Topological type of discriminants of some special families

Abstract

We will describe the topological type of the discriminant curve of the morphism $(\ell , f)$, where $\ell$ is a smooth curve and f is an irreducible curve (branch) of multiplicity less than five or a branch such that the difference between its Milnor number and Tjurina number is less than 3. We prove that for a branch of these families, the topological type of the discriminant curve is determined by the semigroup, the Zariski invariant and at most two other analytical invariants of the branch.

1 Introduction

Let $f(x,y)\in \mathbb C\{x,y\}$ be irreducible. The germ of the irreducible analytic curve (branch) of equation $f(x,y)=0$ is denoted by $C\equiv f(x,y)=0$. Observe that the curves $f(x,y)=0$ and $u(x,y)f(x,y)=0$ are the same, for any unit $u(x,y)\in \mathbb C\{x,y\}$. The multiplicity of C, denoted by m(C), is by definition the order of the power series f(x, y). Suppose that C has multiplicity n. We will say that C is singular if $n>1$. Otherwise C is a smooth curve. The initial form of f(x, y) is the sum of all terms of f(x, y) of degree n. Since f is irreducible, its initial form is a power of a linear form. After a linear change of coordinates, if necessary, we can suppose that the initial form of f(x, y) is $y^n$. Suppose that C has multiplicity $n>1$. We denote by $\mathbb N^*$ the set of positive integers. By Newton’s theorem [7, Theorem 3.8] there is $\alpha (x^{1/n}) \in \mathbb {C}\{x\}^{*}=\bigcup _{m\in \mathbb N^*}\mathbb {C}\{x^{1/m}\}$ with $\alpha (0)=0$ such that $f(x,\alpha (x^{1/n}))=0$ and we say that $\alpha (x^{1/n}) \in \mathbb {C}\{x\}^{*}$ is a Newton–Puiseux root of C. Let us denote by $\hbox {Zer}(f)$ the set of Newton–Puiseux roots of C. Let $\alpha (x^{1/n}) \in \hbox {Zer}(f)$. After Puiseux’s theorem [7, Corollary 3.12] we have that $\hbox {Zer}(f)= \bigl \{\alpha _j:=\alpha (\omega ^j x^{1/n}) \bigr \}_{j=1}^n$, where $\omega$ is an nth-primitive root of unity. Hence

$$\begin{aligned} f(x,y)=u(x,y)\displaystyle \prod _{j=1}^{n}\Bigl (y-(\alpha (\omega ^{j}x^{1/n}))\Bigr ), \end{aligned}$$

(1.1)

where $u \in \mathbb {C}\{x,y\}$ is a unit. After a change of coordinates, if necessary, we can write $\alpha (x)=\sum _{i\ge s_1}a_i x^{i/n}$, where $s_1>n$ and $s_1\not \equiv 0$ mod n.

If we put $x=t^{n}$, where t is a new variable, the Newton–Puiseux root $\alpha (x^{1/n})$ can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t) = t^{n},\\ y(t) = \sum _{i\ge s_1}a_{i}t^{i}, \end{array}\right. } \end{aligned}$$

that we will call the Puiseux parametrisation of C.

There are $g\in \mathbb N$ and a sequence $\bigl (\beta _{0}=n<\beta _1=s_1<\beta _2<\cdots <\beta _{g} \bigr )$ of nonnegative integers such that

$$\begin{aligned} \{\hbox {ord}(\alpha _i-\alpha _j) : \alpha _i,\alpha _j\in \hbox {Zer}(f),\;i\ne j\}=\left\{ \frac{\beta _l}{\beta _0} : 1\le l\le g \right\} \subseteq \mathbb Q\backslash \mathbb Z. \end{aligned}$$

(1.2)

The sequence $(\beta _{0},\cdots ,\beta _{g}) \subseteq \mathbb {N}$ is called the sequence of characteristic exponents of C. The number g is a topological invariant called the genus of the branch C.

Consider the set

$$\begin{aligned} S(C):=\{i_0(f,h) : h\in \mathbb {C}\{x,y\},\ h\not \equiv 0\ mod f\}, \end{aligned}$$

where $i_0(f,h)=\dim _{\mathbb {C}}\mathbb {C}\{x,y\}/(f,h)$ is the intersection number (or intersection multiplicity) of $f(x,y)=0$ and $h(x,y)=0$ at the origin. It is well known that S(C) is a semigroup called the semigroup of values of the branch C. The complement of S(C) in $\mathbb {N}$ is finite. The conductor of S(C) is by definition the smallest natural number $c\in \mathbb {N}$ such that every natural number $N\in \mathbb {N}$ with $N\ge c$ is an element of S(C).

The semigroup S(C) admits a minimal system of generators $(s_0,s_1,\ldots ,s_g)$, where $s_{i-1}<s_{i}$, g is the genus of C, $s_0=n=i_0(f,x)$ and $s_1=m=:i_0(f,y)$. It is a well-known property of S(C) [7, p. 88, (6.5)] that $e_k:=\gcd (s_0,\ldots ,s_k)=\gcd (\beta _0,\ldots ,\beta _k)$ for $0\le k\le g$ and $e_{k-1}s_k<e_ks_{k+1}$ for $1\le k\le g-1$.

If $n>2$, then we have $c\ge s_1+1$. Let q be the number of natural numbers between $s_1$ and c which are not in S(C). We can verify (see [16, p. 21]) that $q=\frac{c}{2}-s_1+ \bigl [\frac{s_1}{s_0} \bigr ]+1$, for $s_0=n>2$, where $\bigl [ z \bigr ]$ denotes the integral part of $z\in \mathbb R$.

Let $f,h\in \mathbb {C}\{x,y\}$ be irreducible power series. Using the Halphen–Zeuthen formula we get

$$\begin{aligned} i_0(f,h)=\sum _{i,j}\hbox {ord}(\gamma _j-\alpha _i), \end{aligned}$$

(1.3)

where $\hbox {Zer}f=\{\alpha _i\}_i$ and $\hbox {Zer}\, h=\{\gamma _j\}_j.$

Two branches C and D have the same topological type (or they are equisingular) if they are topologically equivalent as embedded curves in $\mathbb {C}^2$. It is well known [16, Chapter II] that two branches are equisingular if and only if they have the same semigroup of values or equivalently they have the same characteristic exponents. Denote by ${\mathcal E}(C)$ the set of branches which are equisingular to C. In the set ${\mathcal E}(C)$ we define the next equivalence relation: two branches $D_1$ and $D_2$ in ${\mathcal E}(C)$ are analytically equivalent, and we will denote this by $D_1\cong D_2$, if there exists an analytic isomorphism $T :U_1\longrightarrow U_2$ such that $U_i$ are neighbourhoods of the origin, $D_i$ is defined in $U_i$, $1\le i\le 2$ and $T(D_1\cap U_1)=D_2\cap U_2$.

The moduli space of the equisingularity class ${\mathcal E}(C)$ is the quotient space ${\mathcal E}(C)/\cong$. Let $\nu _1<\nu _2<\cdots <\nu _q$ be the integers of the set $\{s_1+1,\ldots ,c-1\}$ which are not in S(C). Zariski proved [16, Proposition 1.2, Chapter III] that there exists a branch $\overline{C}$ analytically equivalent to C, parametrized as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \bar{x}=t^n,\\ \bar{y}=t^{s_1}+\sum _{i=1}^qa_{i}t^{\nu _i}. \end{array} \right. \end{aligned}$$

(1.4)

Put $\Omega :=\{\omega =g(x,y)dx+h(x,y)dy : g,h\in \mathbb {C}\{x,y\}\}$. If (x(t), y(t)) is a Puiseux parametrisation of C, we put

$$\begin{aligned} \nu (\omega ):=\hbox {ord}\left( f(x(t),y(t))x'(t)+ g(x(t),y(t))y'(t)\right) +1. \end{aligned}$$

Let $\Lambda :=\{\nu (\omega ) : \omega \in \Omega \}$. If $\Lambda \backslash S(C)\ne \emptyset$, then the number $\lambda :=\min \bigl ( \Lambda \backslash S(C) \bigr )-v_0$ is an analytical invariant of C called the Zariski invariant.

Using [16, Lemma 2.6, Chapter IV], we can rewrite the parametrization (1.4) in the next form:

$$\begin{aligned} \left\{ \begin{array}{l} \bar{x}=t^n,\\ \bar{y}=t^{s_1}+at^{\lambda }+\hbox {a finite sum of terms } a_{i}t^{\nu _i}, \end{array} \right. \end{aligned}$$

where $a\ne 0$, $\nu _i>\lambda >s_1$.

The Normal Forms Theorem (see [8, Theorem 1]) states that the plane branch C with semigroup of values $S(C)=\langle s_0, \ldots , s_g\rangle$ and value set of differentials $\Lambda$ is either analytically equivalent to a branch with Puiseux parametrization $(t^{s_0},t^{s_1})$ or Puiseux parametrization $(t^{s_0},t^{s_1}+t^{\lambda }+\sum _{i>\lambda , i\not \in \Lambda -s_0} a_{i} t^{i}$).

Let $f(x,y)=\sum _{i,j}a_{ij}x^iy^j\in \mathbb C\{x,y\}$. The support of f is $\hbox {supp}(f):=\{(i,j)\in \mathbb N^2 : a_{ij}\ne 0\}$. The Newton polygon of f, denoted by ${\mathcal N}(f)$, is by definition the convex hull of $\hbox {supp}(f)+\mathbb R_{\ge 0}^2$. Observe that ${\mathcal N}(f)={\mathcal N}(uf)$ for any unit $u\in \mathbb C\{x,y\}$. Nevertheless, the Newton polygon depends on coordinates. The inclination of any compact face L of ${\mathcal N}(f)$ is by definition the quotient of the length of the projection of L over the horizonal axis by the length of its projection over the vertical axis. The Newton polygon of f gives information on the Newton–Puiseux roots of $f(x,y)=0$. More precisely, if L is a compact face of ${\mathcal N}(f)$ of inclination i and the length of its projection over the vertical axis is $\ell _2$, then f has $\ell _2$ Newton–Puiseux roots of order i (see [3, Lemme 8.4.2]).

We say that $f(x,y)\in \mathbb C\{x,y\}$ is nondegenerate in the sense of Kouchnirenko with respect to the coordinates (x, y), if for any compact edge L of ${\mathcal N}(f)$ the polynomial $f_L(x,y):=\sum _{(i,j)\in L\cap \hbox {supp}(f)}a_{ij}x^iy^j$ does not have critical points outside the axes $x=0$ and $y=0$, or equivalently, the polynomial $F_L(z):=\frac{f_L(1,z)}{z^{j_0}}$ has no multiple roots, where $j_0:=\min \{j\in \mathbb N : (i,j)\in L\}$. Since ${\mathcal N}(f)={\mathcal N}(uf)$, for any unit $u\in \mathbb C\{x,y\}$, the notion of nondegeneracy is extended to curves. The topological type of nondegenerate plane curves are completely determined by their Newton polygons (see [13, Proposition 4.7] and [6, Theorem 3.2]).

Let $\ell (x,y)=0$ be a smooth curve and let $f(x,y)=0$ define an isolated singularity at $0\in \mathbb C^2$. Assume that $\ell (x,y)$ does not divide f(x, y) and consider the morphism

$$\begin{aligned} (\ell ,f):(\mathbb C^{2},0)&\longrightarrow (\mathbb C^2,0),\nonumber \\ (x,y)&\longmapsto (u,v):=(\ell (x,y),f(x,y)). \end{aligned}$$

(1.5)

There are two curves associated with $(\ell ,f)$: the polar curve $\frac{\partial \ell }{\partial x}\frac{\partial f}{\partial y} - \frac{\partial \ell }{\partial y}\frac{\partial f}{\partial x}=0$ and its direct image $D(u,v)=0$ which is called the discriminant curve of the morphism $(\ell ,f)$.

The topological type of the polar curve depends on the analytical type of $\ell (x,y)=0$ and $f(x,y)=0$. In [9] the authors completely determine the topological type of the generic polar curve when the multiplicity of $f(x,y)=0$ is less than 5.

The Newton polygon of D(u, v) in the coordinates (u, v) is called the jacobian Newton polygon of the morphism $(\ell ,f)$. This notion was introduced by Teissier [14], who proved that the inclinations of this jacobian polygon are topological invariants of $(\ell ,f)$ called polar invariants. After Merle [12], when f is irreducible with semigroup of values $S(f)=\langle s_0,s_1,\ldots ,s_g\rangle$ then the jacobian Newton polygon of $(\ell ,f)$ has g compact edges $\{E_i\}_{i=1}^g$. The length of the projection of $E_i$ on the vertical axis is $\bigl (\frac{e_{i-1}}{e_i}-1\bigr )\cdot \frac{e_{i-1}}{e_0}$. The length of the projection of $E_i$ on the horizontal axis is $\bigl (\frac{e_{i-1}}{e_i}-1\bigr )\cdot s_i$. Hence the inclinations (quotient between the length of the horizontal projection and the length of the vertical projection) of the compact edges of the jacobian polygon are $s_1<\frac{e_1}{e_0}s_2<\frac{e_2}{e_0}s_3<\cdots <\frac{e_{g-1}}{e_0}s_g$.

In [5] the authors study the pairs $(\ell ,f)$ for which the discriminant curve is nondegenerate in the Kouchnirenko sense. In particular, when f is irreducible, after [5, Corollary 4.4] the discriminant curve $D(u,v)=0$ is nondegenerate if and only if the multiplicity of $f(x,y)=0$ equals 2 or equals 4 and the genus equals 2. Otherwise the discriminant curve is degenerate. Our aim in this paper will be to describe the topological type of the discriminant curve $D(u,v)=0$ of the morphism $(\ell , f),$ where f is irreducible and belongs to some special families, as for example, branches of multiplicity less than 5, branches C such that the difference between its Milnor number $\mu (C)$ and Tjurina number $\tau (C)$ is less than 3, with $\mu (C)=i_0\bigl (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \bigr )=\hbox {dim}, \hbox {not im}_{\mathbb C}\mathbb C\{x,y\}/ \bigl (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \bigr )$ and $\tau (C)=\hbox {dim}_{\mathbb C}\mathbb C\{x,y\}/ \bigl (f,\frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \bigr )$, where $\bigl (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \bigr )$ (resp. $\bigl (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},f \bigr )$) denotes the ideal of $\mathbb {C}\{x,y\}$ generated by $\frac{\partial f}{\partial x}$ and $\frac{\partial f}{\partial y}$ (resp. by $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$ and f).

For these families of plane branches we determine the topological type of their discriminant curves, in the spirit of [9]. We prove that the topological type of the discriminant curve $D(u,v)=0$ is determined, at most, by the semigroup of values S(f), the Zariski invariant and two other analytical invariants of the curve $f(x,y)=0$. In all cases we explicitly determine such analytical invariants. Hence, in order to describe the topological type of the discriminant curve of a branch, it is necessarily the same number of analytical invariants of the initial branch, as it happens for its generic polar curves (see [9]). Finally in Sect. 5 we summarize the different topological types of the discriminant curve in some tables.

2 Equation of the discriminant curve

An analytic change of coordinates does not affect the discriminant curve of the morphism defined in (1.5) (see for example [2, Section 3]). Hence in what follows we assume that $\ell (x,y)=x$. Then $\frac{\partial f}{\partial y}=0$ is the polar curve of the morphism (x, f).

In this paper we will determine the topological type of the discriminant curve of the morphism (1.5) for $\ell (x,y)=x$ and $f(x,y)\in \mathbb C\{x,y\}$ irreducible belonging to some special families. The corresponding study relative to the polar curves was done in [10] and [11], where the authors characterize the equisingularity classes of irreducible plane curve germs whose general members have nondegenerate general polar curves. In addition, they give explicit Zariski open sets of curves in these equisingularity classes whose general polars are nondegenerate and describe their topology.

Suppose that the Newton–Puiseux factorizations of f(x, y) and $\frac{\partial f}{\partial y}(x,y)$ are of the form

$$\begin{aligned} f(x,y)= & {} u_1(x,y)\prod _{i=1}^n [y-\alpha _i(x)], \end{aligned}$$

(2.1)

$$\begin{aligned} \frac{\partial f}{\partial y}(x,y)= & {} u_2(x,y)\prod _{j=1}^{n-1} [y-\gamma _j(x)], \end{aligned}$$

(2.2)

where $u_1(x,y),u_2(x,y) \in \mathbb C\{x,y\}$ are units, $n=\hbox {ord}f$, $\hbox {Zer}(f)=\{\alpha _i(x)\}_i$ and $\hbox {Zer}\bigl (\frac{\partial f}{\partial y} \bigr )=\{\gamma _j(x)\}_j$. If f is irreducible of order n then n is the smallest natural number such that $\{\alpha _i(x)\}_i\subset \mathbb C\{x^{1/n}\}$. Moreover, if we fix $\alpha _i(x^{1/n})$ then $\alpha _j(x^{1/n})=\alpha _i(\omega x^{1/n})$ for any $1\le j\le n$, where w is an nth root of unity.

Following [4, Lemma 5.4] the discriminant curve of the morphism (x, f) can be written as

$$\begin{aligned} D(u,v) = \prod _{j=1}^{n-1}(v-f(u,\gamma _j(u))) . \end{aligned}$$

(2.3)

3 Discriminants of branches of small multiplicities

In this section we determine the topological type of the discriminant of the morphism given in (1.5), where $C\equiv f(x,y)=0$ has small multiplicity. For this we will make use the results of [16] and the analytic classification of plane branches of multiplicity less than or equal to 4, given in [8].

3.1 Discriminants of branches of multiplicity 2

Let $C\equiv f(x,y)=0$ be a branch of multiplicity 2. The minimal system of generators of the semigroup of C is $\langle 2,s_1\rangle$, where $s_1$ is an odd natural number. By [16, Chapitre V] the moduli space of branches of multiplicity 2 have a unique point whose parametrization is given by $(t^2,t^{s_1})$, that is the branch $y^2-x^{s_1}=0$. Then $f_y(x,y)=2y$ whose Newton–Puiseux root is $y = 0$. Hence, after (2.3) we have $D(u,v)=v-f(u,0)=v+u^{s_1}$, that is the discriminant curve is smooth. The Newton polygon of D(u, v) has only one compact edge. The univariate polynomial associated with this edge is $z+1$, so D(u, v) is nondegenerate.

3.2 Discriminants of branches of multiplicity 3

Let $C\equiv f(x,y)=0$ be a branch of multiplicity 3. The minimal system of generators of the semigroup of C is $\langle 3,s_1\rangle$, where $s_1\in \mathbb N$ is such that $s_1\not \equiv 0$ mod 3. By [16, Chapitre V] the moduli space of branches of multiplicity 3 is completely determined by the semigroup of the branch and its Zariski invariant $\lambda$. The corresponding normal forms are as follows:

$$\begin{aligned} x=t^3,\;\;y=t^{s_1}+at^{\lambda }, \end{aligned}$$

where $a=0$ when $\lambda =0$ or if $\lambda \ne 0$ then we have $a = 1$ and

$$\begin{aligned} \lambda =\left\{ \begin{array}{ll} 3e+3k+4 \; &{}\hbox {when }s_1=3e+2 \\ 3e+3k+2 \; &{}\hbox { when }s_1=3e+1, \end{array} \right. \hbox {where }0\le k\le e-2. \end{aligned}$$

(3.1)

Observe that if $\lambda \ne 0$ then $\frac{s_1+\lambda }{3}$ is a natural number greater than 2.

Proposition 3.1

Let $C\equiv f(x,y)=0$ be a branch of semigroup $\langle 3,s_1\rangle$ and let the Zariski invariant equal $\lambda$. The discriminant curve $D(u,v)=0$ is degenerate and its topological type is determined by $(3,s_1,\lambda )$ in the following way:

• (1) If $\lambda =0$ then the discriminant is the double smooth branch $(v+u^{s_1})^2=0$.

• (2) If $\lambda \ne 0$ then

  • (a) when $\gcd (2,s_1+\lambda )=2$, the discriminant curve is the union of two smooth branches $D_i(u,v)=0$, $1\le i\le 2$, with intersection number $i_0(D_1,D_2)= \frac{s_1+\lambda }{2}$.

  • (b) When $\gcd (2,s_1+\lambda )=1$, the discriminant is a branch of semigroup $\langle 2,s_1+\lambda \rangle$.

Proof

Suppose $\lambda =0$. The implicit equation of the normal form is $f(x,y)=y^3-x^{s_1}=0$. Then $f_y(x,y)=3y^2$ whose Newton–Puiseux root is $y = 0$, with multiplicity 2. Hence, after (2.3) we have $D(u,v)=(v-f(u,0))^2=(v+u^{s_1})^2$, that is the discriminant is a double smooth branch.

Suppose now $\lambda \ne 0$. The normal forms are $x=t^3,\,\,y=t^{s_1} + t^{\lambda },$ with $\lambda$ as in (3.1). After (1.1) the implicit equation is $f(x,y)=y^3-3x^{\frac{s_1+\lambda }{3}}y-(x^{s_1} + x^{\lambda })$. Then $f_y(x,y)=3y^2-3x^{\frac{s_1+\lambda }{3}}$, whose Newton–Puiseux roots are $\gamma _i(x)=\pm x^{\frac{s_1+\lambda }{6}}$ for $1\le i\le 2$. Using (2.3) we have

$$\begin{aligned} D(u,v)=\left( v+u^{s_1}-2u^{\frac{s_1+\lambda }{2}}+u^{\lambda }\right) \left( v+u^{s_1}+2u^{\frac{s_1+\lambda }{2}}+u^{\lambda }\right) . \end{aligned}$$

Hence $\hbox {Zer}(D)= \bigl \{\eta _1:=-u^{s_1}-2u^{\frac{s_1+\lambda }{2}}-u^{\lambda }$, $\eta _2:=-u^{s_1}+2u^{\frac{s_1+\lambda }{2}}-u^{\lambda } \bigr \}$ and $\hbox {ord}(\eta _1-\eta _2)=\frac{s_1+\lambda }{2}$. We distinguish two cases: if $\gcd (2,s_1+\lambda )=2$ then by (1.2) we conclude that $D(u,v)=0$ has two smooth branches of equations $D_1(u,v):=v+u^{s_1}-2u^{\frac{s_1+\lambda }{2}}+u^{\lambda }$ and $D_2(u,v)=v+u^{s_1}+2u^{\frac{s_1+\lambda }{2}}+u^{\lambda }$ such that, after the Halphen–Zeuthen formula, the intersection multiplicity is $i_0(D_1,D_2)=\frac{s_1+\lambda }{2}$. If $\gcd (2,s_1+\lambda )=1$ then the discriminant curve $D(u,v)=0$ is a singular branch of the semigroup $\langle 2,s_1+\lambda \rangle$.

The Newton polygon of D(u, v) is elementary (it has only one compact edge) and the univariate polynomial associated with its compact edge is $(z+1)^2$. Hence the discriminant $D(u,v)=0$ is degenerate.$\square$

Corollary 3.2

If C is a branch of multiplicity 2 or 3 and nonzero Zariski invariant, then the discriminant curve $D(u,v)=0$ has no multiple irreducible branches.

Corollary 3.2 does not hold for branches of multiplicity 4 as the proof of Proposition 3.5 shows.

3.3 Discriminants of branches of multiplicity 4

Let $C\equiv f(x,y)=0$ be a branch of multiplicity 4. The branch C may have genus 1 or 2.

Proposition 3.3

Let $C\equiv f(x,y)=0$ be a branch of the semigroup $\langle 4,s_1, s_2\rangle$. Then the discriminant curve $D(u,v)=0$ is nondegenerate. Moreover, $D(u,v)=D_1(u,v)D_2(u,v)$, where $D_1$ is a smooth branch, $D_2$ is a singular branch of semigroup $\langle 2, s_2\rangle$and the intersection multiplicity between the two branches is $i_0(D_1,D_2)=2s_1$.

Proof

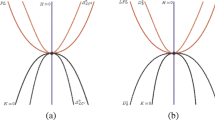
For genus 2, and after the second part of [5, Corollary 4.4] we get that $D(u,v)=0$ is nondegenerate and we can determine its topological type from its Newton polygon (see [13, Proposition 4.7] and [6, Theorem 3.2]), which is the jacobian Newton polygon of (x, f) (see Fig. 1).

Fig. 1

Jacobian Newton polygon of a branch with semigroup $\langle 4,s_1, s_2\rangle$

Since $s_2$ is an odd natural number, $\gcd (s_1+s_2,2)=1$. Moreover, after the properties of S(f), we get $e_0s_1=4s_1<2s_2=e_1s_2$, hence $s_2>2s_1$ and $D(u,v)=D_1(u,v)D_2(u,v)$, where $D_1(u,v)=0$ is a smooth curve admitting as parametrization $(t,t^{s_1}+\cdots )$ and $D_2(u,v)=0$ is a singular curve of genus 1 which semigroup of values is $\langle 2, s_2\rangle$. Finally, after the Halphen–Zeuthen formula, the intersection multiplicity between the two branches is $i_0(D_1,D_2)=2s_1$. $\square$

Suppose now that the branch C has genus 1 and semigroup of values equals $\langle 4, s_1\rangle$. By [8], the moduli space of branches of multiplicity 4 and genus 1 has five families of normal forms:

$$\begin{aligned} \hbox { NF }4.i:\;\;x=t^4,\;\;y_i=\sigma _i(t), \;\;\;\; 1\le i\le 5, \end{aligned}$$

(3.2)

where $\lambda _i$ is the Zariski invariant of the ith normal form family. More precisely, we have

• (1) $(\lambda _1,\sigma _1(t))=(0,t^{s_1})$,

• (2) If $2\le i \le 4$ then $\lambda _i=2s_1-4j$ for $2\le j \le [\frac{{s_1}}{4}]$ and

  $$\begin{aligned} \sigma _2(t)=t^{s_1}+t^{\lambda _2}+a_kt^{3{s_1}-(4[\frac{{s_1}}{4}]+j+1-k)}+ \cdots + a_{j-[\frac{{s_1}}{4}]-2}t^{3{s_1}-4([\frac{{s_1}}{4}]+3-k)}, \end{aligned}$$

  with $a_k \ne 0,\,$ and $1\le k \le [\frac{{s_1}}{4}]-j$.

  $$\begin{aligned} \sigma _3(t)= & {} t^{s_1}+t^{\lambda _3}+ \frac{3{s_1}-4j}{2{s_1}}t^{3{s_1}-8j}+a_{[\frac{{s_1}}{4}]-j+2} t^{3{s_1}-4(2j-1)}+\cdots \\&\quad + a_{[\frac{{s_1}}{4}]}t^{3{s_1}-(j+1)}. \end{aligned}$$
  $$\begin{aligned} \sigma _4(t)= & {} t^{s_1}+t^{\lambda _4}+a_{[\frac{{s_1}}{4}]-j+1}t^{3{s_1}-8j}+a_{[\frac{{s_1}}{4}]-j+2}t^{3{s_1}-4(2j-1)}+ \cdots \\&\quad + a_{[\frac{{s_1}}{4}]-1}t^{3{s_1}-4(j+2)}, \end{aligned}$$

  where $a_{[\frac{{s_1}}{4}]-j+1} \ne \frac{3{s_1}-4j}{2{s_1}}$.

• (3) If $i=5$ then $\lambda _5=3s_1-4j$ for $2\le j \le [\frac{{s_1}}{2}]$ and

  $$\begin{aligned} \sigma _5(t)= & {} t^{s_1}+t^{3s_1-4j}+a_kt^{2s_1-4(j-[\frac{s_1}{4}]-k)} + a_{k+s}t^{2s_1-4(j-[\frac{s_1}{4}] k-s)}\\&\quad +\cdots \end{aligned}$$

After the Newton–Puiseux Theorem, the ith normal form has the equation

$$\begin{aligned} f_i(x,y)=\prod _{\omega ^4=1}(y-\sigma _i(\omega x^{1/4})), \end{aligned}$$

(3.3)

where $\omega$ is a 4th primitive root of unity.

Hence, we obtain the implicit equation for each normal form family:

• NF 4.1: $f_1(x,y)=y^4-x^{s_1}$.

• NF 4.i: For $2\le i \le 4$ we get

  $$\begin{aligned} f_i(x,y)=y^4+P_i(x)y^2+Q_i(x)y+x^{s_1}u(x), \end{aligned}$$

  (3.4)

  where $u(x)\in \mathbb C\{x\}$ is a unit (that is $u(0)\ne 0$), $\lambda _i=2s_1-4j$ for $2\le j \le [\frac{{s_1}}{4}]$, $Q_i(x)=-4x^{s_1-j}+\cdots$ and

  $$\begin{aligned} P_i(x)=\left\{ \begin{array}{ll} -4a_kx^{s_1-\left( \left[ \frac{s_1}{4}\right] +j+1-k\right) }+\cdots &{}\hbox { for } i=2\\ &{}\\ bx^{s_1-2j}+\cdots &{}\hbox {for } i=3 \; \hbox { where }b=\frac{-8(s_1-j)}{s_1}.\\ &{}\\ (-2-4a_{\left[ \frac{s_1}{4}\right] -j+1})x^{s_1-2j}+\cdots &{} \hbox { for } i=4 \; \hbox { and }-2-4a_{\left[ \frac{s_1}{4}\right] -j+1} \ne 0\\ &{}\\ 0&{} \hbox { for } i=4, \;\;-2-4a_{\left[ \frac{s_1}{4}\right] -j+1}=0\\ \; &{} \hbox { and } a_{\left[ \frac{s_1}{4}\right] -j+2}= \cdots =a_{\left[ \frac{s_1}{4}\right] -1}=0 \\ &{}\\ -4a_{\left[ \frac{s_1}{4}\right] -j+k_0}x^{s_1-(2j-(k_0-1))}+\cdots &{} \hbox { for } i=4, \;\;-2-4a_{\left[ \frac{s_1}{4}\right] -j+1}=0\\ \; &{}\hbox { and }a_l\ne 0 \; \hbox { for some }l=\left[ \frac{s_1}{4}\right] -j+2,\ldots , \left[ \frac{s_1}{4}\right] -1 \end{array} \right. \end{aligned}$$

  where $2\le k_0 \le j-1$ such that

  $$\begin{aligned} k:= \min \left\{ l : a_l \ne 0 \, , \ \left[ \frac{s_1}{4}\right] -j+2 \le l < \left[ \frac{s_1}{4}\right] \right\} =\left[ \frac{s_1}{4}\right] -j+k_0. \end{aligned}$$

  Observe that

  $$\begin{aligned} \hbox {ord}P_i(x)\ge \frac{2}{3}(s_1-j). \end{aligned}$$

  (3.5)

• NF 4.5: $f_5(x,y)=y^4+P(x)y^2+Q(x)y+R(x)$, where

  $$\begin{aligned} P(x)= & {} -4x^{s_1-j}-2a_{k}^2x^{s_1-2(j-[\frac{s_1}{4}]-k)}-4a_ka_{k+s}x^{s_1-2(j-s_1-[\frac{s_1}{4}]-k)+s} \nonumber \\&\quad - 2a_{k+s}^2 x^{s_1-2(j-[\frac{s_1}{4}]-k-s )}+\cdots \end{aligned}$$

  (3.6)
  $$\begin{aligned} Q(x)= & {} -4a_kx^{s_1-j+[\frac{s_1}{4}]+k}-4a_{k+s}x^{s_1-j -[\frac{s_1}{4}]+k+s} \nonumber \\&\quad -4a_kx^{2(s_1-j)-(j-[\frac{s_1}{4}]-k)} - 4a_{k+s}x^{2(s_1-j)-(j-[\frac{s_1}{4}]-k-s)}+\cdots )\;\;\;\;\end{aligned}$$

  (3.7)
  $$\begin{aligned} R(x)= & {} -x^{s_1}+2x^{2(s_1-j)} -x^{3s_1-4j}+a_kx^{2s_1-4(j-[\frac{s_1}{4}]-k)}+\cdots \end{aligned}$$

  (3.8)

for $2\le j \le [\frac{{s_1}}{2}]$.

Proposition 3.4

Let $C\equiv f(x,y)=0$ be a branch belonging to the family NF 4.i, for $1\le i\le 4$. Then the discriminant curve $D(u,v)=0$ is degenerate and its topological type is determined by the semigroup $S(f)=\langle 4,s_1\rangle$ and the Zariski invariant $\lambda _i$ of C. Moreover,

• (1) if $\lambda _i=0$ then the discriminant curve is the triple smooth branch $(v+u^{s_1})^3=0$;

• (2) if $\lambda _i\ne 0$ then $\lambda _i=2{s_1}-4j$ for $2\le j \le [\frac{{s_1}}{4}]$ and

  • (a) when $\gcd (3,2s_1+\lambda _i)=1$, the discriminant curve $D(u,v)=0$ is a branch with semigroup $\langle 3,2s_1+\lambda _i\rangle$;

  • (b) when $\gcd (3,2s_1+\lambda _i)=3$, the discriminant curve is the union of three smooth branches $D_i(u,v)=0$, $1\le i\le 3$ with intersection number $i_0(D_l,D_r)=\frac{2s_1+\lambda _i}{3}$ for $l\ne r$.

Proof

Suppose $\lambda _i=0$. By (3.3) the implicit equation of the normal form is $f_1(x,y)=y^4-x^{s_1}$. Then $\frac{\partial f_{1}}{\partial y}(x,y)=4y^3$ whose Newton–Puiseux root is $y = 0$, with multiplicity three. Hence, after (2.3) we have $D(u,v)=(v-f_1(u,0))^3=(v+u^{s_1})^3$, that is the discriminant curve is a triple smooth branch.

Suppose now $\lambda _i\ne 0$. Then $\lambda _i=2{s_1}-4j$ for $2\le j \le [\frac{{s_1}}{4}]$ and the normal form of C is $x=t^4,\;\;y= \sigma _i (t)$ for $2\le i\le 4$.

From the implicit equations $f_i(x,y)$, $2\le i \le 4$, given in (3.4) and from inequality (3.5) we get that the Newton polygon of $\frac{\partial f_{i}}{\partial y}(x,y)$ has only one compact edge whose vertices are (0, 3) and $(s_1-j,0)$. All the parametrisations of $\frac{\partial f_{i}}{\partial y}(x,y)=0$, for $2 \le i \le 4$, have the same order and we can write them as $\gamma _r(u)=\varepsilon u^{\frac{s_1-j}{3}}+\cdots ,$ where $\varepsilon$ is a 3rd root of unity. From (2.3) and for a fixed $i\in \{2,3,4\}$, we have

$$\begin{aligned} D(u,v)=\prod _{\frac{\partial f_{i}}{\partial y}(\gamma _r)=0}(v-f_i(u,\gamma _r(u))), \end{aligned}$$

and considering the development of $f_i(u,\gamma _r(u))$ we obtain

$$\begin{aligned} D(u,v)=\prod _{\varepsilon ^3=1} \bigl (v+u^{s_1}+3\varepsilon u^{4(\frac{s_1-j}{3})}+\cdots \bigr )=\prod _{\varepsilon ^3=1} \bigl (v+u^{s_1}+3\varepsilon u^{(\frac{2s_1+\lambda _i}{3})}+\cdots \bigr ), \end{aligned}$$

so $\hbox {Zer}(D)= \bigl \{\eta _i(\varepsilon ):=-u^{s_1}-3\varepsilon u^{ (\frac{2s_1+\lambda _i}{3} )}+\cdots \bigr \}_{\varepsilon ^3=1}$ and $\hbox {ord}(\eta _l-\eta _r)=\frac{2s_1+\lambda _i}{3}$, for $1\le l\ne r\le 3$. The topological type of $D(u,v)=0$ is determined by the semigroup of the branch $C\equiv f_i(x,y)=0$ and its Zariski analytical invariant $\lambda _i = 2s_1-4j$ for $2\le j \le [\frac{{s_1}}{4}]$. We distinguish two cases: if 3 and $2s_1+\lambda _i$ are coprime then the discriminant $D(u,v)=0$ is a branch of the semigroup $\langle 3,2s_1+\lambda _i\rangle$. Otherwise, by (1.2), we conclude that the discriminant curve is the union of three different smooth branches $D_l(u,v)=0$ with intersection multiplicity $i_0(D_l,D_r)=\frac{2s_1+\lambda _i}{3}$ for $l\ne r$.

In all cases the Newton polygon of D(u, v) is elementary with vertices (0, 3) and $(3s_1,0)$. The polynomial associated with its compact edge is $(z+1)^3$, so the discriminant curve $D(u,v)=0$ is degenerate. $\square$

Proposition 3.5

Let $C\equiv f(x,y)=0$ be a branch belonging to the family NF 4.5. Then the discriminant curve $D(u,v)=0$ is degenerate and its topological type is determined by the semigroup $S(f)=\langle 4,s_1\rangle$, the Zariski invariant $\lambda _5$ and at most two other analytical invariants of C.

Proof

The implicit equation of C has the form $f_5(x,y)=y^4+P(x)y^2+Q(x)y+R(x)$, where P(x), Q(x), R(x) are as in (3.6), (3.7) and (3.8). Hence $\frac{\partial f_{5}}{\partial y}(x,y)=4y^3+2P(x)y+Q(x)$.

We distinguish the following cases:

Case A. If $a_i=0$ in $\sigma _5(t)$ for all i, then we have that $\frac{\partial f_{5}}{\partial y}(x,y)=4y^3-8x^{s_1-j}y=4y(y^2-2x^{s_1-j})$ whose Newton–Puiseux roots are $\bigl \{0, \pm \sqrt{2}x^{\frac{s_1-j}{2}} \bigr \}$. Therefore $f_5(u,0)=R(u)=-u^{s_1}+2u^{2(s_1-j)}-u^{3s_1-4j}$ and $f_5(u,\pm \sqrt{2}u^{\frac{s_1-j}{2}})=-u^{s_1}-2u^{2(s_1-j)}-u^{3s_1-4j}$. From (2.3) we conclude that the discriminant curve is the union of three smooth curves $D_l(u,v)=0,$ where $D_1(u,v)=v+u^{s_1}-2u^{2(s_1-j)}+u^{3s_1-4j}$, $D_2(u,v)=D_3(u,v)=v+u^{s_1}+2u^{2(s_1-j)}+u^{3s_1-4j}$, and $i_0(D_1,D_l)=2(s_1-j)$ for $l\in \{2,3\}$.

Case B. If $a_k\ne 0$ and $a_{k+l}=0$ in $\sigma _5(t)\; \hbox { for }l>0$, then

$$\begin{aligned}\frac{\partial f_{5}}{\partial y}(x,y)= & {} 4y^3+2(-4x^{s_1-j}-2a_{k}^2x^{s_1-2(j-[\frac{s_1}{4}]-k)}+\cdots )y\\- & {} 4a_k\left( x^{s_1-j+[\frac{s_1}{4}]+k}+x^{2(s_1-j)-(j-[\frac{s_1}{4}]-k)}+\cdots \right) .\\ \end{aligned}$$

So the Newton polygon of $\frac{\partial f_{5}}{\partial y}(x,y)$ depends on the position of the point $M=(s_i-j,1)$ with respect to the line passing by $E=(0,3)$ and $F=(s_1-j+[\frac{s_1}{4}]+k,0)$. We have three subcases:

B.1. If $\frac{2}{s_1-j}<\frac{1}{[\frac{s_1}{4}]+k}$ then ${\mathcal N}(\frac{\partial f_{5}}{\partial y})$ has only one compact edge of vertices E and F. Hence the order of the Newton–Puiseux roots $\{\gamma _i\}_{i=1}^3$ of $\frac{\partial f_{5}}{\partial y}(x,y)=0$ equals $\frac{s_1-j+[\frac{s_1}{4}]+k}{3}$. After (2.3) we obtain

$$\begin{aligned} D(u,v)=\prod _{w_i^3=1} \bigl (v-3a^{\frac{4}{3}}w_iu^{4\bigl (\frac{s_1-j+[\frac{s_1}{4}]+k}{3} \bigr )}+u^{s_1}+\cdots \bigr ), \end{aligned}$$

for some nonzero complex number a and where $w_{i}$ is a cubic root of unity. If $\gcd (3,(s_1-j+[\frac{s_1}{4}]+k))=1$ then the discriminant curve is irreducible with semigroup $\langle 3,4(s_1-j+[\frac{s_1}{4}]+k) \rangle .$ In the other case, we get $\gcd (3,(s_1-j+[\frac{s_1}{4}]+k))=3$ and the discriminant curve is the union of three smooth curves $D_l(x,y)=0$ such that $i_0(D_l,D_r)=\frac{4(s_1-j+[\frac{s_1}{4}]+k)}{3}$.

B.2. If $\frac{2}{s_1-j}>\frac{1}{[\frac{s_1}{4}]+k}$ then ${\mathcal N}(\frac{\partial f_{5}}{\partial y})$ has two compact edges of vertices M, E and F. By (2.3) we get

$$\begin{aligned} D(u,v)=(v+u^{s_1} -2u^{2(s_1-j)} +\cdots ) (v+u^{s_1} +2u^{2(s_1-j)} \pm 4\sqrt{2}a_ku^{\frac{3}{2}(s_1-j)+[\frac{s_1}{4}]+k}+\cdots ). \end{aligned}$$

If $s_1-j$ is odd then the discriminant curve is the union of a smooth branch $D_1(u,v)=0$ and a singular branch $D_2(x,y)=0$ with semigroup $\langle 2,3(s_1-j)+2([\frac{s_1}{4}]+k) \rangle$. Moreover, $i_0(D_1,D_2)=4(s_1-j).$ Otherwise, if $s_1-j$ is even then the discriminant curve is the union of three smooth branches $D_l(x,y)=0$ such that $i_0(D_1,D_l)=2(s_1-j)$ for $2\le l \le 3$ and $i_0(D_2,D_3)=\frac{3}{2}(s_1-j)+[\frac{s_1}{4}]+k$ .

B.3. If $\frac{2}{s_1-j}=\frac{1}{[\frac{s_1}{4}]+k}$ then ${\mathcal N}(\frac{\partial f_{5}}{\partial y})$ has only one compact edge of vertices E and F and M is an interior point of this edge. The polynomial in one variable associated with the compact edge of ${\mathcal N}(\frac{\partial f_{5}}{\partial y})$ is $p(z)=z^3-2z-a_k$. After the z-discriminant of p(z) we have that the roots of p(z) are simple if and only if $a_k\ne \pm \bigl (\frac{4\sqrt{6}}{9} \bigr )$. We will study both cases:

B.3.1 Suppose that $a_k\ne \pm \bigl (\frac{4\sqrt{6}}{9} \bigr )$. Denote by $z_i$ the three different roots of the polynomial p(z). For any $\gamma _i(x)\in \hbox {Zer}(\frac{\partial f_{5}}{\partial y})$ we have

$f(u,\gamma _i(u))=-u^{s_1}+q(z_i)u^{2(s_1-j)}+\cdots$, where $q(z)=z^4-4z^2-4a_kz+2$.

Since $z^3-2z=a_k$, we get $q(z)=-3z^4+4z^2+2$ and if $z_r\ne z_l$ then $q(z_r)\ne q(z_l)$. Hence $D(u,v)=\prod _{{i}}(z+u^s_1+q(z_i)u^{2(s_1-j)}+\cdots )$ and the discriminant curve $D(u,v)=0$ is the union of three smooth branches $D_l(x,y)=0$ such that $i_0(D_l,D_r)=2(s_1-j)$.

B.3.2 Suppose that $a_k= \frac{4\sqrt{6}}{9}$. The polynomial p(z) has $z_1=2\sqrt{\frac{2}{3}}$ as a simple root and $z_2=-\sqrt{\frac{2}{3}}$ as a double root. If $\gamma _i\in \hbox {Zer}(\frac{\partial f_{5}}{\partial y})$ corresponds to $z_i$ then

$$\begin{aligned} \begin{array}{l} f_5(u,\gamma _1(u))= u^{s_1}+q(z_1)u^{2(s_1-j)}+\cdots ,\\ f_5(u,\gamma _{2}(u))= u^{s_1}+q(z_2)u^{2(s_1-j)}+r_{2}u^{2(s_1-j)+\frac{s_1-2j}{2}}+\cdots ,\\ f_5(u,\gamma _{3}(u))= u^{s_1}+q(z_2)u^{2(s_1-j)}+r_{3}u^{2(s_1-j)+\frac{s_1-2j}{2}}+\cdots ,\\ \end{array} \end{aligned}$$

where $r_2,r_3 \in \mathbb {C}$ are different. Observe that $q(z_1)\ne q(z_2)$. Hence, if $s_1-2j$ is odd then the discriminant curve is the union of a smooth branch $D_1(u,v)=0$ and a singular branch $D_2(u,v)=0$ with semigroup $\langle 2, 5s_1-6j \rangle ,$ where $i_0(D_1,D_2)=4(s_1-j)$. Otherwise, if $s_1-2j$ is even then the discriminant curve is the union of three smooth branches $D_l(u,v)=0$ such that $i_0(D_1,D_l)=2(s_1-j)$, for $2\le l \le 3$ and $i_{0}(D_2,D_3)=\frac{5s_1-7j}{2}$.

B.3.3 Suppose that $a_k= -\frac{4\sqrt{6}}{9}$. The polynomial p(z) has $2\sqrt{\frac{2}{3}}$ as a double root and $-\sqrt{\frac{2}{3}}$ as a simple root. After a similar procedure we conclude, in this case, that the topological type of the discriminant curve is as in B.3.2.

Case C If $a_k\ne 0\ne a_{k+s}$, then we have $\frac{\partial f_{5}}{\partial y}(x,y)=4y^3+2P(x)y+Q(x)$. The Newton polygon of $\frac{\partial f_{5}}{\partial y}(x,y)$ depends on the position of the point $M=(s_i-j,1)$ with respect to the line passing through $E=(0,3)$ and $F=(s_1-j+[\frac{s_1}{4}]+k,0)$. We have the following subcases:

C.1. If $\frac{2}{s_1-j}<\frac{1}{[\frac{s_1}{4}]+k}$ then the topological type of the discriminant curve $D(u,v)=0$ is as in In emphatic way.

C.2. If $\frac{2}{s_1-j}>\frac{1}{[\frac{s_1}{4}]+k}$ then the topological type of de discriminant curve is as in In emphatic way.

C.3. If $\frac{2}{s_1-j}=\frac{1}{[\frac{s_1}{4}]+k}$ then the Newton polygon of $\frac{\partial f_{5}}{\partial y}(x,y)$ has only one compact edge containing the points E, F, M, as in In emphatic way. The polynomial associated with this compact edge is $p(z)=z^3-2z-a_k$ whose roots are simple if and only if $a_k\ne \pm \bigl (\frac{4\sqrt{6}}{9} \bigr )$. Let us study the different cases:

C.3.1. If $a_k\ne \pm \bigl (\frac{4\sqrt{6}}{9} \bigr )$ then the topological type of the discriminant curve $D(u,v)=0$ is as in In emphatic way.

C.3.2. Suppose that $a_k=\pm \bigl (\frac{4\sqrt{6}}{9} \bigr )$. The polynomial p(z) has $z_1=2\sqrt{\frac{2}{3}}$ as a simple root and $z_2=z_3=-\sqrt{\frac{2}{3}}$ as a double root. If $\gamma _i\in \hbox {Zer}(\frac{\partial f_{5}}{\partial y})$ corresponds to $z_i$ then we can write

$$\begin{aligned} \gamma _i=z_iu^{[\frac{s_1}{4}]+k}+\cdots \end{aligned}$$

(3.9)

Hence

$$\begin{aligned} \begin{array}{l} \delta _1:= f(u,\gamma _1(u))=- u^{s_1}+q(z_1)u^{2(s_1-j)}+\cdots ,\\ \delta _2:= f(u,\gamma _{2}(u))= -u^{s_1}+q(z_2)u^{2(s_1-j)}+\cdots ,\\ \delta _3:= f(u,\gamma _{3}(u))= -u^{s_1}+q(z_2)u^{2(s_1-j)}+\cdots ,\\ \end{array} \end{aligned}$$

where $\delta _2,\delta _3\in \hbox {Zer}D(u,v)$ are different. Observe that $q(z_1)\ne q(z_2)$. So $\hbox {ord}\bigl (\delta _1-\delta _l \bigr )=2(s_1-j)$ for $2\le l\le 3$. Let us determine $\hbox {ord}\bigl (\delta _2-\delta _3 \bigr )$. For that we need to find new terms in $\delta _2$ and $\delta _3$. We apply the Newton procedure for $\frac{\partial f_{5}}{\partial y}$: let $y_1$ be a new variable. Substituting $(x,y):=(x,x^{[\frac{s_1}{4}]+k}(z_2+y_1))$ in $\frac{\partial f_{5}}{\partial y}(x,y)$ we get

$$\begin{aligned} \frac{\partial f_{5}}{\partial y}(x,x^{[\frac{s_1}{4}]+k}(z_2+y_1))=x^{3([\frac{s_1}{4}]+k)}g(x,y_1), \end{aligned}$$

with

$$\begin{aligned} g(x,y_1)= & {} 4\left[ \left( \frac{2}{3}\right) z_2+2y_1+3z_2y_1^2+y_1^3\right] -(4a_k+4a_{k+s}x^s+4a_kx^{s_1-2j}+\cdots ) \nonumber \\&\quad -[8+4a_k^2x^{s_1-2j}+8a_ka_{k+s}x^{s_1-2j+s}+4a_{k+s}^2x^{s_1-2j+2s}+\cdots ]y_1\nonumber \\&\quad -[8+4a_k^2x^{s_1-2j}+8a_ka_{k+s}x^{s_1-2j+s}+ 4a_{k+s}^2x^{s_1-2j+2s}+\cdots ]z_2 \nonumber \\= & {} 4\left[ 3z_2y_1^2+y_1^3\right] -(4a_{k+s}x^s+4a_kx^{s_1-2j}+\cdots ) \nonumber \\&\quad -[4a_k^2x^{s_1-2j}+8a_ka_{k+s}x^{s_1-2j+s}+4a_{k+s}^2x^{s_1-2j+2s}+\cdots ]y_1\nonumber \\&\quad -[4a_k^2x^{s_1-2j}+8a_ka_{k+s}x^{s_1-2j+s}+ 4a_{k+s}^2x^{s_1-2j+2s}+\cdots ]z_2, \end{aligned}$$

(3.10)

where the last equality follows from $p(z_2)=0$.

Hence, in the next step of the Newton procedure it is enough to consider the polynomial

$$\begin{aligned} H(x,y_1)=12z_2 y_1^2-4a_k^2x^{s_1-2j}y_1+(-4z_2a_k^2- 4a_k)x^{s_1-2j}-4a_{k+s}x^s. \end{aligned}$$

(3.11)

The topological type of the discriminant curve will depend on the relation between s and $s_1-2j$:

C.3.2.1 Suppose that $s_1-2j>s$. We obtain

$$\begin{aligned} \gamma _2(u)=-\frac{\sqrt{6}}{3}u^{\frac{s_1-j}{2}}+\frac{\sqrt{-a_{k+s}}}{\root 4 \of {6}}u^{\frac{s_1-j}{2}+\frac{s}{2}}+\cdots ,\\ \gamma _3(u)=-\frac{\sqrt{6}}{3}u^{\frac{s_1-j}{2}}-\frac{\sqrt{-a_{k+s}}}{\root 4 \of {6}}u^{\frac{s_1-j}{2}+\frac{s}{2}}+\cdots . \end{aligned}$$

Hence

$$\begin{aligned} f_5(u,\gamma _2(u))&=-u^s_1+q(z_2)u^{2(s_1-j)}+ p(z_2)u^{ 2(s_1-j)+\frac{s}{2}}+l(a_{k+s})u^{3s_1-4j}\\&\quad +\frac{8}{3}ca_{k+s}u^{2(s_1-j)+\frac{3}{2}s } +\cdots , \end{aligned}$$

and

$$\begin{aligned} f_5(u,\gamma _3(u))&=-u^s_1+q(z_2)u^{2(s_1-j)}- p(z_2)u^{ 2(s_1-j)+\frac{s}{2}}+l(a_{k+s})u^{3s_1-4j}\\&\quad -\frac{8}{3}ca_{k+s}u^{2(s_1-j)+\frac{3}{2}s } +\cdots , \end{aligned}$$

where $c:=\frac{\sqrt{-a_{k+s}}}{\root 4 \of {6}}$, and $l(z)=-4z_2z-1$. As a consequence, when s is odd then the discriminant curve $D(u,v)=0$ is the union of a smooth branch $D_1(u,v)=0$ and a singular branch with semigroup $\langle 2,4(s_1-j)+3s\rangle$, with $i_0(D_1,D_2)=4(s_1-j)$. Otherwise, if s is even then the discriminant curve $D(u,v)=0$ is the union of three smooth braches $D_l(u,v)=0$ such that $i_0(D_1,D_l)=2(s_1-j)$ for $2\le l\le 3$, and... and $i_0(D_2,D_3)=2(s_1-j)+\frac{3}{2}s$.

C.3.2.2 Suppose that $s_1-2j<s$. After (3.11) and for the next step of the Newton procedure we only need the polynomial

$$\begin{aligned} \bar{H}(Z)=12z_2Z^2-4(z_2a_{k}^2+a_k), \end{aligned}$$

whose roots are $\pm \frac{\sqrt{8}}{9}$. Let $d=\frac{\sqrt{8}}{9}$. We obtain

$$\begin{aligned} \gamma _2(u)=z_2u^{\left[ \frac{s_1}{4}\right] +k}+du^{[\frac{s_1}{4}]+k+\frac{s_1-2j}{2}}+\cdots ,\end{aligned}$$

(3.12)

$$\begin{aligned} \gamma _3(u)=z_2u^{\left[ \frac{s_1}{4}\right] +k}-du^{[\frac{s_1}{4}]+k+\frac{s_1-2j}{2}}+\cdots . \end{aligned}$$

(3.13)

Hence

$$\begin{aligned} f_5(u,\gamma _2(u))&=-u^s_1+q(z_2)u^{2(s_1-j)}+ p(z_2)u^{ 2(s_1-j)+\frac{s}{2}}+l(a_{k})u^{3s_1-4j}\\&\quad +\frac{80}{81}z_2du^{\frac{7s_1-10j}{2}}+\cdots , \end{aligned}$$

and

$$\begin{aligned} f_5(u,\gamma _3(u))&=-u^s_1+q(z_2)u^{2(s_1-j)}- p(z_2)u^{ 2(s_1-j)+\frac{s}{2}}+l(a_{k})u^{3s_1-4j}\\&\quad -\frac{80}{81}z_2du^{\frac{7s_1-10j}{2}}+\cdots \end{aligned}$$

Since 4 and $s_1$ are coprime then $7s_1-10$ is odd and the discriminant curve $D(u,v)=0$ is the union of a smooth branch $D_1(u,v)=0$ and a singular branch with semigroup $\langle 2,7s_1-10j\rangle$, where $i_0(D_1,D_2)=4(s_1-j)$.

C.3.2.3 Suppose that $s_1-2j=s$. After (3.11), in order to obtain the next term in the power series $\gamma _i$, it is enough to consider the polynomial

$$\begin{aligned} \bar{H}(Z)=12z_2Z^2-4(z_2a_{k}^2+a_{k+s}+a_k). \end{aligned}$$

The topological type of the discriminant will depend on the value of $a_{k+s}$:

C.3.2.3.1 For $a_{k+s}\ne -4\frac{\sqrt{6}}{81}$, we get

$$\begin{aligned} \bar{H}(Z)=12z_2Z^2-4 \bigl (a_{k+s}+4\frac{\sqrt{6}}{81} \bigr ), \end{aligned}$$

whose roots are $\pm b:=\pm \bigl (\frac{\sqrt{-d_{k+s}}}{\root 4 \of {6}} \bigr )$, where $d_{k+s}=a_{k+s}+4\frac{\sqrt{6}}{81}$. Hence

$$\begin{aligned} \gamma _2(u)=z_2u^{\left[ \frac{s_1}{4}\right] +k}+bu^{[\frac{s_1}{4}]+k+\frac{s}{2}}+\cdots , \\ \gamma _3(u)=z_2u^{\left[ \frac{s_1}{4}\right] +k}-bu^{[\frac{s_1}{4}]+k+\frac{s}{2}}+\cdots . \end{aligned}$$

We conclude that

$$\begin{aligned} f_5(u,\gamma _2(u))=-u^s_1+q(z_2)u^{2(s_1-j)}+ l(a_{k+s})u^{3s_1-4j}+\frac{80}{81}z_2u^{2s_1-j+\frac{3}{2}s}+\cdots , \end{aligned}$$

and

$$\begin{aligned} f_5(u,\gamma _3(u))=-u^s_1+q(z_2)u^{2(s_1-j)}+l(a_{k+s})u^{3s_1-4j}-\frac{80}{81}z_2u^{2s_1-j+\frac{3}{2}s}+\cdots . \end{aligned}$$

So, if s is odd then $D(u,v)=0$ is the union of a smooth branch $D_1(u,v)=0$ and a singular branch of semigroup $\langle 2,7s_1-10j \rangle$, with $i_0(D_1,D_2)=4(s_1-j)$. In the other case, if s is even then $D(u,v)=0$ is the union of three smooth branches $D_l(u,v)=0$ such that $i_0(D_1,D_l)=2(s_1-j)$ for $2 \le l \le 3, and\ldots$, and $i_0(D_2,D_3)= \frac{7s_1-10j}{2}$.

C.3.2.3.2 For $a_{k+s}= -4\frac{\sqrt{6}}{81}$, after (3.10), in order to obtain the next term in the power series $\gamma _i$, it is enough to consider the polynomial

$$\begin{aligned} \bar{H}(Z)=12z_2Z^2-4a_k^2Z-4a_{k+s}(1+2a_k z_2 ), \end{aligned}$$

whose roots $t_1,t_2$ are simple. Hence

$$\begin{aligned} \gamma _2(u)=z_2u^{\left[ \frac{s_1}{4}+k\right] +k}+t_1u^{[\frac{s_1}{4}+k]+k+s}+\cdots , \end{aligned}$$

and

$$\begin{aligned} \gamma _3(u)=z_2u^{\left[ \frac{s_1}{4}+k\right] +k}-t_2u^{[\frac{s_1}{4}+k]+k+s}+\cdots . \end{aligned}$$

We conclude that

$$\begin{aligned} f_5(u,\gamma _2(u))=-u^s_1+q(z_2)u^{2(s_1-j)}-u^{2(s_1-j)+s}+ h(t_1)u^{2(s_1-j)+s2}+\cdots , \end{aligned}$$

and

$$\begin{aligned} f_5(u,\gamma _3(u))=-u^s_1+q(z_2)u^{2(s_1-j)}-u^{2(s_1-j)+s}+ h(t_2)u^{2(s_1-j)+s2}+\cdots , \end{aligned}$$

where $h(z)=-4a_{k+s}z+a_k$. The discriminant curve $D(u,v)=0$ is the union of three smooth branches $D_l(u,v)=0$ such that $i_0(D_1,D_l)=2(s_1-j)$ for $2\le l \le 3$ and... and $i_0(D_2,D_3)=4s_1-6j$. $\square$

From the above computations we obtain

Theorem 3.6

Let $f(x,y)=0$ be a plane branch of multiplicity n. Then the following hold.

• (1) If $n=2$ then the discriminant curve $D(u,v)=0$ is nondegenerate.

• (2) If $n=3$ then the discriminant curve $D(u,v)=0$ is degenerate and its topological type depends on the semigroup S(f) and the Zariski invariant (when it is not zero).

• (3) If $n=4$ then the discriminant curve $D(u,v)=0$ is degenerate and its topological type depends on the semigroup S(f), the Zariski invariant (when it is not zero) and at most two other analytical invariants.

Remark 3.7

In [8], Hefez and Hernandes give explicit normal forms for branches of multiplicity 2, 3 or 4. Thanks to that, the description of the topological type of the discriminant curve of such a branch was possible. The normal forms for branches of multiplicity greater than 4 are not completely determined.

4 Discriminant of branches C with $\mu (C)- \tau (C) \le 2$

Let $C:f(x,y)=0$ be a plane branch. Put $r(C):=\mu (C)-\tau (C)$, where $\mu (C)$ and $\tau (C)$ are the Milnor number and the Tjurina number of C, respectively. Observe that r(C) is a nonnegative integer. In zero characteristic, from [15, Theorem 4] we get $r(C)=0$ if and only if C is analytically equivalent to the curve $y^{s_0}-x^{s_1}=0$ for two coprime integers $s_0$ and $s_1$ greater than 1. Later, in [1], the authors describe all plane branches defined over an algebraically closed field of characteristic zero, modulo analytic equivalence, having the property that the difference between their Milnor and Tjurina numbers is 1 or 2. In particular the authors determined the normal forms of the branches of this family, which show us that the Zariski invariant of these branches are determined by the two first generators of their semigroup. By [1, Corollary 5] we know that if $r(C)\ne 0$ then $r(C)\ge 2^{g-1}$. Hence, if $r(C)=1$ then $g=1$ and if $r(C)=2$ then $g\le 2$. In this section we will describe the topological type of the discriminant curve $D(u,v)=0$ of branches C with $\mu (C)- \tau (C) \le 2$.

Theorem 4.1

Let $C:f(x,y)=0$ be a plane branch with $r(C):=\mu (C)-\tau (C)\le 2$. Then the discriminant curve $D(u,v)=0$ is degenerate and its topological type is given by the semigroup S(f).

Proof

Suppose first that $r(C)=1$. By [1, Corollary 8] the branch C is analytically equivalent to the curve defined by the equation $f(x,y)=y^{s_0}-x^{s_1}+x^{s_1-2}y^{s_0-2}$, where $2\le s_0<s_1$ are coprime integers. Hence $f_y(x,y)=s_0y^{s_0-1}+(s_0-2)x^{s_1-2}y^{s_0-3}=y^{s_0-3}(s_0y^2+(s_0-2)x^{s_1-2})$, whose Newton–Puiseux roots are $\alpha _1=0$ (with multiplicity $s_0-3$ ), $\alpha _2=\sqrt{\frac{2-s_0}{s_0}}x^{\frac{s_1-2}{2}}$ and $\alpha _3=-\sqrt{\frac{2-s_0}{s_0}}x^{\frac{s_1-2}{2}}$. After (2.3) we obtain that the Newton–Puiseux roots of the discriminant curve are

• (1) $\delta _1=u^{s_1}$ with multiplicity ${s_0-3}$,

• (2) $\delta _2=-u^{s_1}+ \left( \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0}+ \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0-2} \right) u^{\frac{(s_1-2)s_0}{2}}$,

• (3) $\delta _3=-u^{s_1}- \left( \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0}+ \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0-2} \right) u^{\frac{(s_1-2)s_0}{2}}$.

Hence, if $s_1$ and $s_0$ are odd then the discriminant curve is given by $D(u,v)=D_1(u,v)^{s_0-3}D_2(u,v),$ where $D_1(u,v)=(v-u^{s_1})$ and $D_2(u,v)$ is a branch of semigroup $\langle 2, (s_1-2)s_0\rangle$ and the intersection multiplicity is $i_0(D_1,D_2)=\min \bigl \{s_1,(s_1-2)n \bigr \}$. Otherwise D(u, v) is the product of $D_1(u,v)^{s_0-3}$ and two smooth branches $D_2(u,v)$ and $D_3(u,v)$, where $i_0(D_1,D_k)=\min \bigl \{s_1,\frac{(s_1-2)s_0}{2} \bigr \}$ for $2\le k \le 3$ and $i_0(D_2,D_3)=\frac{(s_1-2)s_0}{2}$.

Suppose now that $r(C)=2$. In this case we get $g\le 2$. If $g=2$ then by [1, Corollary 13] the multiplicity of C is 4 and we study this case in Proposition 3.3.

For $g=1$, after [1, Theorem 17, Corollary 18], we have two normal forms:

• (A) $f(x,y)=y^{s_0}-x^{s_1}+x^{s_1-3}y^{s_0-2},$ with $2<s_0<s_1$.

• (B) $f(x,y)=y^{s_0}-x^{s_1}+x^{s_1-2}y^{s_0-3}+ \Bigl (\sum _{k \ge 2}^{2+[\frac{s_1}{s_0}]}a_{k}x^{s_1-k} \Bigr )y^{s_0-2},$ with $4\le s_0<s_1$, $\frac{2s_0}{s_0-3}<s_1$ and $a_k\in \mathbb {C}$.

In the case (A) we get $f_y(x,y)=y^{s_0-3}(s_0y^2+(s_0-2)x^{s_1-3}),$ whose Newton–Puiseux roots are $\alpha _1=0$ (with multiplicity $s_0-3$), $\alpha _2=\sqrt{\frac{2-s_0}{s_0}}x^{\frac{s_1-3}{2}}$ and $\alpha _3=-\sqrt{\frac{2-s_0}{s_0}}x^{\frac{s_1-3}{2}}$. After (2.3) we obtain that the Newton–Puiseux roots of the discriminant curve are

• (1) $\delta _1=u^{s_1}$ with multiplicity ${s_0-3}$,

• (2) $\delta _2=-u^{s_1}+ \left( \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0}+ \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0-2} \right) u^{\frac{(s_1-3)s_0}{2}}$,

• (3) $\delta _3=-u^{s_1}- \left( \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0}+ \left( \sqrt{\frac{2-s_0}{s_0}} \right) ^{s_0-2} \right) u^{\frac{(s_1-3)s_0}{2}}$.

Hence, if $s_0$ is odd and $s_1$ is even then the discriminant curve is given by $D(u,v)=D_1(u,v)^{s_0-3}D_2(u,v),$ where $D_1(u,v)=(v-u^{s_1})$ and $D_2(u,v)$ is a branch of the semigroup $\langle 2, (s_1-3)s_0\rangle$ and the intersection multiplicity is $i_0(D_1,D_2)=\min \bigl \{s_1,(s_1-3)s_0 \bigr \}$. Otherwise D(u, v) is the product of $D_1(u,v)^{s_0-3}$ and two smooth branches $D_2(u,v)$ and $D_3(u,v)$, where $i_0(D_1,D_k)=\min \bigl \{s_1,\frac{(s_1-3)s_0}{2} \bigr \}$ for $2\le k \le 3$ and $i_0(D_2,D_3)=\frac{(s_1-3)s_0}{2}$.

In the case (B) we have

$$\begin{aligned} f_y(x,y)=y^{s_0-4}\Biggl (s_0y^3+(s_0-3)x^{s_1-2}+(s_0-2)\Biggl (\sum _{k \ge 2}^{2+[\frac{s_1}{s_0}]}a_{k}x^{s_1-k}\Biggr )y\Biggr ), \end{aligned}$$

hence its Newton polygon coincides with the Newton polygon determined by (0, 3), $(s_1-2,0)$ and $(s_1-2-[\frac{s_1}{s_0}],1)$. But, after the inequality $\frac{2s_0}{s_0-3}<s_1$, we get that this Newton polygon has only two points which are its vertices: (0, 3) and $(s_1-2,0)$. The Newton–Puiseux roots of $f_y(x,y)=0$ are $\alpha _1=0$ (with multiplicity $s_0-4$) and $\alpha _i=\xi _i\root 3 \of {\frac{s_0-3}{s_0}}u^{\frac{s_0-2}{3}}+\cdots$, where $\xi _i$ is a cubic root of unity, $1\le i\le 3$. Then, after (2.3) the Newton–Puiseux roots of the discriminant curve are $\delta _1=u^{s_1}$ with multiplicity ${s_0-4}$ and

$$\begin{aligned} \delta _i= & {} -u^{s_1}+\left[ \left( \xi _i\root 3 \of {\frac{s_0-3}{s_0}}\right) ^{s_0}+\left( \xi _i\root 3 \of {\frac{s_0-3}{s_0}}\right) ^{s_0-3}\right] u^{\frac{(s_1-2)s_0}{3}}\\&+ \left( \xi _i\root 3 \of {\frac{s_0-3}{s_0}}\right) ^{s_0-2}a_{2+[\frac{s_1}{s_0}]}u^{\frac{(s_1-2)(s_0-2)}{3}+(s_1-2)-[\frac{s_1}{s_0}]}+\cdots ,\\ \end{aligned}$$

for $1\le i\le 3$.

If $s_1-2$ (respectively $s_0$) and 3 are coprime then the discriminant curve is given by $D(u,v)=D_1(u,v)^{s_0-4}D_2(u,v),$ where $D_1(u,v)=(v-u^{s_1})$ and $D_2(u,v)$ is a branch of the semigroup $\langle 3, (s_1-2)s_0\rangle$ and, after the Halphen–Zeuthen formula, the intersection multiplicity is $i_0(D_1,D_2)=3s_1$. Otherwise D(u, v) is the product of $D_1(u,v)^{s_0-4}$ and three smooth branches $D_k(u,v)$, $2\le k\le 4$, where $i_0(D_1,D_k)=s_1$ for $2\le k \le 4$ and $i_0(D_l,D_r)=\frac{(s_1-2)s_0}{3}$, for $2\le l\ne r\le 4$. $\square$

Remark 4.2

Observe that in Theorem 4.1 Case (B) with $s_0=4$ coincides with case $\sigma _3$ in (3.2) for $j=2$. Hence this case was studied in Proposition 3.4.

5 Tables

In this section we collect, in some tables, the topological type of the discriminants for branches studied in this paper (See Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11).

Table 1 Discriminants of branches of semigroup $\langle 2,s_1\rangle$

Table 2 Discriminants of branches of semigroup $\langle 3,s_1\rangle$

Table 3 Discriminants of branches of semigroup $\langle 4,6,s_2\rangle$

Table 4 Discriminants of branches of semigroup $\langle 4,s_1\rangle$

Table 5 Multiplicity 4, $g=1$, $\lambda =3s_1-4j\ne 0\;\;2\le j \le [\frac{{s_1}}{2}]$

Table 6 Case B of Proposition 3.5

Table 7 Case C of Proposition 3.5

Table 8 Case C of Proposition 3.5, when $\frac{2}{s_1-j}=\frac{1}{[\frac{s_1}{4}]+k}$ and $a_k=\pm \frac{4\sqrt{6}}{9}$

Table 9 Discriminants of branches with $r(C)=\mu (C)-\tau (C)\le 2$

Table 10 Case $r(C)=\mu (C)-\tau (C)=2$, $S(f)=\langle s_0,s_1\rangle$ and normal form (A)

Table 11 Case $r(C)=\mu (C)-\tau (C)=2$, $S(f)=\langle s_0,s_1\rangle$ and normal form (B)