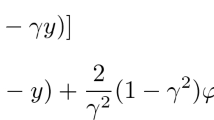Alienation of two general linear functional equations

Abstract

We study the alienation problem for two general linear equations i.e. we compare the solutions of the system of equations

$$\begin{aligned} \left\{ \begin{array}{l}\sum _{i=1}^n\alpha _if(p_ix+q_iy)=0\\ \sum _{j=1}^m\beta _jg(s_jx+t_jy)=0\end{array}\right. \end{aligned}$$

with the solutions of the single equation

$$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=\sum _{j=1}^m\beta _jg(s_jx+t_jy). \end{aligned}$$

To this end we introduce the notion of l-alienation—alienation in the class of monomial functions of order l. We use our results among others to study the alienation properties of two monomial functional equations.

1 Introduction

The alienation problem for functional equations was first studied by Dhombres who in [1] introduced the following definition.

Definition 1

Let $E_1(f)=0$ and $E_2(f)=0$ be two functional equations for a function $f:X\rightarrow Y$, where X and Y are non-empty sets. The equations $E_1$ and $E_2$ are alien with respect to X and Y, if any solution $f:X\rightarrow Y$ of

$$\begin{aligned} E_1(f)+E_2(f)=0 \end{aligned}$$

is a solution of the system

$$\begin{aligned} \left\{ \begin{array}{l} E_1(f)=0\\ E_2(f)=0. \end{array}\right. \end{aligned}$$

Then the problem of alienation was studied by many authors, we cite here just some of them [2,3,4, 6, 9, 11, 13, 17], for the more detailed study of the history and present state of this problem see [7].

In our considerations we use the notion of polynomial functions. Thus we will recall some definitions and results connected with this topic. For details see for example [14, 15].

Let G, S be groups and let $f:G\rightarrow S$ be a function. The difference operator with span h is given by

$$\begin{aligned} \Delta _hf(x)=f(x+h)-f(x). \end{aligned}$$

The iterates $\Delta _h^n$ are defined recursively,

$$\begin{aligned} \Delta _h^0f:=f,\;\Delta _h^{n+1}f:=\Delta _h(\Delta _h^nf),\;n=1,2,\dots \;\;. \end{aligned}$$

Using this operator, we define polynomial functions in the following way.

Definition 2

Let G, S be groups, then a function $f:G\rightarrow S$ is called a polynomial function of order n if it satisfies the equality

$$\begin{aligned} \Delta _h^{n+1}f(x)=0, \end{aligned}$$

for all $x\in G.$

The following theorem is also well known (see for example [14], Corollary 3.3).

Theorem 1

Let n be a positive integer and let G, S be abelian groups such that S is torsion free and is divisible by n!. Then function $f:G\rightarrow S$ is a polynomial function of order n if and only if for all $i=0,1,\dots ,n,$ there exists a symmetric and i-additive function $A_i:G^i\rightarrow S$ such that

$$\begin{aligned} f(x)=\sum _{i=0}^n A_{i}(x,\dots .x),\;x\in G \end{aligned}$$

(1)

where 0-additive functions are understood to be constant functions.

The main tool used in this paper will be the following result of L. Székelyhidi. In this theorem, we use the following definition

Definition 3

([14], Definition 3.5) Let G, S be abelian groups, let n be a nonnegative integer. The function $f:G\rightarrow S$ is said to be of degree n if there exist functions $f_i:G\rightarrow S$ and homomorphisms $\varphi _i.\psi _i:G\rightarrow G$ such that $\varphi (g)\subset \psi (G),$$i=1,2,\dots ,n+1$ and the equation

$$\begin{aligned} f(x)+\sum _{i=1}^{n+1}f_i(\varphi _i(x)+\psi _i(y))=0,\;x,y\in G \end{aligned}$$

holds.

Theorem 2

([14], Theorem 3.6) Let G, S be abelian groups, and suppose that G is divisible, Let n be a nonnegative integer. The function $f:G\rightarrow S$ is of degree n if and only if it is a polynomial function of order n.

For some generalizations of Theorem 2 see for example [12] or [16].

2 Two introductory results

Recently, several authors have dealt with alienation results with respect to two linear equations. Namely, Z. Kominek and J. Sikorska proved that two polynomial equations: $\Delta _nf(x)=0$ and $\Delta _mf(x)=0$ with different m, n are alien whereas R. Ger dealt with the alienation problem of the Cauchy and quadratic functional equations. First we provide a short proof of the result of Kominek and Sikorska [10].

Proposition 1

Let G, H be abelian groups, let $n>m$ be positive integers and let H be torsion free and divisible by n!. Then functions $f,g:G\rightarrow H$ satisfy equation

$$\begin{aligned} \Delta ^n_hf(x)=\Delta ^m_hg(x),\;x,h\in G \end{aligned}$$

(2)

if and only if f is a polynomial function of order $n-1$ and g is a polynomial function of order $m-1.$

Proof

Writing (2) explicitly, we get

$$\begin{aligned}&f(x+nh)-\left( {\begin{array}{c}n\\ 1\end{array}}\right) f(x+(n-1)h)+\cdots +(-1)^nf(x)\nonumber \\&\quad =g(x+mh)-\left( {\begin{array}{c}m\\ 1\end{array}}\right) g(x+(m-1)h)+\cdots +(-1)^mg(x). \end{aligned}$$

(3)

Since $n>m,$ all arguments of g appear on the left hand side as arguments of f. This means that we can rearrange (3) and get

$$\begin{aligned}&((-1)^nf+(-1)^mg)(x)+\left( (-1)^{n-1}\left( {\begin{array}{c}n\\ 1\end{array}}\right) f+(-1)^{m-1}\left( {\begin{array}{c}m\\ 1\end{array}}\right) g\right) (x+h)\nonumber \\&\quad +\cdots + \left( (-1)^{n-m}\left( {\begin{array}{c}n\\ m\end{array}}\right) f+\left( {\begin{array}{c}m\\ m\end{array}}\right) g\right) (x+mh)\nonumber \\&\quad +(-1)^{n-m-1}\left( {\begin{array}{c}n\\ m+1\end{array}}\right) f(x+(m+1)h)+\cdots +f(x+nh)=0. \end{aligned}$$

(4)

Now, our sum contains exactly $n+1$ terms and it is enough to substitute $x-nh$ in place of x to get from Theorem 2 that f is a polynomial function of order at most $n-1$ i.e. $\Delta ^n_hf(x)=0.$ Consequently, using (2) we get $\Delta ^m_hg(x)=0$ which finishes the proof. $\square$

Similarly, it is possible to get an alienation result for the quadratic and additive functional equations which was obtained by Ger in [5].

Proposition 2

Let G and H be abelian groups such that H is torsion free and divisible by 2. Functions $f,g:G\rightarrow H$ satisfy equation

$$\begin{aligned} f(x+y)+g(x+y)+g(x-y)=f(x)+f(y)+2g(x)+2g(y) \end{aligned}$$

(5)

if and only if

$$\begin{aligned} f(x)=a(x)+c \end{aligned}$$

and

$$\begin{aligned} g(x)=q(x)-\frac{c}{2} \end{aligned}$$

where function a is additive, q is quadratic and $c\in H$ is some constant.

3 The general case

In this section we will not restrict ourselves to concrete equations, we will work with two general linear equations. We will include here also the proofs of some known facts to keep the paper as self contained as possible. To use all the tools needed in our approach we need the assumption that the domain and codomain of our functions are abelian and divisible groups. Such structures are simply linear spaces over $\mathbb {Q}.$ However in some of the results presented below it is not essential that the constants involved are rational. Therefore we will work on linear spaces over some field which contains rationals.

Remark 1

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $n,m\in \mathbb {N}$ and let the functions $f_i:X\rightarrow Y,i=1,\dots ,n$ be of the form

$$\begin{aligned} f_i(x)=a_i+F_{i,1}(x)+F_{i,2}(x,x)+\cdots +F_{i,m}(\underbrace{x,\dots ,x}_m),i=1,\dots ,n \end{aligned}$$

where $a_i\in Y,i=1,\dots ,n$ are some constants and functions $F_{i,j}:X^j\rightarrow Y$ are j-additive and symmetric. If

$$\begin{aligned} f_{i,j}(x):= & {} F_{i,j}({x\dots ,x}),i=1,\dots ,n;j=1,\dots ,m,\\ f_{i,0}:= & {} a_i \end{aligned}$$

$p_i,q_i\in \mathbb {H}$ are given and functions $f_1,\dots ,f_n$ satisfy

$$\begin{aligned} \sum _{i=1}^nf_i(p_ix+q_iy)=0,\;x,y\in X \end{aligned}$$

(6)

then for all $j\in \{0,\dots ,m\}$ the system of functions $f_{1,j},\dots ,f_{n,j}$ also satisfies (7).

Indeed, for every rational number r we have

$$\begin{aligned} f_{i,j}(rx)=r^jf_{i,j}(x). \end{aligned}$$

Now, it is enough to take any $r\in \mathbb {Q}$ and substitute rx, ry in places of x, y,  respectively. Then we get

$$\begin{aligned} \sum _{i=1}^n\sum _{j=0}^m r^jf_{i,j}(p_ix+q_iy)=0,\;x,y\in X \end{aligned}$$

i.e.

$$\begin{aligned} \sum _{j=0}^mr^j\sum _{i=1}^n f_{i,j}(p_ix+q_iy)=0,\;x,y\in X. \end{aligned}$$

This equality is satisfied for every rational number r,  thus all the expressions standing at different powers of r must separately be equal to zero. It means that for each j the functions $f_{1,j},\dots ,f_{n,j}$ satisfy our equation.

Lemma 1

Suppose that $\mathbb {H},\mathbb {K}$ are fields so that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $\alpha _i\in \mathbb {K},p_i,q_i\in \mathbb {Q}$ and let l be any positive integer. Then the following conditions are equivalent to each other:

• i) equation

  $$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=0 \end{aligned}$$

  (7)

  is satisfied by some nonzero monomial function of order l, 

• ii) (7) is satisfied by all monomial functions of order l, 

• iii) $\sum _{i=1}^n\alpha _ip_i^kq_i^{l-k}=0,$ for each $k\in \{0,\dots ,l\}.$

Proof

First we assume that i) is satisfied and we show iii). Let $f(x)=F(x,\dots ,x)$ where $F:X^l\rightarrow Y$ is l-additive and symmetric. Then

$$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=\sum _{i=1}^n\alpha _i\sum _{k=0}^lp_i^kq_i^{l-k}\left( {\begin{array}{c}l\\ k\end{array}}\right) F(\underbrace{x,\dots ,x}_k,\underbrace{y,\dots ,y}_{l-k}). \end{aligned}$$

(8)

Similarly as in Remark 1, all expressions of the same degree with respect to x must sum up to zero. Thus for every $k\in \{0,\dots ,l\},$ we have

$$\begin{aligned} \sum _{i=1}^n\alpha _ip_i^kq_i^{l-k} F(\underbrace{x,\dots ,x}_k,\underbrace{y,\dots ,y}_{l-k})=0. \end{aligned}$$

Substituting here x in place of y and using the assumption $f\ne 0,$ we get

$$\begin{aligned} \sum _{i=1}^n\alpha _ip_i^kq_i^{l-k}=0 \end{aligned}$$

as claimed.

In the next part of the proof we show that iii) implies ii). Let $f(x)=F(x,\dots ,x)$ be any monomial function of order l. Using (3) in (8) we get

$$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=0. \end{aligned}$$

i.e. f is a solution of (7).

Finally, the implication $ii) \Rightarrow i)$ is obvious. $\square$

In the next lemma we show that in many cases the solutions of equation

$$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=\sum _{i=1}^m\beta _ig(s_jx+t_jy). \end{aligned}$$

(9)

must be polynomial functions.

Lemma 2

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $\alpha _i,\beta _j\in \mathbb {K}\setminus \{0\},i=1,\dots ,n,j=1\dots ,m$ be some constants and let $p_i,q_i,s_j,t_j\in \mathbb {H},i=1,\dots ,n,j=1\dots ,m.$ Finally, let functions $f,g:X\rightarrow Y$ satisfy Eq. (9). If there exists $i_0\in \{1,\dots ,n\}$ such that for $j\in \{1,\dots ,m\},$ we have

$$\begin{aligned} \left| \begin{array}{ll} p_{i_0}&{} s_j\\ q_{i_0}&{} t_j \end{array}\right| \ne 0 \end{aligned}$$

(10)

and

$$\begin{aligned} \left| \begin{array}{ll} p_{i_0}&{} p_i\\ p_{i_0}&{} q_i \end{array}\right| \ne 0 \end{aligned}$$

(11)

for $i=1,\dots ,n;i\ne i_0$ then f must be a polynomial function of order at most $k-1,$ where k is the maximal number of pairwise independent pairs $(p_i,q_i),(s_j,t_j).$

Further if, additionally, for some $(s_{j_0},t_{j_0})$ we have

$$\begin{aligned} \left| \begin{array}{ll} s_{j_0}&{} s_j\\ t_{j_0}&{} t_j \end{array}\right| \ne 0 \end{aligned}$$

(12)

for $j=1,\dots ,m;j\ne j_0$ then also g must be a polynomial function of order at most $k-1.$

Proof

If $p_{i_o}=0$ then we interchange x with y in (9) and we may use Theorem 2 directly. Now assume that $p_{i_0}\ne 0$ and put $\tilde{x}=\frac{x-q_{i_0}y}{p_{i_0}}$ in place of x in (9). After this substitution we get

$$\begin{aligned} p_{i_0}\tilde{x}+q_{i_0}y=x \end{aligned}$$

and

$$\begin{aligned} p_{i}\tilde{x}+q_{i}y=p_i\frac{x-q_{i_0}y}{p_{i_0}}+q_iy=\frac{p_i}{p_{i_0}} x+\frac{p_iq_{i_0}-q_ip_{i_0}}{p_{i_0}}y. \end{aligned}$$

Using (11), we can see that the coefficient standing here at y is different from zero. Similarly

$$\begin{aligned} s_{i}\tilde{x}+t_{i}y=s_i\frac{x-q_{i_0}y}{p_{i_0}}+t_iy=\frac{s_i}{p_{i_0}} x+\frac{s_iq_{i_0}-t_ip_{i_0}}{p_{i_0}}y, \end{aligned}$$

and from (10) we know that again the coefficient of y is not equal to zero i.e. we may use again Theorem 2 to prove that f is a polynomial function. If there are some linearly dependent pairs among $(p_i,q_i),(s_j,t_j)$ then we group the occurrences of f and g containing these coefficients into new functions so that we achieve the optimal estimation of the order.

Now we will deal with function g. If (12) is satisfied then we have two possibilities.

• 1. If for all $i=1,\dots ,n$ we have

  $$\begin{aligned} \left| \begin{array}{ll} s_{j_0}&{} p_i\\ t_{j_0}&{} q_i \end{array}\right| \ne 0 \end{aligned}$$

  (13)

  then we proceed similarly as in the first part of the proof and we show that g must be a polynomial function.

• 2. The second possibility is that for some $i_1,\dots ,i_r$

  $$\begin{aligned} \left| \begin{array}{ll} s_{j_0}&{} p_{i_\nu }\\ t_{j_0}&{} q_{i_\nu } \end{array}\right| =0,\;\nu =1,\dots ,r. \end{aligned}$$

  (14)

In this case we consider the expression

$$\begin{aligned} \beta _{j_0}g(s_{j_0}x+t_{j_0}y)+\sum _{\nu =1}^r\alpha _{i_\nu } f(p_{i_\nu } x+q_{i_\nu } y) \end{aligned}$$

which in view of (14) may be written as a function of $s_{j_0}x+t_{j_0}y.$ Then we show that this new function is a polynomial function. Finally from the first part of the proof we know that f is a polynomial function thus g also must be a polynomial function. $\square$

Now we give some simple examples of equations which will illustrate the possibilities described in Lemma 2.

Example 1

Equation

$$\begin{aligned} f(x+y)-f(x)-f(y)=2g(x+y)-g(x) \end{aligned}$$

has only polynomial solutions because of the term f(y) on the left hand side, and because of the linear independence of the coefficients of the arguments of g.

Equation

$$\begin{aligned} f(x+y)-f(x)-f(y)=g(x+y)-g(x)-g(y) \end{aligned}$$

has solutions f, g which are not polynomial ($f-g$ must be additive) because there is no occurrence of f or g with coefficients linearly independent from all the others—this shows that the assumptions (10) and (11) cannot be omitted.

The function f occurring in

$$\begin{aligned} f(x+y)-f(x)-f(y)=g(x-y)-g(y-x) \end{aligned}$$

must be polynomial [(10) and (11) are satisfied] but g is not necessarily a polynomial function. Namely, any pair (f, g) where f is additive and g is even satisfies this equation. This shows that the (12) is necessary to guarantee for function g to be a polynomial function.

Remark 2

It may also happen that the assumptions of Lemma 2 are not satisfied and the solutions of a given equation are polynomial functions. Equation

$$\begin{aligned} f(x+y)-f(x)-f(y)=2g(x+y)-g(x)-g(y) \end{aligned}$$

has only polynomial solutions. Indeed, after some rearrangement

$$\begin{aligned} (f-2g)(x+y)-(f-g)(x)-(f-g)(y)=0 \end{aligned}$$

we can see that both $f-2g$ and $f-g$ are polynomial functions. Then $g=f-g-(f-2g)$ and $f=2(f-g)-(f-2g)$ are also polynomial functions, since a linear combination of polynomial functions gives a polynomial function.

As we can see, in many cases functions satisfying (9) must be polynomial. Moreover we know from Remark 1 that the monomial summands of solutions of a given equation also satisfy this equation. Therefore we will study the alienation of linear functional equations in the class of monomial functions of a fixed order. We will use the expression l-alienation if the monomial summands of f and g of the order l alienate. A more precise statement is given by the following definition.

Definition 4

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $\alpha _i,\beta _j\in \mathbb {K}\setminus \{0\},i=1,\dots ,n,j=1\dots ,m$ be some constants and let $p_i,q_i,s_j,t_j\in \mathbb {H},i=1,\dots ,n,j=1\dots ,m.$ If the solutions $f,g:X\rightarrow Y$ of the system of equations

$$\begin{aligned} \sum _{i=1}^n\alpha _if(p_ix+q_iy)=0 \end{aligned}$$

(15)

and

$$\begin{aligned} \sum _{j=1}^m\beta _jg(s_jx+t_jy)=0 \end{aligned}$$

(16)

are different from the solutions of Eq. (9) in the class of monomial functions of order l then we say that Eqs. (15) and (16) are not l-alien. In the opposite case we say that these two equations are l-alien.

We begin with a lemma which gives us some relation between the monomial solutions f, g of (9).

Lemma 3

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $\alpha _i,\beta _j\in \mathbb {K}\setminus \{0\},i=1,\dots ,n,j=1\dots ,m$ be some constants and let $p_i,q_i,s_j,t_j\in \mathbb {Q},i=1,\dots ,n,j=1\dots ,m.$ Let l be a positive integer, let $k\in \{0,\dots ,l\},$ let $F,G:X^l\rightarrow Y$ be l-additive and symmetric functions and let the functions $f,g:X\rightarrow Y$ given by the formulas: $f(x)=F(x,\dots ,x),g(x)=G(x,\dots ,x)$ satisfy Eq. (9). If

$$\begin{aligned} a_{k,l}=\sum _{i=1}^n\alpha _ip_i^kq_i^{l-k} \end{aligned}$$

(17)

and

$$\begin{aligned} b_{k,l}=\sum _{j=1}^m\beta _js_j^kt_j^{l-k}, \end{aligned}$$

(18)

then

$$\begin{aligned} a_{k,l}f(x)=b_{k,l}g(x),\;x\in X. \end{aligned}$$

(19)

Proof

Using the forms of f and g,  we may write (9) in the form

$$\begin{aligned}&\sum _{i=1}^n\sum _{k=0}^l \left( {\begin{array}{c}l\\ k\end{array}}\right) \alpha _ip_i^kq_i^{l-k}F(\underbrace{x,\dots ,x}_k, \underbrace{y,\dots ,y}_{l-k})\nonumber \\&\quad =\sum _{k=0}^l \left( {\begin{array}{c}l\\ k\end{array}}\right) \sum _{i=1}^m\beta _is_i^kt_i^{l-k}G(\underbrace{x,\dots ,x}_k, \underbrace{y,\dots ,y}_{l-k}). \end{aligned}$$

(20)

Thus for every $k\in \{0,\dots ,l\}$ we have

$$\begin{aligned}&\sum _{i=1}^n\alpha _ip_i^kq_i^{l-k}F(\underbrace{x,\dots ,x}_k, \underbrace{y,\dots ,y}_{l-k})\nonumber \\&\quad =\sum _{i=1}^m\beta _is_i^kt_i^{l-k}G(\underbrace{x,\dots ,x}_k, \underbrace{y,\dots ,y}_{l-k}). \end{aligned}$$

(21)

Now it is enough to take $y=x$ in the above equality, to get (19). $\square$

In the next theorem we present the general solution of Eq. (9) in the class of monomial functions of a given order.

Theorem 3

Let l, n, m be any positive integers, Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K},$ let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ let $\alpha _i,\beta _j\in \mathbb {K}\setminus \{0\},i=1,\dots ,n,j=1\dots ,m$ be some constants, let $p_i,q_i,s_j,t_j\in \mathbb {Q},i=1,\dots ,n,j=1\dots ,m$ and let functions f, g be defined on X and take values in Y. For $a_{l,k},b_{l,k}$ given by (17) and (18) we define the sets $A_l,B_l$ by the formulas:

$$\begin{aligned} A_l:=\{k\in \{0,\dots ,l\}:a_{k,l}\ne 0\} \end{aligned}$$

(22)

and

$$\begin{aligned} B_l:=\{k\in \{0,\dots ,l\}:b_{k,l}\ne 0\}. \end{aligned}$$

(23)

The following assertions hold true.

• 1. If $A_l=B_l=\emptyset$ then Eq. (9) is satisfied by every pair (f, g) of monomial functions of order l.

• 2. If $A_l\ne \emptyset ,$$B_l=\emptyset$ and the monomial functions f, g of order l,  satisfy (9) then $f=0.$ Conversely, every pair (0, g) where g is monomial function of order l is a solution of (9).

• 3. If $A_l=\emptyset ,$$B_l\ne \emptyset$ and the monomial functions f, g of order l,  satisfy (9) then $g=0.$ Conversely, every pair (f, 0) where g is monomial function of order l is a solution of (9).

• 4. If $A_l,B_l\ne \emptyset ,$$A_l\ne B_l$ and monomial functions f, g of order l,  satisfy (9) then $f=g=0.$

• 5. If $A_l,B_l\ne \emptyset$ and $A_l=B_l$ then:

  • (i) if there exists c such that $\frac{a_{k,l}}{b_{k,l}}=c$ for all $k\in A_l$ then the solutions of (9) in the class of monomial functions of order l are of the form (f, cf) where f is any monomial function of order l.

  • (ii) if $\frac{a_k}{b_k}$ is not constant on $A_l$ and the monomial functions f, g of order l,  satisfy (9) then $f=g=0.$

Proof

To prove the first statement observe that from Lemma 1 we know that, in the case $A_l=B_l=\emptyset ,$ all monomial functions of order l satisfy (7) and (16). This means that all pairs of monomial functions (f, g) satisfy (9).

Now assume that $A_l\ne \emptyset$ and $B_l=\emptyset .$ Then for some k we have $a_{k,l}\ne 0$ and $b_{k,l}=0.$ In view of Lemma 3 this yields $f=0.$ On the other hand $B_l=\emptyset$ means that all monomial functions of order l satisfy (16). Thus the pair (0, g) where g is any monomial function of order l satisfies (9).

The third assertion is completely analogous to the second one and, therefore, the proof in this case is not needed.

Assume now that $A_l,B_l\ne \emptyset ,$ and $A_l\ne B_l.$ Let for example exist k such that $a_{k,l}\ne 0$ and $b_{k,l}=0.$ Then from Lemma 3 we get $f=0.$ However if $f=0$ then from (9) we get that g satisfies (16) and, since $B_l\ne \emptyset$ we have $b_{k,l}\ne 0$ for some k. In view of Lemma 1, this means that $g=0.$

In the remaining part of the proof we assume that $A_l,B_l\ne \emptyset$ and $A_l=B_l.$ If for some c we have

$$\begin{aligned} \frac{a_{k,l}}{b_{k,l}}=c,\;k\in A_l \end{aligned}$$

then from Remark 3 we know that $g(x)=cf(x).$ Using this form of g in (9), we obtain a linear equation with one unknown function f. Using Lemma 1 it is easy to see that this equation is satisfied by all monomial functions.

Finally, consider the case where $\frac{a_{k,l}}{b_{k,l}}$ is not constant. Then there exist $k_1,k_2$ and $c_1,c_2$ such that

$$\begin{aligned} \frac{a_{k_1,l}}{b_{k_1,l}}=c_1 \end{aligned}$$

and

$$\begin{aligned} \frac{a_{k_2,l}}{b_{k_2,l}}=c_2. \end{aligned}$$

In view of Remark 3 and from the above equalities we get

$$\begin{aligned} g(x)=c_1f(x)\; \text {and}\; g(x)=c_2f(x). \end{aligned}$$

(24)

Thus we have $c_1f(x)=c_2f(x)$ which means that $f=0.$ Now using (24) we get that $g=0$ which finishes the proof. $\square$

Remark 3

Let $A_l,B_l$ be defined as in the above theorem. Equations (16) and (7) are not l-alien if and only if case 4 (i) of Theorem 3 occurs.

Using this theorem, we will give some simple examples of equations that are l-alien and not l-alien, respectively.

Remark 4

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K}.$ Let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K}.$ Let $p,q\in \mathbb {Q}$ and $\alpha ,\beta _1,\beta _2\in \mathbb {K}\setminus \{0\}.$ Let $f,g:X\rightarrow Y$ be some functions. Equations

$$\begin{aligned} \alpha f(px+qy)=0 \end{aligned}$$

and

$$\begin{aligned} \beta _1 g(x)+\beta _2 g(y)=0 \end{aligned}$$

are:

• not 0-alien if $\beta _1+\beta _2\ne 0$

• not 1-alien if $\frac{p}{\beta _1}=\frac{q}{\beta _2}.$

There is no need to test the l-alienation for $l>1,$ since f, g satisfying equation

$$\begin{aligned} \alpha f(px+qy)=\beta _1 g(x)+\beta _2 g(y) \end{aligned}$$

are polynomial functions of order at most 1.

The above remark was connected with the Cauchy equation, now we present a result connected with the quadratic equation.

Remark 5

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K}.$ Let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K}.$ Let $f:X\rightarrow Y$ be some functions, let $q_1,q_2\in \mathbb {Q}$ be any numbers. Equations

$$\begin{aligned} f(x+q_1y)+f(x+q_2y)=0 \end{aligned}$$

and

$$\begin{aligned} g(x)+g(y)=0 \end{aligned}$$

are not 0-alien and are:

• not 1-alien if and only if $q_1+q_2=2$

• not 2-alien if and only if $q_1=1,q_2=-1$ or $q_1=-1,q_2=1.$

Remark 6

Now the alienation of the Fréchet equations obtained in Proposition 1 may be viewed from the perspective of the general theory of Theorem 3. Indeed, as it was shown in the proof of Proposition 1, the solutions f, g of these equation are polynomial functions of order at most m. Let $l<n$ then $A_l,B_l=\emptyset$ i.e. we have l-alienation. Further, if $n<l\le m$ then $A_l\ne \emptyset ,B_l=\emptyset$ i.e. again we have alienation.

Now, using Theorem 3, we will study the alienation problem for two monomial equations.

Theorem 4

Suppose that $\mathbb {H},\mathbb {K}$ are fields such that $\mathbb {Q}\subset \mathbb {H},\mathbb {K}.$ Let X, Y be linear spaces, respectively over the fields $\mathbb {H},\mathbb {K},$ Let m, n be positive integers, $m>n$ and let $f:X\rightarrow Y$ be some functions. Then equations

$$\begin{aligned} \Delta ^m_yg(x)-m!g(y)=0 \end{aligned}$$

(25)

and

$$\begin{aligned} \Delta ^n_yf(x)-n!f(y)=0 \end{aligned}$$

(26)

are not l-alien for $l<n$ and l-alien for $l\in \{n,\dots ,m\}$.

Proof

We will study the equation

$$\begin{aligned} \Delta ^n_yf(x)-n!f(y)=\Delta ^m_yg(x)-m!g(y), \end{aligned}$$

(27)

which certainly is an equation of the form (9). Moreover, it is clear that f, g must be polynomial functions of order at most m.

Let $l<n$ be a fixed positive integer and h b a monomial function of order l,  then

$$\begin{aligned} \Delta ^n_yh(x)=\Delta ^m_yh(x)=0. \end{aligned}$$

In view of Lemma 1 this means that for all $k\in \{0,\dots ,l-1\}$ we have

$$\begin{aligned} a_{k,l}\sum _{i=1}^n\alpha _ip_i^kq_i^{l-k}=0 \end{aligned}$$

and

$$\begin{aligned} b_{k,l}\sum _{j=1}^m\beta _jr_j^ks_j^{l-k}=0. \end{aligned}$$

Whereas for $l=n$

$$\begin{aligned} a_{l,l}=\sum _{i=1}^nq_i^{l}=-n! \end{aligned}$$

and

$$\begin{aligned} b_{l,l}\sum _{j=1}^m\beta _jr_j^ks_j^{l-k}=-m!. \end{aligned}$$

Summarizing these two observations, we can see that $A_l=B_l=\{l\}$ and, in consequence we have the non l-alienation of (25) and (26). Now take $l\in \{n,\dots ,m\},$ then for a non zero monomial function h of order l we have

$$\begin{aligned} \Delta ^n_yh(x)\ne 0 \end{aligned}$$

and

$$\begin{aligned} \Delta ^m_yh(x)=0. \end{aligned}$$

Thus we have $a_{k,l}\ne 0$ for some $k<l$ and $b_{k,l}=0$ for all $k<l$ i.e. $A_l\ne B_l$ and, in view of Theorem 3, Eqs. (26) and (25) are l-alien. $\square$

Of course, in the case of Eqs. (26), (25) considered in the above theorem it would be enough to assume that X and Y are (abelian) groups such that Y is torsion free and divisible by m!. Our assumptions follow from the fact that, in the proof we use Theorem 3.

Remark 7

The result of R. Ger concerning the alienation of the Cauchy equation and the quadratic equation is a particular case of the above result (with $n=1,m=2$).

We conclude the paper with two final remarks.

Remark 8

In this paper we presented results where we first get the solutions of Eq. (9) (using Theorem 3) and then we deduce the alienation properties from the solutions. A similar approach was presented by Gilányi [8], however Gilányi used a computer program to solve the equations.

Remark 9

The non-alienation obtained in Theorem 4 is quite surprising, since it is much more common that two equations are alien than non-alien. The explanation is provided by Theorem 3. It is difficult to obtain non-alienation, since then all elements of $A_l$ and $B_l$ must be proportional. In the case of monomial equations this occurred because each of $A_l$ and $B_l$ consisted of one element only. If we study 0-alienation then the non-alienation effect appears much more frequently, since $A_0$ and $B_0$ can have only one element.