Time-dependent scour processes on granular beds at large scale

Abstract

A theoretical framework, based on the phenomenological theory of turbulence applied to scour-related processes due to plunging jets on cohesionless beds, is considered in this paper. More specifically, its predictive capability is assessed herein for large-scale domains, after it was developed for small scales elsewhere. The analysis focuses on both the time-evolution process and the equilibrium configuration for a wide range of hydraulic structures. After revisiting the theory for the temporal evolution of the scour processes, the scour for large-scale tests is investigated using unpublished experiments performed at Colorado State University by the last author. These tests confirm the existence of two stages in the scour hole development, namely the developing and developed phases. Thus, the scour dynamics at large scales is shown to be consistent with that at smaller scales. Then, the theory recently introduced by the first three authors is used to predict the time evolution of scour, corroborating that the very same equations, together with the same coefficients, provide successful predictions, regardless of scale and granulometric distribution. Finally, the theory is again verified against laboratory data on PK weirs obtained at the University of Pisa. Overall, the work described in the paper offers a tool with general validity.

1 Introduction

Scour holes at plunge pools typically occur downstream of hydraulic structures; they are concerned with the stability of the structure, potentially resulting in its collapse [20]. Because of the risk of structural failure, numerous works have analyzed jet scour to better understand its physical mechanisms. Any improved knowledge can lead to a more accurate prediction of the scour processes, and to effective scour-prevention measures.

Most approaches to evaluate plunge pool scour are based on experimentation; they provide information on the equilibrium condition [7, 40]. Breusers and Raudkivi [8], Hoffmans and Verheij [22], Hoffmans [24], and Mason and Arumugam [29] presented several empirical equations, highlighting some shortcomings. In particular, Hoffmans [24] remarked: “…many of the existing scour relations are not universally applicable but dependent on the data that were used in the regression analyses….”

Pagliara et al. [31, 32] assessed the scour depths for both two- (2D) and three-dimensional (3D) equilibrium configurations. The concepts of static and dynamic scour configurations were defined as follows [31, 32]: (i) the dynamic equilibrium morphology occurs when the jet is still in action; and (ii) the static configuration takes place after the jet has been stopped, and the suspended rotating granulate falls back onto the scour hole. In case (ii), the scour depth can be significantly lower as compared with case (i). Pagliara et al. [33] distinguished between two main phases of the scour process, referred to as the developing and developed scour evolutions, respectively. Their features are [5]: (1) the developing phase is rapid and lasts from jet impact on the granular material to the ridge formation. The upstream ridge portion develops relatively fast, whereas its downstream portion requires longer to be shaped [5]. The sediment removed from the scour hole is mainly transported downstream, thereby increasing the scour depth. Phase (1) is completed once the ridge is formed. (2) the developed phase is characterized by an homothetic expansion of both the scour hole and the ridge, keeping nearly fixed the scour hole origin. Phase (2) is much slower than phase (1), and is completed when the scour morphology variations become negligible. Pagliara et al. [33] evidenced that the duration of phase (1) mainly depends on the impact angle onto water surface measured from horizontal α (the larger α, the shorter is phase (1)). An empirical equation for the non-dimensional transition time between phases (1) and (2) up to α = 60° was proposed, later extended in Bombardelli et al. [5].

The idea of using the Phenomenological Theory of Turbulence (PTT; see also [1, 2]) to address open-channel flow problems was pioneered by Gioia and Bombardelli [16] using the conservation of linear momentum. Bombardelli and Gioia [3, 4] and Gioia and Bombardelli [17] introduced the conservation of energy to apply PTT for scour phenomena, at equilibrium condition. Their approach allowed to theoretically derive the exponents of each parameter for both the 2D and 3D equilibrium configurations via first principles.

Bonetti et al. [6], on the other hand, presented an alternative approach for the derivation of Manning’s formula via the use of the co-spectral budget, the assumption of equilibrium, and the adoption of an ad-hoc version of the spectrum. Following the seminal works of Bombardelli and Gioia, other authors have recently conducted studies to provide insights on scour phenomena in correspondence with a vertical cylinder (e.g., a single bridge pier) in granular beds [9, 28]. In particular, by means of the PTT, Manes and Brocchini [28] clarified the effect of governing parameters on scour mechanisms. Coscarella et al. [9] revised the theory proposed by Manes and Brocchini [28] and further explored the scaling of equilibrium scour depth. Likewise, Musa et al. [30] applied the PTT to scour processes caused by marine hydrokinetic turbines installed in erodible channels. Bonetti et al. [6] scrutinized the PTT-based approach proposed by Gioia and Bombardelli [16] to provide a theoretical explanation of Manning's formula and Strickler's scaling. In doing so, they proposed a modification of some scaling assumptions made by Gioia and Bombardelli [16], introducing two ad hoc scaling functions (α₁ and α₂). According to Coscarella et al. [9], α₁ “links local to global velocity gradients over the bed-normal direction”, whereas α₂ relates the local mean to the bulk Turbulent Kinetic Energy (TKE) dissipation rate. Bonetti et al. [6] concluded that the product α₁α₂ should scale with (k_s/R_h)^−1/3f_d, where k_s indicates the roughness height, R_h the hydraulic radius, and f_d is a friction factor.

Bombardelli et al. [5] extended the theories developed by Bombardelli and Gioia [3, 4] and Gioia and Bombardelli [17] to the temporal evolution of phase (2) by invoking the conservation of sediment mass, and the PTT across the scour hole. Bombardelli et al. [5] also presented new experiments which encompassed jet angles ranging from 45 to 90°, several still water depths, and different particle sizes. The previous and new datasets were used to calibrate the constants in the equilibrium scour formulas, as well as in the time-evolution results.

These analyses [5] were developed for laboratory conditions. For larger scales, the proposed theory needs to be validated. Therefore, in this paper we test the ability of such a theory to address the scour at large scales. To this end, we use unpublished tests developed by Kuroiwa [26]. We show that the theory developed at small scales notably predicts the time evolution of these previously unpublished large-scale tests, without changing the multiplicative constants presented in [5]. In addition, we show that the proposed theory also provides good estimations of scour depths downstream of other hydraulic structures (e.g., weirs, check dams and piano key weirs). This represents a remarkable result because it gives the developed theory unprecedented validity; it also supplements the findings of Bombardelli et al. [5], indicating that the theoretical tools devised to address scour problems are of general nature.

The manuscript is structured as follows. First, unpublished sets of large scale data obtained at the Colorado State University (CSU) are presented; second, we review the theories of Bombardelli et al. [5]; third, we use new and published data pertaining to different structures to validate the proposed theory. Finally, the results are discussed and summarized.

2 Experimental set-up and methodology

Different datasets relative to prototypes and laboratory models were analyzed. A distinction was made between the 2D and 3D cases, following the criteria of Pagliara et al. [31]. These authors conducted experimental tests at ETH-Zurich and University of Pisa, and introduced a quantitative criterion to classify the scour morphology due to plunging jets. Based on their findings, the equilibrium morphology and the flow pattern is 2D if the 3D parameter λ = b/B ≥ 3, where B is the channel width, and b is the maximum scour-hole width. In turn, it is 3D for λ < 3 [31].

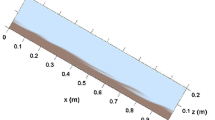
The data used herein are based on four large scale experiments of Kuroiwa [26], supplemented by the tests of Hallmark [21] and Thomas [44]. Kuroiwa [26] analyzed the scour-depth evolution due to a rectangular jet impacting a cohesionless bed in a concrete tailbox. The discharge was provided by a rectangular nozzle whose width and height were equal to W₀ = 3.05 m and b₀ = 0.0873 m, respectively (Figs. 1 and 2). The nozzle angle β was adjusted by rotating the diffuser around its axis. The discharge was regulated using a butterfly valve. The tailbox was 9.14 m-wide, 16.76 m-long, and 4.57 m-deep (Fig. 1c). The tests were 3D, following the criterion mentioned in the previous section. Test duration (t_test) ranged between 6840 and 7200 s. At test end, the scour hole was surveyed.

Fig. 1

Experimental facility (adapted from [26]): a pipeline system; b nozzle detail; c scour hole. Y axis runs parallel to tailbox frontal wall, and is directed from left to rigth. X axis is orthogonal to Y axis, directed from the bottom to the top. The origin O of the reference system is located on left tailbox corner not visible in the figure

Fig. 2

Adapted from Kuroiwa [26]

Main hydraulic and geometric variables for tests of: a Kuroiwa [26]; b Hallmark [21] and Thomas [44].

The granular material was placed in the concrete tailbox and it was levelled before each test. Material samples were analyzed before and after each test. With d_n as the diameter of material for which n% is finer, the non-uniformity coefficient σ = (d₈₄/d₁₆)^1/2 at test end is significantly lower than at test start, indicating that the superficial sediment layer is more uniform at equilibrium condition. It was found that the medium diameter d₅₀ was approximately equivalent to d₈₅ of the original bed material. This confirms the findings of Hoffmans [23] and Pagliara et al. [34] who proposed to adopt d₉₀ for non-uniform bed material. In fact, Pagliara et al. [34] noticed that d₉₀ of the original sediment bed mixture is comparable with that of the equilibrium superficial layer. In Table 1, it is evidenced that this behaviour depends exclusively on the granulometric sorting process of any scour phenomena.

Table 1 Scour depth evolution for tests of Kuroiwa [26] (unpublished data)

In Fig. 2a, we show a sketch of the test apparatus, along with the main parameters. Herein, z is the elevation difference between the jet issuance section and the tailwater, V₀ is the approach flow velocity, g is the gravity acceleration, b₀ is the jet thickness at the issuance section, α is the impact angle onto the water surface, and h = z + V₀²/(2 g) is the theoretical head. In Table 1, the main geometric and hydraulic parameters of tests by Kuroiwa [26] are summarized. The maximum scour depth is Δ_max. At its position, the scour depth evolution Δ(t) is also reported, together with the values of discharge Q, tailwater depth D, and granulometric bed characteristics at test start and test end. The sediment density was ρ_s = 2650 kg/m³.

The laboratory tests of Hallmark [21] and Thomas [44] were also analyzed. They conducted tests with the same experimental apparatus, consisting of a glass-walled flume 0.826 m wide and 7.62 m long and a downstream tailbox containing the granular bed material.

Thomas [44] conducted Series I and II involving a free-falling jet for two bed materials of similar d₅₀ but of different σ. For Series I (Table 2), d₅₀ = 0.0061 m and σ = 1.18, whereas for Series II (Table 3), d₅₀ = 0.00635 m and σ = 1.71, respectively. The sediment density was ρ_s = 2650 kg/m³. Hallmark [21] further extended the scope of Thomas’ tests [44] by using a bed material with d₅₀ = 0.00635 m, σ = 2.87, and ρ_s = 2650 kg/m³, respectively (Table 4). The equilibrium test morphology of both Hallmark [21] and Thomas [44] was 3D. A sketch of their experimental apparatus is presented in Fig. 2b.

Table 2 Experimental data (Series I) of Thomas [44]

Table 3 Experimental data (Series II) of Thomas [44]

Table 4 Experimental data of Hallmark [21]

D’Agostino [10] analyzed the scour process downstream of a vertical weir located in a 0.50 m wide rectangular channel. Its width W₀ was smaller than that of the channel, ranging from 0.15 to 0.30 m, thus resulting in a 3D equilibrium morphology.

Falciai and Giacomin [12] surveyed 29 check dams located in the Arno River Basin, Italy. They took scour data after a flood event [11]. Note the identical widths of the check dams and the streams. Since these structures are located in natural water courses, both non-uniform distributions of sediment size and flow characteristics prevail. It is reasonable to assume that the scour equilibrium morphology is either 3D or 2D/3D. Similar field data were also taken downstream of 13 consecutive check dams in Missiaga River (Italy), whose bottom slope is 15% [11].

Finally, two special tests (termed Test 1 and 2) were conducted at the University of Pisa (especially for this work) to analyze the scour evolution downstream of a four-cycle-Piano Key weir (PK weir). The structure was located in a glass-walled flume, 0.80 m wide and 25 m long. The weir height, measured from the initial bed level, was equal to 27.8 cm and the center line length of the crest was 4.15 m. For both Tests 1 and 2, the discharge Q was set at 50 l/s, whereas the tailwater depth D was equal to 19.2 cm and 24.2 cm, respectively. Tests were conducted using one uniform bed material, with d₅₀ = 0.00148 m, d₉₀ = 0.0017 m, σ = 1.14 and ρ_s = 2467 kg/m³. Test duration was of 5 h Scour depths at different instants were measured using a point gauge equipped with a 30 mm circular plate at its lower end, allowing for measurements in the presence of suspended particles and air bubbles in the scour hole [31]. In addition, a high-resolution camera was located in front of the channel, allowing for a continuous monitoring of the scour evolution. Two pictures of the PK weir during Test 1 are shown on Fig. 3.

Fig. 3

Pictures of the PK weir: a frontal view; b plan view (flow from left to right)

3 Scour evolution at large scale

In this section of the paper, we analyze the experimental data by Kuroiwa [26], elucidating interesting features relative to the scour evolution at large scale. In Fig. 4, we show the data of the scour depth evolution Δ(t) at different streamwise (X), and transverse (Y) coordinates (Fig. 1c), the discharge variation Q(t) and the water depth D(t) for Test 4. Note that Y = 4.57 m corresponds to the basin axis.

Fig. 4

Adapted from Kuroiwa [26]

Test 4: a Scour depth evolution Δ(t) at different locations. Continuous line connects data points pertaining to the position of maximum scour depth; variation of b discharge Q(t) and c tailwater depth D(t).

The maximum scour depth Δ_max not always occurred axially. In Tests 1 and 2, Δ_max was at Y = 7.62 m. Its asymmetric location is reasonably explained by considering that, at large scale, it is complicated to assure the homogenous distribution of the bed material. Also, the time required to set the target discharge and the tailwater depth caused a deformation of the original bed before reaching the target variables, thereby modifying the flow conditions. The location of jet impact shifted downstream during the test, because of combined discharge increase and tailwater decrease. Therefore, these large scale tests resulted in a difficult-to-control scour evolution. In addition, the measurement time might seem “limited”; nevertheless, the scour depth becomes essentially asymptotic at Y = 4.57 m, thus confirming that the equilibrium condition had been practically achieved for Test 1 (Fig. 5a).

Fig. 5

Adapted from Kuroiwa [26]

Scour depth evolution Δ(t) at different locations for Tests a 1, b 2, c 3. Continuous line connects data points pertaining to position of maximum scour depth. The vertical lines represent the transition time between the developing and developed phase calculated using the equation proposed by Bombardelli et al. [5].

In Fig. 5b, in which data are reported for Test 2, the asymptotical behaviour is evident only for two axial positions (i.e., for Y = 4.57 m and X = 4.57 m and 5.49 m), whereas it is not apparent for the other two (i.e., for Y = 4.57 m and X = 6.86 m and 7.62 m). In this case, the gap in time between the last two measurements explains this behaviour. It was not possible to obtain continuous measurements of the scour depth by the adopted procedure. Therefore, the number of measurements appears insufficient to show the asymptotic behavior. As to Tests 3 and 4, similar considerations apply, although the asymptotic behavior is evident, in particular for Test 4 (Figs. 4a and 5c). Note that Tests 3 and 4 differ only in the tailwater depth; Pagliara et al. [33] evidenced that this parameter only slightly affects the time to reach equilibrium. Thus, it is reasonable to state that it was also reached in Test 3.

From Figs. 4a and 5, the distinction between the two phases characterizing the temporal evolution (developing and developed, put forward from laboratory tests) is also apparent for large test scale. Bombardelli et al. [5], by extending as mentioned the findings of Pagliara et al. [33] to vertical jets, found that the non-dimensional transition (subscript T) time τ_T is log(τ_T) =  − 0.02α + 3.62, with τ_T = t_T/T_r. Herein, t_T is the dimensional transition time and T_r = D^*/(g′d₉₀)^1/2, where D^* is the equivalent jet diameter and g′ = [(ρ_s − ρ)/ρ]g is the reduced gravity acceleration [35]. (The previous equation applies for circular jets; D^* should be replaced by the jet width W₀ for rectangular jets. Then, log(τ_T) = log(t_T/T_r*) =  − 0.02α + 3.62, with T_r* = W₀/(g′d₉₀)^1/2.) When applying the above equation, we estimated that that impact angle of the jet onto water surface measured from horizontal (α) was approximately equal to 64° for Tests 1 and 2 and 71° for Tests 3 and 4, and assumed the value of d₉₀ equal to that at t = 0 s. Very interestingly, from Figs. 4 and 5, it can be concluded that this equation also represents large-scale behavior, as indicated by the transition times (vertical lines); this result was completely unexpected but it is a nice confirmation of the validity of the proposed approach. Based on these observations and considering that experimental tests of Kuroiwa [26] lasted some 2 h, the scour was in the developed phase.

In Fig. 6, we show the non-dimensional scour depth data of Kuroiwa [26] against non-dimensional time t/T_r*; the lines representing the non-dimensional transition between the developing and the developed phases according to Bombardelli et al. [5], for the two values of α are also depicted. We calculated T_r* by using both d₉₀ of the original sediment (at t = 0 s in Table 1, Fig. 6a) and d₉₀ of the superficial bed layer at test end (at t = t_test, where t_test = 6840 s, 7140 s, 6900 s, and 7200 s for Tests 1, 2, 3, and 4, respectively, Fig. 6b). As shown in Fig. 6a and b, no significant differences appear in terms of scour-depth evolution. The data of Fig. 6a are characterized by slightly lower values of non-dimensional time, because of the relatively small variation in d₉₀ at t = 0 s and t = t_test. Furthermore, the scour evolution of Tests 3 and 4 is consistent with that found by Bombardelli et al. [5] at small-scale, despite the significant variations in the test conditions. As mentioned, in contrast to Tests 3 and 4, in which the scour evolution was monitored from the very start of the experiment, the first scour depth measurement was taken only at t = 2820 s and t = 1920 s for Tests 1 and 2, respectively. Nonetheless, measurements at the axial section evidence that the equilibrium condition had been reached (Fig. 5).

Fig. 6

Time evolution of the scour depth Δ/W₀ versus t/T_r* for tests by Kuroiwa [26], along with lines indicating transition between developing and developed phases for 64° (Tests 1 and 2) and 71° (Tests 3 and 4). Time is non-dimensionalized with d₉₀ at: a t = 0 s, b t = t_test. Experimemtal data pertain to positions of maximum scour depth

Note that the methodology adopted to reach the target discharge and the tailwater level probably affected the scour depth evolution, yet not the transition time. Hydraulic conditions are easily kept constant in the laboratory. Conversely, it is difficult to reach both the target discharge and tailwater level at the same time and in a short period from test start at large scale.

4 Theoretical model

4.1 Jet energetics and shear stress at interface of the granular material

Here, the theories of Bombardelli and Gioia [3, 4], and Gioia and Bombardelli [17] for the equilibrium condition, and of Bombardelli et al. [5] for the time-dependent behavior of the scour depth are briefly reviewed. There are two basic assumptions related to the PTT, referring to the steady production of turbulent kinetic energy [14, 38]: (i) the Turbulent Kinetic Energy (TKE) per unit mass of a flow is determined by the scales associated with the largest eddies; (ii) the TKE introduced at a rate ε to the flow “cascades” from large to small scales at the same rate ε of the large scales, via an “inviscid” mechanism [43]. The mechanism continues until dissipation into internal energy takes place at sufficiently-small scales.

Based on the above two assumptions, an expression is derived for the rate of dissipation of TKE (i.e., ε) as a function of the velocity of the largest eddies V and the size of the largest eddies (scaling with the sum of the scour depth Δ and the tailwater depth D, R = Δ + D; see Fig. 13a in [5]). From dimensional analysis, it follows at large scale that $\varepsilon \sim V^{3} /R$ [27], where the symbol “ ~ ” indicates “scales with”. Eddies of large sizes split in successive cascading stages such that for the size l and velocity u_l, the transferring of TKE must be $\varepsilon \sim u_{l}^{3} /l$, which together with $\varepsilon \sim V^{3} /R$ leads to the Kolmogorov-Taylor scaling in the inertial sub-range [38]:

$$ u_{l} \sim V\left( {\frac{l}{R}} \right)^{{1/3}} $$

(1)

This relation is valid for l/η >  > 1, where η is the Kolmogorov length-scale ($\eta = \nu ^{{3/4}} \varepsilon ^{{ - 1/4}}$, with ν as the kinematic viscosity of water).

By equating the production of TKE driven by the jet, whose power per unit thickness is P in 2D, or its power (also P) in 3D, to the rate of dissipation of turbulent energy within the scour hole, we obtain for the 2D and 3D conditions, respectively ([3,4,5, 18]:

$$ V\sim \left( {\frac{{qgh}}{R}} \right)^{{1/3}} $$

(2a)

$$ V\sim \left( {\frac{{qgh}}{{R^{2} }}} \right)^{{1/3}} $$

(2b)

where q is the discharge per unit width in Eq. (2a), and the total discharge in Eq. (2b).

To find a scaling for the shear stress at the interface water column-bed sediment, Gioia and Bombardelli [16], Gioia and Chakraborty [18] and Gioia et al. [19] argued that the shear stress acting on a wetted surface tangent to the peaks of the grains at the scour hole surface S is given by (Fig. 13a of [5]):

$$ \tau = \rho \left| {\overline{{v_{n} v_{t} }} } \right|\sim \rho u_{d} V $$

(3)

in which v_n and v_t are the fluctuating velocity components normal and tangent to S, respectively, the overbar denotes time average, and u_d is the velocity scale of the eddy within the roughness coves. If the lengthscale d is within the inertial sub-range ($\eta \ll d \ll R$), then u_d follows the Kolmogorov-Taylor scaling. Substituting V in Eqs. (2a) and (2b), and setting $u_{d} \sim V\left( {d/R} \right)^{{1/3}}$ in Eq. (3):

$$ \tau \sim \rho \frac{{\left( {qgh~} \right)^{{2/3}} d^{{1/3}} }}{R} $$

(4a)

$$ \tau \sim \rho \frac{{\left( {qgh~} \right)^{{2/3}} d^{{1/3}} }}{{R^{{5/3}} }} $$

(4b)

Palermo et al. [36] corroborated that Eq. (4a) adequately predicts the shear stress in the 2D scour hole.

It is convenient to clarify that other authors, based on arguments coming from Roughness SubLayer (RSL) results, have argued that $\varepsilon ={\alpha}_{2}^{3}{V}^{3}/{R}_{h}$, with α₂ ~ (k_s/R_h)^−1/3f_d^1/2 indicating an ad hoc scaling function depending on the relative roughness k_s/R_h for Reynolds number tending to infinity. Likewise, they have stated that the shear stress at the interface should be also related via an ad hoc function α₁, which scales as f_d^1/2, implying that α₁ should depend on the relative roughness k_s/R_h for Reynolds number tending to infinity [6]. Bonetti et al. [6] reasoned that the scaling Eqs. (7a) and (7b) of [16] should be pre-multiplied by (α₁α₂)^−1/2 when the Manning’s equation wants to be recovered. Notably, Bonetti et al. [6] also argued that Strickler scaling needs to be assumed to obtain a constant value of α₁α₂. From a theoretical point of view, the dependence of α₁, α₂ and α₁α₂ on k_s/R_h is indeed correct. However, for practical applications, it can be shown that the product α₁α₂ is mostly constant, and that α₁ and α₂ can be assumed as quasi constant as well (separately) in the range of interest for granular bed materials (i.e., for R_h/k_s > 50). This result can be obtained without appealing to the Strickler scaling, contrary to what was suggested in [6]. Instead, we need only to assume explicit expressions for the friction factor (for instance, Swamee and Jain [42]) to quantify the dependence of α₁, α₂ and α₁α₂ on k_s/R_h. Such dependence is found to be weak, and the apparent discrepancies may only apply for larger values of k_s/R_h corresponding to cases with large gravels and boulders, which fall outside of the analysis devised in Gioia and Bombardelli [16] and in this study. (Note that for such cases the customary resistance formulas also need modification.) The proposed relationships in this paper have nonetheless been successfully validated for larger relative roughness, as we will show in one of the next sections, by contrasting the field values of the parameter Δ + D pertaining to Missiaga River (8.15 < R_h/k_s < 11.15) with those calculated using the present theoretical approach (Fig. 14). Overall, the analysis of hundreds of field and laboratory data revealed that the corrections proposed elsewhere [6, 9] have a negligible impact on the present theory in terms of practical applications.

4.2 Enforcement of the equilibrium condition

As the size of the scour hole increases, the shear stress decreases until reaching a critical (subscript c) value, τ_c, when the scour process ceases. To obtain a scaling expression for τ_c, we use $\tau _{c} ~\sim ~\left( {\rho _{s} - \rho } \right)gd$ for small to coarse sand [15, 25, 39, 45]. (Note that Coscarella et al. [9] argued that τ_c can be assumed to be independent from slope effects where maximum scour depth occurs.) Imposing the equilibrium (subscript eq) condition, the scaling expressions for R_eq and the 2D and 3D cases with K₀ = 0.3 and K₄ = 0.5 [5] are, respectively:

$$ R_{{eq}} = K_{0} \left( {\frac{\rho }{{\rho _{s} - \rho }}} \right)\left( {qh} \right)^{{2/3}} d^{{ - 2/3}} g^{{ - 1/3}} $$

(5a)

$$ R_{{eq}} = K_{4} \left( {\frac{\rho }{{\rho _{s} - \rho }}} \right)^{{3/5}} \left( {qh} \right)^{{2/5}} d^{{ - 2/5}} g^{{ - 1/5}} $$

(5b)

4.3 Theoretical/numerical models for temporal scour depth evolution in the developed stage

We surmise that Eqs. (4a) and (4b), for the shear stress, and the momentum transfer mechanism assumed from within the granular coves hold true at all times during the scour process. It is worth remarking that this hypothesis was already made in Bombardelli et al. [5] and, by judging the results of the agreement with data in that paper, obtained at the laboratory scale, it allowed the authors to furnish a validated and complete theory. Furthermore, this hypothesis is also implicit in the papers since the seminal work by Bombardelli and Gioia [3]. In such papers, Bombardelli and collaborators reasoned that the “kinetics” of the problem indicate that there is a decrease of the shear stress with the growth of the sum of the original water depth and the scour depth (to different powers for 2D and 3D geometries), including the equilibrium condition.

Then, we follow empirical evidence in the developed phase [5] and argue that the scour hole evolution is approximated as homothetic through a circumference with its center located on the free surface (Fig. 13b in [5]). The area of the scoured material scales with the product of the scour depth Δ, and the length of the semi-axis r, i.e., A ~ Δr. By geometric considerations and leading-order analyses, we obtain for the scoured area $A~\sim ~{\varDelta} ^{{3/2}} D^{{1/2}}$. For the scoured volume ∀, a similar expression is ∀ ~ Δ²D. Considering that the rate of change of scoured area and volume is the source of the volumetric transport rate of sediment, then $q_{s} ~\sim ~\frac{{{\text{d}}A}}{{{\text{d}}t}}~\sim \frac{3}{2}~D^{{1/2}} {\varDelta} ^{{1/2}} \frac{{{\text{d}}{\varDelta} }}{{{\text{d}}t}}$ [m²/s] for 2D, and $q_{s} ~ \sim ~\frac{{\text{d}}\forall}{{{\text{d}}t}}~ \sim 2D{\varDelta} \frac{{{\text{d}}{\varDelta} }}{{{\text{d}}t}}$ [m³/s] in 3D. The amount of scoured material scales with the excess of shear stress over the critical shear stress [13, 15, 25, 37, 41, 45]:

$$ \frac{{q_{s} }}{{\sqrt {\frac{{\left( {\rho _{s} - \rho } \right)}}{\rho }gd^{3} } }}\sim \left( {\frac{\tau }{{\tau _{c} }} - 1} \right)^{{m_{1} }} $$

(6a)

$$ \frac{{q_{s} }}{{\sqrt {\frac{{\left( {\rho _{s} - ~\rho } \right)}}{\rho }gd^{5} } }}\sim \left( {\frac{\tau }{{\tau _{c} }} - 1} \right)^{{m_{2} }} $$

(6b)

The exponents m₁ and m₂ vary in the range 1.5–2 for non-cohesive sediment [15, 25, 37, 45]. Considering the equilibrium condition and re-arranging, we obtain the following equations for 2D and 3D cases [5]:

$$ \frac{{{\text{d}}\varDelta }}{{{\text{d}}t}} = K_{3} \sqrt {\frac{{\left( {\rho _{s} - \rho } \right)gd^{3} }}{{\rho D}}} \frac{1}{{\varDelta ^{{1/2}} }}\left( {\frac{{R_{{eq}} }}{R} - 1} \right)^{{m_{1} }} $$

(7a)

$$ \frac{{{\text{d}}\varDelta }}{{{\text{d}}t}} = K_{7} \sqrt {\frac{{\left( {\rho _{s} - \rho } \right)gd^{5} }}{{\rho D^{2} }}} \frac{1}{\varDelta }\left[ {\left( {\frac{{R_{{eq}} }}{R}} \right)^{{5/3}} - 1} \right]^{{m_{2} }} $$

(7b)

where R_eq = Δ_eq + D, and Δ_eq is the equilibrium scour depth. The results of the analysis conducted by Bombardelli et al. [5] indicate that K₃ = 8, K₇ = 80 and m₁ = m₂ = 1.5. These ordinary differential equations (ODEs) are valid for the developed stage, and mathematically represent an initial value problem (IVP). The initial conditions are extracted from the experimental data at the transition point. Importantly, Eqs. (7a) and (7b) are a function solely of the exponents m and the multiplicative constants K. The solutions to the ODEs were implemented in numerical codes in Matlab using the Euler method. For the analysis of scour evolution data at large scale [26], the equilibrium scour depth was assumed to be equal to the maximum scour depth, Δ_eq = Δ_max (i.e., Δ_max = 0.823 m, 1.015 m, 1.362 m, and 1.180 m for Tests 1, 2, 3, and 4).

5 Model validation with field and laboratory data

As the equilibrium scour morphology was 3D (Fig. 1c), we tested the predictive capability of Eq. (7b) with the data of Kuroiwa [26]. Note that Bombardelli et al. [5] validated their equation in the developed phase, stating that their theory has “good prediction capabilities in the developing phase as well” (see Fig. 21 in [5], which compares the model predictions with the experimental data of Stein et al. [41]). Thus, in the present study, we validated our equation including the entire dataset pertaining to both phases. Namely, we numerically solved Eq. (7b), and assumed as initial (subscript in) and equilibrium conditions the first measured scour depth value Δ_in at time t_in (e.g., Δ_in = 0.302 m and t_in = 2820 s for Test 1, Table 1) and the maximum scour depth (Δ_max) measured at test end (e.g., Δ_max = 0.823 m and t_test = 6840 s for Test 1, Table 1), respectively. In Figs. 7 and 8, we compare model predictions with the experimental data relative to the position where the maximum scour depth occurred. To that end, both d₅₀ and d₉₀ at t = 0 s (original granulometric characteristics), and at t = t_test (final granulometric characteristics) were used. Note that in our computations the identical multiplicative constants obtained by Bombardelli et al. [5] were used and that both constants could have been adjusted to improve the agreement with data, as shown in Fig. 7, where we also report the model prediction obtained using m₂ = 1 and K₇ = 250 (dashed lines). But we decided not to do this to obtain a generalized model.

Fig. 7

Numerical solutions Δ/Δ_max versus t/T_r* of Eq. (7b) using d₅₀ and d₉₀ at t = 0 s, K₇ = 80 and m₂ = 1.5 (continuous lines, coefficients by Bombardelli et al. [5]) and K₇ = 250 and m₂ = 1.0 (dashed lines, modified coefficients) against experimental data by Kuroiwa [26], pertaining to position of maximum scour depth

Fig. 8

Numerical solutions Δ/Δ_max versus t/T_r* of Eq. (7b) using d₅₀ and d₉₀ at t = t_test against experimental data by Kuroiwa [26], pertaining to position of maximum scour depth

As shown in Fig. 9a, the theoretical model predicts satisfactorily the experimental data (R² = 0.90 for Test 1, R² = 0.73 for Test 2, R² = 0.97 for Test 3, and R² = 0.94 for Test 4). Notice, however, that the model performs better when using both d₅₀ and d₉₀ at t = t_test. Furthermore, the value of d₅₀ at t = t_test is close to that of d₉₀ at t = 0 s. Once again, this occurrence confirms the findings of Hoffmans [23] and Pagliara et al. [34], and highlights the effect of the granulometric characteristics variation on the scour dynamics for non-uniform material.

Fig. 9

Comparison among measured and calculated values (with Eq. 7b) of Δ(t) for a tests of Kuroiwa [26] using d₅₀ and d₉₀ at t = 0 s and b Tests 1 and 2 with PK weir

We further corroborated our theoretical model for temporal scour depth evolution with data relative to special tests conducted with a PK weir. Also for this structure typology, the distinction between two phases characterizing the temporal evolution (developing and developed) results to be consistent with that found for jet scour processes. In addition, the transition time t_T is well predicted by the equation proposed by Bombardelli et al. [5]. Once again, in Figs. 10a and b we show the two very distinct phases characterizing the temporal scour depth evolution before reaching the equilibrium configuration asymptotically. The developed phase was characterized by an almost homothetic expansion of the scour hole, thus corroborating the basic assumption of the model. We also validated our theory by contrasting numerical solutions of Eq. (7b) against experimental data pertaining to position of maximum scour depth (Fig. 10c and d). To do so, we numerically solved Eq. (7b), assuming as initial and equilibrium conditions the first measured scour depth value Δ_in for t > t_T and the maximum scour depth Δ_max measured at test end, respectively. In Fig. 9b, we show the comparison among measured and calculated values (with Eq. 7b) of Δ(t) for Tests 1 and 2 with PK weir (R² = 0.85 for Test 1 and R² = 0.81 for Test 2). Note that up to 9 scour depth measurements were taken during the developed phase and the predicting capability of the proposed theory is very good (the deviation with respect to perfect agreement is less than 10% for all data points).

Fig. 10

Scour depth evolution Δ(t) for Tests a 1 and b 2 with PK weir. Numerical solutions Δ/Δ_max versus t/T_r* of Eq. (7b) against experimental data pertaining to position of maximum scour depth for Tests c 1 and d 2 with PK weir

We also assessed the prediction capability of Eqs. (5a) and (5b) for the equilibrium condition. As mentioned, a significant amount of laboratory and field data, encompassing a large variety of structures and hydraulic configurations was considered. The experimental data of Hallmark [21] and Thomas [44] were compared against those computed by using Eq. (5b). The result is shown in Fig. 11 (R² = 0.65 for data by Thomas [39]—Series 1, R² = 0.69 for data by Thomas [44]—Series 2, and R² = 0.61 for data by Hallmark [21]). Regardless of sediment gradation and the tailwater depth, our theoretical equation predicts the experimental data reasonably well, considering the complexity of the phenomenon, the basic model assumptions, and the uncertainty in large-scale observations. Furthermore, this shows that our equilibrium equation is not affected by the sediment size non-uniformity, as its predicting capability is essentially the same for both uniform and non-uniform bed material.

Fig. 11

Comparison among measured and calculated values (with Eq. 5b) of variable Δ + D (data by [44]—Series I and II and [21])

Similar considerations apply to the data of D’Agostino [10]. Also, in this case, the equilibrium morphology is 3D, as the weir width is much smaller than the channel width. In Fig. 12a, we show the comparison among measured and calculated values of the parameter Δ + D for W₀/B = 0.3 (R² = 0.81) whereas Fig. 12b applies to W₀/B = 0.6 (R² = 0.83). Our equation performs better for data with W₀/B = 0.3, because for lower values of W₀/B the equilibrium morphology is fully 3D and a surrounding ridge generally forms. As W₀/B increases, the equilibrium morphology three-dimensionality reduces as the scour hole can reach the channel walls and the ridge only forms downstream of it. Nonetheless, our equation shows a good predicting capability for both cases, especially if we consider that the deviation with respect to perfect agreement of almost 90% of the experimental data for W₀/B = 0.6 is smaller than 30%.

Fig. 12

Comparison among measured and calculated values (with Eq. 5b) of variable Δ + D (data by [10, 11]) for W₀/B = (a) 0.3 and (b) 0.6

As to the study of Falciai and Giacomin [12], we should expect a 2D equilibrium morphology downstream of a check dam. But, as clarified above, the equilibrium morphology could be either 3D or (quasi-) 2D. Therefore, in Fig. 13a we compare the measured data with those computed using Eq. (5a) (R² = 0.68) and in Fig. 13b we show the same comparison using Eq. (5b). Although Eq. (5a) performs better, it slightly underestimates the field data, while an over-estimation occurs when applying Eq. (5b). This behavior is reasonable due to the mentioned irregularities of river geometry and mobile bed. In this particular case, it would seem that an intermediate bed morphology occurred. However, it is noticeable that most of the data are predicted reasonably well by Eq. (5a), despite the uncertainties characterizing the in-situ equilibrium morphology.

Fig. 13

Comparison between measured and calculated values of variable Δ + D with a Eq. (5a) and b Eq. (5b) (data by [12])

The same considerations apply to field measurements taken in Missiaga River. In contrast to the rivers monitored by Falciai and Giacomin [12], Missiaga River is located in a mountainous region characterized by a steep slope (≅ 15%) and irregular non-prismatic cross-sections. Therefore, the equilibrium morphology downstream of monitored check dams is reasonably assumed to be 3D. In Fig. 14, we compare measured and calculated values using Eq. (5b) for the parameter Δ + D (R² = 0.82). The proposed comparison reveals that also in this case our equation is able to predict the field data well.

Fig. 14

Comparison between measured and calculated values (with Eq. 5b) of variable Δ + D (Missiaga stream, data available in [11])

All previous comparisons highlight that our theoretical model is able to predict the scour process and its evolution for a large range of hydraulic conditions and structural configurations (see also Appendix). Furthermore, our analysis underscores that scale effects do not affect the predicting capability of our equations, which work well despite the variety of in-situ conditions, including the granulometric characteristics of the bed material, the scour hole geometry and the hydraulic conditions.

6 Conclusion

This study presented a critical validation of a theoretical model for the time-dependent scour evolution in a large range of hydraulic and geometric configurations. The hydraulic structures analyzed encompass weirs located in laboratory flumes (small-scale tests) as well as check dams in natural water courses (large scale).

It appears to be the first time that a fully theoretical methodology is applied to predict the scour evolution. Very importantly, our analysis reveals that the distinction between the developing and the developed phases at large scale is consistent with the laboratory scale findings. In addition, our theoretical model predicts the entire scour evolution process well, regardless of the bed sediment gradation, tailwater depth and the exact plunge pool configuration. The predicting capability of our theoretical model is not affected by the material non-uniformity for both the developing and the developed phase. The equations were additionally tested for the equilibrium condition using both laboratory and field data. Despite the complexity and heterogeneity of in-situ configurations, our theoretical model reasonably predicts the entire database. (The equilibrium morphology of natural water courses cannot be easily predicted.) This study furnishes additional verification of the validity of the approach based on the PTT for the scour problem using a few, unique model constants!

Appendix: validation of equilibrium formulas with scour data downstream of large dam

Our relation was tested to estimate the equilibrium scour depth downstream of Cabora–Bassa Dam (Mozambique) by comparing the measured and computed values of R_eq after a flood event. Based on the above definition, the scour is considered 3D, thus Eq. (5b) applies.

Following Breusers and Raudkivi [8], the flood event was characterized by a discharge Q = 13100 m³/s, h = 100 m, d = 2.1 m and ρ_s = 2400 kg/m³. By substituting these values into Eq. (5b), R_eq,calc = 53.8 m. As the measured value was R_eq,meas = 68 m, the percentage difference is e_% = 100[(68 − 53.8)/68] ≈ 21%. Note that our theoretical equation performs better than most well-known and largely adopted empirical equations (see Table 6.1 in [8]).