1 Introduction

Each year, over 107 kg of material enters the Earth’s atmosphere, mostly composed of particles less than 1 mm wide (Love and Brownlee 1993; Ceplecha et al. 1998; Mathews et al. 2001; Janches et al. 2006). As these meteoroids pass through the atmosphere, they ablate atoms that ionize. HPLA radars can detect the surrounding plasma, called a head echo, at altitudes between 70 km and 140 km (Close 2004). Interferometric HPLA radars, such as the 50 MHz radar at JRO, accurately measure meteoroid trajectories and velocities. Meteoroid characteristics, such as mass, can be calculated from these measurements.

Using conservation of momentum, we find an expression for the meteoroid mass m:

$$ \frac{m} {A} = - v\gamma \rho _{{{\text{air}}}} \sec \chi {\left( {\frac{{dv}} {{dh}}} \right)}^{{ - 1}} $$
(1)

where A is cross sectional area, v is meteoroid velocity, ρair is air density, χ is zenith angle, dv/dh is the rate of change of the meteoroid’s radial velocity with altitude, and γ is the drag coefficient. There are two challenges in applying this relationship. First, various parameters are not precisely known but can be estimated to within a factor of four. The second problem is determining dv/dh. Often, a function is fitted to the data, in range versus time or velocity versus time, in order to determine the deceleration. This function may be a polynomial, such as a line (Janches et al. 2000), or an exponential function (Close et al. 2005). In many cases, the mass calculation produces unphysical results, yielding masses that increase with time instead of decrease (Close et al. 2005).

In this paper, we demonstrate that fitting a polynomial to velocity measurements using artificial data generated by the ablation model outlined in Lebedinets et al. (1973) and Rogers et al. (2005) produces inaccurate results. In addition, we show that polynomial fits to real data yield different solutions depending on the order of the fit. Finally, we show that one obtains more physically plausible masses by fitting observational data to the ablation model.

2 Using Model Data to Calculate Mass

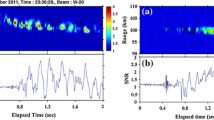
The model used to generate the artificial data involves a system of ordinary differential equations that relate the rate of change of meteoroid mass, velocity, and temperature using values from Rogers et al. (2005). This system is solved at each time step using a Runge-Kutta method. The solid lines in Fig. 1 indicate the resulting mass and velocity values.

Fig. 1
figure 1

Model data and polynomial fits (left) and mass calculations (right)

Full size image

To determine the range over which the meteor would be observed, a simple signal strength model was created, discussed in Close et al. (2004). Signal reflection was assumed when the plasma frequency of the head echo exceeded the radar frequency. We added noise to our theoretical signal and used the values as a way of weighting the ideal data when fitting a polynomial.

We made multiple polynomial fits to our ideal data in order to test the accuracy of a given fit. Meteoroid mass was then calculated from each fitted function. Figure 1 shows the fits and calculated masses. Low-order fits gave unphysical results. A mass that decreases with altitude required a fourth order polynomial fit to the model data. Second and third order fits appear to correspond to the model data, but produce unreasonable mass estimates.

These results highlight the fact that an unphysical mass estimate does not necessarily mean there is a problem with the data. This shows that unphysical results could be obtained from head echo data because of poor velocity fitting, not the data itself. This conclusion becomes stronger when we evaluate the effects of polynomial fitting on real data in Sect. 3.

3 Fitting Data to Model

Another approach to calculating meteoroid mass is to fit the data to the ablation model itself, instead of fitting a function to velocity measurements.

To find the most accurate meteoroid characteristics, we run the simulator repeatedly until we find initial mass and velocity values that minimize the difference between the altitude and velocity measurements from our data and the model. Figure 2 compares the polynomial and model fitting results. An unphysical mass is found each time with a polynomial fit. While the maximum value in the third and fourth order fits is only a factor of ∼4 greater than the model result, the increase and subsequent decrease in mass may lead an observer to discard the data. With higher order fits, noise has a greater effect, changing the velocity derivative and estimated mass. The model provides a reasonable mass estimate and a physically realistic mass along the entire trajectory, with the mass decreasing at all times.

Fig. 2
figure 2

Data with different fits (left) and the resulting mass calculations (right)

Full size image

4 Conclusions

As demonstrated in Sect. 2, Eq. 1 is highly sensitive to the velocity derivative, and small changes in a polynomial fit can greatly affect the resulting mass estimate. Fitting an ablation model to the data allows us to obtain a mass estimate for some cases where a polynomial fit produced unphysical results. We expect that this technique will help researchers make more accurate mass estimates and utilize a greater portion of their data.