In our study, we aimed to create new ways through which young children might experience the mathematical notion of dimension. We show how children as young as 10 years of age were able to work creatively and imaginatively in a three-dimensional (rendered in 2-D) computer-based drawing environment. We analyse the properties of the tools and tasks within that environment that seemed to trigger novel expressions of dimension.

First, though, we need to consider how dimension is encountered informally in everyday settings and formally in scientific ones.

Dimension as a Quality of Object and Space

Our experiences of dimension are in some sense differentiated between a lived-in, unformalised world and an artificial mathematised world, where aspects of space are expressed, for example, in terms of geometry and dimension. For instance, in mathematics, dimension is a powerful mathematical construct integrated within co-ordinate geometry, topology, vectors, projective geometry, statistics, graphs, and calculus (Banchoff 1990). At the same time, children already have an idea of geometry and dimension before entering primary school. Estimating how much water will fit in a glass, cutting enough paper to cover the presents, or drawing their house and family are just some of the many situations in which children experience dimension, though unaware of the mathematical connection.

In everyday life and in scientific endeavour, dimension is sometimes referred to as a quality of an object. For example, in everyday life, dimension might be used to describe the size of a box as, say, 15 cm by 10 cm by 5 cm or a 3-D television. In mathematics, dimension might refer to a line as one-dimensional and a filled-in square as two-dimensional.

On the other hand, dimension might be considered as a quality of space. For example, even in everyday life there is talk of 3-D space. In mathematics, dimension might be expressed as a quality of space by using co-ordinates to locate a given point in space (a Cartesian approach). Roughly speaking, the dimension of a space is the minimum number of co-ordinates needed to specify every point within it. Similarly, in vector geometry, the dimension of a vector space V is the cardinality (i.e. the number of vectors) in a basis of V. In other words, its dimension can be expressed as the least number of linearly independent vectors needed to span the space.

In fact, the qualities of object and space easily become blurred. A line can be considered as a one-dimensional space if we think about a point moving on it, because there is only one direction in which the point can move (regarding back and forth as positive and negative movements in one direction). The same line, however, can exist in a plane and might then be expressed as a relationship between two variables (x, y). In the first case, the line is a space and in the second it is an object within a higher dimensional space.

From another perspective, dimension portrays qualities of both freedom and capacity. There is a sense in which space/objects with greater dimension have the capacity to incorporate space/objects of lower dimensions: for instance, a plane can ‘house’ both a line and a point. At the same time, a freedom quality is expressed by recognising that the greater the dimension of a space/object, the more degrees of freedom for movement lie within that space/object.

Children’s Experience of ‘Dimension’

Although much research has been conducted on the teaching and learning of geometry, most of this research refers either to general facts of geometric thinking (e.g. Fujita and Jones 2002; Gravemeijer 1998; Gutiérrez 1996) or specifically to two-dimensional geometry (e.g. Clements et al. 1999) or three-dimensional geometry (e.g. Pittalis and Christou 2010). In other words, little research has been conducted explicitly on dimension. Nevertheless, the relationship, or ambiguity, between material and theoretical interpretations of geometry and dimension is a recurrent theme in the literature. For instance, geometric objects such as lines and planes are treated in the everyday world as if they can be observed in reality, but they have a theoretical instantiation in mathematics.

Although geometry deals in abstractions as much as any other branch of mathematics – points, lines, and planes are just as much things of the imagination as are polynomials – it is natural to relate visually to geometric objects. (Goldenberg et al. 1998, p. 21)

This ambiguity leads to misinterpretations of representations. These misinterpretations occur mainly because it was not evident for the students that representations present a loss of information and “that the drawing cannot, by itself, substitute for the object” (Parzysz 1988, p. 85). Parzysz identified two main problems of representations: encoding (i.e. producing) representations and decoding (i.e. reading) representations. In terms of coding representations, when he asked sixth-grade students to represent a square-based regular pyramid in a 2-D drawing, he noted that:

For these pupils, there is actually no conscious and deliberate choice of a perspective, as well as a position of the object which ‘presents in order to see’, but a use – more or less important and more or less empirical – of perspective effects, with a concern for preserving some properties of the object. (p. 90)

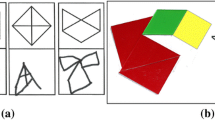
Difficulties exist also while decoding representations, especially when “interpreting two-dimensional diagrams of three dimensional objects” (French 2004, p. 21). French gave an example of a cube that can be equally seen as a two-dimensional picture of a hexagon (Fig. 1).

Fig. 1
figure 1

A cube or a hexagon?

Full size image

As Parzysz (1988) noted, students confuse the drawn 3-D figure with a 2-D figure having the same representation, arguing that this happens because, “what ones knows of a 3D object comes into conflict with what one sees of it” (p. 84). In their longitudinal study of children’s reasoning about 2-D figures and 3-D solids, Lehrer et al. (1998) concluded that children tend to relate to known figures (e.g., “looks like a pushed-in rectangle”) and view figures dynamically (morphing via non-rigid transformations by ‘pushing’ or ‘pulling’ at vertices). In contrast, the 2-D representations create a static and restricted view of shapes, one that conflicts with the dynamic perceptions that students already have about the subject.

Problems of decoding were also recorded when students tried to make sense of space in a representation. Parzysz asked sixth-grade students to state which points are located on the plane below (see Fig. 2, reproduced from his paper) and found that, “if the representation of the point is interior to the representation of the plane, then the point itself is seen as belonging to the plane” (p. 83).

Fig. 2
figure 2

Which points are on the plane P?

Full size image

The above articles suggest that static representations can restrict students’ dynamic perspective of shape and space and, as a result, impede the development of students’ ability for dimensional deconstruction, the analytical breaking down of a solid object into interrelated parts based on relationships (Duval 2005; Laborde and Laborde 2011), as reflected in studies showing the limitation in young students’ judgements of volume by ignoring some vital dimensions.

Piaget (Piaget 1968; Piaget et al. 1960) recognised that primary school children appeared to use only the height of the container when making volume judgments: for example, these children thought that the volume had been reduced when the liquid was poured into a wider glass. Raghubir and Krishna’s (1999) explorations showed that these difficulties continue to exist even in some adults. They observed that when trying to estimate the volume, people’s judgements are likely to be based on one or two dimensions only. This study revealed that perception of volume is mostly influenced by ‘height’ on its own or in a combination with ‘width’. Consequently, taller shapes are perceived as larger than shorter ones, without reference to their other dimensions.

Similar to these studies, but based on explorations of the notion of definition within mathematics, Morgan (2005) argued that students and teachers identify dimension with regard to ‘thickness.’ Her study also showed that they construct “a multi-faceted notion of dimension” (p. 104), including (among others) a description of 2-D as ‘flat’ and 3-D as ‘solid’, and considering 3-D as having something extra compared with 2-D. Additionally, Lehrer et al. (1998) found that students describe 2-D and 3-D shapes in the same manner. They pointed out that children tend to view 2-D and 3-D figures as ‘slanty’ or ‘pointy’, count sides or vertices, or “describe figures in terms of other properties such as parallelism remained stable” (p. 144).

The above studies offer some evidence that the way 2-D and 3-D shapes/spaces are represented and experienced forms students’ construction of the notion of dimension. Panorkou (2011) presented supporting evidence when she studied 10-year-old students’ experiences of dimension by means of three approaches: (i) using the software Elica (http://www.elica.net/site/museum/dalest/dalest.html); (ii) using a sorting task employing physical objects (a variety of 2-D and 3-D shapes that students had to sort and discuss in terms of their similarities and differences); (iii) through discussion based on the film Flatland (Travis 2007). This study showed that students talked of dimension in five specific ways: (i) as a type of measurement (e.g. the more vertices or edges an object has, the greater its dimension); (ii) as a domain incorporating shapes (e.g. dimension is a ‘place’ with different shapes); (iii) as an object having material attributes (e.g. the greater the dimension, the thicker the object); (iv) as a property for distinguishing between 2-D and 3-D shapes (e.g. a square could be in 2-D and a cube could be a square seen in 3-D); (v) as creating a hierarchy of relationships among shapes (point \( \subset \) line, line \( \subset \) square, square \( \subset \) cube). The current study took place shortly after the one reported above and so the five specific ways of talking about dimension provided a basis for knowing which meanings students might have about dimension.

It is instructive to note that some elements of how ‘dimension’ is used in scientific endeavour were absent from, or not clearly articulated in, students’ expressions of dimension in the Panorkou study. In particular, she argued that children sometimes talked of dimension as if it were a property of objects, while at other times they referred to it as a property of space, without indicating any appreciation of the flexibility between the two. What is more, the design of the three settings (Elica, physical objects, Flatland) did not offer opportunities for the students to actively experience dimension as a quality of freedom and capacity. Yet, the frequency of generating expressions of dimension belonging to a specific type was dependent upon the task on which the individuals were working, thereby acknowledging the significance of the setting in shaping the creation of those expressions.

The significance of the setting to the formation of experience about shape and space was also noted by Ferrara and Mammana (2014), who argued that students’ experiences with 2-D and 3-D shapes based on physical manipulation prevent them from discovering the crucial relationships between 2-D and 3-D geometric figures. They pointed out that, “the visual and cognitive potential of interlacing related but different figures is offered by the use of DGEs, allowing for moving back and forth between plane and space” (p. 57). In exploring quadrilaterals and tetrahedra with high-school students utilising Cabri 2D and 3D, they noted that the environment of the software:

encouraged the students to take on multiple perspectives, as if they were taking on various physical positions from which to see a figure, as bodily projecting themselves both beyond and around it. So, they engaged the students in dynamic visual experiences with the diagrams, effecting new kinds of vision that pushed them towards a search for similarities and differences, invariants and changes, between quadrilaterals and tetrahedra. This engagement spoke directly to students’ enhanced visual skills, so that they not only came to see the quadrilateral as a tetrahedron, but also to see them, when thought of as represented in a diagram, as ‘the same thing’. (p. 64)

This study illustrated the power of digital environments, such as Cabri 3D, for developing dynamic experiences of shape and space. Indeed, we recognise in what Ferrara and Mammana call ‘interlacing related but different figures’ and ‘moving back and forth between plane and space’ the flexibility to view geometric entities as objects or spaces and the qualities of freedom or capacity. We conjecture that enhanced flexibility might lead to greater facility in encoding and decoding representations and that new specially designed settings might offer experiences to support such flexibility. More precisely, our research questions asked: (i) What new meanings for dimension might young students articulate, beyond the five specific ways listed above? (ii) How do the features of the setting support these novel meanings?

A Framework for Researching Dimension

The idea of researching ‘experience’ derives from an acknowledgment that, although it is not possible to gain direct access to a child’s mind, it is possible to observe their experiences. We might interpret experience as a realistic articulation of thinking. While experience is evident, thinking – from the researcher’s perspective – is an inference. From the perspective that even very young children might have experiences of dimension (experiences that might be seen by expert others as situated roots of sophisticated mathematical concepts), we set out to identify a setting which might offer experiences of dimension that could trigger the articulation of new meanings for dimension. While we recognised that the articulation of such meanings would not provide evidence that the children ‘understood’ dimension, our primary objective was to understand how such meanings could be shaped by appropriate tools in the setting.

By providing new tools, we hoped that students’ understanding of dimension could be perturbed, an action referred to as ‘thinking-in-change’ by Noss and Hoyles (1996). They regard the setting for these perturbing tools as a ‘window’ through which the researcher is able to examine the thinking process. We have seen how thinking about dimension is sensitive to the context, so in our study the design of the ‘window’ was critical. We have interpreted Ferrara and Mammana as proposing that the affordances of digital technology can offer the flexibility we sought to move between plane and space, so that the child might code or decode representations as either an object’s freedom to move within a space or the capacity of a space to house an object. We now wish to be more precise at a theoretical level about how the use of digital tools might support enhanced flexibility.

The integration of computers into students’ learning has been described as a complex process involving instrumental genesis (Verillon and Rabardel 1995), a dialectical process comprising of how an individual assimilates an artefact (instrumentation) and how the specific artefact is transformed for specific uses (instrumentalisation). The result of instrumental genesis is the “construction of personal schemes or, more generally, the appropriation of social pre-existing schemes” (Artigue 2002, p. 250). However, this process does not necessarily produce individual understanding and ways of working that align to standard mathematics and can be described by the general notion of ‘scheme’.

Following Hoyles et al. (2004) view that there is a need for describing and validating computationally mediated mathematical abstractions that can diverge from standard mathematical norms, we were interested in this study in how students articulate connections between them and the setting in which they explore and develop meaning. In other words, our focus was on the process of abstracting knowledge within the specific context, an idea described by Hoyles and colleagues as webbing:

the process of abstraction of mathematical properties and invariants that is key, and this is necessarily both situated and shaped by the tools being used, the users’ relationship to the tools – including whether the users judge them to be expressive of their developing mathematical meanings – and ultimately whether these meanings are valued and judged by the community (e.g. the classroom) to be mathematical. (p. 314)

Building on the idea of webbing, Noss and Hoyles introduced the notion of situated abstraction, in order “to describe how learners construct mathematical ideas by drawing on the webbing of a particular setting which, in turn, shapes the way the ideas are expressed” (Noss and Hoyles 1996, p. 122). They refer to situated abstractions as generalisations that students form in order to act in specific mathematical contexts (Hoyles and Noss 1992), consequently embedded in the particular context in which they took place. The main idea underlying the notion of situated abstractions is that:

conceptions of mathematics might be situated – in terms of language and connectivity and with the context of their genesis, means of expression and use (that is, with the artefacts, goals and discourse that form part of the activity) – and yet are abstract in that they extend beyond immediate concerns to more general conceptions of knowledge, that is, they can be ‘mapped onto’ parts of formal mathematics. (Hoyles et al. 2004, p. 312)

Adopting the theoretical framework of webbing and situated abstractions, we refer to the enhanced flexibility that we seek as the expansion or refinement of the child’s contextual neighbourhood of situated abstractions for dimension, where the contextual neighbourhood “captures the domain over which the idea has been encountered and found to be powerful by the child in explaining the on-screen behaviour” (Pratt and Noss 2010, p. 94). (Unfortunately, there is scope for confusion in this use of terminology. The reader will note later that our tasks involved the children in building a neighbourhood consisting of streets and buildings so we will refer to ‘contextual neighbourhood’ as ‘c.n.’ for the remainder of the paper to avoid confusion over the use of the term ‘neighbourhood’.)

We also recognised the significance of feedback within the window in response to student activity. Feedback is believed to be one of the most significant aspects of the qualities of a window, as it increases “the likelihood that children would identify the lack of explanatory power of their fragmented knowledge pieces in certain situations” (Pratt and Noss 2010, p. 90). As Healy and Hoyles (2002) have argued, “guided by the visual feedback resulting from their programming activity, users can edit or debug their symbolic constructions until they are satisfied with their final product” (p. 236). This is where learning and expansion of c.ns occurs.

Another critical element of the design of the window lies in its capacity to support expressiveness by the students (diSessa et al. 1995; Hoyles and Noss 2008). A window can be expressive in the sense that it can present abstract mathematical ideas in a concrete form. In this study, the window needed somehow to embed the notion of dimension to support a concretising of dimension by the student (Wilensky 1991). We intended that students would express their ideas about dimension and use feedback to develop the c.n. across which dimension made sense. At the same time, such expressivity would make the students’ ideas more ‘observable’ to the researcher.

With the two key criteria of feedback and expressivity in mind, we chose the software Google SketchUp (http://sketchup.google.com/) as a suitable environment for such young students to experience dimension as capacity of an object or freedom within a space. We can now be more precise about our research questions:

  1. a)

    What new scientific meanings for dimension might young students articulate beyond the five specific ways listed above when using the technological tool Google SketchUp?

  2. b)

    How do the constraints and affordances of Google SketchUp shape thinking-in-change about dimension?

The Opportunities and Constraints of Google SketchUp

Our choice for using SketchUp was influenced both from the geometry that the design of SketchUp embeds, but also from the ways that the environment supports students’ perceptions of the key features of this geometry. Our decisions were based on Jones et al. (2010) analysis of principles for designing digital technologies, which are based on, “how the opening software screen both orients the user to 3D space, and provides a framework for the creation of 3D figures and structures” (p. 53). These principles include: a) the way(s) objects ‘look’ on screen pointing to the idea of perspective; b) the way(s) objects can be constructed, manipulated and dragged using a mouse.

In SketchUp, the basic window is coloured green and light blue in a way to represent the ground floor and sky. There are three axes by default: the red, blue and green axes. They are mutually perpendicular and their extensions are marked with dotted lines (negative direction). There is also a person standing ‘on the ground’, the latter being defined by the red and the green axes (see Fig. 3).

Fig. 3
figure 3

Examples of 2-D and 3-D neighbourhoods in SketchUp

Full size image

After exploring the software further, we decided to create an open task for the students, in order to provide them with the opportunity to explore different features of SketchUp. The aim of the task was for students to use it in order to build a neighbourhood, in that way modelling a real-world phenomenon (Noss and Hoyles 2006; Simpson et al. 2005) and providing opportunities for the students to resolve illusions articulated as errors in coding and decoding when modelling a 3-D world on a 2-D screen.

In designing the learning task, we considered the affordance of the environment to motivate the students to create their own structures. Our notion of structure was based on Jones et al.’s (2010) observations in Cabri 3D:

Such structures included models of ‘real-world’ objects and/or objects that moved, with the creation of such structures necessitating the use of a range of mathematics. […] For instance, in order for an object to have a particular visual property when viewed from all angles (such as a segment being perpendicular to the base plane), the object needs to be constructed using the mathematical tool which creates the desired relationship. (p. 56)

Similar to the notion of mathematical tool mentioned above, SketchUp incorporates what we came to call dimensional tools, tools whose use was likely to raise opportunities for expanding or refining the c.n. of situated abstractions for dimension. These tools have an expressive power (Abelson and diSessa 1986), in that the students used them to build their ideas about a neighbourhood and they provided constructive feedback to the user in the way that they were rendered on the screen according to their orientation and connectivity to other objects on the screen.

The dimensional tools of SketchUp addressed both formal and informal ideas of freedom and capacity. Informally, playing with the tools opens up ideas about space containing equal- or lower-dimensional objects, generated by combinations of those objects. For example, in SketchUp the user can create line segments parallel to the three axes using the Line Tool. The colour of these segments mirrors the colour (blue, red, green) of the axis to which they are parallel. To create a 3-D shape (e.g. a cube), the user has to utilise all three different colours of line segments (blue, red, green) in order to give length, width and height to the cube. Informally, the user might recognise that a cube can be created by an appropriate combination of one-dimensional line segments. The role of the ‘dimensional’ tools incorporated into SketchUp was to make those mathematical ideas apparent. In other words, it became the communication medium between the students and the researcher’s intentions, by making “visible its operations and how they are integrated with the embedded context” (Orhun 1995, p. 310).

In setting out the designer’s perspective on how SketchUp might contribute to the expansion or refinement of the child’s c.n. for dimension, we detail four of its most significant tools (for our purposes). For each tool, we discuss expressivity and feedback and then identify the situated abstractions for dimension that might be articulated by students while working with those tools. It is perhaps worth mentioning that the techniques described, though difficult to express in writing, became quite intuitive for the students through use.

Line Tool

With regard to expressivity, students used the Line tool to render lines, thus creating 2-D shapes that would perhaps represent buildings or streets in their neighbourhood. In relation to feedback, while drawing, the colour of the line changes to mirror that of any parallel axis (red, blue or green) (Fig. 4). If a line is drawn that is not parallel to any of the default axes, then it is given a black colour.

Fig. 4
figure 4

The Line tool

Full size image

The Line tool facilitates the user in creating line segments in different positions or directions and with various orientations in space. It also gives the opportunity to the user to create one-dimensional objects in three different spaces (planes), therefore embedding the object-space duality of dimension with the idea of freedom to move and capacity to house. Our conjecture was that, by creating objects/spaces with the line tool, the child’s attention would be drawn to the relationship with the axes, perhaps leading to an expansion or refinement of the child’s c.n. of situated abstractions for the directional, positional and orientational aspects of dimension.

Shaded Surfaces Tool

This tool is an extension of the Line tool. Expressivity: students could create a surface by drawing a closed loop of edges using the Line tool, perhaps to render walls of a building. Feedback: if this loop of edges is co-planar, the surface created is shaded. If not shaded, at least one of the edges belongs to another plane (Fig. 5).

Fig. 5
figure 5

The Shaded Surfaces tool

Full size image

Furthermore, as soon as a closed co-planar shape is created, its surface is shaded light grey, dark grey or white (see Fig. 6), according to its position in terms of the plane on which the surface is situated.

Fig. 6
figure 6

Dark grey, light grey and white shapes

Full size image

This tool incorporates not only the object–space duality as discussed above for the Line tool, but also the notion of generating and positioning surfaces. For instance, to create a 2-D shape, a student needed to use line segments in two different directions whereas a 3-D shape required line segments in three directions, possibly one parallel to each of the three different axes. If the line is not coloured, it is not parallel to an axis and thus impedes the creation of surfaces. If a shape was created by edges which were not co-planar, then it did not have a shade, and also:

  1. (a)

    it could not be coloured afterwards using another tool (not detailed here);

  2. (b)

    it could not be pushed/pulled into 3-D (see Push/Pull tool below).

We conjectured that the limitations of this tool offered debugging opportunities (Edwards and Benedickt 1995; Papert 1980) for the children to identify and fix problems. We anticipated that such debugging might lead to expansion or refinement of the c.n. of situated abstractions for the cardinality of dimension.

Orbit Tool

Expressivity:

students used the Orbit tool to ‘move’ in 3-D space. Orbiting is like holding an object and turning it around. When using this tool, the user clicks and holds the mouse button and moves the mouse around. Where the user’s cursor is on the screen, it will be the centre of rotation. Feedback: the Orbit tool enables experience of co-planarity or lack of it. Students used the Orbit tool to move their object around and see whether the loop of edges they created was co-planar.

In SketchUp, while moving with the Orbit tool, first the user defines the height (up–down) of rotation and then drags towards an arbitrary direction. If the height remains fixed, then a plane of rotation is created. However, usually the height changes because of the unsteady use of the mouse. In addition, since the orbit tool changes the position of the eye relative to the object, the user sees the object from different perspectives. As well as being a key tool for noticing encoding or decoding errors, we conjectured that use of the Orbit tool might lead to the expansion or refinement of the c.n. of situated abstraction for the plane of rotation and perspective.

Push/Pull Tool

This tool extrudes a 2-D shape into three dimensions in a direction that is perpendicular to the surface. Expressivity: students used this tool for creating 3-D buildings in their neighbourhood by pushing and pulling 2-D surfaces. 2-D surfaces can be created by using the Line tool (as described above) or by using specially designed tools for creating rectangles and circles respectively. Surfaces are extruded along a direction parallel to the red, green or blue axes (normal to the plane being extruded). Feedback: when extruding a circle, for example, the colour of the cursor showed the direction in which the extrusion would go, using the Push/Pull tool. For instance, if the cursor were blue, that means that the extrusion would go in the direction of the blue axis (Fig. 7), as this is normal to the plane being extruded.

Fig. 7
figure 7

Example showing Push/Pull tool

Full size image

The Push/Pull tool emphasises movement between the plane and space, proposed as an important affordance of digital technology by Ferrara and Mammana (2014). We therefore conjectured that this tool might support the expansion or refinement of the c.n. of situated abstractions for how dimension distinguishes and connects different objects and spaces.

Methods

Experiences of dimension were generated from twelve 10-year-old students who worked in six pairs (A–F). The students chosen were upper-middle ability students in mathematics, according to their teachers’ views. Working in pairs was chosen in order for the students to work with a class partner with whom they felt comfortable, according to their teacher, and also because their natural discussion and argument would externalise their thoughts, helping the researcher to interpret their activity.

The specific students were taught the UK’s curriculum as described by the National Numeracy Strategy (DfEE 1999). The Measures, Shape and Space strand of the National Numeracy Strategy consists of four main targets: a) measurement of length, mass, capacity, perimeter, area and time; b) direction and angle; c) position, including co-ordinates; d) properties of 2-D and 3-D shapes, including symmetry. We considered that by age ten, the students were likely to be able to articulate their own thinking about dimension, but that, since the students at this age had not yet experienced formal geometric teaching, the meanings that might emerge would be highly sensitive to how their informal experiences responded to the features in Google SketchUp. We also took the five types of meaning for dimension listed above, which arose in the previously reported study, as a basis for what we might expect to be articulated in the current study. In terms of observing thinking-in-change, we were particularly interested to observe when and how new meanings for dimension emerged during the interactions with Google SketchUp.

The students had not used Google SketchUp before. A semi-structured clinical interview (Hunting 1997; Opper 1977; Piaget 1976), carried out upon completion of tasks using Google SketchUp, was the main method in this study. Each interview lasted around 120–180 minutes. (It is perhaps testimony to the engaging nature of the tasks that these young students were able to concentrate for such an extended period.)

As described previously, the central task of the interview was for students to build their imaginary neighbourhood (Task A). Students were shown the 3-D version of the neighbourhood as in Fig. 3 and then told:

Here is an example of a neighbourhood a pair of students designed. They used special software for designing. The task is to draw your own version of a neighbourhood like the example. For building the neighbourhood, students first designed it like this [the researcher showed the 2-D example of the neighbourhood in Fig. 3] and then used this special tool [the Push/Pull tool] to make it like that [the 3-D example].

The aim of this main task (Task A) was to offer students the opportunity to work in a simulated 3-D environment and experience the capability this facility had to offer. More specifically, it included experiences about:

  1. a)

    the restrictions of movement in a 2-D compared with a 3-D environment (working with 2 or 3 axes; working on a plane; working in space);

  2. b)

    the restrictions of vision in a 2-D compared with a 3-D environment;

  3. c)

    how the objects were created in a 2-D and a 3-D environment (by aggregating other shapes; by dragging lower-dimensional shapes);

  4. d)

    which objects can exist in a 2-D and/or in a 3-D environment.

The main task offered them the chance to explore both the 2-D and the 3-D design and make comparisons pointing to their potentials and constraints. It involved working both in different spaces (2-D floor – 3-D space) and with different objects (lines, 2-D shapes, 3-D shapes) and experiencing the flexibility to move back and forth between spaces and examine ‘interlacing related but different figures’ as described by Ferrara and Mammana (2014). The quality of dimension as freedom could be identified through the experiences a) and b) above. Similarly, the duality of object/space could be identified through the c) and d) type of experiences, by generating different shapes and then identifying the lower-dimensional shapes that were used for their generation.

Our goal in these interviews was to allow the students to be in control of their explorations, decision-makings and consequently construction of knowledge. The interview was conducted by the first-named author acting as a participant observer, as the student pairs worked on their tasks. Most of the interventions involved probing the students to explain their actions further in words, while avoiding changing the direction of students’ thinking. However, some interventions were less neutral and more experimental by intending to make some change in the direction of activity, especially when students were clearly stuck on a path with no apparent learning potential.

For instance, an additional task, the Incomplete Frames task (Task B), was created to enrich the interview plan by being more specific, leading students to the exploration of specific mathematical notions especially in relation to the decoding of specific representations and perspective (French 2004; Parzysz 1988). As was described above, for a surface to be shaded, it has to be created using the Shaded Surfaces tool with a closed loop of co-planar edges. Students were presented some incomplete frames as shown in Fig. 8a and were asked to complete them, as in Fig. 8b. Then they were asked to use the Orbit tool to explore why some of the surfaces remained uncoloured.

Fig. 8
figure 8

Incomplete frames presented to students (a) and frames completed by students (b)

Full size image

The Incomplete Frames task was brought into play according to the needs of the students, which could be either during or after Task A. In other words, this task was complementary, because it offered room for further exploration of specific tools or even notions.

Additionally, during Task A, some prompting questions were used with the students as an extra reinforcement of the notions of direction, position and orientation, asking the students to: (i) discuss the construction of shapes in SketchUp (‘How many ways are there to create a rectangle/ a cube?’); (ii) reflect on the differences between 2D and 3D objects/spaces and make predictions of other dimensional environments (‘What would a 1-D/0-D world look like?’, ‘What shapes might exist in this world and why?’, ‘What would be the difference between this world and their 2-D/3-D world?’); (iii) reflect on how their thinking may have changed throughout the process (‘What do we mean by dimension?’ ‘What is an example of a 2-D/3-D shape?’, ‘What is an example of a 2-D/3-D world?’). We also used the 2-D and 3-D pictures of a neighbourhood (see Fig. 3) and asked the students to comment both on the difference between the two worlds/pictures and on the different shapes that exist in each world/picture.

The aim of our analysis was to describe the nature of the students’ reasoning about dimension and to uncover the constraints and affordances of Google SketchUp for thinking-in-change about dimension. Consequently, the unit of analysis was the variation of situated abstractions about dimension, as articulated by the students. In order for an excerpt to be considered as a situated abstraction of dimension, it had to relate to the definition(s) of dimension as extracted from the literature. For example, the situated abstraction “We have flat shapes and 3-D shapes” was relevant to Morgan’s (2005) study and was included.

In contrast, some excerpts did not qualify, because they referred to mathematics or geometry in general or were even considered to be irrelevant to our study. For example, students talked of the ‘D’ following 1, 2 and 3 as showing dimension, and that, without it, the naming of the shapes would have no meaning i.e. 2/3 shapes instead of 2-D shapes/3-D shapes. Even though the way we name the symbol of dimension is an important notion, and it is mentioned in some excerpts, it was considered irrelevant to include all the excerpts referring to it.

After collecting all the relevant situated abstractions of dimension, we used thematic analysis (Braun and Clarke 2006) to examine themes and patterns across the situated abstractions, based on their similarities and differences. For example, the students’ situated abstractions “Two/three different coloured lines were needed for creating a 2-D/3-D shape” and “3D shapes can be created by pushing/pulling 2-D shapes in three directions” describe dimension in terms of freedom to create objects so they were placed in the same theme category.

On the other hand, the situated abstraction “A 3-D object can go inside the 3-D neighbourhood and its buildings, but it can’t go inside the 2-D one” shows an articulation of dimension in terms of the capacity to house objects and therefore was placed in a different category. Our attention was focused on how the students’ pre-existing experiences of dimension, articulated through the particular situations they had experienced, might be broadened through the situations presented to them in this particular study.

Describing Dimensional Experience

In total, the analysis revealed 190 situated abstractions articulated by the twelve students. The students’ experiences of dimension were sorted into two categories of description, which, roughly speaking, address situated abstractions of the objects/spaces: (i) freedom to move. (ii) capacity to house.

The freedom to move idea incorporates experiences of direction, position and orientation, whereas capacity to house integrates experiences of containment. By containment, one can see the space as incorporating objects; in this sense, the space contains the objects. At the same time, the space can be thought of as generated by the objects.

The following paragraphs describe students’ articulations of each of the categories by presenting some thinking-in-change episodes and giving specific examples of situated abstractions that Pairs A–F expressed during the clinical interviews. (Phrases in the protocols below that are inserted inside square brackets are intended as explanatory commentary and were not part of the students’ articulations.)

Freedom to Move

The majority of the situated abstractions (156 out of 190) expressed situated abstractions of dimension in terms of direction, position and orientation. These can be considered as essential components characterising a particular object/space. In this sub-section, we present findings on these components and then discuss them.

At the beginning of the task, students positioned shapes in more than one plane and they were able to distinguish their orientation in space using the characterisations of ‘flat’, and ‘coming out’ or ‘standing up’. For example, when Pair D used the special tool for creating rectangles, they distinguished ‘flat’ shapes from ‘non-flat’ ones (Fig. 9).

Fig. 9
figure 9

Flat and non-flat shapes

Full size image

Shortly after, the same pair argued that the difference between the two rectangles in their neighbourhood and the new circle they created is that the former were flat while the latter was ‘wrong’, because “it is coming towards you” (Fig. 10).

Fig. 10
figure 10

Characterising shapes in different planes

Full size image

While exploring the Push/Pull tool for extruding their rectangles, students began to identify which rectangles would go ‘up’ (extruded in the direction parallel to the blue axis):

R: Which do you think will go up with the Push/Pull?

S1 and S2: This one, and that one and that one [indicating the dark grey rectangles in Fig. 11]

Fig. 11
figure 11

Students identify which rectangles will go ‘up’ with the Push/Pull tool

Full size image

[They used the Push/Pull tool to show that indeed they went up.]

R: How do you know which ones they are?

S2: Because they are flat on the ground, they are flat.

S1: The other ones are not flat.

[Excerpt 1, Pair D]

Subsequently, students were shown a different dark grey rectangle, which was not on the ground, but was nevertheless going up with the Push/Pull tool:

R: Is this on the ground? [the dark grey rectangle on the top]

Both: No.

R: But it is going up …

S2: It is because they are going up. In different angles, they go in different ways.

R: What is similar between this and this? [the two rectangles above] They both go up, but this is not on the floor. [the top one]

S1: Oh I got it. It has to be flat, it doesn’t matter if it is on the ground or not, it just has to be flat.

R: What about this? [the light grey vertical rectangle shown above] Is this not flat? It looks flat to me … [the Orbit tool was used to show them that it is flat]

S1: It is flat, but it is like straight like that. [showing a vertical direction with his hands] Instead of being this way, [showing vertical movement with a paper] it has to be that way. [showing the ‘flat’ position of a sheet of paper]

[Excerpt 2, Pair D]

Excerpt 2 illustrates that students acknowledged that shapes could face in ‘different ways’ and they also referred to ‘shapes in different angles’. Between them, Excerpts 1 and 2 demonstrated that the students were able to distinguish shapes within the Google SketchUp environment according to their orientation (see situated abstraction a) in Table 1). They used the situated language ‘shapes were put in different ways’ to describe ‘in different planes’.

It is an abstraction in the sense that the students demonstrated their ability to apply the rule across the Google SketchUp environment many times, but situated insofar as the language was strongly couched in the terminology that SketchUp uses. We had no evidence to suggest that the c.n. for this situated abstraction went beyond this setting, and the students would presumably need to have further experiences before such a development was likely. But it is clear, we believe, that this new meaning has a scientific quality that separates it from any of the five meanings previously reported in the literature.

After exploring the tasks and the tools further, these students were also able to relate the colour of the shape’s shade to the way it would go with the Push/Pull i.e. “Maybe white [surface colour] is going like the red [axis], the light grey like the green [axis] and those like the blue [axis]”. (Red, green and blue here refers to the axes that the extruding direction of each surface type is parallel to.) Students also defined parallel shapes arguing that if they used the Push/Pull they would go in the same direction.

Furthermore, while using the Circle tool, the idea of extrusion was noted as a transformation from 2-D to 3-D. Students related the colour of the circle’s cursor to the direction they would go with the Push/Pull tool and they acknowledged the three (or six if the negative directions were included) ways of movement in space. The students exercised control over the process of pushing/pulling 2-D shapes to transform them into 3-D shapes, in order to create the buildings in the neighbourhood they desired. By their actions, they demonstrated a sense of the difference between 2-D and 3-D and how there was freedom to extrude the shape in three directions (see situated abstraction b) in Table 1). Of course, the heuristic they applied generally throughout the setting was nevertheless restricted to that setting.

While exploring the Line tool to create shapes, students noticed the different colours the lines had, arguing that the different colours of the lines followed different directions. Subsequently, their thinking began to change as they recognised that the colour of the lines depended on the colour of the axis of the same direction:

R: Why does it change colour [the line]?

S2: I think it has to do with these lines when it is going in the direction of those lines.

R: Which lines?

S2: These lines [showing the red axis].

R: The red?

S2: The red and the green [the axes].

[Excerpt 3: Pair D]

Pair D also pointed out that some lines were parallel and that even though they did not have the same length, they were of the “same type of shape”. Their thinking was further developed when the students used green and blue lines to create a rectangle and their shape was shaded. We then asked them to explain how it was possible for a shape to be shaded, if it was drawn by using the Line tool. (Before, they had argued that only the special rectangle and circle tools were able to create shaded shapes.) They pointed out that this happened because they used coloured lines to draw the rectangle:

S2: It’s because the green and the blue, if you do it by using the green and the blue then…

S1: The red, the green and the blue.

R: Try it.

S2: For example if you do that is black, and black [They drew a rectangle made out of black lines]. Now it’s blue, red, red, and blue. It’s coloured! [They drew a second rectangle with coloured lines] (see Fig. 12).

Fig. 12
figure 12

Designing with coloured lines vs designing with black lines

Full size image

R: Why does this happen?

S1: Because if it is coloured, [the line segments] it would make a coloured shape.

[Excerpt 4: Pair D]

After using the Orbit tool to look around, they realised that their first shape (the one with the black lines) was not actually a proper rectangle, because “it wasn’t drawn properly”:

S1: No, not wasn’t drawn properly … because when I was watching while [S2] was drawing, I saw that when she drew it, it was black and black and black, [the lines] while when she did it here it was different colours, it was red and blue.

[Excerpt 5: Pair D]

While drawing their next shape, a rectangle, they used a red, a blue, a red line and a black one, and thus the shape was not shaded. However, they identified that this happened “because one of the lines was not coloured” (Pair D). Up to this point, students were able to find a relationship between the colour of the lines and whether or not the shape created was shaded. However, in order for a shape to be shaded, it had to belong to only one plane. Initially, they did not notice that. Therefore, we decided to draw a rectangle by using all the three different colours of lines. The rectangle looked perfect, created by coloured lines, but it was still not shaded! The students then used the Orbit tool to turn around and saw that indeed the rectangle that looked perfect was not even a rectangle:

S1: It’s not symmetry! [He then uses the Orbit tool] See! It’s bending…

R: Why? They were coloured! [the lines]

S1: I think the reason why, it’s because they have to be two same colours. Because that’s what happened with that [a previous coloured rectangle], it was red there and blue there.

R: Try to do it.

S1: Blue, red, blue, red! Yes! I’ve told you! [It turned a shaded colour]

S2: So it has to be two of the same colour.

[Excerpt 6: Pair D]

As shown in Excerpt 6, students concluded that in order for a rectangle to be shaded it had to be made out of only two colours of lines, and noticed the symmetry of the colour of lines within this combination (see Fig. 13).

Fig. 13
figure 13

Symmetry in the colour of lines that create a surface

Full size image

During this thinking-in-change moment, we prompted the students to use the Line tool to create a cube and recognise that for the cube they needed to use lines of all the three colours:

R: What colour of lines did you use?

S2: Red and green.

S1: No, red, green and blue to make a cube.

R: So for making a cube you need three colours? Because if you remember for creating a rectangle you said you need two colours.

S2: No, I think we need two colours. I remember when we did the first square I only used green and red…

R: Yes but when you created the cube?

S2: We used all the different colours.

[Excerpt 7, Pair D]

The two/three different colours of lines showed the different directions which the line could go. At the same time, it expressed a generalisation of how lines could generate 2-D and 3-D shapes, respectively. By acknowledging that they need two different coloured lines to create a 2-D shape, and three coloured lines to create a 3-D shape, and also by talking about the symmetry of those colours (see situated abstractions c) and d) in Table 1), these students showed articulations of new meanings different from the ones reported previously in Panorkou (2011). Although both situated and shaped by the SketchUp environment, these meanings were applied in a consistent way, which suggested they might be useful resources on which to build in the future.

Additionally, when Pair B was asked to explain how many different coloured lines were going to be used for creating a 1-D space/object, they argued: “Because if you realise for three D we used all of them [all different colours], but for two D only two of them, and one D it would be good if we use one.” Following a similar path, Pair D concluded that 1-D would be just a “line on its own.” Likewise, Pairs E and F expressed this generalisation in terms of how many ‘lines’ shapes had in various dimensions (e.g. “You know three D has three lines, two D has two lines, then maybe one D has one line” and “it [1-D] would be just one line, two D two lines, three D three lines, four D would have four lines”).

A new meaning was also evident when students concluded there were two ways for creating a 2-D shape and three ways of creating a 3-D shape (see situated abstraction e) in Table 1):

R: How can we create a square?

S: Press the rectangle button or drawing with the lines.

R: And a cube?

S: By using the rectangle button and pull up or drawing the rectangle and pull up or you draw the whole thing, or use just rectangles.

[Excerpt 8, Pair F]

Students argued that 2-D shapes can be created by the use of lines or rectangles. For 3D shapes, one way was with the Push/Pull tool arguing that “when it is flat two D and then you push it you make it, it will turn three D” (Pair D). A second way was by using a combination of rectangles (2-D shapes) to create a cube. The third way was by arguing that three different coloured lines could combine and result in a ‘proper’ shape.

While drawing the buildings in their neighbourhood, students talked of dimension as positioning, arguing that in two dimensions there were two ways of positioning things, while in three dimensions there were three ways. Pair E even argued that dimension was position and how things were placed. After the students finished their neighbourhood design, a discussion followed about the 2-D and the 3-D versions of their neighbourhood. Pair B recognised the difference in moving around in the 2-D and 3-D neighbourhoods, respectively:

S: Because, that’s two D, you go only left and right and up and down, while if you are in three D you go everywhere. For example, let’s say a house if it was two D, you wouldn’t be able to go into the house.

[Excerpt 9, Pair B]

Similarly, Pair D talked about the bug as being able to walk on anything ‘he’ wanted to in a 2-D neighbourhood. The use of the Orbit tool to turn their 3-D buildings around in order to be able to draw windows at the back was a sign of familiarity of moving in 3-D space, showing the flexibility of generating and positioning shapes in 3-D (see situated abstractions f) and g) in Table 1), meanings that were not evident in previous studies (for instance, the five meanings that the original Panorkou study showed and the difficulties in perspective and coding/decoding of representations that Parzysz reported.)

The excerpts above showed examples of thinking-in-change episodes illustrating the process of students’ development of dimensional abstractions during the activity with Google SketchUp. Table 1 shows an overview of students’ situated abstractions on the object/space’s freedom to move, pointing to the ideas of direction, position and orientation.

Table 1 Sample of students’ situated abstractions on ‘freedom to move’
Full size table

The situated abstractions in Table 1 show that students became familiar with working in a 3-D environment and, more specifically, generating and positioning 2-D and 3-D objects in 2-D and 3-D spaces. In contrast to previous literature on students’ difficulties of decoding representations, situated abstractions a and f show that students were able to describe how objects were placed in space, by drawing on the ideas of position and orientation. Although Parzysz (1988) identified the difficulties of locating objects in different planes, the students in this study showed that they were able to locate objects in different domains. The use of SketchUp made this possible by presenting objects in different shades depending on the plane they are on. Additionally, difficulties of perspective of 2-D/3-D objects (see, for example, French 2004; Parzysz 1988) were eliminated, because students were able to use the Orbit tool as a key means for looking at their shapes from different perspectives and noticing encoding and decoding errors.

Situated abstraction b shows articulation of the extrusion of 2-D shapes following the direction that is perpendicular to their surface. By using the Push/Pull tool, students experienced movement between plane and space, and were able to connect different objects and spaces. Student thinking was challenged and changed to include the generation of objects/spaces using two or three coloured line segments for creating 2-D and 3-D objects/spaces, respectively (situated abstractions c and d). By using the Line tool to create line segments in space, students experienced the directional, positional and orientational aspects of dimension, and also identified the degrees of freedom for generating objects within each space.

These situated abstractions together with situated abstraction e, show students’ ability of coding (producing) representations of 2-D/3-D objects/spaces, surely a precursor to a capability for dimensional deconstruction (Duval 2005; Laborde and Laborde 2011). Although these abstractions are situated in terms of language and connectivity to the SketchUp environment, the fact that the students were consistently able to create cubes and lines from lower-dimensional objects suggests that this resource has potential for abstraction to a wider c.n., one that would be recognised as truly mathematical.

The constraints of SketchUp in terms of both creating objects and moving within each domain led to articulations of dimension as degrees of freedom of an object/space. Two dimensions and three dimensions offer two and three degrees of freedom, respectively. This relationship was expressed for both creating shapes (e.g. situated abstraction e) and for moving within the space (e.g. situated abstraction g).

Capacity to House

A noteworthy amount of students’ situated abstractions (34 out of 190 situated abstractions) referred to dimension as capacity to house. Students’ experiences of dimension as capacity seem to reflect the idea of capacity as containment. In this sub-section, we present examples of students’ articulations and then offer discussion of these ideas.

By using the Orbit tool, students recognised that although a shape would look flat in 3-D, it could be disconnected or twisted. For example, Pair B characterised the shapes, which belonged to more than one plane, as ‘wrong’, ‘not completed’, ‘not done properly’, or ‘wonky’ and, when they finally created a shaded surface, they argued that it was so because it was ‘good’, ‘right’, it was done ‘neatly’, ‘it is perfect’ and ‘it does not change with Orbit’. Students constructed new meanings about representations of shapes and perspective by acknowledging that the additional direction of movement allows the possibility of illusory effects and also the additional freedom throws up the possibility of 2-D shapes that are twisted (see situated abstractions a) and b) in Table 2).

This increasingly helped them through the activity with SketchUp to avoid coding and decoding errors and difficulties in perspective as noted in previous studies (e.g. French 2004; Parzysz 1988). Thus, a key idea about dimension seems to be that, in some sense, it depicts the level of capacity of the space and, more specifically, the containment of that space (edges could be twisted) and the generation of shapes (shapes could be disconnected).

After the students finished their neighbourhood design, a discussion followed about the 2-D and the 3-D versions of their neighbourhood (Fig. 14).

Fig. 14
figure 14

Example of 2-D and 3-D neighbourhoods constructed by one pair of students

Full size image

Pair D, for instance, argued that 2-D is “flat”, “you can see the flat top”, compared to 3D where “you can actually see a big piece compared to that [the 2-D]” and “you can actually see everything inside”. They also pointed out that if we turned the two neighbourhoods into a top view, then they would look the same. They gave the example of a table to support their argument:

S1: Like this table is like that. [showing the table] If you look here you see just that, [the surface] but if you look underneath you see the whole thing.

R: So what is that table?

S1 & S2: three D.

R: And what can be two D in that table?

S1: That [showing the surface]

R: Oh, the surface?

Students 1 & 2: Yeah, the surface.

S2: The surface is always two D.

S1: But everything else is three D.

[Excerpt 10, Pair D]

Students thought of three dimensions as offering something more than two dimensions, like showing the whole picture of something. In their experiences, 2-D was incorporated into 3-D; in other words, 2-D was ‘housed’ by 3-D i.e. surface–whole table, flat-top–everything inside (see situated abstractions c) – f) in Table 2). For example, in Excerpt 9 (Pair B) students argued that a 3-D object can go inside the 3-D neighbourhood and its buildings but it cannot go inside the 2-D one. In Panorkou (2011), students identified dimension as a domain incorporating shapes and as a description of those shapes. During activity with SketchUp, students constructed new more holistic meanings about the relationship between 2-D and 3-D spaces and actively experienced the flexibility of moving between plane and space.

Furthermore, students felt the need to define the planes with which they were working/creating. They gave names to their shapes, depending on the colour of the lines they used to create them. For example, Pair A distinguished between the ‘floor level’ shapes which were created with the use of red and green lines from the ‘red–blue’ lined shapes, and this distinction helped them in creating the cube using only lines. Similarly, Pair F argued, “the floor can be the green thing.” Pair C even connected the SketchUp domain to their familiar co-ordinate plane, arguing that the red line could be the y-axis and the green the x-axis.

It is worth mentioning here that one of the students in Pair D also expressed the idea of the three axes as forming a cube:

S: You see like … this is the bottom [showing the space between the green and the red axes]. It is not a whole cube but a part of it. This is the middle [origin point] and then you go down down, down [across the green line] that’s the edge, that’s like down, that’s the corner [showing the angle created by the blue and the green] and that’s the other line [the red axis].

[Excerpt 11, Pair D]

The student above thought of the axes as forming a cube (object), which included many other objects and, of course, the whole design of their neighbourhood (space). The idea of the axes forming a cube was also noted by Pair B, who pointed out that some shapes were outside of the cube and some inside the cube. Thus, these statements (see situated abstraction g) in Table 2) were a way of expressing dimension both as a quality of object and of space, bringing out the idea of lower-dimensional objects creating higher-dimensional objects/spaces (axes creating a cube), but at the same time showing that higher-dimensional objects/spaces (a cube) can incorporate lower-dimensional objects/spaces (1-D/2-D/3-D objects). Students also talked about the reverse situation of whether it was possible to have higher-dimensional spaces/objects incorporated into lower-dimensional spaces/objects or having higher-dimensional spaces/objects generating lower-dimensional spaces/objects.

The above thinking-in-change episodes are all examples of how students’ thinking about dimension had developed through activity to include generalisations based on the object/space’s capacity to house equal- and lower-dimensional objects/spaces. Table 2 presents a sample of students’ expressions of dimension as capacity.

Table 2 Sample of students’ situated abstractions on ‘capacity to house’
Full size table

Situated abstractions a, b and g, show that by encoding representations of surfaces, students were able to generalise how lines can be composed to create a surface in space. These expressions show that the students see objects/spaces as created (generated) in various ways from lower-dimensional objects, in particular by lines. These articulations show that object/space was thought of as generated by the objects through the way that they span it. Through their experience with SketchUp, students were able to recognize the different dimensions that are composed for defining a space (e.g. situated abstraction g), a finding that contrasts the literature that states that students’ judgements of volume are focused on a single dimension (e.g. Piaget 1968; Piaget et al. 1960; Raghubir and Krishna 1999).

Situated abstractions c, d and e all show that students identified space as incorporating objects by making connections between the surfaces of the 3-D shapes and the 3-D shapes themselves, which we consider as a precursor to a capability of dimensional deconstruction. By moving back and forth between plane and space, students were able to recognise ‘interlacing related but different’ shapes, a notion identified by Ferrara and Mammana (2014). The use of the Push/Pull tool together with the Orbit tool helped students in making those connections by allowing them to view shapes dynamically, comparable with their intuitions noted in the literature (e.g. Lehrer et al. 1998).

These abstractions, together with situated abstraction f, illustrate students’ ability to overcome difficulties of encoding and decoding of representations and describe objects/spaces in terms of their capacity to house other objects/spaces. Although the above abstractions were situated to the SketchUp context and relationships, we recognise their abstraction across the setting as they extend their meanings beyond naive conceptions and the difficulties noted in the literature.

Concluding Discussion

The findings of the study reported here show that further aspects of dimension can be experienced even by very young students, in situated ways, through a setting incorporating SketchUp alongside carefully designed tasks and probing questions. The dimensional tool was an artificial construct (in the sense that the designer created it) that was used to trigger affective responses at the same time as shaping conceptual change. The constraint of working with the dimensional tools perturbed students’ experiences and directed them towards looking for patterns and creating generalisations in the form of abstractions created in situ. As a result, this study confirmed the key significance of the design of the setting in the formation of experience of dimension.

These children working in this setting did not seem afflicted by the difficulties reported elsewhere very often, and, where problems were apparent, the children were able to work through them by trying out ideas in SketchUp using the dimensional tools. More specifically, whereas we might have expected problems in encoding (Parzysz 1988) when the children were expressing their ideas about their neighbourhoods, the use of the Line and Shaded Surface tools enabled them to create two- and three-dimensional shapes and debug them when the feedback did not match their expectations.

Similarly, the use of the Orbit tool enabled the children to observe their creations from many perspectives, thus ameliorating decoding problems that might have been expected when viewing a three-dimensional shape on a two-dimensional screen. A key affordance of the setting seemed to be in the way it supported a flexibility in thinking. For example, the Push/Pull tool helped the children’s webbing (or what Ferrara and Mammana 2014, called ‘interlacing’) of two and three dimensions, articulated as the situated abstractions reported in Tables 1 and 2.

We recognise that it is not possible to map out all the possible ways of experiencing a phenomenon. Thus, the outcomes consist of a subset of all the possible ways of experiencing the phenomenon. Other experiences of dimension are not excluded from this categorisation. The sample of children was not controlled for gender or cultural background, although each of these variables might have an effect in the way a child articulates expressions of dimension.

Therefore, it is more than possible that there are further differences to be observed in how children experience dimension, particularly among children with different backgrounds or who are less competent at school (the children chosen for this study were of upper-middle ability according to their teachers). Furthermore, this study demonstrated that the children were largely oriented towards the way the phenomenon of dimension was presented in an environment like SketchUp and this showed that the setting in which these experiences take place influences their type. Thus, we would argue here that it is quite possible in other settings to have more types of dimensional experience, but the evidence we have presented illustrates two specific categories.

Students’ expressions articulated the duality of dimension as expressing both freedom to move and capacity to house. Their articulations of experience showed that they were able to form situated abstractions, which we recognise as ‘roots of’ (Mason et al. 1985) advanced mathematical ideas such as vector space, and we speculate that these situated abstractions may act as the starting point for ‘routes to’ (Mason et al. 1985) those ideas. Students’ situated abstractions of dimension as freedom to move (as listed in Table 1) could be interpreted as roots of the attributes of vectors such as direction, position and orientation. Similarly, students’ situated abstractions of capacity (as listed in Table 2) could be interpreted as roots of the idea of vector space.

Of course, we do not claim that students as young as these understand vectors or vector spaces. The students’ situated abstractions noted above are truly humble expressions of these sophisticated mathematical ideas. It is the authors, and not the students, who make the connections between the students’ articulations and these mathematical constructs. Nevertheless, the potential significance of such early intuitive learning of situated abstractions of dimension is nicely captured in the following aspirational question, with which we end our article:

Research into language acquisition indicates that […] if a child is not introduced early to other languages, he or she will experience much more difficulty in learning a second tongue. Might the same be true with respect to mathematical perceptions? If we wait until students have developed a great deal of arithmetic sophistication (and a great many misconceptions) before we encourage them to think about solid objects and the interaction between different dimensions, we may be depriving them of the chance to appreciate the full power and scope of geometry. (Banchoff 1990, p. 14)