Artificial Neural Networks-Based Material Parameter Identification for Numerical Simulations of Additively Manufactured Parts by Material Extrusion
Abstract
:1. Introduction
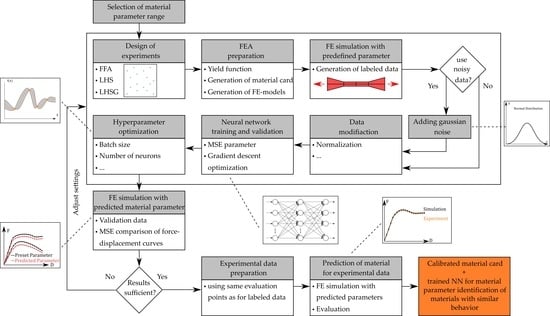
2. Materials and Methods
2.1. Material Parameter Identification
2.1.1. Iterative Optimization Procedure
- The success of optimization algorithms is highly depending on the chosen starting point, which is usually not known
- Many iterations are needed to find appropriate parameters for complex material models, which leads to high computational costs
- A high number of error function evaluations are needed
2.1.2. Direct Neural Network-Based Procedure
2.2. Artificial Neural Networks
2.3. Data Generation by Numerical Simulations
2.4. Additive Manufacturing and Mechanical Characterization of Test Specimens—Experimental Set-Up
3. Results and Discussion
3.1. Iterative Optimization Results
3.2. FFANN Results
3.2.1. Sampling Strategies
3.2.2. Quantity of Input Data
3.2.3. Input Data Range
3.2.4. Validation Set Sizes
3.2.5. Data Modification with Gaussian Noise
3.2.6. Hyperparameters
Gridsearch
Randomsearch
Hyperparameter Optimization
- Epochs per default 250
- Neurons from 50 to 500 in steps of 25
- GD optimizers without SGD
3.3. Comparison of Iterative and Direct Inverse Procedures
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile butadiene styrene |
| AM | Additive Manufacturing |
| ANN | Artificial Neural Network |
| EXP | Experiment |
| FE | Finite Element |
| FFA | Full Factorial Approach |
| FFANN | Feedforward Artificial Neural Network |
| GD | Gradient Descent |
| HL | Hidden Layer |
| HP | Hyperparameter |
| IL | Input Layer |
| LHS | Latin Hypercube Sampling |
| LHSG | Latin Hypercube Sampling with genetic space filling |
| ML | Machine Learning |
| NN | Neural Network |
| OL | Output Layer |
| PI | Parameter Identification |
| SGD | Stochastic gradient descent |
| TPE | Tree-of-Parzen-Estimators |
Appendix A
| Run | Sampling Strategy | Train Set Size | Val. Set Size | Train Range | Val. Range | NN | Noisy Data | Mean MSE Parameter Val. Set (−) | Mean MSE FDC Val. Set () | MSE FDC Exp. () |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | FFA | 2401 | 1 | 2 | Default | No | ||||
| 2 | LHS | 2401 | 1 | 2 | Default | No | ||||
| 3 | FFA | 4096 | 1296 | 1 | 2 | Default | No | |||
| 4 | LHS | 4096 | 1296 | 1 | 2 | Default | No | |||
| 5 | FFA | 2401 | 625 | 1 | 2 | Default | No | |||
| 6 | LHS | 2401 | 625 | 1 | 2 | Default | No | |||
| 7 | FFA | 625 | 256 | 1 | 2 | Default | No | |||
| 8 | LHS | 625 | 256 | 1 | 2 | Default | No | |||
| 9 | LHSG | 625 | 256 | 1 | 2 | Default | No | |||
| 10 | FFA | 256 | 81 | 1 | 2 | Default | No | |||
| 11 | LHS | 256 | 81 | 1 | 2 | Default | No | |||
| 12 | LHSG | 256 | 81 | 1 | 2 | Default | No | |||
| 13 | LHS | 150 | 50 | 1 | 2 | Default | No | |||
| 14 | LHSG | 150 | 50 | 1 | 2 | Default | No | |||
| 15 | LHS | 2401 | 1 | 1 | Default | No | ||||
| 16 | LHS | 2401 | 2 | 1 | Default | No | ||||
| 17 | LHS | 2401 | 3 | 1 | Default | No | ||||
| 18 | LHS | 2401 | 4 | 1 | Default | No | ||||
| 19 | LHS | 5000 | 1 | 1 | Default | No | ||||
| 20 | LHS | 1 | 1 | Default | No | |||||
| 21 | FFA | 2401 | 1 | 2 | Default | Yes | ||||
| 22 | LHS | 2401 | 1 | 2 | Default | Yes | ||||
| 23 | LHS | 625 | 256 | 1 | 2 | Default | Yes | |||
| 24 | FFA | 2401 | 1 | 2 | HPO1 | No | ||||
| 25 | FFA | 2401 | 1 | 2 | HPO2 | No | ||||
| 26 | FFA | 2401 | 1 | 2 | HPO3 | No | ||||
| 27 | FFA | 2401 | 1 | 2 | HPO4 | No | ||||
| 28 | LHS | 2401 | 1 | 2 | HPO5 | No | ||||
| 29 | LHS | 2401 | 1 | 2 | HPO6 | No | ||||
| 30 | LHS | 2401 | 1 | 2 | HPO7 | No | ||||
| 31 | LHS | 2401 | 1 | 2 | HPO8 | No |
| Parameter Range | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 |
| (Hyper-)Parameter | Setting |
|---|---|
| Batch Size | 12 |
| Epochs | 250 |
| Neurons (Input Layer) | 35 |
| Hidden Layers | 1 |
| Neurons | 250 |
| Kernel Initializer (HL) | Normal |
| Activation (HL) | Relu |
| Dropout (HL) | |
| Neurons (Output Layer) | 4 |
| Kernel Initializer (OL) | Normal |
| Activation (OL) | 4 |
| Neurons (Output Layer) | Linear |
| Gradient Descent Optimizer | Adam |
| N | Batch Size | Epochs | Neurons (HL) | Kernel Initializer (HL) | Activation (HL) | Dropout (HL) | Kernel Initializer (OL) | Optimizer |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 75 | 25 | Normal * | Softmax | Normal * | Adam * | |
| 2 | 6 | 100 | 50 | Uniform | Softplus | 0.05 * | Uniform | Rmsprop |
| 3 | 9 | 125 | 75 | Glorot Uniform | Softsign | Glorot Uniform | SGD | |
| 4 | 12 * | 150 | 100 | Lecun Uniform | Relu * | Lecun Uniform | Adagrad | |
| 5 | 15 | 175 | 125 | Zero | Tanh | Zero | Adadelta | |
| 6 | 18 | 200 | 150 | Glorot Normal | Sigmoid | Glorot Normal | Adamax | |
| 7 | 21 | 225 | 175 | He Normal | Hard Sigmoid | He Normal | Nadam | |
| 8 | 24 | 250 * | 200 | He Uniform | Linear | He Uniform | − | |
| 9 | 27 | − | 225 | − | Selu | − | − | |
| 10 | 30 | − | 250 * | − | Elu | − | − | |
| 11 | 33 | − | 275 | − | Exponential | − | − | |
| 12 | 36 | − | 300 | − | − | − | − | − |
| 13 | 39 | − | 325 | − | − | − | − | − |
| 14 | − | − | 350 | − | − | − | − | − |
| 15 | − | − | 375 | − | − | − | − | − |
| 16 | − | − | 400 | − | − | − | − | − |
| 17 | − | − | 425 | − | − | − | − | − |
| 18 | − | − | 450 | − | − | − | − | − |
| 19 | − | − | 475 | − | − | − | − | − |
| 20 | − | − | 500 | − | − | − | − | − |
| N | Batch Size | Epochs | Neurons (HL) | Kernel Initializer (HL) | Activation (HL) | Dropout (HL) | Kernel Initializer (OL) | GD Optimizer |
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | − | |||||||
| 9 | − | − | − | − | ||||
| 10 | − | − | − | − | ||||
| 11 | − | − | − | − | ||||
| 12 | − | − | − | − | − | − | ||
| 13 | − | − | − | − | − | − | ||
| 14 | − | − | − | − | − | − | − | |
| 15 | − | − | − | − | − | − | − | |
| 16 | − | − | − | − | − | − | − | |
| 17 | − | − | − | − | − | − | − | |
| 18 | − | − | − | − | − | − | − | |
| 19 | − | − | − | − | − | − | − | |
| 20 | − | − | − | − | − | − | − |
| Batch Size | Epochs | Neurons (HL) | Kernel Initializer (HL) | Activation (HL) | Dropout (HL) | Kernel Initializer (OL) | GD Optimizer | Mean MSE Parameter Train Set (−) |
|---|---|---|---|---|---|---|---|---|
| 36 | 250 | 325 | He Normal | Selu | Glorot Normal | Nadam | ||
| 21 | 125 | 300 | He Normal | Softsign | Glorot Uniform | Adamax | ||
| 30 | 150 | 400 | He Uniform | Tanh | He Uniform | Adamax | ||
| 18 | 75 | 450 | He Normal | Selu | Glorot Normal | Adamax | ||
| 24 | 250 | 450 | Uniform | Softsign | He Normal | Nadam | ||
| 21 | 100 | 250 | Zero | Softmax | Lecun Uniform | Adadelta | ||
| 39 | 150 | 25 | Lecun Uniform | Exponential | Normal | Adadelta | ||
| 15 | 150 | 75 | Lecun Uniform | Softmax | Lecun Uniform | Adadelta | ||
| 33 | 250 | 450 | Glorot Uniform | Softsign | Glorot Normal | Nadam | ||
| 15 | 150 | 350 | Zero | Relu | Normal | Adadelta |

| (Hyper-) Parameter | HPO1 | HPO2 | HPO3 | HPO4 | HPO5 | HPO6 | HPO7 | HPO8 |
|---|---|---|---|---|---|---|---|---|
| Batch Size | 27 | 12 | 39 | 3 | 27 | 12 | 27 | 30 |
| Epochs * | 250 | 250 | 250 | 250 | 250 | 250 | 250 | 250 |
| Neurons (IL) * | 35 | 35 | 35 | 35 | 35 | 35 | 35 | 35 |
| Number (Hidden) (Layer) | 2 | 2 | 1 | 2 | 2 | 2 | 1 | 1 |
| Neurons (HL1) | 350 | 50 | 400 | 250 | 350 | 50 | 200 | 450 |
| Kernel Initializer (HL1) | He Uniform | He Uniform | Lecun Uniform | He Uniform | He Uniform | He Uniform | He Uniform | Lecun Uniform |
| Activation (HL1) | Hard Sigmoid | Hard Sigmoid | Hard Sigmoid | Softsign | Hard Sigmoid | Hard Sigmoid | Hard Sigmoid | Selu |
| Dropout (HL1) | ||||||||
| Neurons (HL2) | 250 | 300 | − | 350 | 250 | 300 | − | − |
| Kernel Initializer (HL2) * | normal | normal | normal | normal | normal | normal | normal | normal |
| Activation (HL2) * | linear | linear | linear | linear | linear | linear | linear | linear |
| Dropout (HL2) * | ||||||||
| Neurons (OL) * | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Kernel Initializer (OL) | He Uniform | Normal | He Uniform | He Normal | He Uniform | Normal | Glorot Uniform | Zero |
| Activation (OL) * | linear | linear | linear | linear | linear | linear | linear | linear |
| GD Optimizer | Adamax | Adam | Adam | Adagrad | Adamax | Adam | Adam | Adamax |
| HP Optimization Library | Keras Tuner | Keras Tuner | Keras Tuner | Hyperas | Keras Tuner | Keras Tuner | Keras Tuner | Hyperas |
| HP Optimizer | Random- search | Hyper- band | Bayesian | Bayesian TPE | Random- search | Hyper- band | Bayesian | Bayesian TPE |
| Max Trials * | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Exekution per Trial * | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
References
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Kumke, M.; Watschke, H.; Hartogh, P.; Bavendiek, A.K.; Vietor, T. Methods and tools for identifying and leveraging additive manufacturing design potentials. Int. J. Interact. Des. Manuf. (IJIDeM) 2017, 12, 481–493. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. The identification of parameters for visco-plastic models via finite-element methods and gradient methods. Model. Simul. Mater. Sci. Eng. 1994, 2, 597–616. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. A unified approach for parameter identification of inelastic material models in the frame of the finite element method. Comput. Methods Appl. Mech. Eng. 1996, 136, 225–258. [Google Scholar] [CrossRef]
- Morand, L.; Helm, D. A mixture of experts approach to handle ambiguities in parameter identification problems in material modeling. Comput. Mater. Sci. 2019, 167, 85–91. [Google Scholar] [CrossRef]
- Kučerová, A.; Zeman, J. Estimating Parameters of Microplane Material Model Using Soft Computing Methods. In Proceedings of the 6th World Congresses of Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazil, 30 May–3 June 2005. [Google Scholar]
- Goh, G.D.; Sing, S.L.; Yeong, W.Y. A review on machine learning in 3D printing: Applications, potential, and challenges. Artif. Intell. Rev. 2020. [Google Scholar] [CrossRef]
- Mehlig, B. Artifical Neural Networks; Lecture Notes; Department of Physics, University of Gothenburg: Göteborg, Sweden, 2019. [Google Scholar]
- Kučerová, A. Identification of Nonlinear Mechanical Model Parameters Based on Softcomputing Methods. Ph.D. Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2007. [Google Scholar]
- Unger, J.F.; Könke, C. An inverse parameter identification procedure assessing the quality of the estimates using Bayesian neural networks. Appl. Soft Comput. 2011, 11, 3357–3367. [Google Scholar] [CrossRef]
- Soares, C.; de Freitas, M.; Araújo, A.; Pedersen, P. Identification of material properties of composite plate specimens. Compos. Struct. 1993, 25, 277–285. [Google Scholar] [CrossRef]
- Gelin, J.; Ghouati, O. An inverse method for determining viscoplastic properties of aluminium alloys. J. Mater. Process. Technol. 1994, 45, 435–440. [Google Scholar] [CrossRef]
- Araújo, A.; Soares, C.M.; de Freitas, M. Characterization of material parameters of composite plate specimens using optimization and experimental vibrational data. Compos. Part B Eng. 1996, 27, 185–191. [Google Scholar] [CrossRef]
- Fogel, D. An introduction to simulated evolutionary optimization. IEEE Trans. Neural Netw. 1994, 5, 3–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, L.; Sethares, W. Nonlinear parameter estimation via the genetic algorithm. IEEE Trans. Signal Process. 1994, 42, 927–935. [Google Scholar] [CrossRef] [Green Version]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Yagawa, G.; Okuda, H. Neural networks in computational mechanics. Arch. Comput. Methods Eng. 1996, 3, 435–512. [Google Scholar] [CrossRef]
- Jordan, M.I.; Rumelhart, D.E. Forward Models: Supervised Learning with a Distal Teacher. Cogn. Sci. 1992, 16, 307–354. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties fromspherical indentation data using neural networks. Part i:the case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties fromspherical indentation data using neural networks. Part ii:plasticity with nonlinear isotropic and kinematichardening. J. Mech. Phys. Solids 1999, 47, 1589–1607. [Google Scholar] [CrossRef]
- Lefik, M.; Schrefler, B. Artificial neural network for parameter identifications for an elasto-plastic model of superconducting cable under cyclic loading. Comput. Struct. 2002, 80, 1699–1713. [Google Scholar] [CrossRef]
- Nardin, A.; Schrefler, B.; Lefik, M. Application of Artificial Neural Network for Identification of Parameters of a Constitutive Law for Soils. In Developments in Applied Artificial Intelligence, Proceedings of the 16th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems, IEA/AIE, Loughborough, UK, 23–26 June 2003; Springer: Berlin, Germany, 2003; pp. 545–554. [Google Scholar] [CrossRef]
- Helm, D. Pseudoelastic behavior of shape memory alloys: Constitutive theory and identification of the material parameters using neural networks. Tech. Mech. 2005, 25, 39–58. [Google Scholar]
- Chamekh, A.; Salah, H.B.H.; Hambli, R. Inverse technique identification of material parameters using finite element and neural network computation. Int. J. Adv. Manuf. Technol. 2008, 44, 173–179. [Google Scholar] [CrossRef]
- Aguir, H.; Chamekh, A.; BelHadjSalah, H.; Dogui, A.; Hambli, R. Parameter identification of a non-associative elastoplastic constitutive model using ANN and multi-objective optimization. Int. J. Mater. Form. 2009, 2, 75–82. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Mareš, T.; Janouchová, E.; Kučerová, A. Artificial neural networks in the calibration of nonlinear mechanical models. Adv. Eng. Softw. 2016, 95, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Volume II Material Models LS-DYNA, r11 ed. Available online: https://www.dynamore.de/de/download/manuals/ls-dyna/ls-dyna-manual-r11.0-vol-ii-12-mb (accessed on 9 December 2020).
- Stander, N.E.A. LS OPT User’s Manual—A Design Optimization and Probabilistic Analysis Tool for the Engeneering Analyst, v.6.0 ed. 2019. Available online: https://www.lsoptsupport.com/documents/manuals/ls-opt/lsopt_60_manual.pdf (accessed on 9 December 2020).
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Fausett, L.; Fausett, L. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Springer: Vienna, Austria, 1994. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; CRC Press: London, UK, 2018. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Number Bd. 10 in Neural Networks and Learning Machines; Prentice Hall: Hamilton, ON, Canada, 2009. [Google Scholar]
- Da Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial Neural Networks; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Shanmuganathan, S.; Samarasinghe, S. Artificial Neural Network Modelling; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 20 July 2020).
- Pinto, N.; Doukhan, D.; DiCarlo, J.J.; Cox, D.D. A High-Throughput Screening Approach to Discovering Good Forms of Biologically Inspired Visual Representation. PLoS Comput. Biol. 2009, 5, e1000579. [Google Scholar] [CrossRef] [PubMed]
- Moons, B.; Bankman, D.; Verhelst, M. Embedded Deep Learning; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Anders, U.; Korn, O. Model selection in neural networks. Neural Netw. 1999, 12, 309–323. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M. Neural Networks and Deep Learning. 2015. Available online: http://static.latexstudio.net/article/2018/0912/neuralnetworksanddeeplearning.pdf (accessed on 9 December 2020).
- Hutter, F.; Kotthoff, L.; Vanschoren, J. (Eds.) Automated Machine Learning; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. Keras Tuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 6 July 2020).
- Li, L.; Jamieson, K.G.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Efficient Hyperparameter Optimization and Infinitely Many Armed Bandits. arXiv 2016, arXiv:abs/1603.06560. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kegl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems ( NIPS’11), Granada, Spain, 12–14 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. 2018. Available online: http://xxx.lanl.gov/abs/1807.01774 (accessed on 17 August 2020).
- Bengio, Y. Practical Recommendations for Gradient-Based Training of Deep Architectures. Neural Netw. Tricks Trade 2012, 437–478. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]

















| Material | Color | Extrusion Speed | Build Platform Temperature | Nozzle Temperature | Layer Thickness | Raster Angle | Perimeter Shells |
|---|---|---|---|---|---|---|---|
| ABS | black | 40 mm/s | 100 C | 245 C | 0.2 mm | ±45 C | 2 |
| Parameter a | Parameter b | Parameter c | Parameter d | MSE FDC |
|---|---|---|---|---|
| 52,514 | −4056.63 | 11.231 | 539.29 | 163.14 |
| Run | Mean MSE Parameter Val. Set (−) | Mean MSE FDC Val. Set () | MSE FDC Exp. () |
|---|---|---|---|
| 5 | |||
| 25 | |||
| 26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meißner, P.; Watschke, H.; Winter, J.; Vietor, T. Artificial Neural Networks-Based Material Parameter Identification for Numerical Simulations of Additively Manufactured Parts by Material Extrusion. Polymers 2020, 12, 2949. https://doi.org/10.3390/polym12122949
Meißner P, Watschke H, Winter J, Vietor T. Artificial Neural Networks-Based Material Parameter Identification for Numerical Simulations of Additively Manufactured Parts by Material Extrusion. Polymers. 2020; 12(12):2949. https://doi.org/10.3390/polym12122949
Chicago/Turabian StyleMeißner, Paul, Hagen Watschke, Jens Winter, and Thomas Vietor. 2020. "Artificial Neural Networks-Based Material Parameter Identification for Numerical Simulations of Additively Manufactured Parts by Material Extrusion" Polymers 12, no. 12: 2949. https://doi.org/10.3390/polym12122949