An Expert Knowledge Approach to Stochastic Mortality Forecasting in the Netherlands

Abstract

The Dutch population forecasts published by Statistics Netherlands every other year project the future size and age structure of the population of the Netherlands up to 2050. The forecasts are based on assumptions about future changes in fertility, mortality, and international migration. Obviously, the validity of assumptions on changes in the long run is uncertain, even if the assumptions are expected to describe the expected future according to the forecasters. It is important that users of forecasts are aware of the degree of uncertainty. In order to give accurate information about the degree of uncertainty of population forecasts Statistics Netherlands produces stochastic population forecasts. Instead of publishing two alternative deterministic (low and high) variants in addition to the medium variant, as was the practice up to a few years ago, forecast intervals are made. These intervals are calculated by means of Monte Carlo simulations. The simulations are based on assumptions about the probability distributions of future fertility, mortality, and international migration.

1 Introduction

The Dutch population forecasts published by Statistics Netherlands every other year project the future size and age structure of the population of the Netherlands up to 2050. The forecasts are based on assumptions about future changes in fertility, mortality, and international migration. Obviously, the validity of assumptions on changes in the long run is uncertain, even if the assumptions are expected to describe the expected future according to the forecasters. It is important that users of forecasts are aware of the degree of uncertainty. In order to give accurate information about the degree of uncertainty of population forecasts Statistics Netherlands produces stochastic population forecasts. Instead of publishing two alternative deterministic (low and high) variants in addition to the medium variant, as was the practice up to a few years ago, forecast intervals are made. These intervals are calculated by means of Monte Carlo simulations. The simulations are based on assumptions about the probability distributions of future fertility, mortality, and international migration.

In the Dutch population forecasts the assumptions on the expected future changes in mortality primarily relate to life expectancy at birth. In the most recent Dutch forecasts assumptions underlying the medium variant¹ are based on a quantitative model projecting life expectancy at birth of men and women for the period 2001–2050. The model describes the trend of life expectancy in the period 1900–2000 taking into account the effect of changes in smoking behaviour, the effect of the rectangularization of the survival curve and the effect of some other factors on changes in life expectancy at birth. Since the model is deterministic, it cannot be used directly for making stochastic forecasts. For that reason, the assumptions underlying the stochastic forecasts are based on expert judgement, taking into account the factors described by the model.

This paper examines how assumptions on the uncertainty of future changes in mortality in the long run can be specified. More precisely, it discusses the use of expert knowledge for the specification of the uncertainty of future mortality. Section 11.2 briefly describes the methodology underlying the Dutch stochastic population forecasts. Section 11.3 provides a general discussion on the use of expert knowledge in (stochastic) mortality forecasting. Section 11.4 applies the use of expert knowledge to the Dutch stochastic mortality forecasts. The paper ends with the main conclusions.

2 Stochastic Population Forecasts: Methodology

Population forecasts are based on assumptions about future changes in fertility, mortality, and migration. In the Dutch population forecasts assumptions on fertility refer to age-specific rates distinguished by parity, mortality assumptions refer to age- and sex-specific mortality rates, assumptions about immigration refer to absolute numbers, distinguished by age, sex and country of birth, and assumptions on emigration are based on a distinction of emigration rates by age, sex and country of birth.

Based on statistical models of fertility, mortality, and migration, statistical forecast intervals of population size and age structure can be derived, either analytically or by means of simulations. In order to obtain a forecast interval for the age structure of a population analytically a stochastic cohort-component model is needed. Application of such models, however, is very complicated. Analytical solutions require a large number of simplifying assumptions. Examples of applications of such models are given by Cohen (1986) and Alho and Spencer (1985). In both papers assumptions are specified of which the empirical basis is questionable.

Instead of an analytical solution, forecast intervals can be derived from simulations. On the basis of an assessment of the probability of the bandwidth of future values of fertility, mortality, and migration, the probability distribution of the future population size and age structure can be calculated by means of Monte Carlo simulations. For each year in the forecast period values of the total fertility rate, life expectancy at birth of men and women, numbers of immigrants and emigration rates are drawn from the probability distributions. Subsequently age-gender-specific fertility, mortality and emigration rates, and immigration numbers are specified. Each draw results in a population by age and gender at the end of each year. Thus the simulations provide a distribution of the population by age and gender in each forecast year.

To perform the simulations several assumptions have to be made. First, the type of probability distribution has to be specified. Subsequently, assumptions about the parameter values have to be made. The assumption about the mean or median value can be derived from the medium variant. Next, assumptions about the value of the standard deviation have to be assessed. In the case of asymmetric probability distributions additional parameters have to be specified. Finally, assumptions about the covariances between the forecast errors across age, between the forecast years, and between the components have to be specified (see e.g., Lee 1998).

The main assumptions underlying the probability distribution of the future population relate to the variance of the distributions of future fertility, mortality, and migration. The values of the variance can be assessed in three ways:

• (a) an analysis of errors of past forecasts may provide an indication of the size of the variance of the errors of new forecasts;

• (b) estimates of the variance can be based on a statistical (time-series) model;

• (c) on the basis of expert judgement values of the variance can be chosen.

These methods do not exclude each other; rather they may complement each other. For example, even if the estimate of the variance is based on past errors or on a time-series model judgement plays an important role. However, in publications the role of judgement is not always made explicit.

2.1 An Analysis of Errors of Past Forecasts

The probability of a forecast interval can be assessed on the basis of a comparison with the errors of forecasts published in the past. On the assumption that the errors are approximately normally distributed – or can be modelled by some other distribution – and that the future distribution of the errors is the same as the past distribution, these errors can be used to calculate the probability of forecast intervals of new forecasts. Keilman (1990) examines the errors of forecasts of fertility, mortality, and migration of Dutch population forecasts published between 1950 and 1980. He finds considerable differences between the errors of the three components. For example, errors in life expectancy grow considerably more slowly than errors in the total fertility rate. Furthermore, he examines to what extent errors vary between periods and whether errors of recent forecasts are smaller than those of older forecasts, taking into account the effect of differences in the length of the forecast period.

The question whether forecast accuracy has been increasing is important for assessing to what extent errors of past forecasts give an indication of the degree of uncertainty of new forecasts. One problem in comparing old and new forecasts is that some periods are easier to forecast than others. Moreover, a method that performs well in a specific period may lead to poor results in another period. Thus one should be careful in drawing general conclusions on the size of forecast errors on the basis of errors in a given period. For example, since life expectancy at birth of men in the Netherlands has been increasing linearly since the early 1970s, a simple projection based on a random walk model with drift would have produced rather accurate forecasts. Figure 11.1 shows that a forecast that would have been made in 1980 on the basis of a random walk model in which the intercept is estimated by the average change in the preceding 10 years would have been very accurate for the period 1980–2000. However, this does not necessarily imply that forecasts of life expectancy are very certain in the long run. If the same method would have been used for a forecast starting in 1975 the forecast would have been rather poor (Fig. 11.1). Thus simply comparing the forecast errors of successive forecasts does not tell us whether recent forecasts are ‘really’ better than preceding forecasts.

Fig. 11.1

Life expectancy at birth, men, projections of random walk (RW) with drift

The fact that a forecast of life expectancy of men made in 1980 is more accurate than a forecast made in 1975 does not imply that recent forecasts are more accurate than older forecasts. This is illustrated by Fig. 11.2 which shows projections of life expectancy of women. Projections of the life expectancy at birth of women based on a random walk model starting in 1980 are less accurate than projections starting in 1975.

Fig. 11.2

Life expectancy at birth, women, projections of random walk (RW) with drift

In order to be able to assess whether new forecasts are ‘really’ better than older ones, we need to know the reasons why the forecaster chose a specific method for a certain forecast period. This information enables us to conclude whether a certain forecast was accurate, because the forecaster chose the right method for the right period, or whether the forecaster was just more lucky in one period than in another.

Thus, in order to assess whether errors of past forecasts provide useful information about the uncertainty of new forecasts, it is important not only to measure the size of the errors but also to take into account the explanation of the errors. One main explanation of the poor development of life expectancy of men in the 1960s is the increase in smoking in previous decades, whereas the increase in life expectancy in subsequent years can partly be explained by a decrease in smoking. As women started to smoke some decades later than men, the development of life expectancy of women was affected negatively not until the 1980s. This explains why a linear extrapolation of the trend in life expectancy of women starting in 1980 leads to overestimating the increase in the 1980s and 1990s. On the other hand a linear extrapolation of the trend in life expectancy of men starting in 1975 leads to underestimating the increase in subsequent years.

The question to what extent an analysis of past errors provides useful information about the degree of uncertainty of new forecasts depends on the question how likely it is that similar developments will occur again. The 1970- based forecasts were rather poor because forecasters did not recognize that the negative development was temporary (Fig. 11.3). If it is assumed that it is very unlikely that such developments will occur again, one may conclude that errors of new forecasts are likely to be smaller than the errors of the 1970- based forecasts. For that reason, the degree of uncertainty of new forecasts can be based on errors of forecasts that were made after 1970.

Fig. 11.3

Life expectancy at birth, men, observations and historic forecasts

The decision which past forecasts to include is a matter of judgement. Thus, judgement plays a role in using errors of past forecasts for assessing the uncertainty of new forecasts. Obviously one may argue that an ‘objective’ method would be to include all forecasts made in the past. However, this implies that the results depend on the number of forecasts that were made in different periods. Since more forecasts were made after 1985 than in earlier periods, the errors of more recent forecasts weigh more heavily in calculating the average size of errors. On the other hand, for long-run forecasts one major problem in using errors of past forecasts for assessing the degree of uncertainty of new forecasts is that the sample of past forecasts tends to be biased towards the older ones, as for recent forecasts the accuracy cannot yet be checked except for the short run (Lutz et al. 1996a). Forecast errors for the very long run result from forecasts made a long time ago. Figure 11.3 shows that the 30 and 25 years ahead forecasts made in 1970 and 1975 respectively are rather poor, so including these forecasts in assessing the uncertainty of new forecasts may lead to overestimating the uncertainty in the long run. Figure 11.3 suggests that the forecasts made in the 1980s and 1990s may well lead to smaller errors in the long run than the forecasts made in the 1970s, since the former forecasts are closeer to the observations up to now than the latter forecasts were at the same forecast interval.

One way of assessing forecast errors in the long run is to extrapolate forecast errors by means of a time-series model (De Beer 1997). The size of forecast errors for the long run can be projected on the basis of forecast errors of recent forecasts for the short and medium run. Thus, estimates of ex ante forecast errors can be based on an extrapolation of ex post errors.

Rather than calculating errors in forecasts that were actually published, empirical forecast errors can be assessed by means of calculating the forecast errors of simple baseline projections. Alho (1998) notes that the point forecasts of the official Finnish population forecasts are similar to projections of simple baseline projections, such as assuming a constant rate of change of age-specific mortality rates. If these baseline projections are applied to past observations, forecast errors can be calculated. The relationship between these forecast errors and the length of the forecast period can be used to assess forecast intervals for new forecasts.

2.2 Model-Based Estimate of Forecast Errors

Instead of assuming that future forecast errors will be similar to errors of past forecasts, one may attempt to estimate the size of future forecast errors on the basis of the assumptions underlying the methods used in making new forecasts. If the forecasts are based on an extrapolation of observed trends, ex ante forecast uncertainty can be assessed on the basis of the time-series model used for producing the extrapolations. If the forecasts are based on a stochastic time-series model, the model produces not only the point forecast, but also the probability distribution. For example, ARIMA (Autoregressive Integrated Moving Average)-models are stochastic univariate time-series models that can be used for calculating the probability distribution of a forecast (Box and Jenkins 1970). Alternatively, a structural time-series model can be used for this purpose (Harvey 1989). The latter model is based on a Bayesian approach: the probability distribution may change as new observations become available. The Kalman filter is used for updating the estimates of the parameters.

One problem in using stochastic models for assessing the probability of a forecast is that the probability depends on the assumption that the model is correct. Obviously, the validity of this assumption is uncertain, particularly in the long run. If the point forecast of the time-series model does not correspond with the medium variant, the forecaster does apparently not regard the time-series model as correct. Moreover, time-series forecasting models were developed for short horizons, and they are not generally suitable for long run forecasts (Lee 1998). Usually, stochastic time-series models are identified on the basis of autocorrelations for short time intervals only. Alternatively, the form of the time-series model can be based on judgement to constraint the long-run behaviour of the point forecasts such that they are in line with the medium variant of the official forecast (Tuljapurkar 1996). However, one should be careful in using such a model for calculating the variance of ex ante forecast errors, because of the uncertainty of the validity of the constraint imposed on the model. In assessing the degree of uncertainty of the projections of the model one should take into account the uncertainty of the constraint, which is based on judgement.

2.3 Expert Judgement

In assessing the probability of forecast intervals on the basis of either an analysis of errors of past forecasts or an estimate of the size of model-based errors, it is assumed that the future will be like the past. Instead, the probability of forecasts can be assessed on the basis of experts’ opinions about the possibility of events that have not yet occurred. For example, the uncertainty of long-term forecasts of mortality depends on the probability of technological breakthroughs that may have a substantial impact on survival rates. Even though these developments may not be assumed to occur in the expected variant, an assessment of the probability of such events is needed to determine the uncertainty of the forecast. More generally, an assessment of ex ante uncertainty requires assumptions about the probability that the future will be different from the past. If a forecast is based on an extrapolation of past trends, the assessment of the probability of structural changes which may cause a reversal of trends cannot be derived directly from an analysis of historical data and therefore requires judgement of the forecaster. With regard to mortality the assessment of the probability of unprecedented events like medical breakthroughs cannot be derived directly from models. Lutz et al. (1996b) assess the probability of forecasts on the basis of opinions of a group of experts. The experts are asked to indicate the upper and lower boundaries of 90% forecast intervals for the total fertility rate, life expectancy, and net migration up to the year 2030. Subjective probability distributions of a number of experts are combined in order to diminish the danger of individual bias.

In the Dutch population forecasts the assessment of the degree of uncertainty of mortality forecasts is primarily based on expert judgement, taking into account errors of past forecasts and model-based estimates of the forecast errors.

3 Using Expert Knowledge

Expert knowledge or judgement usually plays a significant role in population forecasting. The choice of the model explaining or describing past developments cannot be made on purely objective, e.g., statistical criteria. Moreover, the application of a model requires assumptions about the way parameters and explanatory variables may change. Thus, forecasts of the future cannot be derived unambiguously from observations of the past. Judgement plays a decisive role in both the choice of the method and the way it is applied. “There can never be a population projection without personal judgement. Even models largely based on past time-series are subject to a serious judgemental issue of whether to assume structural continuity or any alternative structure” (Lutz et al. 1996a).

Forecasts of mortality can be based on extrapolation of trends in mortality indicators or on an explanatory approach. In both cases forecasters have to make a number of choices. In projecting future changes in mortality on the basis of an extrapolation of trends, one important question is which indicator is to be projected. If age- and gender-specific mortality rates are projected one may choose to assume the same change for each age (ignoring changes in the age pattern of mortality) or one may project each age-specific rate separately (which may result in a rather irregular age pattern). Instead of projecting separate age-specific mortality rates one may project a limited number of parameters of a function describing the age pattern of mortality, e.g., the Gompertz curve or the Heligman-Pollard model. One disadvantage of the Heligman-Pollard model is that it includes many parameters that cannot be projected separately. This makes the projection process complex. On the other hand, the disadvantage of using a simple model with few parameters is that such models usually do not describe the complete age pattern accurately. Another possible forecasting procedure is based on a distinction of age, period and cohort effects. If cohort effects can be estimated accurately, such models may be appropriate for making forecasts for the long run. However, one main problem in using an APC model is that the distinction between cohort effects and the interaction of period and age effects for young cohorts is difficult. Finally the indicator most widely used in mortality forecasting is life expectancy at various ages, especially life expectancy at birth. Using life expectancy at birth additional assumptions have to be made about changes in the age pattern of mortality rates.

In addition to the choice of the indicator to be projected, other choices have to be made. One main question is which observation period should be the basis for the projections. An extrapolation of changes observed in the last 20 or 30 years may result in quite different projections than an extrapolation of changes in the last 50 or more years. Another important question is the choice of the extrapolation procedure: linear or non-linear. This question is difficult to be answered on empirical grounds: different mathematical functions may describe observed developments about equally well, but may lead to quite different projections in the long run. In summary, judgement plays an important role in extrapolations of mortality.

Instead of an extrapolation of trends forecasts of mortality may be based on an explanatory approach. In making population forecasts usually a qualitative approach is followed. On the basis of an overview of the main determinants of mortality (e.g., changes in living conditions, life style, health care, safety measures, etc.) and of assumptions about both the impact of these determinants on the development of mortality and future changes in the determinants, it is concluded in which direction mortality may change. Clearly, if no quantitative model is specified, the assumptions about the future change in mortality are largely based on judgement. However, even if a quantitative model would be available, judgement would still play an important role, since assumptions would have to be made about the future development in explanatory variables.

In most developed countries life expectancy has been rising during a long period. Therefore, in assessing the uncertainty of forecasts of mortality the main question does not seem to be whether life expectancy will increase or decrease, but rather how strongly life expectancy will increase and how long the increase will continue. Basically, three types of change may be assumed. Firstly, one may assume a linear increase in life expectancy (which is not the same as a linear decrease of age-specific mortality rates) or a linear decline in the logarithm of the age-specific mortality rates. Such a trend may be explained by gradual improvements due to technological progress and increase in wealth. Secondly, one may assume that the rate of change is declining. For example, one may assume that the increase in life expectancy at birth will decline due to the fact that mortality rates for the youngest age groups are already so low that further improvements will be relatively small. More generally, the slowing down of the increase in life expectancy is related to the rectangularisation of the survival curve. Thirdly, it may be assumed that due to future medical breakthroughs life expectancy may increase more strongly than at present.

The assumption about the type of trend is not only relevant for the specification of the medium variant but also for assessing the degree of uncertainty of the forecasts. Obviously, if one assumes that trends will continue and that the uncertainty only concerns the question whether or not the rate of change will be constant or will decline gradually, the uncertainty of the future value of life expectancy is much smaller than if one assumes that life expectancy may change in new, unprecedented directions due to medical breakthroughs.

As discussed above, one problem in determining the long-run trend in life expectancy is the choice of the base period. If one fits a mathematical function to the observed time series of life expectancy in a given period, the results may be quite different than if a model is fitted to another period. Either the estimated values of the parameters of the function may differ or even another function may be more appropriate. One cause of the sensitivity of the fitted function to the choice of the period is that part of the changes in life expectancy are temporary. For example, the increase in smoking by men in the Netherlands starting before the Second World War to a level of about 90% in the 1950s and the decline in the 1960s and 1970s to a level of about 40% had a significant effect on the trend in life expectancy: it caused a negative development in life expectancy in the 1960s and an upward trend in the 1980s and 1990s. It is estimated that smoking reduced life expectancy at birth around 1975 by some 4 years. If the percentage of smokers stabilizes at the present level, the negative effect of smoking can be expected to decline to 2 years. This pattern of change in mortality due to smoking is one explanation why the choice of the base period for projecting mortality has a strong effect on the extrapolation. It makes a lot of difference whether the starting year of the base period is chosen before the negative effect of smoking on life expectancy became visible or around the time that the negative effect reached its highest value. Another example of transitory changes is the decline in mortality at young ages. In the first half of the twentieth century the decline in mortality of newborn children was much stronger than at present. As a consequence, life expectancy at birth increased more strongly than at present. If these transitory changes are not taken into account in fitting a function to the time series of life expectancy, the long-run projections may be biased as temporary changes are erroneously projected in the long run.

In order to avoid these problems, Van Hoorn and De Beer (2001) developed a model in which the development of life expectancy over a longer period, 1900–2000, is described by a long-term trend together with the assumed effects of smoking, the rectangularization of the survival curve, the introduction of antibiotics after the Second World War, the increase and subsequent decline in traffic accidents in the 1970s and changes in the gender difference due to other causes than smoking. The long-run trend is described by a negative exponential curve. Figure 11.4 shows the assumed effects of selected determinants on the level of life expectancy. Figure 11.5 shows that the model fits the data very well (see the appendix for a more extensive description of the model). Figure 11.5 also shows projections up to 2050. This model projects a smaller increase in life expectancy of men than, e.g., a linear extrapolation of the changes in the last 25 years or so would have done.

Fig. 11.4

Effects on life expectancy at birth

Fig. 11.5

Life expectancy at birth: observations and model

Since the model is deterministic, it cannot be used directly for making stochastic forecasts. The projections of the model are uncertain for at least two reasons. Firstly, it is not sure that the model is specified correctly. Several assumptions were made about effects on life expectancy which may be false. Secondly, in the future new unforeseen developments may occur that cannot be specified on the basis of observations. For example, future medical breakthroughs may cause larger increases in life expectancy than what we have seen so far. For this reason expert knowledge is necessary to estimate the probability and the impact of future events that have not occurred in the past.

4 Expert Knowledge in the Dutch Stochastic Mortality Forecasts

For making stochastic forecasts of mortality it is assumed that the projections of the model described in Sect. 11.3 correspond with the expected values of future life expectancy. Assuming future life expectancy to be normally distributed, assumptions need to be made on the values of the standard deviations of future life expectancy.

As mentioned in Sect. 11.2 both an analysis of previous forecasts and model-based estimates of forecast variances can be combined with expert judgement. One problem in using information on historic forecasts to assess the uncertainty of new long-run forecasts is that there are hardly any data on forecast errors for the long run. Alternatively, forecast errors for the long run can be projected on the basis of forecast errors for the short and medium term. Time-series of historic forecast errors can be modelled as a random walk model (without drift). On the basis of this model the standard error of forecast errors 50 years ahead is estimated at 2 years. This implies that the 95% forecast interval for the year 2050 equals 8 years. Alternatively, the standard error of forecast errors can be projected on the basis of a time-series model describing the development of life expectancy. The development of life expectancy at birth for men and women in the Netherlands can be described by a random walk model with drift (Lee and Tuljapurkar 1994, model mortality in the United States as a random walk with drift too). The width of the 95% forecast interval produced by this model for the year 2050 equals 12 years. Thus, on the basis of the time-series models of life expectancy and models of forecast errors of life expectancy it can be expected that the 95% forecast interval of life expectancy in 2050 will be around 8–12 years. The decision which interval is to be used is based on judgement. Judgement ought to be based on an analysis of the processes underlying changes in life expectancy. The judgemental assumptions underlying the Dutch forecasts are based on four considerations.

• (1) It is regarded highly likely that the difference in mortality between men and women will continue to decrease. This difference has arisen in the past decades largely because of differences in smoking habits. As smoking habits of men and women have become more similar, the gender difference in life expectancy is assumed to decrease in the forecasts.

• (2) Changes in life expectancy at birth are the result of changes in mortality for different age groups. In assessing the degree of uncertainty of forecasts of life expectancy, it is important to make a distinction by age as the degree of uncertainty of future changes in mortality differs between age categories. The effect of the uncertainty about the future development of mortality at young ages on life expectancy at birth is only small, because of the current, very low levels of mortality at young ages. On the basis of the current age specific mortality rates, 95.3% of live born men and 96.6% of women would reach the age of 50. Clearly, the upper limits are not far away. According to the medium variant of the 2000 Dutch population forecasts the percentage of men surviving to age 50 will rise to 97.0% in 2050 and the percentage of women to 97.4%. A much larger increase is not possible. A decrease does not seem very likely either. That would, e.g., imply that infant mortality would increase, but there is no reason for such an assumption. The increase in the population with a foreign background could have a negative effect on mortality, since the infant mortality rates for this population group are considerably higher than those for the native population. However, it seems much more likely that infant mortality rates for the foreign population will decline rather than that they would increase. Furthermore, the effect on total mortality is limited. Another cause of negative developments at young ages could be new, deadly diseases. The experience with AIDS, however, has shown that the probability that such developments would have a significant impact on total mortality in the Netherlands (in contrast with, e.g., African countries) does not seem very large. A third possible cause of negative developments at young ages would be a strong increase in accidents or suicides. However, there are no indications of such developments. Thus it can be concluded that the effect of the uncertainty about mortality at young ages on the uncertainty about the future development of life expectancy at birth is limited.

• (3) As regards older age groups one main assumption underlying the Dutch mortality forecasts is that the main cause of the increase in life expectancy at birth is that more people will become old rather than old people becoming still older. This implies the assumption that the survival curve will become more rectangular, an assumption based on an analysis of changes in age-specific mortality rates. The development of mortality rates for the eldest age groups in the 1980s and 1990s has been less favourable than for the middle ages. Another reason for assuming ‘rectangularisation’ of the survival curve is that expectations about a large increase in the maximum life span seem rather speculative, and even if they would become true, it is questionable whether their effect would be large during the next 50 years or so. A very strong progress of life expectancy can only be reached if life styles would change drastically or if medical technology would generate fundamental improvements (and health care would be available for everyone). Assuming a tendency towards rectangularisation of the survival curve implies that uncertainty about the future percentage of survivors around the median age of dying is relatively high. If the percentage of survivors around that age would be higher than in the medium variant (i.e., if the median age would be higher), the decrease in the slope of the survival curve at the highest ages age will be steeper than in the medium variant. Thus, the deviation from the medium variant at the highest ages will be smaller than around the median age. This implies that the degree of uncertainty associated with forecasts of life expectancy at birth mainly depends on changes in the median age of dying rather than on changes in the maximum life span. According to the medium variant of the 2000 population forecasts the percentage of survivors at age 85 in the year 2050 will be little under 50% for men and slightly over 50% for women. For that reason the degree of uncertainty of the mortality forecast is based on the assessment of a forecast interval at age 85.

• (4) The last consideration concerns the important point of discussion whether medical breakthroughs can lead to an unexpectedly strong increase of life expectancy. Even in case of a significant improvement of medical technology, it will be questionable to what extent this future improvement will lengthen the life span of present generations. It should be kept in mind that the mortality forecasts are made for the period up to 2050, and thus primarily concern persons already born. Experts who think that a life expectancy at birth could reach a level of 100 years or higher usually do not indicate when such a high level could be reached. It seems very unlikely that this will be the case in the period before 2050.

The four considerations discussed above are used to specify forecast intervals. According to the medium variant assumptions on the age-specific mortality rates for the year 2050, 41% of men will survive to age 85 (Fig. 11.6). According to the present mortality rates, little more than 25% of men would reach age 85. Because it is assumed to be unlikely that possible negative developments (e.g., a strong increase in smoking or new diseases) will predominate positive effects of improvement in technology and living conditions during a very long period of time, the lower limit of the 95% forecast interval for the year 2050 is based on the assumption that it is very unlikely that the percentage of survivors in 2050 will be significantly lower than the current percentage. For the lower limit it is assumed that one out of five men will survive to age 85. This would imply that the median age of death is 77.5 years. The upper limit of the forecast interval is based on the assumption that it is very unlikely that about two thirds of men will survive past the age of 85. The median age of death would increase to 88 years. Currently, only 16% of men survive past the age of 88. A higher median age at dying than 88 seems thus very unlikely.

Fig. 11.6

Survivors at age 85; medium variant and 95% forecast interval

As discussed above, the medium variant assumes that the gender difference will become smaller. This implies that life expectancy of women will increase less strongly than that of men. This is in line with the observed development since the early 1980s. Consequently, the probability that future life expectancy of women will be lower than the current level is higher than the corresponding probability for men. The lower limit of the 95% forecast interval corresponds with a median age at dying of 81 years, which equals the level reached in the early 1970s. This could become true, e.g., if there would be a strong increase in mortality by lung cancer and coronary heart diseases due to an increase in smoking. The upper limit of the forecast interval is based on the assumption that three quarters of women will reach age 85. This would imply that half of women would become older than 91 years. This is considerably higher than the current percentage of 21. It does not seem very likely that the median age would become still higher.

The intervals for the percentage of survivors at the age of 85 for the intermediate years are assessed on the basis of the random walk model (Fig. 11.6).

On the basis of these upper and lower limits of the 95% forecast interval for percentages of survivors at age 85, forecast intervals for percentages of survivors at the other ages are assessed, based on the judgemental assumption that for the youngest and eldest ages the intervals are relatively smaller than around the median age (Fig. 11.7). The age pattern of changes in mortality rates in the upper and lower limit are assumed to correspond with the age pattern in the medium variant.

Fig. 11.7

Survival curves; medium variant and 95% forecast interval

The assumptions on the intervals of age-specific mortality rates are used to calculate life expectancy at birth. These assumptions result in a 95% forecast interval for life expectancy at birth in 2050 of almost 12 years. For men the interval ranges from 73.7 to 85.4 years and for women from 76.7 to 88.5 years (Fig. 11.8). The width of these intervals closely corresponds with that of the interval based on the random walk with drift model of life expectancy at birth mentioned before.

Fig. 11.8

Life expectancy at birth; medium variant and 95% forecast interval

The intervals for the Netherlands are slightly narrower than the intervals for Germany specified by Lutz and Scherbov (1998). They assume that the width of the 90% interval equals 10 years in 2030. This is based on the assumption that the lower and upper limits of the 90% interval of the annual increase in life expectancy at birth equal 0 and 0.3 years respectively. This would imply that the width of the 90% interval in 2050 equals about 15 years.

5 Conclusions

Long-term developments in mortality are very uncertain. To assess the degree of uncertainty of future developments in mortality and other demographic events several methods may be used: an analysis of errors of past forecasts, a statistical (time-series) model and expert knowledge or judgement. These methods do not exclude each other; rather they may complement each other. For example, even if the assessment of the degree of uncertainty is based on past errors or on a time-series model judgement plays an important role. However, in publications the role of judgement is not always made explicit.

The most recent Dutch mortality forecasts are based on a model that forecasts life expectancy at birth. Implementation of the model is based on literature and expert knowledge. The model includes some important determinants of mortality, such as the effect of smoking and gender differences. Since the model is deterministic, it cannot be used for stochastic forecasting. Therefore, an expert knowledge approach is followed. This approach can be described as ‘argument-based forecasting’. Basically, four quantitative assumptions are made: (1) the difference in mortality between men and women will continue to decrease, (2) the effect of uncertainty about mortality is limited at young ages and is highest around the median age of dying, (3) the effect of medical breakthroughs on the life span will be limited up to 2050, and (4) more people will become old rather than old people will become still older (rectangularisation of the survival curve). Based on these assumptions target values for the boundaries of 95% forecast intervals are specified. It appears that the width of the 95% interval of life expectancy at birth in 2050 is almost 12 years, both for men and women. This interval closely resembles the interval based on a random walk model with drift. It is about 4 years wider than the interval based on a time-series model of errors of historic forecasts.

Appendix: An Explanatory Model for Dutch Mortality

There are several ways to explain mortality. One approach is to assume a dichotomy of determinants of mortality – internal factors and external factors. For instance age, sex and constitutional factors are internal, whereas living and working conditions as well as socio-economic, cultural and environmental conditions are external. Other factors, such as life styles and education are partly internal, partly external.

An alternative approach takes the life course as a leading principle for a causal scheme. Determinants that act in early life are placed in the beginning of the causal scheme, those that have an impact later in life are put at the end. In this way heredity comes first and medical care comes last. Factors like life styles are in the middle. In the following scheme this approach is elaborated, though some elements of the first approach are used also. Eight categories of important determinants are distinguished:

• A. Heredity (including gender)

• B. Gained properties (education, social status)

• C. Life styles (risk factors like smoking, relationships)

• D. Environment (living and working conditions)

• E. Health policy (prevention of accidents, promotion of healthy life styles)

• F. Medical care (technological progress and accessibility of cure and care)

• G. Period effects (wars, epidemics)

• H. Rectangularity of survival curve

Interactions of gender with other factors should be taken in account in forecasting mortality because a lot of differences between men and women exist. Categories A, B, C and D reflect heterogeneity in mortality in the population, while groups E, F and G reflect more general influences. As life expectancy is the dependent variable in the explanatory model, a supplementary factor (H) is needed which is dependent on the age profile of the survival curve. When the survival curve becomes more rectangular, a constant increase in life expectancy can only be achieved through ever-larger reductions of mortality rates.

Most of the eight categories listed above contain many determinants. Of course it is not possible to trace and quantify all determinants. The selection of variables is based on the following criteria:

• 1. there is evidence about the magnitude of the effect and about changes over time;

• 2. independence of effects; and

• 3. there is a good possibility to formulate assumptions for the future.

In category C (life styles), smoking is a good example of a suitable explanatory factor since there is considerable evidence about the prevalence of smoking in the population and the effect on mortality. In category E the effect of safety measures on death from traffic accidents is an example of an independent and relatively easy factor to estimate. The same holds for category F for the introduction of antibiotics which caused a sharp drop in mortality by pneumonia.

On the contrary, general medical progress is not a very suitable factor, because there is much uncertainty and divergence of opinions about the impact on life expectancy. The effect is hard to separate from that of social progress, growth of prosperity, cohort-effects etc.

Part of the variation in mortality (life expectancy) can be modelled by separate effects, the rest is included in the trend. It must be stressed that the model does not quantify the effect of the determinants on causes of death (for instance smoking on death rates of lung cancer and heart diseases), but directly links them with overall mortality (life expectancy).

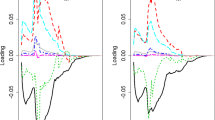
Six determinants that meet the three criteria were included in the model. Figure 11.4 in the paper shows the assumptions about the effect of these determinants on life expectancy at birth in the observation period (1900–2000) and the forecast period (2001–2050).

• A. Heredity: gender difference. Part of the gender difference in mortality can be attributed to differences in smoking behaviour (see C). Gender differences due to other factors were not constant through the entire twentieth century. However, since 1980 the difference seems to have stabilised. The change in the gender difference in life expectancy in the twentieth century can be described by a log normal curve.

• B. Gained properties. There are strong differences in mortality between social groups. However, these effects were not included in the model. One reason is that there is a strong correlation with, e.g., life styles, living and working conditions and access to medical care. Thus, the second criterion mentioned above is violated.

• C. Life style: smoking. On the basis of the literature the different effects for men and women are estimated. The effects can be quantified with a combination of a normal and a logistic curve. Smoking largely explains the quite different developments of life expectancy for men and women in the past decades. As smoking habits of men and women become more similar, in the forecasts the gender difference in life expectancy is assumed to decrease and finally become 3 years (in favour of women).

• D. Environment. These effects can be characterised as gradual long-term changes. It is hard to distinguish these effects from a general long-term trend. Hence these factors are not included in the model as separate effects but are included in the trend.

• E. Health policy: traffic accidents. In the early 1970s measures were taken to improve safety of traffic. As a result the number of deaths by traffic accidents declined. This effect is modelled as a deviation of the trend. Around 1970 the number of traffic accidents reached its highest level. A log normal curve appears to be appropriate for describing changes through time.

• F. Medical care: introduction of antibiotics. After the Second World War the introduction of antibiotics caused a sharp decline of mortality by pneumonia. A logistic function describes the rise in life expectancy and the flattening out to a constant level.

• G. Period effects: outliers. The Spanish flue and the Second World War caused sharp negative deviations of life expectancy, which are modelled by dummies.

• H. Rectangularity. The shape of the survival curve has an important impact on the pace of the increase of life expectancy. If the survival curve in year t is more rectangular than in year s, a given reduction in all age-specific death rates in both years will result in a smaller increase in life expectancy in year t than in year s. We define the rectangularity effect as the growth of life expectancy in year t divided by the growth in the year 1895 caused by the same percentage of decline of all age-specific mortality rates. A linear spline function is used to smooth the results. The increase in life expectancy in 1995 appears to be only 40% of that in 1895.

The new model contains a lot of parameters and simultaneous estimation can be problematic (unstable estimates). Therefore, the parameters were estimated in two steps. In the first step values of parameters of the functions describing the effect of smoking, traffic accidents, the introduction of antibiotics, and rectangularity were chosen in such a way that the individual functions describe patterns that correspond with available evidence. In the second step the values of the trend parameters and the outliers were estimated on the basis of non-linear least squares and some values of parameters fitted in the first step were ‘fine-tuned’.

Several functions were tested to fit the trend. A negative exponential curve appears to fit the development since 1900 best (see Fig. 11.5 in the paper). This function implies that there is a limit to life expectancy. However, according to the fitted model this is not reached before 2100.

The model is:

$$ {e}_{0,g,t}={T}_t+{S}_{g,t}+{V}_t+{A}_t+{G}_{g,t}+\sum \limits_{j=1917}^{1919}{u}_{j,g,t}+\sum \limits_{\mathrm{j}=1940}^{1945}{u}_{j,g,t}+{\varepsilon}_{g,t} $$

$$ {T}_t={a}_0+{H}_t{R}_t $$

$$ {H}_t={a}_1{e}^{-{a}_2\left(t-{t}_1\right)} $$

$$ {R}_t=1-{b}_1\left(t-{t}_2\right)-{b}_2\left(t-{t}_3\right){D}_{1,t} $$

$$ {D}_{1,t}=0\; if\;t<{t}_3\; and\;{D}_{1,t}=1\; if\ge {t}_3 $$

$$ {S}_{g,t}={c}_{g,1}{e}^{-{c}_{g,2}{\left(t-{t}_4\right)}^2}+\frac{c_{g,3}}{1+{c}_{g,4}{e}^{-{c}_{g,5}\left(t-{t}_5\right)}}+\frac{c_{g,6}}{1+{c}_{g,7}{e}^{-{c}_{g,8}\left(t-{t}_6\right)}}+{c}_{g,9} $$

$$ {V}_t={d}_1{e}^{-{d}_2\ln {\left(t/{t}_7\right)}^2} $$

$$ {A}_t=\frac{f_1}{1+{f}_2{e}^{-{f}_3\left(t-{t}_8\right)}}+{f}_4 $$

$$ {\displaystyle \begin{array}{l}{G}_{g,t}=\left({h}_1{e}^{-{h}_2\ln {\left(t/{t}_9\right)}^2}+{h}_3\right){D}_{2,g}\\ {}\end{array}} $$

$$ {D}_{2,g}=1\; if\;g= female\kern0.17em and\;{D}_{2,g}=0\; if\;g= male $$

$$ {u}_{j,g,t}=1\; if\;t=j\; and\;{u}_{j,g,t}=0\; in\kern0.17em other\kern0.17em years, $$

where e _0,g,t is life expectancy at birth for gender g in year t, T is trend, S is the effect of smoking, V is the effect of traffic accidents, A is the introduction of antibiotics, G is the unexplained gender difference, u are outliers, ε is error, H is slope of the trend and R is the effect of the rectangularity of the survival curve.