Abstract
Exact geometric computation (EGC) is a general approach for achieving robust numerical algorithms that satisfy geometric constraints. At the heart of EGC are various Zero Problems, some of which are not-known to be decidable and others have high computational complexity. Our current goal is to introduce notions of “soft- correctness” in order to avoid Zero Problems. We give a bird’s eye view of our recent work with collaborators in two principle areas: computing zero sets and robot path planning. They share a common Subdivision Framework. Such algorithms (a) have adaptive complexity, (b) are practical, and (c) are effective. Here, “effective algorithm” means it is easily and correctly implementable from standardized algorithmic components. Our goals are to outline these components and to suggest new components to be developed. We discuss a systematic pathway to go from the abstract algorithmic description to an effective algorithm in the subdivision framework.
correctness” in order to avoid Zero Problems. We give a bird’s eye view of our recent work with collaborators in two principle areas: computing zero sets and robot path planning. They share a common Subdivision Framework. Such algorithms (a) have adaptive complexity, (b) are practical, and (c) are effective. Here, “effective algorithm” means it is easily and correctly implementable from standardized algorithmic components. Our goals are to outline these components and to suggest new components to be developed. We discuss a systematic pathway to go from the abstract algorithmic description to an effective algorithm in the subdivision framework.
This work is supported by NSF Grants CCF-1423228 and CCF-1564132.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
Monotone means
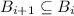 for all i.
for all i. - 3.
The factor \(\sigma >1\) was call the “effectivity factor” in [49]. In the present paper, we avoid this terminology since it conflicts with our notion of “effectivity” of this paper.
- 4.
The
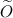 -notation is like the O-notation except that logarithm factors in n and in L are ignored. In the subdivision setting, “near-optimality” may be taken to be
-notation is like the O-notation except that logarithm factors in n and in L are ignored. In the subdivision setting, “near-optimality” may be taken to be
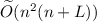 .
. - 5.
Some authors introduce a new symbol, say F, to signal this change.
- 6.
In the spirit of Knuth’s “Literate Programming”.
- 7.
It is possible that such proofs contribute to the poor reputation of error analysis as a topic.
- 8.
We use “precision” for the a priori user-specified bound. The algorithm delivers a value whose a posteriori error is at most this precision.
- 9.
We write \(a = b\pm c\) to mean there exists a constant \(\theta \in [-1,1]\) such that \(a = b+\theta \cdot c\). Alternatively, \(|a-b|\le |c|\).
- 10.
Despite the appearance of asymmetry, x and y are treated symmetrically by this definition.
- 11.
There should no confusion with the notion support of a simplicial complex
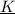 .
. - 12.
Strict inequality may arise in subsets of zero sets: if
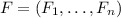 where \(F_i\) are polynomials, and
where \(F_i\) are polynomials, and
 where each \(G_i\) divides \(F_i\), then
where each \(G_i\) divides \(F_i\), then
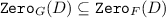 might exhibit this phenomenon.
might exhibit this phenomenon.
References
Abbott, J.: Quadratic interval refinement for real roots. ACM Commun. Comput. Algebra 48(1/2), 3–12 (2014). https://doi.org/10.1145/2644288.2644291. http://doi.acm.org/10.1145/2644288.2644291
Agrawal, A., Requicha, A.: A paradigm for the robust design of algorithms for geometric modeling. In: Computer Graphics Forum, vol. 13, no. 3, pp. 33–44 (1994). 15th Annual Conference and Exhibition. EUROGRAPHICS 1994
Becker, R.: The Bolzano method to isolate the real roots of a bitstream polynomial. Bachelor thesis, University of Saarland, Saarbruecken, Germany, May 2012
Becker, R., Sagraloff, M., Sharma, V., Xu, J., Yap, C.: Complexity analysis of root clustering for a complex polynomial. In: 41st International Symposium on Symbolic and Algebraic Computation, iSSAC 2016, Wilfrid Laurier University, Waterloo, Canada, 20–22 July, pp. 71–78 (2016)
Becker, R., Sagraloff, M., Sharma, V., Yap, C.: A near-optimal subdivision algorithm for complex root isolation based on Pellet test and Newton iteration. J. Symbolic Comput. 86, 51–96 (2018)
Bennett, H., Papadopoulou, E., Yap, C.: Planar minimization diagrams via subdivision with applications to anisotropic Voronoi diagrams. In: Eurographics Symposium on Geometric Processing, SGP 2016, Berlin, Germany, 20–24 June 2016, vol. 35, no. 5 (2016)
Bennett, H., Yap, C.: Amortized analysis of smooth quadtrees in all dimensions. Comput. Geom. Theory Appl. 63, 20–39 (2017). Also, in Proceedings SWAT 2014
de Berg, M., Cheong, O., van Kreveld, M., Overmars, M.: Computational Geometry: Algorithms and Applications, 3rd edn. Springer, Berlin (2008). https://doi.org/10.1007/978-3-540-77974-2
Boissonnat, J.D., Teillaud, M. (eds.): Effective Computational Geometry for Curves and Surfaces. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-33259-6
Brauße, F., et al.: Semantics, logic, and verification of “exact real computation” (2019)
Brent, R.P.: Algorithms for Minimization Without Derivatives. Prentice Hall, Englewood Cliffs (1973)
Burr, M., Krahmer, F.: SqFreeEVAL: an (almost) optimal real-root isolation algorithm. J. Symbolic Comput. 47(2), 153–166 (2012)
Burr, M., Krahmer, F., Yap, C.: Continuous amortization: a non-probabilistic adaptive analysis technique. Electronic Colloquium on Computational Complexity (ECCC) TR09(136), December 2009. http://eccc.hpi-web.de/report/2009/136/
Burr, M.A.: Continuous amortization and extensions: with applications to bisection-based root isolation. J. Symb. Comput. 77, 78–126 (2016). https://doi.org/10.1016/j.jsc.2016.01.007
Burr, M.A., Gao, S., Tsigaridas, E.: The complexity of an adaptive subdivision method for approximating real curves. In: 42nd International Symposium on Symbolic and Algebraic Computation (ISSAC), ISSAC 2017, pp. 61–68. ACM, New York (2017). https://doi.org/10.1145/3087604.3087654
Burr, M.A., Gao, S., Tsigaridas, E.: The complexity of subdivision for diameter-distance tests. J. Symbolic Computation (2019, to appear)
Cucker, F., Ergür, A.A., Tonelli-Cueto, J.: Plantinga-vegter algorithm takes average polynomial time. arXiv:1901.09234 [cs.CG] (2019)
Du, Z., Eleftheriou, M., Moreira, J., Yap, C.: Hypergeometric functions in exact geometric computation. In: Brattka, V., Schoeder, M., Weihrauch, K. (eds.) Proceedings of 5th Workshop on Computability and Complexity in Analysis, Malaga, Spain, 12–13 July 2002, pp. 55–66 (2002). In Electronic Notes in Theoretical Computer Science 66:1 (2002). http://www.elsevier.nl/locate/entcs/volume66.html
Du, Z., Yap, C.: Uniform complexity of approximating hypergeometric functions with absolute error. In: Pae, S., Park, H. (eds.) Proceedings of 7th Asian Symposium on Computer Mathematics, ASCM 2005, pp. 246–249 (2006)
Emiris, I.Z., Pan, V.Y., Tsigaridas, E.P.: Algebraic algorithms. In: Gonzalez, T., Diaz-Herrera, J., Tucker, A. (eds.) Computing Handbook: Computer Science and Software Engineering, 3rd edn., pp. 10: 1–30. Chapman and Hall/CRC, Boca Raton (2014)
Higham, N.J.: Accuracy and Stability of Numerical Algorithms, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2002)
Hsu, C.H., Chiang, Y.J., Yap, C.: Rods and rings: soft subdivision planner for \({ R}^{3}\) x \({S}^{2}\). In: Proceedings of 35th International Symposium on Computational Geometry, SoCG 2019, 18–21 June 2019. CG Week 2019, Portland Oregon. Also in arXiv:1903.09416
Imbach, R., Pan, V.Y., Yap, C.: Implementation of a near-optimal complex root clustering algorithm. In: Davenport, J.H., Kauers, M., Labahn, G., Urban, J. (eds.) ICMS 2018. LNCS, vol. 10931, pp. 235–244. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96418-8_28
Imbach, R., Pouget, M., Yap, C.: Effective subdivision algorithm for isolating zeros of real systems of equations, with complexity analysis, 21st CASC, Moscow (2019, to appear)
Kearfott, R.B.: Rigorous Global Search: Continuous Problems, vol. 13. Springer, Dordrecht (2013). https://doi.org/10.1007/978-1-4757-2495-0
Kerber, M., Sagraloff, M.: Efficient real root approximation. In: Schost, É., Emiris, I.Z. (eds.) ISSAC, pp. 209–216. ACM (2011)
Kincaid, D., Cheney, W.: Numerical Analysis: Mathematics of Scientific Computing, 3rd edn. Brooks/Cole, Boston (2002)
Ko, K.I.: Complexity Theory of Real Functions. Progress in Theoretical Computer Science. Birkhäuser, Boston (1991)
Lien, J.-M., Sharma, V., Vegter, G., Yap, C.: Isotopic arrangement of simple curves: an exact numerical approach based on subdivision. In: Hong, H., Yap, C. (eds.) ICMS 2014. LNCS, vol. 8592, pp. 277–282. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44199-2_43
Lin, L., Yap, C.: Adaptive isotopic approximation of nonsingular curves: the parameterizability and nonlocal isotopy approach. Discrete Comp. Geom. 45(4), 760–795 (2011)
Lin, L., Yap, C., Yu, J.: Non-local isotopic approximation of nonsingular surfaces. Comput. Aided Des. 45(2), 451–462 (2012). Symposium on Solid and Physical Modeling (SPM). U. of Burgundy, Dijon, France, 29–31 October 2012
Mehlhorn, K., Schirra, S.: Exact computation with leda\_real - theory and geometric applications. In: Alefeld, G., Rohn, J., Rump, S., Yamamoto, T. (eds.) Symbolic Algebraic Methods and Verification Methods, pp. 163–172. Springer, Vienna (2001). https://doi.org/10.1007/978-3-7091-6280-4_16
Moore, R.E.: Interval Analysis. Prentice Hall, Englewood Cliffs (1966)
Ó’Dúnlaing, C., Yap, C.K.: A “retraction” method for planning the motion of a disc. J. Algorithms 6, 104–111 (1985). Also, Chapter 6 in Planning, Geometry, and Complexity, eds. Schwartz, Sharir and Hopcroft, Ablex Pub. Corp., Norwood, NJ 1987
Pedersen, P.: Counting real zeros. In: Proceedings of Conference on Algebraic Algorithms and Error Correcting Codes. LNCS, vol. 539, pp. 318–332. Springer (1991)
Pedersen, P.: Counting real zeros. Ph.D. thesis, New York University (1991). Also, Courant Institute Computer Science Technical Report 545 (Robotics Report R243)
Pedersen, P., Roy, M.-F., Szpirglas, A.: Counting real zeros in the multivariate case. In: Eyssette, F., Galligo, A. (eds.) Computational Algebraic Geometry. PM, vol. 109, pp. 203–224. Birkhäuser, Boston (1993). https://doi.org/10.1007/978-1-4612-2752-6_15
Plantinga, S., Vegter, G.: Isotopic approximation of implicit curves and surfaces. In: Proceedings of Eurographics Symposium on Geometry Processing, pp. 245–254. ACM Press, New York (2004)
Preparata, F.P., Shamos, M.I.: Computational Geometry. Springer, New York (1985). https://doi.org/10.1007/978-1-4612-1098-6
Riley, K., Hopson, M., Bence, S.: Mathematical Methods for Physics and Engineering, 3rd edn. Cambridge University Press, New York (2006)
Sagraloff, M., Yap, C.K.: A simple but exact and efficient algorithm for complex root isolation. In: Emiris, I.Z. (ed.) 36th International Symposium on Symbolic and Algebraic Computing, San Jose, California, 8–11 June, pp. 353–360 (2011)
Sagraloff, M., Yap, C.K.: An efficient exact subdivision algorithm for isolating complex roots of a polynomial and its complexity analysis, July 2009, submitted. Full paper from http://cs.nyu.edu/exact/ or http://www.mpi-inf.mpg.de/~msagralo/
Schuurman, P., Woeginger, G.: Approximation schemes: a tutorial. In: Möhring, R., Potts, C., Schulz, A., Woeginger, G., Wolsey, L. (eds.) Lectures in Scheduling (2007, to appear)
Sharma, V., Yap, C.: Near optimal tree size bounds on a simple real root isolation algorithm. In: 37th International Symposium on Symbolic and Algebraic Computing, ISSAC 2012, Grenoble, France, 22–25 July 2012, pp. 319–326 (2012)
Sharma, V., Yap, C.K.: Robust geometric computation. In: Goodman, J.E., O’Rourke, J., Tóth, C. (eds.) Handbook of Discrete and Computational Geometry, 3rd edn., chap. 45, pp. 1189–1224. Chapman & Hall/CRC, Boca Raton (2017)
Snyder, J.: Generative Modeling for Computer Graphics and CAD. Symbolic Shape Design Using Interval Analysis. Academic Press Professional Inc., San Diego (1992)
Trefethen, L.N., Bau, D.: Numerical Linear Algebra. Society for Industrial and Applied Mathematics, Philadelphia (1997)
Ueberhuber, C.W.: Numerical Computation 2: Methods, Software, and Analysis. Springer, Berlin (1997)
Wang, C., Chiang, Y.J., Yap, C.: On soft predicates in subdivision motion planning. Comput. Geom. Theory Appl. 48(8), 589–605 (2015). (Special Issue for SoCG 2013)
Weihrauch, K.: Computable Analysis. Springer, Berlin (2000). https://doi.org/10.1007/978-3-642-56999-9
Xu, J., Yap, C.: Effective subdivision algorithm for isolating zeros of real systems of equations, with complexity analysis. In: 44th International Symposium Symbolic and Algebraic Computing, Beihang University, Beijing, 15–18 July (2019)
Yap, C., Sagraloff, M., Sharma, V.: Analytic root clustering: a complete algorithm using soft zero tests. In: Bonizzoni, P., Brattka, V., Löwe, B. (eds.) CiE 2013. LNCS, vol. 7921, pp. 434–444. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39053-1_51
Yap, C.K.: Soft subdivision search in motion planning, II: axiomatics. In: Wang, J., Yap, C. (eds.) FAW 2015. LNCS, vol. 9130, pp. 7–22. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19647-3_2
Yap, C., Luo, Z., Hsu, C.H.: Resolution-exact planner for thick non-crossing 2-link robots. In: Proceedings of 12th International Workshop on Algorithmic Foundations of Robotics, WAFR 2016, San Francisco, 13–16 December 2016 (2016). The appendix in the full paper (and arXiv from http://cs.nyu.edu/exact/ (and arXiv:1704.05123 [cs.CG]) contains proofs and additional experimental data
Yap, C.K.: On guaranteed accuracy computation. In: Chen, F., Wang, D. (eds.) Geometric Computation, chap. 12, pp. 322–373. World Scientific Publishing Co., Singapore (2004)
Yap, C.K.: In praise of numerical computation. In: Albers, S., Alt, H., Näher, S. (eds.) Efficient Algorithms. LNCS, vol. 5760, pp. 380–407. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03456-5_26
Yu, J., Yap, C., Du, Z., Pion, S., Brönnimann, H.: The design of core 2: a library for exact numeric computation in geometry and algebra. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 121–141. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15582-6_24
Acknowledgements
The author is deeply grateful for the feedback and bug reports from Michael Burr, Matthew England, Rémi Imbach, Juan Xu and Bo Huang.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Yap, C. (2019). Towards Soft Exact Computation (Invited Talk). In: England, M., Koepf, W., Sadykov, T., Seiler, W., Vorozhtsov, E. (eds) Computer Algebra in Scientific Computing. CASC 2019. Lecture Notes in Computer Science(), vol 11661. Springer, Cham. https://doi.org/10.1007/978-3-030-26831-2_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-26831-2_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26830-5
Online ISBN: 978-3-030-26831-2
eBook Packages: Computer ScienceComputer Science (R0)


 then there is some
then there is some 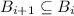 for all i.
for all i.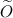 -notation is like the O-notation except that logarithm factors in n and in L are ignored. In the subdivision setting, “near-optimality” may be taken to be
-notation is like the O-notation except that logarithm factors in n and in L are ignored. In the subdivision setting, “near-optimality” may be taken to be
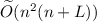 .
.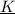 .
.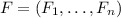 where
where  where each
where each 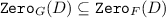 might exhibit this phenomenon.
might exhibit this phenomenon.