Abstract
We consider several macroscopic models, based on systems of conservation laws, for the study of crowd dynamics. All the systems considered here contain nonlocal terms, usually obtained through convolutions with smooth functions, used to reproduce the visual horizon of each individual. We classify the various models according to the physical domain (the whole space \({\mathbb {R}}^N\) or a bounded subset), to the terms affected by the nonlocal operators, and to the number of different populations we aim to describe. For all these systems, we present the basic well posedness and stability results.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
A. Aggarwal, R.M. Colombo, P. Goatin, Nonlocal systems of conservation laws in several space dimensions. SIAM J. Numer. Anal. 53(2), 963–983 (2015)
J.P. Agnelli, F. Colasuonno, D. Knopoff, A kinetic theory approach to the dynamics of crowd evacuation from bounded domains. Math. Models Methods Appl. Sci. 25(1), 109–129 (2015)
P. Amorim, R.M. Colombo, A. Teixeira, On the numerical integration of scalar nonlocal conservation laws. ESAIM Math. Model. Numer. Anal. 49(1), 19–37 (2015)
F. Bagarello, F. Gargano, F. Oliveri, A phenomenological operator description of dynamics of crowds: escape strategies. Appl. Math. Model. 39(8), 2276–2294 (2015)
R. Bailo, J.A. Carrillo, P. Degond, Pedestrian models based on rational behaviour, in Modeling and Simulation in Science, Engineering and Technology (Birkhäuser, New York, 2018), pp. 259–292
N. Bellomo, A. Bellouquid, On multiscale models of pedestrian crowds from mesoscopic to macroscopic. Commun. Math. Sci. 13(7), 1649–1664 (2015)
N. Bellomo, S. Berrone, L. Gibelli, A.B. Pieri, Macroscopic first order models of multicomponent human crowds with behavioral dynamics, in Advances in Computational Fluid-Structure Interaction and Flow Simulation. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2016), pp. 295–306
N. Bellomo, L. Gibelli, N. Outada, On the interplay between behavioral dynamics and social interactions in human crowds. Kinet. Relat. Models 12(2), 397–409 (2019)
F. Berthelin, P. Goatin, Regularity results for the solutions of a non-local model of traffic flow. Discrete Contin. Dyn. Syst. 39(6), 3197–3213 (2019)
S. Bianchini, R.M. Colombo, On the stability of the standard Riemann semigroup. Proc. Am. Math. Soc. 130(7), 1961–1973 (2002)
R. Borsche, R.M. Colombo, M. Garavello, On the coupling of systems of hyperbolic conservation laws with ordinary differential equations. Nonlinearity 23(11), 2749–2770 (2010)
R. Borsche, R.M. Colombo, M. Garavello, Mixed systems: ODEs - balance laws. J. Differ. Equ. 252(3), 2311–2338 (2012)
R. Borsche, R.M. Colombo, M. Garavello, A. Meurer, Differential equations modeling crowd interactions. J. Nonlinear Sci. 25(4), 827–859 (2015)
R. Borsche, A. Klar, F. Schneider, Numerical methods for mean-field and moment models for pedestrian flow, in Crowd Dynamics. Vol. 1. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2018), pp. 167–209
F. Bouchut, B. Perthame, Kružkov’s estimates for scalar conservation laws revisited. Trans. Am. Math. Soc. 350(7), 2847–2870 (1998)
A. Bressan, Hyperbolic Systems of Conservation Laws. Oxford Lecture Series in Mathematics and Its Applications, vol. 20 (Oxford University Press, Oxford, 2000). The one-dimensional Cauchy problem
A. Bressan, B. Piccoli, Introduction to the Mathematical Theory of Control. AIMS Series on Applied Mathematics, vol. 2 (American Institute of Mathematical Sciences, Springfield, 2007)
A. Bressan, W. Shen, On traffic flow with nonlocal flux: a relaxation representation (2019). arXiv: 1911.03636
C. Chalons, P. Goatin, L.M. Villada, High-order numerical schemes for one-dimensional nonlocal conservation laws. SIAM J. Sci. Comput. 40(1), A288–A305 (2018)
G.-Q. Chen, K.H. Karlsen, Quasilinear anisotropic degenerate parabolic equations with time-space dependent diffusion coefficients. Commun. Pure Appl. Anal. 4(2), 241–266 (2005)
F.A. Chiarello, P. Goatin, Global entropy weak solutions for general non-local traffic flow models with anisotropic kernel. ESAIM Math. Model. Numer. Anal. 52(1), 163–180 (2018)
F.A. Chiarello, P. Goatin, Non-local multi-class traffic flow models. Netw. Heterog. Media 14(2), 371–387 (2019)
F.A. Chiarello, P. Goatin, E. Rossi, Stability estimates for non-local scalar conservation laws. Nonlinear Anal. Real World Appl. 45, 668–687 (2019)
A. Colombi, M. Scianna, A. Alaia, A discrete mathematical model for the dynamics of a crowd of gazing pedestrians with and without an evolving environmental awareness. Comput. Appl. Math. 36(2), 1113–1141 (2017)
R.M. Colombo, F. Marcellini, Nonlocal systems of balance laws in several space dimensions with applications to laser technology. J. Differ. Equ. 259(11), 6749–6773 (2015)
R.M. Colombo, L.-M. Mercier, Nonlocal crowd dynamics models for several populations. Acta Math. Sci. 32(1), 177–196 (2012)
R.M. Colombo, E. Rossi, Hyperbolic predators vs. parabolic prey. Commun. Math. Sci. 13(2), 369–400 (2015)
R.M. Colombo, E. Rossi, Nonlocal conservation laws in bounded domains. SIAM J. Math. Anal. 50(4), 4041–4065 (2018)
R.M. Colombo, E. Rossi, Control in a mixed hyperbolic-parabolic predator prey model (2019, in preparation)
R.M. Colombo, E. Rossi, Modelling crowd movements in domains with boundaries. IMA J. Appl. Math. 84(5), 833–853 (2019)
R.M. Colombo, E. Rossi, A modeling framework for biological pest control. Math. Biosci. Eng. 17(mbe-17-02-072), 1413 (2020)
R.M. Colombo, M. Mercier, M.D. Rosini, Stability and total variation estimates on general scalar balance laws. Commun. Math. Sci. 7(1), 37–65 (2009)
R.M. Colombo, M. Herty, M. Mercier, Control of the continuity equation with a non local flow. ESAIM Control Optim. Calc. Var. 17(2), 353–379 (2011)
R.M. Colombo, M. Garavello, M. Lécureux-Mercier, A class of nonlocal models for pedestrian traffic. Math. Models Methods Appl. Sci. 22(4), 1150023, 34 (2012)
M. Colombo, G. Crippa, L.V. Spinolo. Blow-up of the total variation in the local limit of a nonlocal traffic model (2018)
M. Colombo, G. Crippa, M. Graff, L.V. Spinolo. On the role of numerical viscosity in the study of the local limit of nonlocal conservation laws (2019)
M. Colombo, G. Crippa, M. Graff, L.V. Spinolo. Recent results on the singular local limit for nonlocal conservation laws (2019)
M. Colombo, G. Crippa, L.V. Spinolo, On the singular local limit for conservation laws with nonlocal fluxes. Arch. Ration. Mech. Anal. 233(3), 1131–1167 (2019)
A. Corli, L. Malaguti, Viscous profiles in models of collective movement with negative diffusivity. Z. Angew. Math. Phys. 70(2), Art. 47, 22 (2019)
J.-M. Coron, M. Kawski, Z. Wang, Analysis of a conservation law modeling a highly re-entrant manufacturing system. Discrete Contin. Dyn. Syst. Ser. B 14(4), 1337–1359 (2010)
V. Coscia, C. Canavesio, First-order macroscopic modelling of human crowd dynamics. Math. Models Methods Appl. Sci. 18(Suppl.), 1217–1247 (2008)
G. Crippa, M. Lécureux-Mercier, Existence and uniqueness of measure solutions for a system of continuity equations with non-local flow. Nonlinear Differ. Equ. Appl. 20(3), 523–537 (2013)
E. Cristiani, B. Piccoli, A. Tosin, Multiscale Modeling of Pedestrian Dynamics. MS&A. Modeling, Simulation and Applications, vol. 12 (Springer, Cham, 2014)
C.M. Dafermos, Hyperbolic Conservation Laws in Continuum Physics. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 325, 4th edn. (Springer, Berlin, 2016)
E. De Angelis, Nonlinear hydrodynamic models of traffic flow modelling and mathematical problems. Math. Comput. Model. 29(7), 83–95 (1999)
M. Di Francesco, M.D. Rosini, Rigorous derivation of nonlinear scalar conservation laws from follow-the-leader type models via many particle limit. Arch. Ration. Mech. Anal. 217(3), 831–871 (2015)
H. Holden, N.H. Risebro, Front Tracking for Hyperbolic Conservation Laws. Applied Mathematical Sciences, vol. 152, 2nd edn. (Springer, Heidelberg, 2015)
H. Holden, N.H. Risebro, The continuum limit of Follow-the-Leader models—a short proof. Discrete Contin. Dyn. Syst. 38(2), 715–722 (2018)
S.N. Kružhkov, First order quasilinear equations with several independent variables. Mat. Sb. (N.S.) 81(123), 228–255 (1970)
M. Lécureux-Mercier, Improved stability estimates for general scalar conservation laws. J. Hyperbolic Differ. Equ. 8(4), 727–757 (2011). See also the revised version at http://math.univ-lyon1.fr/~mercier
R. Loehner, On the modeling of pedestrian motion. Appl. Math. Model. 34(2), 366–382 (2010)
B.J. Lucier, A moving mesh numerical method for hyperbolic conservation laws. Math. Comput. 46(173), 59–69 (1986)
F. Marcellini, On the stability of a model for the cutting of metal plates by means of laser beams. Appl. Math. Lett. 68, 143–149 (2017)
S. Motsch, M. Moussaïd, E.G. Guillot, M. Moreau, J. Pettré, G. Theraulaz, C. Appert-Rolland, P. Degond, Modeling crowd dynamics through coarse-grained data analysis. Math. Biosci. Eng. 15(6), 1271–1290 (2018)
B. Piccoli, F. Rossi, Measure-theoretic models for crowd dynamics, in Crowd Dynamics. Vol. 1. Modeling and Simulation in Science, Engineering and Technology (Birkhäuser/Springer, Cham, 2018), pp. 137–165
B. Piccoli, A. Tosin, Time-evolving measures and macroscopic modeling of pedestrian flow. Arch. Ration. Mech. Anal. 199(3), 707–738 (2011)
E. Rossi, Definitions of solutions to the IBVP for multi-dimensional scalar balance laws. J. Hyperbolic Differ. Equ. 15(2), 349–374 (2018)
E. Rossi, V. Schleper, Convergence of numerical scheme for a mixed hyperbolic-parabolic system in two space dimensions. ESAIM Math. Model. Numer. Anal. 50(2), 475–497 (2016)
M. Twarogowska, P. Goatin, R. Duvigneau, Macroscopic modeling and simulations of room evacuation. Appl. Math. Model. 38(24), 5781–5795 (2014)
J. Vovelle, Convergence of finite volume monotone schemes for scalar conservation laws on bounded domains. Numer. Math. 90(3), 563–596 (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendices
1.1 Regular Entropy Solutions for IBVP Problems
In this appendix we briefly recall the concept of regular entropy solutions for an initial boundary value problem. To this aim, fix T > 0, an open and bounded subset Ω of \({\mathbb {R}}^N\), and let us consider the system

where  satisfies, for every
satisfies, for every  , \(u(t) \in {\mathbf {C}}^{2} ( \Omega ; {\mathbb {R}}^N)\) and \({\left \|u(t)\right \|}_{{\mathbf {C}}^{2}\left (\Omega ; {\mathbb {R}}^N\right )} \le M\) for a suitable positive constant M. The definition of a boundary entropy–entropy flux pair is as follows.
, \(u(t) \in {\mathbf {C}}^{2} ( \Omega ; {\mathbb {R}}^N)\) and \({\left \|u(t)\right \|}_{{\mathbf {C}}^{2}\left (\Omega ; {\mathbb {R}}^N\right )} \le M\) for a suitable positive constant M. The definition of a boundary entropy–entropy flux pair is as follows.
Definition A.1 ([28, Definition 4.1], [60, Definition 2])
The pair of functions  is said a boundary entropy–entropy flux pair for (7.1) if:
is said a boundary entropy–entropy flux pair for (7.1) if:
-
1.
the function z↦H(z, w) is convex for every \(w \in {\mathbb {R}}\);
-
2.
the equality \(\partial _z Q\left (t, x, z, w\right ) = \left (\partial _z H\left (z, w\right )\right ) u\left (t, x\right )\) holds for every
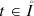 , \(x \in \overline \Omega \), and \(z, w \in {\mathbb {R}}\);
, \(x \in \overline \Omega \), and \(z, w \in {\mathbb {R}}\); -
3.
the equalities \(H\left (w, w\right ) = 0\), \(Q\left (t, x, w, w\right ) = 0\), and \(\partial _z H\left (w, w\right ) = 0\) hold for every
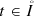 , \(x \in \overline \Omega \), and \(w \in {\mathbb {R}}\).
, \(x \in \overline \Omega \), and \(w \in {\mathbb {R}}\).
It is now possible to state the definition of regular entropy solution.
Definition A.2 ([57, Definition 3.3])
A regular entropy solution to (7.1) is a function  such that, for every boundary entropy–entropy flux pair \(\left (H, Q\right )\), in the sense of Definition A.1, for every \(k \in {\mathbb {R}}\) and for every \(\varphi \in {\mathbf {C}}_c^{1} ({\mathbb {R}} \times {\mathbb {R}}^N; {\mathbb {R}}^+)\), it holds
such that, for every boundary entropy–entropy flux pair \(\left (H, Q\right )\), in the sense of Definition A.1, for every \(k \in {\mathbb {R}}\) and for every \(\varphi \in {\mathbf {C}}_c^{1} ({\mathbb {R}} \times {\mathbb {R}}^N; {\mathbb {R}}^+)\), it holds

where \({\mathcal {H}}^{N-1}\) denotes the Hausdorff measure of dimension N − 1.
1.2 List of Symbols
- C 0, 1(A; B):
-
with A and B subsets of normed vector spaces, is the set of functions defined on A, with values in B, that are Lipschitz continuous on A.
- C k(A; B):
-
with A and B subsets of normed vector spaces, is the set of functions defined on A, with values in B, whose k-derivatives are continuous on A.
- \({\mathbf {C}}_c^{k} (A;B)\) :
-
with A and B subsets of normed vector spaces, is the set of compactly supported functions defined on A, with values in B whose k-derivatives are continuous on A.
- \(\overline {I}\) :
-
is the closure of the set I.
-
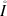 :
: -
is the interior of the set I.
- L p(A; B):
-
with p ≥ 1, \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the set of measurable functions f defined on A, with values in B, such that \({\left |f\right |}^p\) is Lebesgue integrable on A.
- L ∞(A; B):
-
with \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the set of measurable functions f defined on A, with values in B, essentially bounded.
- \({\mathbb {R}}^+\) :
-
is the set \(\left [0, +\infty \right [\) of 0 and all positive real numbers.
-
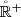 :
: -
is the set \(\left ]0, +\infty \right [\) of all strictly positive real numbers.
- \(\mathbb S^{N-1}\) :
-
is the unit sphere in \({\mathbb {R}}^N\).
- \( \mathop {\mathrm {spt}} \rho \) :
-
is the support of the function ρ.
- W 1, p(A; B):
-
with 1 ≤ p ≤∞, \(A \subseteq {\mathbb {R}}^n\) and \(B \subseteq {\mathbb {R}}^m\), is the Sobolev space of functions defined in A with values in B whose first weak derivative is in L p.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Colombo, R.M., Lecureux-Mercier, M., Garavello, M. (2020). Crowd Dynamics Through Conservation Laws. In: Gibelli, L. (eds) Crowd Dynamics, Volume 2. Modeling and Simulation in Science, Engineering and Technology. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-50450-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-50450-2_5
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-50449-6
Online ISBN: 978-3-030-50450-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


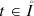 ,
, 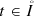 ,
, 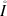 :
: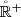 :
: