Abstract
This article revisits the problem of decomposing a Petri net into a network of automata, a problem that has been around since the early 70s. We reformulate this problem as the transformation of an ordinary, one-safe Petri net into a flat, unit-safe NUPN (Nested-Unit Petri Net) and define a quality criterion based on the number of bits required for the structural encoding of markings. We propose various transformation methods, all of which we implemented in a tool chain that combines NUPN tools with third-party software, such as SAT solvers, SMT solvers, and tools for graph colouring and finding maximal cliques. We perform an extensive evaluation of these methods on a collection of more than 12,000 nets from diverse sources, including nets whose marking graph is too large for being explored exhaustively.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The present article addresses the decomposition problem for Petri nets. Precisely, we study the automatic transformation of a (low-level) Petri net into an automata network, i.e., a set of sequential components (such as finite-state machines) that execute asynchronously, synchronize with each other, and exhibit the same global behaviour as the original Petri net. This problem is of practical interest for at least two reasons: (i) Petri nets are expressive, but poorly structured; decomposition is a means to restructure them automatically, making them more modular and, hopefully, easier to understand and reason about; (ii) automata networks contain structural information that formal verification algorithms may exploit to increase efficiency using, e.g., logarithmic encodings of reachable markings, easier detection of independent transitions for partial-order and stubborn-set reduction methods, and divide-and-conquer strategies for compositional verification.
To a large extent, we reformulate the decomposition problem in terms of Nested-Unit Petri Nets (NUPNs) [8], a modern extension of Petri nets, in which places can be grouped into units that express sequential components. Units can be recursively nested to reflect both the concurrent and the hierarchical nature of complex systems. This model of computation, originally developed for translating process calculi to Petri nets, increases the efficiency of formal verification [1, 8, Sect. 6]. It has been so far implemented in thirteen software tools [8, Sect. 7] and adopted for the benchmarks of the Model Checking Contest and the parallel problems of the Rigorous Examination of Reactive Systems. Notice that certain NUPN features, such as the hierarchical nesting of units to an arbitrary depth, are not exploited in the present article.
Related Work. The decomposition of a Petri net into sequential processes has been studied since the early 70s at least [12], and gave rise to a significant body of academic literature. On the theoretical side, one can mention the decomposition of elementary nets into a set of concurrent communicating sequential components [23, Sect. 4.3–4.4], the decomposition of live and bounded free–choice nets into S-components or T-components [6, Chap. 5], and the distribution of a Petri net to geographical locations [5, 11]. On the algorithmic side, one can mention decomposition methods that compute a coverage of a net by strongly connected state machines, e.g., [12], approaches based on invariants and semiflows, e.g., [3, 21, 24], and approaches based on reachability analysis, some using concurrency graphs on which decomposition can be expressed as a graph colouring algorithm [27], others using hypergraphs, which seem more compact that concurrency graphs [28]. On the software implementation side, one can mention the Diane tool [19], which seems no longer accessible today, and the Hippo tool, which is developed at the University of Zielona Góra (Poland) and available on-line through a dedicated web portalFootnote 1. Further references to related work are given throughout the next sections.
Outline. The present paper describes a state-of-the-art approach based on (partial) reachability analysis for translating ordinary, safe Petri nets into automata networks. This approach has been fully implemented in a software tool chain, and successfully applied to thousands of examples. The remainder of this article is organized as follows. Section 2 states the decomposition problem by precisely defining which kind of Petri nets are taken as input, which kind of automata networks are produced as output, and which quality criterion should guide the decomposition. Section 3 defines some key concepts used for decomposition, namely the concurrency relation, the concurrency matrix, and the concurrency graph. Section 4 provides means to efficiently search for solutions. The four next sections present various decomposition approaches based on graph colouring (Sect. 5), maximal-clique algorithms (Sect. 6), SAT solving (Sect. 7), and SMT solving (Sect. 8). Section 9 discusses the experimental results obtained by these various approaches and draws a comparison with the Hippo tool. Finally, Sect. 10 concludes the article.
2 Problem Statement
2.1 Basic Definitions
We briefly recall the usual definitions of Petri nets and refer the reader to classical surveys for a more detailed presentation of Petri nets.
Definition 1
A (marked) Petri Net is a 4-tuple \((P, T, F, M_0)\) where:
-
1.
P is a finite, non-empty set; the elements of P are called places.
-
2.
T is a finite set such that \(P \cap T = \varnothing \); the elements of T are called transitions.
-
3.
F is a subset of \((P \times T) \cup (T \times P)\); the elements of F are called arcs.
-
4.
\(M_0\) is a non-empty subset of P; \(M_0\) is called the initial marking.
Notice that the above definition only covers ordinary nets (i.e., it assumes all arc weights are equal to one). Also, it only considers safe nets (i.e., each place contains at most one token), which enables the initial marking to be defined as a subset of P, rather than a function \(P \rightarrow {\mathbb N}\) as in the usual definition of P/T nets. We now recall the classical firing rules for ordinary safe nets.
Definition 2
Let \((P, T, F, M_0)\) be a Petri Net.
-
A marking M is defined as a set of places (\(M \subseteq P\)). Each place belonging to a marking M is said to be marked or, also, to possess a token.
-
The pre-set of a transition t is the set of places
 .
. -
The post-set of a transition t is the set of places
 .
. -
A transition t is enabled in some marking M iff
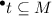 .
. -
A transition t can fire from some marking \(M_1\) to another marking \(M_2\) iff t is enabled in \(M_1\) and
 , which we note
, which we note 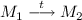 .
. -
A marking M is reachable from the initial marking \(M_0\) iff \(M = M_0\) or there exist \(n \ge 1\) transitions \(t_1, t_2, ..., t_n\) and \((n-1)\) markings \(M_1, M_2, ..., M_{n-1}\) such that
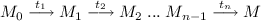 .
. -
A place p is dead if it exists no reachable marking containing p.
-
A transition t is dead if it exists no reachable marking in which t is enabled.
We now recall the basic definition of a NUPN, referring the interested reader to [8] for a complete presentation of this model of computation.
Definition 3
A (marked) Nested-Unit Petri Net (acronym: NUPN) is a 8-tuple \((P, T, F, M_0, U, u_0, \sqsubseteq , \mathsf{unit\,})\) where \((P, T, F, M_0)\) is a Petri net, and where:
-
5.
U is a finite, non-empty set such that \(U \cap T = U \cap P = \varnothing \); the elements of U are called units.
-
6.
\(u_0\) is an element of U; \(u_0\) is called the root unit.
-
7.
\(\sqsubseteq \) is a binary relation over U such that \((U, \sqsupseteq )\) is a tree with a single root \(u_0\), where
 ; intuitivelyFootnote 2, \(u_1 \sqsubseteq u_2\) expresses that unit \(u_1\) is transitively nested in or equal to unit \(u_2\).
; intuitivelyFootnote 2, \(u_1 \sqsubseteq u_2\) expresses that unit \(u_1\) is transitively nested in or equal to unit \(u_2\). -
8.
\(\mathsf{unit\,}\) is a function \(P \rightarrow U\) such that \((\forall u \in U \setminus \{ u_0 \}) \; (\exists p \in P) \; \mathsf{unit\,}(p) = u\); intuitively, \(\mathsf{unit\,}(p) = u\) expresses that unit u directly contains place p.
Because NUPNs merely extend Petri nets by grouping places into units, they do not modify the Petri-net firing rules for transitions: all the concepts of Definition 2 for Petri nets also apply to NUPNs, so that Petri-net properties are preserved when NUPN information is added. Finally, we recall a few NUPN concepts to be used throughout this article; additional information can be found in [8], where such concepts (especially, unit safeness) are defined in a more general manner.
Definition 4
Let \(N = (P, T, F, M_0, U, u_0, \sqsubseteq , \mathsf{unit\,})\) be a NUPN.
-
The local places of a unit u are the set:
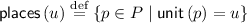 .
. -
A void unit is a unit having no local place.Footnote 3
-
A leaf unit is a minimal element of \((U, \sqsubseteq )\), i.e., a unit having no nested unit.
-
The height of N is the length of the longest chain \(u_n \sqsubseteq ... \sqsubseteq u_1 \sqsubseteq u_0\) of nested units, not counting the root unit \(u_0\) if it is void.
-
The width of N is the number of its leaf units.
-
A flat NUPN is such that its height is equal to one.
-
A trivial NUPN is such that its width is equal to the number of places.Footnote 4
-
A flat NUPN is unit-safe iff any reachable marking contains at most one local place of each unit.
2.2 Input Formalism
From Definition 1 and 2, the Petri nets accepted as input by our methods must be ordinary, safe, and have at least one initially marked placeFootnote 5. Such restrictions are quite natural, given that our goal is the translation of a Petri net to a network of automata, which are also ordinary and safe by essence (this will be further discussed in Sect. 2.3). Unlike, e.g., [21], we do not handle bounded nets that are not safe, given that any bounded net can be converted to a safe net by duplicating (triplicating, etc.) some of its places.
Contrary to other approaches, we do not lay down additional restrictions on the Petri nets accepted as input. For instance:
-
We do not require them to be free choice and well formed (i.e., live and safe) as in [12], nor free choice, live, and bounded as in [18].
-
We do not require them to be state machine coverable [26, Def. 16.2.2 (180)], state machine decomposable [12, Chap. 5], nor state machine allocatable [13] (see [4, Sect. 7.1] for a discussion of the two latter concepts).
-
We do not require them to be pure (i.e., free from self-loop transitions) as in [27], where Petri nets are represented using their incidence matrix, a data structure that cannot describe those transitions t such that
 .
. -
We do not require them to be connected or strongly connected, and accept the presence of dead places and/or dead transitions.
Implementation and Experimentation. Our tool chain accepts as input a “.pnml” file containing a Petri net represented in the PNML standard format [14]. This file is then converted to a “.nupn” file, written in a concise and human-readable textual formatFootnote 6 [8, Annex A] for storing NUPNs. This conversion is performed using PNML2NUPNFootnote 7, a translator developed at LIP6 (Paris, France), which discards those PNML features that are irrelevant to our problem (e.g., colored, timed, or graphical attributes,) to produce a P/T net. All NUPNs generated by PNML2NUPN are trivial, meaning that the translator follows the scheme given in [8, proof of Prop. 11] by putting each place in a separate unit; thus, the translator makes no attempt at discovering concurrency in PNML models.
Our tool chain also accepts a file directly written in the “.nupn” format, rather than being generated from PNML. Such a NUPN model may be trivial or already have a decomposition, either as a network of automata (in the case of flat non-trivial models) or as a hierarchy of nested concurrent units (in the case of non-flat models). We treat non-trivial models like trivial ones by purposely ignoring (most of) the information about the structure of non-trivial models.
The next step is to make sure that each NUPN model to be decomposed is safe. Many NUPN models generated from higher-level specification languages are unit safe by construction, and thus safe, which is indicated by a pragma “!unit_safe” present in the “.nupn” file. In absence of this pragma, one must check whether the underlying Petri net is safe, which is a PSPACE-complete problem. Various tools that can handle “.nupn” files are available for such purpose, e.g., CÆSAR.BDDFootnote 8 or CÆSAR.SDDFootnote 9.
To perform experiments, we used a collection of 12,728 models in “.nupn” format. This collection, which has been patiently built at INRIA Grenoble since 2013, gathers models derived from “realistic” specifications (i.e., written in high-level languages by humans rather than randomly generated, many of which developed for industrial problems). It also contains all ordinary, safe models from the former PetriWeb collectionFootnote 10 and from the Model Checking Context benchmarksFootnote 11. To our knowledge, our collection is the largest ever reported in the scientific literature on Petri nets.
A statistical survey confirms the diversity of our collection of models. Table 1 gives the percentage of models that satisfy or not some usual (structural and behavioural) properties of Petri nets, as well as topological properties of NUPNs; the answer is unknown for some large models that CÆSAR.BDD (with option “-mcc”) could not process entirely. Table 2 gives numerical information about the size of the Petri nets (number of places, transitions, and arcs, as well as arc densityFootnote 12) and the size of the NUPNs (number of units, height, and width).
2.3 Output Formalism
Our goal is to translate ordinary, safe Petri nets into automata networks; however, many automata-based formalisms have been proposed in the literature, most of which are candidate targets for our translation, but differ in subtle details. A thorough survey was given in [4], yet newer proposals have been made since then. In this subsection, we address this issue by precisely stating which constraints a suitable output formalism should satisfy.
Our first constraint is that each automaton should be sequential (contrary to, e.g., [5], where concurrent transitions can be assigned to the same location), that our automata networks should be flat (contrary to, e.g., [7, 16] and [20], where Petri nets are translated to hierarchical models in which processes can have nested sub-processes), and that the semantics of automata networks should be aligned with the usual interpretation of Petri nets, i.e., the states of each automaton should reflect Petri net places, and the global state of the automata network should be the union of all the local states of its component automata. The transitions of each automaton should also behave as Petri net transitions, meaning that synchronization between several automata should be achieved using the Petri-net firing rules (see Definition 2) rather than alternative mechanisms, such as synchronization states in synchronized automata [22], asynchronous message passing in reactive automata [2], or FIFO buffers in communicating automata [10].
Our second constraint goes further by requiring a one-to-one mapping between the places of the Petri net and the states of the automata network, and between each transition of the Petri net and the corresponding (possibly synchronized) transition(s) of the automata network. Consequently, all structural and behavioural properties of the Petri net should be preserved by decomposition; in particular, the graph of reachable markings for the Petri net should be isomorphic (modulo some renaming of places and transitions) to the global state space of the automata network.
Our third constraint demands that the sets of local states of all automata in a network are pairwise disjoint, thus forbidding the possibility of having shared states between two or more automata. Such a criterion draws a clear separation line between the various models proposed in the literature. For instance, open nets [19] rely on shared places for input/output communications between components. Also, among the models surveyed in [4, Sect. 6–7], six models (synchronized state machines, state machine decomposable nets, state machine allocatable nets, proper nets, strict free choice nets, and medium composable nets) allow shared states, while two models (superposed automata nets and basic modular Petri nets) forbid shared states. We opt for the latter approach, which provides a sound model of concurrency (concurrent automata are likely to be executed on different processors and, thus, should not have shared states) and which is mathematically simpler (the local states of all automata form a partition of the set of states). It is worth mentioning that the decomposition approach described in [27] first generates a decomposition with shared states, but later gets rid of these by introducing auxiliary states (noted “NOP”); while we agree with the goal of having pairwise disjoint local state sets, we cannot reuse the same approach, as the addition of extra states in the automata network would violate the one-to-one mapping required by our second constraint.
Our fourth constraint is that a suitable output formalism should be general enough to support, without undue restrictions, all input Petri nets that are ordinary and safe. For instance, among the eight aforementioned models of [4, Sect. 6–7], three models (state machine decomposable nets, state machine allocatable nets, and strict free choice nets) require each automaton to be strongly connected; such a restriction obviously hinders decomposition, as a very simple net with two places and a transition between these places cannot be expressed using a single strongly connected automaton. Another frequent, yet questionable, restriction is the requirement that automata should be state machines, i.e., always have a token in any global state; all the eight aforementioned models of [4, Sect. 6–7] have this restriction, which, we believe, is unsuitable: a very simple net with a single place and a transition going out of this place cannot be represented as a state machine, unless an extra state is added to the post-set of the transition, thus violating our second constraint; more generally, decomposition into state machines assumes that the input Petri net is conservative (i.e., each transition has the same number of input and output places), where Table 1 indicates that only 16.7% of models satisfy this condition in practice; one must therefore consider a more flexible model, in which automata can be started and halted dynamically, meaning that each automaton does not necessary have a token in the initial state, and that it may lose its token in the course of its execution.
Eventually, the suitable output formalism that matches the four above constraints turns out to be a flat, unit-safe NUPN, i.e., nothing else than the input Petri net model augmented with a partition of the set of places into units, each featuring an automaton, such that, in any reachable marking, at most one place of each unit has a token. If there is more than one unit, an additional (root) unit will be created, which is void and encapsulates all other (leaf) units.
A key advantage of this output formalism is that decomposition can be seen as an operation within the NUPN domain, taking as input a trivial, unit-safe NUPN and producing as output a flat, unit-safe NUPN. This makes definitions simpler, as all places, transitions, and arcs of the initial Petri net are kept unchanged, and all structural and behavioural properties are preserved by the translation. In this article, we have so far carefully avoided the term of “state machines”, which implies conservativeness, preferring the more vague term “automata network”. In the sequel, we switch to the precise NUPN terminology, referring to “automata” as “(leaf) units” and “local states” as “places”.
Implementation and Experimentation. Concretely, our tool chain produces as output a “.nupn” file containing the result of the decomposition. To a large extent, this file is identical to the input “.nupn” file, but contains new information about units. Finally, the output “.nupn” file can easily be translated to standard PNML format using the CÆSAR.BDD tool (with option “-pnml”); the information about units produced by the decomposition is retained and stored in the “.pnml” file using a “toolspecific” sectionFootnote 13 [8, Annex B].
2.4 Existence and Multiplicity of Solutions
Our decomposition problem, as stated above, consists in finding an appropriate set of units (namely, a partition of the set of places) to convert an ordinary, safe Petri net into an “isomorphic” flat, unit-safe NUPN.
Contrary to other decomposition approaches (starting from [12]) that may have no solution for certain classes of input nets, our problem always has at least one solution: the trivial NUPN corresponding to the input Petri net (see [8, proof of Prop. 11] for a formal definition) is flat (because its height is one) and it is unit-safe (because its underlying Petri net is safe [8, Prop. 7]).
There may exist several solutions for the decomposition problem. For instance, given a valid solution containing a unit with several places, splitting this unit into two separate units also produces a valid solution; also, if this unit contains a dead place, moving this dead place to any other leaf unit also produces a valid solution. In any valid solution, the number of leaf units belongs to an interval \([{ Min}, { Max}]\), where:
-
\({ Min}\) is the largest value, for any reachable marking M, of \(\text {card}\,(M)\), i.e., the number of tokens in M. For instance, if the initial marking \(M_0\) contains n places, then any valid solution must have at least n leaf units. A valid solution may have more leaf units than Min; by example, a net with 4 places \(p_0, ..., p_3\) (only \(p_0\) is marked initially) and 3 transitions \(t_1, ..., t_3\) such that
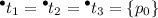 ,
, 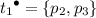 ,
,  , and
, and  has at most 2 tokens but at least 3 leaf units in any valid decomposition.
has at most 2 tokens but at least 3 leaf units in any valid decomposition. -
\({ Max}\) is the number of places (this follows from item 8 of Definition 3). The upper bound Max is reached by, and only by, the trivial solution. Approaches to obtain an upper bound smaller than Max are discussed in Sect. 4 below.
Implementation and Experimentation. The CÆSAR.BDD tool (with option “-min-concurrency”) can quickly compute (an under-approximation of) the value of Min without exploring the reachable marking graph entirely.
2.5 Criteria for Optimal Solutions
Since the decomposition problem usually admits multiple solutions, the next question is to select an “optimal” solution. For instance, the trivial solution is valid, but uninteresting. Various criteria can be used to compare solutions. From a theoretical point of view, and especially for the purpose of formal verification, a suitable criterion is to minimize the number of bits needed to represent any reachable marking. There are different ways of encoding the reachable markings of a safe Petri net. The least compact encoding consists in having one bit per place. The most compact encoding consists in first exploring all reachable markings, then encoding them using \(\lceil \log _2 n \rceil \) bits, where n is the number of reachable markings; of course, this encoding is unrealistic, since exploration cannot be done without already having an encoding.
Between these two extremes, one should select an encoding that can be computed without exploring reachable markings and faithfully measures the compactness of each solution. For such purpose, [8, Sect. 6] lists five encodings for unit-safe NUPNs and evaluates their compactness. We base our approach on the most compact encoding of [8], noted (b), which we further enhance by detecting those units that never get a token or never lose their token.
Definition 5
Let \(N = (P, T, F, M_0, U, u_0, \sqsubseteq , \mathsf{unit\,})\) be a NUPN.
-
Let the projection of a marking M on a unit u be:
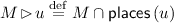 .
. -
A unit u is idle if has no token in the initial marking and no transition puts a token in this unit, i.e.,
 .
. -
A unit u is permanent if has a token in the initial marking and no transition takes the token away from this unit, i.e.,
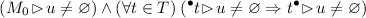 .
.
Notice that, in a flat NUPN, the root unit is always idle, since it is void. Using the encoding (b) of [8, Sect. 6], the state of each unit having n local places can be encoded using \(\lceil \log _2 (n+1) \rceil \) bits. This number of bits can be further reduced if the unit is idle or permanent.
Definition 6
Let \(N = (P, T, F, M_0, U, u_0, \sqsubseteq , \mathsf{unit\,})\) be a NUPN. The number of bits needed to represent the markings of N is defined as \(\varSigma _{u \in U} \; \nu (u)\), where \(\nu (u) = 0\) if u is idle, \(\nu (u) = \lceil \log _2 (\text {card}\,(\mathsf{places\,}(u))) \rceil \) if u is permanent, or \(\nu (u) = \lceil \log _2 (\text {card}\,(\mathsf{places\,}(u))+1) \rceil \) otherwise.
We finally base our comparison criterion upon Definition 6: the smaller the number of bits, the better the decomposition.
Implementation and Experimentation. Given a NUPN obtained by decomposition, its number of bits can be computed using CÆSAR.BDD (option “-bits”). The determination of idle and permanent units is done in linear time, with a simple iteration that examines the pre-set and post-set of each transition.
3 Concurrent Places
3.1 Concurrency Relation
All the decomposition methods presented in this article are based on a concurrency relation defined over places, which appears in many scientific publications under various names: coexistency defined by markings [15, Sect. 9], concurrency graph [27], or concurrency relation [9, 17, 18, 25], etc. Mostly identical, these definitions sometimes differ in details, such as the kind of Petri nets considered, or the handling of reflexivity, i.e., whether a place is concurrent with itself or not. We adopt the following definition:
Definition 7
Let \(N = (P, T, F, M_0)\) be a Petri net. Two places \(p_1\) and \(p_2\) are concurrent, noted “\(p_1 \Vert \,p_2\!\)”, iff there exists a reachable marking M such that \(p_1 \in M\) and \(p_2 \in M\).
This relation is most relevant to the decomposition problem, as it generates weak positive constraints (if two places are not concurrent, they may belong the same unit in the output NUPN) and strong negative constraints (if two places are concurrent, they must not belong to the same unit, i.e.,  —otherwise, the output NUPN would not be unit safe).
—otherwise, the output NUPN would not be unit safe).
For certain classes of Petri nets (namely, extended free choice nets that are bounded and live), there exists a polynomial algorithm for computing the concurrency relation [18]. We have not used this algorithm so far, since, in our collection (see Table 1), less than a half of the models are extended free choice, and most models are not strongly connected, thus not live.
3.2 Concurrency Matrix
We concretely represent the concurrency relation as a matrix indexed by places. The cells of this matrix are equal to “1” if the corresponding two places are concurrent, or to “0” if they are not. The matrix is computed using reachability analysis, but the set of reachable markings may be too large to be explored entirely. In such case, certain cells of the matrix may be undefined, a situation we record by giving them an unknown value noted “.”. A matrix will be said to be incomplete if it contains at least one unknown value, or complete otherwise.
Implementation and Experimentation. In our tool chain for decomposition, the computation of the concurrent matrix is performed by CÆSAR.BDD (with option “-concurrent-places”). Several practical issues are faced.
For a large input model, the matrix can get huge (e.g., several gigabytes). This problem is addressed in two ways: (i) since the concurrency relation is symmetric, only the lower half of the matrix is represented; (ii) each line of the matrix is compacted using a run-length compression algorithm.
To fight algorithmic complexity when generating the matrix of a large input model, CÆSAR.BDD combines various techniques. Initially, the entire matrix is initialized to unknown values. Then, a symbolic exploration (using BDDs) of the reachable markings is undertaken, possibly with a user-specified timeout limitation; during this exploration, all the places reached and all the transitions fired are marked as not dead. If the exploration terminates within the allowed time, then all markings are known, so that the matrix is complete. Otherwise, only a subset of all markings is known, which enables one to write “1” in all the matrix cells corresponding to places found present together in some reached marking; then, various techniques are used to decrease the remaining number of unknown values, stopping as soon as this number drops to zero:
-
If the input model is non-trivial and contains the pragma “!unit_safe”, than all pairs of places in the same unit (resp., in two transitively nested units) are declared to be non-concurrent.
-
If the diagonal of the matrix contains unknown values, an auxiliary explicit-state algorithm that computes a subset of dead places is run.
-
If a place is dead, then it is not concurrent with any other place.
-
If a transition t (dead or not) has a single input place p, then p is not concurrent with any output place of t different from p (otherwise, the net would not be safe).
Although the generation of concurrency matrices is a CPU-intensive operation, we found it to succeed for most models of our collection: 99.9% of all the matrices have been generated; the 12 matrices that could not be generated correspond to large NUPNs, all of which have more than 5556 places, 7868 transitions, and 18,200 arcs. Moreover, 97.3 of all the matrices are complete; the 350 incomplete matrices correspond to large NUPNs, all of which have more than 120 places, 144 transitions, and 720 arcs.
In the sequel, we proceed with the concurrency matrix, which we abstract away by replacing all unknown values by the value “1”, thus assuming that, by default (i.e., in absence of positive information), individual places are live and pairs of places are concurrent. Such pessimistic assumptions are essential to the correctness of our decomposition methods: if the matrix is incomplete, the decomposed NUPN will still be unit-safe, although perhaps suboptimal.
3.3 Concurrency and Sequentiality Graphs
Derived from the (abstracted) concurrency matrix, we introduce two definitions, which have been already given by other authors, e.g., [25, 27], etc.
Definition 8
Given a net and its concurrency matrix, the concurrency graph is an undirected graph, whose vertices correspond to the places of the net, and such that it exists an edge between two different vertices iff the value of the matrix cell for the corresponding places is equal to “1”. There are no self-loops in the concurrency graph.
The decomposition problem can be formulated as a graph colouring problem on the concurrency graph, where leaf units play the role of colours. To ensure unit safeness, any two concurrent places must be put into different units; this amounts to the problem of assigning different colors to any two vertices connected by an edge in the concurrency graph. Then, for each colour, a unit is created, which contains all the vertices (i.e., places) having the same colour.
The concurrency graph is derived from the relation “\(\Vert \,\)”; one can also consider its complement graph (up to self-loops), which is derived from the relation “\(\not \!\Vert \,\)”:
Definition 9
Given a net and its concurrency matrix, the sequentiality graph is an undirected graph, whose vertices correspond to the places of the net, and such that it exists an edge between two different vertices iff the value of the matrix cell for the corresponding places is equal to “0”. There are no self-loops in the sequentiality graph.
4 Solution Search
Bits vs Units. In Sect. 2.5, we have selected the number of bits for encoding reachable markings (see Definition 6) as the most sensible criterion to finely measure the quality of a decomposition. However, this criterion is not easy to express in methods based on graph theory or SAT/SMT solving, because it involves the transcendental function “\(\log _2\)” and the continuous-discrete conversion function “\(\lceil . \rceil \)”. For this reason, our approaches do not directly focus on reducing the number of bits specified in Definition 6, but target instead another goal that is much simpler to implement: reducing the number of units in the output NUPN. Unfortunately, reducing the number of units does not always coincide with reducing the number of bits. Consider a network with 10 places: a decomposition in 2 permanent units with 5 places each will require 6 bits, whereas another decomposition in 3 permanent units with, respectively, 2, 2, and 6 places will require 5 bits onlyFootnote 14. However, a statistical analysis and our experiments show that a search oriented towards reducing the number of units also reduces, on average, the number of bits for encoding reachable markings.
Dichotomy vs Linear Search. We have seen above in Sect. 2.4 that all the solutions of the decomposition problem have their number of leaf units n within an interval \([{ Min}, { Max}]\). Having implemented dichotomy, ascending linear search (i.e., starting from Min and incrementing n until a solution is found), and descending linear search (starting from Max and decrementing n until no solution is found), we observed that the latter is usually more efficient. A key advantage of the latter approach is that it always produces a valid (yet perhaps sub-optimal) solution, even if the search is halted due to some user-specified timeout limitation. Whenever possible, we accelerate the convergence by asking the solver whether it exists a solution having at most n leaf units (rather than a solution having exactly n leaf units). If the solver finds a solution having m leaf units, with \(m < n - 1\), the next iteration will use m rather than \(n-1\).
Upper Bound Reduction. Having opted for descending linear search, we now present three approaches for reducing the value of the upper bound Max (i.e., the number of places). This boosts efficiency by restricting the search space, without excluding relevant solutions (the lower bound Min defined in Sect. 2.4 is kept unchanged):
-
1.
As mentioned in Sect. 2.4, dead places, if present, can be put into any leaf unit of the output NUPN, still preserving the unit-safeness property. With respect to our quality criterion based on the number of bits, it would not be wise to create one extra unit to contain all the dead places nor, even worse, one extra unit per dead place. Instead, our approach is to put dead places into “normal” units, taking advantage of free slots, i.e., unused bit values in logarithmic encoding. For instance, if a non-permanent unit has n places, there are \(m = \lceil \log _2(n+1) \rceil -(n+1)\) free slots, meaning, if m is not zero, that m dead places can be added to this unit without increasing its cost in bits. If there are less free slots than dead places, then we augment the number of free slots by adding one bit (or even more) to the unit having already the largest number of places. Thus, in presence of D dead places, we start by putting these places apart, discarding from the concurrency matrix the corresponding lines and columns, all of which contain only cells equal to “0”. We then perform a descending linear search starting from \({ Max} - D\) rather than \({ Max}\). Finally, we distribute the dead places into the resulting units as explained above.
-
2.
After discarding dead places, one can still start the descending linear search from a lower value than \({ Max} - D\). Let \({ Sum}_p\) be the sum, in the concurrency matrixFootnote 15, of all cell values on the lineFootnote 16 corresponding to place p. Let \({ Sum}\) be the maximum, for all places p, of \({ Sum}_p\). Clearly, \({ Min} \le { Sum} \le { Max} - D\). One can start the search from \({ Sum}\) (rather than \({ Max} - D\)) since no solution has more than \({ Sum}\) leaf units. Indeed, \({ Sum}\) is equal to \(\varDelta + 1\), where \(\varDelta \) is the maximum degree of the concurrency graphFootnote 17 (the increment “\(+1\)” corresponds to the diagonal cell, whose value is always “1”) and, from Brooks’ theorem (extended to possibly non-connected graphs), the number of colours needed for the concurrency graph is at most \(\varDelta + 1\), so there exists at least one solution having at most \({ Sum}\) leaf units.
-
3.
If the concurrency matrix was initially complete, and if the input NUPN contains the “!unit_safe” pragma, let W be the width of the input NUPN. If this NUPN is not flat, one can modify it by keeping only its root unit and leaf units, and by moving, for each non-leaf unit u, the local places of u into any leaf unit nested in u; clearly, the modified NUPN is flat, unit safeFootnote 18, and has also width W. So, there exists at least one solution with W leaf units. Thus, the descending linear search can be started from \({ min} (W, { Sum} - D)\) rather than \({ Sum} - D\), excluding the potential solutions having more leaf units than the input NUPN.
5 Methods Based on Graph Colouring
As stated in Sect. 3.3, the decomposition problem can be expressed as a colouring problem on the concurrency graph (see Definition 8). Thus, the simplest method to perform decomposition is to invoke a graph coloring tool, keeping in mind that graph colouring is an NP-complete problem. Moreover, if the concurrency matrix was initially complete, the minimal number of colours (i.e., the chromatic number of the graph) gives a decomposition with the smallest number of leaf units.
Implementation and Experimentation. We decided to use the Color6 softwareFootnote 19, which is developed at Université de Picardie Jules Verne (France) and is one of the most recent tools for graph colouring. Since Color6 does not necessarily compute an optimal solution (i.e., with the chromatic number) but instead returns a solution having at most a number of colors specified by the user, the tool must be invoked repeatedly, using the linear decreasing search strategy described in 4.
We developed Bourne-shell and Awk scripts that convert the concurrency graph into standard DIMACS format, invoke Color6 iteratively using descending linear search, parse the output of Color6, and finally assign places to units upon completion of the iterations. The results obtained are presented, as for all other decomposition methods, in Sect. 9.
We also experimented with dichotomy and ascending linear search, which we found, on average, 8% and 18% slower than descending linear search; indeed, Color6 often takes much more time to conclude there is no solution (i.e., when given a number of colors smaller than the chromatic number) than to find a solution when it exists.
6 Methods Based on Maximal Cliques
There is another (and, up to our knowledge, novel) approach to the decomposition problem. In the sequentiality graph (see Definition 9), a clique is a set of vertices that are pairwise connected (i.e., a complete subgraph), meaning that a clique corresponds to a potential unit, i.e., a set of places having at most one token in any reachable marking.
Colouring the concurrency graph is equivalent to finding, in the sequentiality graph, a minimal set of cliques that covers all vertices. Instead, we use a software tool that computes a maximal clique, i.e., one single clique containing as many vertices as possible. Although this problem is also NP-complete, it is usually faster to solve in practice than graph colouring.
The tool is invoked repeatedly: at each iteration, a maximal clique is found, from which, a unit is created; the sequentiality graph is then simplified by removing the vertices and edges of the clique, and the next iteration takes place until the sequentiality graph becomes empty. Hence, neither dichotomy nor linear searches apply to the approach described in the present section.
Implementation and Experimentation. We experimented with four maximum-clique tools: MaxCliqueDynFootnote 20, BBMCFootnote 21, MaxCliqueParaFootnote 22—all developed at Institut Jožef Stefan in Ljubljana (Slovenia), and MoMCFootnote 23 developed at Université de Picardie Jules Verne (France). We developed Bourne shell and Awk scripts that generate sequentiality graphs in the DIMACS format, remove cliques from these graphs, invoke the tools, and extract maximal cliques from their output.
7 Methods Based on SAT Solving
We now present methods that encode the constraints of the concurrency matrix as propositional logic formulas passed to a SAT solver, contrary to the methods of Sect. 5 and 6, in which these constraints are expressed using graphs. We believe that the use of SAT solving for the decomposition problem is a novel approach. For efficiency, we generate formulas in Conjunctive Normal Form (CNF), a restriction (natively accepted by most SAT-solvers) of propositional logic.
When applying decreasing linear search (see Sect. 4), one must produce a formula asking whether it exists a decomposition having at most n units. For each place p and each unit u, we create a propositional variable \(x_{pu}\) that is true iff place p belongs to unit u. We then add constraints over these variables: (i) For each unit u and each two places p and \(p'\) such that \(\#p < \#p'\), where \(\#p\) is a bijection from places names to the interval \([1, \text {card}\,(P)]\), if the cell \((p,p')\) of the concurrency matrix contains the value “1”, we add the constraint \(\lnot x_{pu} \vee \lnot x_{p'u}\) to express that two concurrent places cannot be in the same unit; (ii) For each place p, we could add the constraint \(\bigvee _u x_{pu}\) to express that p belongs to at least one unit, but this constraint is too loose and allows n! similar solutions, just by permuting unit names; we thus replace the previous constraint by a stricter one that breaks the symmetry between units: for each place p, we add the refined constraint \(\bigvee _{1 \le \#u \le { min} (\#p, n)} x_{pu}\), where \(\#u\) is a bijection from unit names to the interval [1, n].
Notice that no constraint requires that each place belongs to one single unit, as such a constraint would generate large formulas (quadratic in the number of units) when using the CNF fragment only. Thus, the SAT solver may compute an overly general answer, which includes invalid decompositions in which a place belongs to several units. We then refine this answer by assigning each of these places to a single unit, also trying to minimize the number of bits corresponding to the chosen valid decomposition. Our approach takes inspiration from the first-fit-decreasing bin-packing algorithm: places are first sorted by increasing numbers of units to which they can belong according to the SAT-solver; then, each place is put into the unit having the most free slots (see Sect. 4) and, in case of equality, the most local places.
Implementation and Experimentation. We experimented with two SAT solvers: MiniSat, which was chosen for its popularity, and CaDiCaL, which solved the most problems during the SAT Race 2019 competition. We developed Python scripts that generate formulas in the DIMACS-CNF format, invoke a SAT solver, parse its outputs, and assign places to units.
8 Methods Based on SMT Solving
We also considered SMT solvers, which accept formulas in richer logics than SAT solvers, namely (fragments of) first-order logic. We encoded the decomposition problem into five (quantifier-free) logic fragments: BV, DT, UFDT, IDL, and UFIDL, which we define below. As in Sect. 7, we perform descending linear search, generating formulas from the concurrency matrix for a given number n of units.
BV corresponds to quantifier-free bit-vector logic, which supports fixed-size boolean vectors and logical, relational, and arithmetical operators on these vectors. Our encoding creates, for each place p, a bit vector \(b_p\) of length n such that \(b_p[u]\) is true iff place p can belong to unit u. Constraints are then added in the same way as for SAT solving, shifting from a quadratic set of propositional variables to a linear set of bit vectors.
DT corresponds to quantifier-free data-type logic, which supports the definition of algebraic data types. Our encoding defines an enumerated type Unit, which contains one value per unit; it creates also, for each place p, one variable \(x_p\) of type Unit. Then, constraints are added in the same way as for SAT solving, replacing each propositional variable \(x_{pu}\) by the predicate \(x_p = u\), with the difference that our encoding implicitly warrants that each place is assigned to one, and only one, unit.
UFDT corresponds to quantifier-free uninterpreted-function data-type logic. Our encoding is based on that of DT but, instead of the \(x_p\) variables, defines both an enumerated type Place, which contains one value per place, and an uninterpreted function \(\mathrm{u} : { Place} \rightarrow { Unit}\), each occurrence of \(x_p\) being replaced with \(\mathrm{u} (p)\) in the constraints.
IDL corresponds to quantifier-free integer-difference logic, which supports integer variables and arithmetic constraints on the difference between two variables. Our encoding is based on that of DT but declares the variables \(x_p\) with the integer type instead of Unit. Since integers are unbounded, each variable \(x_p\) whose place number \(\#p\) is greater or equal than n must be constrained by adding \(x_p \in \{ 1, ..., n \}\), since \(x_p\) is not subject to a symmetry-break constraint.
UFIDL corresponds to quantifier-free uninterpreted-function integer-difference logic. Our encoding is based on that of IDL, with the same changes as for evolving from DT to UFDT. The additional constraint for each place p not subject to symmetry breaking is \(\mathrm{u}(x_p) \in \{ 1, ..., n \}\).
Implementation and Experimentation. We experimented with four SMT solvers: Z3 and CVC4, which are general enough to support all the aforementioned logic fragments, as well as Boolector and Yices, which support fewer fragments but were among the two fastest solvers in their respective “single query tracks” of the SMT-COMP 2019 competition. We developed Python scripts to generate formulas in the standard SMT-LIB 2 format, invoke the SMT solvers, analyze their output, and produce the decomposition.
We have 14 combinations (logic fragment, solver), to which we add a 15th combination by processing the IDL fragment with the linear-optimization capabilities of Z3: this is done by enriching the IDL formula with a (Z3-specific) directive “min” that asks Z3 to compute a solution with the smallest number of units; thus, no iteration is required for this approach, which we note “z3opt”.
9 Experiment Results
Validation of Results. We checked each output NUPN systematically to ensure that: (i) it is syntactically and semantically correct, by running CÆSAR.BDD (with option “-check”); (ii) it is presumably unit safe, by checking that none of its units contains two places declared to be concurrent in the concurrency matrix; if the concurrency matrix was initially complete, this guarantees unit safeness; (iii) if the concurrency matrix was initially incomplete, we also check that the output NUPN is presumably unit safe, by exploring (part of) its marking graph, still using CÆSAR.BDD with option “-check”, setting a timeout of one minute for this exploration; (iv) the input and the output NUPNs have the same structural and behavioural properties, including those of Table 1 and 2, but the three last lines devoted to units in both tables; this is done by comparing the outputs of CÆSAR.BDD (with option “-mcc”) under a timeout of one minute.
Presentation of Results. Table 3 summarize the experimental results for all our decomposition methods listed in column 1 of this table. All the methods use the concurrency matrices, which have been pre-computed (when possible) for each input NUPN model of our collection. Each method was tried on each model, with a timeout of two minutes per model. If a method failed (because, e.g., a model was too large, its concurrency matrix absent, the constraints too complex for the solver, etc.), the trivial solution was taken as the result. If a timeout occurred for a method using descending linear search, the last computed intermediate solution was retained. We produced a large number of output NUPNs (potentially 12,728 input NUPNs \(\times \) 22 decomposition methods, actually 265,121 output NUPNs). Column 2 (successes) gives the percentage of models decomposed by the corresponding method, whether a timeout occurred or not. Column 3 (failures) gives the number of models that the method failed to decompose, without occurrence of a timeout. Column 4 (timeouts) give the number of models for which a timeout occurred. Column 5 (total time) gives the time spent by the method on all models, excluding matrix pre-computation and validation of results. Column 6 (bit ratio) measures the quality of the decomposition by giving the quotient of the number of bits in the decomposed model divided by the number of bits in the input modelFootnote 24; the “total” sub-column gives the quotient between the sums of bits for all models, while the “mean” sub-column gives the average of the quotients obtained for each model. Column 7 (unit ratio) does the same as Column 6 for the number of (leaf) units instead of bits.
Many observations can be drawn from Table 3. In a nutshell, the maximal-cliques methods perform best: they are among the fastest approaches, with the fewest timeouts, and produce the most compact decompositions—possibly because they manage to handle large models for which the potential gains in bits and units are the most important. Interestingly, our results contradict the claim that BDD size is smaller when units have a balanced number of places [25]; one rather observes that the most compact encodings are achieved using maximal cliques, which produce fundamentally imbalanced decompositions by computing very large cliques during the first iterations and very small ones at the end.
Comparison with Hippo. We compared our methods with the three decomposition methods (“comparability graphs”, “heuristic invariants”, and “hypergraph colouring”) of Hippo, on all the 223 safe Petri nets available (after removing duplicates) from the Hippo web portal. Our tool chain revealed that several of these nets were incorrect and that the two latter decomposition methods could produce invalid results; we reported these issues, later solved by the Hippo team.
Pursuing our assessment, we measured that the three methods of Hippo took, respectively, 65 seconds, 25 min, and 1 hour 53 min to process the collection of benchmarks. The Hippo portal uses a timeout of nearly 22-minutes, since, for five of the models, [28] reports that decomposition using hypergraphs takes more than one hour. Actually, the three methods could process, respectively, \(70.5\%\), \(92.5\%\), and \(91.1\%\) of the collection. In contrast, our tool chain took only 16 seconds to process 100% of the collection, using the Color6 tool on a 9-year old laptop. The decomposed models produced by our tool chain are also more compact, with an average bit ratio of \(60.6\%\), compared to \(80.6\%\), \(92.2\%\), and \(76.21\%\) for the three methods of Hippo, respectively.
10 Conclusion
For the decomposition problem, which is nearly 50-year old, we presented various methods to automatically translate an ordinary, safe Petri net into a flat NUPN preserving all the structural and behavioural properties of the input model. For such purpose, the concepts and results of the NUPN theory [8] have been found remarkably well-adapted.
Our methods have been implemented in a complete tool chain that accepts and produces models in standard PNML format. The tool chain takes advantage of recent advances in graph algorithms and SAT/SMT solvers, and is modular, allowing certain components to be replaced by more efficient ones. The tool chain is helpful to automatically restructure “legacy” Petri nets and “upgrade” them to NUPNs by inferring their (hidden or lost) concurrent structure.
Decomposition is a difficult problem, and several steps in our tool chain are NP-complete or PSPACE-complete; thus, there will always exist arbitrarily large Petri nets that cannot be decomposed. Yet, this is asymptotic complexity, which does not infirm the high success rate (from 87.3% to 99.2%) of our methods assessed on a large collection of 12,728 models from multiple, diverse origins.
Notes
- 1.
- 2.
\(\sqsubseteq \) is reflexive, antisymmetric, transitive, and \(u_0\) is the greatest element of U for \(\sqsubseteq \).
- 3.
From item 8 of Definition 3, only the root unit \(u_0\) may be void.
- 4.
Each unit has a single local place, except the root unit, which has either zero or one.
- 5.
However, they can have no transition.
- 6.
- 7.
- 8.
http://cadp.inria.fr/man/caesar.bdd.html (see option “-check”).
- 9.
http://github.com/ahamez/caesar.sdd (see option “–check”).
- 10.
- 11.
- 12.
We define arc density as the number of arcs divided by twice the product of the number of places and the number of transitions, i.e., the amount of memory needed to store the arc relation as a pair of place\(\times \)transition matrices.
- 13.
- 14.
The same observation holds for non-permanent units, e.g., \(4+5\) vs \(7+1+1\) places.
- 15.
With or without dead places—this does not change the result since, given that \(M_0 \ne \varnothing \), there is always at least one place that is not dead.
- 16.
Or column, since the concurrency matrix is symmetric.
- 17.
With or without dead places.
- 18.
Based upon the general definition of unit safeness [8, Sect. 3] for non-flat NUPNs.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
If an input model is non-trivial, it is replaced by the equivalent trivial NUPN.
References
Amparore, E.G., Beccuti, M., Donatelli, S.: Gradient-based variable ordering of decision diagrams for systems with structural units. In: D’Souza, D., Narayan Kumar, K. (eds.) ATVA 2017. LNCS, vol. 10482, pp. 184–200. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68167-2_13
Badouel, E., Caillaud, B., Darondeau, P.: Distributing finite automata through Petri net synthesis. Formal Asp. Comput. 13(6), 447–470 (2002)
Balaguer, S., Chatain, T., Haar, S.: A concurrency-preserving translation from time Petri nets to networks of timed automata. Formal Methods Syst. Des. 40(3), 330–355 (2012)
Bernardinello, L., De Cindio, F.: A survey of basic net models and modular net classes. In: Rozenberg, G. (ed.) Advances in Petri Nets 1992. LNCS, vol. 609, pp. 304–351. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55610-9_177
Best, E., Darondeau, P.: Petri net distributability. In: Clarke, E., Virbitskaite, I., Voronkov, A. (eds.) PSI 2011. LNCS, vol. 7162, pp. 1–18. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29709-0_1
Desel, J., Esparza, J.: Free Choice Petri nets. Cambridge University Press, Cambridge (1995)
Eshuis, R.: Translating safe Petri nets to statecharts in a structure-preserving way. In: Cavalcanti, A., Dams, D.R. (eds.) FM 2009. LNCS, vol. 5850, pp. 239–255. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-05089-3_16
Garavel, H.: Nested-unit Petri nets. J. Log. Algebraic Method Program. 104, 60–85 (2019)
Garavel, H., Serwe, W.: State space reduction for process algebra specifications. Theor. Comput. Sci. 351(2), 131–145 (2006)
Genest, B., Kuske, D., Muscholl, A.: On communicating automata with bounded channels. Fundam. Inform. 80(1–3), 147–167 (2007)
van Glabbeek, R., Goltz, U., Schicke-Uffmann, J.-W.: On distributability of Petri nets. In: Birkedal, L. (ed.) FoSSaCS 2012. LNCS, vol. 7213, pp. 331–345. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28729-9_22
Hack, M.: Analysis of Production Schemata by Petri Nets, Master thesis (computer science), MIT, Cambridge, MA, USA (1972)
Hack, M.: Extended State-Machine Allocatable Nets (ESMA), an Extension of Free Choice Petri Net Results. Technical report, 78–1, MIT (1974)
ISO/IEC: High-level Petri Nets - Part 2: Transfer Format. IS 15909–2:2011 (2011)
Janicki, R.: Nets, Sequential components and concurrency relations. Theor. Comput. Sci. 29, 87–121 (1984)
Karatkevich, A., Andrzejewski, G.: Hierarchical decomposition of Petri nets for digital microsystems design. In: Modern Problems of Radio Engineering, Telecommunications, and Computer Science, pp. 518–521. IEEE (2006)
Kovalyov, A.V.: Concurrency relations and the safety problem for Petri nets. In: Jensen, K. (ed.) ICATPN 1992. LNCS, vol. 616, pp. 299–309. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55676-1_17
Kovalyov, A., Esparza, J.: A polynomial algorithm to compute the concurrency relation of free-choice signal transition graphs. In: Workshop on Discrete Event Systems, pp. 1–6 (1996)
Mennicke, S., Oanea, O., Wolf, K.: Decomposition into open nets. In: Algorithmen und Werkzeuge für Petrinetze, pp. 29–34. CEUR-WS.org (2009)
Munoz-Gama, J., Carmona, J., van der Aalst, W.M.P.: Hierarchical conformance checking of process models based on event logs. In: Colom, J.-M., Desel, J. (eds.) PETRI NETS 2013. LNCS, vol. 7927, pp. 291–310. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38697-8_16
Pastor, E., Cortadella, J., Peña, M.A.: Structural methods to improve the symbolic analysis of Petri nets. In: Donatelli, S., Kleijn, J. (eds.) ICATPN 1999. LNCS, vol. 1639, pp. 26–45. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48745-X_3
Petit, A.: Distribution and synchronized automata. Theor. Comput. Sci. 76(2–3), 285–308 (1990)
Rozenberg, G., Engelfriet, J.: Elementary net systems. In: Reisig, W., Rozenberg, G. (eds.) ACPN 1996. LNCS, vol. 1491, pp. 12–121. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-65306-6_14
Schmidt, K.: Using Petri net invariants in state space construction. In: Garavel, H., Hatcliff, J. (eds.) TACAS 2003. LNCS, vol. 2619, pp. 473–488. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36577-X_35
Semenov, A., Yakovlev, A.: Combining partial orders and symbolic traversal for efficient verification of asynchronous circuits. In: CHDL. IEEE (1995)
Starke, P.H.: Analyse von Petri-Netz-Modellen. Teubner, Leitfäden und Monographien der Informatik (1990)
Wiśniewski, R., Karatkevich, A., Adamski, M., Costa, A., Gomes, L.: Prototyping of concurrent control systems with application of Petri nets and comparability graphs. IEEE Trans. Control Syst. Technol. 26(2), 575–586 (2018)
Wiśniewski, R., Wiśniewska, M., Jarnut, M.: C-exact hypergraphs in concurrency and sequentiality analyses of cyber-physical systems specified by safe Petri nets. IEEE Access 7, 13510–13522 (2019)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Bouvier, P., Garavel, H., Ponce-de-León, H. (2020). Automatic Decomposition of Petri Nets into Automata Networks – A Synthetic Account. In: Janicki, R., Sidorova, N., Chatain, T. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2020. Lecture Notes in Computer Science(), vol 12152. Springer, Cham. https://doi.org/10.1007/978-3-030-51831-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-51831-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51830-1
Online ISBN: 978-3-030-51831-8
eBook Packages: Computer ScienceComputer Science (R0)


 .
. .
.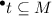 .
. , which we note
, which we note 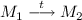 .
.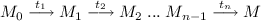 .
. ; intuitively
; intuitively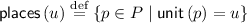 .
. .
.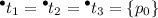 ,
, 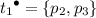 ,
,  , and
, and  has at most 2 tokens but at least 3 leaf units in any valid decomposition.
has at most 2 tokens but at least 3 leaf units in any valid decomposition.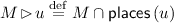 .
. .
.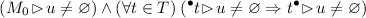 .
.