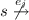Automated Repair of Process Models Using Non-local Constraints

Abstract

State-of-the-art process discovery methods construct free-choice process models from event logs. Hence, the constructed models do not take into account indirect dependencies between events. Whenever the input behavior is not free-choice, these methods fail to provide a precise model. In this paper, we propose a novel approach for the enhancement of free-choice process models, by adding non-free-choice constructs discovered a-posteriori via region-based techniques. This allows us to benefit from both the performance of existing process discovery methods, and the accuracy of the employed fundamental synthesis techniques. We prove that the proposed approach preserves fitness with respect to the event log, while improving the precision when indirect dependencies exist. The approach has been implemented and tested on both synthetic and real-life datasets. The results show its effectiveness in repairing process models discovered from event logs.

1 Introduction

Process mining is a family of methods used for the analysis of event data [1]. These methods include process discovery aimed at constructing process models from event logs; conformance checking applied for finding deviations between real (event logs) and expected (process models) behavior [13]; and process enhancement used for the enrichment of process models with additional data extracted from event logs. The latter also includes process repair applied to realign process models in accordance with the event logs. Event logs are usually represented as sequences of events (or traces). The main challenge of process discovery is to efficiently construct fitting (capturing traces of the event log), precise (not capturing traces not present in the event log) and simple process models.

Scalable process discovery methods, which are most commonly used for the analysis of real-life event data, either produce directly follows graphs, or use them as an intermediate process representation to obtain a Petri net or a BPMN model [24] (see e.g. Inductive miner [21] and Split miner [5]). Directly follows graphs are directed graphs with nodes representing process activities and arcs representing the directly follows (successor) relation between them. Being simple and intuitive, these graphs considerably generalise process behaviour, e.g., they add combinations of process paths that are not observed in the event log. This is because they do not represent higher-level constructs such as parallism and long distance (i.e., non-local) dependencies. The above-mentioned discovery methods construct directly follows graphs from event logs and then recursively find relations between sets of nodes in these graphs, in order to discover a free-choice Petri net [15], which can then be seemlessly converted into a BPMN model – the industry language for representing business process models. In free-choice nets, the choice between conflicting activities (such that only one of them can be executed) is always “free” from additional preconditions. Although parallel activities can be modeled by free-choice nets, non-local choice dependencies are modeled by non-free-choice nets [30]. Several methods for the discovery of non-free-choice Petri nets exist. However, these methods are either computationally expensive [3, 8, 11, 29, 31], or heuristic in nature (i.e., the derived models may fail to replay the traces in the event log) [30]. Even these methods are not heuristic and demonstrate reasonable performance, they usually produce process models with complex structure [22, 32]. In contrast, the approach proposed in this paper, starts with a simple free-choice “skeleton” enhancing it with additional modeling constructs.

In this paper, we propose a repair approach for the enhancement of free-choice nets by adding extra constructs to capture non-local dependencies. To find non-local dependencies, a transition system constructed from the initial event log is analyzed. This analysis checks whether all the free-choice constructs of the initial process model correspond to free-choice relations in the transition system. For process activities with non-free-choice relations in the transition system but with free-choice relation in the Petri net, region theory [7] is applied to identify, whenever possible, additional places and arcs to be added to the Petri net to ensure the non-local relations between the corresponding transitions. Remarkably, although we have implemented our approach over state-based region theory [3, 11, 29], the proposed approach can be also extended to language-based region theory [9, 31], or to geometric or graph-based approaches that have been recently proposed [10, 28].

Importantly, we apply a goal-oriented state-based region algorithm, to those parts of the transition system where the free-choice property is not fulfilled. This allows us to reduce the computation time, relegating region-theory to when it is really needed. We prove that important quality metrics of the initial free-choice (workflow) net are either preserved, or improved for those cases where non-local dependencies exist, i.e., fitness is never reduced and precision can increase. Hence, when using our approach on top of an automated discovery method that returns a free-choice Petri net, one can still keep the complexity of process discovery manageable, obtaining more precise process models that represent more faithfully the process behavior recorded in the event log.

In contrast to the existing process repair techniques, which change the structure of the process models by inserting, removing [4, 17, 25] or replacing tasks and sub-processes [23], the approach proposed in this paper only imposes additional restrictions on the process model behavior, preserving fitness and improving precision where possible.

We implemented the proposed approach as a plugin of Apromore [20]¹ and tested it both on synthetic and real-world event data. The tests show the effectiveness of our approach within reasonable time bounds.

The paper is organized as follows. Section 2 illustrates the approach by a motivating example. Section 3 contains the main definitions used throughout the paper. The state-based region technique is introduced in Sect. 4. The proposed model repair approach is then described in Sect. 5. Additionally, Sect. 5 contains formal proofs of the properties of the repaired process model. High-level process modeling constructs, e.g., BPMN modeling elements representing non-free-choice routing are also discussed in Sect. 5. The results of the experiments are presented in Sect. 6. Finally, Sect. 7 concludes the paper.

2 Motivating Example

This section presents a simple motivating example inspired by real-life event log² and examples discussed in [30]. Consider a process of loan application. The process can be carried out by a client or by a bank employee on behalf of the client. Thus, this process can be described by two possible sequences of events (traces) which together can be considered as an event log: $L=\{\langle send\,application ,\, check\,application , notify\,client ,\, accept\,application \rangle$, $\langle create\,application ,\, check\,application ,\, complete application ,\, accept\,application \rangle \}$. According to one trace, the client sends a loan application to the bank, then this application is checked, after that the client is notified and the application is accepted. The other trace corresponds to a scenario when the application is initially created by a bank employee, then it is checked, after that, the bank employee contacts the client to complete the application, and finally, the application is accepted. Figure 1 presents a workflow net discovered by Inductive miner [21] and Split miner [5] from L. This model accepts two additional traces: $\langle send\,\,application ,\, check\,\,application ,\ complete\,application , accept\,application \rangle$, $\langle create\,application , check\,application ,\, notify\,client ,\, accept application \rangle$ not presented in L. These traces violate the business logic of the process. If the application was sent by a client, it is completed, and there is no need to take $complete\,application$ step. Also, if the application was initially created by a bank employee, the step $complete\,application$ is mandatory.

Fig. 1.

A workflow net discovered from L by Inductive miner and Split miner.

This example demonstrates that the choice between $notify\,client$ and $complete application$ activities depends on the history of the trace. The transition system in Fig. 2 shows a behavior recorded in event log L (Fig. 2). State $s_1$ corresponds to a choice between activities $send\,application$ and $create\,application$. This choice does not depend on any additional conditions. In contrast, for the system being in states $s_4$ and $s_5$ there is no free choice between $notify\,client$ and $complete\,application$ activities; in state $s_4$ only $notify\,client$ step can be taken, in $s_5$ only $complete\,application$ can be performed. This means that there are states in the transition system where activities $notify\,client$ and $complete\,application$ are not in a free-choice relation (the choice depends on additional conditions and is predefined), while they are in a free-choice relation within the discovered model (Fig. 1).

To impose additional restrictions on the process model the state-based region theory can be applied [12, 14, 29]. Figure 2 presents three regions $r_1=\{s_4,s_5\}$, $r_2=\{s_2,s_4\}$, and $r_3=\{s_3,s_5\}$ with outgoing transitions labeled by $notify\,client$ and $complete\,application$ events discovered by the state-based region algorithm [29].

Fig. 2.

Transition system that encodes event log L.

Figure 3 presents a target workflow net obtained from the initial workflow net (Fig. 1) by inserting places which correspond to the discovered regions. As one may note, in addition to $r_1$, two places $r_2$ and $r_3$ were added. These places impose additional constraints, such that the enhanced process model accepts event log L and does not support additional traces and, hence, is more precise.

Fig. 3.

A workflow net enhanced with additional regions (places) $r_2$ and $r_3$.

In the next sections, we formalise this technique and apply it to event data.

3 Preliminaries

In this section, we formally define event logs and process models, such as transition systems, Petri nets, and workflow nets.

3.1 Sets, Multisets, Event Logs

Let S be a finite set. A multiset m over S is a mapping $m: S\rightarrow \mathbb {N}_0$, where $\mathbb {N}_0$ is the set of all natural numbers (including zero), i.e., multiset m contains m(s) copies of element $s\in S$.

For two multisets $m,m'$ we write $m\subseteq m'$ iff $\forall s\in S: m(s) \le m'(s)$ (the inclusion relation). The sum of two multisets m and $m'$ is defined as: $\forall s\in S: (m+m')(s)=m(s)+m'(s)$. The difference of two multisets is a partial function: $\forall s\in S$, such that $m(s)\ge {m(s')}$, $(m-m')(s)=m(s)-m'(s)$.

Let E be a finite set of events. A trace $\sigma$ (over E) is a finite sequence of events, i.e., $\sigma \in {E^*}$, where $E^*$ is the set of all finite sequences over E, including the empty sequence of zero length. An event log L is a set of traces, i.e., $L\subseteq E^*$.

3.2 Transition Systems, Petri Nets, Workflow Nets

Let S and E be two disjoint non-empty sets of states and events, and $B\subseteq {S}\times {E}\times {S}$ be a transition relation. A transition system is a tuple $\mathord {\textit{TS}}=(S,E,B,s_{ i }, S_{ fin })$, where $s_{ i }\in S$ is an initial state and $S_{ fin } \subseteq S$ – a set of final states. Elements of B are called transitions. We write $s{\mathop {\rightarrow }\limits ^{e}}s'$, when $(s,e,s')\in B$ and $s{\mathop {\rightarrow }\limits ^{e}}$, when $\exists s'\in S$, such that $(s,e,s')\in B$; , otherwise.

A trace $\sigma = \left\langle e_1,\dots ,e_n\right\rangle$ is called feasible in $\mathord {\textit{TS}}$ iff $\exists s_1,\dots ,s_{n}\in S: \ s_{ i }{\mathop {\rightarrow }\limits ^{e_1}}s_1 {\mathop {\rightarrow }\limits ^{e_2}}\dots {\mathop {\rightarrow }\limits ^{e_n}}s_{n}$, and $s_n\in S_{ fin }$, i.e., a feasible trace leads from the initial state to some final state. A language accepted by $\mathord {\textit{TS}}$ is defined as the set of all traces feasible in $\mathord {\textit{TS}}$, and is denoted by $\mathcal {L}(TS)$.

We say that a transition system $\mathord {\textit{TS}}$ encodes an event log L iff each trace from L is a feasible trace in $\mathord {\textit{TS}}$, and inversely each feasible trace in $\mathord {\textit{TS}}$ belongs to L. An example of a transition system is shown in Fig. 2. States and transitions are presented by vertices and directed arcs respectively. The initial state $s_1$ is marked by an additional incoming arrow, the only final state $s_7$ is indicated by a circle with double border.

Let P and T be two finite disjoint sets of places and transitions, and $F\subseteq (P\times T)\cup (T\times P)$ be a flow relation. Let also E be a finite set of events, and $l: {T}\rightarrow {E}$ be a labeling function, such that $\forall t_1,t_2\in T, t_1\ne t_2$, it holds that $l(t_1)\ne l(t_2)$, i.e., all the transitions are uniquely labeled. Then $N=(P,T,F,l)$ is a Petri net.

A marking in a Petri net is a multiset over the set of its places. A marked Petri net $(N,m_0)$ is a Petri net N together with its initial marking $m_0$.

Graphically, places are represented by circles, transitions by boxes, and the flow relation F by directed arcs. Places may carry tokens represented by filled circles. A current marking m is designated by putting m(p) tokens into each place $p\in P$. Marked Petri nets are presented in Figs. 1 and 3.

For a transition $t\in T$, an arc (p, t) is called an input arc, and an arc (t, p) an output arc, $p\in P$. The preset ${}^{\bullet }t$ and the postset $t^{\bullet }$ of transition t are defined as the multisets over P, such that ${}^{\bullet }t(p)=1$, if $(p,t)\in F$, otherwise ${}^{\bullet }t(p)=0$, and $t^{\bullet }(p)= 1$ if $(t,p)\in F$, otherwise $t^{\bullet }(p)=0$. A transition $t\in T$ is enabled in a marking m iff ${}^{\bullet }t\subseteq m$. An enabled transition t may fire yielding a new marking (denoted $m{\mathop {\rightarrow }\limits ^{t}}m'$, $m{\mathop {\rightarrow }\limits ^{l(t)}}m'$, or just $m\rightarrow m'$). We say that $m_n$ is reachable from $m_1$ iff there is a (possibly empty) sequence of firings $m_1\rightarrow \dots \rightarrow m_n$ and denote this relation by $m_1{\mathop {\rightarrow }\limits ^{*}}{m_n}$.

${\mathcal R}(N,m)$ denotes the set of all markings reachable in Petri net N from marking m. A marked Petri net $(N,m_0),N=(P,T,F,l)$ is safe iff $\forall p\in P,\forall m\in \mathcal {R}(N,m_0):m(p)\le 1$, i.e., at most one token can appear in a place.

A reachability graph of a marked Petri net $(N,m_0)$, $N=(P,T,F,l)$, with a labeling function $l:T\rightarrow E$, is a transition system $\mathord {\textit{TS}}=(S,E,B,s_{ i }, S_{ fin })$ with the set of states $S= {\mathcal R}(N,m_0)$ and transition relation B defined by $(m,e,m')\in B$ iff $m{\mathop {\rightarrow }\limits ^{t}}m'$, where $e=l(t)$. The initial state in $\mathord {\textit{TS}}$ is the initial marking $m_0$. If some reachable markings in $(N,m_0)$ are distinguished as final markings, they are defined as final states in $\mathord {\textit{TS}}$. The language of a Petri net $(N,m_0)$, denoted by $\mathcal {L}(N,m_0)$ is the language of its reachability graph, i.e., $\mathcal {L}(N,m_0)=\mathcal {L}(\mathord {\textit{TS}})$. We say that a Petri net $(N,m_0)$ accepts a trace iff this trace is feasible in the reachability graph of $(N,m_0)$; a Petri net accepts a language iff this language is accepted by its reachability graph.

Given a Petri net $N=(P,T,F,l)$, two transitions $t_1,t_2\in T$ are in a free-choice relation iff ${}^{\bullet }t_1\cap {}^{\bullet }t_2=\emptyset$ or ${}^{\bullet }t_1={}^{\bullet }t_2$. Since we consider Petri nets with uniquely labeled transitions, we also say that events (or activities) $l(t_1)$ and $l(t_2)$ are in a free-choice relation. Petri net N is called free-choice iff for all $t_1,t_2\in T$, it holds that $t_1$ and $t_2$ are in a free-choice relation. This is one of the several equivalent definitions for free-choice Petri nets presented in [15]. A Petri net is called non-free-choice iff it is not free-choice. Figure 4 presents an example of a non-free-choice Petri net, where for two transitions $t_1$ and $t_2$ holds that ${}^{\bullet }t_1\cap {}^{\bullet }t_2=\{p_1,p_2\}\ne \emptyset$ and ${}^{\bullet }t_1=\{p_1,p_2\}\ne {}^{\bullet }t_2=\{p_1,p_2,p_3\}$.

Fig. 4.

A non-free-choice Petri net.

The choice of which transition will fire depends on an additional constraint imposed by place $p_3$. If $m(p_1)>0$, $m(p_2)>0$, and $m(p_3)=0$, then only $t_1$ is enabled, thus there is no free-choice between $t_1$ and $t_2$. Another example of a non-free-choice Petri net was presented earlier in Fig. 3, where transitions labeled by $notify\,client$ and $complete\,application$ are not in a free-choice relation, thus the Petri net is not free-choice. An example of a free-choice Petri net is presented in Fig. 1.

Workflow nets is a special subclass of Petri nets designed for modeling workflow processes [2]. A workflow net has one initial and one final place, and every place or transition is on a directed path from the initial to the final place.

Formally, a marked Petri net $N=(P,T,F,l)$ is called a workflow net iff

• 1. There is one source place $i\in P$ and one sink place $o\in P$, such that i has no input arcs and o has no output arcs.

• 2. Every node from $P\cup T$ is on a directed path from i to o.

• 3. The initial marking contains the only token in its source place.

We denote by [i] the initial marking in a workflow net N. Similarly, we use [o] to denote the final marking in a workflow net N, defined as a marking containing the only token in the sink place o. The language of workflow net N is denoted by $\mathcal {L}(N)$.

A workflow net N with the initial marking [i] and the final marking [o] is sound iff

• 1. For every state m reachable in N, there exists a firing sequence leading from m to the final state [o]. Formally, $\forall m:[([i]{\mathop {\rightarrow }\limits ^{*}}m)$ implies $(m{\mathop {\rightarrow }\limits ^{*}}[o])]$;

• 2. The state [o] is the only state reachable from [i] in N with at least one token in place o. Formally, $\forall m:[([i]{\mathop {\rightarrow }\limits ^{*}}m)\wedge ([o]\subseteq m)$ implies $(m=[o])]$;

• 3. There are no dead transitions in N. Formally, $\forall t\in T \ \exists m,m':([i]{\mathop {\rightarrow }\limits ^{*}}m{\mathop {\rightarrow }\limits ^{l(t)}}m')$.

Note that both models presented in Figs. 1 and 3 are sound workflow nets.

4 Region State-Based Synthesis

In this section, we give a brief description of the well-known state-based region algorithm [14] applied for the synthesis of Petri nets from transition systems.

Let $\mathord {\textit{TS}}=(S,E,T,s_{ i }, S_{ fin })$ be a transition system and ${r}\subseteq {S}$ be a subset of states. Subset r is a region iff for each event ${e}\in {E}$ one of the following conditions holds:

• all the transitions ${s_1}{\mathop {\rightarrow }\limits ^{e}}{s_2}$ enter r, i.e., ${s_1}\notin {r}$ and ${s_2}\in {r}$,

• all the transitions ${s_1}{\mathop {\rightarrow }\limits ^{e}}{s_2}$ exit r, i.e., ${s_1}\in {r}$ and ${s_2}\notin {r}$,

• all the transitions ${s_1}{\mathop {\rightarrow }\limits ^{e}}{s_2}$ do not cross r, i.e., ${s_1},{s_2}\in {r}$ or ${s_1},{s_2}\notin {r}$.

In other words, all the transitions labeled by the same event are of the same type (enter, exit, or do not cross) for a particular region.

A region $r'$ is said to be a subregion of a region r iff ${r'}\subseteq {r}$. A region r is called a minimal region iff it does not have any other subregions.

The state-based region algorithm covers the transition system by its minimal regions [16]. Figure 5 presents the transition system from Fig. 2 covered by minimal regions: $r_1=\{s_4,s_5\}$, $r_2=\{s_2,s_4\}$, $r_3=\{s_3,s_5\}$, $r_4=\{s_2,s_3\}$, $r_5=\{s_6\}$, $r_6=\{s_1\}$, and $r_7=\{s_7\}$. According to the algorithm in [14], every minimal region is transformed to a place within the target Petri net and connected with transitions corresponding to the exiting and entering events by outgoing and incoming arcs respectively (refer to Fig. 6).

Fig. 5.

Applying the state-based region algorithm to the transition system presented in Fig. 2.

Region r separates two different states $s,s'\in S$, $s\ne s'$, iff $s \in r$ and $s' \notin r$. Finding such a region is the state separation problem between s and $s'$ and is denoted by $SSP (s,s')$. When an event e is not enabled in a state s, i.e., , a region r, containing s may be found, such that e does not exit r. Finding such a region is known as the event/state separation problem between s and e and is denoted by $ESSP (s,e)$.

A well-known result in region theory establishes that if all $SSP$ and $ESSP$ problems are solved, then synthesis is exact [7]:

Theorem 1

A TS can be synthesized into a safe Petri net N such that the reachability graph of N is isomorphic to TS if all $SSP$ and $ESSP$ problems are solvable.

These problems are also known to be NP-complete [7]. In this paper, we reduce the size of the problem by constructing regions corresponding to particular events only.

Fig. 6.

A Petri net model synthesized from the transition system presented in Fig. 5.

5 Repairing Free-Choice Process Models

In this section, we describe our approach for repairing free-choice workflow nets using non-local constraints captured in the event logs. Additionally, we investigate formal properties of the repaired process models.

5.1 Problem Definition

Let N be a free-choice workflow net discovered from event log L and let $\mathord {\textit{TS}}$ be a transition system encoding L. Due to limitations of the automated discovery methods [5, 21] that construct free-choice workflow nets, not all the places that correspond to minimal regions may have been derived, and therefore important $SSP$/$ESSP$ problems may not be solved in N, when considering $\mathcal {R}(N,[i])$ as the behavior to represent with N.

This brings us to the following characterization of the problem. Let $t_1, \ldots , t_n$ be transitions in N with ${}^{\bullet }t_1={}^{\bullet }t_2=\dots ={}^{\bullet }t_n$, i.e., $t_1, \ldots , t_n$ are in the free-choice relation in N, and let $\mathord {\textit{TS}}=(S,E,T,s_{ i }, S_{ fin })$ be a minimal transition system encoding the event log L. If there exists a state $s \in S$, and $1 \le i < j \le n$ such that:

• 1. $e_i$, $e_j$ correspond to transitions $t_i$, $t_j$, respectively,

• 2. ${s}{\mathop {\rightarrow }\limits ^{e_i}}$,

• 3.

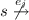
Then, the relation of $t_1, \ldots , t_n$ in N corresponds to a false free-choice relation, not observed in $\mathord {\textit{TS}}$.

There is no place in N corresponding to a region that solves the $ESSP (s,e_j)$ problem, because $t_1, \ldots , t_n$ are in a free-choice relation in N. For instance, the Petri net in Fig. 1 contains places corresponding to regions $r_1$, $r_4$, $r_5$, $r_6$, and $r_7$ shown in Fig. 5, and none of those regions solves the $ESSP (s_4, complete\,application )$ and $ESSP (s_5, notify\,client )$ problems in the transition system.

Note that we define the notion of a false free-choice relation for a minimal transition system (transition system with a minimal number of states [19]) encoding the event log. This is done in order to avoid a case when there exists a state $s'$ which is equivalent to s, such that ${s'}{\mathop {\rightarrow }\limits ^{e_j}}$. During the minimization these equivalent states will be merged into one state with outgoing transitions labeled by $e_i$ and $e_j$ showing that there is no false free-choice relation between corresponding transitions. Another reason to minimize the transition system is to reduce the number of states being analyzed.

Note that there is no guarantee that an $ESSP$ problem can be solved. Nevertheless, in the running example, regions $r_2$ and $r_3$ solve $ESSP (s_4, complete\,application )$ and $ESSP (s_5, notify\,client )$ problems.

5.2 Algorithm Description

In this subsection, we present an algorithm for enhancement of a free-choice workflow net N with additional constraints from event log L (Algorithm 1). Firstly, by applying $ConstructMinTS$, a minimal transitional system encoding the event log L is constructed.³ Then, false free-choice relations and corresponding $ESSP$ problems are identified. According to the definition of a false free-choice relation presented earlier, procedure $FindFalseFreeChoiceRelations$ is polynomial in time. Indeed, to find all the false free-choice relations one needs to check whether all the states of a transition system have none or all outgoing transitions labeled by events assumed to be in free-choice relations within the original workflow net N. When the false free-choice relations are discovered, for each corresponding $ESSP$ problem function $ComputeRegionsESSP$, which finds regions solving the $ESSP$ problem, is applied. Since the problem of finding minimal regions which solve $ESSP$ problem is known to be NP-complete, this is the most time complex part of Algorithm 1. However, in contrast to the original synthesis approach, we do not solve $ESSP$ problems for all the events in the net reducing the size of the problem. For instance, let $\overline{E}\subseteq E$ be the set of events that need to be checked. Let $e\in \overline{E}$, and $S'$ be the states that have incoming or outgoing transitions labeled by e. Then we need to consider $O(2^{|S|-|S'|})$ regions, such that e enters them (for $|S'|$ states their inclusion to the region is predefined) and $O(2^{|S|-\big \lceil {\frac{|S'|}{2}}\big \rceil })$ regions, such that e does not cross them (for $\frac{|S'|}{2}$ states their inclusion to the region depends on the other $\frac{|S'|}{2}$ states). Hence we need to consider $O(|\overline{E}|\cdot 2^{|S|-\big \lceil {\frac{|S'|}{2}}\big \rceil })$ ($|S'|$ is the minimal for all the events from $\overline{E}$) possible regions in contrast to the original region-based approach which exhaustively considers all $O(2^{|S|})$ possible regions. Finally, if new regions solving $ESSP$ problems are found, function $AddNewConstraints$ is applied and corresponding constraints (places) are added to the target workflow net $N'$.

5.3 Formal Properties

In this subsection, we prove formal properties of Algorithm 1. Firstly, we study the relation between the languages of the initial and target workflow nets. Theorem 2 proves that if a trace fits the initial model (initial model accepts the trace), it also fits the target model. Although the proof seems trivial, we need to consider different cases in order to verify that the final marking with only one token in the final place is reached.

Theorem 2 (Fitness)

Let $\sigma \in L$ be a trace of an event log $L\in E^*$, and $N=(P,T,F,l)$, $l:T\rightarrow E$ be a free-choice workflow net, such that its language contains $\sigma$, i.e., $\sigma \in \mathcal {L}(N)$. Workflow net $N'=(P\cup P',T,F',l)$, $l:T\rightarrow E$, is obtained from N and L using Algorithm 1. Then the language of $N'$ contains $\sigma$, i.e., $\sigma \in \mathcal {L}(N')$.

Proof

Let us prove that an insertion of a single place by Algorithm 1 preserves the ability of the workflow net to accept trace $\sigma$. Consider a place r (Fig. 7 b.) constructed from the corresponding region r (Fig. 7 a.) with entering events $b_1,...,b_m$ and exiting events $a_1,...,a_p$. Events $a_1,...,a_p$ can belong to a larger set of events $a_1,...,a_p,..., a_k$ which are in a free-choice relation within N. Let us consider the workflow net $N'$ with a new place r (the fragment of $N'$ is presented in Fig. 7 b.). Next, we consider the following four cases:

• 1. Suppose $\sigma =\langle e_1,...,e_l\rangle \in L$ does not contain events from $\{b_1,...,b_m\}$ and $\{a_1,..., a_p\}$ sets. Since $\sigma \in \mathcal {L}(N)$, there is a sequence of firings in N: $[i]{\mathop {\rightarrow }\limits ^{e_1}}m_1{\mathop {\rightarrow }\limits ^{e_2}}...{\mathop {\rightarrow }\limits ^{e_l}}[o]$, where [i] and [o] are the initial and final markings of the workflow net respectively. The same sequence of firings can be repeated within the target workflow net $N'$, because $\sigma$ does not contain events from the sets $\{b_1,...,b_m\}$ and $\{a_1,...,a_p\}$, and the place r is not involved in this sequence of firings.

• 2. Now let us consider trace $\sigma =\langle e_1,...,b_i,..., a_j,...,e_l\rangle$ in which each occurrence of event $b_i$ from the set $\{b_1,...,b_m\}$ is followed by an occurrence of event $a_j$ from $\{a_1,...,a_p\}$. Similarly, for the firing sequence within N: $\smash {[i]{\mathop {\rightarrow }\limits ^{e_1}}m_1{\mathop {\rightarrow }\limits ^{e_2}}... {\mathop {\rightarrow }\limits ^{b_i}}m_i}\rightarrow \smash {...\rightarrow m_j{\mathop {\rightarrow }\limits ^{a_j}}...{\mathop {\rightarrow }\limits ^{e_l}}[o]}$, there is a corresponding sequence $[i]{\mathop {\rightarrow }\limits ^{e_1}}m_1{\mathop {\rightarrow }\limits ^{e_2}}... {\mathop {\rightarrow }\limits ^{b_i}}m'_i\rightarrow ...\rightarrow m'_j{\mathop {\rightarrow }\limits ^{a_j}}...{\mathop {\rightarrow }\limits ^{e_l}}[o]$ for $N'$, such that $\forall p\in P: m'_i(p)=m_i(p)$, $m'_i(r)>0$, $\forall p\in P: m'_j(p)=m_j(p)$, and $m'_j(r)>0$.

• 3. Consider trace $\sigma$ where an event from $\{b_1,...,b_m\}$ is not followed by an event from $\{a_1,...,a_p\}$. More precisely, there are two possible cases: (1) trace $\sigma$ contains an event from $\{b_1,...,b_m\}$ and does not contain an event from $\{a_1,...,a_p\}$; (2) an occurrence of an event from set $\{b_1,...,b_m\}$ is followed by another occurrence of an event from the same set $\{b_1,...,b_m\}$ and only after that an event from the set $\{a_1,...,a_p\}$ may follow. For the case (1), it is possible that the final state $s_o$ belongs to the region r (Fig. 8a.).

  Let us show that state $s_o$ forms a region itself. Since the transition system constructed from the event log L was minimized, state $s_o$ consolidates all the final states of the initial transition system. Let $f_1,..,f_s$ be events labeling incoming transitions (Fig. 9 a.). These events correspond to workflow net transitions connected with place o by outgoing arcs (Fig. 9 b.).

  If transitions labeled by these events appear in other parts of the transition system (they are not final), then the initial workflow net N does not accept traces with these events. This can be proven by the fact that N is uniquely labeled and hence for marking m reachable by firing an event from $\{f_1,..,f_s\}$ it holds that $m(o)>0$ and $\exists p\in P:p\ne o,m(p)>0$. Obviously, from m the final marking [o] cannot be reached in a workflow net. Thus, we have shown that there is another region $r'=\{s_0\}\subseteq r$, and r is not a minimal. This contradicts Algorithm 1 which builds minimal regions, and hence $s_o\notin r$.

  The other possible scenario for the cases (1) and (2), is that the trace $\sigma$ does not terminate inside region r. In both cases, there is a transition labeled by an event $c\notin \{a_1,...,a_p\}$ which exits region r (Fig. 7 b.). While it is obvious for the case (1), for the case (2) this can be proven by the fact that there are two occurrences of events from $\{b_1,...,b_m\}$ with no occurrences of events from $\{a_1,...,a_p\}$ in between, and hence the trace $\sigma$ leaves the region r in order to enter it again with a transition labeled by an event from $\{b_1,...,b_m\}$. Having a new exiting event $c\notin \{a_1,...,a_p\}$ contradicts the definition of the region r which has $\{a_1,...,a_p\}$ as a set of exiting events. Thus, we have proven that there is no such a trace in the initial event log containing an event from the set $\{b_1,...,b_m\}$ which is not followed by an event from the set $\{a_1,...,a_p\}$.

• 4. Consider the last possible case when an event from $\{a_1,...,a_p\}$ is not preceded by an event from $\{b_1,...,b_m\}$ in trace $\sigma$. Here again we can distinguish two situations: (1) $\sigma$ contains an event from $\{a_1,...,a_p\}$ and does not contain an event from $\{b_1,...,b_m\}$; (2) the occurrence of an event from $\{a_1,...,a_p\}$ is firstly preceded by another occurrence of an event from $\{a_1,...,a_p\}$ which in its turn can be preceded by an event from $\{b_1,...,b_m\}$. Just like in the previous case, two scenarios are possible: the trace starts inside the region r (Fig. 8a.) or there is a transition entering r and labeled by an event $d\notin \{b_1,...,b_m\}$ (Fig. 8 b). Similarly to the previous case, we can prove that in these scenarios r is not a minimal region with entering and exiting events $\{b_1,...,b_m\}$ and $\{a_1,...,a_p\}$, respectively.

Thus, we have proven that if a place corresponding to a region constructed by the Algorithm 1 is added to the initial workflow net N then all the traces form L accepted by N are also accepted by the resulting workflow net $N'$.    $\square$

Fig. 7.

a. A fragment of a transition system that encodes L. b. A fragment of $N'$.

Fig. 8.

Fragments of a transition system that encodes L.

Fig. 9.

Final state of N.

The following theorem states that the resulting model cannot be less precise than the initial process model, i.e., it cannot accept new traces which were not accepted by the initial model.

Theorem 3 (Precision)

Let $N=(P,T,F,l)$, $l:T\rightarrow E$, be a free-choice workflow net and let L be an event log over set of events E. If workflow net $N'$ is obtained from N and L by Algorithm 1, then the language of N contains the language of $N'$, i.e., $\mathcal {L}(N')\subseteq \mathcal {L}(N)$.

Proof

The proof follows from the well-known result that addition of new places (preconditions) can only restrict the behavior and, hence, the language of the Petri net [27].   $\square$

Next, we formulate and prove a sufficient condition for the soundness of resulting workflow nets. This condition is formulated in terms of the state-based region theory.

Theorem 4 (Soundness)

Let L be an event log over set E. Let $N=(P,T,F,l)$, $l:T\rightarrow E$ be a sound free-choice workflow net. Suppose that workflow net $N'=(P\cup P',T,F',l)$ is obtained from N and L by applying Algorithm 1 to one set of events in a free-choice relation within N. Suppose also that $\{r^{(1)},...,r^{(n)}\}$ is a set of regions constructed at line of 8 Algorithm 1 in the transition system encoding L (Fig. 10 b.). Let $E_{ ent }^{(1)}=\{b_1^{(1)},...,b_m^{(1)}\},...,E_{ ent }^{(n)}=\{b_1^{(n)},...,b_t^{(n)}\}$ and $E_{ exit }^{(1)}=\{a_1^{(1)},...,a_p^{(1)}\},...,E_{ exit }^{(n)}=\{a_1^{(n)},...,a_k^{(n)}\}$ be sets of entering and exiting events for the regions $r^{(1)},...,r^{(n)}$ respectively. Consider unions of these sets: $E_{ ent }=E_{ ent }^{(1)}\cup ...\cup E_{ ent }^{(n)}$ and $E_{ exit }=E_{ exit }^{(1)}\cup ...\cup E_{ exit }^{(n)}$. If there exists a (not necessarily minimal) region r in the reachability graph of N (Fig. 10 a.) with entering and exiting sets of events $E_{ ent }$ and $E_{ exit }$, respectively, which does not contain states corresponding to [i] (initial) and [o] (final) markings of N, then $N'$ is sound.

Fig. 10.

a. A fragment of the reachability graph of N. b. A fragment of $N'$.

Proof

Repeating the proof of Theorem 2 and taking into account that the initial and final states of the reachability graph of N do not belong to the region r, we can state that there is a following relation between $E_{ ent }$ and $E_{ exit }$ within $\mathcal {L}(N)$, i.e, for each trace, each occurrence of the event from $E_{ ent }$ is followed by an occurrence of the event from $E_{ exit }$ and there are no other occurrences of events from $E_{ ent }$ between them.

The firing sequences of $N'$ which do not involve firings of transitions labeled by events from $E_{ ent }$ and $E_{ exit }$ repeat the corresponding firing sequences of N and do not violate the soundness of the model.

Let us consider a firing sequence of $N'$ which involves firings of transitions labeled by events from $E_{ ent }$ and $E_{ exit }$. Consider $b\in E_{ ent }$, the firing sequence enabling and firing b in $N'$: $[i]{\mathop {\rightarrow }\limits ^{*}}m'_1{\mathop {\rightarrow }\limits ^{b}}m'_2$, corresponds to the firing sequence performed by N: $[i]{\mathop {\rightarrow }\limits ^{*}}m_1{\mathop {\rightarrow }\limits ^{b}}m_2$, where $\forall p\in P: m_1(p)=m'_1(p)$, $m_2(p)=m'_2(p)$. Without loss of generality suppose that $b\in E^{(i)}_{ ent }$, then $m'_2(r^i)=1$, where $r^i$ is a place constructed by Algorithm 1.

Since $E_{ ent }$ and $E_{ exit }$ events are in a following relation within $\mathcal {L}(N)$, they are in the following relation within $\mathcal {L}(N')$, because $\mathcal {L}(N')\subseteq \mathcal {L}(N)$. Consider sequences of steps leading to some of the events from $E_{ exit }$. These firing sequences will be: $m'_2{\mathop {\rightarrow }\limits ^{*}}m'_3$ and $m_2{\mathop {\rightarrow }\limits ^{*}}m_3$, where $m_3(p)=m'_3(p)$ and $m'_3(r^i)=1$, in $N'$ and N respectively.

In model $N'$ only transitions labeled by the events from $E^{i}_{ exit }$ will be enabled in $m'_3$, because according to Algorithm 1, the new preceding places are added only if they can be found for all the events from $E_{ exit }$. Thus all other activities $E_{ exit }$ have their preceding places empty in the marking $m'_3$: $m'_3(r^j)=0$, $i\ne j$.

In workflow net $N'$ it holds that $m'_3(r^i)=1$ and $m'_3(p^*)=1$ ($p^*$ is a choice place for the transitions in a free-choice relation within N, see Fig. 10 b.) and hence a step: $m'_3{\mathop {\rightarrow }\limits ^{a}}m'_4$, where $a\in E^{(i)}_{ exit }$ can be performed. After a is fired the place $r^i$ is emptied. A corresponding firing step in N: $m_3{\mathop {\rightarrow }\limits ^{a}}m_4$ can be taken, because $m_3(p^*)=1$, and all the transitions labeled by events from $E_{ exit }$ are enabled in $m_3$. These steps lead models to the same markings: $\forall p\in P: m_4(p)=m'_4(p)$ from which firing the same transitions the final marking [o] can be reached. If the rest sequence of firings contains events from $E_{ ent }$ and $E_{ exit }$, we repeat the same reasoning.

Thus, we have shown that all the transitions within $N'$ can be fired. Due to the soundness of N, since all the firing sequences of $N'$ correspond to firing sequences of N, and the number of tokens in each place from P in corresponding markings of $N'$ and N coincide, the final marking can be reached from any reachable marking of $N'$ and there are no reachable markings in $N'$ with tokens in the final place o and some other places.    $\square$

5.4 Using High-Level Constructs to Model Discovered Non-local Constraints

In this subsection, we demonstrate how the discovered process models with non-local constraints can be presented using high-level modeling languages, such as BPMN (Business Process Model and Notation) [24]. Free-choice workflow nets can be modeled by a core set of process modeling elements that includes start and end events, tasks, parallel and choice gateways, and sequence flows. The equivalence of free-choice workflow nets and process models based on the core set of elements is studied in [2, 18]. Most process modeling languages, such as BPMN, support these core elements. A BPMN model corresponding to the discovered free-choice workflow net (shown in Fig. 1) is presented in Fig. 11.

Fig. 11.

A BPMN model that corresponds to the workflow net in Fig. 1.

If a workflow net is not free-choice, then it cannot be presented using core elements only [18]. However, BPMN language offers additional high-level modeling constructs which can be used to model non-free-choice constraints. Figure 12 demonstrates a BPMN model that corresponds to a non-free-choice net (in Fig. 3) constructed by Algorithm 1.

Fig. 12.

A BPMN model that corresponds to the workflow net presented in Fig. 3.

In addition to core modeling elements, signal events and an event-based gateway are used. The signal events capture the discovered non-local dependencies. For instance, after $send\,application$ task is performed, a signal $sent\,by\,client$ is thrown. After that, an event-based gateway is used to select a branch depending on which of the catching signal event that immediately follows the gateway is fired. For example, if the type of the caught event is signal and its value is $sent\,by\,client$, then task $notify\,client$ is performed.

6 Case Study

In this section, we demonstrate the results of applying our approach to synthetic and real-life event logs. The approach is implemented as an Apromore [20] plugin called “Add long-distance relations” and is available as part of Apromore Community Edition.⁴ All the results were obtained in quasi real-time (in the order of milliseconds) using Intel(R) Core(TM) i7-8550U CPU @1.80 GHz with 16 GB RAM.

6.1 Synthetic Event Logs

To assess the ability of our approach to automatically repair process models we have built a set of workflow nets with non-local dependencies. An example of one of these workflow nets is presented in Fig. 13.

Fig. 13.

A workflow net used for the synthesis of an event log.

We simulated each of the workflow nets and generated event logs containing accepted traces. After that, from each event log L we discovered a free-choice workflow net N using Split miner. Then our approach was applied to N and L producing an enhanced workflow net $N'$ with additional constraints. To compare behaviors of N and $N'$ workflow nets, conformance checking techniques [26] assessing fitness (the share of the log behavior accepted by a model) and precision (the share of the model behavior captured by the log) were applied. In all the cases, both models N and $N'$ accept all the traces from L showing maximum fitness values of 1.0 (according to Theorem 2, if N accepts a trace, then $N'$ also accepts this trace). Precision values as well as the structural characteristic of the workflow nets are presented in Table 1. These results demonstrate that our approach is able to automatically reveal hidden non-local constraints discovering precise workflow nets when applied to synthetic event logs.

Table 1. Structural (number of transitions and number of places) and behavioural characteristics (precision) of free-choice (N) and enhanced ($N'$) workflow nets.

At the same time, while other approaches for the discovery of non-free-choice workflow nets, such as $\alpha$++ Miner [30] and the original Petri net synthesis technique [3] can also synthesize precise workflow nets form this set of simple event logs, they often either produce unsound workflow nets with dead transitions (in case of $\alpha$++ Miner), or fail to construct a model in a reasonable time (in case of the original synthesis approach) when applied to real-life event logs. In the next subsection, we apply our approach to a real-life event log showing that our approach can discover a more precise and sound process model in a real-life setting. Note that $\alpha$++ Miner produces a workflow net with dead transitions, which does not accept any of the event log traces, and the original synthesis approach fails to discover a Petri net from this real-life event log.

6.2 Real-Life Event Log

The proposed approach was applied to a real-life event log⁵ of a loan application process. We analyzed car loan applications which had not been cancelled and had not passed the validation procedure at least once. The overall event log L after filtering contains 59 unique traces⁶ and 12 events (each event can appear in the event log traces several times).

Fig. 14.

a. A fragment of the workflow net N discovered from the real-life event log by Split miner. b. A fragment of the corresponding repaired workflow net $N'$ with two places $r_1$ and $r_2$ added by Algorithm 1.

Figure 14 a. demonstrates a fragment of a workflow net N discovered from L by Split miner. N does not accept all the traces from L. The transition system was constructed only from those traces of L which are accepted by N. Algorithm 1 has revealed that there is a false free-choice relation between transitions labeled by $Accepted$ and $Returned$ events, and two additional places (regions) $r_1$ and $r_2$ were discovered and inserted in the repaired workflow net $N'$ (Fig. 14 b.). N and $N'$ have the same fitness values (0.787), i.e., can accept the same share of traces from L, refer to Theorem 2. While their precision values are different (0.806 and 0.866, for N and $N'$ respectively). Indeed, $N'$ is more precise because it does not allow the sequence of events to be repeated more than once, and the repeating sequences are not presented in L traces accepted by N. The fulfillment of Theorem 4 conditions guarantees the soundness of $N'$.

7 Conclusion and Future Work

This paper presented an automated repair approach for obtaining precise process models under the presence of non-local dependencies. The approach identifies opportunities for improving the process model by analyzing the process behavior recorded in the input event log, and then uses goal-oriented region-based synthesis to discover new Petri net fragments that introduce non-local dependencies.

The theoretical contributions of this paper have been implemented as an open-source plugin of the Apromore process mining platform. This implementation has then been used to provide preliminary experiment results. Based on the experiments conducted so far, the proposed approach does not incur into significant performance penalties in practice. This is achieved by restricting the use of region theory to very specific situations.

We foresee different research directions arising from this work. First, implementing the proposed approach for alternative region techniques like language-based [9, 31] or geometric [10, 28], is an interesting avenue to explore. Second, evaluating the impact that well-known problems with event logs, like noise or incompleteness, may have on the approach, and proposing possible ways to alleviate/overcome these problems should be explored. Finally, in this paper, we only presented preliminary experimental results (e.g. we only tested the approach against a single, yet complex, real-life event log). Therefore, a concrete next step to extend this work is to perform more extensive experiments against automated discovery benchmarks such as [6].