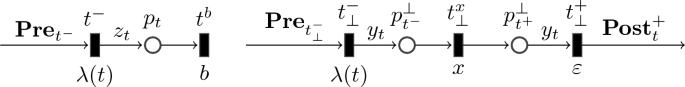Dynamic Recursive Petri Nets

Abstract

In the early two-thousands, Recursive Petri nets (RPN) have been introduced in order to model distributed planning of multi-agent systems for which counters and recursivity were necessary. While having a great expressive power, RPN suffer two limitations: (1) they do not include more general features for transitions like reset arcs, transfer arcs, etc. (2) the initial marking associated with the recursive “call” only depends on the calling transition and not on the current marking of the caller. Here we introduce Dynamic Recursive Petri nets (DRPN) which address these issues. We show that the standard extensions of Petri nets for which decidability of the coverability problem is preserved are particular cases of DPRN. Then we establish that w.r.t. coverability languages, DRPN are strictly more expressive than RPN. Finally we prove that the coverability problem is still decidable for DRPN.

1 Introduction

Limitations of Petri Nets (PN). When modelling dynamic systems, formalisms that can handle infinite transition systems are required in several contexts among them: the concurrent execution of parallel sequential processes that produce and consume resources and the dynamical creation of processes. While Petri nets are well suited for specifying the first pattern, their static structure forbids the modelling of the second pattern. Furthermore even the management of an unbounded number of resources by PNs suffers some limitations: the reset operation that cleans a buffer or the transfer operation of a set of resources from one buffer to another one cannot be performed in an atomic way.

Recursive Petri Nets (RPN). This formalism has been introduced in order to address the issue of modelling dynamic structures with PN [3] (see also [13, 14] for similar models). Roughly speaking, a state of an RPN consists of a tree of threads where the local state of each thread is a marking. Any thread fires an elementary or abstract transition. When the transition is elementary, the firing updates its marking as in Petri nets; when it is abstract, this only consumes the tokens specified by the input arcs of the transition and creates a child thread initialised with the starting marking of the transition. When a marking of a thread covers one of the final markings, it may perform a cut transition pruning its subtree and producing in its parent the tokens specified by the output arcs of the abstract transition that created it. In RPN, reachability, is decidable [9, 10] by reducing this property to several reachability problems of PNs. Furthermore, the coverability and termination problems of RPNS have the same complexity as the ones of PNs (EXPSPACE-complete, see [4]). In [11], several additional features are proposed while preserving the decidability of the verification problems.

Static Extensions of Petri Nets. In another direction, PNs have been extended by adding capabilities of transitions while the static structure given by the set of places is unchanged. The reset and transfer arcs allow to perform the corresponding operations by a single transition [2]. The arcs of self-modifying nets are labelled by expressions in such a way that the numbers of tokens consumed or produced by the transitions depend on the current marking [15]. Affine Petri nets unifies the previous extensions with a concise syntax [6]. While reachability becomes undecidable, depending on the model several properties remain decidable including coverability (implying sometimes weak restrictions).

Our Contribution. While having a great expressive power, RPN suffer two limitations: (1) they do not include more general features for transitions like reset arcs, transfer arcs, etc. (2) the initial marking associated the recursive “call” only depends on the calling transition and not on the current marking of the caller. So we introduce Dynamic Recursive Petri nets (DRPN) which address these issues. We show that the extensions of Petri nets (discussed above) for which decidability of the coverability problem is preserved are particular cases of DPRN. Then we establish that w.r.t. coverability languages, DRPN are strictly more expressive than RPN. Finally we prove that the coverability problem is still decidable for DRPN.

Outline. In Sect. 2 we introduce DRPN, illustrate their modelling capabilities and define a quasi-order between states of DRPN. In Sect. 3, we study from a theoretical point of view, expressiveness of DRPNs. In Sect. 4, we establish that the coverability problem is decidable. Finally in Sect. 5, we conclude and give some perspectives to this work. All missing proofs can be found in [8].

2 Dynamic Recursive Petri Nets

Well Quasi-Ordered Sets. A quasi-ordered set $(X,\le )$ is well quasi-ordered if given any infinite sequence $(x_n)_{n\in \mathbb {N}} \in X^{\omega }$, there exist $i<j$ such that $x_i\le x_j$. For instance, $\mathbb {N}^P$, where P is a finite set, equipped with the component order is well-ordered. From a computability point of view, we assume that the representation of items of X allows to decide whether $x\le x'$ which is obviously the case for $\mathbb {N}^P$. Well quasi-ordered sets fulfill properties that we exploit here:

• Let $Y\subseteq X$. Then Y is upward closed if for all $x\le x' \in X$, $x\in Y$ implies $x' \in Y$. Given an arbitrary set Y, the upward closure of Y, denoted $Y^{\uparrow }$ is defined by $Y^{\uparrow }=\{x'\mid \exists x\in Y\ x\le x' \}$. The set of minimal elements of an upward closed set Y, denoted $\min (Y)$, is finite and fulfills $Y=\min (Y)^{\uparrow }$. So whenever we handle upward closed sets, they are implicitely defined by their set of minimal elements.

• Given any infinite sequence of upward closed sets $(Y_n)_{n\in \mathbb {N}} \in (2^X)^{\omega }$ where for all n, $Y_n\subseteq Y_{n+1}$, there exists $n_0$ such that $\bigcup _{n\in \mathbb {N}} Y_n=\bigcup _{n\le n_0} Y_n$.

• Let f be a partial non decreasing function from X to X, f is effective if (1) there is an algorithm that takes as input $x\in X$, decides whether x belongs to the domain of f and, in the positive case, computes f(x) and (2) there is an algorithm that takes as input $x\in X$ and computes $\min (f^{-1}(\{x\}^{\uparrow }))$.

• Let $\mathcal F$ be a finite set of effective functions and Y be an upward closed set. Define $Cov(\mathcal F,Y)$ as the smallest set C that contains Y and fulfills $\bigcup _{f\in \mathcal F}f^{-1}(C)\subseteq C$. Then $Cov(\mathcal F,Y)$ can be computed the following backward exploration:

  $$\begin{aligned} C \leftarrow Y; \mathbf{~repeat~}oldC \leftarrow C;\ C\leftarrow C \cup \bigcup \nolimits _{f\in \mathcal F}f^{-1}(C) \mathbf{~until~}C=oldC \end{aligned}$$

  For instance, coverability in Petri nets can be decided using this backward exploration (see for instance [7]) and we will apply it in several contexts.

Notation. Let $X\subseteq Y$ be two sets. The mapping Id denotes the identity mapping from X to Y where X and Y should be clear from the context.

Let us introduce dynamic recursive Petri nets (DRPN). Like a Petri net, a DRPN has a set of places P and a set of transitions T partitioned in elementary and abstract transitions (resp. $T_{el}$ and $T_{ab}$). A state s of an SRPN is a tree whose vertices are labelled by markings (defined by the mapping M) and edges are labelled by transitions (defined by the mapping $\varLambda$). A transition t may fire in any vertex u provided that the marking of this vertex M(u) belongs to an upward closed set $\textit{Grd}_t$. If t is elementary then M(u) is updated by applying an effective function $\textit{Upd}_t$. If t is abstract then (1) a vertex v is created as a child of u with $\varLambda (u,v)=t$, (2) marking M(v) is defined by $\textit{Beg}_t(M(u))$ where $\textit{Beg}_t$ is an effective function, and (3) M(u) is updated by applying an effective function $\textit{Upd}^-_t\le \mathbf{Id}$. A DRPN is equipped with $\textit{End}$, an upward closed set of $\mathbb {N}^P$. When for some vertex v, $M(v)\in \textit{End}$ then $\tau$, the cut transition, can be fired whose effect consists to (1) delete the subtree rooted v and (2) when $v\ne r$ where r denotes the root of the state to update M(u) where u is the parent of v by applying the effective function $\textit{Upd}_t^+\ge \mathbf{Id}$. The state consisting in the empty tree is denoted $\bot$.

Definition 1 (DRPN)

A Dynamic Recursive Petri Net is a 6-tuple ${\mathcal {N}}=\langle P,T,\textit{Grd},\textit{Upd}, \textit{Upd}^{-},\textit{Upd}^{+}, \textit{Beg},\textit{End}\rangle$ where:

• P is a finite set of places;

• $T=T_{el}\uplus T_{ab}$ with $P\cap T=\emptyset$ is a finite set of transitions;

• $\textit{Grd}=\{\textit{Grd}_t\}_{t\in T}$ is a family of upward closed sets of $\mathbb {N}^P$;

• $\textit{Upd}=\{\textit{Upd}_t\}_{t\in T_{el}}$ is a family of effective functions with $\textit{Upd}_t \in (\mathbb {N}^P)^{\textit{Grd}_t}$;

• $\textit{Upd}^-=\{\textit{Upd}^-_t\}_{t\in T_{ab}}$ is a family of effective functions with $\textit{Upd}^-_t \in (\mathbb {N}^P)^{\textit{Grd}_t}$;

• $\textit{Upd}^+=\{\textit{Upd}^+_t\}_{t\in T_{ab}}$ is a family of effective functions with $\textit{Upd}^+_t \in (\mathbb {N}^P)^{\mathbb {N}^P}$;

• For all $t\in T_{ab}$, $\textit{Upd}^-_t\le \mathbf{Id}$ and $\mathbf{Id}\le \textit{Upd}^+_t$;

• $\textit{Beg}=\{\textit{Beg}_t\}_{t\in T_{ab}}$ is a family of effective functions with $\textit{Beg}_t \in (\mathbb {N}^P)^{\textit{Grd}_t}$;

• $\textit{End}$ is an upward closed set of $\mathbb {N}^P$.

As discussed above, a state of a DRPN is a labelled tree.

Definition 2 (State)

Let ${\mathcal {N}}$ be a DRPN. Then a state $s=\left\langle V,M,E,\varLambda \right\rangle$ of ${\mathcal {N}}$ is defined by:

• V its finite set of vertices;

• $M: V\rightarrow \mathbb {N}^{P}$, a function that labels vertices with markings;

• $E\subseteq V\times V$, a set of edges such that (V, E) is a directed tree;

• $\varLambda : E \rightarrow T_{ab}$, a function that labels edges with abstract transitions.

One denotes by $Des_s(v)$(respectively $Anc_s(v)$) the set of descendants (respectively ancestors) of $v\in V$ in the underlining tree of s (including v itself). If $v\ne r$ then prd(v) is the parent of v in the tree. Given a $U\subseteq V$ we will denote by $Anc_s(U)=\cup _{v\in U}Anc_s(v)$. The depth of s is the depth of its tree. Given $\mathbf {m}\in \mathbb {N}^P$, $s_{\mathbf {m}}$ denotes a tree consisting of a single vertex r with marking $M(r)=\mathbf {m}$. Let us formally define the firing of elementary, abstract and cut transitions.

Definition 3

Let ${\mathcal {N}}$ be a DRPN, s a state of ${\mathcal {N}}$, $v\in V$ and $t\in T\cup \{\tau \}$.

t is fireable by v from s if either $t\ne \tau$ and $M(v)\in \textit{Grd}_t$ or $t=\tau$ and $M(v)\in \textit{End}$. In this case, its firing leads to the state $s'=\left\langle V',M',E',\varLambda ' \right\rangle$, defined below:

• If $t \in T_{el}$ then $s'=\left\langle V,M',E,\varLambda \right\rangle$ where $M'(u)=M(u)$ for all $u \in V\setminus \{v\}$ and $M'(v)=\textit{Upd}_t(M(v))$;

• If $t \in T_{ab}$ then:

  • $V'=V\cup \{w\}$ where w is a fresh identifier;

  • $M'(u)=M(u)$ for all $u \in V\setminus \{v\}$, $M'(v)=\textit{Upd}^-_t(M(v))$ and $M'(w)=\textit{Beg}_t(M(v))$;

  • $E'=E\cup \{(v,w)\}$ and $\varLambda '(e)=\varLambda (e)$ for all $e \in E$ and $\varLambda '((v,w))=t$.

• If $t =\tau$ and $v=r$ then $s'=\bot$;

• If $t =\tau$ and $v\ne r$ then let $w=prd(v)$:

  • $V'=V\setminus Des_s(v)$;

  • for all $u \ne w$, $M'(u)=M(u)$ and $M'(w)=\textit{Upd}^+_{\varLambda (w,v)}(M(w))$;

  • $E'=E \cap (V'\times V')$ and $\varLambda '$ is the restriction of $\varLambda$ on $E'$.

The transition firing is denoted $s\xrightarrow {(v,t)}s'$ and when there are several nets, $s\xrightarrow {(v,t)}_{{\mathcal {N}}}s'$. A firing sequence is a sequence of transition firings, written in detailed way: $s_0\xrightarrow {(v_1,t_1)}s_1\xrightarrow {(v_2,t_2)}\cdots \xrightarrow {(v_n,t_n)}s_n$, or when the context allows it, in a more concise way like $s_0\xrightarrow {\sigma } s_n$ for $\sigma =(v_1,t_1)(v_2,t_2)\dots (v_n,t_n)$. The length of $\sigma$, denoted $|\sigma |$, is n. The abstract length of $\sigma$, denoted $|\sigma |_{ab}$, is $|\{i\le n\mid t_i\in T_{ab}\}|$. The depth of $\sigma$ is the maximal depth of states $s_0,\ldots ,s_n$. A closing sequence is a firing sequence that reaches $\bot$. Given a firing sequence that includes the firing of an abstract transition t in vertex v creating vertex w and followed later by the cut transition in w, we say that $(v,t),(w,\tau )$ are matched in $\sigma$. The reachability set $Reach({\mathcal {N}},s_0)$ is defined by: $Reach({\mathcal {N}},s_0)=\{s \mid \exists \sigma \ s_0\xrightarrow {\sigma } s \}$.

Discussion. The main limitations of the modelling power of DRPN are the requirements that (1) sets like $\textit{Grd}_t$ must be upward closed and (2) functions like $\textit{Upd}_t$ must be monotonic. Despite these limitations, DRPNs include many models like:

• Petri nets (PN) that can be defined without abstract transitions and such that for all $t\in T$, $\textit{Grd}_t = \{\mathbf {m}\mid \mathbf {m}\ge \mathbf {Pre}(t)\}$ and $\textit{Upd}_{t}=\mathbf{Id}+ \mathbf{C}(t)$ where $\mathbf {Pre}(t)$ (resp. $\mathbf{C}(t)$) is the column vector indexed by t of the backward incidence matrix $\mathbf {Pre}$ (resp. incidence matrix $\mathbf{C}$).

• Affine Petri nets ([6]) that can also be defined without abstract transitions and such that for all $t\in T$, there exist a matrix $\mathbf{A}_t\in \mathbb {N}^{P\times P}$ and a vector $\mathbf{B}_t\in \mathbb {Z}^P$ with $\textit{Grd}_t=\{\mathbf {m}\mid \mathbf{A}_t\mathbf {m}+\mathbf{B}_t\ge 0\}$ and $\textit{Upd}_{t}(\mathbf {m})=\mathbf{A}_t\mathbf {m}+\mathbf{B}_t$.

• Recursive Petri nets (RPN) ([10]) such that for all $t\in T$, $\textit{Grd}_t = \{\mathbf {m}\mid \mathbf {m}\ge \mathbf {Pre}(t)\}$ and when $t\in T_{el}$, $\textit{Upd}_{t}=\mathbf{Id}+ \mathbf{C}(t)$ and when $t\in T_{ab}$, $\textit{Upd}^-_{t}=\mathbf{Id}-\mathbf {Pre}(t)$, $\textit{Upd}^+_{t}=\mathbf{Id} + \mathbf {Post}(t)$ and $\textit{Beg}_t$ is some constant. Here $\mathbf {Post}(t)$ is the column vector indexed by t of the forward incidence matrix $\mathbf {Post}$.

Graphical Representation. For modelling purposes, we equip DRPN with a graphical representation based on net representations. Places (resp. transitions) are depicted by circles (resp. rectangles). However a transition does not have input arcs but only output arcs represented by double-headed arrows and labelled by expressions where a place represents the current value of its marking. The guard of an elementary transition is also represented by a boolean expression inside the rectangle. For instance, the elementary transition t figured below is defined by: $\textit{Grd}_{t}=\{\mathbf {m}\mid \mathbf {m}(p_1)>2\}$ and $\textit{Upd}_t(\mathbf {m})=(\mathbf {m}(p_1)+\mathbf {m}(p_2))\overrightarrow{p_1}+\lfloor \sqrt{\mathbf {m}(p_2)}\rfloor \overrightarrow{p_2}$ where $\overrightarrow{p}$ denotes the vector defined by $\overrightarrow{p}[p]=1$ and for all $p'\ne p$, $\overrightarrow{p}[p']=0$.

The rectangle of an abstract transition t is divided into several parts: on the top corner left (−) starts the edges representing $\textit{Upd}_t^-$, on the top center $\textit{Grd}_t$ is represented, on the bottom corner left $\textit{Beg}_t$ is represented, and on the bottom corner right ($+$) start the edges representing $\textit{Upd}_t^+$. There are no edges for unchanged place markings. For instance, the abstract transition figured below is defined by: $\textit{Grd}(t) = \{\mathbf {m}\mid \mathbf {m}(p_1)>2\vee \mathbf {m}(p_3)>1\}$, $\textit{Upd}^-_t(\mathbf {m})=(\mathbf {m}(p_1)-1)\overrightarrow{p_1}+\lfloor 0.5\mathbf {m}(p_2)\rfloor \overrightarrow{p_2} +\mathbf {m}(p_3)\overrightarrow{p_3}$, $\textit{Upd}^+_t(\mathbf {m})=\mathbf {m}(p_1)\overrightarrow{p_1}+2\mathbf {m}(p_2)\overrightarrow{p_2} +\mathbf {m}(p_3)^2\overrightarrow{p_3}$, and $\textit{Beg}_t=\mathbf {m}(p_1)\overrightarrow{p_2}$. Observe that $\textit{Upd}^-_t\le \mathbf{Id}$ and $\mathbf{Id}\le \textit{Upd}^+_t$.

Example 1 (Hiring an assassin)

In order to illustrate the modelling capabilities of DRPN, we present an example of distributed planning. The DRPN ${\mathcal {N}}_{Jaqen}$ of Fig. 1 represents the possible behaviour of an assassin hired for a job. The transitions filled in black are Petri net transitions and so are presented with input and output arcs as usual.

The assassin is given 3 days (3 tokens in $p_{time}$), an advance of 20 bitcoins (20 tokens in $p_{adv}$), and is promised to get a reward of 20 bitcoins after the job is done (20 tokens in $p_{reward}$). In order to try catching their target he needs to devote one bitcoin and one day of his time. After this day either the assassin is successful ($t_{found}$) or fails ($t_{lost}$) and needs to spend another day. When successful, the assassin can collect the reward ($t_{collect}$). However, the assassin has also another strategy which consists of hiring another assassin by giving him a quarter of his advance money and promise him an equal reward, telling him the number of days left ($t_{hire}$ where $f_{pay}(\mathbf {m})= \mathbf {m}(p_{time})\overrightarrow{p}_{\!time} + \lfloor 0.5\lceil 0.5\mathbf {m}(p_{adv})\rceil \rfloor \overrightarrow{p}_{\!adv} +\lceil 0.5\lceil 0.5\mathbf {m}(p_{adv})\rceil \rceil \overrightarrow{p}_{\!reward}$). If some hired assassin is successful then he can report his success to the hiring guy by firing the cut transition (due to the specification $\textit{End}$). The state presented on the right of Fig. 1 consists of three assassins where the last hired one has killed the target. Observe that as long as a guy has money he can hire several assassins and that even after hiring he can still try to kill the target by himself.

Fig. 1.

A DRPN with a state

A firing sequence of ${\mathcal {N}}_{Jaqen}$ is presented in Fig. 2 where the vertex who fires the transition is filled in black. The initial assassin first tries to find the target but fails ($(r,t_{lost})$), losing one bitcoin and one day. Then he hires another assassin by firing the abstract transition $(r,t_{hire})$, losing half of his advance money and creating a new vertex v), where the hired assassin has two days, an advance of five bitcoins and a promised reward of five bitcoins for completing the job ($M(v)=2\overrightarrow{p}_{\!time}+5\overrightarrow{p}_{\!adv}+ 5\overrightarrow{p}_{\!reward}$). This assassin kills the target and collects the reward ($(v,t_{lost})$ followed by $(v,t_{collect})$). Then using the cut transition he reports it to his employer ($(v,\tau )$), which removes v and adds one token to $p_{dead}$ in M(r). Finally the original assassin can collect his money by firing $t_{collect}$.

Fig. 2.

Firing sequence

Ordering States of a DRPN. We now define a quasi-order on the states of a DRPN. Given two states $s,s'$ of ${\mathcal {N}}$ we say that s is smaller or equal than $s'$ or equivalently that $s'$ covers s if (without considering labels) there is a subtree in $s'$ isomorphic to s (by some matching) such that (1) given any pair of matched vertices $(u,u')$, $M(u)\le M'(u')$ and (2) given any pair of transitions $(t,t')$ labelling matched edges, $\textit{Upd}^+_t\le \textit{Upd}^+_{t'}$.

Definition 4

Let ${\mathcal {N}}$ be DRPN and $s=\left\langle V,M,E,\varLambda \right\rangle$, $s'=\left\langle V',M',E',\varLambda ' \right\rangle$ of a DRPN ${\mathcal {N}}$, be two states of ${\mathcal {N}}$ and $\varphi$ be an injective mapping from V to $V'$. We say that $s'$ covers s by $\varphi$, denoted $s\preceq _\varphi \! s'$ if:

• 1. For all $v\in V$, $M(v)\le M'(\varphi (v))$;

• 2. For all $(u,v)\in E$, $(\varphi (u),\varphi (v)) \in E'$ and $\textit{Upd}^+_{\varLambda (u,v)}\le \textit{Upd}^+_{\varLambda '(\varphi (u),\varphi (v))}$.

We say that $s'$ covers s denoted $s\preceq s'$ if there exists $\varphi$ such that $s\preceq _\varphi \! s'$.

Given states $s, s'$, deciding whether $s'$ covers s is a necessary condition for designing algorithms related to the coverability relation. So we assume that given a DRPN, for all pairs $t,t' \in T_{ab}$ one can decide whether $Upd_t^+\le Upd_{t'}^+$. This hypothesis is satisfied by all “reasonable” effective functions.

The coverability set $Cov({\mathcal {N}},s_0)$ is defined as the upward closure of the reachability set: $Cov({\mathcal {N}},s_0)=Reach({\mathcal {N}},s_0)^{\uparrow }$. As for recursive Petri nets (see [4]) this quasi-order is strongly compatible (and even more): for all $s\preceq _\varphi s'$ and $s\xrightarrow {(v,t)} s_1$ there exists $s'_1 {}_{\varphi _1}\!\!\!\succeq \! s_1$ such that $s'\xrightarrow {(\varphi (v),t)} s'_1$ and $\varphi$ and $\varphi _1$ coincide on the intersection of their domain. However this quasi-order is not a well quasi-order (see also [4]) and thus in order to solve the coverability problem, one cannot apply the backward exploration.

Notation. Let $S_t$ be a finite set of states. We call a sequence $\sigma$ such that $s\xrightarrow {\sigma }s' \succeq s''\in S_t$ a covering sequence.

3 Expressiveness

Expressiveness of a formalism may be defined by the family of languages that it can generate. In [4], expressiveness of RPNs was studied using coverability languages. In order to compare RPN and DRPN we need to define coverability languages of DRPNs and so we equip any transition $t\in T\cup {\tau }$ with a label $\lambda (t)\in \varSigma \cup \{\varepsilon \}$ where $\varSigma$ is an alphabet and $\varepsilon$ is the empty word of $\varSigma ^*$ fulfilling $\lambda (\tau )=\varepsilon$. The labelling is extended to transition sequences in the usual way. Thus given a labelled marked DRPN $({\mathcal {N}},s_{init})$ and a finite set of states $S_t$, the coverability language $\mathcal {L}({\mathcal {N}},s_{init},S_t)$ is defined by:

$$\begin{aligned} \mathcal {L}({\mathcal {N}},s_{init},S_t)=\{\lambda (\sigma ) \mid \exists \ s_0 \xrightarrow {\sigma } s\succeq s'\wedge s' \in S_t\} \end{aligned}$$

i.e. the set of labellings for sequences covering some state $s\in S_t$ of ${\mathcal {N}}$. We say that $\mathcal {L}\subseteq \varSigma ^*$ is a coverability language if $\mathcal {L}=\mathcal {L}({\mathcal {N}},s_{init},S_t)$ for some ${\mathcal {N}}$, $s_{init}$ and $S_t$. We also introduce $\mathcal {L}_B({\mathcal {N}},s_{init},S_t)$ the B-bounded coverability language with $B\in \mathbb {N}$.

$$\begin{aligned} \mathcal {L}_B({\mathcal {N}},s_{init},S_t)=\{\lambda (\sigma ) \mid \exists \ s_0 \xrightarrow {\sigma } s\succeq s'\wedge s' \in S_t\wedge |\sigma |_{ab}\le B\} \end{aligned}$$

We say that $\mathcal {L}\subseteq \varSigma ^*$ is a B-bounded coverability language if $\mathcal {L}=\mathcal {L}_B({\mathcal {N}},s_{init},S_t)$ for some ${\mathcal {N}}$, $s_{init}$ and $S_t$.

The next proposition is an important ingredient for our expressiveness result (see proof in [8]). The main idea of this proof consists in considering a PN with enough copies of P and T such that each copy mimicks the behaviour of a vertex in a state of the RPN with height at most B and outgoing degree at most B for every vertex. Additional places and transitions allow to express the child relation between vertices and the existence of the vertices in the current mimicked state of the RPN.

Proposition 1

Let $\mathcal L$ be a B-bounded coverability language. Then $\mathcal L$ is a PN coverability language.

We say that a function $f:\mathbb {N}\rightarrow \mathbb {N}$ is sublinear if $\lim _{n\rightarrow \infty }\frac{f(n)}{n} = 0$. Let f be sublinear non decreasing with $\lim _{n\rightarrow \infty }f(n)=\infty$, we define on the alphabet $\{a,b\}$ the language $\mathcal {L}_{ f}=~\{a^kb^m\mid ~m\le ~f(k)\}$. Examples of such functions are $\lfloor \log (1+n)\rfloor$ or $\lfloor \sqrt{n}\rfloor$. As an immediate consequence of the properties of f, one defines by induction the strictly increasing sequence $(\alpha (n))_{n\in \mathbb {N}}$: $\alpha (0)=0$ and $\alpha (n+1)=\min (m \mid \alpha (n)<m \wedge f(\alpha (n))<f(m))$. Note that $\alpha$ depends on f, but since in the sequel we consider a single arbitrary f, for sake of readability we write $\alpha$ instead of $\alpha _f$.

The next proposition establishes that $\mathcal {L}_{ f}$ is a DRPN coverability language. Indeed the coverability language of the DRPN below (without abstract transitions) such that the initial state consists of a single vertex with one token in $p_{w_a}$ and the final state consists of a single vertex with one token in $p_{w_b}$ is $\mathcal {L}_{ f}$ (see the full proof in [8]). So we will use $\mathcal {L}_{ f}$ for witnessing that DRPN coverability languages strictly include RPN coverability languages.

Proposition 2

For all f, $\mathcal {L}_{ f}$ is a DRPN coverability language.

The remainder of this section consists in showing that $\mathcal {L}_{ f}$ is not an RPN coverability language. Let us pick an arbitrary labelled RPN ${\mathcal {N}}$ with an initial state $s_{init}$, a finite set of states $S_t$ such that $\mathcal {L}_{ f}\subseteq \mathcal {L}({\mathcal {N}},s_{init},S_t)$. Let $\{\sigma _{n}\}_{n\in \mathbb {N}}$ be a family of sequences covering some state of $S_t$ such that $\lambda (\sigma _{n})=a^{\alpha (n)}b^{f(\alpha (n))}$ where among the possible $\sigma _{n}$’s we pick one with the minimal depth and among those with minimal depth one with the minimal length (i.e. $\min |\sigma _{n}|$). The skeleton of the proof is as follows.

• $\mathcal {L}_{ f}$ is a not a PN coverability language (Proposition 3 proved in [8]). Therefore there does not exist B such that $\mathcal {L}_{ f}$ is a B-bounded language.

• If the depth of $\{\sigma _{n}\}_{n\in \mathbb {N}}$ is bounded then $\mathcal {L}({\mathcal {N}},s_{init},S_t)$ is a B-bounded language (Proposition 4) which shows that $\mathcal {L}_{ f}\subsetneq \mathcal {L}({\mathcal {N}},s_{init},S_t)$.

• If the depth of $\{\sigma _{n}\}_{n\in \mathbb {N}}$ is unbounded $\mathcal {L}({\mathcal {N}},s_{init},S_t)$ contains words that do not belong to $\mathcal {L}_{ f}$, (Proposition 5) which shows that $\mathcal {L}_{ f}\subsetneq \mathcal {L}({\mathcal {N}},s_{init},S_t)$.

The following proposition is obtained by an adaptation of a result related to the (non) weak computability of sublinear functions in PN [12].

Proposition 3

$\mathcal {L}_{ f}$ is not a PN coverability language.

Remark 1

In the appendix of [5] Lemma 6 shows that for any RPN language there exists a marked RPN with an initial state consisting of only one vertex. Therefore we will assume in the following that $s_{init}$ consists of a single vertex.

In order to alleviate notations in RPN and to be consistent with the notations of DRPN, for all $t\in T$, we denote $\mathbf {Pre}(t)$, $\mathbf {Post}(t)$ and $\mathbf {C}(t)$ respectively by $\mathbf {Pre}_t$, $\mathbf {Post}_t$ and $\mathbf {C}_t$.

Given a labelled RPN ${\mathcal {N}}$ and an abstract transition t, we introduce the following languages:

$$\begin{aligned} \mathcal {L}_{\mathcal {N}}(t)=\{\lambda (\sigma )\mid Beg_t\xrightarrow {\sigma } \} \,\,;\,\, \mathcal {L}_{\mathcal {N}}^\bot (t) =\{\lambda (\sigma )\mid Beg_t \xrightarrow {\sigma } \bot \} \end{aligned}$$

Proposition 4

Let ${\mathcal {N}}$ be a labelled RPN, $s_{init}$ be its initial state and $S_t$ be a finite set of states such that $\mathcal {L}_{ f}\subseteq \mathcal {L}({\mathcal {N}},s_{init},S_t)$. Assume that the depths of $\{\sigma _{n}\}_{n\in \mathbb {N}}$ are bounded. Then $\mathcal {L}_{ f}\subsetneq \mathcal {L}({\mathcal {N}},s_{init},S_t)$.

Proof

Let D denote a bound of the depths of the family of $\{\sigma _{n}\}_{n=1}^\infty$, and let $\mathcal {L}_{\mathcal {N}}$ denote more concisely $\mathcal {L}({\mathcal {N}},s_{init},S_t)$. We are going to build a net ${\mathcal {N}}''$ and some $\mathcal L''$, a B-bounded language of ${\mathcal {N}}''$ such that: $\mathcal {L}_{ f}\subseteq \mathcal L''$. Due to Proposition 1 and 3, $\mathcal {L}_{ f}\subsetneq \mathcal L''$. We stop the construction earlier if we can conclude that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{{\mathcal {N}}}$. Otherwise the relation between $\mathcal L''$ and $\mathcal {L}_{{\mathcal {N}}}$ will allow us to conclude.

We first build an RPN ${\mathcal {N}}'$ that fulfills $\mathcal {L}({\mathcal {N}}',s_{init},S_t)=\mathcal {L}_{{\mathcal {N}}}$ as follows. For all $t\in T_{ab}$, one adds places and transitions according to $\mathcal {L}_{\mathcal {N}}(t)$ and $\mathcal {L}_{\mathcal {N}}^\bot (t)$:

• If $a^+ b^+\cap \mathcal {L}_{\mathcal {N}}(t)=\emptyset$ and $z_t=\max \{m\mid b^m\in \mathcal {L}_{\mathcal {N}}(t)\}<\infty$ then one adds elementary transitions $t^-$, $t^b$ and a place $p_t$ (see left side of the figure below), where:

  $$\begin{aligned} \begin{array}{lll} \mathbf {Pre}_{t^-} =\mathbf {Pre}_t,\,\,&{}\mathbf {C}_{t^-} =-\mathbf {Pre}_t+z_t\cdot \overrightarrow{p_t},\,\,&{}\lambda (t^{-})=\lambda (t);\\ \mathbf {Pre}_{t^b} =\overrightarrow{p_t},&{} \mathbf {C}_{t^b} =-\overrightarrow{p_t},&{} \lambda (t^{b})=b; \end{array} \end{aligned}$$

• $a^+ b^+\cap \mathcal {L}^\bot _{\mathcal {N}}(t)=\emptyset$ and $\max \{m\mid b^m\in \mathcal {L}^\bot _{\mathcal {N}}(t)\}<\infty$ then one adds, elementary transitions $t^-_\bot$,$t^x_\bot$, $t^+_\bot$ and places $p^{\bot }_{t^-},p^{\bot }_{t^+}$ such that where the $y_t$ and x are defined below:

  $$\begin{aligned} \begin{array}{lll} \mathbf {Pre}_{t_{\bot }^-} =\mathbf {Pre}_t,&{} \mathbf {C}_{t_{\bot }^-} =y_t\cdot \overrightarrow{p}^{\!\bot }_{\!t^-} -\mathbf {Pre}_{t_{\bot }^-},&{}\lambda (t_{\bot }^-)=\lambda (t);\\ \mathbf {Pre}_{t_\bot ^{x}} =\overrightarrow{p}^{\!\bot }_{\!t^-} ,&{} \mathbf {C}_{t_\bot ^{x}} =\overrightarrow{p}^{\!\bot }_{\!t^+} - \overrightarrow{p}^{\!\bot }_{\!t^-},&{} \lambda (t_{\bot }^x)=x;\\ \mathbf {Pre}_{t_{\bot }^+} =y_t\cdot \overrightarrow{p}^{\!\bot }_{\!t^+},&{} \mathbf {C}_{t_{\bot }^+} =\mathbf {Post}_t-y_t\cdot \overrightarrow{p}^{\!\bot }_{\!t^+} ,&{}\lambda (t_{\bot }^+)=\varepsilon \end{array} \end{aligned}$$

  • $\circ$ If $b^m\in \mathcal {L}_t^\bot$ for $m>0$ then $y_t=\max \{m\mid b^m\in \mathcal {L}_t^\bot \}$ and $x=b$;

  • $\circ$ Else if $a^\ell \in \mathcal {L}_t^\bot$ for $\ell >0$ then $y_t=\min \{\ell \mid a^\ell \in \mathcal {L}_t^\bot \}$ and $x=a$;

  • $\circ$ Otherwise, $y_t=1$ and $x=\varepsilon$.

    

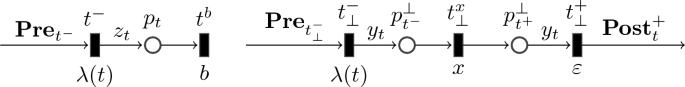
  On the one hand $\mathcal {L}_{\mathcal {N}}\subseteq \mathcal {L}({\mathcal {N}}',s_{init},S_t)$ since any firing sequence in ${\mathcal {N}}$ can be performed in ${\mathcal {N}}'$. On the other hand, the new transitions are built according to $\mathcal {L}_{\mathcal {N}}(t)$ and $\mathcal {L}_{\mathcal {N}}^\bot (t)$ in such a way that every firing of a new transition can be replaced by a firing of a sequence of transitions with the same produced label. Hence $\mathcal {L}({\mathcal {N}}',s_{init},S_t)=\mathcal {L}_{\mathcal {N}}$.

  We now show that for ${\mathcal {N}}'$ there exists some B, such for all $n\in \mathbb {N}$ there is a firing sequence $\sigma _{n}'$ in ${\mathcal {N}}'$ with $|\sigma '_{n}|_{ab}\le B$ and $\lambda '(\sigma '_n)=\lambda (\sigma _n)$. Denote by $G=\max \{|V_{s_t}|\mid s_t\in S_t\}$. Pick an arbitrary $n\in \mathbb {N}$ and denote more explicitely the covering sequence $s_{init}\xrightarrow {\sigma _{n}}s\,\, {}_\varphi \!\!\!\succeq s_t\in S_t$. Assume there is an occurrence $t\in T_{ab}$ by the vertex u in $\sigma _{n}$ creating a vertex v. We transform $\sigma _{n}$ according to whether the firing (u, t) has a matching cut transition $(v,\tau )$ in $\sigma _{n}$:

  The firing (u, t) Does Not Have a Matching Cut.

• If $a^+b^+\cap \mathcal {L}_t\ne \emptyset$ then let us suppose that there are more than $2D+G$ occurrences of t without a matching cut. Then there are two vertices $v,v'$ created by t in $\sigma _n$ which are not: (1) in $\varphi (V_{s_t})$, (2) in the branch leading to it, and (3) both in the same branch. Therefore, one can build a covering sequence $\sigma$ with $\ell _i,m_i>0$ such that $\lambda (\sigma )=~ \ldots a^{\ell _1}b^{m_1} \ldots a^{\ell _2}b^{m_2}\ldots \in \mathcal {L}_{\mathcal {N}}$. So $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done.

• If $\max \{m\mid b^m\in \mathcal {L}_{\mathcal {N}}(t)\}=\infty$ then let us suppose that there are more than $D+G$ occurrences of t without a matching cut. There is a vertex v created by t which is neither in $\varphi (V_{s_t})$ nor in the branch leading to it. Then one can build a covering sequence $\sigma$ with $k\le \alpha (n)$ and $m>f(k)$ such that $\lambda (\sigma )= a^{k}b^{m}\in \mathcal {L}_{\mathcal {N}}$. So $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done.

• Otherwise (i.e. $a^+ b^+\cap \mathcal {L}_{\mathcal {N}}(t)=\emptyset$ and $z_t=\max \{m\mid b^m\in \mathcal {L}_{\mathcal {N}}(t)\}<\infty$), we replace the firing of (u, t) and all firings from Des(v) by:

  $$\begin{aligned} (u,t^-)\overset{z_t \text { times}}{\overbrace{(u,t^b)\ldots (u,t^b)}} \end{aligned}$$

  which will give us a covering sequence $\sigma _{n}'$ such that $\lambda (\sigma _n')=a^{\ell }b^{m}$ with $\ell \le \alpha (n)$ and $m\ge f(\alpha (n))$. If $\ell <\alpha (n)$, and $m>f(\alpha (n))$ then $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done. Otherwise $\lambda '(\sigma _{n}')=\lambda '(\sigma _{n}')$ and $|\sigma '_{n}|_{ab}<|\sigma _{n}|_{ab}$. We can repeat this process until either one concludes that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ or there is no more firing of t without a matching cut transition in $\sigma '_n$.

  The Firing (u, t) Has a Matching Cut.

• Assume that $a^+b^+\cap \mathcal {L}_{\mathcal {N}}^\bot (t)\ne \emptyset$. If there are more than D occurrences of t with a matching cut in $\sigma _{n}$ then there are two occurrences $(w_1,t)$ and $(w_2,t)$ where $w_2$ is neither a descendent nor an ascendent of $w_1$. So one could build a covering sequence $\sigma$ with $\ell _i,m_i>0$ such that $\lambda (\sigma )=\ldots a^{\ell _1}b^{m_1} a^{\ell _2}b^{m_2} \ldots \in \mathcal {L}_{\mathcal {N}}$. So $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done.

• If $\max \{m\mid b^m\in \mathcal {L}_{\mathcal {N}}^\bot (t)\}=\infty$. Consider m the occurrences of b in $\sigma _n$ produced at the subtree rooted in v then there exists $m'>m$ such that one can build a covering sequence $\sigma$ with $m>f(\alpha (n))+1$ such that $\lambda (\sigma )= a^{\alpha (n)}b^{f(\alpha (n))+m'-m}\in \mathcal {L}_{\mathcal {N}}$ So $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done.

• Otherwise (i.e. $a^+ b^+\cap \mathcal {L}^\bot _{\mathcal {N}}(t)=\emptyset$ and $\max \{m\mid b^m\in \mathcal {L}^\bot _{\mathcal {N}}(t)\}<\infty$), we replace the firing of (u, t) by the sequence below and remove all firings from Des(v),

  $$\begin{aligned} (u,t^-_{\bot })\overset{y_t \text { times}}{\overbrace{(u,t^x_{\bot })\ldots (u,t^x_{\bot })}}(u,t^+_{\bot }) \end{aligned}$$

  and obtain a covering sequence $\sigma _{n}'$ such that $\lambda (\sigma _{n}')=a^{\ell }b^{m}$ with $\ell \le \alpha (n)$ and $m\ge f(\alpha (n))$. If $\ell <\alpha (n)$, and $m>f(\alpha (n))$ then $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done. Otherwise $\lambda '(\sigma _{n}')=\lambda '(\sigma _{n}')$ and $|\sigma '_{n}|_{ab}<|\sigma _{n}|_{ab}$. We can repeat this process until either one concludes that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ or there is no more firing of t with a matching cut transition in $\sigma '_n$.

  If we are not yet done, we have built a sequence $\sigma '_{n}$ with $\lambda '(\sigma _{n}')=\lambda '(\sigma _{n}')$ and such that $|\sigma _{n}'|_{ab}\le |T_{ab}|(2D+G)$. So we choose $B=|T_{ab}|(2D+G)$.

  In order that for all $a^\ell b^m\in \mathcal {L}_{ f}$ there is a covering sequence $\sigma$ with $|\sigma |_{ab}\le B$, we build ${\mathcal {N}}''$ from ${\mathcal {N}}'$. We observe that the definition of $\alpha$ implies that: $\mathcal {L}_{ f}=\{a^\ell b^m \mid \exists n,\delta ^-,\delta ^+\ \ell =\alpha (n)+\delta ^+\wedge m =f(\alpha (n))-\delta ^-\}$. Due to the observation about RPN languages, the initial state of ${\mathcal {N}}'$ consists of only one vertex, whose initial marking is denoted $\mathbf {m}_{ini}$. So one builds the RPN ${\mathcal {N}}''$ with initial marking $\overrightarrow{p}_{\!ini}$ from ${\mathcal {N}}'$ as follows.

• Add elementary transitions $t_{a},t_{run},t_{ab}$ and places $p_{ini},p_{run}$ such that:

  $$\begin{aligned} \begin{array}{lll} \mathbf {Pre}''_{t_{a}}=\overrightarrow{p}_{\!ini}, &{} \mathbf {C}''_{t_{a}}=0, &{} \lambda ''(t_{a})=a;\\ \mathbf {Pre}''_{t_{r}}=\overrightarrow{p}_{\!ini}, &{} \mathbf {C}''_{t_{r}}=\mathbf {m}_{ini}-\overrightarrow{p}_{\!ini}+\overrightarrow{p}_{\!run}, &{} \lambda ''(t_{r}) = \varepsilon ;\\ \mathbf {Pre}''_{t_{ab}}=\overrightarrow{p}_{\!run}, &{}\mathbf {C}''_{t_{ab}}=\overrightarrow{p}_{\!run}, &{} \lambda ''(t_{ab})=\varepsilon . \end{array} \end{aligned}$$

• For all $t\in T$, we set:

  $$\begin{aligned} \begin{array}{lll} \mathbf {Pre}''_{t}=\mathbf {Pre}'_{t}+\overrightarrow{p}_{\!run},&\mathbf {C}''_{t}=\mathbf {C}'_{t}-\overrightarrow{p}_{\!run},&\textit{Beg}''_{t}=\textit{Beg}'_{t}+\overrightarrow{p}_{\!run} \text{ when } t\in T_{ab} \end{array} \end{aligned}$$

• For any transition $t\in T$ with $\lambda '(t) = b$, we add the transition $t_\varepsilon$ which is a copy of t with $\lambda ''(t_\varepsilon )= \varepsilon$.

  Let $a^\ell b^m\in \mathcal {L}_{ f}$. Then there exist $n,\delta ^-,\delta ^+$ such that $\ell =\alpha (n)+\delta ^+$ and $m =f(\alpha (n))-\delta ^-$. Let $\sigma _n$ be a covering sequence in ${\mathcal {N}}'$ such that $\lambda '(\sigma _n)=a^{\alpha (n)}b^{f(\alpha (n))}$. We define $\sigma$ a covering sequence of ${\mathcal {N}}''$ as follows.

  $\sigma$ starts by $(r,t_a)^{\delta ^+}(r,t_r)(r,t_{ab})^{|\sigma _n|}$. Then $\sigma$ is completed by $\hat{\sigma }_n$ where $\hat{\sigma }_n$ is obtained from $\sigma _n$ by:

  • changing $\delta ^-$ occurrences of transitions with label b by their copy;

  • whenever $\sigma _n$ creates a new vertex v, one inserts $(v,t_{ab})^{|\sigma _n|}$ firings.

  Observe that $\lambda ''(\sigma )=a^\ell b^m$. Let w be a word. Define $w_{\downarrow b}$ as the set of words obtained from w by omitting some occurrences of b. Define $\mathcal L''=\{w \mid \exists w'\in \mathcal {L}_{\mathcal {N}}\ w\in a^*w'_{\downarrow b}\}$. Therefore $\mathcal {L}_{ f}\subseteq \mathcal {L}_B({\mathcal {N}}'',\overrightarrow{p}_{\!ini},S_t) \subseteq \mathcal L''$. Thus $\mathcal {L}_{ f}\subsetneq \mathcal L''$. If $\mathcal {L}_{{\mathcal {N}}}=\mathcal {L}_{ f}$ then $\mathcal L''=\mathcal {L}_{ f}$ which concludes the proof.    $\blacksquare$

We are now in position to conclude.

Proposition 5

$\mathcal {L}_{ f}$ is not an RPN coverability language.

Proof

Let ${\mathcal {N}}$ be an RPN with initial state $s_{init}$ and final states $S_t$ such that $\mathcal {L}_{ f}\subseteq \mathcal {L}({\mathcal {N}},s_{init},S_t)$. Let us denote more concisely $\mathcal {L}({\mathcal {N}},s_{init},S_t)$ by $\mathcal {L}_{\mathcal {N}}$. By Proposition 4 if $\{\sigma _{n}\}_{n\in \mathbb {N}}$ are bounded then $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$ and we are done.

So assume that the depths of $\{\sigma _{n}\}_{n\in \mathbb {N}}$ are unbounded. Denote by $G = \max \{|s_t|\mid s_t\in S_t\}$. Let $h=(5|T_{ab}|+1)G$. There is some $\sigma _{n}=\sigma _{n}'\sigma _{n}''$ such that $s_0\xrightarrow {\sigma _{n}'}s'$ where the depth of $s'$ is greater than h. There exists $\{v_i\}_{0<i\le 5}\subseteq V_{s'}$ on the same branch which were created by the firing of the same abstract transition with corresponding depths are $\{d_i\}$ and such that $d_{i+1}-d_i>G$. Denote by $T_{ f}$ the subtree of the final state of $\sigma _{n}$ which matches the state to be covered and by Br the branch leading to it. Due to the choice of G there exist three consecutive vertices $v_i,v_{i+1}$ and $v_{i+2}$ such that:

• — The branch $Br_i$ between $v_i$ and $v_{i+2}$ does not intersect with $T_{ f}$;

• — Either $Br_i$ does not intersect with Br or $Br_i$ is included in Br.

Each of these vertex either may or may not have a matching cut in $\sigma _{n}$. We pick two of these vertices $v,v'$ ($v'\in Des(v)$) such that either both of them have a matching cut or both of them do not. Denote by w and $w'$ the labellings of the sequences performed in the subtree rooted in v and $v'$ along $\sigma _{n}$, we split the proof in two cases:

• Case $w\ne w'$. We denote by $\widehat{w}\ne \epsilon$ the trace of the sequence performed in the subtree rooted in v without the one performed in the subtree rooted in $v'$:

  • $\circ$ $\widehat{w}= a^\ell$, for $\ell >0$. Then one can build another covering sequence by mimicking the behavior of $v'$ from v. But then the trace of the new covering sequence will be $a^{\alpha (n)-\ell }b^{f(\alpha (n))}$ and since $\ell >0$ we get that $a^{\alpha (n)k-\ell }b^{f(\alpha (n))}\notin \mathcal {L}_{ f}$, from which we conclude that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$.

  • $\circ$ $\widehat{w}= b^m$, for $m>0$. Then one can build another covering sequence by mimicking the behavior of v from $v'$. But then the trace of the new covering sequence will be $a^{\alpha (n)}b^{f(\alpha (n))+m}\notin \mathcal {L}_{ f}$ from which we conclude that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$.

  • $\circ$ $\widehat{w}= a^\ell b^m$, for $\ell ,m>0$. Then one can build a family of covering sequences $\{\widehat{\sigma }_x\}_{x\in \mathbb {N}}$ by mimicking the behavior of $v_{i}$ from $v_{i+1}$ recursively x times. We would get that $\lambda (\widehat{\sigma }_x) = a^{\alpha (n)+x\ell }b^{f(\alpha (n))+xm}$ for any $x\in \mathbb {N}$. But that would give us that:

    $$\frac{f(\alpha (n))+xm}{\alpha (n)+x\ell }\xrightarrow {x\rightarrow \infty }\frac{m}{\ell }>0 $$

    Since f is sublinear there exists $x\in \mathbb {N}$ such that $\lambda (\widehat{\sigma }_x)\notin \mathcal {L}_{ f}$, from which we conclude that $\mathcal {L}_{ f}\subsetneq \mathcal {L}_{\mathcal {N}}$.

• Case $w=w'$. Then one can build another covering sequence with the trace $a^{\alpha (n)}b^{f(\alpha (n))}$ where we mimic the behavior of $v'$ in v. By doing so we get a covering sequence $\sigma _{n}'$ not deeper then $\sigma _n$ but which is shorter then $\sigma _{n}$, i.e. $|\sigma _{n}|\ge |\sigma _{n}'|$ which is a contradicts to our assumption about $\sigma _n$.   $\blacksquare$

4 Decidability of the Coverability Problem

The coverability problem takes as input a DRPN ${\mathcal {N}}$, and two states $s_0, s$ and asks whether there exists a sequence $s_{0} \xrightarrow {\sigma } s' \succeq s$. Before developing the proof that the coverability problem is decidable let us describe its scheme.

• The algorithm builds a DRPN $\widehat{{\mathcal {N}}}$ by adding elementary transitions to ${\mathcal {N}}$ (Definition 6). The DRPN $\widehat{{\mathcal {N}}}$ is equivalent to ${\mathcal {N}}$ w.r.t. coverability. Furthermore for any firing sequence $\sigma$ of ${\mathcal {N}}$, there is an equivalent firing sequence $\widehat{\sigma }$ of $\widehat{{\mathcal {N}}}$ such that in $\widehat{\sigma }$ there is no occurrence of an abstract transition followed later by a matching cut step.

• The definition of $\widehat{{\mathcal {N}}}$, is based on several upward closed sets of $\mathbb {N}^P$: (1) $\textit{Endable}({\mathcal {N}})$, the set of markings $\mathbf {m}$ such that from $s_{\mathbf {m}}$ one can reach $\bot$ and (2) for all $t \in T_{ab}$, $\textit{Closed}_t$ the set of markings from which one can fire t and create a vertex whose marking belongs to $\textit{Endable}({\mathcal {N}})$. So we establish that one can compute these sets (Proposition 6).

• Afterwards we successively define and solve two intermediate particular coverability problems: (1) the restricted rooted coverability problem which takes as input a DRPN ${\mathcal {N}}$, a marking $\mathbf {m}_0$, and a state s and asks whether there exists a sequence $s_{\mathbf {m}_0} \xrightarrow {\sigma } s' {}_{\mathbf{Id}}\!\!\succeq s$ and (2) the restricted coverability problem which takes as input a DRPN ${\mathcal {N}}$, a marking $\mathbf {m}_0$, and a state s and asks whether there exists a sequence $s_{\mathbf {m}_0} \xrightarrow {\sigma } s' \succeq s$. The decidability of the latter problem (Theorem 2) is partially based on the decidability of the former one (Theorem 1).

• Finally we solve the coverability problem (Theorem 3) by a case based analysis of the covering sequence which, depending on the case, is based on either Theorem 1 or Theorem 2.

As announced above, building the following sets is a key ingredient for the decidability of the coverability problem. Due to the properties of $\preceq$, these sets are upward closed.

Definition 5

Let ${\mathcal {N}}$ be a DRPN. Then $\textit{Endable}({\mathcal {N}})\subseteq \mathbb {N}^P$ is defined by:

$$\begin{aligned} \textit{Endable}({\mathcal {N}})=\{\mathbf {m}\mid \exists \sigma \ s_{\mathbf {m}} \xrightarrow {\sigma } \bot \} \end{aligned}$$

and for all $t\in T_{ab}$, $\textit{Closed}_t$ is defined by:

$$\begin{aligned} \textit{Closed}_t=\textit{Beg}_t^{-1}(\textit{Endable}({\mathcal {N}})) \end{aligned}$$

Example 2

Consider the DRPN of Fig. 1. With one token in $p_{time}$ and in $p_{adv}$ one fires $t_{ {found}}$ producing a token in $p_{dead}$ which allows to fire a cut transition. Furthermore firing the abstract transition $t_{ {hire}}$ does not help to reach $\bot$ since in the new vertex, the marking of $p_{time}$ is equal to the marking of $p_{time}$ in its parent vertex and the marking $p_{adv}$ is smaller than the markingof $p_{adv}$ in in its parent vertex. Thus $\textit{Endable}({\mathcal {N}})= \{p_{time}+p_{adv}\}^{\uparrow }$. The marking of a vertex created by $t_{ {hire}}$ is greater or equal than $p_{time}+p_{adv}$ if in its parent vertex there is at least one token in $p_{time}$ and three tokens in $p_{adv}$. Thus $\textit{Closed}_{t_{ {hire}}}= \{p_{time}+3p_{adv}\}^{\uparrow }$.

If we are able to compute $\textit{Endable}$ and thus $\{\textit{Closed}_t\}_{t \in T_{ab}}$ then we can build a DRPN $\widehat{{\mathcal {N}}}$ which in some sense is equivalent to ${\mathcal {N}}$. The interest of $\widehat{{\mathcal {N}}}$ is that for any firing sequence $\sigma$ of ${\mathcal {N}}$, there is an equivalent firing sequence $\widehat{\sigma }$ where the firing of an abstract transition t followed later by a matching cut transition can be replaced by the firing of an elementary $t^-$ followed later by the firing of another elementary transition $t^+$. So the set of transitions is extended with $T_r=\{t^-,t^+ \mid t \in T_{ab}\}$. To ensure the sequentiality between these firings, the set of places is extended with $P_r=\{p_t \mid t \in T_{ab}\}$ with one token produced (resp. consumed) in $p_t$ by $t^-$ (resp. $t^+$). To ensure that the firing of $t^-$ is performed when the corresponding firing of t can be matched later by the firing of the cut transition, the guard of $t^-$ is the guard of t intersected with $\textit{Closed}_t$. In order to formally define $\widehat{{\mathcal {N}}}$ and to exhibit relations between states and thus markings of ${\mathcal {N}}$ and $\widehat{{\mathcal {N}}}$, we introduce the projection Proj from $\mathbb {N}^{\widehat{P}}$ to $\mathbb {N}^P$ where $\widehat{P}=P \cup P_r$. In addition $\widehat{{\mathcal {N}}}_{el}$, obtained from $\widehat{{\mathcal {N}}}$ by deleting $T_{ab}$, allows to track the evolution of the marking of a vertex in $\widehat{{\mathcal {N}}}$ when no firing of abstract transitions occurs in this vertex.

Definition 6

Let ${\mathcal {N}}$ be a DRPN.

Then $\widehat{{\mathcal {N}}}=\langle \widehat{P},\widehat{T},\widehat{\textit{Grd}},\widehat{\textit{Upd}}, \widehat{\textit{Upd}}{}^{-},\widehat{\textit{Upd}}{}^{+}, \widehat{\textit{Beg}},\widehat{\textit{End}} \rangle$ is a DPRN defined by:

• $\widehat{P}= P \cup P_r$ and $\widehat{T}= T \cup T_r$;

• for all $t\in T$, $\widehat{\textit{Grd}}_t=\mathsf{Proj}^{-1}(\textit{Grd}_t)$

  for all $t^-\in T_r$, $\widehat{\textit{Grd}}_{t^-}=\mathsf{Proj}^{-1}(\textit{Grd}_t\cap \textit{Closed}_t)$

  for all $t^+\in T_r$, $\widehat{\textit{Grd}}_{t^+}=p_t>0$;

• for all $t\in T_{el}$, all $p\in P$ and all $p_{t'}\in P_r$,

  $\widehat{\textit{Upd}}_t(p)= \textit{Upd}_t(p)\circ \mathsf{Proj}$ and $\widehat{\textit{Upd}}_t(p_{t'})= p_{t'}$;

• for all $t^-\in T_r$, all $p\in P$ and all $p_{t'}\in P_r$,

  $\widehat{\textit{Upd}}_{t^-}(p)= \textit{Upd}^-_t(p)\circ \mathsf{Proj}$ and $\widehat{\textit{Upd}}_t(p_{t'})= p_{t'}+\mathsf{1}_{t=t'}$;

• for all $t^+\in T_r$, all $p\in P$ and all $p_{t'}\in P_r$,

  $\widehat{\textit{Upd}}_{t^+}(p)= \textit{Upd}^+_t(p)\circ \mathsf{Proj}$ and $\widehat{\textit{Upd}}_t(p_{t'})= p_{t'}-\mathsf{1}_{t=t'}$;

• for all $t\in T_{ab}$, all $p\in P$ and all $p_{t'}\in P_r$,

  • 1. $\widehat{\textit{Upd}}{}^{-}_t(p)= \textit{Upd}^{-}_t(p)\circ \mathsf{Proj}$, $\widehat{\textit{Upd}}{}^{+}_t(p)= \textit{Upd}^{+}_t(p)\circ \mathsf{Proj}$,

    $\widehat{\textit{Beg}}_t(p) = \textit{Beg}_t(p)\circ \mathsf{Proj}$;

  • 2. $\widehat{\textit{Upd}}{}^{-}_t(p_{t'})= p_{t'}$, $\widehat{\textit{Upd}}{}^{+}_t(p_{t'})= p_{t'}$, $\widehat{\textit{Beg}}_t(p_{t'}) = 0$;

• $\widehat{\textit{End}}=\mathsf{Proj}^{-1}(\textit{End})$;

$\widehat{{\mathcal {N}}}_{el}$ is obtained from $\widehat{{\mathcal {N}}}$ by deleting $T_{ab}$.

The following lemma states the correspondence between ${\mathcal {N}}$, $\widehat{{\mathcal {N}}}$ and $\widehat{{\mathcal {N}}}_{el}$. We extend Proj to states of $\widehat{{\mathcal {N}}}$ by applying it to the marking of vertices and furthermore to sets of states by the standard set extension. In the reverse direction, given a marking $\mathbf {m}\in \mathbb {N}^P$ we define $\widehat{\mathbf {m}}\in \mathbb {N}^{\widehat{P}}$ the extended marking with no token in $P_r$. Similary, given s a state of ${\mathcal {N}}$, we define $\widehat{s}$ a state of $\widehat{N}$ by extending the marking of vertices of s with no token in $P_r$.

Lemma 1

Let ${\mathcal {N}}$ be a DRPN and $s_0$ be a state. Then:

• 1. For all $\widehat{s}_0 \xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} s$, there exists $s_0 \xrightarrow {\sigma '}_{{\mathcal {N}}} s'$ with $\mathsf{Proj}(s)\preceq _{\mathbf{Id}} s'$ and for all $s_0 \xrightarrow {\sigma '}_{{\mathcal {N}}} s$, $\widehat{s}_0 \xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} \widehat{s}$;

• 2. $Cov({\mathcal {N}},s_0)=\mathsf{Proj}(Cov(\widehat{{\mathcal {N}}},\widehat{s}_0))$;

• 3. For all $s\in Reach(\widehat{{\mathcal {N}}},\widehat{s}_0)$, there exists a sequence $\widehat{s}_0 \xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} s$ such that no firing of abstract transition is matched by a cut transition.

• 4. $\mathsf{Proj}(\textit{Endable}(\widehat{{\mathcal {N}}})\cap \bigcap _{t\in T_{ab}} p_t=0) = \mathsf{Proj}(\textit{Endable}(\widehat{{\mathcal {N}}}_{el})\cap \bigcap _{t\in T_{ab}} p_t=0)$ $=\ \textit{Endable}({\mathcal {N}})$.

Proof

• Let $\widehat{s}_0\xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} s$. Consider successively all $t\in T_{ab}$. Observe that due to the presence of place $p_t$ every occurrence of $(v,t^+)$ in $\sigma '$ can be matched with an occurrence of $(v,t^-)$. The unmatched occurrences of $(v,t^-)$ can be omitted since they only produce useless tokens in $p_t$ and do not increase the marking of any other place. So we get a new firing sequence $\widehat{s}_0\xrightarrow {\sigma ^*}_{\widehat{{\mathcal {N}}}} s^*$ with $\mathsf{Proj}(s)\preceq _{\mathbf{Id}} \mathsf{Proj}(s^*)$. We transform this sequence in a sequence $s_0\xrightarrow {\sigma '}_{{\mathcal {N}}} \mathsf{Proj}(s^*)$ as follows. For every pair of matching firings $(v,t^-),(v,t^+)$, we substitute to $(v,t^-)$ the firing (v, t) creating the vertex w with an initial $\mathbf {m}\in \textit{Endable}({\mathcal {N}})$ due to the guard of $t^{-}$. Then we substitute to $(v,t^+)$ a sequence $s_{\mathbf {m}} \xrightarrow {\sigma _{\mathbf {m}}} \bot$ applying it to w. The “reverse” direction is immediate since for all $t \in T \cup \{\tau \}$ and all states s and $s'$, $s\xrightarrow {(v,t)}_{{\mathcal {N}}} s'$ implies $\widehat{s}\xrightarrow {(v,t)}_{\widehat{{\mathcal {N}}}} \widehat{s}'$.

• Assertion 2 is an immediate consequence of Assertion 1 of the lemma.

• Let $\widehat{s}_0 \xrightarrow {\sigma '} s$ be a firing sequence of $\widehat{{\mathcal {N}}}$. Consider successively all $t\in T_{ab}$ and all matching pairs $(v,t),(w,\tau )$ occurring in $\sigma '$ where w is the vertex created by the firing of (v, t). Let $\sigma ^*$ be the subsequence of $\sigma$ of firings in the subtree rooted at w ended by $(w,\tau )$. Then one substitutes to (v, t), the firing $(v,t^-)$ which is fireable as witnessed by $\sigma ^*$ and one deletes $\sigma ^*$ substituting $(w,\tau )$ by $(v,t^+)$. Iterating this process, one gets the sequence we are looking for.

• Let $\mathbf {m}\in \textit{Endable}(\widehat{{\mathcal {N}}})\cap \bigcap _{t\in T_{ab}} p_t=0$. Consider a sequence $s_{\mathbf {m}} \xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} \bot$. Using Assertion 3, one can assume that in $\sigma$, no firing of an abstract transition is matched with a cut transition. Consider (r, t) the firing of an abstract transition in the root occurring in $\sigma$. Since it is not matched by a cut transition one can delete it and all the firings in the subtree rooted at the created vertex and still reaches $\bot$. Such a sequence is thus a firing sequence of $\widehat{{\mathcal {N}}}_{el}$. The other direction is immediate since the set of transitions of $\widehat{{\mathcal {N}}}_{el}$ is included in the one of $\widehat{{\mathcal {N}}}$.

  The inclusion $\textit{Endable}({\mathcal {N}})\subseteq \mathsf{Proj}(\textit{Endable}(\widehat{{\mathcal {N}}})\cap \bigcap _{t\in T_{ab}} p_t=0)$ is immediate since for all $t \in T \cup \{\tau \}$, $s\xrightarrow {(v,t)}_{{\mathcal {N}}} s'$ implies $\widehat{s}\xrightarrow {(v,t)}_{\widehat{{\mathcal {N}}}} \widehat{s}'$. Let $\mathbf {m}\in \mathsf{Proj}(\textit{Endable}(\widehat{{\mathcal {N}}})\cap \bigcap _{t\in T_{ab}} p_t=0)$. One applies Assertion 1 of the lemma with $s_0=s_{\mathbf {m}}$. Let $\widehat{s}_{\mathbf {m}} \xrightarrow {\sigma }_{\widehat{{\mathcal {N}}}} s \xrightarrow {(r,\tau )}_{\widehat{{\mathcal {N}}}}\bot$. Then there exists $s_0 \xrightarrow {\sigma }_{{\mathcal {N}}} s'$ with $\mathsf{Proj}(s)\preceq _{\mathbf{Id}} s'$. Thus $s'\xrightarrow {(r,\tau )}_{{\mathcal {N}}}\bot$ which establishes that $\mathbf {m}\in \textit{Endable}({\mathcal {N}})$.    $\blacksquare$

Let us describe how Algorithm 1 computes Endable and $\{\textit{Closed}_t\}_{t\in T_{ab}}$. During lines 2–14, it builds a version of $\widehat{{\mathcal {N}}}_{el}$ where for every t, $\textit{Closed}_t$ is replaced by $\textit{Closed}[t]$. Since $\textit{Closed}[t]$ will be updated during the loop of lines 15–23, the definition of $\textit{Grd}_{t^-}$ is performed at line 16. Still in this loop, using a standard backward exploration, during lines 17–20, it computes in variable X, Endable for this version of $\widehat{{\mathcal {N}}}_{el}$. Afterwards still in this loop, it updates Y by restricting X to the markings with no token in $P_r$ and then projecting it to P. Then using Y, updates for every t, $\textit{Closed}[t]$. The algorithm terminates when Y is no more enlarged.

Proposition 6

Algorithm 1 terminates and upon termination $Y=\textit{Endable}$ and for all $t\in T_{ab}$, $\textit{Closed}[t]=\textit{Closed}_t$.

Proof

In the sequel $\textit{Closed}[t]$ denotes the value of this variable at some execution point. Let us denote ${\mathcal {N}}'$ the version of $\widehat{N}_{el}$ built by the algorithm and updated at every iteration of loop of lines 15–23.

• Termination. We prove by induction that the sequence of sets $Y_n$ and for all t, $\textit{Closed}_n[t]$ at the beginning of iteration n of the repeat loop is an increasing sequence of upward closed sets of $\mathbb {N}^P$ and $\mathbb {N}^{\widehat{P}}$, respectively. So it must stabilize after a finite number of iterations. Since T is finite this will establish termination of the algorithm. First, for all t, $\emptyset =\textit{Closed}_1[t]\subseteq \textit{Closed}_2[t]$. Assume that for some $1<n$, for all t, $\textit{Closed}_{n-1}[t]\subseteq \textit{Closed}_n[t]$. Then the $n^{th}$ iteration corresponds to the $n-1^{th}$ iteration with $Closed_n[t]$ substituted to $Closed_{n-1}[t]$. Since the operations involving $\textit{Closed}[t]$ are intersection, union and projection, this immediately entails that $\textit{Closed}_{n}[t]\subseteq \textit{Closed}_{n+1}[t]$.

  It remains to prove that for all n, $Y_n$ and (for all t) $\textit{Closed}_n[t]$ are upward closed and that the while loop terminates. We also prove it by induction on n. Consider the $n^{th}$ iteration of the repeat loop and let us prove the sequence of sets $X_k$ at the beginning of iteration k of the while loop is an increasing sequence of upward closed sets. This will establish the termination of this loop. Observe that $X_1=\mathsf{Proj}^{-1}(End)$ is an upward closed set and that at every iteration X is increased because it is updated by union of some set with itself. Furthermore, X remains an upward closed set since (1) upward closed sets are closed by union, intersection, and inverse of non decreasing mappings. Finally while $X\cap \bigcap _{t\in T_{ab}} p_t=0$ is not upward closed, this is the case for $Y_{n+1}=\mathsf{Proj}(X\cap \bigcap _{t\in T_{ab}} p_t=0)$. Thus for every t, $\textit{Closed}_{n+1}[t]$ is upward closed.

• Consistency. We establish by induction on the iterations of the repeat loop that $Y\subseteq \textit{Endable}({\mathcal {N}})$ and for all $\mathbf {m}\in \textit{Closed}[t]$, there is a sequence $s_{\textit{Beg}(t)(\mathbf {m})} \xrightarrow {\sigma _{\mathbf {m}}} \bot$, implying $\textit{Closed}[t]\subseteq \textit{Closed}_t$. Consider an arbitrary iteration of the repeat loop. Thus the while loop computes X the set $\textit{Endable}({\mathcal {N}}')$. Since by induction, $\textit{Closed}[t]\subseteq \textit{Closed}_t$ one deduces that $X\subseteq \textit{Endable}(\widehat{{\mathcal {N}}}_{el})$. Applying Assertion 4 of Lemma 1, one deduces that $Y\subseteq \textit{Endable}({\mathcal {N}})$ and so that at the end of the iteration $\textit{Closed}[t]\subseteq \textit{Closed}_t$.

• Completeness. Let $\mathbf {m}\in \textit{Closed}_t$. Consider a sequence $s_{\textit{Beg}(t)(\mathbf {m})} \xrightarrow {\sigma }_{{\mathcal {N}}} \bot$. Observe that if in $\sigma$, there exists a firing of and abstract transition creating some vertex v not later followed by a cut transition in v, then one can omit this firing and all firings in the subtree rooted at v and still reaches $\bot$. Thus we assume that every vertex v created by the firing of abstract transition is later deleted by a matching cut transition in v.

  We establish the completeness of the algorithm by recurrence on the depth of $\sigma$. If the depth is null, it means that $\sigma$ only includes firing of elementary transitions in r ended by the cut transition. So $\widehat{s}_{\textit{Beg}(t)(\mathbf {m})} \xrightarrow {\sigma }_{{\mathcal {N}}_{el}} \bot$. Furthermore since $\sigma \in (\{r\}\times T_{el})^*(r,\tau )$, $\widehat{s}_{\textit{Beg}(t)(\mathbf {m})} \xrightarrow {\sigma }_{{\mathcal {N}}'} \bot$ for ${\mathcal {N}}'$ built at the beginning of the first iteration of the repeat loop. During every iteration of the repeat loop, the while loop computes in X the set of markings from which a sequence of transitions of ${\mathcal {N}}'$ leads to some marking in $\mathsf{Proj}^{-1}(\textit{End})$. So $\widehat{\textit{Beg}_t(\mathbf {m})} \in X$ at the end of the iteration and after the for loop at line 22, $\mathbf {m}\in \textit{Closed}[t]$.

  Assume that $\sigma$ has depth $h>0$. So every $\mathbf {m}'$ in the root from which there is a firing of an abstract transition $t'$ belongs to $\textit{Closed}[t']$ since the subsequence in the created vertex up to the cut transition has depth strictly less than h. Consider the last iteration of the repeat loop for which such $t'$ is added to $\textit{Closed}[t']$. Then either at this iteration $\mathbf {m}$ already belongs to $\textit{Closed}[t]$ or it will be added at the next iteration (which exists since Y is enlarged) due to execution of the while loop. Indeed consider a closing subsequence of $\sigma$ for a child of the root created by some transition $t'$ and substitute the firing of $t'$ by $t'^-$, delete the closing subsequence and substitute the cut step by the firing of $t^+$ in r. Doing this transformation (and ommitting the cut step in r) one obtains a closing firing sequence in ${\mathcal {N}}'$ as described above from $\widehat{s}_{\textit{Beg}(t)(\mathbf {m})}$. Thus at the beginning of last iteration of the while loop, ${\mathcal {N}}'=\widehat{{\mathcal {N}}}_{el}$. Using Assertion 4 of Lemma 1, one gets that at this end of this iteration, $Y=\textit{Endable}({\mathcal {N}})$.   $\blacksquare$

Theorem 1

The restricted rooted coverability problem is decidable.

Proof

Due to Assertion 1 of Lemma 1, we consider $\widehat{{\mathcal {N}}}$. Applying Assertion 3 of Lemma 1, the sequence we are looking for, does not create other vertices than the vertices of s since (1) the firing of abstract transitions matched by cut transitions are non necessary in $\widehat{{\mathcal {N}}}$ and (2) those that are not matched decrease the marking of a vertex and create a subtree useless for covering $s=(V,E,M,\varLambda )$.

Then for any vertex $v\in V$, one guesses an order of creation of its children along the sequence $\sigma$ and for any transition t labelling an edge of E, one guesses a transition $t'$ with $\textit{Upd}^+_{t'} \ge \textit{Upd}^+_t$. Observe that there are only a finite number of such guesses and so the algorithm enumerates them.

Afterwards the algorithm proceeds bottom-up from the leaves of s to the root. Let v be a leaf. Then the algorithm computes by backward exploration the upward closed set $Cov(v)=\{\mathbf {m}\in \mathbb {N}^{\widehat{P}} \mid \exists \mathbf {m}' \ge M(v)\ \exists \sigma \in \widehat{T}_{el}^*\ \mathbf {m}\xrightarrow {\sigma } \mathbf {m}'\}$.

Let v be an internal vertex with $v_1,\ldots ,v_n$ its children enumerated in the guessed order and $t_1,\ldots ,t_n$ the associated guessed transitions. Then the algorithm computes by backward exploration the upward closed sets $Cov_n(v),\ldots ,Cov_0(v)=Cov(v)$ as follows: $Cov_n(v)=\{\mathbf {m}\in \mathbb {N}^{\widehat{P}} \mid \exists \mathbf {m}' \ge M(v)\ \exists \sigma \in \widehat{T}_{el}^*\ \mathbf {m}\xrightarrow {\sigma } \mathbf {m}'\}$ and for $i<n$,

$$\begin{aligned} Cov_i(v)= \{&\mathbf {m}\in \mathbb {N}^{\widehat{P}}\ \mid \\&\exists \mathbf {m}' \in (\widehat{\textit{Upd}}^-_{t_{i+1}})^{-1}\left( \widehat{\textit{Beg}}_{t_{i+1}}^{-1}(Cov(v_{i+1})) \cap Cov_{i+1}(v)\right) \cap \widehat{\textit{Grd}}_{t_{i+1}}\\&\exists \sigma \in \widehat{T}_{el}^*\ \mathbf {m}\xrightarrow {\sigma } \mathbf {m}'\} \end{aligned}$$

By a straightforward induction, one establishes that $\mathbf {m}\in Cov_i(v)$ if and only from vertex v marked by $\mathbf {m}$ there is a firing sequence $\sigma =\sigma _it_{i+1}\sigma _{i+1}\ldots t_{n}\sigma _{n}$ with for all j, $\sigma _j \in \widehat{T}_{el}^*$ and such that (1) the marking of v reached by $\sigma$ is greater or equal than M(v), and (2) for all $j>i$, from the initial marking of $v_j$ one can fire a sequence that builds a tree covering the subtree of s rooted at $v_i$ using the guessed transitions and orders of creation.

Finally the algorithm returns true if and only if for some guess $\widehat{\mathbf {m}}_0 \in Cov(r)$ where r is the root of s.    $\blacksquare$

Theorem 2

The restricted coverability problem is decidable.

Proof

Let us fix some net ${\mathcal {N}}$ and some state s. As above we substitute $\widehat{{\mathcal {N}}}$ to ${\mathcal {N}}$ but for sake of readability we omit the occurrences of ‘⌃’. Thus one observes that the state $s'$ that should cover s can be chosen as a single branch, say Br, leading to a tree $s^*$ isomorphic to s. Indeed the firings that would create other branches are useless since they only decrease the markings in Br or in $s'$.

Observe that in the previous proof, instead of answering the decision problem, one can compute the set $RRC({\mathcal {N}},s)=\{\mathbf {m}\mid \exists s_{\mathbf {m}}\xrightarrow {\sigma } s^*{}_{\mathbf{Id}}\!\!\succeq s \}$.

Let us define $RC({\mathcal {N}},s,k)=\{\mathbf {m}\mid \exists s_{\mathbf {m}}\xrightarrow {\sigma } s'{}_{\varphi }\!\!\succeq s \wedge |r \rightarrow _{s'} \varphi (r)|\le k\}$ where $|x \rightarrow _{s'} y|$ denotes the length of the elementary path from x to y in $s'$. One immediately observes that $RC({\mathcal {N}},s,0)=RRC({\mathcal {N}},s)$ that for all k, $RC({\mathcal {N}},s,k)$ is upward closed and $RC({\mathcal {N}},s,k)\subseteq RC({\mathcal {N}},s,k+1)$. Furthermore the answer to the restricted coverability problem is positive if and only if $\mathbf {m}_0 \in \bigcup _{k\in \mathbb {N}}RC({\mathcal {N}},s,k)$.

So it only remains to show how to compute $RC({\mathcal {N}},s,k+1)$ when one knows $RC({\mathcal {N}},s,k)$. Observe that:

$$\begin{aligned} RC({\mathcal {N}},s,k+1)=&RC({\mathcal {N}},s,k)\cup \{\mathbf {m}\mid \\&\exists \sigma \in \widehat{T}_{el}^*\ \exists \mathbf {m}'\ \in \bigcup _{t \in T_{ab}}\textit{Grd}_t \cap \textit{Beg}_t^{-1}(RC({\mathcal {N}},s,k))\\&\mathbf {m}\xrightarrow {\sigma } \mathbf {m}'\} \end{aligned}$$

where the second term of this union can be computed by a backward exploration.    $\blacksquare$

Using the previous theorems, we are now in position to decide the coverability problem.

Theorem 3

The coverability problem of DRPN is decidable.

Proof

Let us fix some net ${\mathcal {N}}$ and states $s_0$ and s. As above we substitute $\widehat{{\mathcal {N}}}$ to ${\mathcal {N}}$ and omit the occurrences of ‘⌃’. In order to decide the existence of a sequence $s_{0} \xrightarrow {\sigma } s' {}_{\varphi }\!\!\succeq s$, we consider two cases depending on $\varphi (r)$

• $|\varphi (V_{s})\cap V_{s_0}|\le 1$. So one guesses a vertex $w\in V_{s_0}$ that is the deepest on the branch leading from r to $\varphi (r)$ in $s'$. Then we transform the net (whose current version is in the sequel denoted ${\mathcal {N}}'$) as follows. We examine bottom-up all the (proper) descendants of w in $s_0$ as follows. Let v be such a vertex, u its parent and t the abstract transition labelling the edge (u, v). If $M(v)\in Endable({\mathcal {N}}')$ then one adds a place $p_{u,v}$ with a token in u and no token elsewhere and an elementary transition $t_{u,v}$ such that $\textit{Grd}_{t_{u,v}}=p_{u,v}>0$ and $\textit{Upd}_{t_{u,v}}=\textit{Upd}^+_{t} - p_{u,v}$. By construction, there exists a sequence $s_{0} \xrightarrow {\sigma }_{{\mathcal {N}}} s' {}_{\varphi }\!\!\succeq s$, if and only if there exists a sequence $s_{M(w)} \xrightarrow {\sigma }_{{\mathcal {N}}'} s' {}_{\varphi }\!\!\succeq s$. So this case is decidable by Theorem 2.

• $|\varphi (V_{s})\cap V_{s_0}|>1$. Then one builds a state $s'_0$ with root $\varphi (r)$ and simultaneously transform the net (whose current version is also denoted ${\mathcal {N}}'$) as follows. We eliminate all the vertices of $s_0$ which are not descendants of $\varphi (r)$ since there are irrelevant due to the choice of $\varphi$. Then we eliminate bottom-up all the descendants of $\varphi (r)$ in $s_0$ which do not belong to $\varphi (V_{s})$ as follows. Let v be such a vertex, u its parent and t the abstract transition labelling the edge (u, v). When one examines v, it has become a leaf. If $M(v)\in Endable({\mathcal {N}}')$ then one adds a place $p_{u,v}$ with a token in u and no token elsewhere and an elementary transition $t_{u,v}$ such that $\textit{Grd}_{t_{u,v}}=p_{u,v}>0$ and $\textit{Upd}_{t_{u,v}}=\textit{Upd}^+_{t} - p_{u,v}$. Afterwards one deletes v and (u, v). By construction, there exists a sequence $s_{0} \xrightarrow {\sigma }_{{\mathcal {N}}} s' {}_{\varphi }\!\!\succeq s$, if and only if there exists a sequence $s'_{0} \xrightarrow {\sigma }_{{\mathcal {N}}'} s' {}_{\varphi }\!\!\succeq s$.

  For all vertices u of $s'_0$ denote $s_u$ the subtree of s rooted at $\varphi (u)$ consisting of vertices whose deepest ancestor in s is $\varphi (u)$. Then there exists a sequence $s'_{0} \xrightarrow {\sigma }_{{\mathcal {N}}'} s' {}_{\varphi }\!\!\succeq s$ if and only if the following conditions hold:

  • For all $(u,v)\in E_{s'_{0}}$, $\textit{Upd}^+(\varLambda (u,v))\ge \textit{Upd}^+(\varLambda (\varphi ^{-1}(u),\varphi ^{-1}(v))$;

  • For all $u \in V_{s'_{0}}$ there exists a sequence $s_{M(u)} \xrightarrow {\sigma _u}_{{\mathcal {N}}'} s' {}_{\mathbf{Id}}\!\!\succeq s_u$.

  The first item is decidable by effectiveness of ${\mathcal {N}}$. The second item is decidable by Theorem 1.

Since there are only a finite number of possible $\varphi$ (more precisely their restriction over $s_0$) the coverability problem is decidable.    $\blacksquare$

5 Conclusion

We introduced DRPN that extend recursive Petri nets in several directions. We established that w.r.t. coverability languages, this extension is strict and we have established that the coverability problem is still decidable.

We plan to define a restriction of DRPN for which reachability would be still decidable as in RPN. Moreover since our algorithm is based on backward explorations and our team has already developed an efficient tool for coverability in PN based on such explorations [1], we want to adapt it for DRPN.