Abstract
When a Petri net system of some class is synthesised from a labelled transition system, it may be interesting to derive structural properties of the corresponding reachability graphs and to use them in a pre-synthesis phase in order to quickly reject inadequate transition systems, and provide fruitful error messages. The same is true for simultaneous syntheses problems. This was exploited for the synthesis of choice-free nets for instance, for which several interesting properties have been derived. We exhibit here a new property for this class, and analyse if this gets us closer to a full characterisation of choice-free synthesizable transition systems.
E. Erofeev—Supported by DFG through grant Be 1267/16-1 ASYST.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction: Implementation Issue
Those last years, several works have been dedicated to the (simultaneous) synthesis of choice-free Petri netsFootnote 1, among others [1, 3, 8, 9]. Since this means a loss in the expressive power, we may thus wonder why this class of systems could be especially interesting, besides the known structural properties of their behaviours.
The rather general class of weighted place-transition nets and systems is composed of places and transitions, as indicated by its name, together with weighted arcs between them. A place represents a type of resource; it may contain tokens representing the number of resources of that kind presently available; these (consumable) resources are considered interchangeable, at least as far as the control flow is concerned (“black” tokens), but they may carry some information that will be used (in a way not specified) by the transition that will absorb them. A transition needs some number (possibly zero) of tokens of each kind in order to be able to function, and then produces some (other) tokens. As such, those nets allow to model complex intertwined mixtures of sequences, exclusive choices and concurrency, hence exhibit an interesting expressive power.
But they may also serve as static specifications of systems to build. And a (finite) labelled transition system may serve as a behavioural specification, from which a (bounded) synthesised net system of some class may be built and then serves itself as a structural specification. However, here we may encounter some problems. Since those models allow to represent a concurrency feature between transition firings, a natural implementation strategy would be to build a system composed of data structures to model places and tokens, and parallel agents, one for each transition, interacting only through their competition to access their needed resources, one place at a time to obtain a fully distributed realisation. Note that, since memory resources are finite, we need to restrict our attention to bounded net systems and finite transition systems.
The structure of each implemented transition could then be sketched as follows:
repeat
check availability of needed resources
if some are missing, retry after some time
otherwise, collect the needed tokens
process the action of the transition
(possibly using the hidden information of the black tokens)
produce the output tokens
(possibly with adequate hidden information,
depending on the one of the used tokens.)
There are variants of this schema however; for instance, the production of the output tokens may be performed one by one during the action process, and not all together at the end of the processing.
However there is potentially a big problem with this procedure: between the checking phase and the collection phase, the situation may have changed, due to the parallel action of other transitions, and it may happen that the tokens which were available during the checking phase are no longer there! It may even be possible that this is only discovered in the middle of the collection phase, and that we need to “give back” the tokens that were absorbed during the beginning of the phase. This is illustrated by the system in Fig. 1.
We may partly avoid this problem by absorbing the remainder of the needed tokens whenever the transition discovers they have been produced, but it may still be necessary to give back the absorbed tokens if we observe that it takes too long to get the remaining ones, possibly meaning that we reached a deadlock.
It is possible to avoid this kind of problem by blocking in a critical section all the data structures implementing the places and tokens, in order to check and absorb the needed tokens without being bothered by the other transitions, relaxing the critical section to wait a bit if not all the needed tokens were present, or to start the process and produce phase. However, this seriously reduces the parallelism of the implementation, may lead to starvation problems, and is certainly not distributed in the way we searched for.
We may also slightly alleviate this technique by only blocking together the input places of the transition, by protecting each place separately by a critical section and nesting them while following a predefined ordering in order to avoid deadlocks. However, this still reduces the parallelism of the implementation, may still lead to starvation problems, needs that the transitions first agree on a common ordering of the places, and is again not distributed as expected.
A Petri net system, where transition u may see that all its needed tokens are present, but when it decides to take them, conflicting transitions \(t_1\) and/or \(t_2\) may have taken them before. If u takes a token from \(p_1\) and then sees that the token in \(p_2\) has disappeared, u must give back the token to \(p_1\).
These problems underpin the difficulties encountered when one tries to realise a distributed hardware implementation of Petri nets, as in [13, 18].
The problem we described disappears, whatever the marking, if the places are not shared, that is if each place has (at most) a single output transition (for instance, in Fig. 1, if transition u is dropped, or \(t_1\) and \(t_2\)), which is the definition of choice-free nets (see also Fig. 2 left, Fig. 5 right, and many others in the following).
In that case, it is never necessary to give back some absorbed token(s), and it is even possible to fuse the check and collect phases, leading for each transition to a (parallel) procedure of the kind:
repeat
for each input place do
while the needed tokens are not present do wait for some time
grab the needed tokens
process the action of the transition and produce the output tokens
Of course, it is necessary to protect the data structures representing places, by semaphore-like devices [11] or monitor-like devices [12], in order to ensure that if many producers or the consumer and some producer(s) access the place, the result may be serialised (for instance, if two producers add one token in some common place, the result will be to add two tokens, and not a single one, the last addition wiping out the first one as it can happen in a -badly implemented- parallel system).
There is another class of nets, however, where a distributed implementation may be obtained whatever the initial marking: the join-free nets, where each transition has at most a single input place (called a simple-choice place), as illustrated on the right of Fig. 2. This is in some sense the reverse-dual of the choice-free case, since we have \(\forall t:|{}^\bullet t|\le 1\) instead of \(\forall p:|p^\bullet |\le 1\).
On the left: a general pure (\(h=0\)) or non-pure (\(h>0\)) choice-free place p with initial marking \(\mu _0\) and unique output x (the inputs of \(a_i\)’s and other inputs/outputs of x are not constrained); \(\{a_1,\ldots ,a_m\}=T\setminus \{x\}\), but some \(k_i\)’s may be null. On the right, a general simple-choice place (the outputs of \(a_i\)’s and inputs of p are not constrained).
In an implementation, each transition simply has to check the number of tokens in its unique input place and grab the needed ones in one accessFootnote 2 if present (otherwise, one waits for some time before retrying). If the acquisition succeeded, one then processes the transition action and produces the output tokens, before retrying the whole cycle.
Let us now consider the case of free-choice nets [10], or their extended and weighted version called equal conflict nets [17] (see Appendix A.2 and Fig. 3 left). Here, there possibly are conflicts but they may be solved freely. We may then define an equivalence \(t\sim u \iff {}^\bullet t\cap {}^\bullet u\ne \emptyset \) between transitions, and consider its equivalence classes, called clusters, i.e., the sets of transitions sharing their input places. In a distributed implementation, for each cluster, we may introduce a new process to check the availability of the needed resources (it behaves like in a choice-free net since its input places are not shared); when it works, it produces a single token in an intermediate place (with all the hidden information of the absorbed tokens, if any) which is simply shared by the transitions in the cluster, hence may be implemented as in a join-free net. We thus have a mixture of a choice-free net and a join-free one. This is illustrated in Fig. 3.
2 Introduction: Persistence Issue
A well-known [16] feature of CF-systems is the persistence of their reachability graph, meaning that a label, once firable, remains firable forever till fired (see Appendix A.1). Indeed, suppose that in the reachability graph of a choice-free net system there are a state s and two edge labels \(a\ne b\) such that \(s\,{\mathop {\rightarrow }\limits ^{a}}\,s_1\) and \(s\,{\mathop {\rightarrow }\limits ^{b}}\,s_2\) for two states \(s_1\) and \(s_2\). By the CF property, a and b have no common input place, so that, by the firing rule, firing a cannot disable b and firing b cannot disable a. Hence \(s\,{\mathop {\rightarrow }\limits ^{a}}\,s_1\,{\mathop {\rightarrow }\limits ^{b}}\,s_1'\) and \(s\,{\mathop {\rightarrow }\limits ^{b}}\,s_2\,{\mathop {\rightarrow }\limits ^{a}}\,s_2'\) for states \(s_1',s_2'\). Moreover, \(s_1'=s_2'\) by \(\varPsi (ab)=\varPsi (ba)\) and the fact that the effect of a firing sequence depends only on its Parikh vector. So, the reachability graph is indeed persistent.
In a Petri net, a choice between a and b is indicated structurally by the presence of a place having both a and b as output transitions. In a transition system, on the other hand, a choice may be indicated by a branching state with two or more successor states. These two notions do not coincide however, as illustrated by Fig. 4.
However, we may have a Petri net system with choice-places which nevertheless yields a persistent reachability graph. This is illustrated by Fig. 5. In the plain Petri net system \(PNS_{3}\), place \(p_3\) is a choice place between a and b. However, its reachability graph is isomorphic to \(TS_{3}\), which is persistent (in a trivial way: there is no choice at all). This is due to the fact that, when a is enabled, b is not, and when b is enabled a is not. \(PNS_{3}\) is not the only Petri net solving \(TS_{3}\): \(PNS'_{3}\) is also a solution, and this one is a (non-plain) choice-free net system (it may happen alas, that a persistent transition system is solved by a non-choice-free Petri net system but by no choice-free one: see for instance Figs. 12 and 13 below). There is a difference between these two solutions as to persistence however. If we add an initial token in \(p_1\), a and b are initially enabled, but a disables b and b disables a, so that \(PNS_{3}\) loses its persistence: its persistence is due to a very specific choice of the initial marking. On the contrary, \(PNS'_{3}\) remains persistent, whatever its initial marking: its persistence is due to the underlying net, which is choice-free.
This remark may be related to a rather general property.
Proposition 1
If a pure Petri net presents a choice-place, then there is an initial marking generating a non-persistent reachability graph. This is never the case for a choice-free net.
Proof
Let p be a choice-place in the considered Petri net and let \(w=\max _{t\in p^\bullet }\{F(p,t)\}\). Assume we put initially w tokens in p. Initially, all the output transitions of p are enabled, but if \(F(p,t)=w\), t is no longer enabled after another output transition of p is fired since the net is assumed to be pure. Hence the claim.
If there is no choice-place, the argument given above is valid and all the reachable markings yield diamonds if they enable more than one transition.

If a choice-place presents side-conditions, the previous proposition may be wrong, as shown in Fig. 6: \( PN _4\) is plain but has a choice place \(p_1\) and side conditions between the latter and a, b. If \(p_1\) gets a token, a and b will permanently be enabled, forming (a degenerate kind of) diamonds. However, this does not resist to a splitting of the conflicting transitions into a “check and gather” phase and a “process and produce” phase, as detailed in the previous section and illustrated by the pure Petri net \( PN '_4\) in the same figure. This does not happen with choice-free nets, where the split transforms the net into a pure one, still choice-free (or does not modify the net if we only apply the splitting to conflicting transitions).
3 Simultaneous Choice-Free Synthesis: Preliminary Phase
A generalisation of the synthesis problem, called the simultaneous synthesis problem, has been introduced in [9]. It consists in considering several transition systems \(\{ TS _1,\ldots , TS _m\}\) simultaneously, and in search for a single Petri net N (of some class) together with m initial markings \(\{M_{0,1},\ldots ,M_{0,m}\}\) such that the reachability graph of \((N,M_{0,i})\) is isomorphic to \( TS _i\) for each \(i\in \{1,\ldots ,m\}\). The classic synthesis corresponds to the case \(m=1\), and an example with \(m=2\) is shown in Fig. 7. With a single token on p, \( PN _{5}\) solves \( TS _{5,1}\). Without tokens on p, \( PN _{5}\) solves \( TS _{5,2}\). By contrast, \( TS _{5,1}\) and \(TS'_{5,2}\) can be CF-solved individually, but not simultaneously.
The simultaneous solvability of m transition systems can be reduced to the solvability of a single one by adding a single artificial initial state with m arcs with fresh labels to the m given initial states \(\imath _1,\ldots ,\imath _m\). Solving the augmented transition system and dropping the added auxiliary transitions yields a simultaneous solution, with the various initial markings provided by the markings corresponding to the \(\imath _i\)’s; and conversely, if there is a simultaneous solution, it may be obtained that way.
Such a straightforward approach amounts, however, to consider a large input lts, and we already mentioned that the performance of synthesis procedures is very sensitive to the size of the state space, hence this is not very effective. Also, it fails to preserve the choice-freeness of the underlying unmarked Petri net if \(m\ge 2\), and cannot, therefore, be applied to CF-solvability.
Fortunately, the simultaneous choice-free synthesis may be related to m separate standard but slightly augmented choice-free syntheses.
Let T be the set of all the labels occurring in the various \( TS _i\)’s; this will be the set of transitions in any solution to the simultaneous synthesis. Let also \(\mathcal G_i\) be the set of (T-)Parikh vectors of all the small cycles occurring in \( TS _i\), and \(\mathcal G=\cup _i \mathcal G_i\). An augmented synthesis is a synthesis of some \( TS _i\) which is compatible with all the members of \(\mathcal G\), i.e., which reproduces the markings of all places along all the (small) cycles (not only the ones present in \( TS _i\); this only depends on \(\mathcal G\)). We then have:
Theorem 1
[9] A simultaneous choice-free synthesis problem is solvable if each of its augmented individual synthesis problems is, and the solution may be obtained easily by aggregating all those individual solutions.

Like for the classic choice-free synthesis problem (as well as many other targeted synthesis problems [6]), the synthesis procedure may be separated into a pre-synthesis and a proper synthesis. The pre-synthesis allows to quickly check properties of the structure of the reachability graph(s), from the structure of the class of nets aimed for. If this fails, we avoid a lengthy computation of the places of a tentative solution, get a better intuition about the true causes of the failure, hence are able to produce better error messages.
For this first phase, a series of checks arising from the analysis of choice-free systems, has been elaborated in [9], mainly based on the following observation [16]:
Theorem 2
In the reachability graph of a choice-free system, the Parikh vector of any small cycle (if any) is a minimal semiflow of the underlying net.

This links a behavioural property (on small cycles, from some initial marking) and a structural one (on semiflows of the unmarked net). It also explains why, in a simultaneous synthesis problem, we have to consider the small cycles in all the given transition systems together.
These checks may be summarised as follows:
-
1.
General: Each (finite) \(TS_i\) must be deterministic, totally reachable and persistent.
-
2.
The small cycles property: All the members of \(\mathcal G\) must be prime (no common nontrivial divisor) and two different members must be disjoint.
-
3.
The short distance property: For each state \(s_i\) of each \( TS _i\), all the shortest paths from \(\imath _i\) to \(s_i\) have the same Parikh vector, called the distance \(\varDelta _{s_i}\) to \(s_i\), and none of those distances may dominate a member of \(\mathcal G\).
-
4.
The reduced distance property: For the next checks we need the notion of residue of a T-vector \(\mu \) by another one \(\nu \) which builds the T-vector
 in such a way that
in such a way that 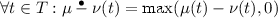 ; then, for each \(i\in \{1,\ldots ,m\}\), state \(s_i\) in \( TS _i\) and member \(\varPhi \in \mathcal G\), there must be a state \(r_i\) in \( TS _i\) such that
; then, for each \(i\in \{1,\ldots ,m\}\), state \(s_i\) in \( TS _i\) and member \(\varPhi \in \mathcal G\), there must be a state \(r_i\) in \( TS _i\) such that  .
. -
5.
The earliest Parikh cycles property: For any member \(\varUpsilon \in \mathcal G\) and state s in some \( TS _i\) with a (small) cycle around s with Parikh vector \(\varUpsilon \) and member \(\varPhi \in \mathcal G\) disjoint from \(\varUpsilon \), there is a cycle with Parikh vector \(\varUpsilon \) around the (unique) state in \( TS _i\) at distance
 (which exists by the previous property).Footnote 3
(which exists by the previous property).Footnote 3
For instance, Condition 2 is not valid in \( TS _{6}\) (Fig. 8) since the (small) cycle \(\imath [aabbcc\rangle \imath \) has Parikh vector (2, 2, 2), which is not prime.
Condition 3 is not valid in \( TS _{7}\) since there are two short paths \(\imath {\mathop {\rightarrow }\limits ^{bac}}s\) and \(\imath {\mathop {\rightarrow }\limits ^{dae}}s\) whose Parikh vectors differ, so that the distance from \(\imath \) to s is not defined here (also, they dominate \(\varPsi (bc)\) and \(\varPsi (de)\), respectively, which are small cycles in \( TS _{7}\)); it is not valid either for the pair \( TS _{5,1}\)–\(TS'_{5,2}\) in Fig. 7, since there is a short path \(\imath _2'{\mathop {\rightarrow }\limits ^{aba}}\) whose Parikh vector is equal to (hence dominates) the Parikh vector of the small cycle \(\imath _1{\mathop {\rightarrow }\limits ^{aab}}\imath _1\) in \( TS _{5,1}\).
Condition 4 is not valid in \( TS _{8}\) since there is a path \(\imath [abb\rangle s\) and a small cycle \(s[abc\rangle s\): if we reduce abb by abc, we get b but the latter is not enabled at \(\imath \).
The importance of Condition 5 is illustrated by the system \( TS _{9}\) in Fig. 8: it satisfies conditions 1 to 4, but not the earliest cycles property since there is a cycle ba at \(s_3\), a cycle d at \(s_2\) and \(\varDelta _{s_2}=(1,0,1,0)\), so that there should be a cycle d at distance  , i.e. at \(s_1\); hence \( TS _{9}\) (or \(\{ TS _{9}\}\)) has no choice-free solution; this is corrected in \( TS '_{9}\), which has the choice-free solution \(PN'_{9}\).
, i.e. at \(s_1\); hence \( TS _{9}\) (or \(\{ TS _{9}\}\)) has no choice-free solution; this is corrected in \( TS '_{9}\), which has the choice-free solution \(PN'_{9}\).
4 A New Criterion for the Choice-Free Simultaneous (and Individual) Synthesis
We shall now consider general paths in a transition system (see Appendix A.1) in addition to the usual directed ones. Referring to the general form of a place \( p\in {}^\bullet {x}\) in a choice-free net as illustrated in the left of Fig. 2, we shall denote \({}^{\bullet \bullet }x\setminus \{x\}\) by A(x).
Lemma 1
Co-enabling along a general path: In a choice-free net N, if \(M_1[x\rangle \), x belongs to the support of some (minimal) semiflow \(\varUpsilon \), \(M_1[\sigma \rangle M_2\) with \(\sigma \in (\pm T)^*\) and \(\forall a\in A(x):\varPsi (\sigma )(a)\ge \varPsi (\sigma )(x)\cdot \varUpsilon (a)/\varUpsilon (x)\), then \(M_2[x\rangle \).
Proof
We only need to show that \(\forall p\in {}^\bullet {x}:M_2(p)\ge M_1(p)\).
In the general form of a place \( p\in {}^\bullet {x}\) (left of Fig. 2), \(k_i=0\) if \(a_i\not \in A(x)\).
We know that \(M_2(p)=M_1(p)+\sum _{a_i\in A(x)}k_i\cdot \varPsi (\sigma )(a_i)-k\cdot \varPsi (\sigma )(x)\), and that \(k\cdot \varUpsilon (x)=\sum _{a_i\in A(x)}k_i\cdot \varUpsilon (a_i)\).
Hence, \(M_2(p)=M_1(p)+\sum _{a_i\in A(x)}k_i\cdot [\varPsi (\sigma )(a_i)-\varPsi (\sigma )(x)\cdot \varUpsilon (a_i)/\varUpsilon (x)]\). The claimed property arises, since no \(k_i\) is negative.

This may be interpreted as follows: if there is a general path \(\sigma \) from some marking \(M_1\) to some marking \(M_2\), and some (possibly fractional, possibly negative) factor \(f\in \mathbb {Q}\) such that \(\varPsi (\sigma )\ge f\cdot \varUpsilon \) on A(x), with \(f=\varPsi (\sigma )(x)/\varUpsilon (x)\) (or \(\varPsi (\sigma )(x)=f\cdot \varUpsilon (x)\)), then \(M_1[x\rangle \Rightarrow M_2[x\rangle \), i.e., we have a kind of co-enabling of x.
If we do not know exactly A(x), we may use any over-approximation:
Corollary 1
In a choice-free net N, if \(M_1[x\rangle \), x belongs to the support of some (minimal) semiflow \(\varUpsilon \), \(A(x)\subseteq A_x\) for some set \(A_x\subseteq T\), \(M_1[\sigma \rangle M_2\) with \(\sigma \in (\pm T)^*\) and \(\forall a\in A_x:\varPsi (\sigma )(a)\ge \varPsi (\sigma )(x)\cdot \varUpsilon (a)/\varUpsilon (x)\), then \(M_2[x\rangle \).

Note that the satisfaction of the constraint on a in this property relies on the sign of \(\varPsi (\sigma )(x)\), i.e. of f, and of the membership of a to the support of \(\varUpsilon \):
-
if \(\varUpsilon (a)=0\), we need \(\varPsi (\sigma )(a)\ge 0\), otherwise
-
if \(\varPsi (\sigma )(x)>0\) (or \(f>0\)) and \(\varPsi (\sigma )(a)\le 0\), the constraint is not satisfied; if \(\varPsi (\sigma )(a)>0\), one needs \(\varPsi (\sigma )(a)\ge f\cdot \varUpsilon (a)\);
-
if \(\varPsi (\sigma )(x)<0\) (or \(f<0\)) and \(\varPsi (\sigma )(a)\ge 0\), the constraint is satisfied; if \(\varPsi (\sigma )(a)<0\), one needs \(|\varPsi (\sigma )(a)|\le |f|\cdot \varUpsilon (a)\);
-
if \(\varPsi (\sigma )(x)=0=f\) and \(\varPsi (\sigma )(a)\ge 0\), the constraint is satisfied; if \(\varPsi (\sigma )(a)<0\), the constraint is not satisfied.
Definition 1
In a simultaneous choice-free synthesis problem, if \(\varUpsilon \in \mathcal G\) we shall denote by \(T_\varUpsilon \) the support of \(\varUpsilon \), and if x belongs to the support of \(\varUpsilon \) we also denote \(T_x=T_\varUpsilon \).
We shall also denote by \(T_0\) the set of labels in T not belonging to the support of some member of \(\mathcal G\), i.e., \(T_0=T\setminus \cup _{\varUpsilon \in \mathcal G}T_\varUpsilon \).

Proposition 2
In a simultaneous choice-free synthesis problem, if x belongs to the support of some \(\varUpsilon \in \mathcal G\), \(s[x\rangle \) and \(\lnot s'[x\rangle \) in some \( TS _\ell \), if \(\forall a\in T_0\cup T_x:(\varDelta _{s'}-\varDelta _s)(a)\ge (\varDelta _{s'}-\varDelta _s)(x)\cdot \varUpsilon (a)/\varUpsilon (x)\), then the problem is not solvable.
Proof
If there is a solution N, from Theorem 2, \(\varUpsilon \) is a minimal semiflow of N.
For any i, if \(a_i\) belongs to the support of some \(\varUpsilon '\in \mathcal G\setminus \{\varUpsilon \}\), we have that x does not belong to the support of \(\varUpsilon '\), from the small cycles property above.
From the definition of semiflows, we must have \(\sum _j \varUpsilon '(a_j)\cdot k_j=k\cdot \varUpsilon '(x)=0\), hence \(k_i=0\). As a consequence we may state that \(A(x)\subseteq T_0\cup T_x\) (we do not have equality since it may happen that \(k_i=0\) while \(a_i\not \in T_0\cup T_x\)).
Let \(\sigma _s\) be a short path from \(\imath _\ell \) to s, and similarly for \(s'\). \((-\sigma _s)(\sigma _{s'})\) is a general path from s to \(s'\) in \( TS _\ell \), and \(\varPsi ((-\sigma _s)(\sigma _{s'}))=\varDelta _{s'}-\varDelta _s\), from the short distance property above.
The proposition then results from Corollary 1, where we may choose \(A_x=T_0\cup T_x\).

In this proposition, we used a special g-path from s to \(s'\), and we could wonder if choosing another one would lead to another condition. We shall now see that this is not the case.
Lemma 2
If, in a simultaneous choice-free synthesis problem, conditions 1 to 5 are satisfied, for each g-cycle \(s[\sigma \rangle s\) in any \( TS _\ell \) (\(\sigma \in (\pm T_\ell )^*\)), we have \(\varPsi (\sigma )=\sum _{\varUpsilon \in \mathcal G_\ell }z_\varUpsilon \cdot \varUpsilon \), for some coefficients \(z_\varUpsilon \in \mathbb {Z}\).
Proof
First, we may observe that each transition system \( TS _\ell \) is weakly periodic. Indeed, if \(s_1{\mathop {\rightarrow }\limits ^{\sigma }}s_2{\mathop {\rightarrow }\limits ^{\sigma }}s_3{\mathop {\rightarrow }\limits ^{\sigma }}s_4{\mathop {\rightarrow }\limits ^{\sigma }}\ldots \), since \( TS _\ell \) is finite, we must have \(s_i=s_j\) for some \(i<j\), hence a cycle \(s_i[\sigma ^{j-i}\rangle s_i\). In a finite, totally reachable, deterministic and persistent system, from Corollary 2 in [8] we have \(\varPsi (\sigma ^{j-i})=(j-i)\cdot \varPsi (\sigma )=\sum _{\varUpsilon \in \mathcal G_\ell }k_\varUpsilon \cdot \varUpsilon \) for some coefficients \(k_\varUpsilon \in \mathbb {N}\). Since, the \(\varUpsilon \)’s are prime and disjoint, \((j-i)\) must divide the \(k_\varUpsilon \in \mathbb {N}\) and \(\varPsi (\sigma )=\sum _{\varUpsilon \in \mathcal G_\ell }k'_\varUpsilon \cdot \varUpsilon \) for some coefficients \(k'_\varUpsilon \in \mathbb {N}\). Then, from the properties of distances in [9], we know that \(\varDelta _{s_2}=\varDelta _{s_1}\) and \(s_1=s_2\).
The claimed property then results from Lemma 4 in [7], which states that general cycles are generated by directed ones when the previous properties are satisfied.

Corollary 2
If, in a simultaneous choice-free synthesis problem, conditions 1 to 5 are satisfied, two g-paths \(\sigma \) and \(\sigma '\) go from s to \(s'\) in \( TS _\ell \), and x belongs to the support of some \(\varUpsilon \in \mathcal G\), then \(\forall a\in T_0\cup T_x:\varPsi (\sigma )(a)\ge \varPsi (\sigma )(x)\cdot \varUpsilon (a)/\varUpsilon (x)\iff \varPsi (\sigma ')(a)\ge \varPsi (\sigma ')(x)\cdot \varUpsilon (a)/\varUpsilon (x)\).
Proof
Since \(s'[(-\!\sigma )(\sigma ')\rangle s'\) is a g-cycle around \(s'\), from Lemma 2, we know that \(\varPsi (\sigma ')=\varPsi (\sigma )+\sum _{\varUpsilon '\in \mathcal G_\ell }z_{\varUpsilon '}\cdot \varUpsilon '\). In particular, from condition 2, that implies \(\varPsi (\sigma ')(x)=\varPsi (\sigma )(x)+z_{\varUpsilon }\cdot \varUpsilon (x)\).
From Proposition 2, we only have to consider \(a\in T_0\cup T_x\).
If a belongs to the support of \(\varUpsilon \), hence to \(T_x\), \(\varPsi (\sigma ')(a)=\varPsi (\sigma )(a)+z_{\varUpsilon }\cdot \varUpsilon (a)\). Since \(z_{\varUpsilon }\cdot \varUpsilon (a)=z_{\varUpsilon }\cdot \varUpsilon (x)\cdot \varUpsilon (a)/\varUpsilon (x)\), we then have the claimed equivalence.
If a belongs to \(T_0\), \(\varPsi (\sigma ')(a)=\varPsi (\sigma )(a)\) and \(\varUpsilon (a)=0\), which again leads to the claimed equivalence.

This corollary immediately leads to the main result of the present paper, a new pre-synthesis condition that may be added to the five ones we already listed for the simultaneous or individual choice-free synthesis (we shall later see that this new condition is not implied by the other ones):
-
6 Co-enabling: For any \(\varUpsilon \in \mathcal G\) and x in its support, for any \( TS _i\) and \(s,s'\in S_i\), if \(s[x\rangle \) and \(\forall a\in T_0\,\cup \,T_x:(\varDelta _{s'}-\varDelta _s)(a)\ge (\varDelta _{s'}-\varDelta _s)(x)\cdot \varUpsilon (a)/\varUpsilon (x)\), then \(s'[x\rangle \).
Two special cases may then be distinguished, corresponding to the cases where \(s'\) occurs before or after s, i.e., that \(s'[\sigma \rangle s\) or \(s[\sigma \rangle s'\) for a directed path \(\sigma \) (but we may have both cases simultaneously):
Corollary 3
Forward fractional reduction: In a choice-free net N, if \(M[\sigma ' t \rangle \) with \(\sigma '\in T^*\) and, for some \(f\in \mathbb {Q}_{>0}\) and semiflow \(\varUpsilon \), \(\varPsi (\sigma ')\le f\cdot \varUpsilon \) and \(\varPsi (\sigma ')(t) = f\cdot \varUpsilon (t)\), then \(M[t\rangle \).
Proof
In this case, we may apply Lemma 1 with \(M_2=M\), \(\sigma =-\sigma '\) and \(\varPsi (\sigma )\le \mathbf {0}\), hence the claim.

From this result, we deduce the following criterion for non-choice-free-solvability.
Corollary 4
Forward fractional reduction in a pre-synthesis: Let \( TS =(S,T,\rightarrow ,\imath )\) be a deterministic and persistent labelled transition system, \(s\in [\imath \rangle \), \(t\in T\), \(\sigma \in T^*\), \(f\in \mathbb {Q}_{>0}\) and \(\varUpsilon \) be any T-vector. If \(\lnot s[t\rangle \), \(s[\sigma t\rangle \), \(\varPsi (\sigma )\le f\cdot \varUpsilon \) and \(\varPsi (\sigma )(t) = f\cdot \varUpsilon (t)\), then there is no choice-free solution of \( TS \) with semiflow \(\varUpsilon \).
Applying these results, the two systems \( TS _{10}, TS _{11}\) in Fig. 9 do not allow a simultaneous choice-free solution. Indeed, \( TS _{11}\) determines a semiflow (3, 2), hence also a fractional semiflow (3/2, 1). With \(s=\imath _1\), \(\sigma =ab\), \(t=b\), \(\varUpsilon =(3,2)\) and \(f=1/2\), since we do not have \(\imath _1[b\rangle \), we may conclude there is no simultaneous choice-free-solution.
This is also true for the two systems \( TS _{11}, TS _{12}\): applying Corollary 3 with \(\imath _3[a\rangle s'\), \(s=s'\), \(\sigma =ab\), \(t=b\), \(\varUpsilon =(3,2)\) and \(f=1/2\), since we do not have \(s'[b\rangle \), we may conclude there is no simultaneous choice-free-solution.
Since these two pairs of systems satisfy conditions 1 to 5, this also shows the independence of condition 6: this last condition is not implied by the other ones.
There is also the symmetric version of those last two Corollaries.
Corollary 5
Backward fractional reduction: In a choice-free net N, if \(M[t\rangle \) and \(M[\sigma '\rangle \) with \(\sigma '\in T^*\) and, for some \(f\in \mathbb {Q}_{>0}\) and semiflow \(\varUpsilon \), \(\varPsi (\sigma ')\le f\cdot \varUpsilon \) and \(\varPsi (\sigma ')(t) = f\cdot \varUpsilon (t)\), then \(M[\sigma ' t\rangle \).
Proof
In this case, we may apply Lemma 1 with \(M_1=M\), \(\sigma =\sigma '\) and \(\varPsi (\sigma )\ge \mathbf {0}\), hence the claim.

Corollary 6
Backward fractional reduction in a pre-synthesis: Let \( TS =(S,T,\rightarrow ,\imath )\) be a deterministic and persistent labelled transition system, \(s\in [\imath \rangle \), \(t\in T\), \(\sigma \in T^*\), \(f\in \mathbb {Q}_{>0}\) and \(\varUpsilon \) be any T-vector. If \( s[t\rangle \), \(s[\sigma \rangle \), \(\varPsi (\sigma )\ge f\cdot \varUpsilon \), \(\varPsi (\sigma )(t) = f\cdot \varUpsilon (t)\) and \(\lnot s[\sigma t \rangle \), then there is no choice-free-solution of \( TS \) with semiflow \(\varUpsilon \).
Applying these results, we get that the two systems in Fig. 10, are not simultaneously choice-free-solvable either. Indeed, in \( TS _{13}\) we have the minimal semiflow \(\varUpsilon =(3,2)\); in \( TS _{14}\), we have \(\imath _{12}[b\rangle \), \(\imath _4[aab\rangle \), \(\varPsi (aab)=(2,1)\), so that with \(f=1/2\) and \(t=b\), from Corollary 6 we should have \(\imath _{12}[aabb\rangle \).
The two systems in Fig. 11, are not simultaneously choice-free-solvable either. Indeed, in \( TS _{16}\) we have the minimal semiflow \(\varUpsilon =(3,2)\); in \( TS _{15}\), we have \(\imath _{13}[b\rangle \), \(\imath _{13}[baa\rangle \), \(\varPsi (baa)=(2,1)\), so that with \(f=1/2\) and \(t=b\), from Corollary 6 we should have \(\imath _{13}[baab\rangle \).
5 But Still, Our Conditions Are Not Sufficient
Now that we accumulated several structural properties of reachability graphs of bounded choice-free systems, and devised corresponding checks to be performed during the (simultaneous) pre-synthesis, we may wonder if they are sufficient to ascertain the existence of a solution, at least in some interesting subclasses of problems.
Since most of these properties concern the small cycles, they are of no help for acyclic transition systems. Let us then restrict our attention to a single (\(m=1\)) reversible system, since then there are small cycles around each state (we mentioned before that cycles are transported Parikh-equivalently along the flow in finite deterministic and persistent systems). We shall also assume that all small cycles have the same Parikh vector, and that there is at least a (non-necessarily choice-free) solution. However, even in these very specific class of systems, there is not always a choice-free solution. We shall give two different counter-examples.
The first one, illustrated in Fig. 12, has already been used in [3]. It has five labels and is remarkable by its small cycles, that all have the Parikh vector \(\mathbf{1}=(1,1,1,1,1)\) (so that fractional semiflows do not introduce any additional constraint since at least one of the components must be an integer: \(f\cdot \varUpsilon (t)\) must count the number of occurrences of t in some path). It has a (non-choice-free) Petri net solution, but not a choice-free one: the numerical construction of the proper synthesis phase (for instance with the use of the APT tool [14]) finds an unsolvable ESSP problem.
The next transition system has four labels, and has a unique small cycle with Parikh vector (5, 3, 1, 1), hence has the form of a simple circle. Here too it has a non-choice-free solution, but no choice-free one (again found by APT). It is illustrated by Fig. 13.
Both counterexamples share the additional condition that they have a Petri net solution. We may then wonder what happens if we still reinforce this condition, in the following way. Let us assume that \(m>1\), that each \( TS _i\) is individually choice-free solvable (not only Petri net-solvable), and reversible, that all the small cycles have the same Parikh vector and that all conditions 1 to 6 are satisfied. Is it still possible that the simultaneous choice-free synthesis fails? Presently, we do not know and we are working on it.
6 Concluding Remarks
We added a new structural criterion to the already long list of available necessary conditions for a labelled transition system to have a bounded choice-free solution. This allows to quickly rule out more inadequate (simultaneous) synthesis problems. However, we are still not in reach of a necessary and sufficient set of criteria fully characterising the state spaces of choice-free systems, in the style of the conditions developed for (bounded or unbounded) marked graphs and T-systems in [2, 4, 5].
Notes
- 1.
Those that would not be familiar with the domain are referred to the Appendix and the Introduction sections.
- 2.
A bit like in a “test and set” instruction, which allow multiprocessors to neatly manage their common memory resource.
- 3.
It is known [1] that in a finite deterministic and persistent transition system, loops are forward Parikh-equivalently transported (in the sense that, if there is a loop \(s[\tau \rangle s\) and a directed path \(s[\sigma \rangle s'\), then there is a loop \(s'[\phi \rangle s'\) with \(\varPsi (\phi )=\varPsi (\tau )\)). The earliest Parikh cycles property means they may also be backward transported, up to some extent.
- 4.
Note that enabledness refers only to outgoing edges and reachability refers only to directed paths, rather than to g-paths.
- 5.
In this paper, whenever we speak of a path or a cycle, a directed path or cycle is meant.
References
Best, E., Darondeau, P.: A decomposition theorem for finite persistent transition systems. Acta Informatica 46, 237–254 (2009). https://doi.org/10.1007/s00236-009-0095-6
Best, E., Devillers, R.: Characterisation of the state spaces of live and bounded marked graph Petri nets. In: Dediu, A.-H., Martín-Vide, C., Sierra-Rodríguez, J.-L., Truthe, B. (eds.) LATA 2014. LNCS, vol. 8370, pp. 161–172. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04921-2_13
Best, E., Devillers, R.: Synthesis of live and bounded persistent systems. Fundamenta Informaticae 140(1), 39–59 (2015)
Best, E., Devillers, R.: State space axioms for T-systems. Acta Informatica 52(2–3), 133–152 (2015). https://doi.org/10.1007/s00236-015-0219-0. In: Lüttgen, G., Corradini, F. (eds.) Special Volume on the Occasion of Walter Vogler’s 60th Birthday
Best, E., Devillers, R.: Characterisation of the state spaces of marked graph Petri nets. Inf. Comput. 253, 399–410 (2017)
Best, E., Devillers, R., Erofeev, E., Wimmel, H.: Target-Oriented Petri Net Synthesis (2019, submitted paper)
Best, E., Devillers, R., Schlachter, U.: A graph-theoretical characterisation of state separation. In: Steffen, B., Baier, C., van den Brand, M., Eder, J., Hinchey, M., Margaria, T. (eds.) SOFSEM 2017. LNCS, vol. 10139, pp. 163–175. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-51963-0_13
Best, E., Devillers, R., Schlachter, U.: Bounded choice-free Petri net synthesis: algorithmic issues. Acta Informatica 55(7), 575–611 (2017). https://doi.org/10.1007/s00236-017-0310-9
Best, E., Devillers, R., Schlachter, U., Wimmel, H.: Simultaneous Petri net synthesis. Sci. Ann. Comput. Sci. 28(2), 199–236 (2018)
Desel, J., Esparza, J.: Free Choice Petri Nets. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge (1995)
Dijkstra, E.W.: The structure of “THE”-multiprogramming system. Commun. ACM 11(5), 341–346 (1968)
Hoare, C.A.R.: Monitors: an operating system structuring concept. Commun. ACM 17(10), 549–557 (1974)
Patil, S.: Circuit Implementation of Petri Nets. Computation Structures Group: Memo 73, Project MAC MIT (1972)
Schlachter, U., et al.: APT: Analysis of Petri Nets and Transition Systems. https://github.com/CvO-Theory/apt
Wimmel, H.: Presynthesis of bounded choice-free or fork-attribution nets. Inf. Comput. (2019). https://doi.org/10.1016/j.ic.2019.104482
Teruel, E., Colom, J.M., Silva Suárez, M.: Choice-free Petri nets: a model for deterministic concurrent systems with bulk services and arrivals. IEEE Trans. Systems Man Cybern. Part A 27(1), 73–83 (1997)
Teruel, E., Silva, M.: Structure theory of equal conflict systems. Theor. Comput. Sci 153(1 & 2), 271–300 (1996)
Yakovlev, A., Gomes, L., Lavagno, L. (eds.): Hardware Design and Petri Nets. Springer, Boston (2000). https://doi.org/10.1007/978-1-4757-3143-9. XII+332 p
Acknowledgements
We are indebted to the anonymous referees for their detailed and helpful remarks.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Basic Definitions
A Basic Definitions
1.1 A.1 Labelled Transition Systems
A labelled transition system with initial state, lts for short, is a quadruple \( TS =(S,T,\mathord {\rightarrow },\imath )\) where S is a set of states, T is a set of labels, \(\mathord {\rightarrow }\subseteq (S\times T\times S)\) is the set of labelled edges, and \(\imath \in S\) is an initial state. \( TS \) is finite if S and T are finite. Let \((-\!T)\) (called backward edges) be a disjoint copy of T:
A g-path is a sequence \(\sigma \in (T\cup (-\!T))^*\); it is a (directed) path if \(\sigma \in T^*\). For \(s,s'\in S\), a g-path \(\sigma =a_1\ldots a_m\) leads from s to \(s'\) (denoted by \(s{\mathop {\rightarrow }\limits ^{\sigma }}s'\)) if
\(\exists r_0,r_1,\ldots ,r_m\in S:\;s=r_0\;\;\wedge \;\;r_m=s'\)
\(\wedge \;\;\forall j\in \{1,\ldots ,m\}:\left\{ \begin{array}{ll} (r_{j-1},a_j,r_j)\in \,\rightarrow &{} \text{ if } a_j\in T \\ (r_j,a_j,r_{j-1})\in \,\rightarrow &{} \text{ if } a_j\in (-\!T){} \end{array}\right. \)
The back-arrow notation is extended to sequences in \((T\cup (-\!T))^*\) inductively as follows:
A label a is enabled at \(s\in S\), or \(s{\mathop {\rightarrow }\limits ^{a}}\) for short, if \(\exists s'\in S:s{\mathop {\rightarrow }\limits ^{a}}s'\). A state \(s'\) is reachable from state s if \(\exists \sigma \in T^*:s{\mathop {\rightarrow }\limits ^{\sigma }}s'\).Footnote 4 Sometimes, we shall use the notation \(s[t\rangle \) instead of \(s{\mathop {\rightarrow }\limits ^{a}}\), and \([s\rangle \) to denote the set of states reachable from s.
For a g-path \(\sigma \in (T\cup (-\!T))^*\), the Parikh vector of \(\sigma \) is a T-vector \(\varPsi (\sigma )\), defined inductively as follows:
For example, \(\varPsi (ab(-\!a)b(-\!c)aa)=(2,2,-1)\). Two finite sequences are Parikh-equivalent if they have the same Parikh vector, and Parikh-disjoint if no label occurs in both of them. The support of a T-vector, hence in particular of a Parikh vector, is the set of indices for which the vector is non-null.
A g-path \(s[\sigma \rangle s'\) is called a g-cycle, or more precisely a g-cycle at (or around) state s, if \(s=s'\).Footnote 5
A finite transition system \( TS =(S,T,\rightarrow ,\imath )\) is called
-
totally reachable if \(\forall s\in S\exists \sigma \in T^*:\imath {\mathop {\rightarrow }\limits ^{\sigma }}s\);
-
deterministic if, for all states \(s,s',s''\in S\), and for any label \(t\in T\), \(s{\mathop {\rightarrow }\limits ^{t}}s'\) and \(s{\mathop {\rightarrow }\limits ^{t}}s''\) imply \(s'=s''\);
-
backward deterministic if, for all states \(s,s',s''\in S\), and for any label \(t\in T\), \(s'{\mathop {\rightarrow }\limits ^{t}}s\) and \(s''{\mathop {\rightarrow }\limits ^{t}}s\) imply \(s'=s''\);
-
fully forward deterministic if, for all states \(s,s',s''\in S\) and for all sequences \(\alpha ,\alpha '\in T^*\), (\(s{\mathop {\rightarrow }\limits ^{\alpha }}s'\wedge s{\mathop {\rightarrow }\limits ^{\alpha '}}s''\wedge \varPsi (\alpha )=\varPsi (\alpha ')\)) entails \(s'=s''\);
-
weakly periodic if for every \(s_1\in S\), label sequence \(\sigma \in T^*\), and infinite sequence \(s_1{\mathop {\rightarrow }\limits ^{\sigma }}s_2{\mathop {\rightarrow }\limits ^{\sigma }}s_3{\mathop {\rightarrow }\limits ^{\sigma }}s_4{\mathop {\rightarrow }\limits ^{\sigma }}\ldots \), \(\forall i,j\ge 1:s_i=s_j\);
-
persistent if for all states \(s,s',s''\in S\), and labels \(t\ne u\), if \(s{\mathop {\rightarrow }\limits ^{t}}s'\) and \(s{\mathop {\rightarrow }\limits ^{u}}s''\), then there is some state \(r\in S\) such that \(s'{\mathop {\rightarrow }\limits ^{u}}r\) and \(s''{\mathop {\rightarrow }\limits ^{t}}r\).
-
live if \(\forall t\in T\) \(\forall s\in [s_0\rangle \) \(\exists s'\in [s\rangle \) such that \(s'[t\rangle \);
-
reversible if \(\forall s\in [s_0\rangle \), \(s_0\in [s\rangle \).
Two lts with the same label set \( TS =(S,T,\rightarrow ,\imath )\) and \( TS '=(S',T,\rightarrow ',\imath ')\) are isomorphic if there is a bijection \(\zeta :S\rightarrow S'\) with \(\zeta (\imath )=\imath '\) and \((r,t,s)\in \mathord {\rightarrow }\Leftrightarrow (\zeta (r),t,\zeta (s))\in \mathord {\rightarrow '}\), for all \(r,s\in S\) and \(t\in T\).
A cycle \(s{\mathop {\rightarrow }\limits ^{\sigma }}s\) with \(\sigma \in T^*\) is small if \(\sigma \ne \varepsilon \) and there is no cycle \(s'{\mathop {\rightarrow }\limits ^{\sigma '}}s'\) with \(\sigma '\ne \varepsilon \) and \(\varPsi (\sigma ')\lneqq \varPsi (\sigma )\) (this should not be confused with a simple cycle, not visiting twice any state). A cycle \(s[\sigma \rangle s\) is prime if the greatest common divisor of the entries in its Parikh vector is 1. A (directed) path \(s[\sigma \rangle s'\) is short if there is no other path between the same states with a smaller Parikh vector: \(s[\sigma '\rangle s'\Rightarrow \lnot (\varPsi (\sigma ')\lneqq \varPsi (\sigma ))\).
1.2 A.2 Petri Nets
A (finite, place-transition, arc-weighted) Petri net is a triple \( PN \!=\!(P,T,F)\) such that P is a finite set of places, T is a finite set of transitions, with \(P\cap T=\emptyset \), F is a flow function \(F:((P\times T)\cup (T\times P))\rightarrow \mathbb {N}\).
The predecessors of a node x is the set \({}^\bullet x=\{y|F(y,x)>0\}\). Symmetrically its successor set is \(x^\bullet =\{y|F(x,y)>0\}\). The incidence matrix C of a Petri net is the integer place-transition matrix with components \(C(p,t)=F(t,p)-F(p,t)\), where p is a place and t is a transition. An elementary property of Petri nets is the state equation which expresses that, if \(M[\sigma \rangle M'\), then \(M'=M+C\cdot \varPsi (\sigma )\). A semiflow of a net N is a T-vector \(\varPhi \) such that \(\varPhi \gneqq \mathbf {0}\) and \(C\cdot \varPhi =\mathbf {0}\). A semiflow is minimal if there is no smaller one.
\( PN \) is plain if no arc weight exceeds 1; pure if \(\forall p\in P:(p^\bullet \,{\cap }\,{}^\bullet p)=\emptyset \); choice-free if \(\forall p\in P:|p^\bullet |\le 1\); join-free if \(\forall t\in T:|{}^\bullet {}t|\le 1\); fork-attribution if choice-free and, in addition, \(\forall t\in T:|{}^\bullet t|\le 1\); a marked graph if \( PN \) is plain and \(|p^\bullet |=1\) and \(|{}^\bullet p|=1\) for all places \(p\in P\); and a T-system if \( PN \) is plain and \(|p^\bullet |\le 1\) and \(|{}^\bullet p|\le 1\) for all places \(p\in P\); free-choice if it is plain and \(\forall t,t'\in T:{}^\bullet t\,\,\cap \,{}^\bullet t'\ne \emptyset \Rightarrow {}^\bullet t={}^\bullet t'\); equal conflict if \(\forall t,t'\in T:{}^\bullet t\,\cap \,{}^\bullet t'\ne \emptyset \Rightarrow \forall p\in P: F(p,t)=F(p,t')\).
A marking is a mapping \(M:P\rightarrow \mathbb {N}\), indicating the number of (black) tokens in each place. A Petri net system is a net provided with an initial marking \((P,T,F,M_0)\); the subclasses defined above for Petri nets extend immediately for Petri net systems. A transition \(t\in T\) is enabled by a marking M, denoted by \(M{\mathop {\rightarrow }\limits ^{t}}\), if for all places \(p\in P\), \(M(p)\ge F(p,t)\). If t is enabled at M, then t can occur (or fire) in M, leading to the marking \(M'\) defined by \(M'(p)=M(p)-F(p,t)+F(t,p)\) and denoted by \(M{\mathop {\rightarrow }\limits ^{t}}M'\). The reachability graph of \( PN \) is the labelled transition system whose initial state is \(M_0\), whose vertices are the reachable markings, and whose edges are \(\{(M,t,M')\mid M{\mathop {\rightarrow }\limits ^{t}}M'\}\). A Petri net system \((P,T,F,M_0)\) is k-bounded for some fixed \(k\in \mathbb {N}\), if \(\forall M\in [M_0\rangle \forall p\in P:M(p)\le k\); bounded if \(\exists k\in \mathbb {N}:N \text{ is } k\text{-bounded }\); and safe if it is 1-bounded. Properties of transition systems extend immediately to Petri net systems through their reachability graphs.
A labelled transition system is PN-solvable if it is isomorphic to the reachability graph of a Petri net system (called the solution); it is CF-solvable if there is a choice-free solution.
1.3 A.3 Regions
When linking transition systems and Petri nets, it is useful to introduce regions.
A region \((\rho ,\mathbb {B},\mathbb {F})\) is a triple of functions \(\rho \) (from states to \(\mathbb {N}\)), and \(\mathbb {B},\mathbb {F}\) (both from labels to \(\mathbb {N}\)), satisfying the property that for any states \(s,s'\) and label a:
since this is the typical behaviour of a place p with token count \(\rho \) during the firing of a with backward and forward connections \(\mathbb {B},\mathbb {F}\) to p (anywhere in \( TS \)). To solve an \(\text {SSP}(s_1,s_2)\) (for State Separation Problem, where \(s_1\ne s_2\)), we need to find an appropriate region \((\rho ,\mathbb {B},\mathbb {F})\) satisfying \(\rho (s_1)\ne \rho (s_2)\), i.e., separating states \(s_1\) and \(s_2\). For an \(\text {ESSP}(s,a)\) (for Event-State Separation Problem, where e is not enabled at s), we need to find a region \((\rho ,\mathbb {B},\mathbb {F})\) with \(\rho (s)<\mathbb {B}(a)\). This can be done by solving suitable systems of linear inequalities which arise from these two requirements, and from the requirement that regions not be too restrictive. If such a system can be solved, an appropriate place has been found, otherwise there does not exist any and \( TS \) is unsolvable.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Best, E., Devillers, R., Erofeev, E. (2020). A New Property of Choice-Free Petri Net Systems. In: Janicki, R., Sidorova, N., Chatain, T. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2020. Lecture Notes in Computer Science(), vol 12152. Springer, Cham. https://doi.org/10.1007/978-3-030-51831-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-51831-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51830-1
Online ISBN: 978-3-030-51831-8
eBook Packages: Computer ScienceComputer Science (R0)









 in such a way that
in such a way that 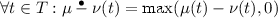 ; then, for each
; then, for each  .
. (which exists by the previous property).
(which exists by the previous property).




