Abstract
Two sorts of circular traffic systems are defined and their minimal length of recurrent transition sequences is computed. The result is used for finding cycloids that have an isomorphic reachability graph. Cycloids are particular Petri nets for modelling processes of actions or events, belonging to the fundaments of Petri’s general systems theory. They have very different interpretations, ranging from Einstein’s relativity theory to elementary information processing gates. The cycloid representation of circular traffic systems allows to identify basic synchronisation mechanisms and leads to a structure theory of such systems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Queues of traffic items like cars, trains, aircrafts, production goods, computer tasks or electronic particles are widespread instances of dynamical systems. Therefore they have been frequently used to illustrate the modelling by Petri nets. Petri himself usually introduced the concept of coordination and synchronization by the regimen or organization rule for people carrying buckets to extinguish a fire [4] or by cars driving in line on a road with varying distances. As Petri always followed the principle of discrete modelling, resulting in finite structures, he defined cycloids by folding such structures with respect to space and time. Cyloids define a subclass of partial cyclic orders and hence generalize the well known token ring structure (a total cyclic order) that is at the core of many solutions to the distributed mutual exclusion problem. This also includes virtual token rings that have been employed in group communication middleware (e.g. the Spread system). Hence, we conjecture that cycloids could more generally play a role as coordination models in new middleware architectures. Another potential application of cycloids might be their use as parallel data flow models for iterative computations. Such data flow models can be directly implemented in hardware (e.g. as systolic arrays) or in a combination of hardware and software, for example on many-core architectures like graphics processing units (GPUs) that are attracting a lot of interest for stream processing and machine learning applications. While Petri introduced cycloids in [4], a more formal definition has been given in [2, 7] and [9]. As a consequence of this formalization some properties could be derived, leading for instance to a synthesis procedure based on observable parameters of the cycloid net, among which is the length of a minimal cycle. However, the concrete structure of a circular traffic queue given by a definite number of c traffic items and g gap instances is not known. In this article two different such systems are defined as transition systems \(tq\text {-}1(c,g)\) and \(tq\text {-}2(c,g)\). For finding the behaviour equivalent cycloids the synthesis theorem from [7] and [9] is used. It requires the number of cycloid transitions, which is computed by the length of recurrent transition sequences of the circular traffic queues in Sect. 2. Also the minimal length cyc of cycles is needed in this theorem. To find it out a particular sequence of c transitions, called release message chain, is introduced, which is the most important synchronisation mechanism of the model. The release message chain is extended to a release message cycle. The length rm of the latter varies for different models and contributes to the determination of cyc. After having found these cycloids their behaviour equivalence is established by proving the isomorphism between their transition systems. Here also the release message cycle plays an important role. As an intermediate step regular cycloid systems are introduced. The obtained cycloids are related to unfoldings of coloured net models of circular traffic queues.
We recall some standard notations for set theoretical relations. If \(R\subseteq A \!\times \! B\) is a relation and \(U \subseteq A\) then \(R[U]:= \{b\,|\,\exists u \in U: (u,b)\in R\}\) is the image of U and R[a] stands for \(R[\{a\}]\). \(R^{-1}\) is the inverse relation and \(R^+\) is the transitive closure of R if \(A=B\). Also, if \(R\subseteq A \!\times \! A\) is an equivalence relation then  is the equivalence class of the quotient A/R containing a. Furthermore
is the equivalence class of the quotient A/R containing a. Furthermore  ,
,  and
and  denote the sets of positive integer, integer and real numbers, respectively. For integers: a|b if a is a factor of b. The modulo-function is used in the form \(a \,mod\,b = a - b \cdot \lfloor \frac{a}{b} \rfloor \), which also holds for negative integers
denote the sets of positive integer, integer and real numbers, respectively. For integers: a|b if a is a factor of b. The modulo-function is used in the form \(a \,mod\,b = a - b \cdot \lfloor \frac{a}{b} \rfloor \), which also holds for negative integers  . In particular, \(-a\,mod\,b = b-a\) for \(0<a\le b\). Due to naming conventions (e.g. the function ind in Definition 1), the range of the modulo-function is supposed to be \(\{1,\cdots ,b\}\) instead of \(\{0,\cdots ,b-1\}\) in some cases. In these cases however, b can be seen to be equivalent to 0.
. In particular, \(-a\,mod\,b = b-a\) for \(0<a\le b\). Due to naming conventions (e.g. the function ind in Definition 1), the range of the modulo-function is supposed to be \(\{1,\cdots ,b\}\) instead of \(\{0,\cdots ,b-1\}\) in some cases. In these cases however, b can be seen to be equivalent to 0.
The author is grateful to U. Fenske, O. Kummer, M.O. Stehr and the anonymous referees for numerous corrections and improvements.
2 Circular Traffic Queues
We define a model of circular traffic queues with two sorts of traffic items. Traffic items \(a\in C\), going from left to right, exchange their position with traffic items \(u\in G\) moving in the opposite direction. See the example after the next definition. By a transition \(\langle \!\langle t_i,a_j \rangle \!\rangle \) traffic item \(a_j\) is moved from the queue position i.
Definition 1
A circular traffic queue tq(c, g) is defined by two positive integers c and g. Implicitly with these integers we consider two finite and disjoint sets of traffic items \(C = \{a_1,\cdots ,a_c\}\) and \(G = \{u_1,\cdots ,u_g\}\) with cardinalities c and g, respectively. A state is a bijective index function \(ind: \{1,\cdots ,n\} \rightarrow C \cup G\), hence \(c+g=n\). The labelled transition system \(LTS(c,g) = (States,T,tr,ind_0)\) of tq(c, g) is defined by a set States of states, a set of transitions \(T = \{ \langle \!\langle t_i,a_j\rangle \!\rangle | 1 \le i \le n,1 \le j \le c \}\), a transition relation tr and a regular initial state \(ind_0\). The regular initial state is given by \(ind_0(i) = a_i\) for \(1 \le i \le c\) and \(ind_0(i) = g_{i-c}\) for \(c < i \le n\). The transition relation \(tr \subseteq States \times T \times States \;\) is defined by
This is written as \(ind_1 \!\!\!\! {\mathop {\longrightarrow }\limits ^{\langle \!\langle t_i,a_j\rangle \!\rangle }} \!\!\! ind_2\) or \(ind_1 \! \rightarrow ind_2\). A transition sequence \(ind_0\rightarrow ind_1 \rightarrow \cdots \rightarrow ind_0\) of minimal length, leading from the initial state \(ind_0\) back to \(ind_0\) is called a recurrent sequence. As usual \(ind_1 \,{\mathop {\rightarrow }\limits ^{*}}\, ind_2\) denotes the reflexive and transitive closure of tr. We restrict the set of states to the states reachable from the initial state: \(States := \mathcal {R}(LTS(c,g),ind_0) :=\{ind | ind_0\, {\mathop {\rightarrow }\limits ^{*}}\,ind\}\).
A more intuitive notation would be to consider a state as a word of length n over the alphabet \(C \cup G\) with distinct letters only, and the rewrite rule \(au \,{\mathop {\rightarrow }\limits ^{}}\, ua\) with \(a \in C\), \(u \in G\) when inside the word and \( u\cdots a \,{\mathop {\rightarrow }\limits ^{}}\, a\cdots u\) at the borders. An example of two such transitions from tq(3, 4) with \(C = \{a,b,c\}, G = \{u,v,w,x\}\) and transitions \(\langle \!\langle t_3,b\rangle \!\rangle , \langle \!\langle t_7,c\rangle \!\rangle \) is \(u \,a\,b\,v\,w\,x\,c \,{\mathop {\rightarrow }\limits ^{}}\, u\,a\,v\,b\,w\,x\,c \,{\mathop {\rightarrow }\limits ^{}}\,c\,a\,v\,b\,w\,x\,u\). When defining the elements of G to be indistinguishable, they can be interpreted as gaps interchanging with the traffic items from C.
Definition 2
A circular traffic queue with gaps \(tq\text {-}g(c,g)\) is defined as in Definition 1, with the difference that \(|G|=1\) and the index function ind is not bijective in general, but only on the co-image \(ind^{-1}(C)\). In addition we require that there is at least one gap: \(ind^{-1}(G) \ne \emptyset \). As the number g from Definition 1 is not longer needed, we use it here to define the number of gaps: \(g := n - c \ge 1\).
With \(G = \{\times \}\) for \(tq\text {-}g(3,4)\) the example above modifies to  . While the regular initial state is natural in the sense that the traffic items start without gaps in between, in a different context (as defined for cycloids by Petri) it is useful that the gaps are equally distributed. If for instance, as in the example after the following definition of a standard initial state, the numbers c and g are even, the queue in its initial state is composed of two equal subsystems with the parameters \(\frac{c}{2}\) and \(\frac{g}{2}\). An analogous situation holds for larger divisors.
. While the regular initial state is natural in the sense that the traffic items start without gaps in between, in a different context (as defined for cycloids by Petri) it is useful that the gaps are equally distributed. If for instance, as in the example after the following definition of a standard initial state, the numbers c and g are even, the queue in its initial state is composed of two equal subsystems with the parameters \(\frac{c}{2}\) and \(\frac{g}{2}\). An analogous situation holds for larger divisors.
Definition 3
A standard initial state \(ind_0\) of a circular traffic queue is defined by the form \(ind_0(1)ind_0(2)\cdots ind_0(n) = a_1w_1a_2w_2\cdots a_cw_c\) with \(a_j \in C, w_j \in G^{r_j}\) and  . \(G^{r_j}\) is the set of words of length \(r_j\) over G.
. \(G^{r_j}\) is the set of words of length \(r_j\) over G.
To be a consistent definition it should be verified that all the \(r_j\) sum up together to \(\sum _{j=1}^c r_j =g \). This follows from the observation that the intervals in the definition of \(r_j\) are disjoint and all together define a set  of cardinality g. To give an example, we consider the case \(c = 4, g = 6\). We obtain \((r_1,r_2,r_3,r_4) = (1,2,1,2)\) and
of cardinality g. To give an example, we consider the case \(c = 4, g = 6\). We obtain \((r_1,r_2,r_3,r_4) = (1,2,1,2)\) and  for the resulting standard initial state.
for the resulting standard initial state.
Theorem 4
Let be \(\varDelta = gcd(c,g)\) the greatest common divisor of c and g. The length of each recurrent sequence (Definition 1) of tq(c, g) is \(\varXi (c,g) := \frac{g}{\varDelta } \cdot (c+g) \cdot c\). For a circular traffic queue with gaps \(tq\text {-}g(c,g)\) this reduces to \(\varGamma (c,g) := c\cdot (c+g)\).
Proof
In both cases we start with a regular initial state \(ind_0 = a_1a_2\cdots a_c\) \(u_1u_2\cdots u_g\) with \(a_i \in C\) and \(u_h \in G\). In the second case all \(u_h\) equal \(\times \). To reach the initial state \(ind_0\) for the first time, each traffic item \(a_j \in C\) has to make \(n= c+g\) steps. Hence in total, we have \(\varGamma (c,g) := c\cdot (c+g)\). Since the general model tq(c, g) is symmetric with respect to G and C, as well as the result \(\varXi (c,g) := \frac{1}{\varDelta }c(c+g)g\) to be proved, it is sufficient to consider the case \(g\ge c\). Furthermore we assume \(g>1\) since for \(g=1\) we also have \(c=1\) and the problem reduces to the case of \(\varGamma (c,g)\). The recurrent sequence to be constructed is split into several pieces. We start by shifting all traffic items to the end of the queue requiring g steps for each and \(g\cdot c\) steps in total: (I)  . Then we move the traffic items back to their initial position, needing \(c\cdot c\) steps: (II)
. Then we move the traffic items back to their initial position, needing \(c\cdot c\) steps: (II)  . Ignoring the individual names of the elements \(u_i \in G\) we have the situation described in the case of \(c\cdot g + c \cdot c = c \cdot (c+g)\) steps. But here in the first case the initial state is not yet reached since the items \(u_h\) are not necessary in their initial order. Therefore the \(c \cdot (c+g)\) steps have to be repeated in a number of different levels. In the following, the step from level k to \(k+1\) is shown. The letter \(u_{i_j^k}\) denotes the item \(u_{i_j} \in G\) of level k in position \(ind^{-1}(u_{i_j}) = j\). (III)
. Ignoring the individual names of the elements \(u_i \in G\) we have the situation described in the case of \(c\cdot g + c \cdot c = c \cdot (c+g)\) steps. But here in the first case the initial state is not yet reached since the items \(u_h\) are not necessary in their initial order. Therefore the \(c \cdot (c+g)\) steps have to be repeated in a number of different levels. In the following, the step from level k to \(k+1\) is shown. The letter \(u_{i_j^k}\) denotes the item \(u_{i_j} \in G\) of level k in position \(ind^{-1}(u_{i_j}) = j\). (III)  . We now consider the sequence \(u_{i_1^1} u_{i_1^2} \cdots u_{i_1^k} \cdots \) of items from G for all levels k in equation (III): \(u_{i_1^1} u_{i_1^2} \cdots u_{i_1^k} \cdots \) starting with \(u_{i_1^1} = u_1\) from \(ind_0\). The initial state is reached when \(u_{i_1^{k}} = u_{i_1^1} = u_1\) for the first time. By induction, beginning with equations (I) and (II): \(u_{i_1^1} = u_1, u_{i_1^2} = u_{1+c} \) and by the induction step from equation (III): \(u_{i_1^{k+1}} = u_{{(i^{k}_1+c)\,mod\, g}}\) we conclude \(u_{i_1^{k}} = u_{(k\cdot c +1)\;mod\; g}\). Hence to determine the value of k for a recurrent sequence we have to find the smallest nontrivial solution in the following equation: (IV) \((k\cdot c + 1)\,mod\, g = 1\). Next we prove \(k = \frac{g}{x}\) to be a solution, where
. We now consider the sequence \(u_{i_1^1} u_{i_1^2} \cdots u_{i_1^k} \cdots \) of items from G for all levels k in equation (III): \(u_{i_1^1} u_{i_1^2} \cdots u_{i_1^k} \cdots \) starting with \(u_{i_1^1} = u_1\) from \(ind_0\). The initial state is reached when \(u_{i_1^{k}} = u_{i_1^1} = u_1\) for the first time. By induction, beginning with equations (I) and (II): \(u_{i_1^1} = u_1, u_{i_1^2} = u_{1+c} \) and by the induction step from equation (III): \(u_{i_1^{k+1}} = u_{{(i^{k}_1+c)\,mod\, g}}\) we conclude \(u_{i_1^{k}} = u_{(k\cdot c +1)\;mod\; g}\). Hence to determine the value of k for a recurrent sequence we have to find the smallest nontrivial solution in the following equation: (IV) \((k\cdot c + 1)\,mod\, g = 1\). Next we prove \(k = \frac{g}{x}\) to be a solution, where  . Applying the formula \((a+b)\,mod\, g = (a \, mod \, g+b \,mod \,g)\,mod \,g\) this is done by \({(\frac{g}{x}\cdot c +1)\;mod\; g} = ([({\frac{c}{x}\cdot g)\;mod\; g}] + [1\; mod \; g ]) \; mod \; g = (0+1)\;mod \; g = 1\) since \(g>1\). In this calculation \( \frac{c}{x}\) has to be an integer, hence x|c. The same holds for \(k = \frac{g}{x}\) and also x|g. For a minimal non-trivial solution we obtain \(x=gcd(c,g) = \varDelta \) and \(k = \frac{g}{\varDelta }\). Recall that k is the number times the step from equation (III) has to be repeated to obtain a recurrent transition sequence. This gives the result \(\varXi (c,g) = k \cdot c \cdot (c+g) = \frac{c \cdot (c+g)\cdot g}{\varDelta }\). All different recurrent transition sequences are obtained by permutations and cannot be shorter. \(\square \)
. Applying the formula \((a+b)\,mod\, g = (a \, mod \, g+b \,mod \,g)\,mod \,g\) this is done by \({(\frac{g}{x}\cdot c +1)\;mod\; g} = ([({\frac{c}{x}\cdot g)\;mod\; g}] + [1\; mod \; g ]) \; mod \; g = (0+1)\;mod \; g = 1\) since \(g>1\). In this calculation \( \frac{c}{x}\) has to be an integer, hence x|c. The same holds for \(k = \frac{g}{x}\) and also x|g. For a minimal non-trivial solution we obtain \(x=gcd(c,g) = \varDelta \) and \(k = \frac{g}{\varDelta }\). Recall that k is the number times the step from equation (III) has to be repeated to obtain a recurrent transition sequence. This gives the result \(\varXi (c,g) = k \cdot c \cdot (c+g) = \frac{c \cdot (c+g)\cdot g}{\varDelta }\). All different recurrent transition sequences are obtained by permutations and cannot be shorter. \(\square \)
The proof has shown that a sequence has to be repeated \(\frac{g}{\varDelta }\) times to reach a state where all traffic items from C are in their initial order. To obtain an adequate labelling of the transitions we add a counter \(k, 0\le k < r\) to represent the repetitive behaviour. The counter is implemented as an exponent of the names of traffic items \(a^k_j\) and transitions \(t^k_v\). Each time the traffic item \(a_j\) starts a new round in its (initial) position \(j \in \{1,\cdots ,c\}\) (with respect to the regular initial state) the counter is increased. With the values of i and k in the following definition, for each traffic item \(a_j\) a number \(p = n\cdot r\) of process states is reached. Later we will restrict to the cases \(r=1\) (no repetition) and \( r = \frac{g}{\varDelta }\).
Definition 5
Let be  and \(C^r := \{a_j^k | a_j \in C, 0\le k < r \}\). A (r-repetitive) labelled transition system \(LTS_p(c,g) = (States,T,tr,ind_0)\) with \(p = r\cdot n\) and
and \(C^r := \{a_j^k | a_j \in C, 0\le k < r \}\). A (r-repetitive) labelled transition system \(LTS_p(c,g) = (States,T,tr,ind_0)\) with \(p = r\cdot n\) and  is defined by a set States of states as in Definition 1 with C replaced by \(C^r\), \(T \! = \!\{ \langle \!\langle t^k_v,a_j\rangle \!\rangle | 1 \!\le \! v \le \! p, 0 \! \le \! k < r,1 \le j \le c \}\) as a set of transitions, The transition relation \(tr \subseteq States \times T \times States \;\) is defined by
is defined by a set States of states as in Definition 1 with C replaced by \(C^r\), \(T \! = \!\{ \langle \!\langle t^k_v,a_j\rangle \!\rangle | 1 \!\le \! v \le \! p, 0 \! \le \! k < r,1 \le j \le c \}\) as a set of transitions, The transition relation \(tr \subseteq States \times T \times States \;\) is defined by
In particular, we consider the special cases \(tq\text {-}2(c,g) :=LTS_p(c,g)\) with \(p = \frac{g}{\varDelta }\cdot n\) and \(tq\text {-}1(c,g) := LTS_n(c,g)\) with \(G = \{\!\times \!\}\). In the latter cases we have \(r=1\) and the labelling of the transitions can be simplified to \(\langle \!\langle t_i,a_j\rangle \!\rangle \).
For preparing the modelling of alternative formalisms, in particular of Petri nets in Sect. 4, we give a specification of circular traffic queues by their properties. To be free from a more sequential specification we prefer a message-oriented formulation. This is similar to Petri’s notion of a permit signal in [5].
Definition 6
A circular traffic queue \(tq\text {-}1(c,g)\) respectively \(tq\text {-}2(c,g)\) has the following properties. Next, \(u \in G\) denotes a gap in the case of \(tq\text {-}1(c,g)\) and a traffic item in the case of \(tq\text {-}2(c,g)\).
-
a)
Each traffic item \(a\in C\) and \(u \in G\) is in exactly in one of \(n = c+g\) positions.
-
b)
Each traffic item \(a\in C\) can make a step from position \(i \in \{1,\cdots ,n\}\) to
position \((i+1)\;mod \; n\), if it has received a message from \(u \in G\) in
position \((i+1)\;mod \; n\). After this step the \(u \in G\) is in position i.
-
c)
The length of recurrent transition sequences is \(\varGamma (c,g) = c \cdot n\) and \(\varXi (c,g) := \frac{g}{\varDelta }\cdot c \cdot n\), respectively.
-
d)
\(tq\text {-}2(c,g)\) is isomorphic to \(\frac{g}{\varDelta }\) copies of transition systems of type \(tq\text {-}1(c,g)\) with \(|G|=g\). After \( c \cdot n\) steps each transition sequence enters the next of these copies.
This specification is denoted as a definition, but requires some justification. The items a), b) and c) follow from the definitions of a circular traffic queue. The supplement concerning \(tq\text {-}2(c,g)\) follows from the proof of Theorem 4.
3 Petri Space and Cycloids
In this section (Petri-) nets and cycloids are defined. Some results are cited from [7] and [9], whereas concepts like regular cycloids and the use of matrix algebra are new. We define Petri nets in the form of condition/event-nets or safe T-nets, while coloured nets are used in Sect. 4.3 without formal definition.
Definition 7
As usual, a net \( \mathcal {N}_{} = (S, T, F)\) is defined by non-empty, disjoint sets S of places and T of transitions, connected by a flow relation  . \(X := S \cup T\). \(\mathcal {N}_{}\simeq \mathcal {N}_{}'\) denote isomorphic nets. A transition \(t \in T\) is active or enabled in a marking \(M \subseteq S\) if
. \(X := S \cup T\). \(\mathcal {N}_{}\simeq \mathcal {N}_{}'\) denote isomorphic nets. A transition \(t \in T\) is active or enabled in a marking \(M \subseteq S\) if  and in this case
and in this case  if
if  , where
, where  denote the input and output elements of an element \(x \in S \cup T\), respectively.
denote the input and output elements of an element \(x \in S \cup T\), respectively.  is the reflexive and transitive closure of \(\rightarrow \). A net together with an initial marking \(M_0 \subseteq S\) is called a net-system \((\mathcal {N}_{},M_0)\) with its reachability set
is the reflexive and transitive closure of \(\rightarrow \). A net together with an initial marking \(M_0 \subseteq S\) is called a net-system \((\mathcal {N}_{},M_0)\) with its reachability set  . The reachability graph \(\mathcal {RG}(\mathcal {N}_{},M_0) = (\mathcal {R}(\mathcal {N}_{},M_0),\rightarrow ,M_0)\) is defined by the reachability set as the set of nodes, the relation \(\rightarrow \) as its set of arrows and the initial marking as distinguished node.
. The reachability graph \(\mathcal {RG}(\mathcal {N}_{},M_0) = (\mathcal {R}(\mathcal {N}_{},M_0),\rightarrow ,M_0)\) is defined by the reachability set as the set of nodes, the relation \(\rightarrow \) as its set of arrows and the initial marking as distinguished node.
Definition 8
A \(Petri \; space\) is defined by the net \(\mathcal {PS}_{1} := (S_1, T_1, F_1)\) where  ,
,  ,
,  (cutout in Fig. 1a).
(cutout in Fig. 1a).  is the set of forward places and
is the set of forward places and  the set of backward places.
the set of backward places.
 is the forward input place of \(t_{\xi ,\eta }\) and in the same way
is the forward input place of \(t_{\xi ,\eta }\) and in the same way
 ,
,  and
and  (see Fig. 1a).
(see Fig. 1a).
By a twofold folding with respect to time and space we obtain the cyclic structure of a cycloid. See [7, 9] for motivation and Fig. 2 a) for an example of a cycloid.
Definition 9
([7, 9]). A cycloid is a net \( \mathcal {C}( \alpha , \beta , \gamma , \delta ) = (S, T, F)\), defined by parameters  , by a quotient of the Petri space \(\mathcal {PS}_{1} := (S_1, T_1, F_1)\) with respect to the equivalence relation
, by a quotient of the Petri space \(\mathcal {PS}_{1} := (S_1, T_1, F_1)\) with respect to the equivalence relation  with
with  \( x_{\xi ,\eta } \equiv x_{\xi +m\alpha +n\gamma ,\,\eta -m\beta +n\delta } \) for all
\( x_{\xi ,\eta } \equiv x_{\xi +m\alpha +n\gamma ,\,\eta -m\beta +n\delta } \) for all  , \( X = X_1/_\equiv \),
, \( X = X_1/_\equiv \),  for all \(x, y \in X_1 \).
for all \(x, y \in X_1 \).
The matrix \(\mathbf {A} = \begin{pmatrix} \alpha &{} \gamma \\ -\beta &{} \delta \end{pmatrix} \) is called the matrix of the cycloid. Petri denoted the number |T| of transitions as the area A of the cycloid and determined in [4] its value to \(|T| =A =\alpha \delta +\beta \gamma \) which equals the determinant \(A = det(\mathbf {A})\). Cycloids are safe T-nets with  for all places \(s\in S\). The embedding of a cycloid in the Petri space is called fundamental parallelogram (see Fig. 1 b), but ignore the tokens for the moment). If the cycloid is represented as a net \(\mathcal {N}_{}\) without explicitly giving the parameters \(\alpha ,\beta ,\gamma ,\delta \), we call it a cycloid in net form \(\mathcal {C}(\mathcal {N}_{})\).
for all places \(s\in S\). The embedding of a cycloid in the Petri space is called fundamental parallelogram (see Fig. 1 b), but ignore the tokens for the moment). If the cycloid is represented as a net \(\mathcal {N}_{}\) without explicitly giving the parameters \(\alpha ,\beta ,\gamma ,\delta \), we call it a cycloid in net form \(\mathcal {C}(\mathcal {N}_{})\).
For proving the equivalence of two points in the Petri space the following procedure is useful.
Theorem 10
Two points \(\varvec{x}_1, \varvec{x}_2\in X_1\) are equivalent \(\varvec{x}_1 \equiv \varvec{x}_2\) if and only if the parameter vector \(\pi (\varvec{v}) = \pi (\varvec{x_2}-\varvec{x_1})\) has integer values, where \(\pi (\varvec{v}) = \frac{1}{A} \cdot \mathbf {B} \cdot \varvec{v}\) with area A and \(\mathbf {B} = \begin{pmatrix} \delta &{} -\gamma \\ \beta &{} \alpha \end{pmatrix}\).
Proof
For \(\varvec{x}_1 := (\xi _1,\eta _1), \varvec{x}_2 := (\xi _2,\eta _2), \varvec{v} := \varvec{x}_2 - \varvec{x}_1\) from Definition 9 we obtain in vector form:  . It is well-known that \(\mathbf {A}^{-1} = \frac{1}{det(\mathbf {A})}\mathbf {B}\) if \(det(\mathbf {A}) > 0\) (see any book on linear algebra). The condition \(det(\mathbf {A}) = A = \alpha \delta + \beta \gamma >0\) is satisfied by the definition of a cycloid. \(\square \)
. It is well-known that \(\mathbf {A}^{-1} = \frac{1}{det(\mathbf {A})}\mathbf {B}\) if \(det(\mathbf {A}) > 0\) (see any book on linear algebra). The condition \(det(\mathbf {A}) = A = \alpha \delta + \beta \gamma >0\) is satisfied by the definition of a cycloid. \(\square \)
Theorem 11
([7, 9]). The following cycloids are isomorphic to \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ) \):
-
a)
\(\mathcal {C}(\beta ,\alpha ,\delta ,\gamma ) \), \(\;\;\;\;\;\;\;\;\;\;\;(\)The dual cycloid of \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ).)\)
-
b)
\(\mathcal {C}(\alpha ,\beta ,\gamma - q \cdot \alpha ,\delta +q \cdot \beta ) \) if
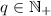 and \(\gamma > q \cdot \alpha \),
and \(\gamma > q \cdot \alpha \), -
c)
\(\mathcal {C}(\alpha ,\beta ,\gamma + q \cdot \alpha ,\delta - q \cdot \beta ) \) if
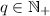 and \(\delta > q \cdot \beta \).
and \(\delta > q \cdot \beta \).
Proof
Part a) has been proved in [7, 9] as well as b) and c) for the special case of \(q = 1\). The current form is derived by iterating the result. \(\square \)
Definition 12
For a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) we define a cycloid-system
\(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ,M_0)\) or \(\mathcal {C}(\mathcal {N}_{},M_0)\) by adding the standard initial marking:

The motivation of this definition is given in [7] and [9]. See Fig. 2 a) for an example of a cycloid with standard initial marking. As in the case of circular traffic queues we define a regular initial marking for cycloids, but not necessarily within the fundamental parallelogram. It is characterized by the absence of gaps between the traffic items whereby only a single transition on the top of the queue is enabled. In the example of \(\mathcal {C}(2,4,3,2)\) from Fig. 1 b) this is the transition \(t_{0,1-\beta } = t_{0,-3}\), which is enabled by the tokens in \(s^\rightarrow _{-1,-3}\) and \(s^\leftarrow _{0,-4}\). After occurring the \(\beta -1 = 3\) transitions \(t_{0,-2}\), \(t_{0,-1}\) and \(t_{0,0}\) can occur in some order. They model the steps of the traffic items following the item at the head of the queue. In this example the regular initial marking is \(\{s^\rightarrow _{-1,0},s^\rightarrow _{-1,-1}, s^\rightarrow _{-1,-2}, s^\rightarrow _{-1,-3}, \} \cup \{s^\leftarrow _{0,-4},s^\leftarrow _{1,-4}\}\), as shown in Fig. 1 b). Equivalent places within the fundamental parallelogram can be computed. For instance, the regular initial marking of \(\mathcal {C}(4,3,3,3)\) is represented by highlighted places in Fig. 2 a).
Definition 13
For a cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) a regular initial marking is defined by a number of \(\beta \) forward places \(\{s^\rightarrow _{-1,i} | \; 0 \ge i \ge 1-\beta \}\) and a number of \(\alpha \) backward places \(\{s^\leftarrow _{i,-\beta } | \; 0 \le i \le \alpha -1\}\).
Theorem 14
([7, 9]). The length of a minimal cycle of a cycloid \(\, \mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is \(cyc(\alpha ,\beta ,\gamma ,\delta ) = cyc = \gamma + \delta + \; \left\{ \begin{array}{lll} \lfloor \frac{\delta }{\beta }\rfloor (\alpha - \beta ) &{} \text {if} &{}\alpha \le \beta \\ -\lfloor \frac{\gamma }{\alpha }\rfloor (\alpha - \beta ) &{} \text {if} &{} \alpha > \beta \end{array} \right. \)
As proved in [7, 9] by the Synthesis-Theorem for cycloids we can compute the parameters \(\alpha ,\beta ,\gamma \) and \(\delta \) of a cycloid from its net presentation using the system parameters \(\tau _0, \tau _a, A\) and cyc. \(\tau _0\) is the number of transitions having at least one marked input place, \(\tau _a\) is the number of active transitions, both w.r.t. the standard initial marking \(M_0\). A is (as before) the number of all transitions and cyc is the minimal length of transition cycles. The following procedures do not necessarily give a unique result, but for \(\alpha \ne \beta \) the resulting cycloids are isomorphic.
Theorem 15
(Synthesis-Theorem, [7, 9]). Cycloid systems with identical system parameters \(\tau _0, \tau _a,\) A and cyc are called \(\sigma \)-equivalent. Given a cycloid system \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta , M_0)\) in its net representation \((S,T,F,M_0)\) where the parameters \(\tau _0, \tau _a, A\) and cyc are known (but the parameters \(\alpha ,\beta ,\gamma ,\delta \) are not). Then a \(\sigma \)-equivalent cycloid \(\mathcal {C}(\alpha ',\beta ',\gamma ',\delta ')\) can be computed by \(\alpha ' = \tau _0\), \(\beta ' = \tau _a\) and for \(\gamma ', \delta '\) by some positive integer solution of the following formulas using these settings of \(\alpha '\) and \(\beta '\):
-
a)
case \(\alpha ' > \beta '\): \(\gamma ' \; mod\; \alpha ' = \frac{\alpha '\cdot cyc - A}{\alpha '-\beta '}\) and \(\delta ' = \frac{1}{\alpha '}(A - \beta '\cdot \gamma ')\),
-
b)
case \(\alpha ' < \beta '\): \(\delta ' \; mod\; \beta ' = \frac{\beta '\cdot cyc - A}{\beta ' - \alpha '}\) and \(\gamma ' = \frac{1}{\beta '}(A - \alpha '\cdot \delta ')\),
-
c)
case \(\alpha ' = \beta '\): \(\gamma ' = \lceil \frac{cyc}{2}\rceil \) and \(\delta ' = \lfloor \frac{cyc}{2}\rfloor \)
These equations may result in different cycloid parameters, however the cycloids are isomorphic in the cases a) and b) as in Theorem 11.
Circular traffic queues are composed by a number of c sequential and interacting processes of equal length. In the formalism of cycloids this corresponds to a number of \(\beta \) disjoint processes of equal length p. Cycloids with such a property are called regular.
Definition 16
A cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) with area A is called regular if for each
\(\eta \in \{0,\cdots ,1-\beta \}\) the set \(\{t_{\xi ,\eta } | 1 \le \xi \le p\}\) with \(p = \frac{A}{\beta }\) of transitions forms an elementary cycleFootnote 1 and all these sets are disjoint.  is called the process length of the regular cycloid. A regular cycloid together with its regular initial marking \(M_0\) is called a regular cycloid system \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ,M_0)\) .
is called the process length of the regular cycloid. A regular cycloid together with its regular initial marking \(M_0\) is called a regular cycloid system \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ,M_0)\) .
Theorem 17
A cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is regular if and only if \(\beta | \delta \).
Proof
We first prove that starting in any point \(t_{\xi ,\eta }\) of the fundamental parallelogram of the cycloid and proceeding in direction of the \(\xi \)-axis we will return to \(t_{\xi ,\eta }\) after passing \(p = \frac{A}{\beta }\) transitions. By Theorem 10, to decide \(t_{\xi +p,\eta }\equiv t_{\xi ,\eta }\) it is sufficient to check whether

\(\frac{A}{\beta }\) is the smallest value for p to obtain an integer value in the second component of the last vector. Therefore an equivalent point is not reached before passing p transitions and the cycle is elementary. By the first component, to fulfill  it is necessary and sufficient that \(\beta | \delta \). It follows that there is a number of \(\beta \) such elementary cycles of length \(\frac{A}{\beta }\) covering the entire set of A transitions. Therefore no pair of these cycles can have a common transition. \(\square \)
it is necessary and sufficient that \(\beta | \delta \). It follows that there is a number of \(\beta \) such elementary cycles of length \(\frac{A}{\beta }\) covering the entire set of A transitions. Therefore no pair of these cycles can have a common transition. \(\square \)
A regular cycloid can be seen as a system of \(\beta \) disjoint sequential and cooperating processes. To exploit this structure we define specific coordinates, called regular coordinates. The process of a traffic item \(a_1\) starts with transition \(t_{0,0}\) which is denoted \([t_1,a_1]\), having the input place \([s_0,a_1]\). The next transitions are \([t_2,a_1]\) up to \([t_p,a_1]\) and then returning to \([t_1,a_1]\). The other processes for \(a_2\) to \(a_c\) (with \(\beta = c\)) are denoted in the same way (see Fig. 2 b). As the process of \(a_j\) starts in position j of the queue, its initial token is in \([s_{j-1},a_j]\).
Definition 18
Given a regular cycloid \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ), \) regular coordinates are defined as follows: transitions of process \(j \in \{1,\cdots ,\beta \}\) each with length p are denoted by \(\{[t_1,a_j],\cdots ,[t_p,a_j]\}\). For each transition we define  and
and  , where we also use \(s_0 := s_p\) and \(s'_0 := s'_p\). Furthermore for \(1 \le j \le \beta \) let
, where we also use \(s_0 := s_p\) and \(s'_0 := s'_p\). Furthermore for \(1 \le j \le \beta \) let  . Regular coordinates are related to standard coordinates of the Petri space by defining the following initial condition \([t_1,a_j] := t_{1-j,1-j}\) for \(1 \le j \le \beta \).
. Regular coordinates are related to standard coordinates of the Petri space by defining the following initial condition \([t_1,a_j] := t_{1-j,1-j}\) for \(1 \le j \le \beta \).
In Fig. 2 b) we obtain for the last formula in Definition 18: \([t_{1},a_{3}] := t_{-2,-2} \equiv t_{1,1}\). While the output place \([s'_i,a_j]\) in regular coordinates takes its name from the input transition, it remains to determine its output transition according to the corresponding standard coordinates.
Lemma 19
The injective mapping stand from regular to standard coordinates is given by \(stand([t_i,a_j])= t_{i-j,1-j}\) for \(1 \le i \le p\) and \(1 \le j \le \beta \) (modulo equivalent transitions). The output transition is  while for \(1< j \le \beta \) we have
while for \(1< j \le \beta \) we have  . If \(\beta = \gamma = \delta \) the two cases coincide.
. If \(\beta = \gamma = \delta \) the two cases coincide.
Proof
For a given j by Definition 18 we have \([t_1,a_j] := t_{1-j,1-j}\). Adding a value \(i-1\) to the index of \(t_1\) we obtain the index of \(t_i\), hence \(stand([t_i,a_j]) := t_{1-j+(i-1),1-j}\). To prove  for \(1< j \le \beta \) we first compute the corresponding standard coordinate \(stand([t_i,a_j]) = t_{i-j,1-j}\). To obtain the output transition of \([s'_i,a_j]\) we go to the next transition in \(\eta \)-direction \(t_{i-j,1-j+1} = t_{i-j,2-j} = stand([t_{i-1},a_{j-1}])\), where \(mod \, p\) and \(mod \, c\) are omitted. To make the proof for \([s'_i,a_1]\) we start with \([t_{i},a_1]\) and compute again \(stand([t_i,a_1]) = t_{i-1,0}\). The next transition in \(\eta \)-direction is \(t_{i-1,1}\). Using Theorem 10 we prove
for \(1< j \le \beta \) we first compute the corresponding standard coordinate \(stand([t_i,a_j]) = t_{i-j,1-j}\). To obtain the output transition of \([s'_i,a_j]\) we go to the next transition in \(\eta \)-direction \(t_{i-j,1-j+1} = t_{i-j,2-j} = stand([t_{i-1},a_{j-1}])\), where \(mod \, p\) and \(mod \, c\) are omitted. To make the proof for \([s'_i,a_1]\) we start with \([t_{i},a_1]\) and compute again \(stand([t_i,a_1]) = t_{i-1,0}\). The next transition in \(\eta \)-direction is \(t_{i-1,1}\). Using Theorem 10 we prove  . Going back to the corresponding regular coordinates the desired result is obtained: \(stand([t_{i+\alpha +\beta -1}, a_{\beta )}] ) = t_{i+\alpha +\beta -1-\beta ,1-\beta } = t_{i+\alpha -1,1-\beta }\) where \(mod \, p\) and \(mod \, c\) are omitted again. If \(\beta = \gamma = \delta \) the two cases coincide as \(p= \alpha + \beta \) in this case. \(\square \)
. Going back to the corresponding regular coordinates the desired result is obtained: \(stand([t_{i+\alpha +\beta -1}, a_{\beta )}] ) = t_{i+\alpha +\beta -1-\beta ,1-\beta } = t_{i+\alpha -1,1-\beta }\) where \(mod \, p\) and \(mod \, c\) are omitted again. If \(\beta = \gamma = \delta \) the two cases coincide as \(p= \alpha + \beta \) in this case. \(\square \)
Corollary 20
The regular initial marking of a regular cycloid system
\(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta ,M_0)\) with process length p is \(M_0 = \{ [s_i,a_{i+1}] | 0\le i\le \beta -1 \} \cup \{ [s'_i,a_1] | p-\alpha +1\le i \le p\}\). For later reference, we note  .
.
Proof
Since the mapping stand is defined on transitions, from the first place of \(M_0\) in Corollary 20 \([s_0,a_{(0+1)\,mod\,\beta }]\) we go to its output transition \([t_1,a_1]\) and apply \(stand([t_1,a_1]) = t_{0,0}\). Going back in \(\xi \)-direction we obtain \(s^\rightarrow _{-1,0} \), which is the first element in Definition 13. Doing the same with \([s_{\beta -1},a_{\beta \,mod\,\beta }]\) we come via \(stand([t_\beta ,a_\beta ]) = t_{\beta -\beta ,1-\beta } = t_{0,1-\beta } \) to \(s^\rightarrow _{-1,1-\beta } \). By this we obtain the entire forward places from Definition 13. Since the mapping stand is injective we can conclude also in the inverse direction. To prove the second part of the union recall that the last traffic item \(a_\beta \) is active (enabled). Therefore also the backward input place \([s'_i,a_1]\) of \([t_\beta ,a_\beta ]\) must be marked. Using Lemma 19 the value of i must satisfy  , hence \((i+\alpha +\beta -1)\,mod\,p = \beta \) and \(i = (1 - \alpha ) \, mod \, p = p - \alpha + 1\). This holds since \(\beta |\delta \; \Rightarrow \;\beta \le \delta \) and therefore \(p = \frac{A}{\beta } = \alpha \frac{\delta }{\beta }+\gamma > \alpha \). The marked place in question is therefore \([s'_i,a_1] = [s'_{ p - \alpha + 1},a_1]\). To determine the other elements of \( \{ [s'_i,a_1] | p-\alpha +1\le i \le p \}\) recall that the last traffic item \(a_\beta \) should be able to make \(\alpha \) steps before any other transition has to occur. Therefore also the places \([s'_{ p - \alpha + 2},a_1] \) to \([s'_{ p - \alpha + \alpha },a_1] \) must be marked in the regular initial marking. \(\square \)
, hence \((i+\alpha +\beta -1)\,mod\,p = \beta \) and \(i = (1 - \alpha ) \, mod \, p = p - \alpha + 1\). This holds since \(\beta |\delta \; \Rightarrow \;\beta \le \delta \) and therefore \(p = \frac{A}{\beta } = \alpha \frac{\delta }{\beta }+\gamma > \alpha \). The marked place in question is therefore \([s'_i,a_1] = [s'_{ p - \alpha + 1},a_1]\). To determine the other elements of \( \{ [s'_i,a_1] | p-\alpha +1\le i \le p \}\) recall that the last traffic item \(a_\beta \) should be able to make \(\alpha \) steps before any other transition has to occur. Therefore also the places \([s'_{ p - \alpha + 2},a_1] \) to \([s'_{ p - \alpha + \alpha },a_1] \) must be marked in the regular initial marking. \(\square \)
In the regular cycloid system \(\mathcal {C}(4,3,3,3,M_0)\) in Fig. 2 b) we obtain  . The given regular initial marking is \(\{[s_0,a_1],[s_1,a_2],\) \([s_2,a_3],[s'_4,a_1],[s'_5,a_1], [s'_6,a_1],[s'_7,a_1]\}\). The standard initial marking is given by bold circles. It is useful in some cases to express the minimal cycle length cyc of a regular cycloid by its process length p. While this can be perfectly done for the case \(\alpha \le \beta \) in the complementary case only partial results are achieved. Compared with general cycloids the lack of symmetry of regular cycloids becomes apparent by these results. However, they cover all the cases required in Sect. 4. In Theorem 23 we consider \(\mathcal {C}(\alpha ,\beta ,\beta ,\beta )\) (in the form \(\alpha = g, \beta = c\)) with \(p = \alpha + \beta \) and \(cyc = min\{\alpha + \beta ,2\cdot \beta \}\), which is covered by the cases a) and c) in Lemma 21. Afterwards in Theorem 24 we have \(\mathcal {C}(\alpha ,\beta ,\frac{1}{\varDelta }\alpha \beta ,\frac{1}{\varDelta }\alpha \beta )\) with \(p = \frac{1}{\varDelta }\alpha (\alpha +\beta )\) and \(cyc = min\{p,\frac{\beta }{\alpha } \cdot p\}\), which is covered by the cases a) and b).
. The given regular initial marking is \(\{[s_0,a_1],[s_1,a_2],\) \([s_2,a_3],[s'_4,a_1],[s'_5,a_1], [s'_6,a_1],[s'_7,a_1]\}\). The standard initial marking is given by bold circles. It is useful in some cases to express the minimal cycle length cyc of a regular cycloid by its process length p. While this can be perfectly done for the case \(\alpha \le \beta \) in the complementary case only partial results are achieved. Compared with general cycloids the lack of symmetry of regular cycloids becomes apparent by these results. However, they cover all the cases required in Sect. 4. In Theorem 23 we consider \(\mathcal {C}(\alpha ,\beta ,\beta ,\beta )\) (in the form \(\alpha = g, \beta = c\)) with \(p = \alpha + \beta \) and \(cyc = min\{\alpha + \beta ,2\cdot \beta \}\), which is covered by the cases a) and c) in Lemma 21. Afterwards in Theorem 24 we have \(\mathcal {C}(\alpha ,\beta ,\frac{1}{\varDelta }\alpha \beta ,\frac{1}{\varDelta }\alpha \beta )\) with \(p = \frac{1}{\varDelta }\alpha (\alpha +\beta )\) and \(cyc = min\{p,\frac{\beta }{\alpha } \cdot p\}\), which is covered by the cases a) and b).
Lemma 21
Let be \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) a regular cycloid with process length p and minimal cycle length cyc. Then a) \(cyc = p\) if \(\alpha \le \beta \), b) If \(\alpha > \beta \) and \(\alpha | \gamma \) then \(cyc = \frac{\beta }{\alpha }\cdot p\) and c) \(cyc = 2 \cdot \beta \) if \(\alpha > \beta = \gamma = \delta \).
Proof
a) By Theorem 14 and \(\delta =m\cdot \beta \) for some  we obtain \(cyc = \gamma + \delta + \lfloor \frac{\delta }{\beta }\rfloor (\alpha - \beta ) = \gamma + m\cdot \beta + \lfloor \frac{m\cdot \beta }{\beta }\rfloor (\alpha - \beta ) = \gamma + m\cdot \alpha \). This term equals \(p = \frac{A}{\beta } = \frac{1}{\beta } (\alpha \delta +\beta \gamma ) = \frac{1}{\beta } (\alpha \cdot m\cdot \beta +\beta \gamma ) = \alpha \cdot m + \gamma \).
we obtain \(cyc = \gamma + \delta + \lfloor \frac{\delta }{\beta }\rfloor (\alpha - \beta ) = \gamma + m\cdot \beta + \lfloor \frac{m\cdot \beta }{\beta }\rfloor (\alpha - \beta ) = \gamma + m\cdot \alpha \). This term equals \(p = \frac{A}{\beta } = \frac{1}{\beta } (\alpha \delta +\beta \gamma ) = \frac{1}{\beta } (\alpha \cdot m\cdot \beta +\beta \gamma ) = \alpha \cdot m + \gamma \).
b) If \(\alpha > \beta \) case a) applies to the dual cycloid \(\mathcal {C}(\beta ,\alpha ,\delta , \gamma )\) (Theorem 11) which is regular since \(\alpha | \gamma \). Hence \(cyc = p'\) where \(p' = \frac{A}{\alpha } = \frac{\beta \cdot p}{\alpha }\) is the process length of the dual cycloid which is isomorphic to \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) by Theorem 11.
c) If \(\alpha > \beta = \gamma = \delta \) then \(cyc = \gamma + \delta - \lfloor \frac{\gamma }{\alpha }\rfloor (\alpha - \beta ) = \beta + \beta - 0 \cdot (\alpha - \beta )\). If \(\alpha = \beta = \gamma = \delta \) then \(cyc = \gamma + \delta + \lfloor \frac{\delta }{\beta }\rfloor (\alpha - \beta ) = \beta + \beta + 1 \cdot 0\). \(\square \)
The regular cycloid \(\mathcal {C}(4,3,3,6)\) does not satisfy any of the conditions of Lemma 21. The parameters in question are \(cyc = 9\), \(p= 11\) and \( \frac{\beta }{\alpha }\cdot p = \frac{3}{4}\cdot 11\).
4 Net Representations of Traffic Queues
From the specification in Definition 6 we deduce different types of cycloids using Theorem 15. This is, however, not a complete proof since it was not shown, that the specifications are correct and complete, but has the great advantage that structural properties of these cycloids are found. Afterwards formal proofs are added, showing that the cycloids are indeed behavioural equivalent to circular traffic queues.
4.1 Cycloids from the Circular Traffic Queue Specification
Theorem 22
From the specifications of a circular traffic queue with gaps \(tq\text {-}1(c,g)\) (Definition 6 a, b) using the Synthesis-Theorem 15 the cycloid \(\mathcal {C}_0(g,c) := \mathcal {C}(g,c,1,1)\) can be deduced, which is isomorphic to the net \(\mathcal {N}_{basic}(c,g)\) of Fig. 3 a).
Proof
From Petri’s papers [3, 4] or [5] it follows definitely that the first two parameters are \(\beta = c\) and \(\alpha = g\). To follow a more formal approach we determine the parameters \(\tau _0, \tau _a, A\) and cyc and then apply Theorem 15 to determine the parameters \(\alpha ,\beta ,\gamma \) and \(\delta \) of the cycloid \(\mathcal {C}(g,c,1,1)\). Consider first the case \(g\ge c\) and the state \(a_1\!\times \! ^{k_1} a_2 \!\times \! ^{k_2} \cdots a_c \!\times \! ^{k_c} \). Due to the assumption \(g\ge c\) it follows \(k_j \ge 1 \;\;(1\le j \le c)\). This means that all traffic items \(a_j\) are able to move right, i.e they are enabled and therefore \(\tau _a = \beta = c\). \(\tau _0\) is the number of transitions having initially at least one marked input place. From all g positions of the queue which are empty a release message was sent to the left. Therefore there is a number of \(\tau _0 = \alpha = g\) such transitions, among these the c active transitions mentioned before. Given a fixed traffic item a and a fixed position in the queue, in a recurrent sequence the traffic item enters the position exactly once. Hence by Definition 6 a) there are \(A =g+c\) transitions, since in this case all \(a_j \in C\) are using the same transitions. In a step the traffic item a gives a release message to enable the access to the position it is leaving. This results in a minimal cycle of length 2. With the parameters \(\tau _a = \beta = c, \tau _0 = \alpha = g, A = g+c\) and \(cyc = 2\) obtained, we compute in the case \(\alpha > \beta \) with Theorem 15: \( \gamma \; mod\; \alpha = \frac{\alpha \cdot cyc -A}{\alpha - \beta } = \frac{g\cdot 2 -(g+c)}{g - c} = \frac{g - c}{g - c} = 1\). With a solution \(\gamma = 1\) of this equation we obtain \(\delta = \frac{1}{\alpha }(A-\beta \cdot \gamma ) = \frac{1}{g}(c+g-c \cdot 1) = 1\). For the case \(\alpha =\beta \) of Theorem 15 we obtain \(\gamma = \delta = \lceil \frac{cyc}{2}\rceil =1\).
Next we prove formally that this cycloid \(\mathcal {C}(g,c,1,1)\) is isomorphic to the basic tq-net \(\mathcal {N}_{basic}(c,g)\) from Fig. 3 a). Starting in the origin (0, 0) of the fundamental parallelogram of \(\mathcal {C}(g,c,1,1)\) using Theorem 10 we compute the smallest point \((\xi ,0)\) on the \(\xi \)-axis equivalent to (0, 0): \(\begin{pmatrix} m \\ n \end{pmatrix} = \frac{1}{A} \begin{pmatrix} \delta &{} -\gamma \\ \beta &{} \alpha \end{pmatrix}\varvec{v} = \frac{1}{g+c} \begin{pmatrix} 1 &{} -1 \\ c &{} g \end{pmatrix}\begin{pmatrix} \xi \\ 0 \end{pmatrix} = \frac{1}{g+c} \begin{pmatrix} \xi \\ \xi \cdot c \end{pmatrix}. \)The smallest positive integer for m is \(\xi =g+c\). Since \(A = g+c\) all transitions have their position on the \(\xi \)-axis from (0, 0) to \((g+c-1,0)\) and form a cycle. This cycle is isomorphic to the cycle \(t_1 \cdots t_{c+g}\) in the net of Fig. 3 a). It remains to prove that \(t_{i,0} \;\; (1 \le i \le c+g)\) is connected to \(t_{i-1,0}\) via a place isomorphic to \(s'_i\) forming a cycle of length 2. As  and
and  (see Fig. 4 a) we have to prove: \(t_{i-1,0} \equiv t_{i,1}\). By Theorem 10 using
(see Fig. 4 a) we have to prove: \(t_{i-1,0} \equiv t_{i,1}\). By Theorem 10 using  For the case \(g < c\) we observe that the net from Fig. 3 a) is symmetric in the following sense. Interpreting the places \(s'_1,s'_2,\cdots s'_{c+g}\) to be the slots of the traffic items instead of \(s_1,s_2,\cdots s_{c+g}\) we obtain an isomorphic system. By the construction in the first part of this proof we obtain the cycloid \(\mathcal {C}(c,g,1,1)\) which is isomorphic to \(\mathcal {C}(g,c,1,1)\) by Theorem 11 a). Therefore the theorem holds also in this case. \(\square \)
For the case \(g < c\) we observe that the net from Fig. 3 a) is symmetric in the following sense. Interpreting the places \(s'_1,s'_2,\cdots s'_{c+g}\) to be the slots of the traffic items instead of \(s_1,s_2,\cdots s_{c+g}\) we obtain an isomorphic system. By the construction in the first part of this proof we obtain the cycloid \(\mathcal {C}(c,g,1,1)\) which is isomorphic to \(\mathcal {C}(g,c,1,1)\) by Theorem 11 a). Therefore the theorem holds also in this case. \(\square \)
As an example, in Fig. 4 b) the cycloid \(\mathcal {C}(4,2,1,1)\) is shown. To illustrate the preceding proof by dashed lines the following equivalent transitions are given: \(t_{3,0} \equiv t_{2,-1}\), \(t_{4,0} \equiv t_{3,-1}\) and \(t_{5,0} \equiv t_{4,-1}\). The transitions \(t_{0,0},\cdots ,t_{5,0}\) on the \(\xi \)-axis are instances of the transitions \(t_{0,0},\cdots ,t_{g+c-1,0}\) in the proof. The places \(s^\leftarrow _{1,0}\), \(s^\leftarrow _{1,-1}\), \(s^\leftarrow _{2,-1}\), \(s^\leftarrow _{3,-1}\), \(s^\leftarrow _{3,-2}\) and \(s^\leftarrow _{4,-2}\) correspond to the complementary places \(s'_1,s'_2,\cdots ,s'_{c+g}\) of the net from Fig. 3 a).
As motivated in the introduction, cyloids are of particular interest and therefore in the focus of this paper. To distinguish them from the preceding model in Theorem 22 we assume \(c>1\) to obtain secure cycloids. To be secure is probably the most important property of cycloids with \(\gamma , \delta > 1\). This has been intensively discussed by Petri in [3, 4] and [5]. For the definition of safe and secure see [4] or [9]. Starting with the specification of circular traffic queues in Definition 6 in Theorems 23 and 24 we will derive cycloid models, that are behavioural equivalent to the models \(tq\text {-}1(c,g)\) and \(tq\text {-}2(c,g)\), respectively. Again, as in Theorem 22, the Synthesis-Theorem 15 will have a prominent role. Therefore, the minimal length cyc of cycles has to be computed. Candidates are the length of the processes \(p = c+g\) and of the release message cycle \(rm = 2\cdot c\). The latter starts with the release message chain which is the sequence of release messages from traffic item \(a_c\) to \(a_{c-1}\), from \(a_{c-1}\) to \(a_{c-2}\) and so on. This can be seen as the synchronization principle of the system. Finally we will obtain \(cyc = min \{p, rm\}\). After this derivation, in Theorem 25 it will be proved by their transition systems, that the cycloid systems \((\mathcal {C}_1(g,c),M_0)\) and \((\mathcal {C}_2(g,c),M_0)\) are in fact behaviour equivalent to \(tq\text {-}1(c,g)\) and \(tq\text {-}2(c,g)\), respectively.
Theorem 23
Within the class of regular cycloids \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) with \(\gamma ,\delta \ge 2\), from the specifications of a circular traffic queue with gaps \(tq\text {-}1(c,g)\) with \(c>1\) (Definition 6) using the Synthesis-Theorem 15 the cycloid \(\mathcal {C}_1(g,c) := \mathcal {C}(g,c,c,c)\) can be deduced. It has process length \(p = g+c\) and minimal cycle length \(cyc = min\{g+c,2\cdot c\}\) (in accordance with Lemma 21 a) and c)).
Proof
For the determination of \(\alpha \) and \(\beta \) we argue as in Theorem 22, i.e. \(\alpha = g\) and \(\beta = c\). If the total number of transitions is A and there are c traffic items with the same process length, this process length is \(p = \frac{A}{c}\). Petri made the assertion [5] that a cycloid with \(\gamma ,\delta \ge 2\) is secure, if and only if every pair of successive arcs lies on a basic cycle. A basic circuit is a cycle with exactly one place marked. This has been proved (also for the more general case of T-systems) by Stehr [6] and it is therefore called the Lemma of Petri/Stehr. Due to this lemma all the marked process cycles are disjoint. As there is a number c of disjoint communicating processes of equal length p the net to be constructed is a regular cycloid (Definition 16) and we can use the naming of Definition 18. The missing places of this net are obtained by considering condition b) of the specification in Definition 6 as follows. Transition \(\langle \!\langle t_i,a_j \rangle \!\rangle \) models the step of traffic item \(a_j\) in position i. To be enabled for this step, it received a release message from \(a_{(j+1)\,mod\, c}\) and when occurring is sending such a message to \(a_{(j-1)\,mod\, c}\). This is modelled by new places  and
and  (Figs. 2 b and 6 c). As a result, we obtain additional \(c\cdot p \) places, i.e. in total \(|S| = 2 \cdot |T|\). To find a minimum length cycle, we next consider a sequence of transitions, which we call the release message chain, rm-chain for short. The rm-chain starts in some transition \([t_i,a_j]\) and continues via place \([s'_i,a_j]\) and transition \([t_{i-1},a_{j-1}]\) down to \([t_{i-c+1},a_{j-c+1}]\), i.e. the process of all traffic items are passed (see Fig. 5 a). Again, first and second index is computed modulo n and c, respectively. In the following the rm-chain is closed to a release message cycle. We continue within the process cycle \(a_{j-c+1}\) a number of c transitions until \([t_{i-c+1+c},a_{j-c+1}] = [t_{i+1},a_{j-c+1}]\) and
(Figs. 2 b and 6 c). As a result, we obtain additional \(c\cdot p \) places, i.e. in total \(|S| = 2 \cdot |T|\). To find a minimum length cycle, we next consider a sequence of transitions, which we call the release message chain, rm-chain for short. The rm-chain starts in some transition \([t_i,a_j]\) and continues via place \([s'_i,a_j]\) and transition \([t_{i-1},a_{j-1}]\) down to \([t_{i-c+1},a_{j-c+1}]\), i.e. the process of all traffic items are passed (see Fig. 5 a). Again, first and second index is computed modulo n and c, respectively. In the following the rm-chain is closed to a release message cycle. We continue within the process cycle \(a_{j-c+1}\) a number of c transitions until \([t_{i-c+1+c},a_{j-c+1}] = [t_{i+1},a_{j-c+1}]\) and  . For the final step by Lemma 19 there are two cases to compute
. For the final step by Lemma 19 there are two cases to compute  (Fig. 5 a). If \(a_{j-c+1} = a_1\) then
(Fig. 5 a). If \(a_{j-c+1} = a_1\) then  since \((i+1+g+c-1)\,mod\,(g+c) = i\) and \(j-c+1 = 1\; \Rightarrow \; c=j\). If \(a_{j-c+1} \ne a_1\) then
since \((i+1+g+c-1)\,mod\,(g+c) = i\) and \(j-c+1 = 1\; \Rightarrow \; c=j\). If \(a_{j-c+1} \ne a_1\) then  since \((j-c) \,mod\, c = j\).
since \((j-c) \,mod\, c = j\).
The length of the rm-cycle is \(rm = 2\cdot c\) transitions and there is no shorter cycle connecting the process cycles. These process cycles have the length of \(p= \frac{A}{c} = \frac{c\cdot (c+g)}{c} = c+g\) transitions and are also candidates for an overall minimal cycle. Therefore the overall minimal cycle of the cycloid is \(cyc = min \{2\cdot c, c+g\}\). For a regular cycloid we construct the following recurrent transition sequence, starting with \([t_{c},a_{c}]\) in the standard initial marking: \([t_{c},a_{c}],[t_{c-1},a_{c-1}], \cdots , [t_{1},a_{1}],\cdots \cdots ,\) \([t_{c+n-1},a_{c}],[t_{c+n},a_{c-1}],\cdots ][t_{n},a_{1}]\) of length \(c\cdot n\). By [9] the cycloid is strongly connected and therefore has a T-invariant of the form  (see reference [1]). This means that all recurrent sequences contain each transition exactly once, as it is in the constructed one and we have \(A = \varGamma (c,g)= c\cdot (g+c)\) (by Definition 6 c, Theorem 4). Together with the value of cyc and the parameters \(\alpha = g\), \(\beta = c\) we can apply Theorem 15 to obtain \(\gamma = \delta = c\) in all cases (see [8] for details). \(\square \)
(see reference [1]). This means that all recurrent sequences contain each transition exactly once, as it is in the constructed one and we have \(A = \varGamma (c,g)= c\cdot (g+c)\) (by Definition 6 c, Theorem 4). Together with the value of cyc and the parameters \(\alpha = g\), \(\beta = c\) we can apply Theorem 15 to obtain \(\gamma = \delta = c\) in all cases (see [8] for details). \(\square \)
In Fig. 2 b) the cycloid \(\mathcal {C}(4,3,3,3)\) is represented as a regular cycloid. Some regular coordinates, like \([s_0,a_1]\) and \([t_1,a_1]\), are added. One of the rm-cycles is highlighted. It has the length \(rm = 2\cdot c = 2\cdot \beta = 6\). The step in the proof where Lemma 19 is applied becomes here  . Also in the next theorem the length rm of the release message cycle is important to determine cyc.
. Also in the next theorem the length rm of the release message cycle is important to determine cyc.
Theorem 24
Within the class of regular cycloids \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) with \(\gamma ,\delta \ge 2\), from the specifications of a circular traffic queue with gaps \(tq\text {-}2(c,g)\) with \(c>1\) (Definition 6) using the Synthesis-Theorem 15 the cycloid \(\mathcal {C}_2(g,c) := \mathcal {C}(g,c,\frac{g \cdot c}{\varDelta },\) \(\frac{g \cdot c}{\varDelta })\) can be deduced. It has process length \(p = \frac{g}{\varDelta }(g+c)\) and minimal cycle length \(cyc = min\{p,\frac{c}{g}\cdot p\}\) (in accordance with Lemma 21 a) and b)).
Proof
The proof is the same as for Theorem 23 until the computation of the length of the rm-chain. Due to the increased length of processes the rm-chain cannot be closed as in this case. By the specification of Definition 6 d) the transition system of \(tq\text {-}2(c,g)\) is a composition of \(\frac{g}{\varDelta }\) copies of the transition system of \(tq\text {-}1(c,g)\). As informally discussed in Sect. 5 this holds also for the corresponding cycloids and is schematically represented in Fig. 5 b) for the case \(\frac{g}{\varDelta } = 2\). At full arcs of this graph one place is omitted. At dotted arcs with label \(\lambda \) a number of \(\lambda \) transitions is supposed (including beginning and end of the arc). For the upper copy the rm-chain from transition a via transitions b and c to d cannot be closed, but is continued to the lower copy. To this end a number \(g-1\) of additional transitions are to be passed. From e via f the rm-chain is closed to complete a rm-cycle. In the general case the structure of the upper copy is repeated a number of \(\frac{g}{\varDelta }\) times. Hence, the overall length of the rm-cycle is the number of transitions on a path from transition a to transition f by repeating the path from b to d a number of \(\frac{g}{\varDelta }-1\) times: \(rm = (c-1) + (\frac{g}{\varDelta }-1)\cdot (c+1+g-1) + c+1 = \frac{g}{\varDelta }\cdot (g+c) + (c-g) = p + (c-g)\). If \(c\ge g\) the length of the rm-cycle is not smaller than the process-length p, which is the minimal cycle in this case, hence \(cyc = p = \frac{g}{\varDelta }\cdot (g+c)\). The model \(tq\text {-}2(c,g)\) is symmetric with respect to c and g. The same proof can be made with c and g interchanged and \(cyc = \frac{c}{\varDelta }\cdot (g+c)\) if \(c \le g\). Using these values of cyc, and the parameters \(\alpha = g\), \(\beta = c\) and \(A = \varXi (c,g) = \frac{g}{\varDelta }\cdot (g+c)\cdot c\) (by the analogous argument as in the proof of Theorem 23) we apply Theorem 15 with \(g =\alpha > \beta = c\). The resulting cycloid is \(\mathcal {C}(g,c,g, c\cdot (\frac{g+c}{\varDelta }-1))\). By Theorem 11 c) this cycloid is equivalent to \(\mathcal {C}(\alpha ,\beta ,\gamma + q\cdot \alpha ,\delta - q\cdot \beta )\). With \(q= \frac{c}{\varDelta }-1\) we obtain \(\gamma ' = \gamma + q\cdot \alpha = g + (\frac{c}{\varDelta }-1)\cdot g = \frac{g\cdot c}{\varDelta }\) and \(\delta ' = \delta - q\cdot \beta = c\cdot (\frac{g+c}{\varDelta }-1) - (\frac{c}{\varDelta }-1)\cdot c = \frac{g\cdot c}{\varDelta } \). Case \(\alpha < \beta \) is similar. See [8] for details of the computation. For \(\alpha = \beta \) we obtain \(\gamma = \delta = \lfloor \frac{cyc}{2}\rfloor = \frac{g\cdot g}{\varDelta }\). \(\square \)
4.2 Isomorphisms
The formal synthesis of cycloids from a less formal specification in Sect. 4.1 is completed in this section by formal analysis. We will prove that the obtained cycloids are behaviour equivalent to the circular traffic queues. This is done using operational semantics, i.e. by comparing the labelled transition systems.
Theorem 25
-
a)
The reachability graph of the cycloid system \((\mathcal {C}_1(g,c),M_0) := \mathcal {C}(g,c,c,c,M_0)\) is isomorphic to the labelled transition system \(LTS_p(c,g) \) with \(p =n=c+g\), where \(M_0\) and \(ind_0\) are the regular initial marking and state, respectively. The same holds for the standard initial marking.
-
b)
The reachability graph of the cycloid system \((\mathcal {C}_2(g,c),M_0) := \mathcal {C}(g,c,\frac{g\cdot c}{\varDelta },\frac{g\cdot c}{\varDelta },\) \(M_0)\) is isomorphic to the labelled transition system \(LTS_p(c,g)\) with \( p=\frac{g}{\varDelta }\cdot n =\frac{g}{\varDelta }\cdot (c+g)\), where \(M_0\) and \(ind_0\) are the regular initial marking and state, respectively. The same holds for the standard initial marking.
Proof
The reachability graph \(\mathcal {RG}(\mathcal {N}_{},M_0) = (\mathcal {R}(\mathcal {N}_{},M_0),\rightarrow )\) of the cycloid net can be seen as a labelled transition system \(LTS' = (States',T',tr',ind'_0)\). Each marking contains the same number \(n = g+c\) of marked places as this holds in the initial marking of the T-net. Therefore we also consider such a marking as an ordered set by an index function \(ind': \{1,\cdots ,n\} \rightarrow S\), where S is the set of places. The labelled transition systems \(LTS := LTS_p(c,g) \) and \(LTS'\) are isomorphic if there are bijective mappings \(\varphi \) and \(\psi \). \(\varphi \) gives for each state \(ind \in States\) a corresponding state \(ind' = \varphi (ind) \in States'\) and \(\psi \) gives for each transition \(t \in T\) a corresponding transition \(t' = \psi (t) \in T'\). The following condition is required: \((ind_1,t,ind_2) \in tr \; \Leftrightarrow \; (\varphi (ind_1),\psi (t),\varphi (ind_2)) \in tr'\). The cycloids of the theorem are regular by Theorem 17 and we can use its regular coordinates (Definition 18, Lemma 19). In the remaining proof, all indices containing j are understood \(modulo \; c\) whereas indices containing i are understood \(modulo \; n\) in a) and \(\,modulo\; p\) in part b). We start with part a) of the theorem:
1. Definition of \(\varphi \) and \(\psi \). We define \(\varphi (ind) := \{ind'(i) | 1 \le i \le n\}\) with \(ind'(i) := [\hat{s}_i,next(i)]\) and \(\hat{s}_i\; = \; \left\{ \begin{array}{lll} s_{i-1} &{} \text {if} &{} ind(i) \in C \\ s'_{i} &{} \text {if} &{} ind(i) = u \in G\\ \end{array} \right. \). The function next is defined by: \(next(i)= a_j \in C \) in a position including or next to i (\(\,mod\,n\)). Hence, if \(ind(i) = a_j \in C\) then \(next(i) = a_j\) and \(ind'(i) = [s_{i-1},a_j]\). If \(ind(i) \in G\) then \(next(i) = a_j \in C\) is the first \(a_j \in C\) after position i (\(\,mod\,n\)) and \(ind'(i) = [s'^{}_{i},a_j]\). The mapping \(\varphi \) is bijective since the image of a state is an encoding of this state. In Fig. 6 a) the case for a state of size \(n=7\) is shown. The mapping \(\psi \) is obviously injective since \(\psi (\langle \!\langle t_i,a_j\rangle \!\rangle ) = [t_i,a_j]\) and also surjective as \(LTS_1(c,g)\) has a number of \(\varGamma (c,g) = (c+g)\cdot c\) transitions (Theorem 4) as well as \((\mathcal {C}_1(g,c),M_0) :=\mathcal {C}(g,c,c,c,M_0)\).
2. \(\mathbf {(s_1,t,s_2) \in tr \Rightarrow (\varphi (s_1),\psi (t),\varphi (s_2) )\in tr}'\). The occurrence of a transition \(\langle \!\langle t_i,a_j \rangle \!\rangle \) of LTS implies that two positions are involved. \(ind(i)ind(i+1) = a_j \!\times \! \) is changed to \(ind(i)ind(i+1) = \!\times \! \,a_j\). By transformation with the mapping \(\varphi \) we obtain that \(ind'(i)ind'(i+1) = [s_{i-1},a_j][s'_{i+1},a_{j+1}] \) is changed to \(ind'(i)ind'(i+1) = [s'_{i},a_j][s_{i},a_j] \) (Fig. 6 b). This is just the result of the occurrence of the transition \(\psi (\langle \!\langle t_i,a_j\rangle \!\rangle ) = [t_i,a_j]\) of \(LTS'\) (Fig. 6 c).
Illustrating the bijections \(\varphi \) and \(\psi \) in the proof of Theorem 25.
3. \(\mathbf {(s_1,t,s_2) \notin tr \Rightarrow (\varphi (s_1),\psi (t),\varphi (s_2) )\notin tr'.}\) A move of a traffic item \(a_j\) at position i by transition \(\langle \!\langle t_i,a_j\rangle \!\rangle \) is impossible if and only if there is a sequence of traffic items \(a_{j+1},\cdots ,a_{j+r}\) (\(r\ge 1\) and all \(\,mod\,c)\) at positions \(i+1,\cdots ,i+r\) (all \(\,mod\,n)\) followed by a gap \(\times \! \in G\) at position \((i+r+1)\,mod\,n\). By the map \(\varphi \) in the cycloid the corresponding transitions \([t_{i+s},a_{j+s}], (0\le s \le r)\) have an empty input place \([s'_{i+s+1},a_{j+s+1}]\), with the exception of \([t_{i+r},a_{j+r}]\). For this transition also \([s'_{i+r+1},a_{j+r+1}]\) is marked since \(a_{j+r}\) can make a move to exchange with the gap \(\times \!\). This sequence is part of a release message chain (Fig. 5). Since the cycloid is live and safe [9] the chain is part of a cycle with exactly one token, which implies that \([s'_{i+1},a_{j+1}]\) is unmarked. Hence, transition \(\psi (\langle \!\langle t_i,a_j\rangle \!\rangle ) =[t_i,a_j]\) cannot occur.
4. Initial state. Applying the mapping \(\varphi \) to Definition 1 of a regular initial state we obtain \(ind'(i) = [s_{i-1},a_i]\) for \(1 \le i \le c\) and \(ind'(i) = [s'_i,a_1]\) for \(c < i \le n\). Hence, for \(1 \le i \le c\) traffic item \(a_i\) is in position i and for \(c < i \le n\) there is a gap and the next traffic item \(modulo\;n\) is \(a_1\). To prove the same for the standard initial state (Definition 3) we have to show that this meets Definition 12 of a standard initial marking of the cycloid. If we substitute j by \(-\eta \) the bound \(1 \le j \le c\) becomes \(-1 \le \eta \le -c\). Then we substitute g, c and x in \(j-1 < \frac{c}{g}\cdot x \le j\) by the cycloid parameters \(\alpha \), \(\beta \) and \(\xi \), respectively. As a result we obtain \(-\eta \,-\,1 < \frac{\beta }{\alpha }\cdot \xi \le -\eta \) which is equivalent to \(\, \beta \xi \,+\, \alpha \eta \,\le \, 0 \ \wedge \ \beta \xi \,+\, \alpha (\eta \,+\,1) \,>\, 0 \) from the definition of the backward places  of \(M_0\) (Definition 12). In this definition the bound \(-1 \le \eta \le -c\) is not needed since it is replaced by the quotient \(/_\equiv \). The standard initial state is completely determined by the distribution of the gaps by the definition of the \(r_i\). The same holds for the cycloid. In fact, the definition of the forward places
of \(M_0\) (Definition 12). In this definition the bound \(-1 \le \eta \le -c\) is not needed since it is replaced by the quotient \(/_\equiv \). The standard initial state is completely determined by the distribution of the gaps by the definition of the \(r_i\). The same holds for the cycloid. In fact, the definition of the forward places  is unambiguously deducible from the definition of the backward places
is unambiguously deducible from the definition of the backward places  . For a more formal proof of this assertion consider the definition of a m-path in [9].
. For a more formal proof of this assertion consider the definition of a m-path in [9].
Figure 6 d) is the analogon to a) in the proof of part b) with respect to \(\mathcal {C}(4,3,12,12)\) with 84 transitions. In principle, the proof is similar to part a), but is omitted due to space limitations and can be found in [8]. \(\square \)
4.3 Representations of Circular Queues by T- and Coloured Nets
In Fig. 3 a) Petri’s queue of cars is represented as net \(\mathcal {N}_{basic}(c,g)\) with a regular initial marking. The positions of a number of c cars are represented by black tokens in the places \(s_0,\cdots ,s_{c-1}\) followed by g tokens in the complementary places \(s'_{c+1},\cdots ,s'_{c+g}\) representing the gaps. By the complementary places the net is safe and the cars cannot pass each other. They cannot be distinguished which is different in the net \(\mathcal {N}_{coul}(c,g)\) from part b) of Fig. 3, where the cars have identifiers \(a_1,\cdots ,a_c\). To handle such individual tokens a coloured net is used containing a variable \(\mathsf {x}\). It has been proved in [8] that applying a light modification of the standard procedure of unfolding the net into a T-net with black tokens only, a net is obtained that is isomorphic to the cycloid \(\mathcal {C}_1(g,c) = \mathcal {C}(g,c,c,c)\). As a result, this cycloid is a folding of the Petri space and an unfolding of the coloured net \(\mathcal {N}_{coul}(c,g)\). As shown, the net has the behaviour of a circular traffic queue with gaps \(tq\text {-}1(c,g)\). In the coloured net \(\mathcal {N}_{sym}(c,g)\) from part c) of Fig. 3 also the places \(s'_k\) have individual tokens representing traffic items moving to the left hand side. A counter place named r has the effect that the initial marking is not reached before a number of \(\frac{g}{\varDelta }\) iterations of the loop. In [8] it is proved that the unfolding of this coloured net into a T-net is isomorphic to \(\mathcal {C}_2(g,c) = \mathcal {C}(g,c,\frac{g\cdot c}{\varDelta },\frac{g\cdot c}{\varDelta })\).
5 Composition of Cyloids and Summary
In this paper the theory of cycloids is extended by new formal methods and new results concerning circular traffic queues. The use of matrix algebra leads to a more mathematical and easier handling of the cycloid equivalence relation. The formalism of regular cycloids is introduced having a process structure like circular traffic queues, but miss some of the clear mathematical properties of general cycloids. The proof of isomorphism of circular traffic queues and special cycloids is facilitated by the use of these regular cycloids as a link. The concept of release message chain and cycle is shown to be useful. It appears to be closely connected to the notion of minimal cycles which was so important in earlier publications on cycloids. Using Theorem 10 it is straight forward to deduce (see [8]), that the equivalence relation \(\equiv \) becomes finer if the cycloid parameters are integer multiples. In particular \(\equiv _1\;\;\subseteq \;\;\equiv _2\) for the equivalence relations of \(\mathcal {C}_1(\alpha ,\beta ,n\cdot \gamma ,n\cdot \delta )\) and \(\mathcal {C}_2(\alpha ,\beta ,\gamma ,\delta )\) with  , respectively. For instance, the cycloid \(\mathcal {C}(\alpha ,\beta ,2\cdot \gamma ,2\cdot \delta )\) has a fundamental parallelogram consisting of two copies of the fundamental parallelogram of \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\), pasted together at the line segment \(\overline{QR}\) (Fig. 1 b) of the first and the line segment \(\overline{OP}\) of the second. Iterating this construction n times the so-called n-fold temporal iteration of \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is obtained and denoted by \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )^{[n]}\). As some kind of a formal summary, this notion allows to characterize the two most important cycloids of this article by iterations of the basic cycloid \(\mathcal {C}(\alpha ,\beta ,1,1)\). Table 1 contains the two models of circular traffic queues \(tq\text {-}1(c,g)\) and \(tq\text {-}2(c,g)\), their modelling by cycloids \(\mathcal {C}_0(g,c)\), \(\mathcal {C}_1(g,c)\) and \(\mathcal {C}_2(g,c)\), the corresponding values of minimal cycles, the numbers of transitions and their representations as iterations of \(\mathcal {C}_0(g,c)\).
, respectively. For instance, the cycloid \(\mathcal {C}(\alpha ,\beta ,2\cdot \gamma ,2\cdot \delta )\) has a fundamental parallelogram consisting of two copies of the fundamental parallelogram of \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\), pasted together at the line segment \(\overline{QR}\) (Fig. 1 b) of the first and the line segment \(\overline{OP}\) of the second. Iterating this construction n times the so-called n-fold temporal iteration of \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )\) is obtained and denoted by \(\mathcal {C}(\alpha ,\beta ,\gamma ,\delta )^{[n]}\). As some kind of a formal summary, this notion allows to characterize the two most important cycloids of this article by iterations of the basic cycloid \(\mathcal {C}(\alpha ,\beta ,1,1)\). Table 1 contains the two models of circular traffic queues \(tq\text {-}1(c,g)\) and \(tq\text {-}2(c,g)\), their modelling by cycloids \(\mathcal {C}_0(g,c)\), \(\mathcal {C}_1(g,c)\) and \(\mathcal {C}_2(g,c)\), the corresponding values of minimal cycles, the numbers of transitions and their representations as iterations of \(\mathcal {C}_0(g,c)\).
Notes
- 1.
An elementary cycle is a cycle where all nodes are different.
References
Desel, J., Esparza, J.: Free Choice Petri Nets. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge (1995)
Kummer, O., Stehr, M.-O.: Petri’s axioms of concurrency - a selection of recent results. In: Azéma, P., Balbo, G. (eds.) ICATPN 1997. LNCS, vol. 1248, pp. 195–214. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63139-9_37
Petri, C.A.: On technical safety and security. Petri Net Newsl. 33, 25–30 (1989). https://www.informatik.uni-augsburg.de/pnnl/
Petri, C.A.: Nets, time and space. Theor. Comput. Sci. 153, 3–48 (1996)
Petri, C.A., Yuan, C.Y.: On technical safety and security (continued). Petri Net Newsl. 35, 8–15 (1990). https://www.informatik.uni-augsburg.de/pnnl/
Stehr, M.O.: Characterizing security in synchronization graphs. Petri Net Newsl. 56, 17–26 (1999). https://www.informatik.uni-augsburg.de/pnnl/
Valk, R.: On the structure of cycloids introduced by Carl Adam Petri. In: Khomenko, V., Roux, O.H. (eds.) PETRI NETS 2018. LNCS, vol. 10877, pp. 294–314. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-91268-4_15
Valk, R.: Formal properties of circular traffic queues and cycloids (2019). http://uhh.de/inf-valk-traffic
Valk, R.: Formal properties of Petri’s cycloid systems. Fundam. Informaticae 169, 85–121 (2019)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Valk, R. (2020). Circular Traffic Queues and Petri’s Cycloids. In: Janicki, R., Sidorova, N., Chatain, T. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2020. Lecture Notes in Computer Science(), vol 12152. Springer, Cham. https://doi.org/10.1007/978-3-030-51831-8_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-51831-8_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51830-1
Online ISBN: 978-3-030-51831-8
eBook Packages: Computer ScienceComputer Science (R0)






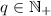 and
and 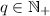 and
and 



