Cryptanalysis of FlexAEAD

Abstract

This paper analyzes the internal keyed permutation of FlexAEAD which is a round-1 candidate of the NIST LightWeight Cryptography Competition. In our analysis, we report an iterated truncated differential leveraging on a particular property of the AES S-box that becomes useful due to the particular nature of the diffusion layer of the round function. The differential holds with a low probability of $2^{-7}$ for one round which allows it to penetrate the same number of rounds as claimed by the designers, but with a much lower complexity. Moreover, it can be easily extended to a key-recovery attack at a little extra cost. We further report a Super-Sbox construction in the internal permutation, which is exploited using the Yoyo game to devise a 6-round deterministic distinguisher and a 7-round key recovery attack for the 128-bit internal permutation. Similar attacks can be mounted for the 64-bit and 256-bit variants. All these attacks outperform the existing results of the designers as well as other third-party results. The iterated truncated differentials can be tweaked to mount forgery attacks similar to the ones given by Eichlseder $et$ $al.$ Success probabilities of all the reported distinguishing attacks are shown to be high. All practical attacks have been experimentally verified. To the best of our knowledge, this work reports the first key-recovery attack on the internal keyed permutation of FlexAEAD.

1 Introduction

In the modern era, the aim is to connect each of the physical devices, even the miniature ones, with the internet so that they can be monitored and controlled remotely for maximum utilization. These devices are powered with the ability of communicating among themselves. Such a huge interconnected system, consisting of numerous tiny devices, is not free from vulnerabilities. Moreover, a security breach in such systems can be catastrophic. So, a major concern in the world of internet-of-things is how to provide security and privacy to each system with the constraints of limited power and area. SKINNY [9], PRESENT [10], QARMA [6], KATAN and KTANTAN [11], GIFT [8] are some of the block ciphers which are designed for such constrained environments. Until recently, no standardization process has been introduced (like AES Development [2], SHA-3 Project [4], CAESAR Competition [1]) for cryptographic schemes in lightweight environments. NIST LightWeight Cryptography (LWC) competition [3] is a major step towards addressing these issues. There are a total of 57 submissions in this competition. Apart from authenticated encryption algorithms in lightweight environment, some of the designs also comprise of hash functions. Some of them have also provided new primitives for block cipher design.

FlexAEAD is one of the round-1 candidates proposed by Nascimento and Xexéo in NIST LWC competition [17]. It is a family of lightweight authenticated encryption schemes with associated data. In this version, the processing of Associate Data (AD) has been added to the original variants [15, 16, 18]. There are mainly three variants of FlexAEAD that have been listed with block sizes of 64, 128 and 256 bits. In general, a FlexAEAD scheme is denoted by FlexAEAD-$b$, with b being the block size. The size of nonce and tag is the same as block size across all variants. The length of key is 128 bits for FlexAEAD-$64$ and FlexAEAD-$128$ whereas it is 256 bits for FlexAEAD-$256$. The nonce in FlexAEAD is used to generate sequence numbers which are eventually XOR-ed with associated data, plaintext and intermediate-state to produce ciphertext-tag pair. The lightweight of FlexAEAD essentially comes from the fact that for computational purposes it uses XOR operations, a look-up table for substitution layer and bit reorganizations for BlockShuffle layer. FlexAEAD has an underlying block cipher; internal keyed permutation ($\text{ PF }_k$) of 64, 128 and 256 bits. We have analyzed the $\text{ PF }_k$ function and reported several results. A brief description of $\text{ PF }_k$ has been provided in Sect. 2.1. The $\text{ PF }_k$ with x-bit state is referred to as Flex-$x$.

Existing Security Claims. The designers have claimed that mounting an attack on Flex-$x$ based on differential and linear characteristics is more difficult than the brute force attack. According to their analysis, the probability of best differential characteristic for Flex-$64$, Flex-$128$ and Flex-$256$ is $2^{-168}$, $2^{-204}$ and $2^{-240}$ respectively. The number of chosen plaintext pairs required for a linear trail in Flex-$64$, Flex-$128$ and Flex-$256$ are $2^{272}$, $2^{326}$ and $2^{380}$ respectively [17]. Eichlseder $et$ $al.$ have claimed several forgery attacks [12, 13] on FlexAEAD. They have followed several different approaches: like changing associated data, truncating ciphertexts and reordering ciphertexts. They have reported differential characteristics for 5-round Flex-$64$, 6-round Flex-$128$ and 7-round Flex-$256$ with probability $2^{-66}$, $2^{-79}$ and $2^{-108}$ respectively. Length extension attacks based on associated data have also been shown [14]. Table 1 shows the comparison of different trail probabilities reported till date with the ones furnished in the current work. For uniformity, we have enlisted trail probabilities for same number of rounds.

Table 1. Comparison of trail probabilities of internal keyed permutation of FlexAEAD

Our Contributions. First of all, we report an iterated truncated differential for all the variants of $\text{ PF }_k$ using the property of AES Difference Distribution Table (DDT) where the output difference of a byte is confined to either upper or lower nibble. The probability of the truncated differential for one round is $2^{-7}$. Its iterative nature makes it possible to penetrate more number of rounds for all Flex-$x$. These differentials are further exploited to devise key-recovery attacks on all the variants.

Next, we explore the application of the Yoyo property which has been introduced by Rønjom $et$ $al.$  [20] on generic 2-round Substitution Permutation Networks and further extended on AES-based permutations and block ciphers [7, 21]. We have been able to devise deterministic Yoyo distinguishers for 4, 6 and 8 rounds of Flex-$64$, Flex-$128$ and Flex-$256$ respectively which are further extended by one more round to mount key recovery attacks. All key recovery attacks (reported in this work) with their respective complexities are summarized in Table 2. For the iterated truncated differential, the maximum number of rounds that is penetrable for a Flex-$x$ variant are enlisted in the table. The attacks with practical complexities are experimentally verified.

Table 2. Comparison of Key Recovery Attacks. Encs, Decs, MAs refers to encryption queries, decryption queries and Memory Accesses respectively. For uniformity, memory accesses and memory complexity has been provided in terms of Flex-$128$ state. 1 MA for Flex-$128$ corresponds to 2 MA in Flex-$64$ and 0.5 MA in Flex-$256$. Memory complexity is also normalized by the same ratio.

Further, we have used the iterated truncated differentials to mount forgery attacks on FlexAEAD similar to the ones reported by Eichlseder $et$ $al.$  [12, 13]. Finally, to measure the effectiveness of all distinguishers reported in this work, their theoretical success probabilities are estimated by following the approach given in [19]. The success probabilities are estimated to be high and some of them with practical complexities are experimentally verified.

All the attacks presented in this paper exploit the vulnerability that merely dividing the bytes into nibbles while using AES S-box is susceptible to differential attacks as diffusion may be slow in some scenarios. Although, FlexAEAD is out of NIST lightweight cryptography competition, this particular vulnerability has a far-reaching impact on designing ciphers using AES S-box. Hence, it forms the basis of continued motivation for this work.

Outline. The necessary details about $\text{ PF }_k$ and Yoyo game are briefly visited in Sect. 2. Section 3 describes the key-recovery attacks based on Iterated Truncated Differential. Section 4 details the attacks based on Yoyo game. The success probabilities of distinguishing attacks and their experimental verification are illustrated in Sect. 5. Forgery attacks based on Iterated Differentials are described in Sect. 6. Finally, the concluding remarks are furnished.

Fig. 1.

Byte representation of Flex-$128$ block cipher

2 Preliminaries

The analysis in this paper is regarding the $\text{ PF }_k$ of FlexAEAD. So, first of all, a brief description of $\text{ PF }_k$ is given. Since a major part of this work uses the Yoyo strategy, for the sake of completeness, a brief description of Yoyo game and its relevant results are provided.

2.1 Internal keyed Permutation $\text{ PF }_k$

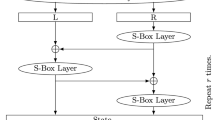
The design strategy of $\text{ PF }_k$ follows the Feistel construction. Let m be the number of bytes in a Flex-$x$ state ($m=x/8$). The state of Flex-$x$ is denoted by B and is divided into two equal halves: the bytes in the left half being numbered from $B[0]$ to $B[\frac{m}{2}-1]$, and the ones on the right half from $B[\frac{m}{2}]$ to $B[m-1]$. Each byte is divided into two parts representing the two nibbles with the upper half (upper nibble) being the most significant one. The other nibble is called as lower nibble. After the BlockShuffle operation, m nibbles from $B[0]$ to $B[\frac{m}{2}-1]$ constitute the upper nibbles of each bytes whereas the nibbles from $B[\frac{m}{2}]$ to $B[m-1]$ constitute the lower ones. The bytes at position $B[i]$ and $B[i+\frac{m}{2}]$ are referred to as a “pair of symmetric bytes". Application of BlockShuffle operation on state s in r-th round is denoted by $BS^{r}(s)$. Figure 1 shows the byte representation in Flex-$128$ state.

Figure 2 shows the round function of Flex-$128$. Each round of Flex-$x$ starts with the BlockShuffle operation. Then the state is bifurcated and the right half goes through subbytes operation. AES S-box is used for byte substitution. The left half is modified by XOR-ing it with the right half and applying the subbytes operation. The modified values of the left half are XOR-ed with the right half values and subbytes is applied to get new values of the right half. Then the left and right half are combined to form the new state and the next round follows. In Flex-$x$ there are no round keys; there are only two subkeys $K_{\alpha }$, $K_{\beta }$ which are used at the beginning and the end of round functions respectively. The total number of rounds for Flex-$64$, Flex-$128$ and Flex-$256$ are 5, 6 and 7 respectively [17]. In authenticated encryption modes, three $\text{ PF }_k$ are used sequentially for encrypting a block of plaintext, which makes the effective number of rounds 15, 18 and 21 in FlexAEAD-$64$, FlexAEAD-$128$ and FlexAEAD-$256$ respectively.

Key Generation. Key generation in Flex-$x$ uses the $\text{ PF }_k$ where the master key K is divided into two parts and used as two subkeys. State is initialized with $0^{\mid K \mid /2}$ and three times $\text{ PF }_k$ is applied to generate part of the subkey to be used for encryption of the plaintext. This process is repeated several times till the required number of subkeys is obtained. Apart from the first round, each time the state is initialized with the output of the previous round. The key generation algorithm makes it difficult to recover the master key from a known subkey. The key recovery attacks presented in this paper refers to the recovery of subkeys.

2.2 Yoyo Game

By applying the Yoyo game strategy, a deterministic distinguisher for two generic Substitution-Permutation (SP) rounds have been reported [20]. This has been used to devise a 6-round Flex-$128$ distinguisher and a 7-round Flex-$128$ key recovery attack. To apply their results, first Zero Difference Pattern and Swapping of Words need to be defined which were originally given in  [20].

Let $F:\mathbb {F}^n_q \rightarrow \mathbb {F}^n_q$ be a permutation with $q=2^k$ and

$$F(x) = S \circ L \circ S \circ L \circ S(x).$$

Here, S is the concatenation of several smaller S-boxes operating on elements from $\mathbb {F}_q$ in parallel and L is the linear layer over $\mathbb {F}^n_q$. A state is defined as the vector of words $\alpha =(\alpha _0,\alpha _1,\cdots ,\alpha _{n-1}) \in \mathbb {F}^n_q$.

Definition 1

Zero Difference Pattern. [20] Let $\alpha \in \mathbb {F}_{q}^{n}$ for $q=2^{k}$. The Zero Difference Pattern for $\alpha$ is

$\nu (\alpha )=(z_0,z_1,...,z_{n-1})$,

where $\nu (\alpha )$ takes values in $\mathbb {F}_{2}^{n}$ and $z_i=1$ if $\alpha _i=0$ or $z_i=0$ otherwise.

Fig. 2.

Round function of Flex-$128$ block cipher

Definition 2

Swapping of Words. [20] Let $\alpha ,\beta \in \mathbb {F}_{q}^{n}$ be two states and $v \in \mathbb {F}_{2}^{n}$ be a vector, then $\rho ^{v}(\alpha ,\beta )$ is a new state in $\mathbb {F}_{q}^{n}$ created from $\alpha , \beta$ by swapping components among them. The $i^{th}$ component of $\rho ^{v}(\alpha ,\beta )$ is defined as

$$\begin{aligned} \rho ^{v}(\alpha ,\beta )_i= {\left\{ \begin{array}{ll} \alpha _i, &{} \text {if }v_i=1;\\ \beta _i, &{} \text {if }v_i=0. \end{array}\right. } \end{aligned}$$

(1)

The following theorem describes the deterministic distinguisher for 2 generic SP-rounds ($G_2$).

Theorem 1

[20] Let $p^0,p^1 \in \mathbb {F}_{q}^{n}$, $c^0=G_{2}(p^0)$ and $c^1=G_{2}(p^1)$. For any vector $v \in \mathbb {F}_{2}^{n}$, $c^{'0}=\rho ^{v}(c^0,c^1)$ and $c^{'1}=\rho ^{v}(c^1,c^0)$. Then

$$\begin{aligned} \nu (G_2^{-1}(c^{'0}) \oplus G_2^{-1}(c^{'1})) =\nu (p^{'0} \oplus p^{'1}) =\nu (p^{0} \oplus p^{1}). \end{aligned}$$

(2)

The notion behind devising such distinguisher is to choose a plaintext pair according to some Zero Difference Pattern and query this plaintext pair to the cipher to obtain a ciphertext pair. Words are swapped between the two ciphertexts on the basis of the substitution layer to produce modified ciphertexts that are queried to obtain new pair of plaintexts. Theorem 1 states that the Zero Difference Pattern of the original plaintext pair and the modified plaintext pair should be the same if the cipher is of the form $S \circ L \circ S$. In the following section, details regarding iterated truncated differential attacks on $\text{ PF }_k$ are discussed.

3 Iterated Truncated Differential Attacks on $\text{ PF }_k$

Differential of iterative characteristics can be easily exploited to penetrate full rounds of a cipher. The fundamental strategy behind devising an iterated differential is to choose the output differential in a way such that after some operations the input differential can be produced easily. Alkhzaimi $et$ $al.$ have reported such differentials for SIMON family of block ciphers [5]. In this work, iterated differentials in truncated form have been considered. First of all, a particular property of AES S-box which has been exploited needs to be discussed.

Property of AES DDT Table. From AES DDT table it has been observed that the number of randomly chosen input differences that map to output differences, such that the non-zero bits in each output difference are confined to the upper nibble is 4096. Same is true if they are confined to the lower nibble. In other words,

where S is the AES S-box. Therefore, with probability $\frac{4096}{2^{16}}= 2^{-4}$ a random input difference transits to upper nibble in the output difference. With same probability, random input difference transits to lower nibble. The way this property is exploited to devise iterated truncated differential is provided in the next subsection.

3.1 One Round Probabilistic Iterated Truncated Differential

Refer to Fig. 3 for the iterated differential of Flex-$128$. In $X_1$, keeping the difference in B[0] ensures that in $Y_1$ difference are in B[0] and B[8]. With probability $2^{-7}$ both differences are confined in either upper nibble or lower nibble in those bytes. Therefore, after BlockShuffle only one byte is active in $X_2$. In $X_2$ the active byte can be either B[0] or B[1], depending on whether the upper or lower nibbles in $Y_1$ are active. The iterative nature of the differential comes from the fact that in $X_2$ only one byte is active at the cost of $2^{-7}$ probability under the constraints that only one byte is active in $X_1$, and this particular event can be repeated an infinite number of times. Similar kinds of iterated truncated differential with the same probability exists for Flex-$64$ and Flex-$256$. Now, how these one round differentials are exploited to penetrate more number of rounds is discussed.

Fig. 3.

Iterated Truncated Differential with One-round probability of $2^{-7}$. Note that the key-addition is not shown, since it has no effect on the trail

Application to Variants of $\mathbf{PF }_{\varvec{k}}$. The one round iterated truncated differential can be applied to all the versions of $\text{ PF }_k$. The iterated differential occurs with probability $2^{-7}$. Depending on the blocksize, last few rounds can be made free as no byte to nibble transition is needed for those rounds.

Let the iterated truncated differential is kept free for last $f$ rounds for Flex-$x$. Then the probability of the trail is $2^{-7\times (r-f)}$. For uniform random discrete distribution, the same event will occur with probability $2^{-8 \times (\frac{x}{8}-2^{f})}= 2^{-(x-8\times 2^{f})}$. For devising a distinguisher for x-bit flex,

$$\begin{aligned}&2^{-7\times (r-f)} > 2^{-(x-8 \times 2^{f})}\nonumber \\ \implies&r < \frac{(x-8 \times 2^{f})}{7} + f. \end{aligned}$$

(3)

Table 3. Iterated differential trails

Table 4. Comparison of differential probabilities

Then, the probability of the iterated truncated differential trail for r-round Flex-$x$ is $2^{-7 \times (r-f)}$. Table 3 shows the trail probabilities for different Flex-$x$. $r_{max}$ denotes the maximum number of rounds reachable under the constraints of fixed $f$. Table 4 compares the differential probabilities claim of the designers with our claim using the iterated differential. $\mathcal {P}_D$ denotes the designers’ claim whereas $\mathcal {Q}_D$ denotes our claim.

Another aspect of such kind of trails is the position of active byte in each round. As mentioned in 3.1, if $B[0]$ is active in $X_0$, then either $B[0]$ or $B[1]$ is active in $X_2$. If $B[1]$ is active in $X_2$, then either $B[2]$ or $B[3]$ is active in $X_3$. In general, for Flex-$x$ if $B[m]$ or $B[\frac{x}{2 \times 8}+m]$ is active in $X_i$, then either $B[2m]$ or $B[2m+1]$ is active in $X_{(i+1)}$. Now, the mechanism of transforming these distinguishers to key recovery attacks is detailed.

3.2 Key Recovery Using Iterated Truncated Differential

At the end of each round, the difference in a pair of symmetric bytes after S-box transits to the same nibble with probability $2^{-7}$. This has been used as a filtering technique to eliminate wrong key bytes. Let the first subkey, $K_{\alpha }$ for Flex-$128$ is being recovered. Using iterated truncated differential for r rounds a right pair can be identified with probability $2^{-7\times (r-f)}$, where $f$ is number free rounds. Suppose, in the right pair the initial difference is in $B[i]$ and $B[i+8]$. So, we guess key byte $K_{\alpha }[i]$ and $K_{\alpha }[i+8]$. There are $2^{16}$ possible guesses and these are used to verify whether at the end of first-round byte to nibble transition occur. Out of $2^{16}$, $2^{9}$ key-byte candidates remain. For further filtering, two more right pairs are used. The second right pair reduces the candidate numbers to $2^2$. After filtering using three different right pairs, it is expected only one candidate should remain for the key byte pair . For the remaining symmetric key bytes, the procedure is repeated 7 more times. In the end, it is expected that only one key candidate should pass the test. The other subkeys can be recovered similarly. After recovering the first subkey, the values of the plaintexts are exactly known till the second subkey whitening. The same key recovery attacks are applicable for Flex-$64$ and Flex-$256$. In the next subsections, details about the complexities of all attacks and experimental verification of practical ones are provided.

3.3 Complexity Evaluation

Distinguisher. To distinguish iterated truncated differential for r rounds, $2^{7 \times (r-f)}$ number of plaintext pairs are required, where $f$ is the number of free rounds at the end. In devising the distinguishers, difference can be kept in 2 bytes only in $X_1$, which yields ${2^{16} \atopwithdelims ()2} \approx 2^{31}$ pairs of plaintexts. For distinguishers requiring more than $2^{31}$ pairs, a different set of states is needed. So, the data complexity is $\frac{2^{7 \times (r-f)}}{2^{31}} \times 2^{16}= \frac{2^{7 \times (r-f)}}{2^{15}}$ encryption queries. Time complexity involves the memory accesses required to compute the specified collisions, which is the number of plaintext pairs needed, i. e., $2^{7 \times (r-f)}$. Memory complexity is $2^{16}$ Flex-$x$ states, which is the memory required for storing different states.

Consider a particular case for 21-round Flex-$256$. According to Inequality 3, the value of $f$ can be set to 4. For this case

• 1. Data Complexity is $\frac{2^{7 \times 17}}{2^{15}}$ = $2^{104}$ encryption queries..

• 2. Time Complexity is $2^{119}$ memory accesses.

• 3. Memory Complexity is $2^{16}$ Flex-$256$ states = $2^{17}$ Flex-$128$ states.

Key Recovery. Complexities of key recovery attack of Flex-$x$ depends on distinguisher. To recover each pair of key-byte, three different right pairs are required. This procedure also needs to be repeated $\frac{x}{16}$ times for recovering the full key. Therefore, data complexity, time complexity and memory complexity of distinguisher needs to be multiplied by a factor of $3\times \frac{x}{16}$. Moreover, candidate key-byte recovery for each pair of byte can be computed in parallel. To recover the other subkey, a plaintext, ciphertext pair $\big (p_1, c_1\big )$ is chosen and $\text{ PF }_k$ round functions till the second subkey whitening is computed offline and XOR-ed with $c_1$. So, the complexities of r-round Flex-$x$ with $f$ free rounds are-

• 1. Data Complexity is $3\times \frac{x}{16} \times \frac{2^{7 \times (r-f)}}{2^{15}}$ encryption queries.

• 2. Time Complexity is $3\times \frac{x}{16} \times 2^{7 \times (r-f)}$ memory accesses.

• 3. Memory Complexity is $3\times \frac{x}{16} \times 2^{16}$ Flex-$x$ states.

The complexities of particular cases for 7-round Flex-$64$ with $f$ = 1, 16-round Flex-$128$ with $f$ = 1 and 21-round Flex-$256$ with $f$ = 4 have been listed in Table 2.

3.4 Experimental Verification

The key recovery attack using iterated differentials has been experimentally verified for 8 rounds Flex-$128$ with $f$ = 3. The attack initiates after a key is chosen randomly. The number of key candidates after using the first right pairs for each pair of symmetric bytes (from ($K_{\alpha }[0]$, $K_{\alpha }[8]$) to ($K_{\alpha }[7]$, $K_{\alpha }[15]$)) are 316, 520, 632, 448, 568, 484, 368 and 356 respectively. It conforms to the theoretical analysis, which states that the number of candidates should be around $2^9$. After using the second right pairs, the number of candidates is reduced to 2, 12, 4, 4, 6, 5, 2 and 5 respectively which is close to the theoretical value of $2^2$. The third right pair reduces the number for all pairs of bytes to 1. The key recovery attack correctly recovers the subkeys.

In the next section, details regarding attacks on $\text{ PF }_k$ using Yoyo game strategy are provided.

4 Yoyo Attacks on $\text{ PF }_k$

The Yoyo distinguishing attack has been briefly described in Sect. 2.2. First, the result of Yoyo game on 2-generic SP rounds has been applied for devising r-round Flex-$x$ deterministic distinguisher. Then cipher specific properties has been exploited to penetrate one more extra round and recover the key. Here, r is 4, 6 and 8 for Flex-$64$, Flex-$128$ and Flex-$256$ respectively. First, details about Super-Sbox of Flex-$x$ is given.

4.1 Super-Sbox

Refer to Fig. 4 for the Super-Sbox construction in Flex-$128$ block cipher. Consider the bytes $\{B[0], B[2], \cdots B[7]\}$ at $X_1$. Due to round function, only the symmetric bytes affect each other. So, in $Y_1$ every symmetric bytes depends on every symmetric bytes at $X_1$. Due to $BS^2$, B[2i], $B[2i+8]$ $(0 \le i \le 3)$ from $Y_1$ constitutes the B[4i], $B[4i+1]$ $(0 \le i \le 3)$ at $X_2$. Due to application of $BS^3$, $\{B[2i],B[2i+1],B[2i+8],B[2i+9]\},\, (0 \le i \le 1)$ at $Y_2$ affects $\{B[8i],B[8i+1],B[8i+2],B[8i+3]\},\, (0 \le i \le 1)$ at $X_3$. This constitutes a Super-Sbox which spans over 2.5 rounds (omitting the initial BlockShuffle). There are two 64-bit Super-Sbox in the Flex-$128$ state. In similar way, Flex-$64$ and Flex-$256$ has 32-bit and 128-bit Super-Sbox which span over 1.5 and 3.5 rounds respectively. In the next subsection, how these Super-Sbox es are used to design deterministic Yoyo distinguishers is discussed.

Fig. 4.

Super-Sbox of Flex-$128$ Block Cipher

4.2 Deterministic Distinguisher for r-round Flex-$x$

In devising this distinguisher, Theorem 1 has been used directly. For this purpose, the $S \circ L \circ S$ layers need to be identified in this construction. The S here corresponds to Super-Sbox described in Sect. 4.1 whereas the L corresponds to the BlockShuffle layer. A pair of plaintexts is chosen such that only one of the Super-Sbox is active at $X_1$. Yoyo game is played using these two plaintexts to obtain a new pair of texts. The same Super-Sbox should be active in the new pair of texts and the other should be inactive. For a uniform random discrete distribution, this occurs with probability $\frac{1}{2^{\frac{x}{2}}}$. Next, attack procedures and their corresponding complexities are provided. In the attack procedure, steps pertaining to Flex-$128$ has been described. Same attack strategy follows for Flex-$64$ and Flex-$256$.

Attack Procedure

• 1. Choose two 128-bit plaintexts $p_1,p_2$ such that, $wt(\nu (p_1 \oplus p_2))=1$. Inverse BlockShuffle is applied to $p_1, p_2$ and then they are queried to encryption oracle to obtain $c_1, c_2$.

• 2. As there is two Super-Sbox es, so only one swapping is possible. One of the Super-Sbox is swapped between $c_1$ and $c_2$ to form $c'_{1}, c'_{2}$, which are queried to decryption oracle and $p'_{1}, p'_{2}$ is obtained.

• 3. Check whether $wt(\nu (BS(p'_{1}) \oplus BS(p'_{2})))=1$ or not. If it is 1, then distinguish it as Flex-$128$; otherwise it is a random permutation.

Complexity Evaluation. The attack needs 2 encryption queries and 2 decryption queries; its time complexity is 2 BlockShuffle, 2 inverse BlockShuffle operation and 2 Flex-$128$ state XOR, and the memory complexity is negligible.

4.3 Key Recovery for $(r+1)$-round Flex-$x$

For attacking $(r+1)$-round Flex-$x$, Yoyo distinguishing attack on r-round is composed with the one round trail of iterated truncated differential. The attack for Flex-$128$ is shown in Fig. 5. With probability $2^{-7}$ only one Super-Sbox is active at $X_2$. By virtue of Yoyo game, only one Super-Sbox should be active in $W_2$. Due to inverse BlockShuffle, the differences should be confined to either upper nibbles or lower nibbles in $Z_1$; the other half should be free. With probability $2^{-8}$, two symmetric bytes become free at $Z_1$. There are 8 (4 and 16 for Flex-$64$ and Flex-$256$ respectively) choices for symmetric byte positions which increases the probability to $2^{-5}$ and $2^{-4}$ for Flex-$64$ and . Therefore, at the cost of $2^{-12}$, two symmetric bytes become free for the 7-round Flex-$128$. Probability of the same event for 5-round Flex-$64$ and 9-round Flex-$256$ is $2^{-13}$ and $2^{-11}$ respectively. Now, the attack steps of Flex-$128$, it’s corresponding complexities and experimental verifications are discussed.

Attack Procedure

• 1. Choose $2^{6}$ plaintexts such that they differ only in $B[0]$ and $B[8]$. Apply inverse BlockShuffle on them and query them to encryption oracle to obtain corresponding ciphertexts. Consider all ciphertext pairs, swap bytes between them according to the Super-Sbox output and query them to the decryption oracle to obtain new pairs of plaintexts. Check whether the pair has a pair of free symmetric bytes. At least one such pair is expected.

• 2. Repeat step 1 two more times to obtain two more right pairs. Let $(c_1,c_2)$, $(c_3,c_4)$ and $(c_5,c_6)$ be such pairs and their corresponding plaintexts are $(p_1,p_2)$, $(p_3,p_4)$ and $(p_5,p_6)$. After byte swapping, $(c_1,c_2)$, $(c_3,c_4)$ and $(c_5,c_6)$ becomes $(c'_1,c'_2)$, $(c'_3,c'_4)$ and $(c'_5,c'_6)$. BlockShuffle is applied on the decrypted value of these modified ciphertexts to obtain $(p'_1,p'_2)$, $(p'_3,p'_4)$ and $(p'_5,p'_6)$.

• 3. Guess key bytes 0 and 8 for $K_{\alpha }$, run one round encryption for $p'_1,p'_2$ and observe whether same nibble in $B[0]$ and $B[8]$ remains free or not for the pair. Using nibble transition, out of $2^{16}$ candidates, $2^7$ are filtered out. Then the remaining two right pairs subsequently reduces the number of candidates for $K_{\alpha }[0]$ and $K_{\alpha }[8]$ to $2^2$ and 1 respectively.

• 4. For the remaining 7 symmetric pairs of bytes, step 3 is repeated 7 more times. At, the end 1 key candidates are expected for $K_{\alpha }$. For each $K_{\alpha }$, $K_{\beta }$ is computed by using a plaintext-ciphertext pair. If there is more than one $K_{\alpha }$, $K_{\beta }$ pair, they are exhaustively tried for finding the right key candidate.

Fig. 5.

7-round Yoyo Distinguisher for Flex-$128$

Complexity Evaluation. Let probability of the event that “two symmetric bytes become free" is $2^{-p}$. So, for retrieving a right pair, $2^{\frac{p}{2}}$ encryption queries and $2^{p}$ decryption queries are required. For guessing each pair of key byte, 3 such right pairs are needed and to recover the key, this process need to be repeated $\frac{x}{16}$ times. Therefore, data complexity of the attack is $\frac{3\times x}{16} \times 2^{\frac{p}{2}}$ encryption queries and $\frac{3\times x}{16} \times 2^{p}$ decryption queries.

Time complexity is $\frac{3\times x}{16} \times 2^{p}$ memory accesses for retrieving the stored ciphertexts.

Memory complexity is $\frac{3\times x}{16} \times 2^{\frac{p}{2}+1}$ Flex-$x$ states for storing the plaintexts and ciphertexts.

The complexities of 7-round Flex-$128$ key recovery attack are-

• 1. Data Complexity is $24 \times 2^6 \approx 2^{10.5}$ encryption queries and $24 \times 2^{12} \approx 2^{16.5}$ decryption queries.

• 2. Time Complexity is $2^{16.5}$ memory accesses.

• 3. Memory Complexity is $2^{11.5}$ Flex-$128$ states.

Experimental Verification. The Yoyo attack for 7-round Flex-$128$ has been experimentally verified. Initially the oracle chooses a master key randomly and computes the subkeys. Adversarial algorithm queries according to attack steps in Sect. 4.3 and retrieves right pairs. The number of key candidates corresponding to each symmetric bytes after filtering with first right pairs are 502, 618, 546, 496, 510, 486, 552 and 538 respectively which conforms to the theoretical value of $2^9$. The second right pairs further reduces it to 6, 7 6, 7, 7, 3, 3 and 5 respectively which is close to the theoretical value of $2^2$. The third pairs reduces all these values to 1. This reduction in the number of key candidates using the right pairs conforms to the theoretical analysis. At last, the algorithm successfully recovers the subkeys.

In the next section, we discuss the success probability of distinguishing attacks reported in this work.

5 Success Probability of Distinguishing Attacks

The effectiveness of an attack depends on its success probability. First, the success probability of all reported distinguishers is computed. Then, the success probability of practical ones is experimentally verified. To deduce the theoretical estimation of success probabilities, the following theorem from [19] has been applied.

Theorem 2

[19] Suppose, the event e happens in uniform random bitstream with probability p and in keystream of a stream cipher with probability $p(1+q)$. Then the data complexity of the distinguisher with false positive and false negative rates $\alpha$ and $\beta$ is given by

$$\begin{aligned} n>\frac{\Big (\kappa _1 \sqrt{1-p} + \kappa _2 \sqrt{\big (1+q\big )\big (1-p(1+q)\big )}\Big )^2}{pq^2} \end{aligned}$$

(4)

where $\varPhi (-\kappa _1)=\alpha$ and $\varPhi (\kappa _2)=1-\beta$.

For computing success probability, we consider $\kappa _1=\kappa _2$ in theorem 2, which gives us $\alpha =\beta$. Then the success probability is given by $(1-\beta )$. Note that, in the theorem data complexity essentially refers to sample complexity. Table 5 lists the success probabilities of different distinguishers presented in this paper.

Table 5. Success probabilities of various distinguishers

Experimental Verification. For experimental verification of success probabilities, the strategy from [21] has been followed. First, consider a blackbox which can act as either a cipher $\mathcal {C}$ or a uniform discrete random permutation $\mathcal {R}$. Then the experiment is run two times in the following ways:

• 1. Consider the blackbox as $\mathcal {C}$ and repeat the experiment $a_c$ times.

• 2. Consider the blackbox as $\mathcal {R}$ and repeat the experiment $a_r$ times.

Let out of ($a_c$+$a_r$) experiments, distinguisher decides it as $\mathcal {C}$ $o_c$ times and as $\mathcal {R}$ $o_r$ times. $n_{FP}$ and $n_{FN}$ denotes the number of false positives and false negatives respectively. Based on this parameters, the confusion matrix is shown in Table 6.

Table 6. Confusion matrix of $\mathcal {C}$ and $\mathcal {R}$

Then the success probability is calculated by:

$$\begin{aligned} Pr[Success]&=\frac{(o_c-n_{FP})+(o_r-n_{FN})}{o_c+o_r}\\&=\frac{(o_c-n_{FP})+(o_r-n_{FN})}{a_c+a_r}.\\ \end{aligned}$$

The values of success probabilities for 5-round and 6-round Flex-$64$ derived using experiments and theoretical estimations are listed in Table 7.

Table 7. Experimental verification of success probability

Trade-Off Between Success Rate and Free Rounds. The iterated truncated differentials can have a different number of free rounds at the end. More number of free rounds reduces the trail complexity at the expense of success rate. For analysis, consider the case pertaining to 6-round Flex-$64$ with the number of free rounds 1 and 2. The success rate for both cases is listed in Table 8.

Table 8. Comparison of Success Rate for Flex-$64$

For 21-round Flex-$128$, the number of free rounds can take any value between 1 and 4. For each of the cases, the theoretical estimation of success probability is almost equal. The estimated success probabilities have been shown in Table 9. The difference between the distribution of random bitstream and 21-round Flex-$128$ for each case is so huge, that it has a negligible effect on the success probability.

Table 9. Comparison of Success Rate for Flex-$256$

In the following section, we show how to mount forgery attacks on FlexAEAD variants using the idea of iterated truncated differentials.

6 Forgery Attacks on FlexAEAD

Eichlseder $et$ $al.$ have shown forgery attacks on FlexAEAD by applying several strategies [12]. All those strategies are also applicable using the differentials described in this paper. The main difference between these two approaches is the differential characteristics for the sequence generation. First, the differential characteristic of the sequence generation step is shown.

6.1 Differential Characteristics in Sequence Generation

A sequence of bits is used by FlexAEAD for authenticated encryption. These sequences are generated by using $\text{ PF }_k$, with initial state being the nonce. For details on sequence generation refer to [17]. The difference between two consecutive sequence numbers is that their last call to $\text{ PF }_k$ differ by a INC32 call. INC32 is a 32-bit word operation which acts as an XOR operation with probability $2^{-1}$.

Fig. 6.

Differential Characteristics of Sequence Generation for FlexAEAD-$128$. Note that, plaintext difference or associated data difference can cancel out difference in $S_i \oplus S_{i+1}$ with probability $2^{-8}$.

Consider, m 32-bit words in a r-round Flex-$x$ state. Due to INC32 with probability $2^{-m}$, m nibbles at $\frac{m}{2}$ symmetric positions become active between two subsequent sequence generation steps. Due to BlockShuffle, those m active nibbles is converted to $\frac{m}{2}$ active bytes which occupies $\frac{m}{4}$ symmetric positions. In the next round, those active bytes transits to $\frac{m}{8}$ symmetric positions ($\frac{m}{4}$ active bytes) at the cost of $2^{-2m}$. In the next round, $\frac{m}{16}$ symmetric positions get occupied at the cost of $2^{-m}$. After repeating the process, $\big (\log _2(m)-2\big )$ times, only one symmetric position remains occupied by the active byte. For the rest $\big (r-\log _2(m)+2\big )$ rounds, with probability $2^{-8}$ for each round the position of two active nibbles in the output get fixed (Note that, in the iterated truncated differential, the position of active is not fixed and that is why the probability of $2^{-7}$ is paid). With $2^{-8}$ probability the value of the active nibbles can be fixed to a specific value.

Table 10. Comparison of Forgery Attacks on FlexAEAD

By following this approach, the difference of two consecutive sequence numbers can be fixed to a specific value with probability $2^{-50}$ for FlexAEAD-64, $2^{-60}$ for FlexAEAD-128 and $2^{-80}$ for FlexAEAD-256 (Corresponding complexities of forgery attacks are computed by taking the inverse of these probabilities). Differential characteristics of sequence generation for FlexAEAD-128 is shown in Fig. 6. Once the output difference value is fixed, the techniques (Changing Associated Data, Truncating Ciphertext, Reordering Ciphertext) in [12] can be applied to forge ciphertext-tag pair. Comparison between several approaches regarding forgery attack is enlisted in Table 10.

7 Conclusion

In this work, we analyzed all variants of $\text{ PF }_k$ of FlexAEAD. We reported a one round differential characteristic of $\text{ PF }_k$, which due to its iterative nature was exploited to penetrate a large number of rounds. We also showed that the generalized Yoyo distinguishing attack on SPN ciphers was applicable for $\text{ PF }_k$. While deploying Yoyo attack, a Super-Sbox construction of 1.5, 2.5 and 3.5 rounds in 64-bit, 128-bit and 256-bit $\text{ PF }_k$ respectively were reported. All these attacks were easily exploited to recover the subkeys. In addition, the iterated truncated differential attack strategy was applied to the nonce-based sequence number generator which was exploited to devise similar kinds of forgery attacks on FlexAEAD as given by Eichlseder $et$ $al.$  [12]. The success probabilities of all distinguishing attacks were shown to be high. All attacks reported in this work with practical complexities were experimentally verified. All these attacks have exploited a vulnerability in the design which is based on dividing the nibbles into two parts while using AES S-box.