Keywords

1 Introduction

In various assessment fields, essay-writing tests have attracted much attention as a way to measure practical and higher-order abilities such as logical thinking, critical reasoning, and creative thinking [1, 4, 13, 18, 33, 35]. In essay-writing tests, examinees write essays about a given topic, and human raters grade those essays based on a scoring rubric. However, grading can be an expensive and time-consuming process when there are many examinees [13, 16]. In addition, human grading is not always sufficiently accurate even when a rubric is used because assigned scores depend strongly on rater characteristics such as strictness and inconsistency [9, 11, 15, 26, 31, 43]. Automated essay scoring (AES), which utilizes natural language processing (NLP) and machine learning techniques to automatically grade essays, is one approach toward resolving this problem.

Many AES methods have been developed over the past decades, and can generally be classified as feature-engineering or automatic feature extraction approaches [13, 16].

The feature-engineering approach predicts scores using manually tuned features such as essay length and number of spelling errors (e.g., [3, 5, 22, 28]). Advantages of this approach include interpretability and explainability. However, these approaches generally require extensive feature redesigns to achieve high prediction accuracy.

To obviate the need for feature engineering, automatic feature extraction based on deep neural networks (DNNs) has recently attracted attention. Many DNN-AES models have been proposed in the last few years (e.g., [2, 6, 10, 14, 23, 24, 27, 37, 47]) and have achieved state-of-the-art accuracy. This approach requires a large dataset of essays graded by human raters as training data. Essay grading tasks are generally shared among many raters, assigning a few raters to each essay to lower assessment burdens. However, assigned scores are known to be strongly biased due to the effects of rater characteristics [8, 15, 26, 31, 34, 39, 40]. Performance of DNN models rapidly drops when biased data are used for model training, because the resulting model reflects bias effects [3, 12, 17]. This problem has been generally overlooked or ignored, but it is a significant issue affecting all AES methods using supervised machine learning models, including DNN, and because cost concerns make it generally difficult to remove rater bias in practical testing situations.

In the fields of educational and psychological measurement, statistical models for estimating essay scores while considering rater characteristic effects have recently been proposed. Specifically, they are formulated as item response theory (IRT) models that incorporate parameters representing rater characteristics [9, 29, 30, 38, 42,43,44,45]. Such models have been applied to various performance tests, including essay writing. Previous studies have reported that they can provide reliable scores by removing adverse effects of rater bias (e.g., [38, 39, 41, 42, 44]).

This study therefore proposes a new DNN-AES framework that integrates IRT models to deal with rater bias in training data. Specifically, we propose a two-stage architecture that stacks an IRT model over a conventional DNN-AES model. In our framework, the IRT model is first applied to raw rating data to estimate reliable scores that remove effects of rater bias. Then, the DNN-AES model is trained using the IRT-based scores. Since the IRT-based scores are theoretically free from rater bias, the DNN-AES model will not reflect bias effects. Our framework is simple and easily applied to various conventional AES models. Moreover, this framework is highly suited to educational contexts and to low- and medium-stakes tests, because preparing high-quality training data in such situations is generally difficult. To our knowledge, this study is a first attempt at mitigating rater bias effects in DNN-AES models.

2 Data

We assume the training dataset consists of essays written by J examinees and essay scores assigned by R raters. Let \(e_{j}\) be an essay by examinee \(j \in \mathcal{J} = \{ 1, \cdots , J \}\) and let \(U_{jr}\) represent a categorical score \(k \in \mathcal{K} = \{1,\cdots ,K\}\) assigned by rater \(r \in \mathcal{R} = \{1,\cdots , R\}\) to \(e_{j}\). The score data can then be defined as \(\varvec{U} = \{ U_{jr} \in \mathcal{K} \cup \{-1\} \mid j \in \mathcal{J},r \in \mathcal{R}\}\), with \(U_{jr} = -1\) denoting missing data. Missing data occur because only a few graders in \(\mathcal{R}\) can practically grade each essay \(e_{j}\) to reduce assessment workload. Furthermore, letting \(\mathcal{V} = \{1, \cdots , V\}\) be a vocabulary list for essay collection \(\varvec{E} = \{ e_{j} \mid j \in \mathcal{J} \}\), essay \(e_{j} \in \varvec{E}\) is definable as a list of vocabulary words \(e_{j} = \{\varvec{w}_{jt} \in \mathcal{V} \mid t = \{1, \cdots , N_{j} \} \}\), where \(\varvec{w}_{jt}\) is a one-hot representation of the t-th word in \(e_{j}\), and \(N_{j}\) is the number of words in \(e_{j}\). This study aimed at training DNN-AES models using this training data.

3 Neural Automated Essay Scoring Models

This section briefly introduces the DNN-AES models used in this study. Although many models have been proposed in the last few years, we apply the most popular model that uses convolution neural networks (CNN) with long short-term memory (LSTM) [2], and an advanced model based on bidirectional encoder representations from transformers (BERT) [7].

3.1 CNN-LSTM-Based Model

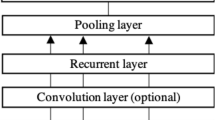
A CNN-LSTM-based model [2] proposed in 2016 was the first DNN-AES model. Figure 1(a) shows the model architecture. This model calculates a score for a given essay, which is defined as a sequence of one-hot word vectors, through the following multi-layered neural networks.

  • Lookup table layer: This layer transforms each word in a given essay into a D-dimensional word-embedding representation, in which words with the same meaning have similar representations. Specifically, letting \(\varvec{A}\) be a \(D \times V\)-dimensional embeddings matrix, the embedding representation corresponding to \(\varvec{w}_{jt} \in e_{j}\) is calculable as the dot-product \(\varvec{A}\cdot \varvec{w}_{jt}\).

  • Convolution layer: This layer extracts n-gram level features using CNN from the sequence of word embedding vectors. These features capture local textual dependencies among n-gram words. Zero padding is applied to outputs from this layer to preserve the word length. This is an optional layer, often omitted in current studies.

  • Recurrent layer: This layer is a LSTM network that outputs a vector at each timestep to capture long-distance dependencies of the words. A single-layer unidirectional LSTM is generally used, but bidirectional or multilayered LSTMs are also often used.

  • Pooling layer: This layer transforms outputs of the recurrent layer \(\mathcal {H}=\{ \varvec{h}_{j1},\) \(\varvec{h}_{j2},\) \(\cdots ,\) \(\varvec{h}_{jN_{j}}\}\) into a fixed-length vector. Mean-over-time (MoT) pooling, which calculates an average vector \(\varvec{M}_{j}=\frac{1}{N_{j}}\sum _{t=1}^{N_{j}}\varvec{h}_{jt}\), is generally used because it tends to provide stable accuracy. Other frequently used pooling methods include the last pool, which uses the last output of the recurrent layer \(\varvec{h}_{jN_{j}}\), and a pooling-with-attention mechanism.

  • Linear layer with sigmoid activation: This layer projects pooling-layer output to a scalar value in the range [0, 1] by utilizing the sigmoid function as \(\sigma (\varvec{W}\varvec{M}_{j}+\text{ b })\), where \(\varvec{W}\) is a weight matrix and \(\text{ b }\) is a bias. Model training is conducted by normalizing gold-standard scores to [0, 1], but the predicted scores are rescaled to the original score range in the prediction phase.

Fig. 1.
figure 1

Architectures of DNN-AES models.

Full size image

3.2 BERT-Based Model

BERT, a pretrained language model released by the Google AI Language team, has achieved state-of-the-art results in various NLP tasks [7]. BERT has been applied to AES [32] and automated short-answer grading (SAG) [19, 21, 36] since 2019, and provides good accuracy.

BERT is defined as a multilayer bidirectional transformer network [46]. Transformers are a neural network architecture designed to handle ordered sequences of data using an attention mechanism. Specifically, transformers consist of multiple layers (called transformer blocks), each containing a multi-head self-attention and a position-wise fully connected feed-forward network. See Ref. [46] for details of this architecture.

BERT is trained in pretraining and fine-tuning steps. Pretraining is conducted on huge amounts of unlabeled text data over two tasks, masked language modeling and next-sentence prediction, the former predicting the identities of words that have been masked out of the input text and the latter predicting whether two given sentences are adjacent.

Using BERT for a target NLP task, including AES, requires fine-tuning (retraining), which is conducted from a task-specific supervised dataset after initializing model parameters to pretrained values. When using BERT for AES, input essays require preprocessing, namely adding a special token (“CLS”) to the beginning of each input. BERT output corresponding to this token is used as the aggregate sequence representation [7]. We can thus score an essay by inputting its representation to a linear layer with sigmoid activation, as illustrated in Fig. 1(b).

3.3 Problems in Model Training

Training of CNN-LSTM-based AES models and fine-tuning of BERT-based AES models are conducted using large datasets of essays by graded human raters. For model training, the mean-squared error (MSE) between predicted and gold-standard scores is used as the loss function. Specifically, letting \(y_{j}\) be the gold-standard score for essay \(e_j\) and letting \(\hat{y}_{j}\) be the predicted score, the MSE loss function is defined as \(\frac{1}{J}\sum _{j=1}^J(y_{j}-\hat{y}_{j})^2\).

The gold-standard score \(y_{j}\) is a score for essay \(e_j\) assigned by a human rater in a set of raters \(\mathcal{R}\). When multiple raters grade each essay, the gold-standard score should be determined by selecting one score or by calculating an average or total score. In any case, such scores depend strongly on rater characteristics, as discussed in Sect. 1. The accuracy of a DNN model drops when such biased data are used for model training, because the trained model inherits bias effects [3, 12, 17]. In educational and psychological measurement research, item response theory (IRT) models that can estimate essay scores while considering effects of rater characteristics have recently been proposed [9, 29, 30, 38, 42,43,44]. The main goal of this study is to train AES models using IRT-based unbiased scores. The next section introduces the IRT models.

4 Item Response Theory Models with Rater Parameters

IRT [20] is a test theory based on mathematical models. IRT represents the probability of an examinee response to a test item as a function of latent examinee ability and item characteristics such as difficulty and discrimination. IRT is widely used for educational testing because it offers many benefits. For example, IRT can estimate examinee ability considering effects of item characteristics. Also, the abilities of examinees responding to different test items can be measured on the same scale, and missing response data can be easily handled.

Traditional IRT models are applicable to two-way data (examinees \(\times \) test items), consisting of examinee test item scores. For example, the generalized partial credit model (GPCM) [25], a representative polytomous IRT model, defines the probability that examinee j receives score k for test item i as

$$\begin{aligned} P_{ijk}= \frac{\exp \sum _{m=1}^{k}\left[ \alpha _i (\theta _j-\beta _{i}-d_{im}) \right] }{\sum _{l=1}^{K} \exp \sum _{m=1}^{l}\left[ \alpha _i (\theta _j-\beta _{i}-d_{im}) \right] }, \end{aligned}$$
(1)

where \(\theta _j\) is the latent ability of examinee j, \(\alpha _i\) is a discrimination parameter for item i, \(\beta _{i}\) is a difficulty parameter for item i, and \(d_{ik}\) is a step difficulty parameter denoting difficulty of transition between scores \(k-1\) and k in the item. Here, \(d_{i1}=0\), and \(\sum _{k=2}^{K} d_{ik} = 0\) is given for model identification.

However, conventional GPCM ignores rater factors, so it is not applicable to rating data given by multiple raters as assumed in this study. Extension models that incorporate parameters representing rater characteristics have been proposed to resolve this difficulty [29, 30, 38, 42,43,44,45]. This study introduces a state-of-the-art model [44, 45] that is most robust for a large variety of raters. This model defines the probability that rater r assigns score k to examinee j’s essay for a test item (e.g., an essay task) i as

$$\begin{aligned} P_{ijrk} = \frac{\exp \sum _{m=1}^{k}\left[ \alpha _r\alpha _i(\theta _j-\beta _{r} - \beta _i-d_{rm}) \right] }{\sum _{l=1}^{K} \exp \sum _{m=1}^{l}\left[ \alpha _r\alpha _i(\theta _j-\beta _{r} - \beta _i-d_{rm} )\right] } , \end{aligned}$$
(2)

where \(\alpha _r\) is the consistency of rater r, \(\beta _{r}\) is the strictness of rater r, and \(d_{rk}\) is the severity of rater r within category k. For model identification, we assume \(\sum _{i=1}^{I} \log \alpha _{i} = 0\), \(\sum _{i=1}^{I} \beta _{i} = 0\), \(d_{r1}=0\), and \(\sum _{k=2}^{K} d_{rk} = 0\).

This study applies this IRT model to rating data \(\varvec{U}\) in training data. Note that DNN-AES models are trained for each essay task. Therefore, rating data \(\varvec{U}\) are defined as two-way data (examinees \(\times \) raters). When the number of tasks is fixed to one in the model, the above model identification constraints make \(\alpha _i\) and \(\beta _i\) ignorable, so Eq. (2) becomes

$$\begin{aligned} P_{jrk} = \frac{\exp \sum _{m=1}^{k}\left[ \alpha _r(\theta _j-\beta _{r} - d_{rm}) \right] }{\sum _{l=1}^{K} \exp \sum _{m=1}^{l}\left[ \alpha _r(\theta _j-\beta _{r} - d_{rm} )\right] }. \end{aligned}$$
(3)

This equation is consistent with conventional GPCM, regarding use of item parameters as the rater parameters. Note that \(\theta _j\) in Eq. (3) represents not only the ability of examinee j but also the latent unbiased scores for essay \(e_j\), because only one essay is associated with each examinee. This model thus provides essay scores with rater bias effects removed.

5 Proposed Method

We propose a DNN-AES framework that uses IRT-based unbiased scores \(\varvec{\theta } = \{\theta _j \mid j \in \mathcal{J}\}\) to deal with rater bias in training data.

Fig. 2.
figure 2

Proposed architectures.

Full size image

Figure 2 shows the architectures of the proposed method. As that figure shows, the proposed method is defined by stacking an IRT model over a conventional DNN-AES model. Training of our models occurs in two steps:

  1. 1.

    Estimate the IRT scores \(\varvec{\theta }\) from the rating data \(\varvec{U}\).

  2. 2.

    Train AES models using the IRT scores \(\varvec{\theta }\) as the gold-standard scores. Specifically, the MSE loss function for training is defined as \(\frac{1}{J}\sum _{j=1}^J(\theta _{j}-\hat{\theta }_{j})^2\), where \(\hat{\theta }_j\) represents the AES’s predicted score for essay \(e_j\). Since scores \(\varvec{\theta }\) are estimated while considering rater bias effects, a trained model will not reflect bias effects. Note that the gold-standard scores must be rescaled to the range [0, 1] for training because sigmoid activation is used in the output layer. In IRT, \(99.7\%\) of \({\theta }_j\) fall within the range [−3, 3] because a standard normal distribution is generally assumed. We therefore apply a linear transformation from the range [−3, 3] to [0, 1] after rounding the scores lower than \(-3\) to \(-3\), and those higher than 3 to 3.

Note that the increase in training time for the proposed method compared with a conventional method is the time for IRT parameter estimation.

In the testing phase, the score for new essay \(e_{j'}\) is predicted in two steps:

  1. 1.

    Predict the IRT score \(\theta _{j'}\) from a trained AES model, and rescale it to the range [−3,3].

  2. 2.

    Calculate the expected score \(\hat{U}_{j'}\), which corresponds to an unbiased original-scaled score of \(e_{j'}\) [39], as

    $$\begin{aligned} \hat{U}_{j'} =\frac{1}{R} \sum _{r=1}^R \sum _{k=1}^K k\cdot P_{j'rk}. \end{aligned}$$
    (4)

6 Experiments

This section describes evaluation of the effectiveness of the proposed method through actual data experiments.

6.1 Actual Data

Fig. 3.
figure 3

Score statistics (average and SD) for each rater.

Full size image
Table 1. Category usage rates.
Full size table

These experiments used the Automated Student Assessment Prize (ASAP) dataset, which is widely used as benchmark data in AES studies. This dataset consists of essays on eight topics, originally written by students from grades 7 to 10. There are 12,978 essays, averaging 1,622 essays per topic. However, this dataset cannot be directly used to evaluate the proposed method, because despite its essays having been graded by multiple raters, it contains no rater identifiers.

We therefore employed other raters and asked them to grade essays in the ASAP dataset. We used essay data for the fifth ASAP topic, because the number of essays in that topic is relatively large (\(n=1805\)). We recruited 38 native English speakers as raters through Amazon Mechanical Turk and assigned four raters to each essay. Each rater graded around 195 essays. The assessment rubric used the same five rating categories as ASAP. Average Pearson’s correlation between the collected rating scores and the original ASAP scores was 0.675.

To confirm any differences in rater characteristics, we plotted averaged score values and standard deviations (SD) for each rater, as shown in Fig. 3. In that figure, each plot represents a rater, and horizontal and vertical axes respectively show the average and SD values. In addition, Table 1 shows appearance rates in the five rating categories for 10 representative raters. The figure and table show extreme differences in grading characteristics among the raters, suggesting that consideration of rater bias is required.

6.2 Experimental Procedures

This subsection shows that the proposed method can provide more robust scores than can conventional AES models, even when the rater grading each essay in the training data changes. The experimental procedures, which are similar to those used in previous studies examining IRT scoring robustness [39,40,41,42], were as follows:

  1. 1.

    We estimated IRT parameters by the Markov chain Monte Carlo (MCMC) algorithm [30, 42] using all rating data.

  2. 2.

    We created a dataset consisting of (essay, score) pairs by randomly selecting one score for each essay from among the scores assigned by multiple raters. We repeated this data generation 10 times. Hereafter, the m-th generated dataset is represented as \(\varvec{U}^{\prime }_m\).

  3. 3.

    From each dataset \(\varvec{U}^{\prime }_m\), we estimated IRT scores \(\varvec{\theta }\) (referred to as \(\varvec{\theta }_m\)) given the rater parameters obtained in Step 1, and then created a dataset \(\varvec{U}^{\prime \prime }_m\) comprising essays and \(\varvec{\theta }_m\) values.

  4. 4.

    Using each dataset \(\varvec{U}^{\prime \prime }_m\), we conducted five-fold cross validation to train AES models and to obtain predicted scores \(\varvec{\hat{\theta }}_m\) for all essays.

  5. 5.

    We calculated metrics for agreement between the expected scores calculated by Eq. (4) given \(\varvec{\hat{\theta }}_m\) and those calculated given \(\varvec{\hat{\theta }}_{m^{\prime }}\) for all unique \(m, m^{\prime } \in \{1,\cdots ,10\}\) pairs (\(_{10} C_2 = 45\) pairs in total). As agreement metrics, we used Cohen’s kappa, weighted kappa, root mean squared error (RMSE), and Pearson correlation coefficient.

  6. 6.

    We calculated average metric values obtained from the 45 pairs.

High kappa and correlation and low RMSE values obtained from the experiment indicate that score predictions are more robust for different raters.

We conducted a similar experiment using conventional DNN-AES models without the IRT model. Specifically, using each dataset \(\varvec{U}^{\prime }_m\), we predicted essay scores from a DNN-AES model through five-fold cross validation procedures as in Step 4. We then calculated the four agreement metrics among the predicted scores obtained from different datasets \(\varvec{U}^{\prime }_m\), and averaged them.

Table 2. Evaluations of prediction robustness.
Full size table

These experiments were conducted with several DNN-AES models. Specifically, we examined CNN-LSTM models using MoT pooling or last pooling, those models without a CNN layer, and the BERT model. These models were implemented in Python with the Keras library. For the BERT model, we used the base-sized pretrained model. The hyperparameters and dropout settings were determined following Refs. [2, 7, 46].

6.3 Experimental Results

Table 2 shows the results, which indicate that the proposed method sufficiently improves agreement metrics as compared to the conventional models in all cases. The results indicate that the proposed method provides stable scores when the rater allocation for each essay in training data is changed, thus demonstrating that it is highly robust against rater bias. Note that the values in Table 2 are not comparable with the results of previous AES studies because our experiment and previous experiments evaluated different aspects of AES performance.

In addition, as in previous AES studies, we evaluated score (\(\theta \)) prediction accuracy of the proposed method through five-fold cross-validation. We measured accuracy using mean absolute error (MAE), RMSE, the correlation coefficient, and the coefficient of determination (\(R^2\)), because \(\theta \) is a continuous variable. Table 3 shows the results, which indicate that the CNN-LSTM and LSTM models with MoT pooling achieved higher performance than did those with last pooling. The table also shows that the CNN did not effectively improve accuracy. These tendencies are consistent with a previous study [2]. In addition, the BERT provided the highest accuracy, which is also consistent with current NLP studies.

Tables 2 and 3 show that the score prediction robustness in Table 2 tends to increase with score prediction accuracy. This might be because scores in low-performance DNN-AES models are strongly biased not only by rater characteristics, but also by prediction errors arising from the model itself. With increasing accuracy of DNN-AES models, rater bias effects as a percentage of overall error increases, suggesting that the impact of the proposed method increases.

Table 3. Prediction accuracy for IRT score \(\theta \) by the proposed method
Full size table

7 Conclusion

We showed that DNN-AES model performance strongly depends on the characteristics of raters grading essays in training data. To resolve this problem, we proposed a new DNN-AES framework that integrates IRT models. Specifically, we formulated our method as a two-stage architecture that stacks the IRT model over a conventional DNN-AES model. Through experiments using an actual dataset, we demonstrated that the proposed method can provide more robust essay scores than can conventional DNN-AES models. The proposed method is simple but powerful, and is easily applicable to any AES model. As described in the Introduction, our method is also highly suited to situations where high-quality training data are hard to prepare, including educational contexts.

In future studies, we expect to evaluate effectiveness of the proposed method using various datasets. Although this study mainly focused on robustness against rater bias, the proposed method might also improve prediction accuracy for each rater’s score. In future studies, the accuracy should be evaluated. Our method is defined as a two-stage procedure for separately training IRT models and DNN-AES models. However, conducting end-to-end optimization would further improve the performance. This extension is another topic for future study.