Abstract
In a lockable obfuscation scheme [28, 39] a party takes as input a program P, a lock value \(\alpha \), a message \(\mathsf {msg}\) and produces an obfuscated program \(\tilde{P}\). The obfuscated program can be evaluated on an input x to learn the message \(\mathsf {msg}\) if \(P(x)= \alpha \). The security of such schemes states that if \(\alpha \) is randomly chosen (independent of P and \(\mathsf {msg}\)), then one cannot distinguish an obfuscation of P from a “dummy” obfuscation. Existing constructions of lockable obfuscation achieve provable security under the Learning with Errors assumption. One limitation of these constructions is that they achieve only statistical correctness and allow for a possible one sided error where the obfuscated program could output the \(\mathsf {msg}\) on some value x where \(P(x) \ne \alpha \).
In this work we motivate the problem of studying perfect correctness in lockable obfuscation for the case where the party performing the obfuscation might wish to inject a backdoor or hole in correctness. We begin by studying the existing constructions and identify two components that are susceptible to imperfect correctness. The first is in the LWE-based pseudo random generators (PRGs) that are non-injective, while the second is in the last level testing procedure of the core constructions.
We address each in turn. First, we build upon previous work to design injective PRGs that are provably secure from the LWE assumption. Next, we design an alternative last level testing procedure that has additional structure to prevent correctness errors. We then provide a surgical proof of security (to avoid redundancy) that connects our construction to the construction by Goyal, Koppula, and Waters (GKW) [28]. Specifically, we show how for a random value \(\alpha \) an obfuscation under our new construction is indistinguishable from an obfuscation under the existing GKW construction.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In cryptographic program obfuscation a user wants to take a program P and publish an obfuscated program \(\widetilde{P}\). The obfuscated program should maintain the same functionality of the original while intuitively hiding anything about the structure of P beyond what can be determined by querying its input/output functionality.
One issue in defining semantics is whether we demand that \(\widetilde{P}\) always match the functionality exactly on all inputs or we relax correctness to allow for some deviation with negligible probability. At first blush such differences in semantics might appear to be very minor. With a negligible correctness error it is straightforward for the obfsucator to parameterize an obfuscation such that the probability of a correctness error is some minuscule value such as \(2^{-300}\) which would be much less than say the probability of dying from an asteroid strike (1 in 74 million).
The idea that statistical correctness is always good enough, however, rests on the presumption that the obfuscator itself wants to avoid errors. Consider for example, a party that is tasked with building a program that screens images from a video feed and raises an alert if any suspicious activity is detected. The party could first create a program P to perform this function and then release an obfuscated version \(\widetilde{P}\) that could hide features of the proprietary vision recognition algorithm about how the program was built. But what if the party wants to abuse their role? For instance, they might want to publish a program \(\widetilde{P}\) that unfairly flags a certain group or individual. Or perhaps is programmed with a backdoor to let a certain image pass.
In an obfuscation scheme with perfect correctness, it might be possible to audit such behavior. For example, an auditor could require that the obfuscating party produce their original program P along with the random coins used in obfuscating it. Then the auditor could check that the original program P meets certain requirements as well as seeing that \(\widetilde{P}\) is indeed an obfuscation of P.Footnote 1 (We emphasize that if one does not want to reveal P to an auditor that such a proof can be done in zero knowledge or by attaching a non-interactive zero knowledge proof to the program. This proof will certify that the program meets some specification or has some properties; e.g. “there are at most three inputs that result in the output ‘010’.") However, for such a process to work it is imperative that the obfuscation algorithm be perfectly correct. Otherwise, a malicious obfuscator could potentially start with a perfectly legitimate program P, but purposefully choose coins that would flip the output of a program at a particular input point.
Another important context where perfect correctness matters is when a primitive serves as a component or building block in a larger cryptosystem. We present a few examples where a difference in perfect versus imperfect correctness in a primitive can manifest into fundamentally impacting security when complied into a larger system.
-
1.
Dwork, Naor and Reingold [25] showed that the classical transformations of IND-CPA to IND-CCA transformations via NIZKs [22, 33] may not work when the IND-CPA scheme is not perfectly correct. They addressed this by amplifying standard imperfect correctness to what they called almost-all-keys correctness.
-
2.
Bitansky, Khurana, and Paneth [10] constructed zero knowledge arguments with low round complexity. For their work, they required lockable obfuscation with one-sided perfect correctness.Footnote 2
-
3.
Recently, [4, 11] constructed constant-round post-quantum secure constant-round ZK arguments. These protocols use lockable obfuscation as a means to commit a message with pefect-binding property. Without both-sided perfect correctness, the commitment scheme and thereby the ZK argument scheme fails to be secure.
In this paper we study perfect correctness in lockable obfuscation, which is arguably the most powerful form of obfuscation which is provably secure under a standard assumption. Recall that a lockable obfuscation [28, 39] scheme takes as input a program P, a message \(\mathsf {msg}\), a lock value \(\alpha \) and produces an obfuscated program \(\widetilde{P}\). The semantics of evaluation are such that on input x the evaluation of the program outputs \(\mathsf {msg}\) if and only if \(P(x) = \alpha \). Lockable obfuscation security requires that the obfuscation of any program P with a randomly (and independently of P and \(\mathsf {msg}\)) chosen value \(\alpha \) will be indistinguishable from a “dummy” obfuscated program that is created without any knowledge of P and \(\mathsf {msg}\) other than their sizes. While the power of lockable obfuscation does not reach that of indistinguishability obfuscation [8, 26, 37], it has been shown to be sufficient for many applications such as obfuscating conjunction and affine testers, upgrading public key encryption, identity-based encryption [14, 20, 38] and attribute-based encryption [36] to their anonymous versions and giving random oracle uninstantiatability and circular security separation results, and most recently, building efficient traitor tracing systems [15, 18].
The works of Goyal, Koppula, and Waters [28] and Wichs and Zirdelis [39] introduced and gave constructions of lockable obfuscation provably secure under the Learning with Errors [35] assumption. A limitation of both constructions (inherited from the bit-encryption cycle testers of [30]) is that they provide only statistical correctness. In particular, there exists a one-sided error in which it is possible that there exists an input x such that \(P(x) \ne \alpha \) yet the obfuscated program outputs \(\mathsf {msg}\) on input x.
Our Results. With this motivation in mind we seek to create a lockable obfuscation scheme that is perfectly correct and retains the provable security under the LWE assumption. We begin by examining the GKW lockable obfuscation for branching programs and identify two points in the construction that are susceptible to correctness errors. The first is in the use of an LWE-based pseudo random generator that could be non-injective. The second is in the “last level testing procedure” comprised in the core construction. We address each one in turn. First, we build over the previous work to design and prove a new PRG construction that is both injective and probably secure from the LWE assumption. (We also create an injective PRG from the learning parity with noise (LPN) assumption as an added bonus.) Then we look to surgically modify the GKW construction to change the last level testing procedure to avoid the correctness pitfall. We accomplish this by adding more structure to a final level of matrices to avoid false matches, but doing so makes the new construction incompatible with the existing security proof. Instead of re-deriving the entire proof of security, we carefully show how an obfuscation under our new construction with a random lock value is indistinguishable from an obfuscation under the previous construction. Security then follows.
While the focus of this work has been on constructing lockable obfuscation schemes with perfect correctness building upon the schemes of [28, 39], we believe our techniques can also be applied to the recent obfuscation scheme by Chen, Vaikuntanathan, and Wee [19].
1.1 Technical Overview
We first present a short overview of the statistically correct lockable obfuscation scheme by Goyal, Koppula and Waters [29, Appendix D], (henceforth referred to as the GKW scheme), and discuss the barriers to achieving perfect correctness. Next, we discuss how to overcome each of these barriers in order to achieve perfect correctness.
Overview of the GKW Scheme. The GKW scheme can be broken down into three parts: (i) constructing a lockable obfuscation scheme for \(\mathsf {NC}^1\) circuits and 1-bit messages, (ii) bootstrapping to lockable obfuscation for poly-depth circuits, and (iii) extending to multi-bit message space. It turns out that steps (ii) and (iii) preserve the correctness properties of the underlying lockable obfuscation scheme, thus in order to build a perfectly correct lockable obfuscation scheme for poly-depth circuits and multi-bit messages, we only need to build a perfectly correct lockable obfuscation scheme for \(\mathsf {NC}^1\) and 1-bit messages.Footnote 3 We start by giving a brief overview of the lockable obfuscation scheme for \(\mathsf {NC}^1\), and then move to highlight the barriers to achieving perfect correctness.
One of the key ingredients in the GKW construction is a family of log-depth (statistically injective) PRGs with polynomial stretch (mapping \(\ell \) bits to \(\ell _{\mathrm {PRG}}\) bits for an appropriately chosen polynomial \(\ell _{\mathrm {PRG}}\)). Consider a log-depth circuit C that takes as input \(\ell _{\mathrm {in}}\)-bits and outputs \(\ell \)-bits. To obfuscate circuit C with lock value \(\alpha \in \{0,1\}^{\ell }\) and message \(\mathsf {msg}\), the GKW scheme first chooses \(\mathrm {PRG}\) from the family and computes an “expanded” lock value \(\beta = \mathrm {PRG}(\alpha )\). It then takes the circuit \(\widehat{C}= \mathrm {PRG}(C(\cdot ))\) that takes as input \(\ell _{\mathrm {in}}\)-bits and outputs \(\ell _{\mathrm {PRG}}\)-bits, and generates the permutation branching program representation of \(\widehat{C}\). Let \(\mathsf {BP}^{(i)}\) denote the branching program that computes \(i^{th}\) output bit of \(\widehat{C}\). Since C and \(\mathrm {PRG}\) are both log-depth circuits, we know (due to Barrington’s theorem [9]) that \(\mathsf {BP}^{(i)}\) is of some polynomial length L and width 5.Footnote 4 The obfuscator continues by sampling \(5 \ell _{\mathrm {PRG}}\) matrices, for each level except the last one, using lattice trapdoor samplers such that all the matrices at any particular level share a common trapdoor. Let \(\varvec{\mathrm {B}}^{(i)}_{j, k}\) denote the matrix corresponding to level j, state k of the \(i^{th}\) branching program \(\mathsf {BP}^{(i)}\). Next, it chooses the top level matrices \(\left\{ \varvec{\mathrm {B}}^{(i)}_{L, 1}, \ldots , \varvec{\mathrm {B}}^{(i)}_{L, 5}\right\} \) for each \(i \in [\ell _{\mathrm {PRG}}]\) uniformly at random subject to the following “sum-constraint":
Looking ahead, sampling the top level matrices in such a way helps to encode the expanded lock value \(\beta \) such that an evaluator can test for this relation if it has an input x such that \(C(x) = \alpha \).
Next step in the obfuscation procedure is to encode the branching programs using the matrices and trapdoors sampled above. The idea is to choose a set of \(\ell _{\mathrm {PRG}}\cdot L\) “transition matrices” \(\{\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j}\}_{i, j}\) such that each matrix \(\varvec{\mathrm {C}}^{(i, b)}_{j}\) is short and can be used to evaluate its corresponding state transition permutation \(\sigma _{j, b}^{(i)}\). The obfuscation of C is set to be the \(\ell _{\mathrm {PRG}}\) base-level matrices \(\{\varvec{\mathrm {B}}^{(i)}_{0,1}\}_i\) and \(\ell _{\mathrm {PRG}}\cdot L\) transition matrices \(\{\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j}\}_{i, j}\).
Evaluating the obfuscated program on input \(x \in \{0,1\}^{\ell _{\mathrm {in}}}\) is analogous to evaluating the \(\ell _{\mathrm {PRG}}\) branching programs on x. For each \(i \in [\ell _{\mathrm {PRG}}]\), the evaluation algorithm first computes \(\varvec{\mathrm {M}}_i = \varvec{\mathrm {B}}^{(i)}_{0,1} \cdot \prod _{j=1}^L \varvec{\mathrm {C}}^{(i, x_{\mathsf {inp}(j)})}_j\) and then sums them together as \(\varvec{\mathrm {M}} = \sum _i \varvec{\mathrm {M}}_i\). To compute the final output, it looks at the entries of matrix \(\varvec{\mathrm {M}}\), if all the entries are small (say less than \(q^{1/4}\)) it outputs 0, else if they are close to \(\sqrt{q}\) it outputs 1, otherwise it outputs \(\perp \).
To argue correctness, they first show that the matrix \(\varvec{\mathrm {M}}\) computed by the evaluator is close to \(\varvec{\mathrm {\Gamma }} \cdot \sum _i \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {st}^{(i)}}\) where \(\varvec{\mathrm {\Gamma }}\) is some low-norm matrix and \(\mathsf {st}^{(i)}\) denotes the final state of \(\mathsf {BP}^{(i)}\).Footnote 5 It is easy to verify that if \(C(x) = \alpha \), then \(\widehat{C}(x) = \beta \), and therefore
As a result, if \(C(x) = \alpha \), then the evaluation is correct. However, it turns out that even when \(C(x) \ne \alpha \) the evaluation algorithm could still output 0/1 (recall that if \(C(x) \ne \alpha \), then the evaluation algorithm must output \(\perp \)). There are two sources of errors here.
-
Non-Injective PRGs. First, it is possible that the \(\mathrm {PRG}\) chosen is not injective. In this event (which happens with negligible probability if \(\mathrm {PRG}\) is chosen honestly), there exist two inputs \(y \ne y'\) such that \(\mathrm {PRG}(y) = \mathrm {PRG}(y')\). As a result, if there exist two inputs \(x, x' \in \{0,1\}^{\ell _{\mathrm {in}}}\) such that \(C(x) = y, C(x') = y'\), then the obfuscation of C with lock y and message \(\mathsf {msg}\), when evaluated on \(x'\), outputs \(\mathsf {msg}\) instead of \(\perp \). Note that this source of error can be eliminated if we use a perfectly injective PRG family instead of a statistically injective PRG family.
-
Sum-Constraints. The second source of error is due to the way we encode the lock value in the top-level matrices. Let \(x \ne x'\) be two distinct inputs, and let \(\alpha = C(x)\), \(\alpha ' = C(x')\), \(\beta = \mathrm {PRG}(\alpha )\) and \(\beta ' = \mathrm {PRG}(\alpha ')\). Suppose we obfuscate C with lock value \(\alpha \). Recall that the obfuscator samples the top-level matrices uniformly at random with the only constraint that the top-level matrices corresponding to the expanded lock value \(\beta \) either sum to 0 (if \(\mathsf {msg}= 0\)), else they sum to certain medium-ranged matrix (i.e., entries \(\approx \sqrt{q}\)). Now this corresponds to sampling all but one top-level matrix uniformly at random (and without any constraint), and that one special matrix such that the constraint is satisfied. Therefore, it is possible (although with small probability) that summing together the top-level matrices for string \(\beta '\) is close to the top-level matrix sum for string \(\beta \). That is,
$$ \sum _{i :\ \beta _i = 0} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i :\ \beta _i = 1} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {acc}^{(i)}} \approx \sum _{i :\ \beta '_i = 0} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i :\ \beta '_i = 1} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {acc}^{(i)}}. $$As a result, if we obfuscate C with lock \(\alpha \) and message \(\mathsf {msg}\), and evaluate this on input \(x'\), then it could also output \(\mathsf {msg}\) instead of \(\perp \). This type of error is trickier to remove as it is crucial for security in the GKW construction that these matrices look completely random if one doesn’t know the lock value \(\alpha \). To get around this issue, we provide an alternate top-level matrix sampling procedure that guarantees perfect correctness.
We next present our solutions to remove the above sources of imperfectness. First, we construct a perfectly injective PRG family that is secure under the LWE assumption. This resolves the first problem. Thereafter, we discuss our modifications to the GKW construction for resolving the sum-constraint error. Later we also briefly talk about our perfectly injective PRG family that is secure under the LPN assumption.
Perfectly Injective PRG Family. We will first show a perfectly injective PRG family based on the LWE assumption. The construction is a low-depth PRG family with unbounded (polynomial) stretch. The security of this construction relies on the Learning with Rounding (LWR) assumption, introduced by Banerjee, Peikert and Rosen. [7], which in turn can be reduced to LWE (with subexponential modulus/error ratio). First, let us recall the LWR assumption. This assumption is associated with two moduli p, q where \(p < q\). The modulus q is the modulus of computation, and p is the rounding modulus. Let \(\lfloor \cdot \rceil _p\) denote a mapping from \(\mathbb {Z}_q\) to \(\mathbb {Z}_p\) which maps integers based on their higher order bits. The LWR assumption states that for a uniformly random secret vector \(\varvec{\mathrm {s}} \in \mathbb {Z}_q^n\) and uniformly random matrix \(\varvec{\mathrm {A}}\in \mathbb {Z}_q^{n \times m}\), \(\lfloor \varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\rceil _p\) looks like a uniformly random vector in \(\mathbb {Z}_p^m\), even when given \(\varvec{\mathrm {A}}\). We will work with a ‘binary secrets’ version where the secret vector \(\varvec{\mathrm {s}}\) is a binary vector.
Let us start by reviewing the PRG construction provided by Banerjee et al. [7]. In their scheme, the setup algorithm first chooses two moduli \(p < q\) and outputs a uniformly random \(n \times m\) matrix \(\varvec{\mathrm {A}}\) with elements from \(\mathbb {Z}_q\). The PRG evaluation takes as input an n bit string \(\varvec{\mathrm {s}}\) and outputs \(\lfloor \varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\rceil _p\), where \(\lfloor x\rceil _p\) essentially outputs the higher order bits of x. Assuming m is sufficiently larger than n and moduli p, q are appropriately chosen, for a uniformly random matrix \(\varvec{\mathrm {A}}\leftarrow \mathbb {Z}_q^{n \times m}\), the function \(\lfloor \varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\rceil _p\) is injective with high probability (over the choice of \(\varvec{\mathrm {A}}\)). In order to achieve perfect injectivity, we sample the public matrix \(\varvec{\mathrm {A}}\) in a special way.
In our scheme, the setup algorithm chooses a uniformly random matrix \(\varvec{\mathrm {B}}\) and a low norm matrix \(\varvec{\mathrm {C}}\). It sets \(\varvec{\mathrm {D}}\) to be a diagonal matrix with medium-value entries (\(\varvec{\mathrm {D}}\) is a fixed deterministic matrix). It sets \(\varvec{\mathrm {A}}= [\varvec{\mathrm {B}}~ | ~ \varvec{\mathrm {B}}\cdot \varvec{\mathrm {C}}+ \varvec{\mathrm {D}}]\) and outputs it as part of the public parameters, together with the LWR moduli p, q. To evaluate the PRG on input \(\varvec{\mathrm {s}} \in \{0,1\}^n\), one outputs \(\varvec{\mathrm {y}} = \lfloor \varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\rceil _p\). Intuitively, the \(\varvec{\mathrm {D}}\) matrix acts as a error correcting code, and if \(\varvec{\mathrm {s}}_1 \ne \varvec{\mathrm {s}}_2\), then there is at least one coordinate such that \(\lfloor \varvec{\mathrm {s}}_1^T \cdot \varvec{\mathrm {D}}\rceil _p\) and \(\lfloor \varvec{\mathrm {s}}_2^T \cdot \varvec{\mathrm {D}}\rceil _p\) are far apart.
Suppose \(\varvec{\mathrm {s}}_1\) and \(\varvec{\mathrm {s}}_2\) are two bitstrings such that \(\lfloor \varvec{\mathrm {s}}_1^T\cdot \varvec{\mathrm {A}}\rceil _p = \lfloor \varvec{\mathrm {s}}_2^T \cdot \varvec{\mathrm {A}}\rceil _p\). Then \(\lfloor \varvec{\mathrm {s}}_1^T \cdot \varvec{\mathrm {B}}\rceil _p\) = \(\lfloor \varvec{\mathrm {s}}_2^T \cdot \varvec{\mathrm {B}}\rceil _p \), and as a result, \(\lfloor \varvec{\mathrm {s}}_1^T \cdot \varvec{\mathrm {B}}\cdot \varvec{\mathrm {C}}\rceil _p\) and \(\lfloor \varvec{\mathrm {s}}_2^T \cdot \varvec{\mathrm {B}}\cdot \varvec{\mathrm {C}}\rceil _p\) have close enough entries as \(\varvec{\mathrm {C}}\) has small entries. However, this implies that \(\lfloor \varvec{\mathrm {s}}_1^T \cdot \varvec{\mathrm {D}}\rceil _p\) and \(\lfloor \varvec{\mathrm {s}}_2^T \cdot \varvec{\mathrm {D}}\rceil _p\) also have close enough entries, which implies that \(\varvec{\mathrm {s}}_1 = \varvec{\mathrm {s}}_2\).
Pseudorandomness follows from the observation that \(\varvec{\mathrm {A}}\) looks like a uniformly random matrix. Once we replace \([ \varvec{\mathrm {B}}~|~ \varvec{\mathrm {B}}\cdot \varvec{\mathrm {C}}+ \varvec{\mathrm {D}}] \) with a uniformly random matrix \(\varvec{\mathrm {A}}\), we can use the binary secrets version of LWR to argue that \(\varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\) is indistinguishable from a uniformly random vector. This is discussed in detail in Sect. 3.
Relation to the Perfectly Binding Commitment Scheme of [27]: The perfectly injective PRG family outlined above builds upon some core ideas from the perfectly binding commitments schemes in [27]. Below, we will describe the constructions from [27], and discuss the main differences in our PRG schemes.
In the LWE based commitment scheme, the sender first chooses a modulus q, matrices \(\varvec{\mathrm {B}}, \varvec{\mathrm {C}}, \varvec{\mathrm {D}}\) and \(\varvec{\mathrm {E}}\) of dimensions \(n \times n\), where \(\varvec{\mathrm {B}}\) is a uniformly random matrix, entries in \(\varvec{\mathrm {C}}\), \(\varvec{\mathrm {E}}\) are drawn from the low norm noise distribution, and \(\varvec{\mathrm {D}}\) is some fixed diagonal matrix with medium-value entries. It sets \(\varvec{\mathrm {A}}= [\varvec{\mathrm {B}}\left| \right| \varvec{\mathrm {B}}\cdot \varvec{\mathrm {C}}+ \varvec{\mathrm {D}}+ \varvec{\mathrm {E}}]\). Next, it chooses a vector \(\varvec{\mathrm {s}}\) from the noise distribution, vector \(\varvec{\mathrm {w}}\) uniformly at random, vector \(\varvec{\mathrm {e}}\) from the noise distribution and f from the noise distribution. To commit to a bit b, it sets \(\varvec{\mathrm {y}} = \varvec{\mathrm {A}}^T \cdot \varvec{\mathrm {s}} + \varvec{\mathrm {e}}\), \(z = \varvec{\mathrm {w}}^T \cdot \varvec{\mathrm {s}} + f + b (q/2)\), and the commitment is \((\varvec{\mathrm {A}}, \varvec{\mathrm {w}}, \varvec{\mathrm {y}}, z)\). The opening simply consists of the randomness used for constructing the commitment.
The main differences between our PRG construction and their commitment scheme are as follows: (i) we need to separate out their initial commitment step into PRG setup and evaluation phase, (ii) since the PRG evaluation is deterministic, we cannot add noise (unlike in the case of commitments). Therefore, we need to use Learning with Rounding. Finally, we need to carefully choose the rounding modulus p as we want to ensure that the rounding operation does not round off the contribution from the special matrix \(\varvec{\mathrm {D}}\) while still allowing us to reduce to the LWR assumption.
Sum-Constraint on the Top-Level Matrices. We will now discuss how the top-level matrices can be sampled to ensure perfect correctness. In order to do so, let us first consider the following simplified problem which captures the essence of the issue. Given a string \(\beta \in \{0,1\}^\ell \), we wish to sample \(2\ell \) matrices \(\{\varvec{\mathrm {M}}_{i,b}\}_{i \in [\ell ], b\in \{0,1\}}\) such that they satisfy the following three constraints:
-
1.
\(\sum _i \varvec{\mathrm {M}}_{i, \beta _i}\) has ‘small’ entries (say \(< q^{1/4}\)).
-
2.
For all \(\beta ' \ne \beta \), \(\sum _i \varvec{\mathrm {M}}_{i, \beta '_i}\) has ‘large’ entries (say greater than \(q^{1/2}\)).
-
3.
For a uniformly random choice of string \(\beta \), the set of \(2\ell \) matrices \(\left\{ \varvec{\mathrm {M}}_{i,b}\right\} _{i,b}\) ‘look’ like random matrices.
In the GKW construction, the authors use a simple sampler that the sampled matrices satisfy the first constraint, and by applying the Leftover Hash Lemma (LHL) they also show that the corresponding matrices satisfy the third constraint. However, to achieve perfect correctness, we need to build a matrix sampler such that its output always satisfy all the three constraints. To this end, we show that by carefully embedding LWE samples inside the output matrices we can achieve the second constraint as well. We discuss our approach in detail below.
We now define a sampler \(\mathsf {Samp}\) that takes an \(\ell \)-bit string \(\beta \) as input, and outputs \(2\ell \) matrices satisfying all the above constraints, assuming the Learning with Errors assumption (in addition to relying on LHL). The sampler first chooses \(2\ell \) uniformly random square matrices \(\{\varvec{\mathrm {A}}_{i,b}\}_{i \in [\ell ], b \in \{0,1\}}\) subject to the constraint that \(\sum _{i} \varvec{\mathrm {A}}_{i, \beta _i} = \varvec{\mathrm {0}}^{n \times n}\). This can be achieved by simply sampling \(2\ell - 1\) uniformly random \(n\times n\) matrices, and setting \(\varvec{\mathrm {A}}_{\ell , \beta _{\ell }} = - \sum _{i<\ell } \varvec{\mathrm {A}}_{i, \beta _i}\). Let \(\varvec{\mathrm {D}}= q^{3/4} \left[ \varvec{\mathrm {I}}_n \left| \right| \varvec{\mathrm {0}}^{n\times (m-2n)} \right] \) be a \(n \times (m - n)\) matrix with a few ‘large’ entries. The sampler then chooses a low norm \(n\times (m-n)\) matrix \(\varvec{\mathrm {S}}\) and low-norm \(n\times (m-n)\) error matrices \(\left\{ \varvec{\mathrm {E}}_{i,b}\right\} _{i \in [\ell ], b \in \{0,1\}}\). It sets the \(2\ell \) output matrices as
In short, our sampler samples the first n columns of the output matrix in a similar way to GKW scheme, whereas the remaining \((m - n)\) columns are sampled in a special way such that if we sum up the matrices corresponding to string \(\beta \) then the last \((m - n)\) columns of the summed matrix have small entries, whereas summing up matrices corresponding to any other string \(\beta ' \ne \beta \), the last \((m - n)\) columns of the summed matrix have distinguishably large entries. Below we briefly argue why our sampler satisfies the three properties specified initially.
-
1.
(First property): Note that \(\sum _{i} \varvec{\mathrm {A}}_{i, \beta _i} = \varvec{\mathrm {0}}^{n \times n}\), therefore we have that
$$\varvec{\mathrm {M}}_{\beta } = \sum _i \varvec{\mathrm {M}}_{i, \beta _i} = \left[ \varvec{\mathrm {0}}^{n\times n} \left| \right| \varvec{\mathrm {0}}^{n \times n} \cdot \varvec{\mathrm {S}}+ \sum _{i} \varvec{\mathrm {E}}_{i, \beta _i} \right] = \left[ \varvec{\mathrm {0}}^{n\times n} \left| \right| \sum _{i} \varvec{\mathrm {E}}_{i, \beta _i} \right] . $$Since the error matrices are drawn from a low-norm distribution, the entries of \(\varvec{\mathrm {M}}_{\beta } \) are ‘small’.
-
2.
(Second property): We need to check that \(\varvec{\mathrm {M}}_{\beta '} = \sum _i \varvec{\mathrm {M}}_{i, \beta '_i}\) has ‘large’ entries for \(\beta ' \ne \beta \). Suppose \(\beta \) and \(\beta '\) differ at t positions (\(t>0\)). Then
$$\sum _i \varvec{\mathrm {M}}_{i, \beta '_i} = \left[ \sum _{i} \varvec{\mathrm {A}}_{\beta '} \left| \right| \varvec{\mathrm {A}}_{\beta '} \cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_{\beta '} + t\cdot \varvec{\mathrm {D}} \right] ,$$where \(\varvec{\mathrm {A}}_{\beta '} = \sum _i \varvec{\mathrm {A}}_{i, \beta '_i}\) and \(\varvec{\mathrm {E}}_{\beta '} = \sum _i \varvec{\mathrm {E}}_{i, \beta '_i}\). If \(\varvec{\mathrm {A}}_{\beta '}\) has large entries (greater than \(q^{1/2}\)), then we are done. On the other hand, if \(\varvec{\mathrm {A}}_{\beta '}\) has small entries (less than \(q^{1/2}\)), then we can argue that \(\varvec{\mathrm {A}}_{\beta '} \cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_{\beta '}\) also has entries less than \(q^{3/4}\), and therefore \(\varvec{\mathrm {A}}_{\beta '} \cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_{\beta '} + t\cdot \varvec{\mathrm {D}}\) has large entries. This implies that \(\varvec{\mathrm {M}}_{\beta '}\) has large entries, and hence the second constraint is also satisfied.
-
3.
(Third property): To argue about the third property, we use the LWE assumption in conjunction with LHL. First, we can argue that the \(\{\varvec{\mathrm {A}}_{i, b}\}\) matrices look like uniformly random matrices (using the leftover hash lemma). Next, using the LWE assumption, we can show that \(\left\{ \left[ \varvec{\mathrm {A}}_{i,b} \left| \right| \varvec{\mathrm {A}}_{i,b}\cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_{i,b} \right] \right\} _{i,b}\) are indistinguishable from \(2\ell \) uniformly random matrices, and hence the third property is also satisfied.
We can also modify the above sampler slightly such that \(\sum _i \varvec{\mathrm {M}}_{i,\beta _i}\) has ‘medium’ entries (that is, entries within the range \([q^{1/4}, q^{1/2})\)). The sampler chooses random matrices \(\{\varvec{\mathrm {A}}_{i,b}\}_{i,b}\) subject to the constraint that \(\sum _{i} \varvec{\mathrm {A}}_{i, \beta _i} = q^{1/4} \varvec{\mathrm {I}}_n\), and the remaining steps are same as above. Let \(\mathsf {Samp}_{\mathrm {med}}\) be the sampler for this ‘medium-entries’ variant.
We observe that if we plug in these samplers into the GKW scheme for sampling their top-level matrices, then that leads to a perfectly correct lockable obfuscation scheme. Specifically, let \(\alpha \) be the lock used, \(\mathrm {PRG}\) chosen from a perfectly injective PRG family, and \(\beta = \mathrm {PRG}(\alpha )\) be the expanded lock value. The obfuscation scheme chooses matrices \(\left\{ \varvec{\mathrm {M}}_{i,b}\right\} _{i,b}\) using either \(\mathsf {Samp}\) or \(\mathsf {Samp}_{\mathrm {med}}\) depending on the message \(\mathsf {msg}\). That is, if \(\mathsf {msg}= 0\), it chooses \(\left\{ \varvec{\mathrm {M}}_{i,b}\right\} _{i,b} \leftarrow \mathsf {Samp}(\beta )\), else it chooses \(\left\{ \varvec{\mathrm {M}}_{i,b}\right\} _{i,b} \leftarrow \mathsf {Samp}_{\mathrm {med}}(\beta )\). It then sets \(\varvec{\mathrm {B}}^{(i)}_{L, \mathsf {acc}^{(i)}} = \varvec{\mathrm {M}}_{i,1}\) and \(\varvec{\mathrm {B}}^{(i)}_{L, \mathsf {rej}^{(i)}} = \varvec{\mathrm {M}}_{i,0}\) for each \(i \in [\ell _{\mathrm {PRG}}]\). From the properties of \(\mathsf {Samp}/\mathsf {Samp}_{\mathrm {med}}\), it follows that
which has ‘low’ or ‘medium’ norm depending on \(\mathsf {msg}\) bit. The remaining top level matrices are chosen uniformly at random. Everything else stays the same as in the GKW scheme.
For completeness, we now check that this scheme indeed satisfies perfect correctness. Consider an obfuscation of circuit C with lock \(\alpha \) and message \(\mathsf {msg}\). If this obfuscation is evaluated on input x such that \(C(x) = \alpha \), then the evaluation outputs \(\mathsf {msg}\) as expected. If \(C(x) = \alpha ' \ne \alpha \), then \(\mathrm {PRG}(C(x)) = \beta ' \ne \beta \) (since the PRG is injective). This means the top level sum is
Using the second property of \(\mathsf {Samp}/\mathsf {Samp}_{\mathrm {med}}\), we know that this sum has ‘large’ entries, and therefore the evaluation outputs \(\perp \). This completes our perfect correctness argument. Now for proving that our modification still give a secure lockable obfuscation, we do not re-derive a completely new security proof but instead we show that no PPT attacker can distinguish an obfuscated program generated using our scheme from the one generated by using the GKW scheme. Now combining this claim with the fact that the GKW scheme is secure under LWE assumption, we get that our scheme is also secure. Very briefly, the idea behind indistinguishability of these two schemes is that since the lock \(\alpha \) is chosen uniformly at random, then \(\mathrm {PRG}(\alpha )\) is computationally indistinguishable from a uniformly random string \(\beta \), and thus these top level matrices also look like uniformly random matrices for uniformly random \(\beta \) (using the third property of \(\mathsf {Samp}/\mathsf {Samp}_{\mathrm {med}}\)). Now to complete argument we show the same hold for GKW scheme as well, thereby completing the proof. More details on this are provided in the main body.
Perfectly Injective PRGs from the LPN Assumption. Finally, we also build a family of perfectly injective PRGs based on the Learning Parity with Noise assumption. While the focus of this work has been getting an end-to-end LWE solution for perfectly correct lockable obfuscation, we also build perfectly injective PRGs based on the LPN assumption, which could be of independent interest. Recently, there has been a surge of interest towards new constructions of cryptographic primitives based on LPN [16, 17, 23, 40,41,42], and we feel that our perfectly injective PRGs fit this theme. Our LPN solution uses a low-noise variant (\(\beta \approxeq \frac{1}{\sqrt{n}}\)) of the LPN assumption that has been used in previous public key encryption schemes [1]. Below we briefly sketch the main ideas behind our PRG construction.
To build perfectly injective PRGs from LPN, we take a similar approach to one taken in the LWE case. The starting idea is to use the PRG seed (as before) as the secret vector \(\varvec{\mathrm {s}}\) and compute the PRG evaluation as \(\varvec{\mathrm {B}}^T \varvec{\mathrm {s}})\) but now, unlike the LWE case, we do not have any rounding equivalent for LPN, that is we do not know how to avoid generating the error vector \(\varvec{\mathrm {e}}\) during PRG evaluation. Therefore, to execute the idea we provide an (efficient) injective sampler for error vectors which takes as input a bit string and outputs an error vector \(\varvec{\mathrm {e}}\) of appropriate dimension. (The injectivity property here states that the mapping between bit strings and the error vectors is injective.) So now in our PRG evaluation the input string is first divided in two disjoint components where the first component is directly interpreted as the secret vector \(\varvec{\mathrm {s}}\) and second component is used to sample the error vector \(\varvec{\mathrm {e}}\) using our injective sampler.
Although at first it might seem that building an injective sampler might not be hard, however it turns out there are a couple of subtle issues that we have taken care of while proving security as well as perfect injectivity. Concretely, for self-composability of our PRG (i.e., building PRGs which take as input bit strings of fixed length instead having a special domain sampling algorithm), we require that the size of support of distribution of error vectors \(\varvec{\mathrm {e}}\) used is a ‘perfect power of two’. As otherwise we can not hope to build a perfectly injective (error vector) sampler which takes as input a fixed length bit string and outputs the corresponding error vector. Now we know that the size of support of noise distribution in the LPN assumption might not be a perfect power of two, thus we might not be able to injectively sample error vectors from the fixed length bit strings. To resolve this issue, we define an alternate assumption which we call the ‘restricted-exact-LPN’ assumption and show that (a) it is as hard as standard LPN, (b) sufficient for our proof to go through, and (c) has an efficiently enumerable noise distribution whose support size is a perfect power of two (i.e., we can define an efficient injective error sampler for its noise distribution). More details are provided later in Sect. 5.
1.2 Related Works on Perfect Correctness
In this section, we discuss some related work and approaches for achieving perfect correctness for lockable obfuscation and its applications. First, a recent concurrent and independent work by Asharov et al. [6] also addresses the question of perfect correctness for obfuscation. They show how to generically achieve perfect correctness for any indistinguishability obfuscation scheme, assuming hardness of LWE. Below, we discuss other related prior works.
Perfect Correctness via Derandomization. Bitansky and Vaikuntanathan [13] showed how to transform any obfuscation scheme (and a large class of cryptosystems) to remove correctness errors using Nisan-Wigderson (NW) PRGs [34]. In their scheme, the obfuscator runs the erroneous obfuscation algorithm sufficiently many times, and for each execution of the obfuscator, the randomness used is derived pseudorandomly (by adding the randomness derived from the NW PRGs and the randomness from a standard cryptographic PRG). As the authors show, such a transformation leads to a perfectly correct scheme as long as certain circuit lower bound assumptions hold (in particular, they require that the NW-PRGs can fool certain bounded-size circuits). Our solution, on the other hand, does not rely on additional assumptions as well as it is as efficient as existing (imperfect) lockable obfuscation constructions [28, 39].
Using a Random Oracle for Generating Randomness. A heuristic approach to prevent the obfuscator from using malicious randomness is to generate the random coins using a hash function H applied on the circuit. Such a heuristic might suffice for some applications such as the public auditing example discussed previously, but it does not seem to provide provable security in others. Note that our construction with perfect correctness is proven secure in the standard model, and does not need rely on ROs or a CRS.
Lastly, we want to point out that in earlier works by Bitansky and Vaikuntanathan [12], and Ananth, Jain and Sahai [3], it was shown how to transform any obfuscation scheme that has statistical correctness on \((1/2 + \epsilon )\) fraction of inputs (for some non-negligible \(\epsilon \)) into a scheme that has statistical correctness for all inputs. However, this does not achieve perfect correctness. It is an interesting question whether their approach could be extended to achieve perfect correctness. Similar correctness amplification issues were also addressed by Ananth et al. [2].
2 Preliminaries
In this section, we review the notions of injective pseudorandom generators with setup and Lockable Obfuscation [28, 39]. Due to space constraints, we review fundamentals of lattices and homomorphic encryption in the full version of the paper.
2.1 Injective Pseudorandom Generators with Setup
We will be considering PRGs with an additional setup algorithm that outputs public parameters. The setup algorithm will be important for achieving injectivity in our constructions. While this is weaker than the usual notion of PRGs (without setup), it turns out that for many of the applications that require injectivity of PRG, the setup phase is not an issue.
-
\(\mathsf {Setup}(1^{\lambda }){:}\) The setup algorithm takes as input the security parameter \(\lambda \) and outputs public parameters \(\mathsf {pp}\), domain \(\mathcal {D}\) and co-domain \(\mathcal {R}\) of the PRG. Let \(\mathsf {params}\) denote \((\mathsf {pp}, \mathcal {D}, \mathcal {R})\).
-
\(\mathrm {PRG}(\mathsf {params}, s \in \mathcal {D}):\) The PRG evaluation algorithm takes as input the public parameters and the PRG seed \(s \in \mathcal {D}\), and outputs \(y \in \mathcal {R}\).
Perfect Injectivity. A pseudorandom generator with setup \((\mathsf {Setup}, \mathrm {PRG})\) is said to have perfect injectivity if for all \((\mathsf {pp}, \mathcal {D}, \mathcal {R}) \leftarrow \mathsf {Setup}(1^{\lambda })\), for all \(s_1 \ne s_2 \in \mathcal {D}\), \(\mathrm {PRG}(\mathsf {params}, s_1) \ne \mathrm {PRG}(\mathsf {params}, s_2)\).
Pseudorandomness. A pseudorandom generator with setup \((\mathsf {Setup}, \mathrm {PRG})\) is said to be secure if for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\),

2.2 Lockable Obfuscation
In this section, we recall the notion of lockable obfuscation defined by Goyal et al. [28]. Let n, m, d be polynomials, and \(\mathcal {C}_{n,m,d}(\lambda )\) be the class of depth \(d(\lambda )\) circuits with \(n(\lambda )\) bit input and \(m(\lambda )\) bit output. Let \(\mathcal {M}\) be the message space. A lockable obfuscator for \(\mathcal {C}_{n,m,d}\) consists of algorithms \(\mathsf {Obf}\) and \(\mathsf {Eval}\) with the following syntax.
-
\(\mathsf {Obf}(1^{\lambda }, P, \mathsf {msg}, \alpha ) \rightarrow \widetilde{P}.\) The obfuscation algorithm is a randomized algorithm that takes as input the security parameter \(\lambda \), a program \(P \in \mathcal {C}_{n,m,d}\), message \(\mathsf {msg}\in \mathcal {M}\) and ‘lock string’ \(\alpha \in \{0,1\}^{m(\lambda )}\). It outputs a program \(\widetilde{P}\).
-
\(\mathsf {Eval}(\widetilde{P}, x) \rightarrow y \in \mathcal {M}\cup \{ \perp \}.\) The evaluator is a deterministic algorithm that takes as input a program \(\widetilde{P}\) and a string \(x \,{\in }\, \{0,1\}^{n(\lambda )}\). It outputs \(y \,{\in }\, \mathcal {M}\cup \{ \perp \}\).
Correctness. For correctness, we require that if \(P(x) = \alpha \), then the obfuscated program \(\widetilde{P}\leftarrow \mathsf {Obf}(1^{\lambda }, P, \mathsf {msg}, \alpha )\), evaluated on input x, outputs \(\mathsf {msg}\), and if \(P(x) \ne \alpha \), then \(\widetilde{P}\) outputs \(\perp \) on input x. Formally,
Definition 1 (Perfect Correctness)
Let n, m, d be polynomials. A lockable obfuscation scheme for \(C_{n,m,d}\) and message space \(\mathcal {M}\) is said to be perfectly correct if it satisfies the following properties:
-
1.
For all security parameters \(\lambda \), inputs \(x \in \{0,1\}^{n(\lambda )}\), programs \(P \in \mathcal {C}_{n,m,d}\) and messages \(\mathsf {msg}\in \mathcal {M}\), if \(P(x) = \alpha \), then
$$ \mathsf {Eval}(\mathsf {Obf}(1^{\lambda }, P, \mathsf {msg}, \alpha ), x) = \mathsf {msg}.$$ -
2.
For all security parameters \(\lambda \), inputs \(x \in \{0,1\}^{n(\lambda )}\), programs \(P \in \mathcal {C}_{n,m,d}\) and messages \(\mathsf {msg}\in \mathcal {M}\), if \(P(x) \ne \alpha \), then
$$ \mathsf {Eval}(\mathsf {Obf}(1^{\lambda }, P, \mathsf {msg}, \alpha ), x) =\ \perp .$$
Remark 1 (Weaker notions of correctness)
We would like to point out that GKW additionally defined two weaker notions of correctness - statistical and semi-statistical correctness. They say that lockable obfuscation satisfies statistical correctness if for any triple \((P, \mathsf {msg}, \alpha )\), the probability that there exists an x s.t. \(P(x) \ne \alpha \) and the obfuscated program outputs \(\mathsf {msg}\) on input x is negligible in security parameter. The notion of semi-statistical correctness is even weaker where each obfuscated program could potentially always output message \(\mathsf {msg}\) for some input x s.t. \(P(x) \ne \alpha \), but if one fixes the input x before obfuscation, then the probability of the obfuscated program outputting \(\mathsf {msg}\) on input x is negligible.
Security. We now present the simulation based security definition for Lockable Obfuscation.
Definition 2
Let n, m, d be polynomials. A lockable obfuscation scheme \((\mathsf {Obf},\) \( \mathsf {Eval})\) for \(\mathcal {C}_{n,m,d}\) and message space \(\mathcal {M}\) is said to be secure if there exists a PPT simulator \(\mathsf {Sim}\) such that for all PPT adversaries \(\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)\), there exists a negligible function \(\text {negl}(\cdot )\) such that the following function is bounded by \(\text {negl}(\cdot )\):

3 Perfectly Injective PRGs from LWR
In this construction, we will present a construction based on the Learning With Rounding (LWR) assumption. At a high level, the construction works as follows: the setup algorithm chooses a uniformly random matrix \(\varvec{\mathrm {A}}\in \mathbb {Z}_q^{n \times 2m}\), where m is much greater than n. The PRG evaluation outputs \(\lfloor \varvec{\mathrm {x}}^T \cdot \varvec{\mathrm {A}}\rceil _p\), where \(p = 2^{\ell _{\mathrm {out}}}\). Note that this already gives us a PRG with statistical injectivity. However, to achieve perfect injectivity, we need to ensure that the matrix \(\varvec{\mathrm {A}}\) is full rank, and that injectivity is preserved even after rounding. In order to achieve this, we need to make some modifications to the setup algorithm.
The new setup algorithm chooses a uniformly random matrix \(\varvec{\mathrm {B}}\), a random matrix \(\varvec{\mathrm {R}}\) with \(\pm 1\) entries. Let \(\varvec{\mathrm {D}}\) be a fixed full rank matrix with ‘medium sized’ entries. It then outputs \(\varvec{\mathrm {A}}= [\varvec{\mathrm {B}}~ | ~ \varvec{\mathrm {B}}\varvec{\mathrm {R}}+ \varvec{\mathrm {D}}]\). The PRG evaluation is same as described above.
We will now describe the algorithms formally.
-
\(\mathsf {Setup}(1^\lambda )\) The setup algorithm first sets the parameters \(n, m, q, \ell _{\mathrm {out}}, \rho \) in terms of the security parameter. These parameters must satisfy the following constraints.
-
\(n = \mathsf {poly}(\lambda )\)
-
\(q \le 2^{n^{\epsilon }}\)
-
\(m > 2 n \log q\)
-
\(p = 2^{\ell _{\mathrm {out}}}\)
-
\(n < m \cdot \ell _{\mathrm {out}}\)
-
\( (q/p)m< \rho < q\)
One particular setting of parameters which satisfies the constraints above is as follows: set \(n = \mathsf {poly}(\lambda )\), \(q = 2^{n^\epsilon }\), \(p = \sqrt{q}\), \(m = n^2\) and \(\rho = q/4\).
Next, it chooses a matrix \(\varvec{\mathrm {B}}\leftarrow \mathbb {Z}_q^{n \times m}\), matrix \(\varvec{\mathrm {R}}\leftarrow \{+1, -1\}^{m \times m}\). Let \(\varvec{\mathrm {D}}= \rho \cdot [\varvec{\mathrm {I}}_n ~ | ~ \varvec{\mathrm {0}}^{n \times (m-n)}]\) and \(\varvec{\mathrm {A}}= [\varvec{\mathrm {B}}~ | ~ \varvec{\mathrm {B}}\cdot \varvec{\mathrm {R}}+ \varvec{\mathrm {D}}]\). The setup algorithm outputs \(\varvec{\mathrm {A}}\) as the public parameters. It sets the domain \(\mathcal {D}= \{0,1\}^{n}\) and co-domain \(\mathcal {R}= \{0,1\}^{m\cdot \ell _{\mathrm {out}}}\).
-
-
\(\mathrm {PRG}(\varvec{\mathrm {A}}, \varvec{\mathrm {s}})\): The PRG evaluation algorithm takes as input the matrix \(\varvec{\mathrm {A}}\) and the seed \(\varvec{\mathrm {s}}\in \{0,1\}^{n}\). It computes \(\varvec{\mathrm {y}} = \varvec{\mathrm {s}}^T \cdot \varvec{\mathrm {A}}\). Finally, it outputs \(\lfloor \varvec{\mathrm {y}}\rceil _p \in \mathbb {Z}_p^m\) as a bit string of length \(2m \cdot \ell _{\mathrm {out}}\).
Depth of \(\mathrm {PRG}\) Evaluation Circuit and \(\mathrm {PRG}\) Stretch. First, note that the the \(\mathrm {PRG}\) evaluation circuit only needs to perform a single matrix-vector multiplication followed by discarding the \(\lceil {\log _2 q/p}\rceil \) least significant bits of each element. Clearly such a circuit can be implemented in \(\varvec{\mathrm {TC}}^0\), the class of constant-depth, poly-sized circuits with unbounded fan-in and threshold gates (which is a subset of \(\varvec{\mathrm {NC}}^1\)). Additionally, the stretch provided by the above \(\mathrm {PRG}\) could be arbitrarily set during setup. Thus, the above construction gives a \(\mathrm {PRG}\) that provides a polynomial stretch with a \(\varvec{\mathrm {TC}}^0\) evaluation circuit.
We now prove the following theorem where we show that our \(\mathrm {PRG}\) construction satisfies perfect injectivity property. Due to space constraints, we argue the pseudorandomness property of the construction in the full version of the paper.
Theorem 1
If the LWR assumption with parameters n, m, p and q holds, then the above construction is a perfectly injective PRG.
Due to space constraints, we prove the Theorem in the full version of the paper.
4 Lockable Obfuscation with Perfect Correctness
4.1 Construction
In this section, we present our perfectly correct lockable obfuscation scheme. We note that the construction is similar to the statistically correct lockable obfuscation scheme described in Goyal et al. [28]. A part of the description has been taken verbatim from [28]. For any polynomials \(\ell _{\mathrm {in}}, \ell _{\mathrm {out}}, d\) such that \(\ell _{\mathrm {out}}= \omega (\log \lambda )\), we construct a lockable obfuscation scheme \(\mathcal {O}= (\mathsf {Obf}, \mathsf {Eval})\) for the circuit class \(\mathcal {C}_{\ell _{\mathrm {in}}, \ell _{\mathrm {out}}, d}\). The message space for our construction will be \(\{0,1\}\), although one can trivially extend it to \(\{0,1\}^{\ell (\lambda )}\) for any polynomial \(\ell \) [28].
The tools required for our construction are as follows:
-
A compact leveled homomorphic bit encryption scheme \((\mathsf {LHE}.\mathsf {Setup}, \mathsf {LHE}.\mathsf {Enc},\) \(\mathsf {LHE}.\mathsf {Eval}, \mathsf {LHE}.\mathsf {Dec})\) with decryption circuit of depth \(d_{\mathsf {Dec}}(\lambda )\) and ciphertexts of length \(\ell _{\mathsf {ct}}(\lambda )\).
-
A perfectly injective pseudorandom generator scheme \((\mathrm {PRG}.\mathsf {Setup}, \mathrm {PRG}.\mathsf {Eval})\), where \(\mathrm {PRG}.\mathsf {Eval}\) has depth \(d_{\mathrm {PRG}}(\lambda )\), input length \(\ell _{\mathrm {out}}(\lambda )\) and output length \(\ell _{\mathrm {PRG}}(\lambda )\).
For notational convenience, let \(\ell _{\mathrm {in}}= \ell _{\mathrm {in}}(\lambda )\), \(\ell _{\mathrm {out}}= \ell _{\mathrm {out}}(\lambda )\), \(\ell _{\mathrm {PRG}}= \ell _{\mathrm {PRG}}(\lambda )\), \(d_{\mathsf {Dec}}= d_{\mathsf {Dec}}(\lambda )\), \(d_{\mathrm {PRG}}= d_{\mathrm {PRG}}(\lambda )\) and \(d = d(\lambda )\).
Fix any \(\epsilon < 1/2\). Let \(\chi \) be a B-bounded discrete Gaussian distribution with parameter \(\sigma \) such that \(B = \sqrt{m} \cdot \sigma \). Let \(n, m, \ell , \sigma , q, \mathsf {Bd}\) be parameters with the following constraints:
-
\(n = \mathsf {poly}(\lambda )\) and \(q \le 2^{n^{\epsilon }}\) (for LWE security)
-
\(m \ge \widetilde{c} \cdot n \cdot \log q\) for some universal constant \(\widetilde{c}\) (for \(\mathsf {SamplePre}\))
-
\(\sigma = \omega (\sqrt{n\cdot \log q \cdot \log m})\) (for Preimage Well Distributedness)
-
\(\ell _{\mathrm {PRG}}= n \cdot m \cdot \log q + \omega (\log n)\) (for applying Leftover Hash Lemma)
-
\(\ell _{\mathrm {PRG}}\cdot (L+1) \cdot (m^2 \cdot \sigma )^{L+1} < q^{1/8}\) (where \(L = \ell _{\mathrm {out}}\cdot \ell _{\mathsf {ct}}\cdot 4^{d_{\mathsf {Dec}}+ d_{\mathrm {PRG}}}\)) (for correctness of scheme)
It is important that \(L = \lambda ^{c}\) for some constant c and \(\ell _{\mathrm {PRG}}\cdot (L+1) \cdot (m^2 \cdot \sigma )^{L+1} < q^{1/8}\). This crucially relies on the fact that the LHE scheme is compact (so that \(\ell _{\mathsf {ct}}\) and \(\ell _{\mathrm {PRG}}\) are bounded by a polynomial independent of the size of the circuits supported by the scheme, and that the LHE decryption and PRG computation can be performed by a log depth circuit (i.e, have poly length branching programs). The constant c depends on the LHE scheme and PRG.
One possible setting of parameters is as follows: \(n = \lambda ^{4c/\epsilon }\), \(m = n^{1+ 2\epsilon }\), \(q = 2^{n^{\epsilon }}\), \(\sigma = n\) and \(\ell _{\mathrm {PRG}}= n^{3\epsilon + 3}\).
We will now describe the obfuscation and evaluation algorithms.
-
\(\mathsf {Obf}(1^{\lambda }, P, \mathsf {msg}, \alpha )\): The obfuscation algorithm takes as input a program \(P \in \mathcal {C}_{\ell _{\mathrm {in}}, \ell _{\mathrm {out}}, d}\), message \(\mathsf {msg}\in \{0,1\}\) and \(\alpha \in \{0,1\}^{\ell _{\mathrm {out}}}\). The obfuscator proceeds as follows:
-
1.
It chooses the LHE key pair as \((\mathsf {lhe}.\mathsf {sk}, \mathsf {lhe}.\mathsf {ek}) \leftarrow \mathsf {LHE}.\mathsf {Setup}(1^{\lambda }, 1^{d \log d})\).Footnote 6
-
2.
Next, it encrypts the program P. It sets \(\varvec{\mathrm {\mathsf {ct}}} \leftarrow \mathsf {LHE}.\mathsf {Enc}(\mathsf {lhe}.\mathsf {sk}, P)\).Footnote 7
-
3.
It runs \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\), and assigns \(\beta = \mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, \alpha )\).
-
4.
Next, consider the following circuit Q which takes as input \(\ell _{\mathrm {out}}\cdot \ell _{\mathsf {ct}}\) bits of input and outputs \(\ell _{\mathrm {PRG}}\) bits. Q takes as input \(\ell _{\mathrm {out}}\) LHE ciphertexts \(\left\{ \mathsf {ct}_i\right\} _{i \le \ell _{\mathrm {out}}}\), has LHE secret key \(\mathsf {lhe}.\mathsf {sk}\) hardwired and computes the following — (1) it decrypts each input ciphertext \(\mathsf {ct}_i\) (in parallel) to get string x of length \(\ell _{\mathrm {out}}\) bits, (2) it applies the PRG on x and outputs \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, x)\). Concretely, \(Q(\mathsf {ct}_1, \ldots , \mathsf {ct}_{\ell _{\mathrm {out}}}) = \mathrm {PRG}.\mathsf {Eval}\big (\mathsf {pp},\) \(\mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk}, \mathsf {ct}_1) \left| \right| \cdots \left| \right| \mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk},\) \(\mathsf {ct}_{\ell _{\mathrm {out}}})\big )\).
For \(i \le \ell _{\mathrm {PRG}}\), we use \(\mathsf {BP}^{(i)}\) to denote the fixed-input selector permutation branching program that outputs the \(i^{th}\) bit of output of circuit Q. Note that Q has depth \(d_{\mathsf {tot}}= d_{\mathsf {Dec}}+ d_{\mathrm {PRG}}\). In the full version of the paper, we show that each branching program \(\mathsf {BP}^{(i)}\) has length \(L = \ell _{\mathrm {out}}\cdot \ell _{\mathsf {ct}}\cdot 4^{d_{\mathsf {tot}}}\) and width 5.
-
5.
The obfuscator creates matrix components which enable the evaluator to compute \(\mathsf {msg}\) if it has an input strings (ciphertexts) \(\mathsf {ct}_1, \ldots , \mathsf {ct}_{\ell _{\mathrm {out}}}\) such that \(Q(\mathsf {ct}_1, \ldots , \mathsf {ct}_{\ell _{\mathrm {out}}}) = \beta \). Concretely, it runs the (randomized) routine
 (defined in Figs. 1, 2). This routine takes as input the circuit Q in the form of \(\ell _{\mathrm {PRG}}\) branching programs \(\{\mathsf {BP}^{(i)}\}_i\), string \(\beta \) and message \(\mathsf {msg}\). Let
(defined in Figs. 1, 2). This routine takes as input the circuit Q in the form of \(\ell _{\mathrm {PRG}}\) branching programs \(\{\mathsf {BP}^{(i)}\}_i\), string \(\beta \) and message \(\mathsf {msg}\). Let  .
. -
6.
The final obfuscated program consists of the LHE evaluation key \(\mathsf {ek}= \mathsf {lhe}.\mathsf {ek}\), LHE ciphertexts \(\varvec{\mathrm {\mathsf {ct}}}\), together with the components \(\Big (\left\{ \varvec{\mathrm {B}}^{(i)}_{0, 1}\right\} _i,\) \(\left\{ (\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j})\right\} _{i, j}\Big )\).
-
1.
-
\(\mathsf {Eval}(\tilde{P}, x)\): The evaluation algorithm takes as input \(\tilde{P}= \Big (\mathsf {ek}, \varvec{\mathrm {\mathsf {ct}}}, \left\{ \varvec{\mathrm {B}}^{(i)}_{0, 1}\right\} _i,\) \(\left\{ (\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j})\right\} _{i, j}\Big )\) and input \(x \in \{0,1\}^{\ell _{\mathrm {in}}}\). It performs the following steps.
-
1.
The evaluator first constructs a universal circuit \(U_x(\cdot )\) with x hardwired as input. This universal circuit takes a circuit C as input and outputs \(U_x(C) = C(x)\). Using the universal circuit of Cook and Hoover [21], it follows that \(U_x(\cdot )\) has depth O(d).
-
2.
Next, it performs homomorphic evaluation on \(\varvec{\mathrm {\mathsf {ct}}}\) using circuit \(U_x(\cdot )\). It computes
 . Note that \(\ell _{\mathsf {ct}}\cdot \ell _{\mathrm {out}}\) denotes the length of
. Note that \(\ell _{\mathsf {ct}}\cdot \ell _{\mathrm {out}}\) denotes the length of  (as a bitstring), and let
(as a bitstring), and let  denote the \(i^{th}\) bit of
denote the \(i^{th}\) bit of  .
. -
3.
The evaluator then obliviously evaluates the \(\ell _{\mathrm {PRG}}\) branching programs on input
 using the matrix components. It calls the component evaluation algorithm
using the matrix components. It calls the component evaluation algorithm  (defined in Fig. 3). Let
(defined in Fig. 3). Let  \(\left( \left\{ \varvec{\mathrm {B}}^{(i)}_{0, 1}\right\} _i, \left\{ (\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j})\right\} _{i, j} \right) \Big )\). The evaluator outputs y.
\(\left( \left\{ \varvec{\mathrm {B}}^{(i)}_{0, 1}\right\} _i, \left\{ (\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j})\right\} _{i, j} \right) \Big )\). The evaluator outputs y.
-
1.
4.2 Correctness
We will prove that the lockable obfuscation scheme described above satisfies the perfect correctness property (see Definition 1). To prove this, we need to prove that if \(P(x) = \alpha \), then the evaluation algorithm always outputs the message, and if \(P(x) \ne \ \alpha \), then it always outputs \(\perp \).
First, we will prove the following lemma about the  and
and  routines. For any \(z \in \{0,1\}^{\ell _{\mathrm {in}}(\lambda )}\), let \(\mathsf {BP}(z) = \mathsf {BP}^{(1)}(z) \left| \right| \ldots \left| \right| \mathsf {BP}^{(\ell _{\mathrm {PRG}})}(z)\). Intuitively, this lemma states that for all fixed input branching programs \(\{\mathsf {BP}^{(i)}\}_i\), strings \(\beta \), input z, and messages \(\mathsf {msg}\), if \(\mathsf {BP}(z) = \beta \), then the component evaluator outputs \(\mathsf {msg}\).
routines. For any \(z \in \{0,1\}^{\ell _{\mathrm {in}}(\lambda )}\), let \(\mathsf {BP}(z) = \mathsf {BP}^{(1)}(z) \left| \right| \ldots \left| \right| \mathsf {BP}^{(\ell _{\mathrm {PRG}})}(z)\). Intuitively, this lemma states that for all fixed input branching programs \(\{\mathsf {BP}^{(i)}\}_i\), strings \(\beta \), input z, and messages \(\mathsf {msg}\), if \(\mathsf {BP}(z) = \beta \), then the component evaluator outputs \(\mathsf {msg}\).
Lemma 1
For any set of branching programs \(\{\mathsf {BP}^{(i)}\}_{i\le \ell _{\mathrm {PRG}}}\),
string \(\beta \in \{0,1\}^{\ell _{\mathrm {PRG}}}\), message \(\mathsf {msg}\in \{0,1\}\) and input z,
-
1.
if \(\mathsf {BP}(z) = \beta \), then

-
2.
if \(\mathsf {BP}(z) \ne \beta \), then

Proof
Recall that the component generation algorithm chooses matrices \(\varvec{\mathrm {B}}^{(i)}_j\) for each \(i\le \ell _{\mathrm {PRG}}\), \(j \le L\), \(\varvec{\mathrm {S}}^{(0)}_{j}, \varvec{\mathrm {S}}^{(1)}_{j}\) for each \(j \le L\) and \(\varvec{\mathrm {E}}^{(i, 0)}_{j}, \varvec{\mathrm {E}}^{(i, 1)}_{j}\) for each \(i \le \ell _{\mathrm {PRG}}, j \le L\). Note that the \(\varvec{\mathrm {S}}^{(b)}_{j} \) and \(\varvec{\mathrm {E}}^{(i, b)}_{j}\) matrices have \(l_{\infty }\) norm bounded by \(\sigma \cdot m^{3/2}\) since they are chosen from truncated Gaussian distribution with parameter \(\sigma \).
We start by introducing some notations for this proof.
-
\(\mathsf {st}^{(i)}_j\) : the state of \(\mathsf {BP}^{(i)}\) after j steps when evaluated on z
-
\(\varvec{\mathrm {S}}_j= \varvec{\mathrm {S}}^{(z_{\mathsf {inp}(j)})}_{j}\), \(\varvec{\mathrm {E}}^{(i)}_j= \varvec{\mathrm {E}}^{(i, z_{\mathsf {inp}(j)})}_{j}\), \(\varvec{\mathrm {C}}^{(i)}_j= \varvec{\mathrm {C}}^{(i, z_{\mathsf {inp}(j)})}_{j}\) for all \(j \le L\)
-
\(\mathbf {\Gamma }_{j^{*}}= \prod _{j = 1}^{j^{*}} \varvec{\mathrm {S}}_j\) for all \(j^{*}\le L\)
-
\(\varvec{\mathrm {\Delta }}^{(i)}_{j^{*}}= \varvec{\mathrm {B}}^{(i)}_{0, 1} \cdot \left( \prod _{j = 1}^{j^{*}} \varvec{\mathrm {C}}^{(i)}_j \right) \), \(\widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{j^{*}}= \mathbf {\Gamma }_{j^{*}}\cdot \varvec{\mathrm {B}}^{(i)}_{j^{*}, \mathsf {st}^{(i)}_{j^{*}}}\), \(\varvec{\mathrm {Err}}^{(i)}_{j^{*}}= \varvec{\mathrm {\Delta }}^{(i)}_{j^{*}}- \widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{j^{*}}\) for all \(j^{*}\le L\)
-
For any string \(x \in \{0,1\}^{\ell _{\mathrm {PRG}}}, \varvec{\mathrm {A}}_x = \sum _{i : x_i = 0} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : x_i = 1} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {acc}^{(i)}}\)
-
Similarly, \(\varvec{\mathrm {B}}_x = \sum _{i : x_i = 0} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : x_i = 1} \varvec{\mathrm {B}}^{(i)}_{L, \mathsf {acc}^{(i)}}\) & \(\varvec{\mathrm {F}}_x = \sum _{i : x_i = 0} \varvec{\mathrm {F}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : x_i = 1} \varvec{\mathrm {F}}^{(i)}_{L, \mathsf {acc}^{(i)}}\) & \(\varvec{\mathrm {E}}_x = \sum _{i : x_i = 0} \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : x_i = 1} \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {acc}^{(i)}}\).
Observe that the  algorithm computes matrix \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\). First, we show that for all \(i\le \ell _{\mathrm {PRG}}\), \(j^{*}\le L\), \(\varvec{\mathrm {Err}}^{(i)}_{j^{*}}\) is small and bounded. This would help us in arguing that matrices \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\) and \(\widetilde{\varvec{\mathrm {M}}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{L}\) are very close to each other. We then prove the below bounds on \(\varvec{\mathrm {M}}\) by proving the corresponding bounds on \(\widetilde{\varvec{\mathrm {M}}}\) in each of the cases.
algorithm computes matrix \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\). First, we show that for all \(i\le \ell _{\mathrm {PRG}}\), \(j^{*}\le L\), \(\varvec{\mathrm {Err}}^{(i)}_{j^{*}}\) is small and bounded. This would help us in arguing that matrices \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\) and \(\widetilde{\varvec{\mathrm {M}}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{L}\) are very close to each other. We then prove the below bounds on \(\varvec{\mathrm {M}}\) by proving the corresponding bounds on \(\widetilde{\varvec{\mathrm {M}}}\) in each of the cases.

First, we show that \(\varvec{\mathrm {Err}}^{(i)}_{j^{*}}\) is bounded with the help of the following claim.
Claim 1
([28, Claim 4.1]) \(\forall \ i \in \left\{ 1, \ldots , \ell _{\mathrm {PRG}}\right\} , j^{*}\in \left\{ 1, \ldots , L\right\} ,\)
\(\left\Vert \varvec{\mathrm {Err}}^{(i)}_{j^{*}}\right\Vert _\infty \le j^{*}\cdot \left( m^2 \cdot \sigma \right) ^{j^{*}}\).
The remaining proof of the lemma will have two parts, (1) when \(\mathsf {BP}(z) = \beta \) and (2) when \(\mathsf {BP}(z) \ne \beta \). Recall that the  algorithm computes matrix \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\). Let \(\widetilde{\varvec{\mathrm {M}}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{L}\) and \(\mathsf {Err}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {Err}}^{(i)}_{L}\). Also, we parse these matrices as \(\varvec{\mathrm {M}}= \left[ \varvec{\mathrm {M}}^{(1)}\left| \right| \varvec{\mathrm {M}}^{(2)} \right] \), \(\widetilde{\varvec{\mathrm {M}}}= \left[ \widetilde{\varvec{\mathrm {M}}}^{(1)}\left| \right| \widetilde{\varvec{\mathrm {M}}}^{(2)} \right] \) and \(\mathsf {Err}= \left[ \mathsf {Err}^{(1)}\left| \right| \mathsf {Err}^{(2)} \right] \), where \(\varvec{\mathrm {M}}^{(1)}, \widetilde{\varvec{\mathrm {M}}}^{(1)}\) and \(\mathsf {Err}^{(1)}\) are \(n \times n\) (square) matrices.
algorithm computes matrix \(\varvec{\mathrm {M}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {\Delta }}^{(i)}_{L}\). Let \(\widetilde{\varvec{\mathrm {M}}}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \widetilde{\varvec{\mathrm {\Delta }}}^{(i)}_{L}\) and \(\mathsf {Err}= \sum _{i = 1}^{\ell _{\mathrm {PRG}}} \varvec{\mathrm {Err}}^{(i)}_{L}\). Also, we parse these matrices as \(\varvec{\mathrm {M}}= \left[ \varvec{\mathrm {M}}^{(1)}\left| \right| \varvec{\mathrm {M}}^{(2)} \right] \), \(\widetilde{\varvec{\mathrm {M}}}= \left[ \widetilde{\varvec{\mathrm {M}}}^{(1)}\left| \right| \widetilde{\varvec{\mathrm {M}}}^{(2)} \right] \) and \(\mathsf {Err}= \left[ \mathsf {Err}^{(1)}\left| \right| \mathsf {Err}^{(2)} \right] \), where \(\varvec{\mathrm {M}}^{(1)}, \widetilde{\varvec{\mathrm {M}}}^{(1)}\) and \(\mathsf {Err}^{(1)}\) are \(n \times n\) (square) matrices.
First, note that \(\varvec{\mathrm {M}}= \widetilde{\varvec{\mathrm {M}}}+ \mathsf {Err}\). Using Claim 1, we can write that
Next, consider the following scenarios.
Part 1: \(\mathsf {BP}(z) = \beta \). First, recall that the top level matrices always satisfy the following constraints during honest obfuscation:
Note that
Next, we consider the following two cases dependending upon the message being obfuscated — (1) \(\mathsf {msg}= 0\), (2) \(\mathsf {msg}= 1\).
Case 1 \((\mathsf {msg}= 0)\). In this case, we bound the \(l_\infty \) norm of the output matrix \(\varvec{\mathrm {M}}\) (computed during evaluation) by \(q^{1/8}\). We do this by bounding the norm of \(\widetilde{\varvec{\mathrm {M}}}\) and using the error bound in Eq. 1. Recall that when \(\mathsf {msg}= 0\), \(\widetilde{\varvec{\mathrm {M}}}= \left[ \varvec{\mathrm {0}}^{n \times n} \left| \right| \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {E}}_\beta \right] \). First, we bound the norms of \(\mathbf {\Gamma }_{L}\) and \(\varvec{\mathrm {E}}_\beta \) as follows.
The last inequality follows from the fact that the matrices \(\varvec{\mathrm {E}}^{(i)}_{L, \mathsf {acc}^{(i)}}, \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {rej}^{(i)}}\) are sampled from truncated gaussian distribution. We can also write that,
This implies,
Now we bound the \(l_\infty \) norm of \(\varvec{\mathrm {M}}\). Recall that, \(\left\Vert \mathsf {Err}\right\Vert _\infty \le \ell _{\mathrm {PRG}}\cdot L \cdot (\sigma \cdot m^2)^{L}\). Therefore,
The last inequality follows from the constraints described in the construction. Thus, matrix \(\varvec{\mathrm {M}}\) (computed during evaluation) always satisfies the condition that \(\left\Vert \varvec{\mathrm {M}}\right\Vert _\infty < q^{1/8}\) if \(\mathsf {msg}= 0\).
Case 2 \((\mathsf {msg}= 1)\). In this case, we prove that the \(l_\infty \) norm of the output matrix \(\varvec{\mathrm {M}}\) (computed during evaluation) lies in \((q^{1/8}, q^{1/2})\). We do this by first computing upper and lower bounds on \(\left\Vert \widetilde{\varvec{\mathrm {M}}}\right\Vert _\infty \) and using the bound on \(\mathsf {Err}\) from Eq. 1. Recall that when \(\mathsf {msg}= 1\), \(\widetilde{\varvec{\mathrm {M}}}= \left[ q^{1/4} \cdot \mathbf {\Gamma }_{L} \left| \right| q^{1/4}\cdot \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {S}}+ \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {E}}_\beta \right] \). To prove a bound on \(\left\Vert \widetilde{\varvec{\mathrm {M}}}\right\Vert _\infty \), we first prove bounds on individual components of \(\widetilde{\varvec{\mathrm {M}}}\) : \(\mathbf {\Gamma }_{L}, \varvec{\mathrm {S}}, \varvec{\mathrm {E}}_\beta \).
By Eq. 3, we have \(\left\Vert \mathbf {\Gamma }_{L}\right\Vert _\infty < (\sigma \cdot m^2)^L\). Note that during obfuscation we sample secret matrices \(\varvec{\mathrm {S}}^{(b)}_{\mathsf {level}}\) (for each \(\mathsf {level}\) and bit b) such that they are short and always invertible. Therefore, matrix \(\mathbf {\Gamma }_{L}\) (which is product of L secret matrices) is also invertible. Thus, we can write that \(\left\Vert \mathbf {\Gamma }_{L}\right\Vert _\infty \ge 1\). The lower bound of 1 follows from the fact that \(\mathbf {\Gamma }_{L}\) is non-singular (and integral) matrix. By Eq. 2, we know that \(\left\Vert \varvec{\mathrm {E}}_\beta \right\Vert _\infty < \ell _{\mathrm {PRG}}\cdot \sigma \cdot m^2\). Also, \(\left\Vert \varvec{\mathrm {S}}\right\Vert _\infty \le \sigma \cdot n \cdot \sqrt{m} < \sigma \cdot m^2\) as \(\varvec{\mathrm {S}}\) is sampled from truncated gaussian distribution.
We finally prove bounds on \(\left\Vert \widetilde{\varvec{\mathrm {M}}}\right\Vert _\infty \). We know that \(\widetilde{\varvec{\mathrm {M}}}^{(1)}= q^{1/4} \cdot \mathbf {\Gamma }_{L}\) and \(\widetilde{\varvec{\mathrm {M}}}^{(2)}= q^{1/4}\cdot \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {S}}+ \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {E}}_\beta \).

This implies,
The last inequality follows from the constraints described in the construction. Next, we show that matrix \(\varvec{\mathrm {M}}^{(1)}\) has large entries. In other words, matrix \(\varvec{\mathrm {M}}\) has high \(l_{\infty }\) norm. Concretely,

Hence if \(\mathsf {msg}= 1\), \(\left\Vert \varvec{\mathrm {M}}\right\Vert _\infty \in (q^{1/8}, q^{1/2})\) and the evaluation always outputs 1.
Part 2: \(\mathsf {BP}(z) \ne \beta \). In this case, we prove that the \(l_\infty \) norm of output matrix \(\varvec{\mathrm {M}}\) is at least \(q^{1/2}\). Let \(x = \mathsf {BP}(z)\) and \(\delta _x\) be the edit distance between x and \(\beta \), which is clearly greater than 0 if \(x \ne \beta \). By construction, \(\widetilde{\varvec{\mathrm {M}}}= \mathbf {\Gamma }_{L} \cdot \left[ \varvec{\mathrm {A}}_x \left| \right| \varvec{\mathrm {A}}_x\cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_x + \delta _x \cdot \varvec{\mathrm {D}} \right] \) and \(\varvec{\mathrm {M}}= \widetilde{\varvec{\mathrm {M}}}+ \mathsf {Err}\). We now split this case into two subcases: 1) \(\left\Vert \varvec{\mathrm {M}}^{(1)}\right\Vert _\infty > q^{1/2}\) and 2) \(\left\Vert \varvec{\mathrm {M}}^{(1)}\right\Vert _\infty \le q^{1/2}\).
Case 1. \(\left\Vert \varvec{\mathrm {M}}^{(1)}\right\Vert _\infty > q^{1/2}\). In this case, \(\left\Vert \varvec{\mathrm {M}}\right\Vert _\infty > q^{1/2}\) and the evaluator always outputs \(\perp \).
Case 2. \(\left\Vert \varvec{\mathrm {M}}^{(1)}\right\Vert _\infty \le q^{1/2}\). In this case, we prove that \(\varvec{\mathrm {M}}^{(2)}\) has high \(l_\infty \) norm. Recall that \(\left\Vert \varvec{\mathrm {S}}\right\Vert _\infty \le \sigma \cdot n \cdot \sqrt{m} < \sigma \cdot m^2\) as \(\varvec{\mathrm {S}}\) is sampled from truncated gaussian distribution and \(\left\Vert \varvec{\mathrm {E}}_x\right\Vert _\infty \le \ell _{\mathrm {PRG}}\cdot \sigma \cdot m^2\) by an analysis similar to Eq. 2. Also, \(\left\Vert \mathbf {\Gamma }_{L}\right\Vert _\infty < (\sigma \cdot m^2)^L\) by Eq. 3. We now prove an upper bound on norm of \(\mathbf {\Gamma }_{L} \cdot \left[ \varvec{\mathrm {A}}_x \cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}_x \right] \).
The last 2 inequalities follow from the constraints described in the construction. As \(\mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {D}} = \left[ q^{3/4} \cdot \mathbf {\Gamma }_{L} \left| \right| \varvec{\mathrm {0}}^{n \times (m - 2\cdot n)} \right] \), we know that \(\left\Vert \mathbf {\Gamma }_{L} \cdot \varvec{\mathrm {D}}\right\Vert _\infty = q^{3/4} \cdot \left\Vert \mathbf {\Gamma }_{L}\right\Vert _\infty \), which lies in \([q^{3/4}, q^{3/4} \cdot (\sigma \cdot m^2)^L]\) as discussed earlier. This along with Eq. 4 implies the following upper bound on \(\left\Vert \widetilde{\varvec{\mathrm {M}}}^{(2)}\right\Vert _\infty \).
The last inequality follows from the constraints described in the construction. We can also prove the following lower bound on \(\left\Vert \widetilde{\varvec{\mathrm {M}}}^{(2)}\right\Vert _\infty \).
Now, we prove upper and lower bounds on \(\varvec{\mathrm {M}}^{(2)}= \widetilde{\varvec{\mathrm {M}}}^{(2)}+ \mathsf {Err}^{(2)}\).
This implies, \(\left\Vert \varvec{\mathrm {M}}^{(2)}\right\Vert _\infty > q^{1/2}\) in this case. Therefore, \(\left\Vert \varvec{\mathrm {M}}\right\Vert _\infty > q^{1/2}\) and the evaluator always outputs \(\perp \).
Using the above lemma, we can now argue the correctness of our scheme. First, we need to show correctness for the case when \(P(x) = \alpha \).
Claim 2
For any security parameter \(\lambda \in \mathbb {N}\), any input \(x \in \{0,1\}^{\ell _{\mathrm {in}}}\), any program \(P \in \mathcal {C}_{\ell _{\mathrm {in}}, \ell _{\mathrm {out}}, d}\) and any message \(\mathsf {msg}\in \{0,1\}\), if \(P(x) = \alpha \), then
Proof
First, the obfuscator encrypts the program P using an LHE secret key \(\mathsf {lhe}.\mathsf {sk}\), and sets \(\mathsf {ct}\leftarrow \) \(\mathsf {LHE}.\mathsf {Enc}(\) \(\mathsf {lhe}.\mathsf {sk}, P)\). The evaluator evaluates the LHE ciphertext on universal circuit \(U_x(\cdot )\), which results in an evaluated ciphertext  . Now, by the correctness of the LHE scheme, decryption of
. Now, by the correctness of the LHE scheme, decryption of  using \(\mathsf {lhe}.\mathsf {sk}\) outputs \(\alpha \). Therefore, \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, \mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk}, \widetilde{\varvec{\mathrm {\mathsf {ct}}}})) = \beta \), where \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\).Footnote 8 Then, using Lemma 1, we can argue that
using \(\mathsf {lhe}.\mathsf {sk}\) outputs \(\alpha \). Therefore, \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, \mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk}, \widetilde{\varvec{\mathrm {\mathsf {ct}}}})) = \beta \), where \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\).Footnote 8 Then, using Lemma 1, we can argue that  outputs \(\mathsf {msg}\), and thus \(\mathsf {Eval}\) outputs \(\mathsf {msg}\).
outputs \(\mathsf {msg}\), and thus \(\mathsf {Eval}\) outputs \(\mathsf {msg}\).
Claim 3
For all security parameters \(\lambda \), inputs \(x \in \{0,1\}^{\ell _{\mathrm {in}}}\), programs \(P \in \mathcal {C}_{\ell _{\mathrm {in}}, \ell _{\mathrm {out}}, d}\), \(\alpha \in \{0,1\}^{\ell _{\mathrm {out}}} \) such that \(P(x) \ne \alpha \) and \(\mathsf {msg}\in \{0,1\}\),
Proof
Fix any security parameter \(\lambda \), program P, \(\alpha \), x such that \(P(x) \ne \alpha \) and message \(\mathsf {msg}\). The evaluator evaluates the LHE ciphertext on universal circuit \(U_x(\cdot )\), which results in an evaluated ciphertext  . Now, by the correctness of the LHE scheme, decryption of
. Now, by the correctness of the LHE scheme, decryption of  using \(\mathsf {lhe}.\mathsf {sk}\) does not output \(\alpha \). Therefore, by the perfect injectivity of \(\mathrm {PRG}\) scheme, for all \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\), we have \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, \mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk}, \widetilde{\varvec{\mathrm {\mathsf {ct}}}})) \ne \beta \). Then, using Lemma 1, we can argue that
using \(\mathsf {lhe}.\mathsf {sk}\) does not output \(\alpha \). Therefore, by the perfect injectivity of \(\mathrm {PRG}\) scheme, for all \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\), we have \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp}, \mathsf {LHE}.\mathsf {Dec}(\mathsf {lhe}.\mathsf {sk}, \widetilde{\varvec{\mathrm {\mathsf {ct}}}})) \ne \beta \). Then, using Lemma 1, we can argue that  outputs \(\perp \), and thus \(\mathsf {Eval}\) outputs \(\perp \).
outputs \(\perp \), and thus \(\mathsf {Eval}\) outputs \(\perp \).
4.3 Security
In this subsection, we prove the security of the above construction. Concretely, we prove the following theorem.
Theorem 2
Assuming that \(\mathsf {LHE}\) is a secure leveled homomorphic encryption scheme, and \(\mathsf {PRG}\) is a secure perfectly injective pseudorandom generator, lattice trapdoors are secure and \((n, 2n\cdot \ell _{\mathrm {PRG}}, m - n, q, \chi )\)- , \((n, 5m\cdot \ell _{\mathrm {PRG}}, n, q, \chi )\)-
, \((n, 5m\cdot \ell _{\mathrm {PRG}}, n, q, \chi )\)- assumptions hold, the lockable obfuscation construction described in Sect. 4.1 is secure as per Definition 2.
assumptions hold, the lockable obfuscation construction described in Sect. 4.1 is secure as per Definition 2.
Proof
We prove the above theorem by proving that our construction is computationally indistinguishable from the construction provided in [28, Appendix D] that uses perfectly injective PRGs. Note that Goyal et al. [28] construct a simulator \(\mathsf {Sim}(1^\lambda , 1^{|P|}, 1^{|\alpha |})\) and prove that their construction is computationally indstinguishable from the simulator. By a standard hybrid argument, this implies that our construction is computationally indstinguishable from the simulator. Formally, we prove the following theorem.
Theorem 3
Assuming that \(\mathsf {PRG}\) is a secure perfectly injective pseudorandom generator and \((n, 2n\cdot \ell _{\mathrm {PRG}}, m - n, q, \chi )\)- assumption holds, the lockable obfuscation construction described in Sect. 4.1 is computationally indistinguishableFootnote 9 from [28, Appendix D] construction that uses perfectly injective PRGs.
assumption holds, the lockable obfuscation construction described in Sect. 4.1 is computationally indistinguishableFootnote 9 from [28, Appendix D] construction that uses perfectly injective PRGs.
We prove the theorem using the following sequence of hybrids. The first hybrid corresponds to the security game in which the challenger uses our lockable obfuscation scheme (Sect. 4.1) for obfuscating the challenge program. The last hybrid corresponds to the security game in which the challenger uses lockable obfuscation scheme provided in [28]. We note that some portions of the proof are similar to those used in [28].
\(\mathsf {Game}~\) 0. This game correponds to the challenger using our lockable obfuscation scheme for obfuscating the challenge program.
-
1.
The adversary sends a program P and message \(\mathsf {msg}\) to the challenger.
-
2.
The challenger first chooses the LWE parameters n, m, q, \(\sigma \), \(\chi \) and \(\ell _{\mathrm {PRG}}\). Recall L denotes the length of the branching programs.
-
3.
The challenger then chooses \((\mathsf {sk}, \mathsf {ek}) \leftarrow \mathsf {LHE}.\mathsf {Setup}(1^{\lambda }, 1^{d \log d})\) and sets \(\mathsf {ct}\leftarrow \mathsf {LHE}.\mathsf {Enc}(\mathsf {sk}, P)\).
-
4.
Next, it chooses a uniformly random string \(\alpha \leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\), runs \(\mathsf {pp}\leftarrow \mathrm {PRG}.\mathsf {Setup}(1^\lambda )\) and sets \(\beta = \mathrm {PRG}.\mathsf {Eval}(\mathsf {pp},\alpha )\).
-
5.
Next, consider the following program Q. It takes as input an LHE ciphertext \(\mathsf {ct}\), has \(\mathsf {sk}\) hardwired and does the following: it decrypts the input ciphertext \(\mathsf {ct}\) to get string x and outputs \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp},x)\). For \(i \le \ell _{\mathrm {PRG}}(\lambda )\), let \(\mathsf {BP}^{(i)}\) denote the branching program that outputs the \(i^{th}\) bit of \(\mathrm {PRG}.\mathsf {Eval}(\mathsf {pp},x)\).
-
6.
For \(i = 1 \) to \(\ell _{\mathrm {PRG}}\) and \(j = 0\) to \(L - 1\), it chooses \((\varvec{\mathrm {B}}^{(i)}_j, T^{(i)}_j) \leftarrow \mathsf {TrapGen}(1^{5 n}, 1^m, q)\).
-
7.
Let \(\varvec{\mathrm {D}} = q^{3/4}\cdot \left[ \varvec{\mathrm {I}}_n \left| \right| \varvec{\mathrm {0}}^{n \times (m - 2\cdot n)} \right] \).
-
(a)
For the top level, it first chooses the matrices \(\varvec{\mathrm {A}}^{(i)}_{L, k}\) (of dimension \(n \times n\)) for each \(i \le \ell _{\mathrm {PRG}}, k \le 5\), uniformly at random, subject to the following constraints:
$$ \sum _{i : \beta _i = 0} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : \beta _i = 1} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {acc}^{(i)}} = \varvec{\mathrm {0}}^{n \times n} \text { if } \mathsf {msg}= 0. $$$$ \sum _{i : \beta _i = 0} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \sum _{i : \beta _i = 1} \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {acc}^{(i)}} = q^{1/4}\cdot \varvec{\mathrm {I}}_n \text { if } \mathsf {msg}= 1. $$ -
(b)
It then samples a matrix \(\varvec{\mathrm {S}}\leftarrow \chi ^{n \times (m - n)}\), and matrices \(\varvec{\mathrm {E}}^{(i)}_{L, \mathsf {rej}^{(i)}} \leftarrow \chi ^{n \times (m - n)}, \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {acc}^{(i)}} \leftarrow \chi ^{n \times (m - n)}\) for each \(i \le \ell _{\mathrm {PRG}}\). Next, it chooses matrices \(\varvec{\mathrm {F}}^{(i)}_{L, k}\) as follows
$$\begin{aligned} \begin{aligned} \varvec{\mathrm {F}}^{(i)}_{L, \mathsf {acc}^{(i)}}&= \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {acc}^{(i)}}\cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {acc}^{(i)}} + (1 - \beta _i)\cdot \varvec{\mathrm {D}}\\ \varvec{\mathrm {F}}^{(i)}_{L, \mathsf {rej}^{(i)}}&= \varvec{\mathrm {A}}^{(i)}_{L, \mathsf {rej}^{(i)}}\cdot \varvec{\mathrm {S}}+ \varvec{\mathrm {E}}^{(i)}_{L, \mathsf {rej}^{(i)}} + \beta _i\cdot \varvec{\mathrm {D}}\\ \varvec{\mathrm {F}}^{(i)}_{L, k}&\leftarrow \mathbb {Z}_q^{n \times (m-n)}\text { if } k \notin \{\mathsf {acc}^{(i)}, \mathsf {rej}^{(i)}\} \end{aligned} \end{aligned}$$ -
(c)
The top level matrices \(\varvec{\mathrm {B}}^{(i)}_{L, k}\) for each \(i \le \ell _{\mathrm {PRG}}, k \le 5\) are set to \(\varvec{\mathrm {B}}^{(i)}_{L, k} = \left[ \varvec{\mathrm {A}}^{(i)}_{L, k} \left| \right| \varvec{\mathrm {F}}^{(i)}_{L, k} \right] \).
-
(a)
-
8.
Next, it generates the components for each level. For each \(i \in [1,\ell _{\mathrm {PRG}}]\) and each level \(\mathsf {level}\in [1,L]\), do the following:
-
(a)
Choose matrices \(\varvec{\mathrm {S}}^{(0)}_{\mathsf {level}}, \varvec{\mathrm {S}}^{(1)}_{\mathsf {level}}\leftarrow \chi ^{n \times n}\) and \(\varvec{\mathrm {E}}^{(i, 0)}_{\mathsf {level}}, \varvec{\mathrm {E}}^{(i, 1)}_{\mathsf {level}}\leftarrow \chi ^{5 n \times m}\) for \(i\le \ell _{\mathrm {PRG}}\). If either \(\varvec{\mathrm {S}}^{(0)}_{\mathsf {level}}\) or \(\varvec{\mathrm {S}}^{(1)}_{\mathsf {level}}\) has determinant zero, then set it to be \(\varvec{\mathrm {I}}_n\).
-
(b)
For \(b \in \{0,1\}\), set matrix \(\varvec{\mathrm {D}}^{(i, b)}_{\mathsf {level}}\) as a permutation of the matrix blocks of \(\varvec{\mathrm {B}}^{(i)}_\mathsf {level}\) according to the permutation \(\sigma ^{(i)}_{\mathsf {level}, b}(\cdot )\).
-
(c)
Set \(\varvec{\mathrm {M}}^{(i, b)}_{\mathsf {level}}= \left( \varvec{\mathrm {I}}_5 \otimes \varvec{\mathrm {S}}^{(b)}_{\mathsf {level}} \right) \cdot \varvec{\mathrm {D}}^{(i, b)}_{\mathsf {level}}+ \varvec{\mathrm {E}}^{(i, b)}_{\mathsf {level}}\) for \(i \le \ell _{\mathrm {PRG}}\).
-
(d)
Compute \(\varvec{\mathrm {C}}^{(i, b)}_{\mathsf {level}}\leftarrow \mathsf {SamplePre}(\varvec{\mathrm {B}}^{(i)}_{\mathsf {level}-1}, T^{(i)}_{\mathsf {level}-1}, \sigma , \varvec{\mathrm {M}}^{(i, b)}_{\mathsf {level}})\)
-
(a)
-
9.
The challenger sends the final obfuscated program which consists of the LHE evaluation key \(\mathsf {ek}\), LHE encryption \(\mathsf {ct}\), together with the components \(\left( \left\{ \varvec{\mathrm {B}}^{(i)}_{0, 1}\right\} _i, \left\{ (\varvec{\mathrm {C}}^{(i, 0)}_{j}, \varvec{\mathrm {C}}^{(i, 1)}_{j})\right\} _{i, j} \right) \) to the adversary.
-
10.
The adversary outputs a bit \(b'\).
\(\mathsf {Game}~\) 1: In this hybrid, the string \(\beta \) is chosen uniformly at random.
-
4.
Next, it chooses a uniformly random string
 .
.
\(\mathsf {Game}~\) 2: In this hybrid, the matrices \(\varvec{\mathrm {A}}^{(i)}_{L, k}\) are chosen uniformly at random without any constraints.
-
7.
-
(a)
For the top level, it first chooses the matrices \(\varvec{\mathrm {A}}^{(i)}_{L, k}\) (of dimension \(n \times n\)) for each \(i \le \ell _{\mathrm {PRG}}, k \le 5\), uniformly at random
 .
.
-
(a)
\(\mathsf {Game}~\) 3: In this hybrid, all the matrices \(\varvec{\mathrm {F}}^{(i)}_{L, k}\) are chosen uniformly at random.

\(\mathsf {Game}~\) 4: In this hybrid, all the top level matrices \(\varvec{\mathrm {B}}^{(i)}_{L, k}\) are chosen uniformly at random.
-
7.
For the top level,
 .
.
\(\mathsf {Game}~\) 5: In this hybrid, the top level matrices \(\varvec{\mathrm {B}}^{(i)}_{L, k}\) are chosen according to GKW17 construction.
-
7.
For the top level, for each \(i \le \ell _{\mathrm {PRG}}\) and \(k \le 5\), it chooses the matrices \(\varvec{\mathrm {B}}^{(i)}_{L, k}\) uniformly at random from \(\mathbb {Z}_q^{n \times m}\)
 .
. 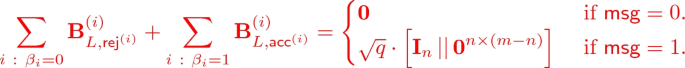
\(\mathsf {Game}~\) 6: This hybrid corresponds to challenger using GKW17 lockable obfuscation scheme for obfuscating the challenge program.
-
7.
Next, it chooses a uniformly random string
 .
.
Due to space constraints, we prove that \(\mathsf {Game}~0\) is indistinguishable from \(\mathsf {Game}~6\) in the full version of the paper.
5 Perfectly Injective PRGs from LPN
In this section, we give our construction of (perfectly) injective PRGs (with Setup) from the Learning Parity with Noise assumption.Footnote 10
Overview. Let the input length of PRG be \(n + \ell \). We parse input \(x \in \{0, 1\}^{n + \ell }\) as \(x = y \left| \right| z\), where \(|y| = n\) and \(|z| = \ell \). Now, string y is parsed as \(\varvec{\mathrm {s}}\), and z will be used to sample the error vector \(\varvec{\mathrm {e}}\). Note that for injectivity argument to go through, it is important that the mapping between input y, z and vectors \(\varvec{\mathrm {s}}, \varvec{\mathrm {e}}\) is also injective. Now both y and \(\varvec{\mathrm {s}}\) are already of length n, thus we only need to make sure that our error vector sampling procedure is injective. Before describing our sampling procedure, we would like to point out that, in the PRG security game, the PRG seed is sampled uniformly at random, thus the distribution over error vectors will be a uniform distribution as well. This suggests that for basing pseudorandomness security we can’t rely on the standard LPN assumption as the noise distribution is not Bernoulli, but uniform. However, we could instead rely on the exact-LPN assumption (or \(\mathsf {xLPN}\)) which is polynomially related to standard LPN assumption, and in which the noise distribution is uniform as the error vectors are sampled such that they have fixed hamming weight.
Next, we observe that the size of support of noise distribution in the \(\mathsf {xLPN}\) assumption need not be a perfect power of two, thus we might not be able to injectively sample error vectors from the fixed length binary string z. To resolve this issue, we simply truncate the noise distribution to contain only lexically smallest error vectors such that the size of truncated set is equal to the nearest power of two. However, with this modification we need to rely on an alternate assumption which we call the restricted-exact-LPN assumption (or \(\mathsf {rxLPN}\)). It turns out that the sample-preserving reduction of [5] also holds for \(\mathsf {rxLPN}\). This suggests that \(\mathsf {rxLPN}\) and \(\mathsf {LPN}\) assumptions are (polynomially) equivalent, therefore we could still reduce the security to the \(\mathsf {LPN}\) assumption. Now to injectively map vectors with a fixed hamming weight to bitstrings, we employ a simple combinatorial trick to give a total ordering over vectors with efficient recursive sampling procedure. First, note that a total ordering over vectors can be trivially defined by denoting each vector with its corresponding integer representation. Now, our sampling procedure works as follows—let \(x \in \{0, 1\}^{\ell }\) and we want to sample vector \(\varvec{\mathrm {v}} \in \mathbb {Z}_2^m\) such that \(\mathsf {HW}(\varvec{\mathrm {v}}) = k\). The sampling algorithm first checks whether \(\mathsf {int}(x) > {^{m - 1}C_{k}}\) (where \(\mathsf {int}(x)\) is the integer corresponding to string x). If the check succeeds, then it sets the first position in \(\varvec{\mathrm {v}}\) to be 1, else it sets it 0, and continues. Also, if the check succeeds, then it updates \(x = x - {^{m - 1}C_{k}}\). In other words, each vector \(\varvec{\mathrm {v}} \in \mathbb {Z}_2^m\) with \(\mathsf {HW}(\varvec{\mathrm {v}}) = k\) is uniquely ranked from 0 to \({^{m}C_{k}} - 1\), and the sample algorithm outputs vector \(\varvec{\mathrm {v}}\) with rank \(\mathsf {int}(x)\). For example, \(0^{m - k}1^{k}\) has rank 0 and \(1^{k}0^{m - k}\) has rank \({^{m}C_{k}} - 1\). The sampling procedure has been formally described later in the full version of the paper.
Finally, to sample matrix \(\varvec{\mathrm {B}}\) as a generator matrix of some good but random code, we employ ideas similar to that used in our LWE solution. To sample \(\varvec{\mathrm {B}}\) in this special way, we simply choose a uniformly random matrix \(\varvec{\mathrm {A}}\), a matrix \(\varvec{\mathrm {C}}\) with low hamming weight rows and set \(\varvec{\mathrm {B}}= [\varvec{\mathrm {A}}~ | ~ \varvec{\mathrm {A}}\varvec{\mathrm {C}}+ \varvec{\mathrm {G}}]\), where \(\varvec{\mathrm {G}}\) is the generator matrix of an error correcting code. Here the role of \(\varvec{\mathrm {G}}\) is similar to the role of \(\varvec{\mathrm {D}}\) in the previous solution, that is to map any non-zero vector to a high hamming weight vector. A crucial point here is that the rows of \(\varvec{\mathrm {C}}\) must have low hamming weight. This is because if \(\varvec{\mathrm {A}}^{T} \varvec{\mathrm {s}}\) has low hamming weight, then so does \(\varvec{\mathrm {C}}^{T} \varvec{\mathrm {A}}^{T} \varvec{\mathrm {s}}\), and later this will be crucial in arguing that \(\varvec{\mathrm {B}}\) is a generator matrix of a good code. Finally, for pseudorandomness of our construction, we want that \(\varvec{\mathrm {B}}\) should look like a random matrix to any computationally bounded adversary. To this end, we use the Knapsack LPN assumption which was also shown to be (polynomially) equivalent to LPN assumption [32].Footnote 11 Due to space constraints, we defer the formal description of the construction to the full version of the paper.
Notes
- 1.
The above argument relies on the ability of one being able to test the original program meets a certain template or is otherwise well-formed. Our work does not address under which circumstances this is possible.
- 2.
- 3.
Strictly speaking, [29, Appendix C] shows how to extend the message space for semi-statistically correct lockable obfuscation schemes. However, the same transformation also works for perfectly correct schemes.
- 4.
Recall, a permutation branching program of length L and width w can be represented using w states, 2L permutations \(\sigma _{j, b}\) over states for each level \(j\le L\), an input-selector function \(\mathsf {inp}(\cdot )\) which determines the input read at each level, and an accepting and rejecting state. The program execution starts at state \(\mathsf {st}= 1\) of level 0, and iteratively carried out as \(\mathsf {st}= \sigma _{i, b}(\mathsf {st})\) (where b is the input bit read at level i). Depending upon the final state (i.e., at level L), the program either accepts or rejects.
- 5.
That is, \(\mathsf {st}^{(i)}= \mathsf {acc}^{(i)}\) if \(\widehat{C}(x)_i = 0\) and \(\mathsf {rej}^{(i)}\) otherwise.
- 6.
We set the LHE depth bound to be \(d \log d\), where the extra \(\log \) factor is to account for the constant blowup involved in using a universal circuit. In particular, we can set the LHE depth bound to be \(c \cdot d\) where c is some fixed constant depending on the universal circuit.
- 7.
Note that LHE scheme supports bit encryption. Therefore, to encrypt P, a multi-bit message, the \(\mathsf {FHE}.\mathsf {Enc}\) algorithm will be run independently on each bit of P. However, for notational convenience throughout this section we overload the notation and use \(\mathsf {FHE}.\mathsf {Enc}\) and \(\mathsf {FHE}.\mathsf {Dec}\) algorithms to encrypt and decrypt multi-bit messages respectively.
- 8.
As before, we are overloading the notation and using \(\mathsf {LHE}.\mathsf {Dec}\) to decrypt multiple ciphertexts.
- 9.
Consider a game in which the adversary sends a program P and message \(\mathsf {msg}\) to the challenger, which either obfuscates (\(P, \mathsf {msg}\)) using [28] construction or our construction and sends back the obfuscated program. No PPT adversary can distinguish the two scenarios with non-negligible advantage.
- 10.
Our PRG construction bears some resemblance to the IND-CCA secure encryption schemes provided by Döttling et al. [24] and Kiltz et al. [31], but requires new ideas. We point that if we try to build PRGs using the techniques from [24, 31], then that only gives ‘statistically injective’ PRGs, whereas in this paper our goal is to get perfectly injective PRGs.
- 11.
The Knapsack LPN assumption states that for a uniformly random matrix \(\varvec{\mathrm {A}}\) and a matrix \(\varvec{\mathrm {E}}\) such that each entry is 1 with probability p and \(\varvec{\mathrm {A}}\) has fewer rows than columns, then \((\varvec{\mathrm {A}}, \varvec{\mathrm {A}}\varvec{\mathrm {E}})\) look like uniformly random matrices.
References
Alekhnovich, M.: More on average case vs approximation complexity. In: FOCS 2003 (2003)
Ananth, P., Jain, A., Naor, M., Sahai, A., Yogev, E.: Universal constructions and robust combiners for indistinguishability obfuscation and witness encryption. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 491–520. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_17
Ananth, P., Jain, A., Sahai, A.: Robust transforming combiners from indistinguishability obfuscation to functional encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 91–121. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_4
Ananth, P., Placa, R.L.L.: Secure quantum extraction protocols. IACR Cryptol. ePrint Arch. (2019). https://eprint.iacr.org/2019/1323
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography with constant input locality. J. Cryptol. 22(4), 429–469 (2009). https://doi.org/10.1007/s00145-009-9039-0
Asharov, G., Ephraim, N., Komargodski, I., Pass, R.: On perfect correctness without derandomization. IACR Cryptol. ePrint Arch. 2019, 1025 (2019)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Barak, B., et al.: On the (Im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Barrington, D.A.: Bounded-width polynomial-size branching programs recognize exactly those languages in NC1. In: STOC 1986 (1986)
Bitansky, N., Khurana, D., Paneth, O.: Weak zero-knowledge beyond the black-box barrier. In: STOC 2019 (2019)
Bitansky, N., Shmueli, O.: Post-quantum zero knowledge in constant rounds. In: STOC (2020)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation: from approximate to exact. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016-A. LNCS, vol. 9562, pp. 67–95. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_4
Bitansky, N., Vaikuntanathan, V.: A note on perfect correctness by derandomization. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 592–606. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_20
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_34
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Brakerski, Z., Lyubashevsky, V., Vaikuntanathan, V., Wichs, D.: Worst-case hardness for LPN and cryptographic hashing via code smoothing. IACR Cryptology ePrint Archive 2018, 279 (2018)
Chen, Y., Vaikuntanathan, V., Waters, B., Wee, H., Wichs, D.: Traitor-tracing from LWE made simple and attribute-based. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 341–369. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_13
Chen, Y., Vaikuntanathan, V., Wee, H.: GGH15 beyond permutation branching programs: proofs, attacks, and candidates. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 577–607. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_20
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45325-3_32
Cook, S.A., Hoover, H.J.: A depth-universal circuit. SIAM J. Comput. 14(4), 833–839 (1985)
Dolev, D., Dwork, C., Naor, M.: Nonmalleable cryptography. SIAM J. Comput. 45, 727–784 (2000)
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Döttling, N., Müller-Quade, J., Nascimento, A.C.A.: IND-CCA secure cryptography based on a variant of the LPN problem. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 485–503. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_30
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_21
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indstinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Goyal, R., Hohenberger, S., Koppula, V., Waters, B.: A generic approach to constructing and proving verifiable random functions. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 537–566. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_18
Goyal, R., Koppula, V., Waters, B.: Lockable obfuscation. In: FOCS 2017 (2017)
Goyal, R., Koppula, V., Waters, B.: Lockable obfuscation. Cryptology ePrint Archive, Report 2017/274 (2017). https://eprint.iacr.org/2017/274
Goyal, R., Koppula, V., Waters, B.: Separating semantic and circular security for symmetric-key bit encryption from the learning with errors assumption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 528–557. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_18
Kiltz, E., Masny, D., Pietrzak, K.: Simple chosen-ciphertext security from low-noise LPN. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 1–18. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_1
Micciancio, D., Mol, P.: Pseudorandom knapsacks and the sample complexity of LWE search-to-decision reductions. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 465–484. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_26
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: STOC 1990 (1990)
Nisan, N., Wigderson, A.: Hardness vs randomness. J. Comput. Syst. Sci. 49(2), 149–167 (1994). https://doi.org/10.1016/S0022-0000(05)80043-1
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC 2005 (2005)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC 2014 (2014)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Wichs, D., Zirdelis, G.: Obfuscating compute-and-compare programs under LWE. In: FOCS 2017 (2017)
Yu, Y., Steinberger, J.: Pseudorandom functions in almost constant depth from low-noise LPN. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 154–183. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_6
Yu, Yu., Zhang, J.: Cryptography with auxiliary input and trapdoor from constant-noise LPN. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 214–243. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_9
Yu, Y., Zhang, J., Weng, J., Guo, C., Li, X.: Collision resistant hashing from learning parity with noise. IACR Cryptology ePrint Archive 2017, 1260 (2017)
Acknowledgements
We thank anonymous reviewers for useful feedback. The work is done in part while the first and second authors were at UT Austin. The first author is supported by IBM PhD Fellowship, and the Simons Institute for the Theory of Computing (supported by Simons-Berkeley research fellowship). The second author is supported by the Simons Institute for the Theory of Computing (supported by the Simons-Berkeley research fellowship), Binational Science Foundation (Grant No. 2016726), and by the European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482) and via Project PROMETHEUS (Grant 780701). The third author is supported by Provost Fellowship. The fourth author is supported by NSF CNS-1908611, CNS-1414082, DARPA SafeWare and Packard Foundation Fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Goyal, R., Koppula, V., Vusirikala, S., Waters, B. (2020). On Perfect Correctness in (Lockable) Obfuscation. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12550. Springer, Cham. https://doi.org/10.1007/978-3-030-64375-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-64375-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64374-4
Online ISBN: 978-3-030-64375-1
eBook Packages: Computer ScienceComputer Science (R0)







 (defined in Figs.
(defined in Figs.  .
. . Note that
. Note that  (as a bitstring), and let
(as a bitstring), and let  denote the
denote the  .
. using the matrix components. It calls the component evaluation algorithm
using the matrix components. It calls the component evaluation algorithm  (defined in Fig.
(defined in Fig. 

 Continued
Continued



 .
. .
. .
. .
. 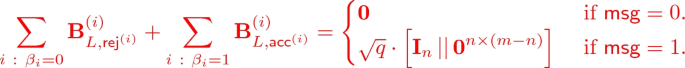
 .
.