Beyond Birthday Bound Secure Fresh Rekeying: Application to Authenticated Encryption

Abstract

Fresh rekeying is a well-established method to protect a primitive or mode against side-channel attacks: an easy to protect but cryptographically not so involved function generates a subkey from the master key, and this subkey is then used for the block encryption of a single or a few messages. It is an efficient way to achieve side-channel protection, but current solutions only achieve birthday bound security in the block size of the cipher and thus halve its security (except if more involved primitives are employed). We present generalized solutions to parallel block cipher rekeying that, for the first time, achieve security beyond the birthday bound in the block size n. The first solution involves, next to the subkey generation, one multiplication and the core block cipher call and achieves $2^{2n/3}$ security. The second solution makes two block cipher calls, and achieves optimal $2^n$ security. Our third solution uses a slightly larger subkey generation function but requires no adaptations to the core encryption and also achieves optimal security. The construction seamlessly generalizes to permutation based fresh rekeying. Central to our schemes is the observation that fresh rekeying and generic tweakable block cipher design are two very related topics, and we can take lessons from the advanced results in the latter to improve our understanding and development of the former. We subsequently use these rekeying schemes in a constructive manner to deliver three authenticated encryption modes that achieve beyond birthday bound security and are easy to protect against side-channel attacks.

1 Introduction

The security of cryptographic constructions is typically analyzed in a black-box model. The analysis is based on the assumption that the adversary adheres to the conditions and limitations set by the security model, and that it only obtains information about the cryptographic function by model-wise permitted evaluations of that function. The emerging threat of side-channel attacks questions the credibility of this approach. Side-channel attackers obtain additional information about a cryptographic function, typically via passive attacks such as timing attacks  [52], differential power analysis  [54], or electromagnetic radiation  [56]. With black-box security of cryptographic schemes improving, side-channel security is often the weak spot. In particular, a cryptographic function could achieve very strong black-box security, but its security may be nullified if its implementation is in an unprotected environment.

Securing a cryptographic function against side-channel attacks is a serious challenge. One way of doing so is at the implementation level, namely through hiding  [62] or masking  [24, 31, 44, 85]. However, these approaches are often design-specific and could be prohibitively expensive. An alternative approach is to change the mode at the protocol level, i.e., to develop the protocol in such a way that secret-key material is used scarcely and its usage is easier to protect.

One of the most basic and practically appealing expositions of this idea is fresh parallel rekeying. In this approach one does not use a block cipher in its naive fashion, but rather uses a subkey generation function on top of that. This subkey generation function has access to the master key (hence needs strong side-channel protection) but does not need to be a cryptographically strong primitive. The block cipher evaluation itself must of course be cryptographically strong, but only uses every subkey once or a few number of times, and does not need strong side-channel protection. In practical cases, the subkey generation needs to be protected against the stronger differential power analysis (DPA) whereas the core encryption only needs to be protected against simple power analysis (SPA) and related techniques  [9, 93]. This concept is called a “leveled implementation”  [79]. The first appearance of the idea of rekeying was by Abdalla and Bellare  [1], and it was independently introduced and proposed as side-channel countermeasure by Borst  [21, Section 6.6.1]. The approach was recently reconsidered and popularized by Medwed et al.  [64]: they suggest multiplication as subkey generation (but, see Sect. 7). In this way, the cryptographic strength and the side-channel resistance of the scheme are virtually disconnected into a light but strongly protected multiplication and a strong but lightly protected core encryption. Medwed et al.  [63] generalized it to a multi-party variant, but later, Dobraunig et al.  [28] demonstrated that Medwed et al.’s solutions allowed for birthday bound key recoveries in the block size of the cipher. Dobraunig et al.  [30] later resolved this by introducing two fresh rekeying solutions: one based on the subkey generation function and two block cipher calls that is still birthday bound secure (though optimally key recovery secure), and one based on a subkey generation function and a tweakable block cipher call that is optimally secure (in the ideal model). Patented ideas on the topic appeared in [35, 53]. We refer to Sect. 3 for a detailed survey of the schemes and their relation.

One might argue that the idea to separate cryptographic building blocks into a part that must be DPA-protected and a part that must be SPA-protected has been overtaken by time. Most notably, single trace attacks have improved over the last decades, in particular with the soft-analytical side-channel attacks enhanced with belief propagation [37, 50, 92]. These attacks, however, focus on unprotected implementations of which the behavior was known prior to the attack (e.g., how the implementation responds to known inputs with known key). In practical applications, such as smart cards, this is usually not the case. More fundamentally, in [37, Section 6] it is already confirmed that for noisy implementations, multiple traces simply give more information to an attacker than a single trace, and likewise [50, Section 1] conclude that DPA attacks are more powerful in the context of noisy implementation. From this viewpoint, it is fair to conclude that in practical settings, multiple traces simply give more information to an attacker than a single trace. The separation of schemes into a DPA-protected part and an SPA-protected part is thus a very valuable approach towards efficient cryptography.

None of the solutions so far is particularly desirable: rekeying a plain block cipher halves its security (this applies to the schemes of Medwed et al.  [63, 64] and the first one of Dobraunig et al.  [30]), and beyond birthday bound security is only achieved using heavier machinery, namely a tweakable block cipher (this applies to the second one of Dobraunig et al.  [30]). Of course, dedicated tweakable block cipher designs such as SKINNY or MANTIS  [11] or QARMA  [4] exist, but this solution is unsatisfying for securing implementations of the plain AES or lightweight block ciphers like PRESENT  [19], CLEFIA  [90], Midori  [5], GIFT  [6], and others  [10, 20, 39, 89].

Strikingly, it turns out that the idea of fresh rekeying is very related to generic tweakable block cipher design  [60]: not only in its appearance as underlying primitive in Dobraunig et al.’s second construction, but more importantly from a bigger picture (see also  [38]). Contrary to the field of rekeying, generic tweakable block cipher design has faced extensive research, in particular in the design and understanding of beyond birthday bound secure solutions. This direction was initiated by Landecker et al.  [58], and optimally secure solutions (in the ideal model) were given by Mennink  [65], Wang et al.  [94], and Jha et al.  [49]. A detailed survey of the state of the art and the relations among these schemes is given in Sect. 4.

1.1 Beyond Birthday Bound Security Block Cipher Rekeying

We tackle the problem of developing beyond birthday bound secure yet efficient parallel rekeying solutions of block ciphers. First, one may suggest that an instantiation of Dobraunig et al.’s tweakable block cipher based construction with a beyond birthday bound secure tweakable block cipher immediately reaches our goal, but this is not true: the analysis of Dobraunig et al. is performed in the ideal tweakable cipher model and thus only holds under the assumption that the tweakable block cipher is perfectly random. No generic construction can be perfectly secure, and as we will demonstrate in Sect. 5.2, composition may already collapse at the birthday bound. Instead, a direct analysis is necessary. In addition, Dobraunig et al. built a rekeying scheme on top of a tweakable block cipher, but it appears that one can use (variants of) tweakable block ciphers as rekeying schemes. Although the difference is subtle, this gives an efficiency gain as we will see later on (in Sect. 8).

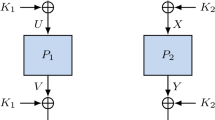
Therefore, in Sect. 5, we investigate how to use beyond birthday bound secure tweakable block ciphers more efficiently in the context of rekeying. This is a delicate task: not all state of the art solutions are suitable. The first scheme is based on the simplest beyond birthday bound secure tweakable block cipher from Mennink  [65], along with some cosmetic simplifications that appear unnecessary in the composition. The scheme, called $R\mathrm {1}$, consists of one subkey generation function, one multiplication, and one block cipher call. It is depicted in Fig. 1, and achieves security up to complexity $2^{2n/3}$, where n is the block size of the cipher. The second solution is an instantiation of Dobraunig et al.’s scheme with an optimally secure tweakable block cipher from Wang et al.  [94], along with some necessary changes to avoid that security collapses at $2^{n/2}$. The adjusted scheme, called $R\mathrm {2}$, is depicted in Fig. 2 and achieves optimal $2^n$ security.

Albeit the two solutions achieve beyond birthday bound security and are reasonably efficient, they may be unsatisfying in certain settings. This is in part as they use a block cipher whose key size and block size are the same, but also as they consist of a sequential evaluation of three operations (subkey generation, then multiplication/block cipher, then block cipher). For our third generalized solution, we depart from state of the art on rekeying, and note that the tweakable block cipher $\mathrm {XHX}$ from Jha et al.  [49] in itself is already well-suited for rekeying. Our third scheme $R\mathrm {3}$ is a simplification and adaptation of $\mathrm {XHX}$ in such a way that it is easy to understand and analyze and at the same time general enough to be broadly applicable in a side-channel setting. The resulting scheme is introduced in Sect. 6 and depicted in Fig. 3. It uses a larger key than $R\mathrm {1}$ and $R\mathrm {2}$, but performs subkey generation more efficiently and flexibly, and consists of only two functions (subkey generation, then block cipher). In addition, key size reduction is possible. The scheme achieves optimal $2^n$ security. The scheme easily generalizes to a permutation based variant, concretely a rekeying scheme for Even-Mansour  [33], in birthday bound security in the state size of the permutation, where we remark that the state of a permutation is typically much larger than the block size of a block cipher (see Sect. 6).

We elaborate on instantiations of the schemes in Sect. 7, where we also discuss possible key size reduction of $R\mathrm {3}$, and we describe and discuss the costs of the schemes relative to the state of the art in Sect. 8. This comparison, summarized in Table 1, indicates that our schemes $R\mathrm {1}$, $R\mathrm {2}$, and $R\mathrm {3}$, compare favorably. For example: $R\mathrm {2}$ is equally expensive as the block cipher based solution of Dobraunig et al., yet optimally secure. The scheme $R\mathrm {1}$, in turn, achieves a lower level of provable security than $R\mathrm {2}$, but it is also cheaper and intuitively more appealing. Scheme $R\mathrm {3}$, finally, has higher subkey generation cost and a priori larger key, but it achieves optimal security and is more generic.

1.2 Application: Rekeying-Based Authenticated Encryption

Tweakable block ciphers have played an important role in the design and analysis of authenticated encryption schemes. Either implicitly or explicitly, 18 out of 57 submissions to the CAESAR competition for the development of a portfolio of authenticated encryption schemes  [22] were based on a tweakable block cipher. The reason for this is a technical one: in analyzing the authenticated encryption mode, one can discard many technicalities and argue security of the mode assuming that the tweakable block cipher is secure. Then, these technicalities are dealt with at the tweakable block cipher level, which is by design a smaller and easier to handle object.

In Sect. 9, we benefit from the solid state of the art on authenticated encryption, and use our observation that generic tweakable block cipher design and fresh parallel rekeying are very related. We take the $\varTheta \mathrm {CB}$ authenticated encryption mode of Krovetz and Rogaway  [55] as application, and instantiate it with our rekeying schemes $R\mathrm {1}$, $R\mathrm {2}$, and $R\mathrm {3}$. The three resulting modes are parallelizable, have a security bound dominated by that of the underlying tweakable rekeying scheme (hence, $2^{2n/3}$, $2^n$, and $2^n$, respectively), and are by design easy to protect against side-channel attacks (as $R\mathrm {1}$, $R\mathrm {2}$, and $R\mathrm {3}$ are). We compare the solutions among each other, with $\mathrm {OCB}\mathrm {3}$, with DTE  [16, 17], and other alternatives in Sect. 9.3.

It is important to note that the gains we achieve here are independent of the fact that we used $\varTheta \mathrm {CB}$: they are purely caused by the use of our rekeying schemes. Further applications can be found in tweakable block cipher based MAC or AE schemes such as ZMAC  [47] or ZOCB/ZOTR  [7], and the achieved efficiency and security gains are comparable to that of the application outlined in Sect. 9.

1.3 Outline

Section 2 includes the preliminaries of this work. An in-depth survey of rekeying schemes is given in Sect. 3 and of tweakable block ciphers in Sect. 4. The first two schemes, $R\mathrm {1}$ and $R\mathrm {2}$, are given in Sect. 5. The third scheme, $R\mathrm {3}$, is given in Sect. 6. We elaborate on instantiations of the schemes in Sect. 7, and perform a cost analysis of the schemes in Sect. 8. In Sect. 9, we apply our findings to authenticated encryption and instantiate $\varTheta \mathrm {CB}$ with our rekeying solutions. The work is concluded in Sect. 10.

2 Preliminaries

For natural $n\in \mathbb {N}$, $\{0,1\}^{n}$ denotes the set of all n-bit strings. $\{0,1\}^{*}$ denotes the set of arbitrarily sized strings. For a finite set $\mathcal {X}$, $x\xleftarrow {{\scriptscriptstyle \$}}\mathcal {X}$ denotes the random sampling of an element x from $\mathcal {X}$. For natural $m,n\in \mathbb {N}$ such that $m\le n$, we denote by $(n)_m=n(n-1)\cdots (n-m+1)$ the falling factorial.

2.1 (Tweakable) Block Ciphers

For $\kappa ,\rho ,n\in \mathbb {N}$, a block cipher $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is a mapping such that for every key $k\in \{0,1\}^{\kappa }$, the function $E_k(\cdot )=E(k,\cdot )$ is a permutation on n-bit strings. Its inverse is denoted $E_k^{-1}(\cdot )$. A tweakable block cipher $\widetilde{E}:\{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is a mapping such that for every key $k\in \{0,1\}^{\kappa }$ and every tweak $r\in \{0,1\}^{\rho }$, the function $\widetilde{E}_k(r,\cdot )=\widetilde{E}(k,r,\cdot )$ is a permutation on n-bit strings. Its inverse is denoted $\widetilde{E}_k^{-1}(r,\cdot )$.

Note that a block cipher is a family of $2^\kappa$ n-bit permutations, and a tweakable block cipher is a family of $2^{\kappa +\rho }$ n-bit permutations (gluing together key and tweak). For arbitrary $\mu ,n\in \mathbb {N}$, we denote by $\mathrm {tperm}(\mu ,n)$ the set of all families of $2^\mu$ n-bit permutations.

2.2 Universal Hashing

For $\kappa ,\rho ,n\in \mathbb {N}$, let $h:\{0,1\}^{\kappa }\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{n}$ be a family of keyed hash functions. Let $\alpha \ge 0$. We say that $h$ is $\alpha$-uniform if for any $x\in \{0,1\}^{\rho }$ and $y\in \{0,1\}^{n}$:

$$\begin{aligned} \mathbf {Pr}_{k}\left( h(k,x)=y\right) \le \alpha \,, \end{aligned}$$

where the probability is taken over $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$. For $m\le n$, we say that $h$ is $\alpha$-m-partial-XOR-uniform if for any distinct $x,x'\in \{0,1\}^{\rho }$ and $y\in \{0,1\}^{m}$:

$$\begin{aligned} \mathbf {Pr}_{k}\left( h(k,x)\oplus h(k,x') = 0^{n-m}\Vert y\right) \le \alpha \,, \end{aligned}$$

where the probability is taken over $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$. Partial-XOR-uniformity is a generalization of the well-known XOR-uniformity condition on hash function families. It was introduced in [73]. We simply refer to $\alpha$-XOR-uniformity in case $m=n$.

2.3 Rekeying Schemes and Security Model

A rekeying scheme $R:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is a mathematical function that gets as input a key $k\in \{0,1\}^{\kappa '}$, a tweak $r\in \{0,1\}^{\rho }$, and bijectively encrypts an input m to a ciphertext c. The tweak r is typically restricted to be a counter, nonce, or random value. For secret k, $R$ should behave as a family of n-bit permutations indexed by r: for different choices of r the outcomes are uniformly random, whereas identical r’s will give distinct outputs naturally. This means that a rekeying scheme has the same functionality as a tweakable block cipher, and we can inherit the security model.

The security of a rekeying scheme $R$ considers a distinguisher $D$ that has bi-directional query access to either $R_k$ for $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa '}$ or to $\tilde{\pi }\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\rho ,n)$, and tries to distinguish both worlds. The capabilities of the distinguisher are typically bounded by the number of queries it can make to its oracle, q, and the time it can use for offline computations, p. (We do not take storage into account.) In our work, we consider $R$ to be based on a block cipher $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$, and logically, the distinguisher may want to evaluate $E$ offline as much as possible. Assuming that one evaluation of $E$ takes one unit of time, it can make at most p evaluations of $E$ offline. In our setting, we will consider security of $R$ in the ideal cipher model, which means that the distinguisher has query access to $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$ and can make p queries to it. Besides these queries, we allow $D$ to have unlimited time, we consider it computationally unbounded. We end up with the following definition.

Definition 1

Let $\kappa ',\kappa ,\rho ,n\in \mathbb {N}$. Consider $R:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be any computationally unbounded distinguisher. The “strong tweakable pseudorandom permutation security” security of $R$ is defined as

$$\begin{aligned} \mathbf {Adv}_{R}^{\mathrm {stprp}}(D) = \left| \mathbf {Pr}_{k,E}\left( D^{R_k^{\pm },E^{\pm }} = 1 \right) - \mathbf {Pr}_{\tilde{\pi },E}\left( D^{\tilde{\pi }^{\pm },E^{\pm }} = 1 \right) \right| \,, \end{aligned}$$

(1)

where the probabilities are taken over $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa '}$, $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$, and $\tilde{\pi }\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\rho ,n)$. The superscript “±” indicates that the distinguisher has bi-directional access to the oracle.

Above model poses no restriction on the choice of r by the distinguisher: it can freely choose it. In practical rekeying schemes, however, r is typically restricted to be a counter, nonce, or random value, as explicitly outlined in the schemes below. This does not change the security model, yet it does influence the security analysis and the scope of the schemes.

3 State of the Art on Rekeying Schemes

Throughout this section, let $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ be a block cipher. If the block cipher is used many times under the same key, a poorly protected block cipher may leak this key. Abdalla and Bellare  [1] formalized the idea of rekeying, where a particular function is used to generate subkeys for $E$. They introduced two variants, a parallel and a serial one; we will only be concerned with the parallel one. Using a PRF $F:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$, they considered

$$\begin{aligned} \begin{aligned} \mathrm {AB}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(F(k,r),m)\,, \end{aligned} \end{aligned}$$

(2)

where r is in principle a counter (the scheme could also be implemented with random r, but this may induce extra collisions for $F$). The approach was introduced independently, and suggested for side-channel protection, by Borst  [21, Section 6.6.1]. Abdalla and Bellare proved that if $F$ is a secure PRF and $E$ is a secure cipher, $\mathrm {AB}$ is a perfectly secure rekeying mechanism (as a pseudorandom function).

Medwed et al.  [64] initiated the investigation of the minimal conditions needed on the block cipher and the subkey generation to obtain side-channel security. They introduced a function

$$\begin{aligned} \begin{aligned} \mathrm {MSGR}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(h(k,r),m)\,, \end{aligned} \end{aligned}$$

(3)

for some function $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$, and where r is necessarily a random value for each evaluation. The idea of the scheme is that $E$ is cryptographic machinery that does not need to be equipped with strong side-channel protection (just against SPA) and $h$ is a function that does not need to have strong cryptographic properties but it processes the master key and hence needs to resist strong side-channel attacks (SPA and DPA). For a block cipher with 256-bit key, Medwed et al. suggested to take $\kappa '=\kappa =256$, and to define $h$ as multiplication in $\mathrm {GF}_{2^8}[\mathtt {x}]/f(\mathtt {x})$ for $f(\mathtt {x})=\mathtt {x}^d+1$ for $d\in \{4,8,16\}$. In other words, $h(k,r)=r\cdot k$ in above-mentioned ring. The scheme does not come with a theoretical security analysis, but the authors do provide extensive side-channel analysis. The scheme was later generalized to the multi-party setting by Medwed et al.  [63].

In their introduction, Medwed et al.  [64] did not draw the equivalence with the scheme of Abdalla and Bellare. Most importantly, $h$ does not behave as a PRF. Dobraunig et al.  [28] subsequently described a birthday bound key recovery attack on both schemes of Medwed et al.  [63, 64].¹ The attack is based on the idea that if a session key is recovered, the master key can be derived by invertibility of $h$. In other words, the attack relies on two weaknesses of $\mathrm {MSGR}$:

• (i) a subkey can be recovered in total complexity around $2^{n/2}$;

• (ii) once a subkey is recovered, the master key can be recovered by invertibility of $h$.

Later, Dobraunig et al.  [30] presented two solutions to remedy the situation. The first one does so by enhancing the subkey generation function, and works for $\kappa =n$:

$$\begin{aligned} \begin{aligned} \mathrm {DKM}^{+}1&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(E(h(k,r),r)\oplus r\oplus h(k,r),m)\,. \end{aligned}\end{aligned}$$

(4)

Also in this scheme, $h$ needs to be secured against SPA and DPA, whereas the block cipher only needs to be SPA secure. The value r can be random or a counter. $\mathrm {DKM}^{+}1$ differs from $\mathrm {MSGR}$ by having a one-way subkey generation function, and reducing the security to that of $\mathrm {AB}$. To wit, the subkey generation function in $\mathrm {DKM}^{+}1$ is the function $h$ followed by the Miyaguchi-Preneel compression function  [82]. Nonetheless, the resulting subkey generation only behaves like a PRF up to the birthday bound: the authors prove that if $h$ is bijective for either the left or the right of its inputs fixed and if $E$ is an ideal cipher, the resulting scheme is secure up to complexity $2^{n/2}$. For $h$, they suggest multiplication in $\mathrm {GF}_2[\mathtt {x}]/f(\mathtt {x})$ for any irreducible polynomial $f(\mathtt {x})$ of degree n.

The second scheme of Dobraunig et al.  [30] achieves security beyond the birthday bound, but it is based on a tweakable block cipher $\widetilde{E}:\{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$:

$$\begin{aligned} \begin{aligned} \mathrm {DKM}^{+}2&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto \widetilde{E}(h(k,r),r,m)\,. \end{aligned}\end{aligned}$$

(5)

One can see this construction as an abstraction of $\mathrm {DKM}^{+}1$ by “uniting” the two block cipher calls into a single tweakable block cipher call. The value r can, again, be random or a counter. This construction is perfectly secure under the assumption that $h$ is bijective for either the left or the right of its inputs fixed and that $\widetilde{E}$ is an ideal tweakable block cipher.

For future discussion, it is of importance to understand how the schemes of Dobraunig et al.  [30] improve over the one of Medwed et al.  [64]. The first scheme, $\mathrm {DKM}^{+}1$, improves over $\mathrm {MSGR}$ by resolving weakness (ii) above, namely by assuring that the subkey generation is non-invertible. It may still be possible to recover a session key in complexity $2^{n/2}$; this is no problem, but de facto contributes to the fact that the scheme only achieves $2^{n/2}$ security. The second scheme, $\mathrm {DKM}^{+}2$, resolves both weaknesses (i) and (ii) and is the first scheme in the line to achieve beyond birthday bound security, but at a considerable cost: it assumes that $\widetilde{E}$ is an ideal tweakable block cipher. This particularly means that it is only meaningful for instantiation with a dedicated tweakable block cipher design (assumed to be perfectly secure). Any instantiation with a generic tweakable block cipher design (such as the ones in next section) violates the “ideal tweakable block cipher” assumption, and does not necessarily induce a secure scheme; to the contrary, as we will demonstrate in Sect. 5.2.

4 State of the Art on Tweak-Rekeyable Tweakable Block Ciphers

Throughout this section, let $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ be a block cipher. A tweakable block cipher extends a conventional one by the extra input of a “tweak” $r\in \{0,1\}^{\rho }$: the tweakable block cipher behaves as an independent block cipher for every tweak. The initial formalization of a tweakable block cipher is by Liskov et al.  [60]. As part of their formalization, Liskov et al. suggested that changing the tweak should be cheaper than changing the key. Their formalization included two designs, most notably a construction currently known as $\mathrm {LRW2}$:

$$\begin{aligned} \begin{aligned} \mathrm {LRW2}&: \{0,1\}^{\kappa +\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k_1\Vert k_2,r,m) \mapsto E(k_1,m\oplus h(k_2,r))\oplus h(k_2,r)\,, \end{aligned}\end{aligned}$$

(6)

where $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{n}$ is a universal hash function family. Various generalizations of the scheme have appeared  [23, 70, 87]. A cascade of multiple $\mathrm {LRW2}$’s was proven to be secure beyond the birthday bound  [57, 58, 68, 84].

Cascading, however, makes the scheme more expensive, and alternatives to achieving beyond birthday bound secure tweakable block ciphers have been considered. Minematsu  [71] introduced the following scheme based on block cipher $E$ and a PRF $F:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$:

$$\begin{aligned} \begin{aligned} \mathrm {Min}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(F(k,r),m)\,, \end{aligned}\end{aligned}$$

(7)

where, depending on the application, the user can choose the tweak input r. Minematsu proved security up to $\max \{2^{n/2},2^{n-\rho }\}$ and the bound is known to be tight  [67]. Note that $\mathrm {Min}$ is equivalent to $\mathrm {AB}$ but the security bounds are different: this is because Minematsu poses no restriction on repeated usage of r.

Mennink  [65] introduced two constructions that achieve beyond birthday bound security with minimal key material. Both constructions assume $\kappa =\rho =n$ (but we will keep using $\kappa ,\rho ,n$ as this more clearly describes the roles of the different sets). The first construction makes one call to $E$ and one multiplication:

$$\begin{aligned} \begin{aligned} \mathrm {Men1}&: \{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(k\oplus r,m\oplus r\cdot k) \oplus r\cdot k\,, \end{aligned}\end{aligned}$$

(8)

where multiplication is in $\mathrm {GF}_2[\mathtt {x}]/f(\mathtt {x})$ for any irreducible polynomial $f(\mathtt {x})$ of degree n. The scheme is proven secure up to total complexity $2^{2n/3}$ in the ideal cipher model. Mennink’s second construction,

$$\begin{aligned} \begin{aligned} \mathrm {Men2}&: \{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(k\oplus r,m\oplus E(2\cdot k,r)) \oplus E(2\cdot k,r)\,, \end{aligned}\end{aligned}$$

(9)

makes two block cipher calls (instead of one block cipher call and one multiplication) and is proven to achieve optimal $2^n$ security in the ideal cipher model  [65, 66].² One can simply take $E(k,r)$ for mask, provided that one restricts the tweak to $r\ne 0$.

Clearly, $\mathrm {Men1}$ and $\mathrm {Men2}$ are not so interesting from a leakage resilience point of view: the key input to the (possibly unprotected) block cipher is $k\oplus r$ from which k can be recovered with knowledge of r. Nevertheless, the work of Mennink  [65] set the stage for a line of research on tweak-rekeyable schemes, where the key input to the internal primitive may change depending on the tweak. Wang et al.  [94] generalized the construction $\mathrm {Men2}$ to 32 variants $\mathrm {WGZ}^{+}i$ for $i\in \{1,\dots ,32\}$ that are based on two block cipher calls and achieve optimal $2^n$ security. The approach is systematic and gives an exhaustive list of all “interesting” solutions. We will highlight one of them, $\mathrm {WGZ}^{+}12$, which we consider to be the simplest and most elegant scheme, as well as the most suitable one for our purposes (the reason being that for $\mathrm {WGZ}^{+}12$ the masking $E(0,k)$ needs to be computed only once). Also this construction assumes $\kappa =\rho =n$:

$$\begin{aligned} \begin{aligned} \mathrm {WGZ}^{+}12&: \{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(k\oplus r,m\oplus E(0,k)) \oplus E(0,k)\,. \end{aligned}\end{aligned}$$

(10)

Naito  [74] introduced $\mathrm {XKX}$, a generalization of $\mathrm {Min}$ specifically targeting authenticated encryption. In addition to the PRF $F:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$, it uses a hash function family $h:\{0,1\}^{\kappa ''}\times \{0,1\}^{\rho '}\rightarrow \{0,1\}^{n}$ and is defined as

$$\begin{aligned} \begin{aligned} \mathrm {XKX}&: \{0,1\}^{\kappa '+\kappa ''}\times \{0,1\}^{\rho +\rho '}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k_1\Vert k_2,N\Vert r,m) \mapsto E(F(k_1,N),m\oplus h(k_2,r)) \oplus h(k_2,r)\,. \end{aligned}\end{aligned}$$

(11)

Here, N is a nonce and r a counter, such that $N\Vert r$ is unique for every query. The PRF $F$ is then instantiated using the sum of permutations  [14, 15, 18, 27, 46, 61, 77, 78].

Jha et al. presented the generalized construction $\mathrm {XHX}$  [49]. It uses a universal hash function family $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }\times \{0,1\}^{n}\times \{0,1\}^{n}$, and is defined as

$$\begin{aligned} \begin{aligned} \mathrm {XHX}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(u,m\oplus v)\oplus w \text {, where } (u,v,w)\leftarrow h(k,r)\,. \end{aligned}\end{aligned}$$

(12)

They subsequently consider $h$ to be constructed of three universal hash function families $h_1,h_2,h_3$, all receiving subkeys $k_1,k_2,k_3$ derived from k using the block cipher $E$. The construction generalizes $\mathrm {Men2}$ as well as the 32 $\mathrm {WGZ}^{+}i$ constructions. Jha et al.  [49] derive minimal conditions on the functions and on the subkey generation for $\mathrm {XHX}$ to be secure, and prove that security up to $2^{(\kappa +n)/2}$ is achieved. Note that the $\mathrm {XHX}$ scheme is quite general (and in fact it is not described in full generality here), but this generality goes at the cost of simplicity, and in fact, if $E$-based subkey generation for $h$ is omitted the scheme simplifies drastically. Also, security turns out not to be sacrificed if one uses identical masking before and after the block cipher, i.e., if one sets $v=w$.

It is important to note that, although Minematsu’s $\mathrm {Min}$ and Naito’s $\mathrm {XKX}$ can still be proven secure in the standard cipher model, the analyses of Mennink’s $\mathrm {Men1}$ and $\mathrm {Men2}$, Wang et al.’s $\mathrm {WGZ}^{+}i$, and Jha et al.’s $\mathrm {XHX}$ are performed in the ideal cipher model. This difference comes from the fact that the adversary can change tweaks, subsequently influence the key input to the block cipher, and the model of related-key secure block ciphers has to be deployed in order to get standard model security. The construction can subsequently never be properly proven to be beyond birthday bound secure. Mennink  [67] performed an extensive theoretical analysis of this phenomenon and demonstrated that provably optimal security is impossible in the standard model, under the assumption that no non-tweak-rekeyable scheme based on approximately $\sigma$ block cipher calls achieves security beyond $2^{\sigma n/(\sigma +1)}$. This assumption, in turn, is still open, and the security of cascaded $\mathrm {LRW2}$ is known to reside on the edge of this bound  [68]. Cogliati  [25] recently considered multi-user beyond birthday bound security of tweakable block ciphers, and presented refinements of [68] in the case of block ciphers whose key space is larger than the block size.

5 Improved $\mathrm {DKM}^{+}2$ Instantiations

The rekeying scheme $\mathrm {DKM}^{+}1$  [30] (see (4)) is seen as a specific instantiation of $\mathrm {AB}$, namely by putting PRF $F$:

$$\begin{aligned} \begin{aligned} F&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }\,,\\&(k,r) \mapsto E(h(k,r),r)\oplus r\oplus h(k,r)\,. \end{aligned}\end{aligned}$$

(13)

Instead, in hindsight it is more reasonable to think of it as an instantiation of $\mathrm {DKM}^{+}2$ for an inconveniently designed tweakable block cipher design:

$$\begin{aligned} \widetilde{E}&: \{0,1\}^{\kappa }\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(E(k,r)\oplus r\oplus k,m)\,. \end{aligned}$$

As a tweakable block cipher, this function can be broken in complexity $2^{n/2}$. In the remainder of this section, we start from $\mathrm {DKM}^{+}2$ and consider two of the most suitable ways of instantiating the tweakable block cipher.

5.1 First Scheme

The simplest choice, following Sect. 4, is to instantiate $\mathrm {DKM}^{+}2$ with the $\mathrm {Men1}$ tweakable block cipher  [65] (see (8)). We call this scheme $R\mathrm {1}$. It is based on a block cipher $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ and internally uses a hash function family $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$, where $\kappa =\rho =n$ (and typically, but not necessarily, $\kappa '=\kappa$):

$$\begin{aligned} \begin{aligned} R\mathrm {1}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(h(k,r),m\oplus r\cdot h(k,r)) \oplus r\cdot h(k,r)\,, \end{aligned}\end{aligned}$$

(14)

where multiplication is in $\mathrm {GF}_2[\mathtt {x}]/f(\mathtt {x})$ for any irreducible polynomial $f(\mathtt {x})$ of degree n. The scheme is depicted in Fig. 1. We remark that this is not exactly a composition of $\mathrm {DKM}^{+}2$ with $\mathrm {Men1}$: such a composition would have $h(k,r)\oplus r$ as key input to $E$. As we have included subkey generation $h(k,r)$ to the scheme, the addition of r is not needed.

Fig. 1.

Generalized rekeying construction $R\mathrm {1}$ of (14) with $\kappa =\rho =n$: subkey generation (left) and core encryption (right).

Intuitively, as $\mathrm {DKM}^{+}2$ is optimally $2^n$ secure and $\mathrm {Men1}$ is $2^{2n/3}$ secure, one expects $R\mathrm {1}$ to be $2^{2n/3}$ secure. Unfortunately, one cannot simply claim security of $R\mathrm {1}$ in such a hybrid argument. The reason is that $\mathrm {DKM}^{+}2$ is proven secure under the assumption that $\widetilde{E}$ is an ideal tweakable block cipher, and $\mathrm {Men1}$ does not meet this criterion. Fortunately, however, a dedicated proof would be similar to that of $\mathrm {Men1}$, the overlay of $\mathrm {DKM}^{+}2$ coming at limited effort.

Formally, in the security model of Definition 1, we will prove that $R\mathrm {1}$ achieves security up to complexity $2^{2n/3}$. The proof is given in the full version  [69]. It is inspired by that of Mennink  [65], but it is not quite the same due to the usage of the subkey generation function. In fact, the security of $R\mathrm {1}$ cannot be concluded from the security results on $\mathrm {DKM}^{+}2$ and $\mathrm {Men1}$. The proof of $R\mathrm {1}$ is, as that of  [65], based on the Szemerédi-Trotter theorem [91], which claims that if one takes q lines and p points in a two-dimensional finite field $\mathbb {F}^2$, the number of point-line incidences is at most $\min \{q^{1/2}p+q,qp^{1/2}+p\}$.

Theorem 1

Let $\kappa ',\kappa ,\rho ,n\in \mathbb {N}$ with $\kappa =\rho =n$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$ be a family of keyed hash functions that is injective for fixed $k\in \{0,1\}^{\kappa '}$ and $\alpha$-uniform. Let $D$ be a distinguisher making at most q construction queries and p primitive queries. Then,

$$\begin{aligned} \mathbf {Adv}_{R\mathrm {1}}^{\mathrm {stprp}}(D)&\le 2\min \{q^{1/2}p+q,qp^{1/2}+p\}\alpha \,. \end{aligned}$$

(15)

Note that for $q=p$, the bound simplifies to $2(q^{3/2}+q)\alpha$. There exist hash function families $h$ that meet the conditions for $\alpha =2^{-\kappa }$ (see Sect. 7). Recalling that $\kappa =n$, this implies $2^{2n/3}$ security.

The condition that $h$ needs to be injective for fixed $k\in \{0,1\}^{\kappa '}$ can be traded for the requirement that for any distinct $r,r'\in \{0,1\}^{\rho }$ and $y\in \{0,1\}^{\kappa }$,

$$\begin{aligned} \mathbf {Pr}_{k}\left( h(k,r)=h(k,r')=y\right) \le \alpha ^2\,. \end{aligned}$$

(16)

This relaxation will add $\left( {\begin{array}{c}q\\ 2\end{array}}\right) \alpha ^2$ to the security bound. The proof is trivial: it simply considers the event $h(k,r)=h(k,r')=y$ as a bad event for any two construction queries.

5.2 Second Scheme

The first scheme $R\mathrm {1}$ is efficient, but achieves security up to $2^{2n/3}$ only. We consider an alternative instantiation of $\mathrm {DKM}^{+}2$ with a tweakable block cipher based on two block cipher calls. We will not take $\mathrm {Men2}$  [65] (see (9)), but rather one of the solutions of Wang et al., $\mathrm {WGZ}^{+}12$  [94] (see (10)) to be precise, which we found more suitable. The resulting scheme $R\mathrm {2}$ is based on the same primitives as $R\mathrm {1}$ and is defined as follows:

$$\begin{aligned} \begin{aligned} R\mathrm {2}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(h(k,r),m\oplus E(r,h(k,r))) \oplus E(r,h(k,r))\,. \end{aligned}\end{aligned}$$

(17)

The scheme is depicted in Fig. 2.

Fig. 2.

Generalized rekeying construction $R\mathrm {2}$ of (17) with $\kappa =\rho =n$: subkey generation (left) and core encryption (right).

It is important to note that the scheme is not exactly a composition of $\mathrm {DKM}^{+}2$ with $\mathrm {WGZ}^{+}12$. First of all, as for $R\mathrm {1}$, the subkey input $h(k,r)\oplus r$ is simplified to $h(k,r)$. More importantly, a literal composition would have $E(0,h(k,r))$ as masking rather than $E(r,h(k,r))$. This would make it easier to attack: an adversary can make q construction queries with $m=0$ for varying r, and p primitive evaluations $E(0,l)=y$ for varying l, and the proof aborts at the point that the adversary has a correct guess $h(k,r)=l$, which happens with probability $qp/2^n$. This also perfectly marks the weak spot of the ideal tweakable cipher model used to prove $\mathrm {DKM}^{+}2$: composition does not work as nicely as hoped for. It is also for the same reason that not any of the 32 $\mathrm {WGZ}^{+}i$ schemes could do the job, as became clear after experimentation.

In the full version  [69], we will give a formal analysis in the security model of Definition 1 that $R\mathrm {2}$ achieves security with complexity $2^n$. The proof is inspired by that of Wang et al.  [94], but it is more complex due to the changes in the construction and the usage of the subkey generation function. In fact, the security of $R\mathrm {2}$ cannot be concluded from the security results on $\mathrm {DKM}^{+}2$ and $\mathrm {WGZ}^{+}12$.

Theorem 2

Let $\kappa ',\kappa ,\rho ,n\in \mathbb {N}$ with $\kappa =\rho =n$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }$ be a family of keyed hash functions that is $\alpha$-uniform and $\alpha$-XOR-uniform. Let $D$ be a distinguisher making at most q construction queries and p primitive queries. Then,

$$\begin{aligned} \mathbf {Adv}_{R\mathrm {2}}^{\mathrm {stprp}}(D)&\le \frac{q(3q-3+2p)\alpha }{2^n} + (q+p)\alpha + \frac{p}{2^n}\,. \end{aligned}$$

(18)

For $q=p$ and for simplicity of reasoning taking $h$ to meet the conditions for $\alpha =2^{-\kappa }=2^{-n}$ (see Sect. 7), the bound simplifies to $\frac{5q^2}{2^{2n}} + \frac{3q}{2^n}$. This implies security up to complexity $2^n$.

6 Simpler Optimally Secure Block Cipher Rekeying

The links between fresh rekeying and generic tweakable block cipher design are apparent, but in-depth analyses of the problems in both directions have been performed mostly disjointly, and the equivalence has never been properly drawn and exploited. This is, in part, caused by the fact that the design incentives are different. For example, whereas Minematsu’s tweakable block cipher $\mathrm {Min}$  [71] (see (7)) is identical to Abdalla and Bellare’s $\mathrm {AB}$  [1] (see (2)) and almost identical to Medwed et al.’s rekeying scheme $\mathrm {MSGR}$  [64] (see (3)), schemes like $\mathrm {Men1}$ and $\mathrm {Men2}$ do not achieve leakage resilience in the sense that $\mathrm {MSGR}$, $\mathrm {DKM}^{+}1$, or $\mathrm {DKM}^{+}2$ do, at least not with the same minimal leakage resilience assumptions.

Yet, there is resemblance in the directions, and we can take advantage of this in our quest to optimally secure block cipher rekeying. Our third generalized solution discards the earlier rekeying schemes in its entirety and takes inspiration of the state of the art on tweakable block ciphers. The resulting scheme is reminiscent of $\mathrm {XHX}$  [49] (see (12)) but we make significant simplifications to balance between generality, simplicity, and the possibility to achieve leakage resilience under reasonable conditions. Our rekeying construction for block cipher $E:\{0,1\}^{\kappa }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ internally uses a hash function family $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }\times \{0,1\}^{n}$, and is defined as

$$\begin{aligned} \begin{aligned} R\mathrm {3}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r,m) \mapsto E(u,m\oplus v)\oplus v \text {, where } u\Vert v\leftarrow h(k,r)\,. \end{aligned}\end{aligned}$$

(19)

The scheme is depicted in Fig. 3. Note that we pose no restrictions on $\kappa ',\kappa ,\rho ,n$. We remark that $\mathrm {XHX}$ is a particularly useful choice in the context of lightweight applications. For instance, due to its beyond birthday bound security (in the block size) it has been the base of the tweakable block cipher in REMUS  [45], a first-round submission to the NIST lightweight cryptography competition  [75].

Fig. 3.

Generalized rekeying construction $R\mathrm {3}$ of (19): subkey generation (left) and core encryption (right).

In the security model of Definition 1, we will prove that $R\mathrm {3}$ achieves security up to complexity $2^{(\kappa +n)/2}$. The proof is given in the full version  [69]; it is a simplification of that of Jha et al.  [49].

Theorem 3

Let $\kappa ',\kappa ,\rho ,n\in \mathbb {N}$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }\times \{0,1\}^{n}$ be a family of keyed hash functions that is $\alpha$-uniform and $\alpha$-n-partial-XOR-uniform. Let $D$ be a distinguisher making at most q construction queries and p primitive queries. Then,

$$\begin{aligned} \mathbf {Adv}_{R\mathrm {3}}^{\mathrm {stprp}}(D)&\le q(q - 1 + 2p)\alpha \,. \end{aligned}$$

(20)

As we will discuss in Sect. 7, there exists a hash function family $h$ that meets the requested conditions for $\alpha =2^{-(\kappa +n)}$. Equating $q=p$ for simplicity, above bound simplifies to $3q^2/2^{\kappa +n}$. This roughly gives security up to complexity $2^{(\kappa +n)/2}$.

We remark that using a universal hash function family with $(\kappa =n)$-bit output and setting

$$\begin{aligned} (k,r,m) \mapsto E(h(k,r),m\oplus h(k,r))\oplus h(k,r) \end{aligned}$$

does not allow to achieve security beyond the birthday bound. An adversary can make q evaluations with $m=0$ and varying r. It can additionally make p primitive evaluations $E(l,l)$ for varying l. Any construction query collides with any primitive query if $h(k,r)=l$, which happens with probability $qp/2^n$.

Recall that in $R\mathrm {3}$ we pose no restriction on $\kappa$. One could consider $\kappa =0$: in this case, $E\in \mathrm {tperm}(0,n)$ is simply a permutation, and one can consider $R\mathrm {3}$ to be a rekeying scheme for Even-Mansour  [33]. Following Theorem 3, it achieves security up to around $2^{n/2}$, where n is the state size of the permutation. Practical permutations are typically much larger than block ciphers. For example, the AES  [26] has a block size of $n=128$ bits, but the Keccak/SHA-3  [34] permutation has a state size of $n=1600$ bits.

7 Instantiations

Medwed et al. and Dobraunig et al. initially suggested multiplication for $h$. Later, it was demonstrated  [12, 13, 40, 80] that its use should be done with care as the algebraic structure enables certain types of attacks. A formal treatment was delivered by Dziembowski et al.  [32]. In their introduction of a side-channel secure authenticated encryption scheme ISAP, Dobraunig et al.  [29] suggested the sponge for subkey generation.

Nonetheless, for the sake of comparison in Sect. 8, we will adopt the approach of using finite field multiplication for $h$ in our schemes. For $R\mathrm {1}$ and $R\mathrm {2}$, the same approach as that of Dobraunig et al. works. In detail, finite field multiplication in $\mathrm {GF}_2[\mathtt {x}]/f(\mathtt {x})$ for any irreducible polynomial $f(\mathtt {x})$ of degree n is known to be $2^{-n}$-uniform and $2^{-n}$-XOR-uniform (assuming $r\ne 0^\rho$). For $R\mathrm {3}$, multiplication also works but one would need a hash function family with $(\kappa +n)$-bit range, meaning multiplication in $\mathrm {GF}_{2}[\mathtt {x}]/f(\mathtt {x})$ for irreducible polynomial $f(\mathtt {x})$ of degree $\kappa +n$. It is possible to improve the efficiency to smaller multiplications by instantiating $h$ using two independent keys. Let $\kappa ,n\in \mathbb {N}$ be the parameters of the underlying block cipher $E$, set $\rho \le \min \{\kappa ,n\}$ and $\kappa '=\kappa +n$, and consider the folklore construction

$$\begin{aligned} \begin{aligned} h_{\mathrm {mult}}&: \{0,1\}^{\kappa '}\times \{0,1\}^{\rho }\rightarrow \{0,1\}^{\kappa }\times \{0,1\}^{n}\,,\\&(k_1\Vert k_2,r) \mapsto (r\cdot k_1 \,,\, r\cdot k_2)\,, \end{aligned}\end{aligned}$$

(21)

where multiplication is in $\mathrm {GF}_2[\mathtt {x}]/f(\mathtt {x})$ for any irreducible polynomial $f(\mathtt {x})$ of degree n, and r is always injectively padded to obtain a string of size $\kappa$ resp. n bits. Assuming $r\ne 0^\rho$, it is straightforward to prove that $h_{\mathrm {mult}}$ is $2^{-(\kappa +n)}$-uniform and $2^{-(\kappa +n)}$-n-partial-XOR-uniform.

Proposition 1

$h_{\mathrm {mult}}$ of (21) is $2^{-(\kappa +n)}$-uniform and $2^{-(\kappa +n)}$-n-partial-XOR-uniform.

Proof

Starting with $2^{-(\kappa +n)}$-uniformity, consider any $r\in \{0,1\}^{\rho }\backslash \{0^\rho \}$ and $(u,v)\in \{0,1\}^{\kappa }\times \{0,1\}^{n}$. Then,

$$\begin{aligned} \mathbf {Pr}_{k_1,k_2}\left( h_{\mathrm {mult}}(k_1\Vert k_2,r)=(u,v)\right)&= \mathbf {Pr}_{k_1}\left( r\cdot k_1=u\right) \cdot \mathbf {Pr}_{k_2}\left( r\cdot k_2=v\right) = 1/2^{\kappa +n}\,, \end{aligned}$$

where the randomness is taken over $k_1\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$ and $k_2\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$.

For $2^{-(\kappa +n)}$-n-partial-XOR-uniformity, consider any distinct $r,r'\in \{0,1\}^{\rho }$ and $v\in \{0,1\}^{n}$. Then,

$$\begin{aligned}&\mathbf {Pr}_{k_1,k_2}\left( h_{\mathrm {mult}}(k_1\Vert k_2,r)\oplus h_{\mathrm {mult}}(k_1\Vert k_2,r') = (0^{\kappa },v)\right) \\&= \mathbf {Pr}_{k_1}\left( (r\oplus r')\cdot k_1 = 0^{\kappa }\right) \cdot \mathbf {Pr}_{k_2}\left( (r\oplus r')\cdot k_2 = v\right) \\&= 1/2^{\kappa +n}\,, \end{aligned}$$

where the randomness is taken over $k_1\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$ and $k_2\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$.    $\square$

Alternative solutions, particularly for larger and possibly variable length values of $\rho$, are described in  [49].

The universal hash function family $h_{\mathrm {mult}}$ is thus optimally secure, and yields a construction $R\mathrm {3}$ that is secure as long as, roughly, $q^2+2qp\le 2^{\kappa +n}$ (see Theorem 3). It has the disadvantage that two keys are needed. It is possible to reduce this key material. An obvious choice for this is to use the block cipher $E$. A direct simplification of the technique used in $\mathrm {XHX}$ suggests the following key generation that takes a single $\kappa$-bit key k:

$$\begin{aligned} h(k,r) = (r\cdot E(k,0) \,,\, r\cdot E(k,1))\,, \end{aligned}$$

(22)

assuming for a moment that $\kappa =n$.³ This works fine as long as none of the construction queries or primitive queries made by the distinguisher matches the evaluations of $E(k,0)$ or $E(k,1)$. Incorporating this in the proof is simple but technically involved; we refer to [49] for details.

From the perspective of leakage resilience, there is not much gain in this approach: computing the subkeys every evaluation of $R\mathrm {3}$ would imply that $E$ needs to be DPA protected (it evaluates the master key multiple times for each query). Alternatively, the subkeys can be precomputed and stored, but in this case the advantage over simply generating and storing random subkeys $(k_1,k_2)$ is marginal.

8 Cost Comparison

We perform a comparison of the symmetric-cryptographic solutions around, i.e., those of Abdalla and Bellare  [1], Medwed et al.  [64], Dobraunig et al.  [30], and ours. The comparison is given in Table 1. The cost is split into a subkey generation cost and a core generation cost: the subkey generation must be secure against differential power analysis (DPA) whereas the core part needs to be secure against simple power analysis (SPA). All security bounds are derived in the ideal model for the core (that is, the ideal cipher model or ideal tweakable cipher model).

Here, for simplicity of comparison, we keep $\kappa =\rho =n$ and take the instantiation of $h$ using finite field multiplications of Sect. 7. In particular, any evaluation of $h$ in $R\mathrm {1}$ and $R\mathrm {2}$ is considered to cost one multiplication and any evaluation of $h$ in $R\mathrm {3}$ to cost two multiplications. The main characteristics of the comparison hold for arbitrary choice of $h$: de facto, that of $R\mathrm {3}$ is simply considered to be twice as expensive as that of the others.

Table 1. Cost comparison. Here, $F$ a random function, $\widetilde{E}$ is a tweakable block cipher, $E$ a block cipher, and $\otimes$ finite field multiplication of n-bit elements. We estimate the cost of subkey generation $h$ with finite field multiplications as outlined in Sect. 7. (We stress that instantiation can also be done using different hash function families, as long as the conditions of Theorems 1–3 are met.) Cost is split into “subkey” to generate a session key from the master key and “core” that corresponds to the core encryption performed using the session key. For the number of finite field multiplications, key size, and security bound, we assume that $\kappa =\rho =n$ for simplicity.

Clearly, DPA protection is most expensive, so in the subkey generation a minimal primitive is desirable. This, in particular, led Dobraunig et al.  [30] to instantiating the PRF $F$ in $\mathrm {AB}$ as (13). Yet, $\mathrm {DKM}^{+}1$ only achieved birthday bound security. The transition to $\mathrm {DKM}^{+}2$ was to replace the two block cipher calls by a tweakable block cipher: the resulting construction is optimally secure, yet, the security loss is implicit in the ideal tweakable block cipher. If the scheme is instantiated with a dedicated tweakable block cipher such as SKINNY or MANTIS  [11] or QARMA  [4], this is reasonable. On the other hand, instantiations using generic block cipher constructions cost at least two expensive operations (either two block cipher calls or a block cipher call and a multiplication, see Sect. 4) to become beyond birthday bound secure  [65]. Stated differently, if $\mathrm {DKM}^{+}2$’s security is wished for using a conventional block cipher rather than a tweakable block cipher as underlying primitive, at least two block cipher calls or at least a block cipher call and a multiplication are needed.

Needless to say, it is preferable to have as few block cipher calls as possible. Instantiating $\mathrm {DKM}^{+}2$ with $\mathrm {Men1}$ gives 2n/3-security using a single key, as given by our construction $R\mathrm {1}$. We had to perform a dedicated analysis, as the analysis of the original $\mathrm {DKM}^{+}2$ is in the ideal tweakable cipher model. Our construction $R\mathrm {2}$ achieves optimal $2^n$ security at cost identical to $\mathrm {DKM}^{+}1$.

Our construction $R\mathrm {3}$ generalizes. Assuming $\kappa =n$ and using two independent n-bit keys (as suggested in Sect. 7), it achieves optimal $2^n$ security as well. Using a 2n-bit key may be arguably worse from a practitioner’s perspective, and in some settings $R\mathrm {1}$ is preferable over $R\mathrm {3}$. From a theoretical perspective, the use of an extra key in $R\mathrm {3}$ is justifiable compared to the analysis of $\mathrm {DKM}^{+}2$. To wit, both analyses are in the ideal model for the core primitive. This means that the formal security analysis of $\mathrm {DKM}^{+}2$ is based on the random generation of $\widetilde{E}\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa +\rho ,n)$ and of $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa }$,⁴ i.e., the random elements are taken uniformly randomly from a pool of

$$\begin{aligned} (2^n!)^{2^{\kappa +\rho }} \cdot 2^{\kappa } \end{aligned}$$

elements. In the analysis of $R\mathrm {3}$, the security is based on the random generation of $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$ and of $k_1\Vert k_2\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa +n}$ (see Sect. 7), i.e., the random elements are taken uniformly randomly from a pool of

$$\begin{aligned} (2^n!)^{2^\kappa } \cdot 2^{\kappa +n} \end{aligned}$$

elements. It is clear to see that this is a much smaller pool of randomness. As a general rule, the larger the pool of randomness, the stronger the security assumption, and the easier a security analysis is performed.

In addition, as discussed in Sect. 6, $R\mathrm {3}$ also generalizes to permutation based rekeying, namely by setting $\kappa =0$ and instantiating it with an n-bit permutation $P\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(0,n)$. The resulting scheme generates a subkey at cost 1 evaluation of $\otimes$/$h$, and encrypts data at cost 1 evaluation of P. It has keysize n and achieves $2^{n/2}$ security.

9 Authenticated Encryption from Fresh Rekeying

Tweakable block ciphers have historically been used a lot in the context of authenticated encryption  [3, 41, 55, 72, 81, 87, 88]. They serve as an intermediate construction in a generic security proof: one can argue security of the authenticated encryption scheme via the tweakable block cipher to the underlying block cipher. Leading in this respect is the $\varTheta \mathrm {CB}$ (formally named $\varTheta \mathrm {CB}{3}$) authenticated encryption mode that was proven secure relative to the security of its underlying tweakable block cipher  [55]. It forms the base of $\mathrm {OCB}\mathrm {1}$-$\mathrm {OCB}\mathrm {3}$ if instantiated with (a variant of) $\mathrm {XEX}$  [55, 87, 88], of $\mathrm {OPP}$ if instantiated with $\mathrm {MEM}$  [36], and Deoxys-I if instantiated with a dedicated tweakable block cipher  [48].⁵

In this section, we will combine this approach with our insights that tweakable block ciphers and block cipher rekeying are related. In more detail, we will instantiate $\varTheta \mathrm {CB}$ with the rekeying schemes $R\mathrm {1}$, $R\mathrm {2}$, and $R\mathrm {3}$, and compare the resulting solutions with state of the art side-channel secure authenticated encryption schemes. We remark that $\varTheta \mathrm {CB}$ purely serves as example here. The security and efficiency gains that are achieved in this section are attributed to the use of our rekeying schemes. Comparable results can be achieved when these rekeying schemes are used to instantiate other tweakable block cipher based MAC or AE schemes such as ZMAC  [47] or ZOCB/ZOTR  [7].

The model of authenticated encryption is discussed in Sect. 9.1 and we describe $\varTheta \mathrm {CB}$ in Sect. 9.2. We instantiate $\varTheta \mathrm {CB}$ with our rekeying schemes in Sect. 9.3, and discuss the security and efficiency of the resulting schemes from a side-channel protection point of view.

9.1 Authenticated Encryption

We will be concerned with authenticated encryption schemes defined by parameters $\kappa ',\kappa ,\rho ,n,\tau \in \mathbb {N}$ such that $\tau \le n$, and that internally use a block cipher $E\in \mathrm {tperm}(\kappa ,n)$.

An authenticated encryption scheme $AE$ consists of an encryption function $\mathcal {E}$ and a decryption function $\mathcal {D}$. The encryption function $\mathcal {E}$ gets as input a key $k\in \{0,1\}^{\kappa '}$, initial value $iv \in \{0,1\}^{n}$, associated data $a\in \{0,1\}^{*}$, and message $m\in \{0,1\}^{*}$, and outputs a ciphertext $c\in \{0,1\}^{|m|}$ and a tag $t\in \{0,1\}^{\tau }$. Decryption $\mathcal {D}$ gets as input a key $k\in \{0,1\}^{\kappa '}$, initial value $iv \in \{0,1\}^{n}$, associated data $a\in \{0,1\}^{*}$, ciphertext $c\in \{0,1\}^{*}$, and tag $t\in \{0,1\}^{\tau }$, and it outputs a message $m\in \{0,1\}^{|c|}$ (if the authentication is correct) or a dedicated failure symbol $\bot$:

$$\begin{aligned} \mathcal {E}(k, iv ,a,m)&= (c,t)\,,\\ \mathcal {D}(k, iv ,a,c,t)&= m \text { or } \bot \,, \end{aligned}$$

in such a way that for any $(k, iv ,a,m)$, we have $\mathcal {D}(k, iv ,a,\mathcal {E}(k, iv ,a,m))=m$.

The security of an authenticated encryption scheme $AE =(\mathcal {E},\mathcal {D})$ consists of confidentiality and authenticity (these could be merged into a single definition, but it is convenient to treat them separately). In confidentiality, a distinguisher $D$ has query access to either $\mathcal {E}_k$ for $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa '}$ or to a random function $\$$ that for each input $( iv ,a,m)$ returns a random $(c,t)\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{|m|+\tau }$. As in Sect. 2.3, we consider security in the ideal cipher model, which means that the distinguisher also has bi-directional query access to $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$. It can make q queries to its construction oracle, in total of size at most $\sigma$ n-bit blocks, and it can make p queries to the ideal cipher. The q construction queries must be made for non-repeated $iv$ (i.e., the $iv$ is a nonce). Besides these queries, we allow $D$ to have unlimited time, we consider it computationally unbounded.

For authenticity, the distinguisher $D$ has query access to $\mathcal {E}_k$, and in addition to either $\mathcal {D}_k$ or a function $\bot$ that always returns the $\bot$-sign. As before, it has bi-directional access to the underlying ideal cipher $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$. Its goal is to generate a forgery: a query $( iv ,a,c,t)$ to $\mathcal {D}_k$ that returns a valid message m, in such a way that $( iv ,a,m)$ has not been queried to $\mathcal {E}_k$ before. The query and computational complexities of $D$ are as before, with the difference that it is allowed to repeat an $iv$ for decryption queries. It can make $q_v$ forgery attempts.

We obtain the following definitions for confidentiality and authenticity.

Definition 2

Let $\kappa ',\kappa ,n,\tau \in \mathbb {N}$. Consider $AE =(\mathcal {E},\mathcal {D})$ based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be any computationally unbounded distinguisher. The “confidentiality” of $AE$ is defined as

$$\begin{aligned} \mathbf {Adv}_{ AE }^{\mathrm {conf}}(D) = \left| \mathbf {Pr}_{k,E}\left( D^{\mathcal {E}_k,E^{\pm }} = 1 \right) - \mathbf {Pr}_{\$,E}\left( D^{\$,E^{\pm }} = 1 \right) \right| \,, \end{aligned}$$

(23)

and the “authenticity” of $AE$ is defined as

$$\begin{aligned} \mathbf {Adv}_{ AE }^{\mathrm {auth}}(D) = \left| \mathbf {Pr}_{k,E}\left( D^{\mathcal {E}_k,\mathcal {D}_k,E^{\pm }} = 1 \right) - \mathbf {Pr}_{E}\left( D^{\mathcal {E}_k,\bot ,E^{\pm }} = 1 \right) \right| \,, \end{aligned}$$

(24)

where the probabilities are taken over $k\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{\kappa '}$, $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$, and the function $\$$ that returns a random $(c,t)\in \{0,1\}^{|m|+\tau }$ for each input $( iv ,a,m)$. The distinguisher is not allowed to make two encryption queries for the same $iv$, and it is not allowed to query $\mathcal {D}_k/\bot$ on the outcome of an earlier query to $\mathcal {E}_k$. The superscript “±” indicates that the distinguisher has bi-directional access to the oracle.

9.2 $\varTheta \mathrm {CB}$

The $\varTheta \mathrm {CB}$ authenticated encryption scheme was first described by Krovetz and Rogaway  [55]. It is internally based on a tweakable block cipher $\widetilde{E}:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho '}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ with $\rho '=n+\rho$. The encryption function of $\varTheta \mathrm {CB}$ for integral data is depicted in Fig. 4. We refer to [55] for a formal description of the function and its corresponding decryption function.

Fig. 4.

The $\varTheta \mathrm {CB}$ encryption function $\mathcal {E}_k$  [87] for integral data. The associated data a and message m are padded into n-bit blocks. The tweak to each tweakable block cipher call consists of an n-bit string (either 0 or the initial value $iv$) and a $\rho$-bit string $tw _i^{a/\oplus /m}$ that unambiguously determines the position of the tweakable block cipher within the $\varTheta \mathrm {CB}$ construction.

Krovetz and Rogaway proved optimal security of $\varTheta \mathrm {CB}$ under the assumption that the underlying tweakable block cipher is secure  [55]. It is important to note that their result is in the standard model, but we will directly phrase it in the ideal cipher model (Definitions 1 and 2 are both in the ideal cipher model), where we look ahead and observe that our application is internally based on an ideal cipher $E\xleftarrow {{\scriptscriptstyle \$}}\mathrm {tperm}(\kappa ,n)$. For now, this does not bias the discussion; we will elaborate on this in Sect. 9.3.1.

Theorem 4

Let $\kappa ',\kappa ,\rho ,n,\tau \in \mathbb {N}$, and write $\rho '=n+\rho$. Consider $\varTheta \mathrm {CB}$ based on a tweakable block cipher $\widetilde{E}\in \mathrm {tperm}(\kappa ',\rho ',n)$, that is in turn based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be a distinguisher making at most q construction queries (in total of length at most $\sigma$ blocks), $q_v$ forgery attempts, and at most p offline evaluations of $E$. Then,

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}}^{\mathrm {conf}}(D) \le 0\qquad + \mathbf {Adv}_{\widetilde{E}}^{\mathrm {stprp}}(D'), \end{aligned}$$

(25)

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}}^{\mathrm {auth}}(D) \le \frac{2^{n-\tau }q_v}{2^n-1} + \mathbf {Adv}_{\widetilde{E}}^{\mathrm {stprp}}(D'), \end{aligned}$$

(26)

for some distinguisher $D'$ making at most $\sigma$ construction queries and p primitive queries.

As mentioned before, $\mathrm {OCB}\mathrm {1}$-$\mathrm {OCB}\mathrm {3}$ are designed by instantiating $\varTheta \mathrm {CB}$ with variants of $\mathrm {XEX}$  [87]. Here, we focus on $\mathrm {OCB}\mathrm {3}$  [55], which can be seen as being instantiated using the following simplified version of $\mathrm {XEX}$:

$$\begin{aligned} \begin{aligned} \mathrm {XEX}&: \{0,1\}^{\kappa }\times (\{0,1\}^{n}\times \{0,1\}^{n})\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}\,,\\&(k,r\Vert a,m) \mapsto E(k,m\oplus 2^aE(k,r))\oplus 2^aE(k,r)\,. \end{aligned}\end{aligned}$$

(27)

Here, exponentiation and multiplication are over an appropriate finite field, and the value $a\in \{0,1\}^{\rho }$ is first interpreted as a non-negative integer. In fact, the domain of a must be limited in some way to avoid colliding masks $2^a=2^{a'}$, but this fine-tuning is irrelevant for the current discussion (refer to Rogaway  [87] or Granger et al.  [36]). In particular, in $\mathrm {OCB}\mathrm {3}$ the value a is updated according to the Gray code as this allows for optimization in the mask update. This tweakable block cipher is tightly birthday bound secure (in both the standard cipher model and the ideal cipher model), and from Theorem 4 it can be deduced that $\mathrm {OCB}\mathrm {3}$ is tightly birthday bound secure.

9.3 Instantiation of $\varTheta \mathrm {CB}$ with $R\mathrm {1}$-$R\mathrm {3}$

The security of $\varTheta \mathrm {CB}$ instantiated with $R\mathrm {1}$, $R\mathrm {2}$, or $R\mathrm {3}$ follows readily from Theorem 4 on $\varTheta \mathrm {CB}$ and the security result on the respective rekeying scheme in Theorem 1, 2, or 3. The corresponding results are stated in Corollaries 1, 2, and 3, respectively.

Corollary 1

Let $\kappa ',\kappa ,\rho ,n,\tau \in \mathbb {N}$, and write $\rho '=n+\rho$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho '}\rightarrow \{0,1\}^{\kappa }$ be a family of keyed hash functions that is $\alpha$-uniform and $\alpha$-n-partial-XOR-uniform. Consider $\varTheta \mathrm {CB}$ based on rekeying scheme $R\mathrm {1}\in \mathrm {tperm}(\kappa ',\rho ',n)$ of (14), that is in turn based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be a distinguisher making at most q construction queries (in total of length at most $\sigma$ blocks), $q_v$ forgery attempts, and at most p offline evaluations of $E$. Then,

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {1}}^{\mathrm {conf}}(D) \le 0 \qquad + 2\min \{\sigma ^{1/2}p+\sigma ,\sigma p^{1/2}+p\}\alpha , \end{aligned}$$

(28)

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {1}}^{\mathrm {auth}}(D) \le \frac{2^{n-\tau }q_v}{2^n-1} + 2\min \{\sigma ^{1/2}p+\sigma ,\sigma p^{1/2}+p\}\alpha . \end{aligned}$$

(29)

Corollary 2

Let $\kappa ',\kappa ,\rho ,n,\tau \in \mathbb {N}$, and write $\rho '=n+\rho$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho '}\rightarrow \{0,1\}^{\kappa }$ be a family of keyed hash functions that is $\alpha$-uniform and $\alpha$-XOR-uniform. Consider $\varTheta \mathrm {CB}$ based on rekeying scheme $R\mathrm {2}\in \mathrm {tperm}(\kappa ',\rho ',n)$ of (17), that is in turn based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be a distinguisher making at most q construction queries (in total of length at most $\sigma$ blocks), $q_v$ forgery attempts, and at most p offline evaluations of $E$. Then,

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {2}}^{\mathrm {conf}}(D) \le 0 \qquad + \frac{\sigma (3\sigma -3+2p)\alpha }{2^n} + (\sigma +p)\alpha + \frac{p}{2^n}\,, \end{aligned}$$

(30)

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {2}}^{\mathrm {auth}}(D) \le \frac{2^{n-\tau }q_v}{2^n-1} + \frac{\sigma (3\sigma -3+2p)\alpha }{2^n} + (\sigma +p)\alpha + \frac{p}{2^n}\,. \end{aligned}$$

(31)

Corollary 3

Let $\kappa ',\kappa ,\rho ,n,\tau \in \mathbb {N}$, and write $\rho '=n+\rho$. Let $h:\{0,1\}^{\kappa '}\times \{0,1\}^{\rho '}\rightarrow \{0,1\}^{\kappa }\times \{0,1\}^{n}$ be a family of keyed hash functions that is $\alpha$-uniform and $\alpha$-n-partial-XOR-uniform. Consider $\varTheta \mathrm {CB}$ based on rekeying scheme $R\mathrm {3}\in \mathrm {tperm}(\kappa ',\rho ',n)$ of (19), that is in turn based on a block cipher $E\in \mathrm {tperm}(\kappa ,n)$. Let $D$ be a distinguisher making at most q construction queries (in total of length at most $\sigma$ blocks), $q_v$ forgery attempts, and at most p offline evaluations of $E$. Then,

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {3}}^{\mathrm {conf}}(D) \le 0 \qquad + \sigma (\sigma - 1 + 2p)\alpha \,, \end{aligned}$$

(32)

$$\begin{aligned} \mathbf {Adv}_{\varTheta \mathrm {CB}\text {-}R\mathrm {3}}^{\mathrm {auth}}(D) \le \frac{2^{n-\tau }q_v}{2^n-1} + \sigma (\sigma - 1 + 2p)\alpha \,. \end{aligned}$$

(33)

Efficiency-wise, the cost of authenticating and encrypting $\ell _a$ associated data blocks and $\ell _m$ message blocks (each of size n bits) using either of $\varTheta \mathrm {CB}\text {-}R\mathrm {1}$, $\varTheta \mathrm {CB}\text {-}R\mathrm {2}$, or $\varTheta \mathrm {CB}\text {-}R\mathrm {3}$ can be obtained by multiplying the cost of the corresponding underlying rekeying scheme from Table 1 by $\ell _a+\ell _m+1$ (the number of times that the rekeying scheme is evaluated in one evaluation of the construction). As $\varTheta \mathrm {CB}$ itself is optimally secure (see Theorem 4), the security of the rekeying scheme will dominate that of the resulting construction: $\varTheta \mathrm {CB}\text {-}R\mathrm {1}$ achieves $2^{2n/3}$ security, and $\varTheta \mathrm {CB}\text {-}R\mathrm {2}$ and $\varTheta \mathrm {CB}\text {-}R\mathrm {3}$ achieve $2^n$ security. Even though $R\mathrm {3}$ (and thus $\varTheta \mathrm {CB}\text {-}R\mathrm {3}$) has a larger key than $R\mathrm {1}$ and $R\mathrm {2}$, it achieves optimal security based on only one evaluation of the underlying ideal cipher, and it can arguably considered to be the best alternative of the three. Therefore, in the remainder, we focus on $\varTheta \mathrm {CB}$-$R\mathrm {3}$. The scheme is depicted in Fig. 5. We compare $\varTheta \mathrm {CB}$-$R\mathrm {3}$ with $\mathrm {OCB}\mathrm {3}$ and with alternative leakage resilient authenticated encryption schemes in Sects. 9.3.1 and 9.3.2, respectively.

Fig. 5.

The $\varTheta \mathrm {CB}$-$R\mathrm {3}$ encryption function $\mathcal {E}_k$ for integral data. The associated data a and message m are padded into n-bit blocks. The universal hash function $h_k$ transforms a $(n+\rho )$-bit tweak into $(\kappa +n)$-bit subkey. The tweaks themselves are identical to those in $\varTheta \mathrm {CB}$ (see Fig. 4).

9.3.1 Comparison with $\mathrm {OCB}\mathrm {3}$

We acknowledge that the resulting construction $\varTheta \mathrm {CB}$-$R\mathrm {3}$ is more expensive than $\mathrm {OCB}\mathrm {3}$. Indeed, for the authenticated encryption of an input consisting of $\ell _a$ associated data blocks and $\ell _m$ message blocks (each of size n bits), $\mathrm {OCB}\mathrm {3}$ makes $\ell _a+\ell _m+2$ block cipher calls, whereas $\varTheta \mathrm {CB}$-$R\mathrm {3}$ makes $\ell _a+\ell _m+1$ block cipher calls and around $2(\ell _a+\ell _m+1)$ universal hash function calls (taking the scaling of Sect. 8 on the number of universal hash function calls in $R\mathrm {3}$ for granted).

On the other hand, Corollary 3 shows that our construction $\varTheta \mathrm {CB}\text {-}R\mathrm {3}$ achieves $2^n$ security whereas $\mathrm {OCB}\mathrm {3}$ achieves tight birthday bound security, only. The comparison must be taken with a grain of salt, though: $\mathrm {OCB}\mathrm {3}$ can be proven in the standard cipher model, but for $\varTheta \mathrm {CB}$-$R\mathrm {3}$ we have to resort to the ideal cipher model. That said, no standard model attack on $\varTheta \mathrm {CB}$-$R\mathrm {3}$ is known, and the difference seems to arise mostly due to the standard-versus-ideal phenomenon investigated by Mennink  [67] in the context of tweakable block ciphers (cf. the last paragraph of Sect. 4).

More importantly, $\varTheta \mathrm {CB}$-$R\mathrm {3}$ is easier to protect against side-channel attacks than $\mathrm {OCB}\mathrm {3}$. For $\mathrm {OCB}\mathrm {3}$, all block cipher calls are performed for the same key, and the implementation of $E$ needs to be DPA protected. In addition, a typical instantiation of $\mathrm {OCB}\mathrm {3}$ makes use of multiplications in the masking that are hard to protect due to their algebraic structure (recall the first paragraph of Sect. 7). In $\varTheta \mathrm {CB}$-$R\mathrm {3}$, only the “lighter” function $h_k$ needs DPA protection. It is possible to incorporate a cheaper rekeying function in $\mathrm {OCB}\mathrm {3}$, for instance $\mathrm {MSGR}$  [64] (see (3))  [2], but the resulting authenticated encryption mode would only be birthday bound secure and security analysis must likewise be performed in the ideal cipher model.

We conclude by remarking that the efficiency of $\mathrm {OCB}\mathrm {3}$ in part comes from the fact that the computation of $E(k, iv )$ needs to be computed only once per evaluation of the construction. A similar efficiency improvement may be achieved in $\varTheta \mathrm {CB}$-$R\mathrm {3}$ by smart selection of $h_k$. In that case, the total cost of the evaluations of $h_k$ in one evaluation of $\varTheta \mathrm {CB}$-$R\mathrm {3}$ may reduce to around $\ell _a+\ell _m+2$.

9.3.2 Comparison with Leakage Resilient Authenticated Encryption Schemes

State of the art on leakage resilient authenticated encryption is slim. The most relevant proposal is by Berti et al.  [16, 17], that improves upon earlier proposals of Pereira et al.  [79]. Their proposal DTE (Digest, Tag, and Encrypt), in a nutshell, operates as follows:

• Evaluate a hash function on the initial value $iv$ and the message m;

• Transform the output through a side-channel-protected evaluation of $E_k$. The resulting value is the tag t;

• Transform the tag through another evaluation of the side-channel-protected evaluation of $E_k$. The resulting value is the subkey $k_0$;

• Evaluate a two-layer encryption part: the top layer evolves the subkey as $k_i=E_{k_{i-1}}(\mathrm {const}_1)$ and the second layer derives a key stream block as $s_i=E_{k_{i-1}}(\mathrm {const}_2)$, where $\mathrm {const}_1$ and $\mathrm {const}_2$ are two distinct constants.

Thus, for the authenticated encryption of a message of length $\ell _m$ n-bit blocks, DTE makes one cryptographic hash function evaluation on $\ell _m+1$ blocks, two side-channel-protected E-calls, and $2\ell _m$ E-calls. Associated data of $\ell _a$ blocks can be covered by feeding these blocks to the cryptographic hash function as well. Assuming, for simplicity of counting, that hashing $\ell$ blocks is approximately as expensive as $\ell$ E-calls (this is the case for generic Merkle-Damgård hash functions based on the Davies-Meyer compression function), we obtain that DTE takes $\ell _a+\ell _m+1$ unprotected E-calls, $2\ell _m$ SPA-protected E-calls, and 2 DPA-protected E-calls.

Comparing DTE with $\varTheta \mathrm {CB}$-$R\mathrm {3}$ is like comparing apples with oranges: the security models and incentives are different. In particular, DTE is proven to be misuse resistant and to achieve security against decryption leakages, a much stronger security requirement. Effectively, this leads to an efficiency gain in $\varTheta \mathrm {CB}$-$R\mathrm {3}$, in the number of primitive evaluations as well as in the fact that it is parallelizable. Furthermore, both security proofs require E to be an ideal cipher, but DTE is only birthday bound secure while $\varTheta \mathrm {CB}$-$R\mathrm {3}$ is optimally secure. Also, in $\varTheta \mathrm {CB}$-$R\mathrm {3}$, E needs only SPA-protection as long as $h_k$ is DPA-protected; DTE requires two evaluations of E to have strong side-channel protection (the remaining $\ell _a+3\ell _m+1$ can have lighter protection).

Dobraunig et al.  [29] took a different avenue. Their proposal ISAP is sponge based: it uses the sponge with a very small rate to compress key material. ISAP relies on the philosophy that once the sponge has a state with sufficient entropy, it can perform authentication and encryption with a larger rate without any security sacrifice. ISAP is inherently sequential; in addition, it is infeasible to compare $\varTheta \mathrm {CB}$-$R\mathrm {3}$ with ISAP as its design rationale is different (block cipher versus permutation).

An alternative approach to design an authenticated encryption scheme is by generic composition of a MAC function and an authenticated encryption scheme. Barwell et al.  [8] studied generic composition (MtE, M&E, EtM) under leakage and concluded that only the latter is leakage resilient. They present a generic solution, called SIVAT, a three-layer misuse resistant and leakage secure authenticated encryption scheme. The resulting construction can be instantiated with a PRF, an encryption scheme, plus a MAC function. Overall, Barwell et al.  [8] target a different (stronger) security goal, and in part due to the generic nature of the approach, the resulting construction becomes more expensive.

10 Concluding Remarks

Depending on the subkey generation function, one may have to require the tweak to be unpredictable. In our formal security analyses, there is no issue, the adversary can freely choose it (provided that the tweakable block cipher is strong enough). The analysis does not limit the number of times a user may use a certain tweak, but one typically needs to limit it, in order to ensure that no subkey to the underlying block cipher is used too often. Indeed, in this case, for the functions to be side-channel secure it suffices for the block cipher to be secure against SPA (rather than DPA). It is possible to improve the bounds of Theorems 1–3 if the number of appearances per tweak is restricted. In the field of generic tweakable block cipher design and analysis, such a condition appeared before in [59, 68].

We remark that the rekeying solutions serve as an alternative to other strong side-channel countermeasures, at least for specific scenarios. Still, the primitives of the rekeying functions still require certain level of protection. It would be an interesting direction to investigate in what degree the cost of countermeasures gets reduced in practice.

It is fascinating to see that, as this work shows, two seemingly disjoint directions have such a strong relation that the knowledge from one direction (generic tweakable block cipher design) can be used to improve the state of the art of the other field (fresh rekeying). Other conclusions from the former field may likewise result in fruitful solutions to side-channel security, and it is worth exploring this direction. Conversely, there may be possibilities of using the extensive state of the art on, for example, leakage resilient pseudorandom number generators to classical cryptography.