Abstract
Alasdair Urquhart’s work on models for relevant logics is distinctive in a number of different ways. One key theme, present in both his undecidability proof for the relevant logic R (Urquhart 1984) and his proof of the failure of interpolation in R (Urquhart 1993), is the use of techniques from geometry (Urquhart 2019). In this paper, inspired by Urquhart’s work, I explore ways to generate natural models of R \(^+\) from geometries, and different constraints that an accessibility relation in such a model might satisfy. I end by showing that a set of natural conditions on an accessibility relation, motivated by geometric considerations, is jointly unsatisfiable.
Second Reader
P. Balbiani
Institut de Recherche en Informatique de Toulouse – IRIT
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
There are many different things we could say about how we might interpret ‘combination’, and much ink has been spilled on this very issue (Beall et al. 2012; Mares 2004; Restall 1994, 2000; Slaney 1990), both concerning this semilattice semantics and its generalisation, the ternary relational semantics of Routley and Meyer (1972, 1973). It is not my place in this short paper to address those issues. Instead, we will look at how geometries provide a rich playground for developing models for these logics.
- 3.
The axioms correspond to the I, B, C and W combinators. Noticeably absent is the K combinator, with the axiom \(A\rightarrow (B\rightarrow A)\), which reeks of irrelevance. Adding this axiom strengthens the logic to the implicational fragment of intuitionistic logic.
- 4.
To cut down on parentheses, we use the convention that \(\wedge \) and \(\vee \) bind more tightly than the conditional. So, \(A\wedge B\rightarrow A\) is a conditional with \(A\wedge B\) as its antecedent, and so on.
- 5.
If we added the weakening axiom K to give intuitionistic logic, the distribution axiom would come along for the ride.
- 6.
This is Lloyd Humberstone’s approach, in his ‘Operational Semantics for Positive R’ (Humberstone 1988).
- 7.
Bimbó et al. (2018) give an account of the historical origins of the ternary semantics.
- 8.
To add these to our axiomatisation, it suffices to take \(\circ \) to residuate the conditional, like this. We have \((A\circ B\rightarrow C)\rightarrow (A\rightarrow (B\rightarrow C))\) and its converse, \((A\rightarrow (B\rightarrow C))\rightarrow (A\circ B\rightarrow C)\) (so \(\circ \) acts like a kind of conjunction, and with \(\wedge \) it binds more tightly than the conditional). For t, it suffices to set \(t\rightarrow (A\rightarrow A)\) and t as our axioms.
- 9.
In models for relevant logics, extending the ternary R to relate triples and quadruples, by setting R(ab)cd to mean that there is some x where Rabx and Rxcd have become standard notation. For this reason, we continue to use ‘R’ to name this collection relation, since context will determine whether we mean a collection relation or a ternary relation, as appropriate.
- 10.
How ‘represented’ may be understood can, of course, vary from application to application, or model to model.
- 11.
This may be reminiscent to a Cut rule, taking us from and
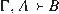 and
and 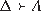 to
to 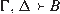 .
. - 12.
For more details concerning set frames, and their cousins, multiset frames, list frames and the like, the reader is referred to the paper ‘Collection Frames’ (Restall and Standefer 2020), written with Shawn Standefer.
References
Beall, J., Brady, R., Dunn, J. M., Hazen, A. P., Mares, E., Meyer, R. K., et al. (2012). On the ternary relation and conditionality. Journal of Philosophical Logic, 41(3), 595–612.
Bimbó, K., Dunn, J., & Ferencz, N. (2018). Two manuscripts, one by Routley, one by Meyer: The origins of the Routley-Meyer semantics for relevance logics. The Australasian Journal of Logic, 15(2), 171–209.
Humberstone, I. L. (1988). Operational semantics for positive r. Notre Dame Journal of Formal Logic, 29(1), 61–80.
Mares, E. D. (2004). Relevant logic: A philosophical interpretation. Cambridge: Cambridge University Press.
Martin, E. P. (1978). The P-W problem. PhD thesis, Australian National University.
Martin, E. P., & Meyer, R. K. (1982). Solution to the P-W problem. The Journal of Symbolic Logic, 47, 869–886.
Restall, G. (1994). A useful substructural logic. Bulletin of the Interest Group in Pure and Applied Logic, 2(2), 135–146.
Restall, G. (2000). An introduction to substructural logics. London: Routledge.
Restall, G., & Standefer, S. (2020). Collection frames for substructural logics. Paper in progress.
Routley, R., & Meyer, R. K. (1972). Semantics of entailment – II. Journal of Philosophical Logic, 1(1), 53–73.
Routley, R., & Meyer, R. K. (1973). Semantics of entailment. In H. Leblanc (Ed.), Truth, Syntax and Modality, Proceedings of the Temple University Conference on Alternative Semantics (pp. 194–243). North Holland.
Slaney, J. K. (1990). A general logic. Australasian Journal of Philosophy, 68, 74–88.
Urquhart, A. (1972). Semantics for relevant logics. The Journal of Symbolic Logic, 37, 159–169.
Urquhart, A. (1984). The undecidability of entailment and relevant implication. The Journal of Symbolic Logic, 49(4), 1059–1073.
Urquhart, A. (1993). Failure of interpolation in relevant logics. Journal of Philosophical Logic, 22(5), 449–479.
Urquhart, A. (2019). Relevant implication and ordered geometry. The Australasian Journal of Logic, 16(8), 342–354.
Acknowledgements
Thanks to Shawn Standefer for many helpful conversations on the material discussed here, including correcting a few of my stumbles along the way, to referees for this volume, for helpful suggestions, and to an (online) audience of the Melbourne Logic Group, including Graham Priest, Shay Logan, Yale Weiss and Tomasz Kowalski, for feedback on this material. Many thanks to Philippe Balbiani and Alasdair Urquhart for helpful comments on a draft of this chapter. This research was supported by the Australian Research Council, Discovery Grant DP150103801.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Restall, G. (2022). Geometric Models for Relevant Logics. In: Düntsch, I., Mares, E. (eds) Alasdair Urquhart on Nonclassical and Algebraic Logic and Complexity of Proofs. Outstanding Contributions to Logic, vol 22. Springer, Cham. https://doi.org/10.1007/978-3-030-71430-7_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-71430-7_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-71429-1
Online ISBN: 978-3-030-71430-7
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


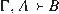 and
and 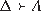 to
to 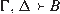 .
.