Abstract
Virtual black-box obfuscation is a strong cryptographic primitive: it encrypts a circuit while maintaining its full input/output functionality. A remarkable result by Barak et al. (Crypto 2001) shows that a general obfuscator that obfuscates classical circuits into classical circuits cannot exist. A promising direction that circumvents this impossibility result is to obfuscate classical circuits into quantum states, which would potentially be better capable of hiding information about the obfuscated circuit. We show that, under the assumption that Learning With Errors (LWE) is hard for quantum computers, this quantum variant of virtual black-box obfuscation of classical circuits is generally impossible. On the way, we show that under the presence of dependent classical auxiliary input, even the small class of classical point functions cannot be quantum virtual black-box obfuscated.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
If, apart from the targets of the aforementioned CNOTs, the circuit C contains any other wires that are initialized in the \(\left| 0\right\rangle \) state inside the circuit, those wires are also considered part of the input of the unitary \(U_C\). They should be initialized to \(\left| 0\right\rangle \) here as well.
- 2.
The total number of blocks, \(K(\lambda ,d)\), will be the number of gates in \(\mathsf {KeyGen} (1^{\lambda }, 1^d, r)\). Since the number of gates is polynomial in \(\lambda \), it suffices for the length of the PRF seed \(r'\) to be linear in \(\lambda \).
References
Aaronson, S.: Ten semi-grand challenges for quantum computing theory. Blog post (2005). https://www.scottaaronson.com/writings/qchallenge.html
Aharonov, D., Brakerski, Z., Chung, K.-M., Green, A., Lai, C.-Y., Sattath, O.: On quantum advantage in information theoretic single-server PIR. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 219–246. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_8
Alagic, G., Fefferman, B.: On quantum obfuscation. arxiv preprint arXiv: 1602.01771 (2016)
Ambainis, A., Hamburg, M., Unruh, D.: Quantum security proofs using semi-classical oracles. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 269–295. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_10
Ananth, P., La Placa, R.L.: Secure quantum extraction protocols. In: Pass, R., Pietrzak, K. (eds.) TCC 2020. LNCS, vol. 12552, pp. 123–152. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_5
Ananth, P., La Placa, R.L.: Secure software leasing. arXiv arXiv: 2005.05289 (2020)
Applebaum, B.: Garbled circuits as randomized encodings of functions: a primer. Tutorials on the Foundations of Cryptography. ISC, pp. 1–44. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57048-8_1
Barak, B., et al.: On the (Im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Bellare, M., Hoang, V.T., Rogaway, P.: Foundations of garbled circuits. In: Proceedings of the 19th ACM SIGSAC Conference on Computer and Communications Security (CCS), pp. 784–796. ACM (2012). https://doi.org/10.1145/2382196.2382279
Broadbent, A., Jeffery, S.: Quantum homomorphic encryption for circuits of low T-gate complexity. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 609–629. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_30
Broadbent, A., Kazmi, R.A.: Indistinguishability obfuscation for quantum circuits of low t-count. arXiv: 2005.14699 (2020)
Brakerski, Z.: Quantum FHE (Almost) as secure as classical. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 67–95. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_3
Bitansky, N., Shmueli, O.: Post-quantum zero knowledge in constant rounds. In: Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, pp. 269–279 (2020)
Canetti, R., Dakdouk, R.R.: Obfuscating point functions with multibit output. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 489–508. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_28
Christiano, P.: Quantum obfuscation of classical circuits. Seminar talk in the Quantum Games and Protocols program, Simons Insitute for the Theory of Computing (2014). Online: https://simons.berkeley.edu/talks/paul-christiano-2014-02-25
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_19
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC), pp. 169–178. ACM (2009). https://doi.org/10.1145/1536414.1536440
Goldwasser, S., Kalai, Y.T.: On the impossibility of obfuscation with auxiliary input. In: Proceedings of the 46th Annual Symposium on Foundations of Computer Science (FOCS), pp. 553–562. IEEE (2005). https://doi.org/10.1109/SFCS.2005.60
Goyal, R., Koppula, V., Waters, B.: Lockable obfuscation. In: Proceedings of the 58th Annual Symposium on Foundations of Computer Science (FOCS), pp. 612–621. IEEE (2017). https://doi.org/10.1109/FOCS.2017.62
Mahadev, U.: Classical homomorphic encryption for quantum circuits. In: Proceedings of the 59th Annual Symposium on Foundations of Computer Science (FOCS), pp. 332–338. IEEE (2018). https://doi.org/10.1109/FOCS.2018.00039
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of ring-LWE for any ring and modulus. In: Proceedings of the 49th Annual ACM Symposium on Theory of Computing (STOC), pp. 461–473. ACM (2017). https://doi.org/10.1145/3055399.3055489
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing (STOC), pp. 84–93. ACM (2005). https://doi.org/10.1145/1060590.1060603
Wee, H.: On obfuscating point functions. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing (STOC), pp. 523–532. ACM (2005). https://doi.org/10.1145/1060590.1060669
Wichs, D., Zirdelis, G.: Obfuscating compute-and-compare programs under LWE. In: Proceedings of the 58th Annual Symposium on Foundations of Computer Science (FOCS), pp. 600–611. IEEE (2017). https://doi.org/10.1109/FOCS.2017.61
Yao, A.C.: How to generate and exchange secrets. In: Proceedings of the 27th Annual Symposium on Foundations of Computer Science (FOCS), pp. 162–167. IEEE (1986). https://doi.org/10.1109/SFCS.1986.25
Acknowledgements
We thank Andrea Coladangelo, Urmila Mahadev and Alexander Poremba for useful discussions, and Serge Fehr for pointing out an error in the proof of Lemma 2.9. GA acknowledges support from the NSF under grant CCF-1763736, from the U.S. Army Research Office under Grant Number W911NF-20-1-0015, and from the U.S. Department of Energy under Award Number DE-SC0020312. ZB is supported by the Binational Science Foundation (Grant No. 2016726), and by the European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482) and via Project PROMETHEUS (Grant 780701). YD is supported by the Dutch Research Council (NWO/OCW), as part of the Quantum Software Consortium programme (project number 024.003.037). CS is supported by a NWO VIDI grant (Project No. 639.022.519). Part of this work was done while the authors were attending https://simons.berkeley.edu/programs/quantum2020. The Quantum Wave in Computing at the Simons Institute for the Theory of Computing.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Lemma 2.9
Proof
The input-recovering circuit \(C_\mathsf {rec}\) will consist of running C coherently, copying out the output register, and reverting the coherent computation of C. Suppose the circuit C contains k measurement gates, \(\ell \) initializations of wires in the \(\left| 0\right\rangle \) state, and outputs of length n. Define \(C_\mathsf {rec}\) as:
-
1.
Run \(U_C\) on input
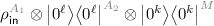 , where \(U_C\) is the unitary that coherently executes C, \(A = (A_1, A_2)\) is a register that contains the actual input and the auxiliary input \(\left| 0\right\rangle \) states for C, and M is the register that contains the auxiliary wires for the coherent measurements.
, where \(U_C\) is the unitary that coherently executes C, \(A = (A_1, A_2)\) is a register that contains the actual input and the auxiliary input \(\left| 0\right\rangle \) states for C, and M is the register that contains the auxiliary wires for the coherent measurements. -
2.
Copy the wires that are supposed to contain the output \(C(\rho _\mathsf {in})\) into a register Y, initialized to \(\left| 0^n\right\rangle \!\left\langle 0^n\right| \), using \(\mathsf {CNOT} \)s. The source of the \(\mathsf {CNOT} \)s is a register O, the subregister of A containing those output wires. Write \(\overline{O}\) for the registers in A that are not in O (these wires are normally discarded after the execution of C).
-
3.
Run \(U_C^{\dagger }\) to recover the original input, and discard the registers \(A_2\) and M.
The behavior of \(C_\mathsf {rec} \) can be summarized as

To see that \(C_\mathsf {rec}\) acts as promised, let \(\rho _{\mathsf {in}}\), x, and \(\varepsilon \) be s.t. \(\left\| \,C(\rho _{\mathsf {in}}) - \left| x\right\rangle \!\left\langle x\right| \,\right\| _{\mathrm {tr}} \le \varepsilon \). If \(\varepsilon \) is small, the \(\mathsf {CNOT}\) in Step 2 does not create a lot of entanglement, since the control wires are (close to) the computational-basis state \(\left| x\right\rangle \!\left\langle x\right| \). The output is therefore (almost) perfectly copied out.
More formally, note that \(C(\rho _{\mathsf {in}}) = {\mathop Tr }_{\overline{O}M}\left[ U_C(\rho _{\mathsf {in}} \otimes \left| 0^{\ell + k}\right\rangle \!\left\langle 0^{\ell + k}\right| )U_C^{\dagger }\right] \). By Lemma A.1 in [ABC+19], the closeness of \(C(\rho _{\mathsf {in}})\) and \(\left| x\right\rangle \!\left\langle x\right| \) implies that there exists a density matrix  such that
such that

Next, we use the fact that a quantum map cannot increase the trace distance between two states to derive two inequalities from Eq. 34.
For the first inequality, we append \(\left| x\right\rangle \!\left\langle x\right| \) on both sides (into a separate Y register):

For the second inequality, we instead append \(\left| 0\right\rangle \!\left\langle 0\right| \) into the Y register, followed by \(\mathsf {CNOT} \)s from O onto Y. Note that on the second term inside the trace norm, the effect is the same as before:

Thus, by the triangle inequality, the left-hand terms inside the trace norms in Eqs. 35 and 36 are \(2\sqrt{\varepsilon }\)-close. Applying the map \({\mathop Tr }_{A_2M}\left[ U_C^{\dagger } (\cdot ) U_C\right] \) to both terms, which again does not increase the trace difference, we arrive at the desired statement:
B Auxiliary Lemmas for Theorem 5.1
Lemma B.1
Let \(g : \{0,1\}^m \rightarrow \{0,1\}^n\) for \(m, n \in \mathbb {N}\), and let \(c \in \{0,1\}^n\). Let \(f : \{0,1\} \times \{0,1\}^m \rightarrow \{0,1\}^n\) be defined by
Then for every QPT A, there exists a simulator S such that for all f, g of the form described above, and all input states \(\rho \):
Proof
Recall that since A and S are quantum algorithms, they access their oracles in superposition: that is, A has access to the map defined by \(\left| x\right\rangle \left| z\right\rangle \mapsto \left| x\right\rangle \left| z \oplus f(x)\right\rangle \), and S has access to the map defined by \(\left| x\right\rangle \left| z\right\rangle \mapsto \left| x\right\rangle \left| z \oplus g(x)\right\rangle \). The simulator S runs A on input \(\rho \), and simulates any oracle calls to f (on inputs registers BX and output register Z) using two oracle calls to g. It only needs to prepare an auxiliary register in the state \(\left| 0^n\right\rangle \), and run the following circuit:

To see that this circuit exactly simulates a query to f on BXZ, consider an arbitrary query state
where R is some purifying register. The state on BXZR (plus the two auxiliary registers containing \(\left| 0^n\right\rangle \) and \(\left| c\right\rangle \)) after the above circuit is executed, is equal to
which is exactly the state that would result from a direct query to f.
Corollary B.2
Let \(\hat{\mathcal {C}}^{\mathsf {point}} _{\lambda }\) and q be as in Sect. 5. Then for any QPT \(\mathcal {S} _0\), there exists a QPT simulator \(\mathcal {S} _1\) such that for all \(\alpha ,r \in \{0,1\}^{\lambda }\),
A similar statement holds for circuits from \(\hat{\mathcal {C}}^{\mathsf {zero}} _{\lambda }\).
Proof
The statement is proven via an intermediate simulator \(\mathcal {S} _2\). This simulator is constructed by repeated application of Lemma B.1, so that for all \(\alpha ,r\),
is at most \(\mathsf {negl}\left( \lambda \right) \), where \(K = K(q,\lambda )\) as in Definition 3.1. On the right-hand side, the probability is additionally over a random choice of \(r'\) (resulting in the sequence \((c_0, c_1, c_2, \dots , c_K)\)).
Next, we apply the simulatability property of Definition 3.1. It states that there exists a simulator \(\mathcal {S} _3\) that, given a public key, can generate the distribution over \((c_0, c_1, c_2, \dots , c_K)\) itself. Define
and the corollary follows.
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Alagic, G., Brakerski, Z., Dulek, Y., Schaffner, C. (2021). Impossibility of Quantum Virtual Black-Box Obfuscation of Classical Circuits. In: Malkin, T., Peikert, C. (eds) Advances in Cryptology – CRYPTO 2021. CRYPTO 2021. Lecture Notes in Computer Science(), vol 12825. Springer, Cham. https://doi.org/10.1007/978-3-030-84242-0_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-84242-0_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84241-3
Online ISBN: 978-3-030-84242-0
eBook Packages: Computer ScienceComputer Science (R0)


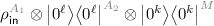 , where
, where 