Microbial Community Decision Making Models in Batch and Chemostat Cultures

Abstract

Microbial community simulations using genome scale metabolic networks (GSMs) are relevant for many application areas, such as the analysis of the human microbiome. Such simulations rely on assumptions about the culturing environment, affecting if the culture may reach a metabolically stationary state with constant microbial concentrations. They also require assumptions on decision making by the microbes: metabolic strategies can be in the interest of individual community members or of the whole community. However, the impact of such common assumptions on community simulation results has not been investigated systematically. Here, we investigate four combinations of assumptions, elucidate how they are applied in literature, provide novel mathematical formulations for their simulation, and show how the resulting predictions differ qualitatively. Crucially, our results stress that different assumption combinations give qualitatively different predictions on microbial coexistence by differential substrate utilization. This fundamental mechanism is critically under explored in the steady state GSM literature with its strong focus on coexistence states due to crossfeeding (division of labor).

1 Introduction

Microbial communities perform essential functions in diverse environments such as the soil [11] and the human gut [13]. While the experimental characterization of community composition is relatively easy with metagenomics methods, this is not true for the analysis of functional metabolic interactions between community members [10]. The paradigm of constraint based modelling of metabolism with genome scale models (GSMs) [4] has therefore become increasingly popular for the analysis of microbial communities [1, 3]. For example, a recent GSM-based study stipulated that whether a microbial community is cooperative or competitive correlates strongly with the nutrient abundance in its natural habitat [20].

Approaching community functions with GSMs requires two key ingredients: models and simulation methods. Models are no longer a main limitation because of the ease with which large, organism-specific and relatively predictive GSMs can be derived automatically from genome sequences [15]. However, the main simulation methods for GSMs such as flux balance analysis (FBA) [16] and stochastic sampling [14] were originally developed for single species, not communities.

In single-species FBA, a key assumption is that the simulated species optimizes its fitness (e.g., growth). This can be interpreted as a decision making problem where the organism needs to optimally control its (evolved) metabolic network. However, in co-culture, the degree to which one species reaches its objective may depend on the metabolic activity of all species, for example, when species compete for nutrients. Dynamic FBA (dFBA) explicitly accounts for nutrient concentrations and thereby for such interactions; it combines the FBA principle with iterations over time to reflect changing environmental conditions [28]. Recently, also scalable methods for dFBA simulation of communities have been proposed [23]. Yet, a drawback of dFBA is that it requires reliable knowledge on the form and parameters of uptake kinetics. These are hard to obtain and without them, the simulation results can be unreliable [3].

Incomplete information on uptake kinetics raises a new frontier in decision making for the simulation of interacting microbes in co-culture: the presence of multiple decision making entities with potentially conflicting objectives. For example, in d-OptCom, an influential method for dFBA of a community of GSMs, decisions are based on a community objective (high community biomass production) as well as individual objectives (high growth rate) [29]. In other methods, the emergence of multiple decision makers has stimulated the use of game theory for the analysis of microbial interactions [24].

To alleviate the dependence on uptake kinetics, community analyses with GSMs are often restricted to metabolically stationary states (that is, metabolic fluxes are constant over time) [7, 31]. The long term behavior, represented by the steady states, is the primary interest of most investigations. This makes investment of computational resources into predicting transient behavior less attractive. Furthermore, dynamics make the conceptualization of microbial decision making more complex (raising questions about when a consortium strives to achieve an objective).

However, as we will detail in Sect. 2, going from one to several microbial species, the interpretation of the metabolically stationary state assumption in constraint-based modeling suddenly depends on the type of cultivation environment. Moreover, it turns out that differences in the environment also have implications for models of decision making in FBA-type analyses. In particular, assumptions on environment and decision making have fundamental impact on whether organisms in a community of GSMs can coexist or not. These dependencies have not yet been investigated systematically.

Here, we formulate four methods for simulating metabolically stationary states, corresponding to combinations of two different environments, batch and chemostat cultivation, and two different modes of microbial decision making, distributed (rational agent) and centralized (rational community). In these formulations, we put a novel emphasis on what information (local/global) the decision makers have access to. The combination steady state batch/rational community resembles the SteadyCom formulation [8]; the chemostat formulations applicable to GSMs are new. We demonstrate the qualitative differences between the approaches on two toy-examples, a prisoners dilemma (PD) model for decision making and a nutrient limitation model for coexistence. As expected, switching from rational agent to rational community, PD switches from defection to cooperation. For nutrient limitation, the four models yield qualitatively different results. We argue that, which model to apply in a practical scenario should be considered carefully and has to reflect both the chemical environment and whether the community can be expected to have developed community strategies. We believe that the chemostat formulations are of particular value because important microbial environments such as the human gut resemble a chemostat [9].

Fig. 1.

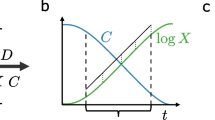
Cultivation systems and their implications for metabolically stationary state conditions. For definitions of mathematical variables, see Sect. 2.1. (A) Chemostat as an open system in steady state. Black: time-constant entities; bold arrows: flows; normal arrows: metabolic fluxes; rounded rectangle: cell. (B) Dynamics in batch cultivation of cells with a phase of metabolically stationary state (constant growth rate, implying linear increase of the logarithm of the species concentration, insensitive to external concentrations) between dashed vertical lines. (C) Metabolically stationary state in the closed batch system (time-constant entities in black).

2 Concepts

The two main environments for cultivating microbes are (assumed) chemostat and batch processes. For FBA-based analysis, they imply different concepts of metabolically stationary state, leading to different forms of microbial coexistence and of models for decision making.

2.1 Chemostat vs Batch Environment

In a chemostat as an open system, a fluid flow (dilution rate D) adds nutrients (inflow concentrations $C_{in}$) and flushes out parts of the cultivation medium, keeping the cultivation volume constant (see Fig. 1A). A metabolically stationary state requires that metabolic fluxes ($\nu$), species abundances (X), and environmental nutrient concentrations (C) are constant over time (t). For the (non-zero) absolute microbial species abundances to be constant, the growth rates ($\mu$) must be equal to the dilution rate D (henceforth called D-growth).

Assuming growth maximization, the growth rate depends on the environmental nutrient concentrations via uptake kinetic functions that determine the upper bounds of uptake fluxes. In turn, environmental nutrient concentrations depend on fluxes and species abundances. Assume that the kinetic functions increase monotonically with environmental nutrient concentrations. Then, starting from low species abundances and high environmental nutrient concentrations, growth rates higher than D (if existent) will increase species abundances and decrease environmental nutrient concentrations, thereby decreasing the growth rate, until the growth rate equals D and a (nutrient limited) metabolically stationary state is reached. As a consequence, to simulate the microbial abundances at which the nutrient limited steady state(s) occurs, we need an explicit representation of extracellular substrate concentrations. Different combinations of microbial and substrate concentrations may give rise to multiple valid steady states. Models that take the extracellular environment into account are frequent in the chemostat literature [18, 19]. However, the illustrative small scale models conventionally used in chemostat modelling do not possess intracellular metabolic networks with degrees of freedom in the fluxes, and are thus not concerned with decision making in the same way as FBA-models that use internal degrees of freedom to optimize some objective.

In a batch process as a closed system, all nutrients are provided at the beginning of the cultivation and nothing is flushed out (Fig. 1B, C). Here, a modeled metabolically stationary state refers to the condition that metabolic fluxes as well as growth rates are time-constant. This can hold, for example, during exponential growth. It has two important implications: First, relevant environmental nutrient concentrations are assumed to be in a regime where the kinetic functions determining the upper bounds of the growth limiting uptake fluxes are insensitive to the nutrient concentrations. This allows for community models without a representation of environmental nutrient concentrations. Second, the relative species concentrations must be constant, implying that all species with non-zero abundance grow at the same rate averaged over time (henceforth called balanced growth). This allows to properly model inter species crossfeeding of compounds. Some GSM-based studies of communities apply balanced growth [8, 17]. However, others do not [6, 7, 30], thus assuming a non-closed system. Throughout this manuscript, any system operating a metabolically stationary state under non-limiting extracellular nutrient conditions will be called a steady state batch. Though such a system may not have to be a batch cultivation, we will use the name batch throughout the manuscript, since batch cultivation is the model system addressed in this manuscript.

2.2 Implications for Coexistence

As demonstrated, in the context of GSMs, chemostat and batch imply distinct conditions on metabolically stationary states. These distinctions have crucial consequences for the possibility of co-existence of microbes. For non-interacting microbes in a batch, balanced growth will only occur if all concerned species have the exact same growth rate by chance, a situation that never happens in practice. Therefore, to simulate coexistence in a consortium, an explicit interaction between microbes, such as crossfeeding [8] or some form of agreement to grow at the same rate is mandatory. In contrast, for a chemostat operated with constant nutrient concentrations in the feed, competing species may coexist under D-growth, if they are limited by different nutrients [2]. Indeed, this enables models with coexistence states originating from both crossfeeding and differential nutrient limitations [22].

2.3 Implications for Decision Making

The assumptions on the environment—implying observability of nutrient concentrations or lack of observability—also have implications for models of decision making in FBA-type analyses. As mentioned for the GSM community simulation method d-OptCom [29], as well as for its metabolically stationary state sibling OptCom, [30], decision making is modeled as a bi-level optimization problem. On one level, the community strives towards a fitness goal (high community biomass production) and on the other level each microbial species optimizes its own fitness (growth rate). Abstractly, there are two types of decision makers, one making community decisions and one making decisions for individuals. The existence of an apparent community decision maker is hypothetical—it could result from species co-evolution [27, 31]. Generally, it has been shown that cooperative (generous) strategies are evolutionarily robust in repeated PD games in simulations [25].

Because community and individual decision makers may follow contradictory strategies, a principle for conflict resolution is needed. Some possibilities used for GSMs are: the community strategy takes precedence over individual decision makers [30], a community strategy must be Pareto optimal for the individual decision makers [6], and a community strategy must be a Nash equilibrium for the individual decision makers [7].

Table 1. Generic prisoners dilemma payoff matrix (numbers unrelated to Fig. 2). The first and second number in the round brackets denote the payoffs for player 1 and 2, respectively.

In particular, Cai et al. [7] makes the differences in conflict resolution mechanisms concrete by converting the so-called called Prisoners Dilemma (PD) [12] game theory example to a metabolic network setting. PD is a two player symmetric game with payoffs shown in Table 1. Mutual cooperation generates the largest overall benefit, but defection by one player yields a higher payoff for this player if the other player cooperates. Figure 2 shows a metabolic community version of PD, where species 1 and 2 both have the capacity to produce metabolites A and B and need both to grow, but where species 1 produces A and species 2 produces B at lower yield than the other. Thus, for the community, mutual cooperation (crossfeeding) will lead to the highest biomass yield, whereas for the individual species, the highest yield is obtained by not secreting anything, while still being fed by the other species. PD is a good testing ground for conflict resolution: it pits the community and individual decision makers against each other. As expected, the Nash equilibrium mechanism suggested in [7] results in no crossfeeding, whereas giving the community decision maker precedence [30] yields crossfeeding. Yeast cells feeding off sucrose may be a biological PD. The sucrose is hydrolyzed to glucose and fructose extracellularly by the enzyme invertase. It is expected that producing and secreting invertase comes at a metabolic cost. However, it may also give a growth benefit, if being an invertase producer means that more sugars will be hydrolyzed close to the producer. If the cost is relatively high and the benefit relatively low, cheating by producing no invertase becomes a desirable strategy [7].

Fig. 2.

A PD microbial consortium [7]. Rectangles are metabolites and diamonds are reactions. Red rectangles are extracellular metabolites. Numbers next to lines are stoichiometric coefficients. The subscripts c and e denote intra- and extracellular compounds, respectively. Species 1 and 2 (blue and brown symbols) can choose to crossfeed the compounds A and B to increase their yields by activating the reactions with the red dashed lines. (Color figure online)

3 Community Models

To cover the two principal dimensions environment (chemostat vs batch) and decision making model (rational agent vs rational community), we developed four models of microbial community growth at metabolically stationary state using metabolic networks. We first introduce the general system of equations and differential equations governing the metabolite and species concentrations that the models are based on. Then we impose assumptions about steady state conditions and decision making that lead to the models.

3.1 General Consortium Models

We are interested in the time development of the extracellular compound concentrations $C \ge 0\in \mathcal {R}^{n_C}$ (we denote dimensionalities of variable x by $n_x$) and the organism concentrations $X \ge 0 \in \mathcal {R}^{n_X}$ (see also Fig. 1). We consider a system with inflow rate $D_{in}$ and outflow rate $D_{out}$. The inflow has nutrient concentrations $C_{in}\in \mathcal {R}^{n_C}$. The vector of metabolic fluxes (reaction rates) of microbial species i is denoted $\nu _i \in \mathcal {R}^{n_{\nu _i}}$. One element of each flux vector $\nu _i$ is the biomass production (growth) rate $\nu _{\mu , i}$. The matrix $T_i \in \mathcal {R}^{n_C \times n_{\nu _i}}$ maps reactions to exchanges of extracellular compounds. Assuming that compounds and cells are flushed out at a rate proportional to their concentrations, the dynamics of C and X are described by:

$$\begin{aligned} \frac{dC}{dt} = D_{in}C_{in}-D_{out}C - \sum _{i} T_i \nu _i X_i\end{aligned}$$

(1)

$$\begin{aligned} \frac{dX_i}{dt} = X_i(\nu _{\mu , i} - D_{out}),\ \forall i \;. \end{aligned}$$

(2)

For steady state, left-hand sides of the system of ordinary differential equations (ODEs) Eqs. (1–2) are zero.

Common in both FBA and dFBA, as well as used here, is the assumption of intracellular (metabolically) stationary state [16, 21]. Modelling reactions between $n_S$ intracellular compounds at constant concentrations, intracellular stationary state introduces a stoichiometric matrix ${S_i\in \mathcal {R}^{n_S \times n_{\nu _i}}}$ for which holds that

$$\begin{aligned} S_i\nu _i=0,\ \forall i \;. \end{aligned}$$

(3)

Furthermore, for some matrix $A_i \in \mathcal {R}^{n_A \times n_{\nu _i}}$ and a vector $b_i \in \mathcal {R}^{n_A}$, the fluxes have capacity constraints

$$\begin{aligned} A_i\nu _i \le b_i,\ \forall i\ . \end{aligned}$$

(4)

The steady state models of interest here are chemostat and steady state batch. In a chemostat at steady state, $D_{in}=D_{out}=D$ and the steady state algebraic relations from Eqs. (1)–(4) apply directly.

In contrast, in steady state batch, the extracellular compound concentrations are assumed to have no influence on the fluxes. To avoid infinite uptakes, flux exchanges with the environment, modeled by changes in C in Eq. (1), are captured by a vector of culture uptake bounds, $u \in \mathcal {R}^{n_C}$. The species concentrations X are exchanged for the relative species concentrations x. The change to relative species concentrations allows them to stay constant over time under balanced growth. To represent balanced growth, a community growth rate $\nu _{\mu }^{\star }$ is introduced. In combination, the steady state batch system is then:

$$\begin{aligned} u - \sum _{i} T_i \nu _i \cdot x_i \ge 0\\ S_i\nu _i=0,\ \forall i \\ A_i\nu _i \le b_i,\ \forall i\\ x_i (\nu _{\mu }^{\star }-\nu _{\mu , i}) = 0, \forall i\\ \sum _{i} x_i = 1\ . \end{aligned}$$

We use these formulations of chemostat and batch in metabolically stationary state to introduce four models. For ease of comparison, all model equations, plus extra information such as Karush Kuhn Tucker (KKT) [26] conditions used for solving the models, can be seen side-by-side in Table A.1.

3.2 Rational Agents

We assume that each cell is a decision making entity, using the extracellular concentrations as information to maximize its growth rate. As foundation for its decision making, each cell uses local information, in this case the extracellular compound concentrations, as well as its own flux constraints Eqs. (3–4). This assumption seems intuitive for microbial species that do not share an evolutionary history of interactions.

Assuming a chemostat environment and denoting variables resulting from an optimization problem with hat notation $\hat{\nu _i}$, the rational agent (CA, where ‘C’ stands for chemostat and ‘A’ for agent) model becomes:

$$\begin{aligned} \begin{aligned} D(C_{in}-C) - \sum _{i} T_i \hat{\nu }_i(C) X_i = 0\\ X_i(D -\hat{\nu }_{\mu , i}(C)) = 0,\ \forall i\\ C, X \ge 0\\ \hat{\nu }_i(C) = \mathop {\mathrm {argmax}}\limits _{\nu _i\in \mathcal {R}^{n_{\nu _i}}} \nu _{\mu , i}, \forall i\\ s.t.\ S_i \nu _i=0,\ \forall i\\ A_i \nu _i \le b_i(C),\ \forall i \;. \end{aligned} \end{aligned}$$

(5)

Importantly, here the right hand side of the capacity constraints b(C) depends on the extracellular concentrations C through uptake kinetics. Without implementing a concentration dependency, the optimization problem is independent of the substrate and organism concentrations. This means that the modeled cells do not adapt their growth to changes in extracellular nutrient concentrations. In most cases, this will imply that no solution will fulfill the D-growth requirement and only the trivial solution $X=0$ will be feasible.

Correspondingly, the steady state batch rational agent (BA) system is:

$$\begin{aligned} \begin{aligned} u - \sum _{i} T_i\hat{\nu }_i \cdot x_i \ge 0 \\ x_i (\nu _{\mu }^{\star }-\hat{\nu }_{\mu , i}) = 0, \forall i \\ \sum _{i} x_i = 1\\ x \ge 0\\ \hat{\nu }_i = \mathop {\mathrm {argmax}}\limits _{\nu _i\in \mathcal {R}^{n_{\nu _i}}} \nu _{\mu , i}, \forall i\\ s.t.\ S_i \nu _i=0,\ \forall i\\ A_i \nu _i \le b_i,\ \forall i \;. \end{aligned} \end{aligned}$$

(6)

Contrary to practice in the GSM consortium literature [3], the rational agent assumption does not include the global equations (first lines) in the optimization problem. Furthermore, since the extracellular substrate concentrations are assumed to be constant, the optimization problem is independent of the first two lines of Eq. (6). Combined with the balanced growth assumption, this means that coexistence is only possible for organisms that independently developed the exact same growth rate, a situation that will never occur in practice. The steady state batch rational agent model is therefore of little practical relevance and we included it only for completeness.

3.3 Rational Community

The rational community model assumes that, through a time of coexistence, a community has learnt to optimize its (D- or balanced-) growth rate while cooperating to create a favourable nutrient environment.

To model a chemostat environment and a rational community (CC), note that what the community wants to achieve through cooperation, and with it the formal community objective function, may vary. A biologically relevant community objective, so far not formulated as FBA objective, is resistance to invasion by pathogenic species [5]. Here, for simplicity and in line with the literature [3], we consider only the community objective of maximizing total biomass production. Using a concatenated flux variable $\nu = [\nu _1,,,\nu _{n_X}] \in \mathcal {R}^{n_{\nu }}$, the CC model reads:

$$\begin{aligned} \begin{aligned} X_i(D -\hat{\nu }_{\mu , i}(X)) = 0, \forall i\\ X \ge 0\\ \hat{\nu }(X) = \mathop {\mathrm {argmax}}\limits _{\nu \in \mathcal {R}^{n_{\nu }}, C\in \mathcal {R}^{n_C}} \sum _{i} \nu _{\mu , i}X_i\\ s.t.\ D(C_{in}-C) - \sum _{i} T_i \nu _i X_i = 0\\ S_i \nu _i=0,\ \forall i\\ A_i \nu _i \le b_i(C),\ \forall i\\ C\ge 0 \;. \end{aligned} \end{aligned}$$

(7)

Contrary to the rational agent models, Eq. (1) is now inside the optimization problem, and therefore, so are also all instances of the global variables C. This encodes our assumption that the community has knowledge of and power over the global cellular exchanges of compounds.

An important detail of the CC model is that the abundances X do not enter the optimization problem as optimization variables. Since different community decisions may benefit different organisms (in terms of species abundances and other factors), having a range of community optimal strategies in terms of fluxes and extracellular concentrations, but given different species abundances, it is not possible to know which strategy the community will settle for without detailed knowledge of the “negotiation” process leading up to a decision. Thus, the step from rational agent to rational community is not about assuming full knowledge of how the community decides, but that actively influencing C is taken into account in its decision, while optimizing some assumed objective.

In the steady state batch rational community (BC) case, having no explicit representation of C, the community decision maker cannot take C into account in the optimization problem. Thus, the difference to the rational agent steady state batch model is that the community takes the macroscopic equation $u + \sum _{i} T_i\nu _i \cdot x_i \ge 0$ into account in the decision making process, leading to the system:

$$\begin{aligned} \begin{aligned} x_i (\nu _{\mu }^{\star }-\hat{\nu }_{\mu , i}(x)) = 0, \forall i\\ \sum _{i} x_i = 1\\ x \ge 0\\ \hat{\nu }(x) = \mathop {\mathrm {argmax}}\limits _{\nu \in \mathcal {R}^{n_{\nu }}} \sum _{i} \nu _{\mu , i}x_i\\ s.t.\ u - \sum _{i} T_i\nu _i \cdot x_i \ge 0 \\ S_i \nu _i=0,\ \forall i\\ A_i \nu _i \le b_i,\ \forall i \;. \end{aligned} \end{aligned}$$

(8)

4 Applications

We tested the CA, CC and BC models on two toy examples: PD (Fig. 2) for exploring decision making and a competition scenario for exploring coexistence. For named reactions and compounds in Figs. 2 and 3, such as $t_{S,1}$ and $S_e$, the corresponding fluxes and concentrations will be referred to as $\nu _{t_{S}, 1}$ and $C_{S_e}$. All examples were solved symbolically in Mathematica 9 using the KKT formulations in Table A.1. Notice that the optimization problems in Eqs. (5)–(8) are all linear in the optimization arguments, implying that KKT provides sufficient conditions for global optimality [26]. By solving the respective systems symbolically, we are confident that all solutions are found.

4.1 Prisoners Dilemma

For PD (Fig. 2), we are interested in whether, using a specific simulation model, the community achieves a fitness bonus by utilizing crossfeeding (using reactions with dashed red arrows in Fig. 2) or whether the organisms refuse to cooperate. For CA and CC simulations, we set the inflow nutrient concentration mixture to $C_{in, A_e}=0$, $C_{in, B_e}=0$ and $C_{in, S_e}=10$. The flow rate was set to $D=0.5$. Similarly for BC, we used the culture uptake bounds $u_{A_e}=0$, $u_{B_e}=0$ and $u_{S_e}=10$.

Table 2. Flux values of PD simulations for CA, CC and BC. The variable names correspond to the reactions in Fig. 2. In the last column, CC was run with a higher flow rate, $D=1.2$.

Quantitative simulation results are shown in Table 2. As expected, without a joint objective for the organisms, CA finds no crossfeeding. CC and BC find crossfeeding solutions, but these solutions differ. In CC, the secretion fluxes are greater than the uptake fluxes because some of the secreted material will be flushed out of the chemostat, rather than taken up by another organism. This generally makes crossfeeding in chemostats less attractive. For example when increasing the flow rate D from 0.5 to 1.2, the benefit of crossfeeding vanishes and CC switches to a solution without crossfeeding. In BC, void of an active out flush mechanism, all secreted material is taken up. Apart from the symmetric (non-zero) solutions, non-symmetric solutions where one species has zero abundance occur. These solutions, with only one participating species and thereby no potential for cooperation, are not considered here.

4.2 Coexistence Microbial Consortium

In a chemostat with two supplied nutrients $A_e$ and $B_e$, coexistence of two distinct species may emerge if, depending on the supply concentrations, the species reach a state in which they are limited by different nutrients [2, 19]. This (potentially competitive) coexistence does not rely on direct interactions such as crossfeeding. For the CA, CC and BC models, we investigated under what circumstances coexistence emerges for the non-crossfeeding metabolic network models in Fig. 3. There, species 1 needs more of compound $A_c$ to grow and species 2 needs more of compound $B_c$ to grow.

Fig. 3.

A coexistence microbial consortium. Rectangles are metabolites and diamonds are reactions. Red rectangles are extracellular metabolites. The subscripts c and e denotes intra- and extracellular compounds, respectively. Numbers next to lines are stoichiometric coefficients. (Color figure online)

Fig. 4.

Coexistence results for the network in Fig. 3 for varying environmental conditions using CA, CC and BC. Abbreviations: ZS - zero solution shows the value of a variable for one species; for the other species, all variables are zero. CS - coexistence solution shows the value of a variable for one species, while for the other species, the value of the same variable is given by the other CS curve. (A) Species concentrations X for changing supply mixtures $C_{in}$ in CA or CC; they yield identical solutions. (B) Relative species concentrations x for changing input flux mixtures u for BC. ZS curves for the two species coincide. (C) Selected fluxes of species 1 for changing input flux mixtures u for BC. (D) Same information as in (A), but only using CC and with an alternative objective function. (E) Same information as in (B), but with an alternative objective function.

For CA and CC, we varied the nutrient composition of the inflow, ($C_{in, A_e} / C_{in, B_e}$), linearly from (0/10) to (10/0). We set the flow rate $D=1$ and the uptake flux limitations $\nu _{t_{A},i} \le 2\cdot C_{A_e}$ and $\nu _{t_{B},i} \le 2\cdot C_{B_e}$ (symbols defined in Fig. 3). Lacking a potential to crossfeed, CA and CC generated identical results. Figure 4A shows identical, horizontally mirrored, zero solutions (ZS), that is, solutions where only one species exists. The ZS of species 1 starts flat at zero, which is a regime where the concentration of $C_{A_e}$ is so low that species 1 cannot grow at the flow rate $(D=1)$; it is flushed out of the chemostat. After the zero regime comes a regime in which the growth rate of species 1 is limited by $C_{A_e}$ and the concentration of species 1 increases linearly with $C_{in, A_e}$. This continues with increasing $C_{in, A_e}$ and decreasing $C_{in, B_e}$, until $C_{B_e}$ becomes growth limiting, and the species concentration goes down linearly. A coexistence solution (CS) exists in one central regime, throughout which species 1 is limited by $C_{A_e}$ and species 2 is limited by $C_{B_e}$. At the concentration mixture where the dark blue curve (CS) goes to zero and ends, the light blue curve (CS) touches the light green curve (ZS). At this point, where the lower CS goes to zero, the upper CS becomes a ZS.

For BC, we varied the culture uptake bounds $u_{A_e}$ and $u_{B_e}$ linearly from (0/1) to (1/0). The uptake bounds were $\nu _{t_{A},i} \le 2$ and $\nu _{t_{B},i} \le 2$. The main distinction from the chemostat scenario is that in BC, the ZSs are identically one (Fig. 4B), due to the relative species concentrations.

Despite the apparent similarity between CA and BC, the interpretation of the coexistence solutions (CSs) differs. For CA, a CS emerges without interspecies communication, simply because, at the species level, the growth rates of species 1 and 2 are limited by the uptake rates of $A_e$ and $B_e$, respectively. This is a known result from chemostat modelling [18]. Thus, at their steady state concentrations, the species reach a self stabilizing equilibrium, where neither species can grow faster than $D=1$.

In contrast, the growth rates of the species in the CS in BC (Fig. 4B) are not restricted by individual species uptake fluxes. Figure 4C shows for species 1 (a horizontal mirror image of species 2) that the uptake flux $\nu _{t_{A}, 1}$ always remains below its upper bound of 2. Instead, the growth rates are restricted by the global nutrient restrictions $u - \sum _{i} T_i\nu _i \cdot x_i \ge 0$. With regard to the global nutrient restrictions, the balanced growth solutions, where the species grow at the same rate are not the only solutions. As shown in Fig. 4C, in the CS, species 1 voluntarily grows at a rate that is lower than its maximal growth rate (CS max $\nu _{\mu , 1}$ exceeds the take-all solution ZS $\nu _{\mu , 1}$ since it is operating at a lower relative species concentration). If the species did not communicate that growing at the same rate maximizes community biomass production, single species would claim more resources for themselves and break the metabolically stationary state. Thus, the CS solution we see is a result of the objective function.

To elucidate the dependence of the CSs of CC and BC on the community objective function, we changed the objective of CC and BC to maximizing the sum of growth rates, $\sum _{i} \nu _{\mu , i}\delta (X_i>0)$, rather than total community biomass production, $\sum _{i} \nu _{\mu , i}X_i$ ($X_i$ is replaced by $x_i$ in BC). Figure 4D-E shows that the changed objective function results in CSs that differ from the ones in Fig. 4A-B.

5 Discussion

Our study draws heavily on the long tradition of chemostat community models [19]. We followed in the same spirit: to keep models small and to use them to demonstrate general system properties, rather than detailed properties of cells with specific genomes. On the contrary, GSMs facilitate a detailed, species-specific analysis of intracellular fluxes and related properties. We consider the work presented here as an early-stage attempt to combine the two worlds.

To incorporate FBA models in the chemostat community model frame work, due to the internal degrees of freedom of FBA models, the fundamentally game theoretic problem of multiple decision makers has to be taken into account [24]. Here, and in line we previous proposals for community modeling, we therefore explored two flavors: rational agent and rational community. For our rational community models, we allowed the community to optimize both its shared metabolism and the environmental nutrient concentrations to achieve a community objective. However, we did not explicitly optimize the species concentration variables. This acknowledges that, if different species concentrations favor different species, and thereby yield multiple optima in terms of fluxes and nutrient concentrations, we do not know which optimum the community would choose.

One would expect that the decision a community takes depends on the overarching frame work (here: rational agent and rational community) and on the particular objective imposed. For example, by maximizing biomass production of the community, crossfeeding emerges in the PD scenario. However, our community models demonstrates that also environmental variables play a role. For example, by increasing the flow rate in the chemostat, the benefit of crossfeeding decreased, so that CC switched from crossfeeding to no crossfeeding. This phenomenon might be relevant for the gut microbiome, where the significance of other aspects of flow has been investigated [9].

More specifically, we believe that the qualitative results of PD are relatively robust to changes in the community objective, such as switching to a sum of growth rates objective. Contrarily, for the coexistence example, we saw that changing the community objective function gave a new set of coexistence states.

Our models also suggest that coexistence in batch (BC) relies on a different mechanism than in chemostat (CA and CC). In BC, the community steady state is not a consequence of nutrient limitations caused by community growth. Coexistence requires agreement to coexist in the community, without any external enforcement mechanism, contrary to the chemostat models. Agreement without enforcement may amount to forced altruism, a modelling artifact discussed in detail in the context of PD by Chan et al. [8]. The emergence of forced altruism in terms of coexistence at balanced growth, rather than in terms of crossfeeding, is to our knowledge a new perspective that may be relevant for future community simulation methods.

A limitation of the present work is that we considered only toy metabolic networks. This choice was intentional to provide general insights. It also allows us to solve the problems symbolically, which certified that all roots to the equations were found. However, this approach is of course not scalable. Before any real applications can be considered, an efficient numerical solution scheme needs to be developed. As alternative to solving the KKT equations, one could directly run corresponding dFBA simulations until stationarity. However, also this approach would need to be complemented with a mechanism for finding multiple solutions.

Lastly, in the chemostat literature [19], stability of stationary solutions of ODEs is a central topic, which we did not address. If we assume that the microbial species can make decisions and actively uphold a state or an equilibrium, exactly what stability means in this scenario may need additional theoretical attention. Such concepts may be important to evaluate resistance of microbial communities to invasion by pathogens.

Appendix

Table A.1. Models, Lagrangians and KKT formulations. For BA and CA, Lagrangian multipliers (inequality, $\lambda _1$, and equality, $\lambda _2$, multipliers) are introduced on a per species level (subscript i), whereas for BC and CC, global multipliers are introduced. Dimensionalities of multipliers vary between formulations. Rows #var and #EQ confirm that the numbers of unknowns and equations are equal.