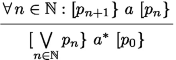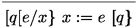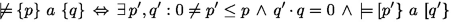Abstract
Variants of Kleene algebra have been used to provide foundations of reasoning about programs, for instance by representing Hoare Logic (HL) in algebra. That work has generally emphasised program correctness, i.e., proving the absence of bugs. Recently, Incorrectness Logic (IL) has been advanced as a formalism for the dual problem: proving the presence of bugs. IL is intended to underpin the use of logic in program testing and static bug finding. Here, we use a Kleene algebra with diamond operators and countable joins of tests, which embeds IL, and which also is complete for reasoning about the image of the embedding. Next to embedding IL, the algebra is able to embed HL, and allows making connections between IL and HL specifications. In this sense, it unifies correctness and incorrectness reasoning in one formalism.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Context
My basic mistake was to set up proof in opposition to testing, where in fact both of them are valuable and mutually supportive ways of accumulating evidence of the correctness and serviceability of programs. T. Hoare [17]
Beginning with fundamental work of Kozen and others, variants of Kleene algebra have been used as foundations for program logics. Typically, a translation is given from a logic, such as Hoare Logic (HL, [16]), into the algebra [22]. This approach has been extended to other program logics such as modal [11] and concurrency logics [18]. Work has generally emphasised correctness, i.e., proving the absence of bugs. While that is a worthy ideal, significant programs are often not wholly free of bugs and may never be as they continue evolving. So much attention and energy is spent in engineering practice on testing and other methods of finding specific bugs, rather than proving that none can ever occur.
Despite the practical importance of bug finding, theoretical research on reasoning about programs has concentrated to a much greater extent on correctness. Testing and verification are sometimes even seen in opposition to one another. The third author described his regret for this in the quotation above, from a retrospective in 2009, 40 years after the appearance of Hoare’s Logic. In recent years he and the second author have turned attention to theories of testing and static analysis as ways of showing program incorrectness, and the second author introduced Incorrectness Logic (IL) as a dual formalism to HL, oriented to proving the presence of bugs rather than their absence [25]. It was shown in [25] that IL can be used to represent a variety of bug finding approaches, ranging from traditional testing, to symbolic execution [8], to compositional analyses which use logic to summarise the effect of a program component [14].
The present paper deals with representing IL in Kleene algebra. We don’t repeat the motivations for IL or the examples illustrating it, and instead refer the reader to the developments in [25, 26]. Our interest here is to extend Kleene algebra’s successful treatment of program correctness to encompass incorrectness as well. The first aim is to pinpoint the algebraic properties needed to represent IL; secondly we want to represent both IL and HL in the same algebra. This second aim replaces the opposition described in the quotation at the beginning with theoretical unification. We are building on work on the unifying role of Kleene algebra in connecting denotational and operational semantics and program logics for correctness (e.g., [18, 19]); we are adding incorrectness to the picture here. Note that both HL and IL deal with partial correctness, not with termination. Other limitations of our results are mentioned at the end of the paper.
1.2 Technical Approach
IL uses an under-approximate triple [25, 27], dual to Hoare’s triple:

Here, \(\mathsf {sp}(c,p)\) is the strongest postcondition: in a binary relation model, c is a relation, p a set of states, and \(\mathsf {sp}(c,p)\) the image of the restriction of c to p. In the sequel we abbreviate pre/postcondition by just pre/post. The Hoare triple \(\{ p \}\ c\ \{ q \}\) stipulates that the post q be a superset, an over-approximation, of the states reachable via c from p, while the under-approximate triple  requires that q be a subset, an under-approximation.
requires that q be a subset, an under-approximation.
The terminology over/under-approximation comes from automatic program analysis. The method of Floyd [13] associates an assertion describing a superset of the reachable states with each program point, and this corresponds to Hoare triples (or more generally to abstract interpretations [10]). Over-approximation may lead to false positives (bug claims that are not true) in program analysis, but not false negatives (missed bugs). Dually, an analysis computing an under-approximation at each program point avoids false positives but may suffer from false negatives. Under-approximate analysis is performed by testing and symbolic bug-finding tools. In such an analysis there would be an under-approximate triple relating the program start state with any given program point.
It is well known that \(\mathsf {sp}(c,p)\) can be seen as a backwards diamond modality in the sense of dynamic logic. So, it is natural to employ a Modal Kleene Algebra [12] to represent the under-approximate triple algebraically. This has the pleasant consequence that the Hoare triple, which is usually defined in Kleene algebra without recourse to \(\mathsf {sp}(c,p)\), enjoys a description that can be connected at once to its under-approximate cousin in a way that formalises aspects of testing and verification as mutually supportive ways of obtaining evidence (see Theorem 4.1 and Theorem 4.5). In addition to connecting over- and under-approximate triples, we also study a version of IL as in [25] in which assertions are embedded as statements within programs in such a way that their violation signals an error.
We start from one of Kozen’s variants of Kleene algebra [21], an idempotent semiring (equivalently, an ordered monoid with all finite joins, cf. Definition 2.1) with an additional operator \(^*\) satisfying two unfolding and two induction axioms. Modal Kleene Algebra enriches that with diamond operators [12]. This indeed gives us a way to interpret all IL proof rules except an infinitary proof principle which is used to obtain a completeness theorem for under-approximate reasoning:

To model this rule we need countable joins of tests, where a test is a complemented algebra element below the unit of sequential composition. We show that Kleene Algebra with diamonds and countable joins of tests is sound and (relatively) complete for under-approximate triples. A version of this infinitary principle is actually sound in Hoare logic but usually not stated because loop invariants provide a complete reasoning technique for over-approximation. Loop invariants are not complete for under-approximation.
Our technical development begins in Sect. 2 with the algebraic framework, viz. Modal Kleene algebra with countable suprema of tests (CTC algebras). In Sect. 3 we prove soundness and completeness of a proof system for under-approximate triples over CTC algebras. Section 4 connects under-approximation to incorrectness by showing how under-approximate triples can be used to disprove Hoare triples, as well as treating a language with embedded assertions with \({ error}\) and \({ ok}\) information. In Sect. 5 we use the algebra to present another variant of incorrectness reasoning based on backwards rather than forwards under-approximation. Section 6 concludes.
2 Modal Kleene Algebra
Throughout the paper we refer to a particular example, the “relation model”, which is an algebra where the carrier \(A = P(S\times S)\) is the set of binary relations on a set S. \(a\mathbin {\cdot }b\) denotes the composition in diagrammatic order (sequential composition) of relations, \(+\) denotes their union, 1 is the identity relation, 0 the empty relation, and \(a^*\) is the reflexive-transitive closure of a. If \(p \subseteq S\) then \(\mathsf {sp}(a,p)\) is the image \(\{s' \mid \exists s\in p : (s,s') \in a\}\). The relation model is a Boolean quantale (details below) where \(a^*\) is a certain least fixed-point. Some Boolean quantales, like the algebras of relations and of sets of graph paths, satisfy the algebraic properties we need to interpret IL, thus giving us a wide range of models, but we seek to identify lesser structure that supports interpretation.
2.1 Idempotent Semirings, Tests and Diamonds
Definition 2.1
-
1.
An idempotent semiring, briefly I-semiring, is a structure \((A,+,\mathbin {\cdot },0,1)\) such that \((A,+,0)\) is a commutative monoid with idempotent addition, \((A,\mathbin {\cdot },1)\) is a monoid, multiplication distributes from both sides over addition and 0 is an annihilator for multiplication, that is, \(0 \mathbin {\cdot }a = 0 = a \mathbin {\cdot }0\) for all \(a\in A\).
-
2.
Every I-semiring can be partially ordered by setting
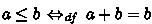 . Then \(+\) and \(\mathbin {\cdot }\) are isotone w.r.t. \(\le \) and 0 is the least element. This makes A an upper semilattice with join operator \(+\) and least element 0. If existing, the least upper bound (lub) of a subset \(B \subseteq A\) is denoted by
. Then \(+\) and \(\mathbin {\cdot }\) are isotone w.r.t. \(\le \) and 0 is the least element. This makes A an upper semilattice with join operator \(+\) and least element 0. If existing, the least upper bound (lub) of a subset \(B \subseteq A\) is denoted by 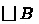 . With this,
. With this, 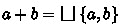 . For uniformity we write \(\mathrel {\mathop {\bigsqcup }\limits _{i < k}} a_i\) instead of
. For uniformity we write \(\mathrel {\mathop {\bigsqcup }\limits _{i < k}} a_i\) instead of 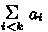 .
.
Definition 2.2
A test in an I-semiring is an element p that has a complement \(\lnot p\) relative to the multiplicative unit 1, namely \(p + \lnot p = 1\) and \(p \mathbin {\cdot }\lnot p = 0 = \lnot p \mathbin {\cdot }p\). The set of all tests in A is denoted by \(\textsf {test}(A)\). A is called countably test-complete (CTC) if every countable subset of \(\textsf {test}(A)\) has a lub. (This is equivalent to stipulating that every countable chain of tests has a lub.)
The complement \(\lnot p\) is unique when it exists. The composition \(p \mathbin {\cdot }q\) of tests represents logical conjunction and is the meet of p and q. Symmetrically, \(p+q\) represents disjunction and is the join. Finally, \(p \le q\) represents implication.
Using tests we can axiomatise the modal operators diamond and box. For IL we only need the backward diamond. For \(a \in A\) and \(p \in \textsf {test}(A)\) the test  characterises the set of states that can be reached from p in a single a-step, i.e., the image of p under a. We use the following axiomatization of diamond.
characterises the set of states that can be reached from p in a single a-step, i.e., the image of p under a. We use the following axiomatization of diamond.
Definition 2.3
A backward diamond semiring is a structure  such that \((A,+,\mathbin {\cdot },0,1)\) is an I-semiring and
such that \((A,+,\mathbin {\cdot },0,1)\) is an I-semiring and  is an operator satisfying the axioms
is an operator satisfying the axioms

The backward box is the De Morgan dual of the diamond:  .
.
(bdia1) implies that diamond is additive in both arguments, while (bdia2) stipulates that it is multiplicative in its first argument and hence preserves composition. In the relation model the diamond  corresponds to \(\mathsf {sp}(a,p)\).
corresponds to \(\mathsf {sp}(a,p)\).
Our presentation uses a direct axiomatisation of backward modalities. An alternative is to axiomatise a codomain operator  and then define
and then define  . Conversely, one can define codomain in terms of diamond as
. Conversely, one can define codomain in terms of diamond as  . Adopting a definition based on Kleene Algebra with (Co)Domain [12] or based on diamonds is just a presentational choice.
. Adopting a definition based on Kleene Algebra with (Co)Domain [12] or based on diamonds is just a presentational choice.
Definition 2.4
A modal semiring is a structure  such that
such that  is a backward diamond semiring and the forward diamond operator
is a backward diamond semiring and the forward diamond operator  satisfies the (dual) axiom
satisfies the (dual) axiom

The test  algebraically represents the inverse image of q under a. It has been shown in [12] (Cor. 5.8) that (bdia1), (bdia2) and (fdia1) imply multiplicativity of forward diamond, i.e.,
algebraically represents the inverse image of q under a. It has been shown in [12] (Cor. 5.8) that (bdia1), (bdia2) and (fdia1) imply multiplicativity of forward diamond, i.e.,  . The forward box is
. The forward box is  ; it corresponds to the weakest liberal precondition \(\mathsf {wlp}(a,q)\).
; it corresponds to the weakest liberal precondition \(\mathsf {wlp}(a,q)\).
The following property is fundamental for our completeness results; see [23] for more details. Moreover, forward diamonds have good other use later.
Lemma 2.5
Assume a modal semiring.
-
1.
We have Galois connections
 and
and  .
. -
2.
As lower adjoints of Galois connections the diamonds preserve all existing lubs in their second argument.
We discuss some related axiomatisations. The purely relational monotype factor of [3] coincides with the forward box and \(\mathsf {wlp}\). The dynamic negation of [20] in dynamic relation algebras (reducts of relation algebras) coincides with the complement of domain. In Boolean quantales, the domain operator was defined via a Galois connection in [5]. Since here we strive for a maximally general algebraic basis, we have decided for an axiomatisation equivalent to that in [11, 12].
2.2 Iteration and Kleene Algebra
Next we represent arbitrary finite iteration by an additional operator  .
.
Definition 2.6
An I-semiring with star is called a Kleene algebra if \(^*\) satisfies

The following property (by an easy induction on n) is essential for a number of rules of IL.
Lemma 2.7
In an I-semiring with star and one of the star unfold axioms, the element \(a^*\) is an upper bound of the sets  and
and  , where
, where  .
.
Lemma 2.8
[12]. In a Kleene algebra with backward diamond one has, without any further assumptions, the rules

Dual rules hold for the forward diamond.
Definition 2.9
A quantale (e.g. [28]) is an I-semiring in which the order \(\le \) induces a complete lattice and \(\mathbin {\cdot }\) preserves arbitrary lubs in both arguments. It is Boolean if its complete lattice is a Boolean algebra.
Lemma 2.10
[12]. Any Boolean quantale is a CTC Kleene Algebra (cf. Definition 2.2) and admits pre-diamonds satisfying (bdia1) and (fdia1).
3 Under-Approximation and Over-Approximation
It is standard that one can encode
 programs into Kleene algebra. Given test p and algebra elements a, b, we can represent
programs into Kleene algebra. Given test p and algebra elements a, b, we can represent  as \((p \cdot a)^* \cdot \lnot p\),
as \((p \cdot a)^* \cdot \lnot p\),  as \(p \cdot a +\;\lnot p \cdot b\), a; b as \(a \cdot b\) and the identity \({ skip}\) as 1. 0 is equivalent to
as \(p \cdot a +\;\lnot p \cdot b\), a; b as \(a \cdot b\) and the identity \({ skip}\) as 1. 0 is equivalent to  . Throughout this section, by a program we mean a Kleene algebra element generated from 0, 1 and a set of atomic commands and arbitrary tests using \(+\), \(\cdot \) and \(^*\). (In the next section we will need to distinguish programs from algebra when working with expressions that map less directly to algebra.)
. Throughout this section, by a program we mean a Kleene algebra element generated from 0, 1 and a set of atomic commands and arbitrary tests using \(+\), \(\cdot \) and \(^*\). (In the next section we will need to distinguish programs from algebra when working with expressions that map less directly to algebra.)
3.1 Under-Approximate Triples
Definition 3.1
We assume a CTC Kleene algebra A with backward diamond.
-
1.
An under-approximate (or IL) triple is a formula
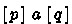 , where \(p,q \in \textsf {test}(A)\) and \(a\in A\) is a program.
, where \(p,q \in \textsf {test}(A)\) and \(a\in A\) is a program. -
2.
 is valid in A, in signs \(\models \,[[\, p\, ]]\ a\ [[\, q\, ]]\), iff
is valid in A, in signs \(\models \,[[\, p\, ]]\ a\ [[\, q\, ]]\), iff  .
. -
3.
\([[\, p\, ]]\ a\ [[\, q\, ]]\) is provable iff it can be derived using the rules in Fig. 1.
As in [22] we are dealing with a “propositional” program logic: rules involving variables are left out. Some of these, such as an axiom for assignment statements

could be covered (in a particular model) by the axiom for atoms in Fig. 1, which requires that the strongest post be present for each atomic command. Others, such as the frame rule for variable mutation and substitution rules, would require additional inference rules.
An example triple is \([[\, x=0\, ]]\ (x:=x+1)^*\ [[\, x\ge 0\, ]]\), saying that execution of the loop can result in x taking on any non-negative integer. This property can be proven using (Iteration) with \(p_n = (n \ge 0 \wedge x=n)\). The triple \([[\, x=n\, ]]\ x:=x+1\ [[\, x=n+1\, ]]\) used in the premise of the rule shows n decreasing in the backwards direction (hence the name Backwards Variant for this rule in [25]). The post can be written as an infinite disjunction, or finitely using a quantifier:  . This is where the CTC assumption has its place; without it such countable disjunctions are not well defined. The assertion \(x\ge 0\) is the strongest post, and this pre/post pair actually gives us a valid Hoare triple as well. But we can shrink the post using (Consequence) to go below the strongest post, to obtain
. This is where the CTC assumption has its place; without it such countable disjunctions are not well defined. The assertion \(x\ge 0\) is the strongest post, and this pre/post pair actually gives us a valid Hoare triple as well. But we can shrink the post using (Consequence) to go below the strongest post, to obtain  : the positive integers are a valid under-aproximation.
: the positive integers are a valid under-aproximation.
We record this example as loop1() in Fig. 4, where presumes is used for the pre-assertion in an under-approximate triple, and achieves for the post-assertion. In a program analysis tool we would not expect the human to specify the presumes and achieves, or the variant p; they would (hopefully) be inferred.
It can be helpful to contrast these rules with those from the over-approximate logic HL (see Fig. 3). The rule for divergence has “false” as the post for under-approximation, where “true” is the post in HL, the choice rule has an \(\exists \) in the premise where HL has \(\forall \), the consequence rule uses \(\le \) where over-approximation uses \(\ge \), and the iterate rule uses a possibly infinite disjunction while for over-approximation we can use loop invariance with no need for infinitary constructs.
It is worth noting that \(\le \) of the algebra is used in the proof rules only between tests (assertions), and not general algebra elements (commands). In program logic this is done because one expects to have a reasonable way to decide \(\le \) between tests, by means of a theorem prover or an abstract interpreter, but deciding \(\le \) between commands has been less common (at least, historically). However, rules involving \(\le \) between commands can be handy, especially for metatheory.
One such is the rule (Isotony in Command) from Fig. 2. (In contrast, Hoare triples are anti-isotone in their command.) Isotony together with (Star Unfold) of Kleene algebra justifies the three (Unfold) rules (all of which are unsound in HL). It turns out that these are what is called in logic admissible rules: if the premises are derivable from the given rules then so is the conclusion (but there might not be a single direct derivation from the premises to the conclusion). O’Hearn [25] included the first and second rules as they allow a direct derivation of a rule for bounded model checking. De Vries and Koutavas [27] avoided unrolling rules, and a justification for this decision is a completeness theorem (where all true triples can be derived, if not all true proof rules).
The two further admissible but non-derivable rules (Full Disjunction) and (False Post) deal with choice. Note that in the premise of (Full Disjunction) we use semiring lub (sum), whereas in the conclusion we use meta-conjunction.
Theorem 3.2
(Soundness and Completeness). Assume a modal CTC semiring with star.
-
1.
With star unfold, the rules in Figs. 1 and 2 are sound (preserve validity).
-
2.
If also star induction holds then the rules in Fig. 1 are complete, i.e., every valid triple is provable.
Note that these results do not require any form of \(*\)-continuity.
Proof
[Iteration Soundness]. Here is the proof for the iteration rule. First we show by induction on n that  for all
for all  .
.
-
For \(n = 0\), by \(1 \le a^*\) with isotony of diamond,
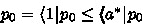 .
. -
Assume
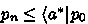 . Then by the rule premise with the definition of underapproximate triples, the induction hypothesis with isotony of diamond, multiplicativity of diamond and \(a \mathbin {\cdot }a^* \le a^*\) with isotony of diamond:
. Then by the rule premise with the definition of underapproximate triples, the induction hypothesis with isotony of diamond, multiplicativity of diamond and \(a \mathbin {\cdot }a^* \le a^*\) with isotony of diamond: 
Hence  is an upper bound of all the \(p_n\) and by the definition of a lub we obtain
is an upper bound of all the \(p_n\) and by the definition of a lub we obtain  , which is the conclusion of the rule.
, which is the conclusion of the rule.
The proofs for the other rules are not difficult, and do not use CTC at all. \(\square \)
The completeness result (proof overleaf) is sometimes termed “relative” completeness because it uses a proof theory with potential incomputable elements that we assume oracles for deciding or writing: in our case \(\le \) queries and infinite disjunctions. Also, an assumption that posts  be expressible is sidestepped by allowing arbitrary tests instead of those built following a specific syntax.
be expressible is sidestepped by allowing arbitrary tests instead of those built following a specific syntax.
The completeness argument is standard: first we show that triples for strongest posts are provable. This, in turn, relies on a characterization of the strongest post for iteration, which is where induction principles from Kleene algebra are used.
Lemma 3.3
In a modal CTC Kleene algebra all elements a and tests p satisfy  .
.
Proof
(\(\ge \)). This is immediate from \(a^n \le a^*\) for all  (Lemma 2.7), isotony of diamond and the definition of lubs.
(Lemma 2.7), isotony of diamond and the definition of lubs.
(\(\le \)) We use (Diamond Star Induction) for  . The premise of that rule is by lattice algebra equivalent to
. The premise of that rule is by lattice algebra equivalent to  . The first conjunct is true, since
. The first conjunct is true, since  . For the second conjunct we calculate by the definition of q, diamond preserving existing lubs (Lm. 2.5.1), multiplicativity of diamond, laws of powers, lattice algebra and definition of q:
. For the second conjunct we calculate by the definition of q, diamond preserving existing lubs (Lm. 2.5.1), multiplicativity of diamond, laws of powers, lattice algebra and definition of q:

\(\square \)
Lemma 3.4
In a modal CTC Kleene algebra the triple  is provable.
is provable.
Proof
By induction on the generation of the program a. For atomic a the claim holds by the proof rule for atoms.
-
For choice, additivity of diamond yields
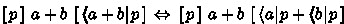 . Now, by (Disjunction), (Choice) twice and the induction hypothesis for a, b:
. Now, by (Disjunction), (Choice) twice and the induction hypothesis for a, b: 
-
For composition, multiplicativity of diamond yields
 . Now, by (Sequencing) and induction hypothesis for a, b:
. Now, by (Sequencing) and induction hypothesis for a, b: 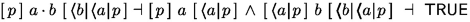
-
For iteration, by the induction hypothesis for a, all triples \([[\, p_n\, ]]\ a\ [[\, p_{n+1}\, ]]\) are derivable, since
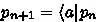 . Therefore, (Iteration) yields the triple
. Therefore, (Iteration) yields the triple  , which is equivalent to
, which is equivalent to 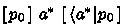 by Lemma 3.3.
by Lemma 3.3.
\(\square \)
Completeness then follows since from  we can shrink the post using (Consequence) to obtain that \([[\, p\, ]]\ a\ [[\, q\, ]]\) is provable for any
we can shrink the post using (Consequence) to obtain that \([[\, p\, ]]\ a\ [[\, q\, ]]\) is provable for any  .
.
3.2 Over-Approximate Triples
We have established that the algebra provides a faithful representation of under-approximate reasoning. In this section we briefly indicate how the prior strength of Kleene algebra for correctness (over-approximation) is maintained.
Definition 3.5
-
1.
An over-approximate triple is a formula \(\{ p \}\ a\ \{ q \}\), where \(p,q \in \textsf {test}(A)\) and \(a\in A\) is a program.
-
2.
\(\{ p \}\ a\ \{ q \}\) is valid in A, in signs \(\models \,\{ p \}\ a\ \{ q \}\), just if
 .
. -
3.
\(\{ p \}\ a\ \{ q \}\) is provable iff it can be derived using the rules in Fig. 3.
Theorem 3.6
(Soundness and Completeness) [23]. The proof rules in Fig. 3 are sound and complete in any modal Kleene algebra.
Revisiting our earlier example, \(\{ x=0 \}\ (x:=x+1)^*\ \{ x\ge 1 \}\) is not valid but \(\{ x=0 \}\ (x:=x+1)^*\ \{ x\ge -1 \}\) is, as can be proven by selecting \(x\ge -1\) as the loop invariant, together with use of the Consequence rule with the implication from \(x=0\) to \(x\ge -1\). \(x\ge -42\) is strictly over-approximate, and \([[\, x=0\, ]]\ (x:=x+1)^*\ [[\, x\ge -1\, ]]\) can’t be proven because (Consequence) reverses the implications between tests and the implication from \(x=0\) to \(x\ge -1\) is in the wrong direction for under-approximate reasoning.
In contrast to our result for under-approximation (Theorem 3.2(1)), we do not need the CTC hypothesis to show soundness here: the iteration rule is based on loop invariants rather than an infinite disjunction. But, we do need to have a Kleene algebra requirement for soundness, where the under-approximate case (Theorem 3.2(1)) does not: star induction implies the over-approximate iteration rule. These differences underline that the under-approximate theory is not obtained from the over-approximate theory at once by appeal to order duality.
The completeness proof for Theorem 3.6 follows the same pattern as our earlier completeness result: we establish by generation induction on a that  is derivable and then apply the rule of consequence. An algebraic relative completeness result for HL was given already in [23] using forwards diamonds, and a proof with backwards diamonds is possible and omitted. (Note that the under-approximate triple does not admit a backwards predicate transformer semantics [25], and that is why we have used backwards diamonds in the present paper.)
is derivable and then apply the rule of consequence. An algebraic relative completeness result for HL was given already in [23] using forwards diamonds, and a proof with backwards diamonds is possible and omitted. (Note that the under-approximate triple does not admit a backwards predicate transformer semantics [25], and that is why we have used backwards diamonds in the present paper.)
This result extends at once to CTC algebras. We have included it to emphasise: in modal CTC Kleene algebras, we have sound and complete representations of both under-approximate and over-approximate triples, in the same algebra.
Aside: The Ideal Formulation. We have axiomatised the strongest post via a backwards diamond. There are other algebraic encodings which avoid modalities, as in a generalized representation of \(\{ b \}\ a\ \{ c \}\) as \(b\cdot a \le c\), where b and c are not required to be tests [18]. Here, \(\le \) judges approximation between entire programs and not just tests. A similar under-approximate triple is obtained by defining \([[\, b\, ]]\ a\ [[\, c\, ]]\) as \(b\cdot a \ge c\). Let’s call this the generalized under-approximate triple.
To connect the generalized and classical triples we represent pres and posts in terms of the programs b and c. If p is a test and our semilattice has a greatest element \(\mathsf {T}\), then \(\mathsf {T}\mathbin {\cdot }p\) is the test ideal for p. Intuitively, \( \mathsf {T}\mathbin {\cdot }p\) represents a program that can do anything but, if it terminates, must leave p being true at the end. In the relation model, it is the relation that maps any input state to every state in p. Using test ideals, we can define under- and over-approximate triples as

The right hand sides of the equivalences are generalized triples, with \(\mathsf {T}\mathbin {\cdot }p\) and \(\mathsf {T}\mathbin {\cdot }q\) for b and c. Let us call these the ideal interpretations of the two triples, and the ones in rest of the paper the modal interpretations. The ideal and modal interpretations agree in the concrete relation model ([25], Fact 11). We chose to work with modalities as their direct connection to the official definition of the under-approximate triple seemed natural, but we emphasize that it is possible to develop a full treatment of IL based on ideals rather than modalities.
Another encoding represents \(\{ p \}\ a\ \{ q \}\) as \(p\mathbin {\cdot }a \mathbin {\cdot }\lnot q = 0\): assuming p then executing a cannot contradict q [22]. We are not aware of a similar interpretation, avoiding ideals and modalities, for the under-approximate triple. End of Aside
4 Incorrectness
An under-approximate triple \([[\, p\, ]]\ a\ [[\, q\, ]]\) on its own tells us nothing about whether a program is incorrect: it just tells us a subset of what can happen. In the terminology of program testing, such a triple gives us information that is similar to a “test case”, with the generalization that if p and q are assertions describing multiple program states then a single triple can cover more than a single input or output. A test case is not yet a test, as it has no way to judge violation: we also need a “test oracle”, which tells us if a run is considered erroneous.
4.1 Disproving Hoare Triples
Suppose we are given a Hoare triple \(\{ p \}\ c\ \{ q \}\), but we are not told whether it is valid. We can consider such a triple as “putative”, a test oracle (or a specification): given an input/output pair of states the oracle says “no” if the input state satisfies p and the output state doesn’t satisfy q.
See Fig. 4 for an example. In specloop1() we use the keywords requires and ensures to indicate the pre and post in a putative Hoare triple. The presumes and ensures assertions from loop1() are those of an under-approximate triple, and give us a way to prove falsity of the Hoare triple: the achieves assertion in loop1() says that x can be any positive integer, and this is incompatible with the ensures assertion in specloop1(). Note also that if we were to change specloop1() by replacing 42,000,000 with 86,000,000 then we could re-use the achieves assertion in loop1() to give us another disproof.
These ideas on testing and oracles/specification are captured in the following result, which refers to interpretations of triples in modal Kleene algebra.
Theorem 4.1
 .
.
Proof
(\(\Rightarrow \)) By the definitions,  and
and  . Hence we may choose \(p' = p\) and
. Hence we may choose \(p' = p\) and  .
.
(\(\Leftarrow \)) By generalised contraposition, the definitions and isotony of diamond with transitivity of \(\le \),

Informally, if an execution of a lands outside the post, then the post can’t hold. In concrete program testing in the relation model, \(p'\) and \(q'\) denote singleton sets. But the theorem also covers cases where we use assertions to cover many states at once, as in loop1(). Connecting back to the discussion of false positives and under-approximation in the Introduction: if we were to attempt to apply Theorem 4.1, if \(q'\) did not under-approximate the reachable states we might get incorrect suggested disproofs; false positives. Also, under-approximation furnishes information for verification: when we shouldn’t try to verify. Conversely, if a Hoare triple holds, we needn’t try to use testing to falsify it.
These remarks connecting verification and testing are obvious intuitively in concrete models [25]. The point of stating this theorem is as a sanity check that the algebra faithfully represents their connection.
4.2 Error Statements and Embedded Assertions
Hoare triples provide a popular form of specifications/test oracles, especially in theoretical work. An even more popular method, in widespread use across industry in program testing, is embedded “assert” statements. When an assert fails it indicates program error and execution halts. This gives us a facility similar to the post in a Hoare triple, as in testloop1() in Fig. 4. But, an assert statement does not need to be in post position, and in this sense is more flexible than pre/post specs. A concocted example is loop2() from Fig. 4. A more realistic example is testing code in Fig. 5, taken from the open source code of the toolkit OpenSSL. The call to test_dtls1_heartbleed_excessive_plaintext_length() in the main() program eventually calls dtls1_write_bytes() after executing other instructions and, as we can see from the comment, the embedded assert statement catches a bug which was present in earlier versions of the software. The assert statement functions like the post in a Hoare triple, in that its failure indicates a program error, but it has further statements following it: it is a program statement, and it need not be placed at the end of a function.
Turning back to theory, these assert statements are distinct from the “tests” used in Kleene algebra. The latter corresponds more to the “assume” statement in programming language theory: \({ assume}{(p)}\) simply discards the current program path when p is false but does not halt execution, whereas \({ assert}{(p)}\) results in abnormal program termination. Hence, c is not executed in \({ assert}(p);c\) when p fails. Abnormal termination is itself different from the 0 of Kleene algebra, which means program divergence, since it is equivalent to  (or \(1^*;\lnot 1\)).
(or \(1^*;\lnot 1\)).
We approach the use of embedded assertions to specify incorrectness following Incorrectness Logic, which itself follows the lead of C and other programming languages. A special instruction \({ error}\), distinct from 1 and 0, is used to cause abnormal termination before a program’s end is reached; assert statements can be described using a combination of tests/Booleans and \({ error}\).
We consider the following grammar of commands,

and set  . Although \({ error}\) does not correspond directly to a Kleene algebra element, we can do a semantics of a language with \( { error}\) by representing a program as a pair (a, e) of Kleene algebra expressions. The a component describes what happens in executions where no errors are raised, while the e component describes what happens when errors do occur. In terms of the relation model, a program denotes a pair of relations \((a,e) \in P(S\times S) \times P(S\times S)\), and this model is equivalent to a treatment of exceptions in denotational semantics via the isomorphism with \(P(S\times (S+S))\).
. Although \({ error}\) does not correspond directly to a Kleene algebra element, we can do a semantics of a language with \( { error}\) by representing a program as a pair (a, e) of Kleene algebra expressions. The a component describes what happens in executions where no errors are raised, while the e component describes what happens when errors do occur. In terms of the relation model, a program denotes a pair of relations \((a,e) \in P(S\times S) \times P(S\times S)\), and this model is equivalent to a treatment of exceptions in denotational semantics via the isomorphism with \(P(S\times (S+S))\).
The mapping of such program expressions to pairs of Kleene algebra elements is given in Fig. 6. This semantics, when specialised to the relation model, is that of [25]. Notice how neither sequencing nor iteration map pointwise to their Kleene cousins \(\mathbin {\cdot }\) and \(^*\): Sequencing uses “short circuiting”, where upon an error in the first operand execution halts and does not continue with the second, while iteration allows an error to happen on a final execution of a loop body, after some number of normally terminating executions. Finally, note that  is distinct from
is distinct from  .
.
4.3 Incorrectness Logic
We are now in a position to formulate a general algebraic form of the program logic from [25]. This is based on distinguishing two post-assertion forms, one \([[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]] \) for normal termination and the other \([[\, p\, ]]\ c\ [[\, \mathsf {er}: q\, ]] \) for erroneous.
Definition 4.2
-
1.
An under-approximate triple with error information is a formula \([[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]]\) or \([[\, p\, ]]\ c\ [[\, \mathsf {er}: q\, ]]\), where \(p,q \in \textsf {test}(A)\) and c is a program.
-
2.
-
(a)
\([[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]]\) is valid, in signs \(\models \,[[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]]\), iff
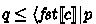 .
. -
(b)
\([[\, p\, ]]\ c\ [[\, \mathsf {er}: q\, ]]\) is valid, in signs \(\models \,[[\, p\, ]]\ c\ [[\, \mathsf {er}: q\, ]]\), iff
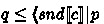 .
.
-
(a)
For the proof rules, first we translate all of the earlier proof rules for under-approximate triples \([[\, p\, ]]\ c\ [[\, q\, ]]\) into the \([[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]]\) form.
Definition 4.3
For each rule in Fig. 1 define a corresponding proof rule for \([[\, p\, ]]\ c\ [[\, \mathsf {ok}: q\, ]]\) triples by replacing \(\mathbin {\cdot }\) with ; , 0 with \({ diverge}\), 1 with \({ skip}\) and add strongest post axioms for atomic commands. Also, add (Choice) and (Disjunction) with \(\mathsf {er}\) and \(\mathsf {ok}\) conclusions. Call the resulting set of rules Fig. 1 translated.
Theorem 4.4
(Soundness and Completeness). Assume a modal CTC semiring with star.
-
1.
With star unfold, the rules in Figs. 7 plus Fig. 1 translated are sound.
-
2.
If also star induction holds then every true triple is provable.
There is a departure from [25]: we include the rule (Iterate:er) for \(\mathsf {er}\) conclusions only. The soundness of this rule follows from the semantics of iteration in the error case. If we included this rule for \(\mathsf {ok}\) conclusions as well (as in [25]), then we would appeal to the Kleene law \(c^*;c \le c^*\) plus isotony in command for soundness, and this would require stronger assumptions than Theorem 4.4(1). From the point of view of provability it is possible to leave out the stronger rule for \(\mathsf {ok}\) conclusions, as the backwards variant rule lets us prove all true \(\mathsf {ok}\) conclusions. The proof of completeness of each error case is straightforward and omitted.
An example which utilises (Iterate:er) is loop2() from Fig. 4. The assertion eventually fails after the loop body is successfully executed 42,000,000 times, and then upon the next iteration abnormal termination occurs. We leave as an exercise for the reader to supply the assertions formalizing this argument.
4.4 Over-Approximating Errors
It is possible to formulate an over-approximate system for reasoning about errors as well. We define \(\{ p \}\ c\ \{\mathsf {ok}: q \} \) to be valid iff  , and \(\{ p \}\ c\ \{\mathsf {er}: q \} \) to be valid iff
, and \(\{ p \}\ c\ \{\mathsf {er}: q \} \) to be valid iff  . Such triples can be used to show that a program doesn’t raise an error (when the \(\mathsf {er}\) conclusion is empty), or that it doesn’t terminate normally (when the \(\mathsf {ok}\) conclusion is empty).
. Such triples can be used to show that a program doesn’t raise an error (when the \(\mathsf {er}\) conclusion is empty), or that it doesn’t terminate normally (when the \(\mathsf {ok}\) conclusion is empty).
As before there are properties in the algebra connecting testing and verification. Specifically, if 0 over-approximates the error states, then no non-0 under-approximate error conclusion is possible (we needn’t test for it); and, if a non-0 under-approximates error, then some errors must occur (we needn’t verify).
Theorem 4.5
-
1.
 .
. -
2.
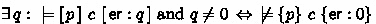 .
.
We don’t give a full treatment of proof theory for this extension of HL, but it is worth contrasting some rules with those for under-approximation. First, sequencing again takes into account short-circuit evaluation, but now must consider the short-circuit and normal cases together top achieve over-approximation.

Second, iteration cannot (however implicitly) make use of \(c^*;c \le c^*\) plus isotony in command, because in over-approximate logic isotony fails (anti-isotony holds). Instead, even in the error case, can make use of a loop invariant (cf. [9]).

5 Backwards Under-Approximation and Incorrectness
A broadly similar technical development can be done if we replace the strongest post, or the image of a relation, by the inverse image. We obtain a triple \([[p \}\}\ a\ [[q \}\}\) where p under-approximates the states obtained executing a backwards from q.
More precisely, in the relation model define the weakest possible pre of a relation,  . Then we can define
. Then we can define

Another way to describe \([[p \}\}\ a\ [[q \}\}\) is by saying that every state in p can reach some state in q via a [27]. Note that \(\mathsf {wpp}\) is neither Dijkstra’s weakest precondition, nor the weakest liberal precondition. This triple is different from \(\{ p \}\ a\ \{ q \}\), because a still might land outside of q when executing in the forwards direction.
This yields a logic for reasoning about backwards under-approximation. We don’t develop the logic in full, but mention several salient points.
-
1.
Algebraically, \(\mathsf {wpp}(q,a)\) is represented by the forward diamond
 from Definition 2.4, and we define
from Definition 2.4, and we define 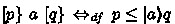 .
. -
2.
The iteration rule becomes
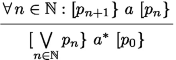
This is in the form of variant rules for total correctness [1] except that the triple does not ensure termination on every path or that no path leads outside the post. It is similar to a rule for diamonds in first-order dynamic logic [15].
-
3.
The assignment axiom is now the backwards-running one
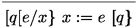
-
4.
Disproving a Hoare triple can still be done but requires a different approach than Theorem 4.1: landing outside q falsifies a Hoare triple.
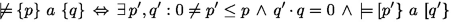
Kleene algebra can serve as a foundation for reasoning about backwards under-approximation; e.g., must transitions [4] and reachability witnesses [2].
6 Conclusion and Outlook
Kleene algebra encapsulates basic principles of simple imperative programs, and many works have shown how these principles can provide a foundation for program verification. In this paper we have studied how Kleene algebra can also be used as a foundation for reasoning about the presence of bugs, as in (static or dynamic) program testing. This has the potential to significantly expand the application area of Kleene algebra. While logics for verification have received voluminous treatment in theoretical research, the practical impact of program testing currently dwarfs that of verification: it is much more widely deployed in engineering practice, helping the creation of almost all software products.
In this paper we looked at two specific theories, Hoare Logic (HL) and Incorrectness Logic (IL). The main difference between them is that HL (like verification of safety properties, generally) is a formalism of over-approximation, where IL (like testing generally) rests on under-approximation. We used Modal Kleene algebra to express the under-approximate triple directly. As a happy consequence, the power of Kleene algebra to describe HL is preserved, and properties can be stated linking HL and IL specifications. In this sense, the modal Kleene algebra of the current paper can be said to unify HL and IL.
Our technical results pertain to the specific theories of HL and IL, not to the entire broader informal concepts of correctness and incorrectness. The results here concern safety properties and not liveness properties or hyperproperties. Also, HL and IL are basic theories, and the extension of our results to further programming features is not obvious. For example, Concurrent Kleene Algebra [18] through its exchange law supports a proof rule for over-approximate and not under-approximate reasoning about concurrent processes, and reversing the law furnishes a rule for under-approximation, but how to treat correctness and incorrectness in one algebra for concurrency is not immediately obvious. For another, sequential separation logic relies on an interpretation of triples which avoids memory errors, where the incorrectness version does not use such an interpretation [26]; again, they do not connect at once as HL and IL do here.
A contribution of the paper has been to pinpoint properties relevant to completeness of under-approximate reasoning (test completeness), when Kleene properties are and are not needed, and that \(*\)-continuity is not. These observations should persist into extensions to other programming features, whether or not the exact form of unification achieved here can survive extension.
To conclude, under-approximation and incorrectness have been under-studied in foundational theory, and there is much to be learnt about them and their relation to correctness theories (see [7] for an example of recent theoretical learnings in the area between them, albeit without algebra). It is our hope that some of the problems in this area will be taken up by others.
References
Apt, K.: Ten years of Hoare’s logic: a survey – part 1. ACM TOPLAS 3(4), 431–483 (1981)
Asadi, A., Chatterjee, K., Fu, H., Goharshady, A., Mahdavi, M.: Polynomial reachability witnesses via Stellensätze. In: PLDI (2021)
Backhouse, R., van der Woude, J.: Demonic operators and monotype factors. Math. Struct. Comp. Sci. 3, 417–433 (1993)
Ball, T., Kupferman, O., Yorsh, G.: Abstraction for falsification. In: CAV, pp. 67–81 (2005)
Brunn, T., Möller, B., Russling, M.: Layered graph traversals and Hamiltonian path problems – an algebraic approach. Tech. Rep. 1997–08, Institute of Computer Science, University of Augsburg, December 1997. Revision in Jeuring, J. (ed.): Math. Prog. Constr. LNCS 1422, 96–121. Springer (1998)
Brookes, S., O’Hearn, P.W.: Concurrent Separation Logic. ACM SIGLOG News 3(3), 47–65 (2016)
Bruni, R., Giacobazzi, R., Gori, R., Ranzato, F.: A logic for locally complete abstract interpretations. In: LICS (2021)
Cadar, C., Sen, K.: Symbolic execution for software testing: three decades later. CACM 65(2), 82–90 (2013)
Clint, M., Hoare, T.: Program proving: jumps and functions. Acta Informatica 1, 214–224 (1972)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: POPL, pp. 238–252 (1977)
Desharnais, J., Möller, B., Struth, G.: Modal Kleene algebra and applications – a survey. J. Rel. Meth. Comp. Sci. 1, 93–131 (2004)
Desharnais, J., Möller, B., Struth, G.: Kleene algebra with domain. ACM TOCL 7, 798–833 (2006)
Floyd, R.W.: Assigning meanings to programs. Mathematical aspects of computer science. In: Proceedings of Symposium on Applied Mathematics. vol. 19, pp. 19–32. AMS (1967)
Godefroid, P.: Compositional dynamic test generation. In: POPL, pp 47–54 (2007)
Harel, D. (ed.): First-Order Dynamic Logic. LNCS, vol. 68. Springer, Heidelberg (1979). https://doi.org/10.1007/3-540-09237-4
Hoare, C.A.R.: An axiomatic basis for computer programming. CACM 12(10), 576–580 (1969)
Hoare, T.: Retrospective: an axiomatic basis for computer programming. CACM 52(10), 30–32 (2009)
Hoare, T., Möller, B., Struth, G., Wehrman, I.: Concurrent Kleene algebra and its foundations. J. Log. Algebr. Program 80(6), 266–296 (2011)
Hoare, T., van Staden, S.: In praise of algebra. Formal Aspects Comput. 24(4–6), 423–431 (2012)
Hollenberg, M.: An equational axiomatization of dynamic negation and relational composition. J. Logic Lang. Inf. 6, 381–401 (1997)
Kozen, D.: A completeness theorem for Kleene algebras and the algebra of regular events. Inf. Comp. 110, 366–390 (1994)
Kozen, D.: On Hoare logic and Kleene algebra with tests. ACM TOCL 1(1), 60–76 (2000)
Möller, B., Struth, G.: Algebras of modal operators and partial correctness. TCS 351, 221–239 (2006)
O’Hearn, P.W.: Separation logic. Commun. ACM 62(2), 86–95 (2019)
O’Hearn, P.W.: Incorrectness logic. PACML(POPL) 4, 10:1–10:32 (2020)
Raad, A., Berdine, J., Dang, H.-H., Dreyer, D., O’Hearn, P.W., Villard, J.: Local reasoning about the presence of bugs: incorrectness separation logic. CAV 2, 225–252 (2020)
de Vries, E., Koutavas, V.: Reverse Hoare logic. In: Barthe, G., Pardo, A., Schneider, G. (eds.) SEFM 2011. LNCS, vol. 7041, pp. 155–171. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24690-6_12
Rosenthal, K.: Quantales and their applications. In: Pitman Research Notes in Math, vol. 234 (1990)
Acknowledgements
Helpful comments were provided by Jules Desharnais, Roland Glück, Mark Harman and the anonymous referees.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Möller, B., O’Hearn, P., Hoare, T. (2021). On Algebra of Program Correctness and Incorrectness. In: Fahrenberg, U., Gehrke, M., Santocanale, L., Winter, M. (eds) Relational and Algebraic Methods in Computer Science. RAMiCS 2021. Lecture Notes in Computer Science(), vol 13027. Springer, Cham. https://doi.org/10.1007/978-3-030-88701-8_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-88701-8_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-88700-1
Online ISBN: 978-3-030-88701-8
eBook Packages: Computer ScienceComputer Science (R0)





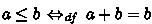 . Then
. Then 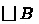 . With this,
. With this, 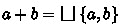 . For uniformity we write
. For uniformity we write 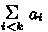 .
. and
and  .
.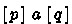 , where
, where  is valid in A, in signs
is valid in A, in signs  .
.

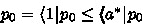 .
.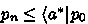 . Then by the rule premise with the definition of underapproximate triples, the induction hypothesis with isotony of diamond, multiplicativity of diamond and
. Then by the rule premise with the definition of underapproximate triples, the induction hypothesis with isotony of diamond, multiplicativity of diamond and 
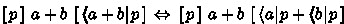 . Now, by (Disjunction), (Choice) twice and the induction hypothesis for a, b:
. Now, by (Disjunction), (Choice) twice and the induction hypothesis for a, b: 
 . Now, by (Sequencing) and induction hypothesis for a, b:
. Now, by (Sequencing) and induction hypothesis for a, b: 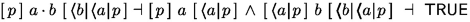
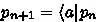 . Therefore, (Iteration) yields the triple
. Therefore, (Iteration) yields the triple  , which is equivalent to
, which is equivalent to 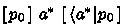 by Lemma
by Lemma  .
.




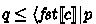 .
.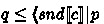 .
.
 .
.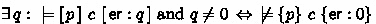 .
. from Definition
from Definition 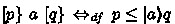 .
.