Skip to main content
SpringerLink
Log in

Quantifying Degrees of E-admissibility in Decision Making with Imprecise Probabilities

  • Chapter
  • First Online:
Reflections on the Foundations of Probability and Statistics

Part of the book series: Theory and Decision Library A: ((TDLA,volume 54))

Abstract

This paper is concerned with decision making using imprecise probabilities and looks at extensions and aspects of the criterion of E-admissibility, as introduced by Levi and extensively studied and advocated by Teddy Seidenfeld. In the first part, we introduce a decision criterion that allows for explicitly modeling how far maximal decisions in Walley’s sense are accepted to deviate from E-admissibility. We also provide an efficient and simple algorithm based on linear programming theory for this criterion. In the second part of the paper, we propose two measures for quantifying what we call the extent of E-admissibility of an E-admissible act, i.e. the size of the set of measures for which the corresponding act maximizes expected utility. The first measure is the maximal diameter of this set, while the second one relates to the maximal barycentric cube that can be inscribed into it. Also here, for both measures, we give linear programming algorithms capable to deal with them. Finally, we discuss some ideas in the context of ordinal decision theory. The paper concludes with a stylized application example illustrating all introduced concepts.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
eBook
USD 16.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 129.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 129.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    The one exception is the discussion in Sect. 13.4, where we do not assume a cardinal utility representation.

  2. 2.

    See Schervish et al. (2013) for the situation where multiple utilities through different currencies are available and exchange rates have to be taken into account.

  3. 3.

    It should, however, be emphasized that in the context of imprecise probabilistic models (like for instance credal sets or interval probabilities) the relationship between optimal decision functions in terms of prior risk and posteriori loss optimal acts may be more subtle than in the context of precise probability: the main theorem of Bayesian decision theory may fail (cf., e.g., Augustin (2003, Section 2.3)). This failure is in essence a variant of the general phenomenon of potential sequential incoherence in decision making and discrepancy between extensive and normal forms, as investigated in depth by Seidenfeld (e.g., Seidenfeld (1988, 1994)). Immediate counter-examples arise from the phenomenon of dilation, which has intensively been studied by Seidenfeld and co-authors (cf., e.g., Seidenfeld (1994), Seidenfeld and Wassermann (1993), Wassemann and Seidenfeld (1994)), see also, e.g., Hailin (2015).

  4. 4.

    See, however, e.g., Seidenfeld et al. (1989), Wheeler (2012), Majo-Wilson and Wheeler (2016, Section 2), and the references therein, for arguments to consider also non-convex sets of probabilities.

  5. 5.

    Note that if \(\mathcal {M}\) is described by functions (f 1, …, f r) and bounds \((( \underline {b_1}, \overline {b}_1) , \dots , ( \underline {b_r}, \overline {b}_r))\) not meeting this assumptions, we can always equivalently characterize it by functions (f 1 − c 1, …, f r − c r) and bounds \((( \underline {b_1}-c_1, \overline {b}_1-c_1) , \dots , ( \underline {b_r}-c_r, \overline {b}_r -c_r))\), where, for all s = 1, …, r, we set \(c_s= \underline {b}_s \) if \( \underline {b}_s> 0\) and \(c_s=-\overline {b}_s \) if \( \overline {b}_s < 0\) and c s = 0 if \(0 \in [ \underline {b}_s, \overline {b}_s]\). This assumption is technically convenient in the context of the optimization results later in the paper, since it allows to directly specify an admissible solution whenever \(\mathcal {M}\) is interpreted as the set of (potential) admissible solutions of some linear programming problem.

  6. 6.

    See, for instance, Kofler and Menges (1976) and Gilboa and Schmeidler (1989). Many authors denote \(\mathcal {M}\) by Γ, and thus the term Γ-maximin is common as well.

  7. 7.

    This criterion is mainly advocated by Walley (1991) and work following him.

  8. 8.

    Compare also Seidenfeld et al. (2010) and (Vicig and Seidenfeld 2012, Section 3).

  9. 9.

    This criterion is introduced by Levi (1974).

  10. 10.

    Both criteria just discussed are also of high interest in forecasting with imprecise probabilities. While for imprecise probabilities there is no real-valued strictly proper scoring rule, it is possible to formulate an appropriate lexicographic strictly proper scoring rule with respect to \(\mathcal {M}\)-maximinity and E-admissibility, supplemented by \(\mathcal {M}\)-maximinity (Seidenfeld et al. (2012)).

  11. 11.

    Note that considering criteria additional to E-admissibility seems very natural, since, by introducing the criteria of P- and S-admissibility, this was already done in the original work of Levi (1974).

  12. 12.

    Note that, due to standard results from linear programming theory, such an optimal solution always exists since the constraint set is bounded and there always exists an admissible solution since \(a_z \in \mathbb {A}_{\mathcal {M}}\).

  13. 13.

    Another, very prominent, way for proceeding in such situations is working with partially cardinal preference relations as done in Seidenfeld et al. (1995).

  14. 14.

    For a simple example consider the decision problems \((\mathbb {A} ,\Theta ,u)\) and \((\mathbb {A}\cup \{a^*\} , \Theta , \tilde {u})\) given by

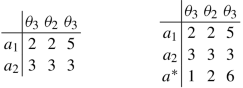
    and the prior π on Θ induced by (π({θ 1}), π({θ 2}), π({θ 3})) = (0.2, 0.2, 0.6). Here we have that \(D^{\mathbb {A}}_{\pi }(a_1)=0.6 >0.4= D^{\mathbb {A}}_{\pi }(a_2)\) but \(D_{\pi }^{\mathbb {A}^*}(a_2)=0.4 > 0 = D_{\pi }^{\mathbb {A}^*}(a_1)\).

  15. 15.

    The calculation was performed with the rcdd package (see Geyer and Meeden (2019)), which provides an interface for using Fukuda (2018)’s cdd library in the R statistical computing environment (see R Core Team (2020)).

References

  • Antonucci, A., Corani, G., Couso, I., and S. Destercke. eds. 2017. Proceedings of the tenth international symposium on imprecise probability: theories and applications (ISIPTA ’17, Lugano), vol 62. Proceedings of machine learning research, PMLR.

    Google Scholar 

  • Augustin, T. 2003. On the suboptimality of the generalized Bayes rule and robust Bayesian procedures from the decision theoretic point of view: a cautionary note on updating imprecise priors. In Proceedings of the third international symposium on imprecise probability: theories and applications (ISIPTA ’03, Lugano), eds. Bernard, J.-M., Seidenfeld, T., and Zaffalon, M., 31–45. Ottawa: Carleton Scientific.

    Google Scholar 

  • Augustin, T., Coolen, F., De Cooman, G., and M. Troffaes. eds. 2014. Introduction to imprecise probabilities. Chichester: Wiley.

    Google Scholar 

  • Bradley, S. 2015. How to choose among choice functions. In Proceedings of the ninth international symposium on imprecise probability: theories and applications (ISIPTA ’15, Pescara), eds. Augustin, T., Doria, S., Miranda, E., and E. Quaeghebeur, 57–66. Rome: Aracne.

    Google Scholar 

  • Bradley, S. 2019. Imprecise probabilities. In The Stanford encyclopedia of philosophy (Spring 2019 Edition). Available via https://plato.stanford.edu/archives/spr2019/entries/imprecise-probabilities/. Last access February 20th, 2022.

  • Cozman, F., and C. de Campos. 2007. Inference in credal networks through integer programming. In Proceedings of the fifth international symposium on imprecise probability: theories and applications (ISIPTA ’07, Prague), eds. De Cooman, G., Vejnarová, J., and M. Zaffalon, 145–154. Lugano: SIPTA.

    Google Scholar 

  • De Bock, J., de Campos, C., De Cooman , G., Quaeghebeur, E., and G. Wheeler. eds. 2019. Proceedings of the eleventh international symposium on imprecise probability: theories and applications (ISIPTA ’19, Gent), vol 103. Proceedings of machine learning research, PMLR.

    Google Scholar 

  • de Campos, L., Huete, J., and S. Moral. 1994. Probability interval: a tool for uncertain reasoning. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 2:167–196.

    Article  Google Scholar 

  • Derks, J., and J. Kuipers. 2002. On the number of extreme points of the core of a transferable utility game. In Chapters in game theory in honour of Stef Tijs, eds. Borm, P., and H. Peters, 83–97. Alphen aan den Rijn: Kluwer.

    Google Scholar 

  • Etner, J., Jeleva, M., and J.-M. Tallon (2012). Decision theory under ambiguity. Journal of Economic Surveys 26:234–270.

    Article  Google Scholar 

  • Fukuda, K. (2018). The cdd and cddplus homepage. Available via https://www.inf.ethz.ch/personal/fukudak/cdd_home/. Last access June 30th, 2021.

  • Geyer, C., and G. Meeden. 2019. Package ‘rcdd’ (Version 1.2–2). Available via https://CRAN.R-project.org/package=rcdd and www.stat.umn.edu/geyer/rcdd/. Last access February 20th, 2022.

  • Gilboa, I., and D. Schmeidler. 1989. Maxmin expected utility with non-unique prior. Journal of Mathematical Economics 18:141–153.

    Article  Google Scholar 

  • Hable, R., and M. Troffaes. 2014. Computation. In Introduction to imprecise probabilities, eds. Augustin, T., Coolen, F., De Cooman, G., and M. Troffaes, 329–337. Chichester: Wiley.

    Google Scholar 

  • Hailin, L. 2015. Common knowledge, ambiguity, and the value of information in games. In Proceedings of the ninth international symposium on imprecise probability: theories and applications (ISIPTA ’15, Pescara), eds. Augustin, T., Doria, S., Miranda, E., and E. Quaeghebeur, 167–176. Rome: Aracne.

    Google Scholar 

  • Herron, T., Seidenfeld, T., and L. Wasserman. 1997. Divisive conditioning: further results on dilation. Philosophy of Science 64:411–444.

    Article  Google Scholar 

  • Hodges, J., and E. Lehmann. 1952. The use of previous experience in reaching statistical decisions. Annals of Mathematical Statistics 23:396–407.

    Article  Google Scholar 

  • Huntley, N., Hable, R., and M. Troffaes. 2014. Decision making. In Augustin, T., Coolen, F., De Cooman, G., and M. Troffaes. eds. Introduction to imprecise probabilities, 190–206. Chichester: Wiley.

    Google Scholar 

  • Jansen, C., Schollmeyer, G., and T. Augustin. 2017. Decision theory meets linear optimization beyond computation. In Symbolic and quantitative approaches to reasoning with uncertainty. ECSQARU 2017, eds. Antonucci, A., Cholvy, L., and O. Papini, vol 10369. Lecture notes in computer science, 57–66. New York: Springer.

    Google Scholar 

  • Jansen, C., Schollmeyer, G., and T. Augustin. 2018. Concepts for decision making under severe uncertainty with partial ordinal and partial cardinal preferences. International Journal of Approximate Reasoning 98:112–131.

    Article  Google Scholar 

  • Kikuti, D., Cozman, F., and R. Shirota Filho. 2011. Sequential decision making with partially ordered preferences. Artificial Intelligence 175:1346–1365.

    Article  Google Scholar 

  • Kofler, E. 1989. Prognosen und Stabilität bei unvollständiger Information (in German) [Forecasts and stability under incomplete information]. Frankfurt: Campus.

    Google Scholar 

  • Kofler, E., and G. Menges. 1976. Entscheiden bei unvollständiger Information (in German) [Decision making under incomplete information]. Berlin: Springer.

    Google Scholar 

  • Lehmann, E. 1955. Ordered families of distributions. Annals of Mathematical Statistics 26:399–419.

    Article  Google Scholar 

  • Levi, I. 1974. On indeterminate probabilities. The Journal of Philosophy 71:391–418.

    Article  Google Scholar 

  • Majo-Wilson, C., and G. Wheeler. 2016. Scoring imprecise credences: a mildly immodest proposal. Philosophy and Phenomenological Research 93, 55–78.

    Article  Google Scholar 

  • Miranda, E., and S. Destercke. 2015. Extreme points of the credal sets generated by comparative probabilities. Journal of Mathematical Psychology 64:44–57.

    Article  Google Scholar 

  • Montes, I. 2014. Comparison of Alternatives under Uncertainty and Imprecision. PhD Thesis, University of Oviedo. Available via http://digibuo.uniovi.es/dspace/bitstream/10651/28953/6/TD_IgnacioMontesGutierrez.pdf. Last access February 20th, 2022.

  • Montes, I., and S. Destercke. 2017. On extreme points of p-boxes and belief functions. In Soft methods for data science, eds. Ferraro, M., Giordani, P., Vantaggi, B., Gagolewski, M., Gil, M., Grzegorzewski, P., and O. Hryniewicz, 363–371. Berlin: Springer.

    Chapter  Google Scholar 

  • Montes, I., Miranda, E. and S. Destercke. 2017. A study of the pari-mutuel model from the point of view of imprecise probabilities. In Proceedings of the tenth international symposium on imprecise probability: theories and applications (ISIPTA ’17, Lugano), eds. Antonucci, A., Corani, G., Couso, I., and S. Destercke, vol 62. Proceedings of machine learning research, PMLR, 229–240.

    Google Scholar 

  • Mosler, K., and M. Scarsini. 1991. Some theory of stochastic dominance. In Stochastic orders and decision under Risk, eds. Mosler, K., and M. Scarsini, 203–212. Hayward, CA: Institute of Mathematical Statistics.

    Google Scholar 

  • R Core Team. 2020. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. Available via https://www.R-project.org. Last access February 20th, 2022.

  • Ristic, B., Gilliam, C., Byrne, M., and A. Benavoli. 2020. A tutorial on uncertainty modeling for machine reasoning. Information Fusion 55:30–44.

    Article  Google Scholar 

  • Schervish, M., Seidenfeld, T., Kadane, J., and I. Levi. 2003. Extensions of expected utility theory and some limitations of pairwise comparisons. In Proceedings of the third international symposium on imprecise probability: theories and applications (ISIPTA ’03, Lugano), eds. Bernard, J.-M., Seidenfeld, T., and M. Zaffalon, 496–510. Ottawa: Carleton Scientific.

    Google Scholar 

  • Schervish, M., Seidenfeld, T., and J. Kadane. 2013. The effect of exchange rates on statistical decisions. Philosophy of Science 80:504–532.

    Article  Google Scholar 

  • Schollmeyer, G. 2015. On the number and characterization of the extreme points of the core of necessity measures on finite spaces. In Proceedings of the ninth international symposium on imprecise probability: theories and applications (ISIPTA ’15, Pescara), eds. Augustin, T., Doria, S., Miranda, E., and E. Quaeghebeur, 277–286. Rome: Aracne.

    Google Scholar 

  • Schollmeyer, G., Jansen, C., and T. Augustin. 2017. Detecting stochastic dominance for poset-valued random variables as an example of linear programming on closure systems. Technical Report 209, Department of Statistics, LMU Munich. Available via https://epub.ub.uni-muenchen.de/40450/. Last access February 20th, 2022.

  • Seidenfeld, T. 1988. Decision theory without independence or without ordering, What is the difference? (with discussion). Economics and Philosophy 4:267–315.

    Article  Google Scholar 

  • Seidenfeld, T. 1994. When normal form and extensive form solutions differ. In Logic, methodology and philosophy of science IX (Uppsala, 1991), eds. Prawitz, D., Skyrms, B., and D. Westerstahl, 451–463. Amsterdam: Elsevier.

    Google Scholar 

  • Seidenfeld, T. 2004a. A contrast between two decision rules for use with (convex) sets of probabilities: Γ-maximin versus E-admissibility. Synthese 140:69–88.

    Article  Google Scholar 

  • Seidenfeld, T. 2004b. Some decision theoretic issues for imprecise probability theory. Slides of a lecture given on the First SIPTA School on Imprecise Probabilities. Available via http://www.sipta.org/ssipta04/topics.htm. Last access February 20th, 2022

  • Seidenfeld, T., Kadane, J., and M. Schervish. 1995. A representation of partially ordered preferences. Annals of Statistics 23:2168–2217.

    Article  Google Scholar 

  • Seidenfeld, T., Kadane, J., and M. Schervish. 1989. On the shared preferences of two Bayesian decision makers. The Journal of Philosophy 86:225–244.

    Article  Google Scholar 

  • Seidenfeld, T., Schervish, M., and J. Kadane. 2010. Coherent choice functions under uncertainty. Synthese 172:157–176.

    Article  Google Scholar 

  • Seidenfeld, T., Schervish, M., and J. Kadane. 2012. Forecasting with imprecise probabilities. International Journal of Approximate Reasoning 53:1248–1261.

    Article  Google Scholar 

  • Seidenfeld, T., and L. Wassermann. 1993. Dilation for sets of probabilities. Annals of Statistics 21:1139–1154.

    Article  Google Scholar 

  • Seidenfeld, T., and L. Wassermann. 1996. Discussion of “Inferences from multinomial data: learning about a bag of marbles” by P. Walley. Journal of the Royal Statistical Society. Series B (Methodological) 58:49.

    Google Scholar 

  • Troffaes, M. 2007. Decision making under uncertainty using imprecise probabilities. International Journal of Approximate Reasoning 45:17–29.

    Article  Google Scholar 

  • Utkin, L., and T. Augustin. 2005. Powerful algorithms for decision making under partial prior information and general ambiguity attitudes. In Proceedings of the forth international symposium on imprecise probability: theories and applications (ISIPTA ’05, Pittsburgh), eds. Cozman, F., Nau, R., and T. Seidenfeld, 349–358. Pittsburgh: SIPTA.

    Google Scholar 

  • Utkin, L., and T. Augustin. 2007. Decision making under imperfect measurement using the imprecise Dirichlet model. International Journal of Approximate Reasoning 44:322–338.

    Article  Google Scholar 

  • Vicig, P., and T. Seidenfeld. 2012. Bruno de Finetti and imprecision: imprecise probability does not exist! International Journal of Approximate Reasoning 53:1115–1123.

    Article  Google Scholar 

  • Walley, P. 1991. Statistical reasoning with imprecise probabilities. London: Chapman and Hall.

    Book  Google Scholar 

  • Walley, P. 1996. Inferences from multinomial data: learning about a bag of marbles (with discussion). Journal of the Royal Statistical Society. Series B (Methodological) 58:3–57.

    Article  Google Scholar 

  • Wallner, A. (2007). Extreme points of coherent probabilities on finite spaces. International Journal of Approximate Reasoning, 44, pp. 339–357.

    Article  Google Scholar 

  • Wassemann, L., and T. Seidenfeld. 1994. The dilation phenomenon in robust Bayesian inference (With discussion). Journal of Statistical Planning and Inference 40:345–356.

    Article  Google Scholar 

  • Weichselberger, K. 2001. Elementare Grundbegriffe einer allgemeineren Wahrscheinlichkeitsrechnung I: Intervallwahrscheinlichkeit als umfassendes Konzept (in German) [Elementary Foundations of a More General Calculus of Probability I: Interval Probability as a Comprehensive Concept]. Heidelberg: Physica.

    Google Scholar 

  • Weichselberger, K., and S. Poehlmann. 1990. A Methodology for Uncertainty in Knowledge-Based Systems. Berlin: Springer.

    Google Scholar 

  • Wheeler, G. 2012. Objective Bayesianism and the problem of non-convex evidence. British Journal for the Philosophy of Science 63:841–850.

    Article  Google Scholar 

  • Wheeler, G. 2022. A gentle approach to imprecise probablities. In Reflections on the Foundations of Probability and Statistics: Essays in Honor of Teddy Seidenfeld, eds. Augustin, T., Cozman, F., and G. Wheeler, 37–67. Berlin: Springer.

    Google Scholar 

Download references

Acknowledgements

We are grateful to two referees for their very helpful comments and to Sebastien Destercke for valuable discussions about decision criteria. Moreover, we want to express our gratitude to Jean Baccelli, Seamus Bradley, Stephan Hartmann, Arthur Merin, Jürgen Landes, Gregory Wheeler and many other (former) members of the Munich Center for Mathematical Philosophy for stimulating talks and discussions on decision theory and imprecise probabilities during the last years, and to Teddy Seidenfeld for inspiring lectures and discussions not only during his visits to Munich.

Author information

Authors and Affiliations

  1. Department of Statistics, Ludwig-Maximilians-University of Munich, Munich, Germany

    Christoph Jansen, Georg Schollmeyer & Thomas Augustin

Authors
  1. Christoph Jansen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Georg Schollmeyer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas Augustin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christoph Jansen .

Editor information

Editors and Affiliations

  1. Department of Statistics, Ludwig-Maximilians-University of Munich, Munich, Germany

    Thomas Augustin

  2. Universidade de São Paulo, São Paulo, Brazil

    Fabio Gagliardi Cozman

  3. Frankfurt School of Finance & Management, Frankfurt am Main, Germany

    Gregory Wheeler

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Jansen, C., Schollmeyer, G., Augustin, T. (2022). Quantifying Degrees of E-admissibility in Decision Making with Imprecise Probabilities. In: Augustin, T., Cozman, F.G., Wheeler, G. (eds) Reflections on the Foundations of Probability and Statistics. Theory and Decision Library A:, vol 54. Springer, Cham. https://doi.org/10.1007/978-3-031-15436-2_13

Download citation

Publish with us

Policies and ethics

Search

Navigation