Generating Synthetic Graph Data from Random Network Models

Abstract

Network models are developed and used in various fields of science as their design and analysis can improve the understanding of the numerous complex systems we can observe on an everyday basis. From an algorithmics point of view, structural insights into networks can guide the engineering of tailor-made graph algorithms required to face the big data challenge.

By design, network models describe graph classes and therefore can often provide meaningful synthetic instances whose applications include experimental case studies. While there exist public network libraries with numerous datasets, the available instances do not fully satisfy the needs of experimenters, especially pertaining to size and diversity. As several SPP 1736 projects engineered practical graph algorithms, multiple sampling algorithms for various graph models were designed and implemented to supplement experimental campaigns. In this chapter, we survey the results obtained for these so-called graph generators. This chapter is partially based on [43 SPP].

1 Motivation

Networks are the very fabric that makes societies [5, 40]. As such, humanity is seeking to understand their structures, rules, and implications for centuries (see also Sect. 1). The practical importance of networks, however, only sky-rocketed with the advent of the information age. Nowadays, modern computers offer sufficient storage and processing capacity to map out most aspects of human life and the world we inhabit. They are fed by billions of interconnected sensors and computerized personal devices that produce enormous volumes of network data to be exploited.

Computer science provides the means to face this big data challenge. However, a formal grammar capturing the inner structure of the data expected to be processed is required to provide tailor-made solutions. Network models are just that: a mathematical tool to describe and analyze realistic graphs. Research into and applications of these models are deeply intertwined with various fields of science.

Networks are commonly modeled by so-called random graphs and, therefore, represent probability distributions over the set of graphs [8]. These distributions are almost always parametrized (e.g., for the graph size or density) and typically follow implicitly from some randomized construction algorithm. Popular models are designed such that we¹ can expect certain topological properties from a randomly drawn instance: a particularly interesting goal is to reproduce the loosely defined class of complex networks which, among others, encompasses most social networks.

By expressing network models as random graphs, we inherit a rich set of tools from combinatorics, stochastics, and graph theory. In algorithmics we may, for instance, assume that meaningful inputs are random instances of a suitable network model. Then we can derive realistic formal performance predictions using average-case analysis, smoothed complexity, et cetera. In practice, such results tend to be more relevant than worst-case analysis based on pathologic structures that are implausible in applications.

Network models also enable or supplement experimental campaigns as a versatile source of synthetic data with controllable independent variables. Synthetic benchmarks are especially useful in the context of large instances where real data is typically unavailable in sufficient size, quantity, or variety. Even if the data exists, procuring and archiving it may be difficult for legal or technical reasons; this threatens the independent reproducibility of results and thus infringes on one of science’s cornerstones [45].

1.1 Structure

In Sects. 1.2 and 1.3, we introduce the definitions and notation used in this chapter. The main part of the chapter is then organized by the network model type. Section 2 discusses the notation of random graphs in detail and introduces sampling algorithms for the $\mathcal {G}(n,p)$ and $\mathcal {G}(n,m)$ models.

Sections 3 to 5 deal with random graph classes that focus on the distribution of degrees. Preferential attachment models, and especially the BA model by Barabási and Albert, explain the emergence of powerlaw degree distributions in growing networks; we discuss suitable sampling algorithms, so-called (graph) generators, in Sect. 3. The R-MAT, also capable of producing powerlaw degree distributions, is presented in Sect. 4. In Sect. 5, we consider several solutions for the following problem: given a list of degrees, produce a uniform sample from the set of all simple graphs that satisfy these degrees. Section 6 discusses geometrically embedded random graphs including the popular Random Hyperbolic Graphs.

Finally, in Sect. 7, we introduce network analysis and generator software supported by the SPP 1736.

1.2 Notation

A graph $G=(V,E)$ models a set of objects (nodes) $V = \{v_1, \ldots , v_n\}$ and their connections E (edges). Throughout this chapter, we will denote the numbers of nodes and edges as $n = |V|$, and $m = |E|$ respectively. A graph class is called sparse if $m = \mathcal {O}{(n {{\,\textrm{polylog}\,}}n)}$ and dense if $m = \varTheta (n^2)$.

Edges can encode a direction (i.e., $E \subseteq V \times V$) or be undirected (i.e., $E \subseteq \{ \{u,v\}\,| u,v \in V\}$). If not stated differently, we assume undirected graphs. An edge that exists multiple times is called multi-edge and part of a multi-graph. A graph without multi-edges or self-loops (edges between one node) is called simple.

Two nodes u and v connected by an edge e are neighbors or said to be adjacent; the nodes u and v, in turn, are incident to the edge e. The number of neighbors of a given node $u \in V$ is called its degree $\deg (u)$. A sequence $(\deg (v_1), \ldots , \deg (v_n))$ is called a degree sequence. The related concept of a degree distribution refers to the probability distribution of the degree of a randomly sampled node (possibly in a randomly sampled graph). Many observed networks exhibit a powerlaw degree distribution where the probability of degree k is proportional to $k^{-\gamma }$ for some $2 < \gamma$ (and often $\gamma < 3$). A property applies with high probability (w.h.p.) if it holds with probability of at least $1 - x^{-\alpha }$ for $\alpha \ge 1$ where x depends on the context and is often the problem size n or m.

1.3 Models of Computation

The design of an algorithm is heavily influenced by the assumed model of computation. If not state differently we suppose the unit-cost RAM in which operations for control-flow, data access, and basic arithmetic are handled in constant time. For shared-memory parallel algorithms, its parallel variant PRam is used. In a parallel context, we use the term processing unit (PU) to refer to an abstract machine executing a sequential algorithm (e.g., a core in a CPU or an individual processor in a distributed computer cluster). A problem is said to be pleasingly parallel if it consists of sufficiently many subproblems that can trivially be computed independently.

To model the cost of data transfer, the external memory model by Aggarwal and Vitter [1] assumes a two-level memory hierarchy. It consists of an internal memory of size M and an unbounded external disk which holds the algorithm’s input and output. Computation is free, but is only possible on data in internal memory and therefore has to be move to and fro. Data access is block-oriented and transfers B data items per I/O. Reading and writing N contiguous items is referred to as scanning and requires $\text {scan}(N) = \varTheta (N/B)$ I/Os. Sorting such items triggers $\text {sort}(N) = \varTheta ( (N/B) \log _{M/B}(N/B))$ I/Os and constitutes a lower-bound for most intuitively hard problems.

Analogously, the cost of communication is often a bottleneck for distributed machines consisting of interconnected processors. Communication-agnostic algorithms are an extreme case of communication avoidance. Each PU is only aware of its rank, the total number of PUs, and some input configuration. However, exchange of any further information during the execution of the algorithm is prohibited.

2 Random Graphs and the G(n, p) and G(n, m) Models

A random graph is a probability distribution $P:\mathbb G \rightarrow [0, 1]$ where $\mathbb G$ is the set of all graphs. Virtually all random graph models² are parameterized and thus form families of probability distributions. The underlying distributions are typically specified implicitly, and often have a finite support defined by some combinatorial constraints.

As an example, consider the popular $\mathcal {G}(n,p)$ model introduced by E. Gilbert [20] in 1959. In its original formulation, the model’s support consists of all $2^{n(n+1)/2}$ undirected graphs with exactly n nodes. The probability distribution is given indirectly via the following sampling algorithm:

“Pick one of these graphs by the following random process. For all pairs of points [nodes] make random choices, independent of each other, whether or not to join the points of the pair by a line [edge]. Let the common probability of joining be p.” [20]

In other words, in a random instance of $\mathcal {G}(n,p)$ any edge e exists independently with probability p. Observe that G(n, 1/2) hence implies the uniform distribution of all graphs with n nodes. It is therefore a so-called maximum entropy model and sometimes even referred to as the random graph [5].

Erdős and Rényi [17] propose the related and well-known $\mathcal {G}(n,m)$ model as the uniform distribution over all undirected graphs with n nodes and m edges. The models $\mathcal {G}(n,p)$ and $\mathcal {G}(n,m)$ with $m = \left( {\begin{array}{c}n\\ 2\end{array}}\right) p$ are equivalent in the limit of $n \rightarrow \infty$.

Neither $\mathcal {G}(n,p)$ nor $\mathcal {G}(n,m)$ explain the non-trivial structural properties of observed networks. Since all edges are chosen (mostly) independently with identical probabilities, we do not expect the formation of any complex features. Several ways to formalize this intuition are discussed in [44 SPP]. Still, the models are commonly used to generate synthetic data, e.g., as a null-model.

2.1 Sampling from $\mathcal {G}(n,p)$ and $\mathcal {G}(n,m)$

Gilbert’s sampling algorithm is designed to communicate the model’s spirit to a human reader and, as such, is not optimized for performance. The generator thus requires $\varOmega (n^2)$ work independently of the linking probability p which is suboptimal for non-dense graphs.

Batagelj and SPP 1736 PI Brandes [6] describe an optimal sequential generator requiring work linear in the number m of edges produced. The algorithm fixes a convenient order of all possible edges (i.e., a bijection $\pi :[\left( {\begin{array}{c}n\\ 2\end{array}}\right) ] \rightarrow \{ \{u,v\}\, |\, u, v \in V \wedge u \ne v \}$) and considers them in this sequence. Since each edge in a $\mathcal {G}(n,p)$ graph is the result of an independent Bernoulli trial, the number of “non-edges” between any two successful trials follows a geometric distribution. The generator therefore draws a random geometric variate, jumps over that many non-edges, writes out the next edge, and repeats until all possible edges have been considered.

Since all edges are drawn independently, the generator can be parallelized by partitioning the sequence of possible edges into independent sub-problems of roughly equal size. Later, Bringmann and Friedrich [9] give an exact variant of the algorithm that does not require real-valued arithmetic to sample the skip distances.

Sampling from $\mathcal {G}(n,m)$ is more challenging than $\mathcal {G}(n,p)$ since faithful $\mathcal {G}(n,m)$ generators can not assume independent trials. This is due to the fact that partially sampled edges and non-edges affect the probability distribution of the remaining candidates. While Batagelj and Brandes remark that their $\mathcal {G}(n,p)$ generator can be extended to $\mathcal {G}(n,m)$ by modifying the skip distance distribution accordingly, they continue to develop a more efficient alternative requiring work linear in the number of edges produced [6].

In the following, we however focus on a parallel approach by Funke  et al.  [18 SPP] and showcase general divide-and-conquer techniques used to yield communication-agnostic generators. The resulting generator is a variant of a parallel sampling algorithm [47 SPP] for the related problem of randomly selecting m distinct elements from a finite universe (i.e., sampling without replacement).

For simplicity’s sake, we only consider the directed variant of $\mathcal {G}(n,m)$.³ In order to parallelize, we partition the set of nodes V into disjoint subsets $V_1, \ldots , V_p$ of roughly equal size. Then, processing unit i is tasked to produce the $m_i$ out-going edges of nodes in $V_i$. By definition of $\mathcal {G}(n,m)$, we require that $\sum _i m_i = m$. Observe that this is the only dependency between subproblems. Thus, if $m_i$ is known a priori, PU i can work independently.

Consequently, we need to find a communication-agnostic way to agree on a consistent and randomly chosen $\textbf{m}= (m_1, \ldots , m_P)$ where each PU only needs to know its own value $m_i$. The vector $\textbf{m}$ follows a multinomial hypergeometric distribution where the number of “positive instances” for the i-th entry are given by the number $n\cdot |V_i|$ of potential edges processed by PU i. Under the assumption that the number P of PUs satisfies $P = \mathcal {O}{(n / \log n)}$ the values of $m_i$ are sufficiently concentrated to bound the complexity of the previous local sampling to $\mathcal {O}{((n+m) / P)}$ w.h.p..

A traditional distributed generator may sample $\textbf{m}$ on a central PU and then broadcast the values—this is, however, not possible in a communication-agnostic setting since it incurs a communication volume $\varOmega (P)$. Alternatively, each PU can independently sample $\textbf{m}$ with pseudo-random number generators that use a common seed value. This approach requires expected time $\varTheta (P)$ and, thus, dominates the total runtime for $P = \omega (\sqrt{m})$.

Thus, we rather follow a divide-and-conquer approach which works for various distributions and is also used in Sect. 6.3. Roughly speaking, each $m_i$ corresponds to a leaf in a binary tree of depth $\mathcal {O}{(\log P)}$. At each inner node, we draw a random variate x from an appropriately parametrized hypergeometric distribution and interpret x as the number of edges to be produced in the left subtree. Each PU follows its unique path from the root to the i-th leaf to sample its own value of $m_i$. To achieve consistent values, the sampling at each inner node is carried out using a pseudo-random number generator whose seed is deterministically derived from a unique node index.

The authors show that combining these ideas yields a communication-agnostic generator with a runtime complexity of $\mathcal {O}{((n+m)/P + \log P)}$ w.h.p..

3 Preferential Attachment

Barabási and Albert [4] propose a simple stochastic process to explain the emergence of scale-free networks and show that two ingredients, namely growth and selection bias, suffice to yield networks with powerlaw degree distributions.⁴

At its core, their BA model relies on preferential attachment, a positive feedback loop in dynamic systems where selecting an item at one point in time increases the probability of selecting it again in the future. It is proverbially summarized as “the rich get richer”.

Based on this idea, the authors describe the following random graph. Starting with an arbitrary seed graph $G_0$ with $n_0$ vertices and $m_0$ edges, we iteratively add $n - n_0$ nodes—one node at a time. For each new node, we choose d neighbors at random where the probability to select node v is proportional to the degree of v at that time.

The main algorithmic challenge of BA lies in this dynamic weighted sampling. Depending on the assumed model of computation, quite different solutions are available. Batagelj and Brandes [6] observe that each node with degree k appears exactly k-times in the edge list produced so far. Therefore, the underlying dynamic weighted sampling problem can be reduced to uniformly selecting entries from the edge list, leading to the linear-time generator BB-BA.

As BB-BA requires unstructured I/Os, it cannot efficiently produce graphs that do not fit into main memory. Meyer and Penschuck [36 SPP] introduce TFP-BA and MP-BA, the first two I/O-efficient sampling approaches for random graph models based on preferential attachment. The authors initially focus on BA graphs to demonstrate the techniques and subsequently discuss additional features such as seed graphs exceeding main memory, nodes with inhomogenous initial degrees, the inclusion of uniform node sampling, directed graphs, and edges between two randomly chosen nodes.

• TFP-BA is a simple and easily generalizable sequential generator inspired by BB-BA. Rather than reading from random positions in the edge list, TFP-BA first precomputes all necessary read operations and sorts them by the memory address they read from. As the algorithm produces the edge list monotonously moving from beginning to end, it scans through the sorted read request and forwards the still cached values to the target positions using an I/O-efficient priority queue. This approach requires $\mathcal {O}{(\text {scan}(m_0) + \text {sort}(m))}$ I/Os, where $m_0$ is the number of edges in the seed graph and m is the number of edges produced.

• MP-BA is a parallel generator that offloads a number of subtasks onto a general-purpose graphics processor. The algorithm implements dynamic weighted sampling using a binary tree T partially stored in external memory. Each node u of the generated graph corresponds to a leaf in T labeled with the degree of u; any inner node stores the total weight of all leaves contained in its left subtree.

  In order to select a neighbor, MP-BA first has to sample a leaf according to the current degree distribution and then increment the leaf’s weight to account for the newly gained edge. The key insight is that we can do both in a single top-down traversal from the root to the sampled leaf. This allows us to combine the queries for sampling and updating into a single operation and, in turn, to coalesce queries into batches. MP-BA requires $\mathcal {O}{(\text {sort}(n_0 + m))}$ I/Os, where $n_0$ is the number of nodes in the seed graph and m is the number of edges produced.

  The algorithm uses two forms of parallelism: firstly, T is cut at a certain depth to process the subtrees rooted there pleasingly parallel. In order to handle the high volume of requests near T’s root, a dedicated PRam algorithm processes multiple requests to the same tree node in parallel. MP-BA ’s implementation executes the latter part on a GPU for maximal throughput.

Sanders and Schulz [48 SPP] describe CA-BA, a communication-agnostic generator for distributed-memory parallelism. Their algorithm builds on top of BB-BA and uses pseudo-randomization to avoid all lookups to edges generated. By doing so, several PUs can work on the problem without exchanging information other than an initial broadcast of the seed graph and a few parameters. In contrast to the original algorithm, CA-BA does not maintain an edge list to sample from explicitly. To simplify the description, we still presume its existence as a concept for addressing.

In order to add an edge, the generator needs to place the indices of the two incident nodes into the edge list. Recall that each generated edge consists of a newly introduced node and a randomly selected neighbor. By convention, we store the former at even positions of the edge list, and the latter at odd positions. Since by definition of the BA model, each newly introduced node is initially incident to exactly d edges, all entries at even positions follow from a simple index transformation.

Sampling random neighbors involves a shared random hash function $h(\cdot )$ with the property that $h(i) < i$. Then, in order to choose the node index of the random neighbor to be written to the edge list’s i-th position, we conceptually copy the value from position $j=h(i)$. To do so, we distinguish three cases:

• 1. If $j < 2m_0$, we need to retrieve a value from the seed graph which is a simple read access to the input data. It is the only case where an actual memory access needs to be carried out.

• 2. If $j \ge 2m_0$ and j is even, we can compute the value stored there using the aforementioned index transformation.

• 3. If $j \ge 2m_0$ and j is odd, we retrace the sampling carried out. To do so, we recurse on $j' = h(j) = h(h(i))$.

The first two cases imply constant work on a unit-cost RAM. Since we assume $h(\cdot )$ to be a random function, the first two cases are chosen with probability of at least 1/2. Thus, the recursion of the last case has an expected depth of at most 2 and is $\mathcal {O}{(\log m)}$ with high probability. Assuming $h(\cdot )$ can be evaluated in constant time, CA-BA therefore requires expected linear work.

4 R-MAT

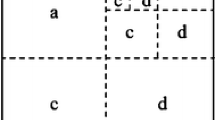
R-MAT [15] graphs are a well-accepted network model which is especially known for its use in the Graph500 benchmark [38]. The model is defined for graphs on $2^k$ nodes and m edges. To sample an edge, we recursively subdivide the adjacency matrix into four quadrants, assign them probabilities $p_a + p_b + p_c + p_d=1$ provided as model parameters, and randomly select one. We repeat this k times until we reach a matrix of size $1 \times 1$ which corresponds to the edge. Depending on the model, we either allow multi-edges, or reject and resample to avoid duplicates. Undirected graphs are possible and typically imply additional symmetry constraints on the quadrant probabilities. For certain sets of parameters, the model exhibits similarities to observed networks such a powerlaw degree distribution [34].

Following the recursive definition, there exists a bijection between each possible edge and the set of words $\varSigma ^k$ over $\varSigma = \{\mathtt a, \mathtt b, \mathtt c, \mathtt d\}$ where each $x \in \varSigma$ represents the quadrant chosen. A naive R-MAT generator explicitly samples the k characters, one after another, and thus requires $\varOmega (\log n)$ work per edge.

Hübschle-Schneider and Sanders [27 SPP] propose a communication-agnostic scheme that instead samples edges in constant time under the reasonable assumption that $m = \varOmega (n)$. The algorithms performs a preprocessing step to construct an urn which contains $n^\alpha$ path fragments (for some $\alpha < 1$) weighted by their probabilities in time $\mathcal {O}{(n)}$, e.g., by considering all words $\varSigma ^\ell$ of fixed length $\ell = \log _2\sqrt{n} = k / 2$.

To draw an edge we sample $\lceil k / \ell \rceil = \mathcal {O}{(1)}$ fragments. We then concatenate them using bit-parallel shifting and masking operations available in virtually all modern computers. Both steps require only constant time per edge.

5 Simple Graphs from Prescribed Degree Sequence

The sampling of random graphs matching a prescribed degree sequence is a common task in network analysis. Its various applications range from to the construction of null-models (e.g.,  Sect. 3) to use-cases as building blocks in graph generators. Instances of the latter are the popular LFR benchmark [28] or the derived ReCon  [51 SPP] model to generate scaled-replicas of an input graph.

The computational cost of this approach heavily depends on the exact formulation of the model. Two models with linear work sampling algorithms are the Chung-Lu (CL) model and the Configuration Model (CM). The CL model produces the prescribed degree sequence only in expectation (see [44 SPP] for details). The CM, on the other hand, exactly matches the prescribed degree sequence but permits self-loops and multi-edges. These parallel edges affect the uniformity of the model [39, p. 436] and are inappropriate for certain applications; however, erasing them may lead to significant changes in topology [49 SPP]. In the following, we focus on simple graphs (i.e., without self-loops or multi-edges) matching a prescribed degree sequence exactly. Several generators and models for such graphs were considered within the SPP 1736.

5.1 The Edge Switching Markov Chain Model

The Fixed-Degree-Sequence-Model (FDSM) is a common solution to obtain simple graphs from a prescribed degree sequence. It first manifests a biased deterministic graph (e.g., using the Havel-Hakimi algorithm [23, 26]) and then uses an Edge Switching (ES) Markov chain process [21] to perturb the graph. In each step, the process selects two edges uniformly at random and exchanges their incident nodes—by doing so the degrees of all nodes involved do not change. If a step were to result in a self-loop or multi-edge, it is rejected without replacement. Despite intensive research, it remains an open problem to find practical upper bounds on the Markov chain’s mixing time; i.e., the number of steps required to obtain a uniform sample. In practice, a small multiple of the number of edges typically suffices (cf. Sect. 3).

The main issue when implementing ES is the large number of unstructured accesses to memory; for each switch it is necessary to identify the involved nodes, check whether the updated edges already exist, and finally to write out the updates.

Hamann et al.  [25 SPP] describe EM-LFR, an I/O-efficient pipeline to sample large instances from the LFR model. From an algorithmic point of view, two central parts of the pipeline are EM-HH and EM-ES which together implement FDSM. EM-HH is designed to avoid memory accesses as best as possible especially for graphs with powerlaw distributions. EM-ES, on the other hand, batches $\varTheta (m)$ individual swaps and processes them out-of-order without changing the outcome; due to the large number of swaps in each batch, we can amortize the I/O volume and stream through the whole graph a constant number of times rather than executing $\varTheta (m)$ more expensive unstructured accesses.

Later, [24 SPP] propose a modification of the FDSM model and provide empirical evidence of faster mixing. The previous combination of EM-HH followed by EM-ES starts with a highly biased simple graph. The novel EM-CM/ES takes another route: It starts with a random but non-simple graph and switches edges until a simple random graph is obtained. It uses an I/O-efficient generator for the Configuration Model and a variant of EM-ES which accepts non-simple inputs without increasing its I/O complexity. The modified algorithm executes all switches that neither increase the multiplicity of a given edge nor introduce self-loops. Non-simple edges are also switched more frequently than legal edges to accelerate the repair phase. Observe, however, that it does not suffice to rewire non-simple edges using the presented variant of ES as it produces a biased sample [2, 3]. Instead, additional ES steps are necessary.

Brugger  et al.  [12 SPP] implement ES in hardware (see Sect. 4 for details). Their design maintains the graph in a hybrid data structure combining an adjacency list to efficiently sample edges and an adjacency matrix for fast edge existence queries. Then, the authors investigate two cases:

• First they perturb several independent graphs pleasingly parallel where each graph is stored in a dedicate physical region (DRAM channel) of common memory chips. In this setting, the authors optimize the memory controller to address channels independently and interleave these requests.

• In a second step, parallelism within a single ES run is exposed using the following observation: If the graph is sufficiently large, the probability that a short run of multiple switches target a common edge is small (cf. birthday problem). The authors therefore describe a hardware design that checks whether 12 contiguous switches are collision-free and if so, execute them in parallel.

5.2 Curveball

Curveball (CB) [52] is a more recent process but structurally similar to ES; instead of selecting random edges, CB selects two random nodes $u \ne v$, and trades their neighborhoods as follows. CB begins by freezing all edges that either connect u and v themselves or link to neighbors which u and v have in common. Then, the remaining neighbors are randomly shuffled while maintaining the degrees of u and v. A single CB trade can therefore inflict “more change” to a graph than a single edge switch; depending on the processed graph, a state in CB ’s Markov chain may have up to $2^{\varTheta (n)}$ neighbors while the degrees in ES ’s chain are bounded by $\mathcal {O}{(n^4)}$ [13]. Empirical data suggests that fewer trades are necessary to mix a graph (though each trade may require more work).

CB exposes more data locality than ES since all information required to carry out a trade is contained in the two neighborhoods. This is in contrast to ES, which requires additional unstructured reads to prevent a switch from introducing multi-edges. Note, however, that an undirected edge is classically stored twice—once for each endpoint. In this scenario, frequent unstructured updates are necessary and negate the previously mentioned locality benefits.

The I/O-efficient EM-CB algorithm [14 SPP] thus relies on a dynamic data structure and assigns each edge only to the endpoint that is traded next. EM-CB uses the external-memory technique Time Forward Processing (TFP, see [35]) to ensure that the complete neighborhood of a node is available when needed.

The algorithm works in batches. At the beginning of each batch, it samples the node pairs to be traded within the batch and organizes them in dedicated indices. These auxiliary data structures are used to address the TFP messages and to determine which endpoint of an edge will be traded first. EM-CB requires $\mathcal {O}{(r[\text {sort}(n) + \text {sort}(m)])}$ I/Os to carry out r global trades (see below).

Carstens  et al.  [14 SPP] generalize Global Curveball (G-CB) to undirected graphs. An undirected global trade is a sequence of $\lfloor n / 2 \rfloor$ single trades such that the neighborhood of each node is traded at most once. They show that the process converges to a uniform distribution over the set of all graphs and give empirical evidence of its superior performance compared to CB.

Since each node participates once⁵ in a global trade, we can interpret a global trade as a random permutation of nodes where we trade pairwise adjacent nodes. The authors then propose an algorithm that eliminates the auxiliary data structures by maintaining the permutation implicitly using a collision-free (on the relevant domain) and invertible hash function, and finally give a parallel version of it.

6 Geometrically Embedded Random Graphs

Random Hyperbolic Graphs (RHGs) are a popular network model which naturally exhibits many features commonly observed in complex networks. RHG assigns each node a position on a two-dimensional hyperbolic disk of radius R. These positions are conveniently expressed in polar coordinates where each point is located in terms of its distance r (radius) to the disk’s center and an angular coordinate $\theta$.

In the so-called Threshold RHG  [22], we connect all pairs of points $(r_i, \theta _i)$ and $(r_j, \theta _j)$ with $i \ne j$ whose hyperbolic distance $d(p_i, p_j)$ is smaller than R, where

$$\begin{aligned} \cosh ( d(p_i, p_j) ) = \cosh (r_i)\cosh (r_j) - \sinh (r_i)\sinh (r_j)\cos (\theta _i - \theta _j). \end{aligned}$$

(1)

Thus, the hyperbolic distance is a function of the relative and absolute positions of both points; the closer a point is to the disk’s center, the more neighbors it is expected to have. We obtain a powerlaw degree distribution with a controllable exponent by choosing an appropriate radial density for the randomly placed points.

Binomial RHG extends Threshold RHG by adding a positive temperature parameter T that affects the local cohesion. In the binomial variant, each pair of nodes $p_i \ne p_j$ is independently connected by an edge with probability $p_T(d(p_i, p_j))$ defined as follows:

$$\begin{aligned} p_T(d) = \left[ \exp \left( \frac{d-R}{2T}\right) + 1\right] ^{-1} \end{aligned}$$

(2)

Binomial RHG contains Threshold RHG as $p_T$ becomes a step function for $T \rightarrow 0$. Looz and Meyerhenke [31 SPP] propose an extension of the RHG model to generate dynamic graph data sets: their model adds movement of nodes which in turn translates to a stream of edge insertions and deletions.

6.1 Efficient Generators Based on Geometric Data Structures

A naive RHG generator that checks each node pair for an edge requires $\varOmega (n^2)$ work and little parallel depth⁶. All efficient generators we are aware of reduce the computational complexity in a two step process: they cheaply identify a set of edge candidates (i.e., a super-set of the true result), and then filter the candidates more carefully. The identification typically exploits geometrical or stochastic arguments, while the filtering process tends to involve costly per edge distances computations.

All geometric generators discussed in the remainder of this chapter use one of two geometric partitioning schemes, namely a quad-tree or a band structure.

• Looz et al.  [32 SPP] describe NkQuad, the first sub-quadratic work RHG generator. NkQuad is based on a polar quad-tree which recursively subdivides the space into four quadrants each (i.e., each inner tree-node introduces two cuts, one in the angular and one in radial dimension, respectively). The generator then iterates over all nodes and computes for each $v \in V$ the neighbor candidates $C_v$. The set $C_v$ consists of all nodes in quad-tree leaf cells which intersect the hyperbolic circle of radius R around v. The identification of such leafs is simplified by working in the Poincare projection which translates hyperbolic circles into (radially shifted) Euclidean circles. The authors show that such a query examines $\mathcal {O}{(\sqrt{n} + |C_v|)}$ leafs w.h.p., leading to total work of $\mathcal {O}{((n^{3/2} + m) \log n)}$ w.h.p..

  Later, Looz and Meyerhenke [30 SPP] generalize the data structure and extend the generator to Binomial RHG while maintaining the asymptotic complexity. The efficient sampling of low-probability edges is implemented by bounding the probability to connect to any edge within a leaf from above. These bounds are used to carry out geometric jumps (cf. Sect. 2) followed by rejection sampling to account for the over-estimation.

• Looz  et al.  [33 SPP] improve NkQuad by proposing NkBand featuring a novel partitioning scheme. NkBand covers the hyperbolic disk with $\varTheta (\log n)$ disjoint concentrical bands where each band is maintained as an array of points sorted by their angles. To find the neighbor candidates of a node v in band $b_i$, the algorithms considers $b_i$ and all bands containing larger radii. For each such band $b_j$, the smallest and largest angular coordinate of a potential neighbor of v in $b_j$ is computed; then two binary search yield the left- and right-most candidates in the sorted array. By doing so, the authors effectively over-estimate the upper half of the hyperbolic circle around node v by a discrete stack of shrinking band-segments. The generator has an empirical runtime of $\mathcal {O}{(n \log n + m)}$. Later, Looz [29 SPP] extends NkBand to Binomial RHG using ideas similarly to the generalization described for NkQuad.

6.2 A Fast and Memory-Efficient Streaming Generator for RHG

As the geometric data structures discussed for NkQuad, NkBand, and HyperGirgs have a large memory footprint that can render them unsuitable for accelerator hardware with a small dedicated memory, [42 SPP] presents HyperGen, a streaming generator for Threshold RHGs which instead samples the points on demand. The generator requires $\mathcal {O}{([n^{1- \alpha } \bar{d}^\alpha + \log n] \log n)}$ words of memory w.h.p.. For realistic average degrees $\bar{d} = o(n / \log ^{1/\alpha }(n))$ this is a significant asymptotic reduction over classical approaches.

HyperGen executes a sweep-line algorithm and stores the set of nodes that may still find neighbors in its sweep-line state; we refer to them as candidates. Roughly speaking, the algorithm randomly samples points with non-decreasing angular coordinates.⁷ For each new point, the algorithm identifies all sufficiently close candidates and emits edges to them. The generator then marks the point a candidate itself and advances the sweep-line. HyperGen stops the sweep-line at additional points, e.g., to prune candidates whose distances to the sweep-line are so large that they cannot find neighbors anymore.

To manage the computational cost of maintaining the sweep state, HyperGen includes conservative approximations that do not infringe on the generator’s faithful reproduction of RHGs. They exploit the distribution of points as well as properties of the hyperbolic distance function. The majority of points can be quickly pruned from the algorithm’s state. In contrast, the few points that have small radii stay candidates for a significantly longer period of time. To accommodate the different requirements, HyperGen partitions the hyperbolic disk into $\varTheta (\log n)$ concentrical bands. Each band has its own sweep-line and state which remain synchronized with the states of its adjacent bands.

Observe that, due to the angular periodicity of the hyperbolic disk, points sampled late (i.e., with angles near $2\pi$) can be adjacent to points discovered and pruned much earlier. HyperGen accounts for this by restarting the sampling process until all candidates of the first phase are processed. It exploits pseudorandomness to obtain consistent point coordinates in both phases.

Parallelization is possible by splitting the disk into segments of equal size. Some care has to be taken to manage the dependencies near the segments’ borders. HyperGen also significantly accelerates the frequent distance computations by preparing auxiliary values per point. This removes all transcendental functions (here $\sinh$, $\cosh$, and $\cos$) from Eq. (1). Refined versions of these techniques carry over to Sects. 6.3 and 6.4.

The implementation of HyperGen is designed with SIMD (Single-Instruction-Multiple-Data) in mind and is explicitly vectorized. It uses SIMD instructions to compute eight hyperbolic distances simultaneously (which is only possible because we first removed the aforementioned transcendental functions).

6.3 Communication-Agnostic Generators for RHG

Funke et al.  [19 SPP] present Rhg, a communication-agnostic generator for Threshold RHG. The generators Rhg and HyperGen were developed independently at roughly the same time, and share ideas to sample specific subsections of the hyperbolic disk using pseudorandomization. While HyperGen uses a monotonous sweep-like motion optimized for memory usage, Rhg uses less structured queries. These “random” queries are answered using a fine-grained partitioning of the hyperbolic space which ingeniously allows random access to any cell (the geometry is similar to the one discussed in Sect. 6.1).

For huge graph instance, the number of nodes may be too large to sample —let alone store— all nodes on every distributed machine. Fortunately, a key property of relevant RHG graphs is that most nodes only have a very local neighborhood, i.e., a hyperbolic circle around each node suffices to compute all its links. Observe that many of these subsets overlap due to common edges. In general, there is no balanced mapping of nodes to processing units without overlaps. Thus, any two PUs with overlapping subsets have to have a consistent view of the underlying region of hyperbolic space.

We achieve this by partitioning the hyperbolic space into k cells. Then, the following process reproducibly samples points within a cell. First, a hash function f is used to seed a pseudorandom number generator with the value f(i). For each cell i, we seed a pseudorandom generator with a value deterministically derived from the cell’s index i and, subsequently, use the generator to sample the $n_i$ points contained within the cell. By construction, this process yields consistent results even if executed by multiple independent processing units.

The only information missing is the number $n_i$ of points in cell i. The vector $\textbf{N}= (n_1, \ldots , n_k)$ follows a multinomial hypergeometric distribution due to the side condition that exactly n points need to be scattered in total, i.e., $\sum _i n_i = n$. All PUs obtain consistent values for $\textbf{N}$ using common seeds for their pseudorandom generators analogously to the divide-and-conquer approach in Sect. 2.1.

In [18 SPP], this techniques is combined with HyperGen (see Sect. 6.2) yielding the communication-agnostic sweep-line generator sRhg which consistently outperforms Rhg. We demonstrate its scalability to up to 32 768 cores and produce a graph with $n=2^{39}$ nodes in less than a minute.

6.4 GIRG-Based Generator

Bringmann et al. propose Geometric Inhomogenous Random Graphs as a flexible and simple model, that asymptotically contains RHG  [11]. Roughly speaking, the model embeds a graph into an d-dimensional torus and uses node weights to control the degree sequence similarly to the Chung-Lu model. The authors also give an expected linear time sampling algorithm for GIRGs [10] which we engineer adapt⁸ it to Binomial RHGs in [7 SPP]. We refer to our algorithms as Girgs and HyperGirgs, respectively. To the best of our knowledge, Girgs is the first practically efficient generator for the GIRG model. Here, we focus on RHGs since the algorithmic treatment of both models is very similar.

HyperGirgs first samples all points and builds a data structure that can be interpreted as a polar quad-tree. While the structure is similar to the previous state-of-the-art generator NkQuad (see Sect. 6.1), differences in details result in a polynomial gap in their running times. In the following, we refer to nodes of the quad-tree as tree-nodes (to distinguish them from the hyperbolic nodes contained).

Bringmann et al. propose the following neighborhood search which is adapted by HyperGirgs. For simplicity, we initially restrict ourselves to Threshold RHGs. The generator enumerates all pairs of tree-nodes that may contain point pairs sufficiently close to imply an edge. This is done in a pessimistic and oblivious fashion, i.e., without considering the actual points represented by the tree-nodes. HyperGirgs then emits edges by testing all point pairs contained in each previously enumerated pair of tree-nodes. To avoid asymptotically significant overheads, the algorithm pairs tree-nodes as high up in the quad-tree as possible without adding unintended distance computations.

The quad-tree needs to support efficient random access to all points contained within any tree-node at any depth. Similarly to [10], HyperGirgs achieves this using z-order space-filling curves [41] to map the tree to memory. This choice allows us to efficiently build and query the quad-tree using Morton codes [37].

In case of Binomial RHGs with $T > 0$, any node pair has a positive (yet mostly negligible) probability $p_T(d)$ to be connected. HyperGirgs therefore has to consider all tree-node pairs—even those with a tiny connection probability. In the latter case, the connection probability is bounded from below. Then, we use geometric jumps followed by rejection sampling to prune the search space. The authors also engineer an exact look-up table-based sampling scheme to reduce the evaluation of transcendental functions during the computation of linking probabilities $p_T(d)$.

HyperGirgs processes the tree-node pairs pleasingly parallel. As a special feature, its implementation guarantees reproducibility in the sense that two runs with the same set of parameters and seed values output the same set of edges (though not necessarily in the same order). At the time of writing, the implementation of HyperGirgs is the fastest sequential RHG generator and competitive for shared-memory parallelism.

7 Software Packages

From a practical point of view, it is crucial that a generator interacts well with the software used to analyze the emitted graphs. A common choice is to write the produced graph into a file which then can be processed by a tool of choice. There are, however, notable drawbacks of this approach; for one, there are a plethora of file formats which may be incompatible. Also reading and writing files can have surprisingly high overheads (e.g., [42 SPP]).

The network analysis framework NetworKit (partially supported by the SPP 1736) includes generators for all network models that are discussed in depth in this chapter. As detailed in Sect. 1, this software package combines various types of graph algorithms efficiently implemented in C++ with an easy to use Python interface. The tight interaction between network generation and analysis promises a fast and convenient processing pipelines.

KaGen is a graph generator suite for distributed computing and contains a number of communication-agnostic generators [18 SPP]. The suite includes generators for the following models accessible via a common interface $\mathcal G(n, p)$, $\mathcal G(n,m)$, Kronecker Graph, Random Geometric Graph, Random Delaunay Triangulation, Barabási-Albert, and Threshold RHG.