Supervised Cluster Analysis of miRNA Expression Data Using Rough Hypercuboid Partition Matrix

Abstract

The microRNAs are small, endogenous non-coding RNAs found in plants and animals, which suppresses the expression of genes post-transcriptionally. It is suggested by various genome-wide studies that a substantial fraction of miRNA genes is likely to form clusters. The coherent expression of the miRNA clusters can then be used to classify samples according to the clinical outcome. In this background, a new rough hypercuboid based supervised similarity measure is proposed that is integrated with the supervised attribute clustering to find groups of miRNAs whose coherent expression can classify samples. The proposed method directly incorporates the information of sample categories into the miRNA clustering process, generating a supervised clustering algorithm for miRNAs. The effectiveness of the rough hypercuboid based algorithm, along with a comparison with other related algorithms, is demonstrated on three miRNA microarray expression data sets using the $B.632+$ bootstrap error rate of support vector machine. The association of the miRNA clusters to various biological pathways are also shown by doing pathway enrichment analysis.

1 Introduction

Micro RNAs/miRNAs are a class of short approximately 22-nucleotide non-coding RNAs found in many plants and animals. They inhibit the expression of mRNA expression post-transcriptionally. It has been shown by [1] that the miRNAs on a genome tend to present in a cluster. Large scale surveys [2] have established the fact that miRNAs have tendency to present in clusters. Existence of co-expressed miRNAs is also demonstrated using expression profiling analysis in [3]. These findings suggest that members of a miRNA cluster, which are at a close proximity on a chromosome, are highly likely to be processed as co-transcribed units. In [4, 15], different approaches are introduced to discover miRNA cluster patterns. Expression data of miRNAs can be used to detect clusters of miRNAs as it is suggested that co-expressed miRNAs are co-transcribed, so they should have similar expression pattern.

Several unsupervised clustering techniques like hierarchical clustering algorithms [8] and self organizing maps [2] are used to cluster a miRNA expression data. However, the groups of miRNAs discovered by these unsupervised clustering algorithms are not potential enough to do tissue classification [5], as the miRNAs are grouped based on their similarity without incorporating the class label information. In this regard, several supervised clustering algorithms are proposed to cluster gene expression data [5, 10, 11]. In [5], genes are clustered by incorporating the knowledge of tissue. On the other hand, hierarchical clustering is employed on the gene expression data and the average of resultant clustering solutions are further used to do sample classification. Only in the later part, information of the class label is incorporated [10]. In [11], a fuzzy-rough supervised gene clustering algorithm is described. The algorithm uses fuzzy equivalence classes to compute relevance of the clusters, that makes the algorithm sensitive to the fuzzy parameter. However, none of the works has addressed the problem of supervised clustering of miRNAs.

However, one of the main problems in expression data analysis is uncertainty. Some of the sources of this uncertainty include imprecision in computations and vagueness in class definition. In this background, the rough set [16] provides a mathematical framework to capture uncertainties associated with human cognition process. In [11, 13, 14], rough sets have been successfully used to analyze a microarray expression data.

In this regard, this paper presents a new rough hypercuboid based supervised clustering algorithm. It is developed by integrating the concepts of rough hypercuboid equivalence partition matrix [12, 14] and supervised attribute clustering algorithm [11]. It finds coregulated clusters of miRNAs whose collective expression is strongly associated with the sample categories. Using the concept of rough hypercuboid equivalence partition matrix, the degree of dependency is calculated for miRNAs, which is used to compute both relevance and significance of the miRNAs. Hence, the only information required in the proposed method is in the form of equivalence classes for each miRNA, which can be automatically derived from the data set. A new measure is developed for calculating similarity between two miRNAs. Based upon the similarity values, the miRNAs are grouped into cluster. The new supervised clustering algorithm divides the miRNA expression data in distinct clusters. In each cluster, the first selected miRNA has high relevance value with respect to the class label and it is the representative of the cluster. The representative is modified in such a way that the averaged expression value has high relevance value with the class label. Finally, the proposed method generates a set of clusters, whose coherent average expression levels allow perfect discrimination of tissue types. The concept of B.632+ error rate [7] is used to minimize the variability and biasedness of the derived results. The support vector machine is used to compute the B.632+ error rate as well as several other types of error rates as it maximizes the margin between data samples in different classes. The effectiveness of the proposed approach, along with a comparison with other related approaches, is demonstrated on several miRNA expression data sets.

2 Rough Hypercuboid Based Supervised Attribute Clustering

In this paper, a new algorithm is developed based on rough hypercuboid equivalence partition matrix. Every clustering algorithm need a distance or similarity measure to group objects. Accordingly, a new rough hypercuboid based similarity measure is proposed. The concept of rough hypercuboid was presented in [20], while that of rough hypercuboid equivalence partition matrix was proposed in [12, 14]. It has also been successfully applied for feature/gene/miRNA selection in [12, 14]. The relevance of a cluster is calculated using rough hypercuboid equivalence partition matrix based dependency measure. The proposed rough hypercuboid based supervised similarity measure is integrated into the supervised attribute clustering algorithm developed by Maji [11]. Prior to describe about the new supervised attribute clustering algorithm, next the concept of rough hypercuboid equivalence partition matrix is described.

2.1 Rough Hypercuboid Equivalence Partition Matrix

Let ${\mathbb U}=\{s_1,\cdots ,s_i,\cdots ,s_n\}$ be the set of $n$ objects or samples and ${\mathbb C}=\{{\fancyscript{M}}_1,\cdots , \cdots ,{\fancyscript{M}}_{m}\}$ denotes the set of $m$ attributes or miRNAs of a given microarray data set. Let ${\mathbb D}$ be the set of class labels or sample categories of $n$ samples.

If ${\mathbb U}/{{\mathbb D}}=\{\beta _1,\cdots ,\beta _i,\cdots ,\beta _c\}$ denotes $c$ equivalence classes or information granules of ${\mathbb U}$ generated by the equivalence relation induced from the decision attribute set ${{\mathbb D}}$, then $c$ equivalence classes of ${\mathbb U}$ can also be generated by the equivalence relation induced from each condition attribute or miRNA ${\fancyscript{M}}_k \in {\mathbb C}$. If ${\mathbb U}/{\fancyscript{M}}_k=\{\mu _1,\cdots ,\mu _i,\cdots ,\mu _c\}$ denotes $c$ equivalence classes or information granules of ${\mathbb U}$ induced by the condition attribute or miRNA ${\fancyscript{M}}_k$ and $n$ is the number of objects in ${\mathbb U}$, then $c$-partitions of ${\mathbb U}$ are the sets of ($cn$) values $\{\mathrm{h}_{ij}({{\fancyscript{M}}_k})\}$ that can be conveniently arrayed as a ($c \times n$) matrix ${\mathbb H}({\fancyscript{M}}_k) =[\mathrm{h}_{ij}({\fancyscript{M}}_k)]$. The matrix ${\mathbb H}({\fancyscript{M}}_k)$ is denoted by

$$\begin{aligned} {\mathbb H}({\fancyscript{M}}_k)= \left( \begin{array}{llll} \mathrm{h}_{11}({\fancyscript{M}}_k) &{} \mathrm{h}_{12}({\fancyscript{M}}_k) &{} \cdots &{} \mathrm{h}_{1n}({\fancyscript{M}}_k) \\ \mathrm{h}_{21}({\fancyscript{M}}_k) &{} \mathrm{h}_{22}({\fancyscript{M}}_k) &{} \cdots &{} \mathrm{h}_{2n}({\fancyscript{M}}_k) \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \mathrm{h}_{c1}({\fancyscript{M}}_k) &{} \mathrm{h}_{c2}({\fancyscript{M}}_k) &{} \cdots &{} \mathrm{h}_{cn}({\fancyscript{M}}_k) \\ \end{array} \right) \end{aligned}$$

(1)

$$\begin{aligned} \text{ where }~~\mathrm{h}_{ij}({\fancyscript{M}}_k)= \left\{ \begin{array}{ll} 1 &{} \text{ if } \mathrm{L}_i \le x_j({\fancyscript{M}}_k) \le \mathrm{U}_i\\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(2)

The tuple $[\mathrm{L}_i,\mathrm{U}_i]$ represents the interval of $i$th class $\beta _i$ according to the decision attribute set ${\mathbb D}$. The interval $[\mathrm{L}_i,\mathrm{U}_i]$ is the value range of condition attribute or miRNA ${\fancyscript{M}}_k$ with respect to class $\beta _i$. It is spanned by the objects with same class label $\beta _i$. That is, the value of each object $s_j$ with class label $\beta _i$ falls within interval $[\mathrm{L}_i,\mathrm{U}_i]$. This can be viewed as a supervised granulation process, which utilizes class information.

On employing a condition attribute or miRNA ${\fancyscript{M}}_k$ a $c \times n$ matrix ${\mathbb H}({\fancyscript{M}}_k)$ termed as hypercuboid equivalence partition matrix is generated. The $c \times n$ matrix ${\mathbb H}({\fancyscript{M}}_k)$ is termed as hypercuboid equivalence partition matrix of the condition attribute or miRNA ${\fancyscript{M}}_k$. Each row of the matrix ${\mathbb H}({\fancyscript{M}}_k)$ is a hypercuboid equivalence partition or class. Here $\mathrm{h}_{ij}({\fancyscript{M}}_k) \in \{0,1\}$ represents the membership of object $s_j$ in the class $\beta _i$ satisfying following two conditions:

$$\begin{aligned} 1\le \displaystyle {\sum _{j=1}^n \mathrm{h}_{ij}({\fancyscript{M}}_k)\le n,\forall i};~~ 1 \le \displaystyle {\sum _{i=1}^c \mathrm{h}_{ij}({\fancyscript{M}}_k) \le c,\forall j}. \end{aligned}$$

(3)

The above axioms should hold for every equivalence partition, which correspond to the requirement that an equivalence class is non-empty. However, in real data analysis, uncertainty arises due to overlapping class boundaries. Hence, such a granulation process does not necessarily result in a compatible granulation in the sense that every two class hypercuboids or intervals may intersect with each other. The intersection of two hypercuboids also forms a hypercuboid, which is referred to as implicit hypercuboid. The implicit hypercuboids encompass the misclassified samples or objects those belong to more than one classes. The degree of dependency of the decision attribute set or class label on the condition attribute set depends on the cardinality of the implicit hypercuboids. The degree of dependency increases with the decrease in cardinality.

Using the concept of hypercuboid equivalence partition matrix, the misclassified objects of boundary region present in the implicit hypercuboids can be identified based on the confusion vector defined next

$$\begin{aligned} {\mathbb V}({\fancyscript{M}}_k)=[\mathrm{v}_1({\fancyscript{M}}_k),\cdots ,\cdots ,\mathrm{v}_n({\fancyscript{M}}_k)];~ \text{ where }~\mathrm{v}_j({\fancyscript{M}}_k)= \min \{1,\sum _{i=1}^c \mathrm{h}_{ij}({\fancyscript{M}}_k) -1 \}. \end{aligned}$$

(4)

In rough sets if an object $s_j$ belongs to the lower approximation of any class $\beta _i$, then it does not belong to the lower or upper approximations of any other classes and $\mathrm{v}_j({\fancyscript{M}}_k)=0$. On the other hand, if the object $s_j$ belongs to the boundary region of more than one classes, then it should be encompassed by the implicit hypercuboid and $\mathrm{v}_j({\fancyscript{M}}_k)=1$. Hence, the hypercuboid equivalence partition matrix and corresponding confusion vector of the condition attribute ${\fancyscript{M}}_k$ can be used to define the lower and upper approximations of the $i$th class $\beta _i$ of the decision attribute set ${\mathbb D}$. Let $\beta _i \subseteq {\mathbb U}$. $\beta _i$ can be approximated using only the information contained within ${\fancyscript{M}}_k$ by constructing the $M$-lower and $M$-upper approximations of $\beta _i$:

$$\begin{aligned} \underline{M}(\beta _i)=\{s_j|~\mathrm{h}_{ij}({\fancyscript{M}}_k)=1~\mathrm{and}~\mathrm{v}_j({\fancyscript{M}}_k)=0 \};~~ \overline{M}(\beta _i)=\{s_j|~\mathrm{h}_{ij}({\fancyscript{M}}_k)=1 \}; \end{aligned}$$

(5)

where equivalence relation $M$ is induced from attribute ${\fancyscript{M}}_k$. The boundary region of $\beta _i$ is then defined as

$$\begin{aligned} BN_M(\beta _i)=\{s_j|~\mathrm{h}_{ij}({\fancyscript{M}}_k)=1~\mathrm{and}~\mathrm{v}_j({\fancyscript{M}}_k)=1 \}. \end{aligned}$$

(6)

Dependency. The dependency between condition attribute ${\fancyscript{M}}_k$ and decision attribute ${\mathbb D}$ can be defined as follows:

$$\begin{aligned} \gamma _{{\fancyscript{M}}_k}({\mathbb D})=\frac{1}{n} \sum _{i=1}^c \sum _{j=1}^n \mathrm{h}_{ij}({\fancyscript{M}}_k) \cap [1-\mathrm{v}_j({\fancyscript{M}}_k)]; ~ \mathrm{that~is,}~\gamma _{{\fancyscript{M}}_k}({\mathbb D})=1-\frac{1}{n} \sum _{j=1}^n \mathrm{v}_j({\fancyscript{M}}_k),~~~~~ \end{aligned}$$

(7)

where $0 \le \gamma _{{\fancyscript{M}}_k}({\mathbb D}) \le 1$. If $\gamma _{{\fancyscript{M}}_k}({\mathbb D})=1$, ${\mathbb D}$ depends totally on ${\fancyscript{M}}_k$, if $0 < \gamma _{{\fancyscript{M}}_k}({\mathbb D})< 1$, ${\mathbb D}$ depends partially on ${\fancyscript{M}}_k$, and if $\gamma _{{\fancyscript{M}}_k}({\mathbb D})=0$, then ${\mathbb D}$ does not depend on ${\fancyscript{M}}_k$. The $\gamma _{{\fancyscript{M}}_k}({\mathbb D})$ is also termed as the relevance of attribute ${\fancyscript{M}}_k$ with respect to class ${\mathbb D}$.

Significance. The resultant hypercuboid equivalence partition matrix ${\mathbb H}(\{{\fancyscript{M}}_k,{\fancyscript{M}}_l\})$ of size $c \times n$ can be computed from ${\mathbb H}({\fancyscript{M}}_k)$ and ${\mathbb H}({\fancyscript{M}}_l)$ as follows:

$$\begin{aligned} {\mathbb H}(\{{\fancyscript{M}}_k,{\fancyscript{M}}_l\})= {\mathbb H}({\fancyscript{M}}_k) \cap {\mathbb H}({\fancyscript{M}}_l);~ \mathrm{where}~~\mathrm{h}_{ij}(\{{\fancyscript{M}}_k,{\fancyscript{M}}_l\})= \mathrm{h}_{ij}({\fancyscript{M}}_k) \cap \mathrm{h}_{ij}({\fancyscript{M}}_l). \end{aligned}$$

(8)

The significance of the attribute $\fancyscript{M}_k$ with respect to the condition attribute set $\{{\fancyscript{M}}_k,{\fancyscript{M}}_l\}$ is given by

$$\begin{aligned} {\sigma _{\mathbb M}}({\mathbb D},\fancyscript{M}_k)= \frac{1}{n} \sum _{j=1}^n \left[ \mathrm{v}_j({\mathbb M}-\{{\fancyscript{M}}_k\})-\mathrm{v}_j({\mathbb M}) \right] ; \end{aligned}$$

(9)

where $0 \le {\sigma _{\{{\fancyscript{M}}_k,{\fancyscript{M}}_l\}}}({\mathbb D},\fancyscript{M}_k) \le 1$. Hence, the higher the change in dependency, the more significant the attribute $\fancyscript{M}_k$ is. If significance is 0, then the attribute is dispensable.

2.2 Rough Hypercuboid Based Supervised Similarity Measure

The simple concepts of rough hypercuboid based dependency and significance is used to calculate distance between two miRNAs and then the non-linear transformation of the distance is used to calculate similarity between two miRNAs. This subsection presents the proposed rough hypercuboid based supervised similarity measure.

Let ${\mathbb C}=\{{\fancyscript{M}}_1,\cdots , {\fancyscript{M}}_i,\cdots ,{\fancyscript{M}}_j,\cdots ,{\fancyscript{M}}_{\mathcal {D}}\}$ denotes the set of ${\mathcal {D}}$ condition attributes or miRNAs of a given data set. Define ${\mathrm {R}}_{{\fancyscript{M}}_i}({\mathbb D})$ as the relevance of the condition attribute ${\fancyscript{M}}_i$ with respect to the class label or decision attribute ${\mathbb D}$. The dependency function of rough hypercuboid can be used to calculate the relevance of condition attributes or miRNAs. Hence, the relevance ${\mathrm {R}}_{{\fancyscript{M}}_i}({\mathbb D})$ of the condition attribute ${\fancyscript{M}}_i$ with respect to the decision attribute ${\mathbb D}$ using rough hypercuboid can be calculated as follows:

$$\begin{aligned} {\mathrm {R}}_{{\fancyscript{M}}_i}({\mathbb D})=\gamma _{{\fancyscript{M}}_i}({\mathbb D}) \end{aligned}$$

(10)

where $\gamma _{{\fancyscript{M}}_i}({\mathbb D})$ represents the degree of dependency between condition attribute or miRNA ${\fancyscript{M}}_i$ and decision attribute or class label ${\mathbb D}$ that is given by (7).

At first, the distance between two miRNAs ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$ is calculated using rough hypercuboid based approach. Then the non-linear transformation of the distance is done for getting the similarity between these two miRNAs. The non-linear transformation is done to detect nonlinear interdependencies between the underlying two miRNAs. The rough hypercuboid based significance (9) is used to compute similarity between two miRNAs and it is defined next.

Definition 1

The rough hypercuboid based similarity measure between two attributes or miRNAs ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$ is defined as follows:

$$\begin{aligned} \psi ({\fancyscript{M}}_i,{\fancyscript{M}}_j)=\frac{1}{\sqrt{{\kappa }^2+1}};~~ \mathrm{where}~~\kappa =\left\{ \frac{\sigma _{{\fancyscript{M}}_i}({\mathbb D},{\fancyscript{M}}_j)+ \sigma _{{\fancyscript{M}}_j}({\mathbb D},{\fancyscript{M}}_i)}{2} \right\} \end{aligned}$$

(11)

Hence, the supervised similarity measure $\psi ({\fancyscript{M}}_i,{\mathcal A}_j)$ directly takes into account the information of sample categories or class labels ${\mathbb D}$ while computing the similarity between two attributes or miRNAs ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$. If attributes ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$ are completely correlated with respect to class labels ${\mathbb D}$, then $\kappa =0$ and so $\psi ({\fancyscript{M}}_i,{\fancyscript{M}}_j)$ is 1. If ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$ are totally uncorrelated, $\psi ({\fancyscript{M}}_i,{\fancyscript{M}}_j) = \frac{1}{\sqrt{2}}$. Hence, $\psi ({\fancyscript{M}}_i,{\fancyscript{M}}_j)$ can be used as a measure of supervised similarity between two miRNAs ${\fancyscript{M}}_i$ and ${\fancyscript{M}}_j$.

2.3 Supervised miRNA Clustering Algorithm

In this work the proposed rough hypercuboid based similarity measure is incorporated into the Fuzzy-Rough Supervised Attribute Clustering Algorithm [11]. In the proposed method a new rough hypercuboid based similarity measure is developed to calculate similarity between two miRNAs. Whereas, in [11] a fuzzy-rough supervised similarity measure is proposed. However, the fuzzy-rough supervised similarity measure is sensitive to the fuzzy parameter that is used to calculate the similarity between two objects.

Let ${\mathbb C}$ represents the set of miRNAs of the original data set, while ${\mathbb S}$ and ${\bar{\mathbb S}}$ are the set of actual and augmented attributes, respectively, selected by the miRNA clustering algorithm. Let ${\mathbb V}_i$ is the coarse cluster associated with the miRNA ${\fancyscript{M}}_i$ and ${\bar{\mathbb V}}_i$, the finer cluster of ${\fancyscript{M}}_i$, represents the set of miRNAs of ${\mathbb V}_i$ those are merged and averaged with the attribute ${\fancyscript{M}}_i$ to generate the augmented cluster representative ${\bar{\fancyscript{M}}}_i$. The main steps of the integrated miRNA clustering algorithm are reported next.

• 1. Initialize ${\mathbb C} \leftarrow \{{\fancyscript{M}}_1,\cdots , {\fancyscript{M}}_i,\cdots ,{\fancyscript{M}}_j,\cdots ,{\fancyscript{M}}_{\mathcal {D}}\}$, ${\mathbb S} \leftarrow \emptyset$, and ${\bar{\mathbb S}} \leftarrow \emptyset$.

• 2. Calculate the rough hypercuboid based relevance value ${\mathrm {R}}_{{\fancyscript{M}}_i}({\mathbb D})$ of each miRNA ${\fancyscript{M}}_i \in {\mathbb C}$.

• 3. Repeat the following nine steps (steps 4 to 12) until ${\mathbb C}=\emptyset$ or the desired number of attributes are selected.

• 4. Select miRNA ${\fancyscript{M}}_i$ from ${\mathbb C}$ as the representative of cluster ${\mathbb V}_i$ that has highest rough hypercuboid based relevance value. In effect, ${\fancyscript{M}}_i \in {\mathbb S}$, ${\fancyscript{M}}_i \in {\mathbb V}_i$, ${\fancyscript{M}}_i \in {\bar{\mathbb V}}_i$, and ${\mathbb C}={\mathbb C} \setminus {\fancyscript{M}}_i$.

• 5. Generate coarse cluster ${\mathbb V}_i$ from the set of existing attributes/miRNAs of ${\mathbb C}$ satisfying the following condition:

  $$\begin{aligned} {\mathbb {V}}_i=\{{\fancyscript{M}}_j|\psi ({\fancyscript{M}}_i,{\fancyscript{M}}_j)\ge \delta ; {\fancyscript{M}}_j \ne {\fancyscript{M}}_i \in {\mathbb {C}}\}. \end{aligned}$$

  (12)

• 6. Initialize ${\bar{\fancyscript{M}}}_i \leftarrow {\fancyscript{M}}_i$.

• 7. Repeat following four steps (steps 8–11) for each miRNA ${\fancyscript{M}}_j \in {\mathbb {V}}_i$.

• 8. Compute two augmented cluster representatives by averaging ${\fancyscript{M}}_j$ and its complement with the attributes of ${\bar{\mathbb {V}}}_i$ as follows:

  $$\begin{aligned} {\bar{\fancyscript{M}}}_{i+j}^{+}=\frac{1}{|{\bar{\mathbb {V}}}_i|+1} \left\{ \sum _{\fancyscript{M}_k \in {\bar{\mathbb {V}}}_i} {\fancyscript{M}}_k+{\fancyscript{M}}_j \right\} ; {\bar{\fancyscript{M}}}_{i+j}^{-}=\frac{1}{|{\bar{\mathbb {V}}}_i|+1} \left\{ \sum _{\fancyscript{M}_k \in {\bar{\mathbb {V}}}_i} {\fancyscript{M}}_k-{\fancyscript{M}}_j \right\} \end{aligned}$$

  (13)

• 9. The augmented cluster representative ${\bar{\fancyscript{M}}}_{i+j}$ after averaging ${\fancyscript{M}}_j$ or its complement with ${\bar{\mathbb {V}}}_i$ is as follows:

  $$\begin{aligned} {\bar{\fancyscript{M}}}_{i+j} = \left\{ \begin{array}{ll} {\bar{\fancyscript{M}}}_{i+j}^{+} &{} \text{ if } {\mathrm R}_{{\bar{\fancyscript{M}}}_{i+j}^{+}}({\mathbb D}) \ge {\mathrm R}_{{\bar{\fancyscript{M}}}_{i+j}^{-}}({\mathbb D})\\ {\bar{\fancyscript{M}}}_{i+j}^{-} &{} \text{ otherwise. }\\ \end{array} \right. \end{aligned}$$

  (14)

• 10. The augmented cluster representative ${\bar{\fancyscript{M}}}_i$ of cluster ${\mathbb V}_i$ is ${\bar{\fancyscript{M}}}_{i+j}$ if ${\mathrm R}_{{\bar{\fancyscript{M}}}_{i+j}}({\mathbb D}) \ge {\mathrm R}_{{\bar{\fancyscript{M}}}_i}({\mathbb D})$, otherwise ${\bar{\fancyscript{M}}}_i$ remains unchanged.

• 11. Select attribute ${\fancyscript{M}}_j$ or its complement as a member of the finer cluster ${\bar{\mathbb V}}_i$ of attribute ${\fancyscript{M}}_i$ if ${\mathrm R}_{{\bar{\fancyscript{M}}}_{i+j}}({\mathbb D}) \ge {\mathrm R}_{{\bar{\fancyscript{M}}}_i}({\mathbb D})$.

• 12. In effect, ${\bar{\fancyscript{M}}}_i \in {\bar{\mathbb S}}$ and ${\mathbb C}={\mathbb C} \setminus {\bar{\mathbb V}}_i$.

• 13. Stop.

3 Experimental Results

The performance of the proposed rough hypercuboid equivalence partition matrix based supervised miRNA clustering (RH-SAC) method is extensively studied and compared with that of some existing feature selection and clustering algorithms on three miRNA expression data sets GSE17846, GSE21036, and GSE28700. The algorithms compared are mutual information based InfoGain [17] and minimum redundancy-maximum relevance (mRMR) algorithm [6], method proposed by Golub et al. [9], rough set based maximum relevance-maximum significance (RSMRMS) algorithm [13], $\mu$HEM [14], fuzzy-rough supervised attribute clustering algorithm (FR-SAC) [11]. The error rate of support vector machine (SVM) [18] is used to evaluate the performance of different algorithms. To compute the error rate of SVM, bootstrap approach ($B.632+$ error rate) [7] is performed on each miRNA expression data set. For each training set, a set of differential miRNA groups is first generated, and then SVM is trained with the selected coherent miRNAs. After the training, the information of miRNAs those were selected for the training set is used to generate test set and then the class label of the test sample is predicted using the classifier. The maximum number of features selected by the new integrated supervised miRNA clustering algorithm are 50.

3.1 Optimal Value of $\delta$ Parameter

The threshold $\delta$ in (12) plays an important role in the performance of the proposed supervised miRNA clustering algorithm. It controls the size of a cluster. Hence, it has direct influence in the performance of the proposed algorithm. Higher the value of $\delta$ sparse the cluster becomes. To find the optimal value of $\delta$ parameter the proposed algorithm is implemented on three data sets. The value for which the $B.632+$ error rate is minimum is considered to be the optimum $\delta$ value for the corresponding data set.The value of $\delta$ is varied from 0.90 to 1.00. Hence, the optimum value of $\delta$ for three miRNA data sets are calculated using the following relation:

$$\begin{aligned} \delta ^\star =\mathrm{arg}\min _\delta \{B.632+ \mathrm{error}\}. \end{aligned}$$

(15)

The optimum values of $\delta ^{*}$ obtained using (15) are 0.99, 1.00, 0.95 for GSE17846, GSE21036, and GSE28700 data sets, respectively. The number of miRNAs at which optimal $\delta ^{*}$ value is obtained for miRNA data sets are 31, 49, and 43 for GSE17846, GSE21036, and GSE28700 data sets, respectively.

3.2 Different Types of Errors

This section describes about the different types of errors generated by the SVM classifier. The importance of $B.632+$ error over apparent error ($AE$), gamma error ($\gamma$), and bootstrap ($B1$) error is also established. All the errors are calculated using the SVM for the proposed method. The results are presented for the optimum values of $\delta$. Figure 1 represents different types of errors obtained for three different data sets. From the figure it is seen that the $\gamma$ error rate is higher than any other type of errors for each data set, while $B1$ error is lower than the $\gamma$ error rate but higher than the $B.632+$ error and $AE$. The average of $B1$ error and $AE$ leads to $B.632+$ error rate lower than the $B1$ error but higher than $AE$. Table 1 represents minimum values of different types of errors and corresponding number of miRNAs at which the error is obtained for each miRNA data sets. From the table it is seen that the $B.632+$ estimator rectifies the upward bias of $B1$ error and downward bias of $AE$.

Fig. 1.

Different error rates of the proposed algorithm on different data sets obtained using the SVM averaged over 50 random splits

Table 1. Comparative analysis of different types of errors for proposed method

3.3 Comparative Performance Analysis

In this section comparative performance analysis of the proposed supervised miRNA clustering algorithm has been shown. The proposed algorithm has been compared with some popular feature selection and supervised attribute clustering algorithms.

Table 2 represents the different types of error obtained by different methods at their optimal parameters. It also contains the number of miRNAs at which the corresponding lowest error rate is obtained by each method. From the table it is seen that the almost all the algorithms generate $AE$ equal to zero. However, the RSMRMS generates non zero $AE$ in 2 cases. From the table it is seen that the proposed supervised miRNA clustering algorithm generates $B.632+$ error rate lower than any other method except in one case. Only in one case the $\mu$-HEM miRNA selection algorithm generates better result than the proposed method.

Table 2. Comparative performance analysis of different algorithms

Fig. 2.

miRNAs versus pathways heat map for different miRNA data sets

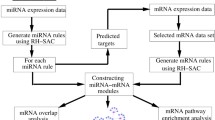
3.4 Pathway Enrichment Analysis of Obtained miRNAs

In this section biological importance of the obtained miRNAs using proposed supervised miRNA clustering algorithm is described. Those miRNAs which are selected by the proposed method in all the 50 bootstrap samples were used for further analysis. The association of those miRNAs with different biological pathways were determined. The DIANA-miRPath v2.0 [19] interface has been used to identify the miRNA-pathway relationship. The server performs an enrichment analysis of miRNA gene targets in KEGG pathways. The tool first identifies the target genes of the uploaded miRNAs.

The DIANA-miRPath v2.0 has been applied on the selected miRNAs of miRNA data sets. Those pathways are selected whose $P$-value is lower than 0.05. The miRNA-pathway relation is represented by a heatmap. Figure 2 represents the heatmap of the miRNA-pathways which are found to be statistically significant. The darker colors represent that the miRNA is associated with the pathway more significantly. In data set GSE17846 the miRNA profiling of total blood of multiple sclerosis and control samples is performed. From the figure it is seen the miRNAs selected by the proposed method are statistically related with 29 pathways. Multiple Sclerosis is a autoimmune disorder and from the Fig. 2 it is seen that around 7 pathways are significant and they are related to autoimmune disorder. They are Cell adhesion molecules (CAMs), TGF-beta signaling pathway, PI3K-Akt signaling pathway, Leukocyte transendothelial migration, MAPK signaling pathway, Fc gamma R- mediated phagocytosis, and Calcium signaling pathway. On the other hand around 48 pathways-miRNAs relationship are found to be statistically significant for GSE21036 data set. This data set is generated using metastatic prostate cancer samples and normal adjacent benign prostate. From Fig. 2 it is seen that the proposed method is able to select those miRNAs that are associated with prostate cancer. In addition to that it is also able to identify other significant pathways like Progestrone-mediated oocyte maturation, Inositol phosphate metabolism, mTOR signaling pathway, and so forth. Similarly, several significant miRNA-pathway relations are obtained using the DIANA-miRPath tool for the data set GSE28700. In this data set, expression profiles of microRNAs in gastric cancer are stored. From Fig. 2 it is clear several cancer related pathways are found to be significant using the proposed method. From the figure it is seen that total 22 pathways are found to be significant and few of them are Colorectal cancer, Pancreatic cancer, Non-small cell lung cancer, Chronic myeloid leukemia, Hepatitis B, Small cell lung cancer, HIF-1 signaling pathway, Focal adhesion, Prostate cencer, Pathways in cancer.

4 Conclusion

The paper presents a new rough hypercuboid based supervised similarity measure that is incorporated into the supervised miRNA clustering algorithm. It uses the concept of rough hypercuboid for calculating similarity between two miRNAs and thus improves the performance of the method. The rough hypercuboid based similarity measure uses the information of class label for calculating similarity between two miRNAs and hence, makes it a supervised measure. The proposed method fetches cluster of miRNAs whose collective expressions are strongly associated with the class label. The effectiveness of the proposed rough hypercuboid based supervised miRNA clustering algorithm is shown and compared with other existing methods on three miRNA expression data sets. The selected miRNAs are also found to be significantly associated with different important pathways that are related to the data set.