Focal Flow: Measuring Distance and Velocity with Defocus and Differential Motion

Abstract

We present the focal flow sensor. It is an unactuated, monocular camera that simultaneously exploits defocus and differential motion to measure a depth map and a 3D scene velocity field. It does so using an optical-flow-like, per-pixel linear constraint that relates image derivatives to depth and velocity. We derive this constraint, prove its invariance to scene texture, and prove that it is exactly satisfied only when the sensor’s blur kernels are Gaussian. We analyze the inherent sensitivity of the ideal focal flow sensor, and we build and test a prototype. Experiments produce useful depth and velocity information for a broader set of aperture configurations, including a simple lens with a pillbox aperture.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Computational sensors reduce the data processing burden of visual sensing tasks by physically manipulating light on its path to a photosensor. They analyze scenes using vision algorithms, optics, and post-capture computation that are jointly designed for a specific task or environment. By optimizing which light rays are sampled, and by moving some of the computation from electrical hardware into the optical domain, computational sensors promise to extend task-specific artificial vision to new extremes in size, autonomy, and power consumption [1–5].

Fig. 1.

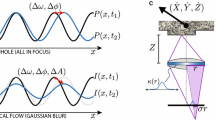
The focal flow principle. A: When a 1D pinhole camera observes a world plane with sinusoidal texture, the image is also a sinusoid (black curve). Motion between camera and scene causes the sinusoidal image to change in frequency and phase (blue curve), and these two pieces of information reveal time to contact and direction of motion. B: When a finite-aperture camera images a similar moving scene, the motion additionally induces a change in image amplitude, because the scene moves in or out of focus. This third piece of information resolves depth and scene velocity. C: We show that, with an ideal thin lens and Gaussian blur $\kappa (r)$, depth and 3D velocity can be measured through a simple, per-pixel linear constraint, similar optical flow. The constraint applies to any generic scene texture. (Color figure online)

We introduce the first computational sensor for depth and 3D scene velocity. It is called a focal flow sensor. It is passive and monocular, and it measures depth and velocity using a per-pixel linear constraint composed of spatial and temporal image derivatives. The sensor simultaneously exploits defocus and differential motion, and its underlying principle is depicted in Fig. 1. This figure shows the one-dimensional image values that would be measured from a front-parallel, Lambertian scene patch with a sinusoidal texture pattern, as it moves relative to a sensor. If the sensor is a pinhole camera, the patch is always in focus, and the images captured over time are variously stretched and shifted versions of the patch’s texture pattern (Fig. 1A). The rates of stretching and shifting together resolve the time to contact and direction of motion (e.g., using  [6]), but they are not sufficient to explicitly measure depth or velocity. The focal flow sensor is a real-aperture camera with a finite depth of field, so in addition to stretching and shifting, its images exhibit changes in contrast due to defocus (Fig. 1B). This additional piece of information resolves depth and velocity explicitly.

Our main contribution is the derivation of a per-pixel linear equation,

that relates spatial and temporal image derivatives to depth and 3D scene velocity, and that is valid for any generic scene texture. Over an image patch, depth and velocity are recovered simply by computing spatial and temporal derivatives, solving a $4\times 4$ linear system for vector $\mathbf {v} \in \mathbb {R}^4$, and then evaluating analytic expressions for depth $Z(\mathbf {v})$ and 3D velocity $(\dot{X},\dot{Y},\dot{Z})(\mathbf {v})$ determined by the physical characteristics of the calibrated sensor.

The focal flow cue is distinct from conventional passive depth cues like stereo and depth from defocus because it directly measures 3D velocity in addition to depth. It is also different because it does not require inferences about disparity or blur; instead, it provides per-pixel depth in closed form, using a relatively small number of multiply and add operations. The focal flow sensor might therefore be useful for applications, such as micro-robotics [3], that involve motion and that require visual sensing with low power consumption and small form factors.

We prove that this linear constraint is invariant to scene texture, that it exists analytically whenever the optical system’s point spread functions are Gaussian, and that no other class of radially symmetric point spread functions—be they discs, binary codes, or continuous functions—provides the same capability. We also analyze the inherent sensitivity of the focal flow sensor, and show the effectiveness in practice of non-Gaussian aperture configurations including filter-free apertures. We demonstrate a working prototype that can measure depth within $\pm 5.5$ mm over a range of more than 15 cm using an f / 4 lens.

1 Related Work

Motion & Linear Constraints. Differential optical flow, which assumes that all images are in focus, is computable from a linear system of equations in a window [7]. A closely related linear system resolves time to contact [6, 8]. The focal flow equation has a similar linear form, but it incorporates defocus blur and provides additional scene information in the form of depth and 3D velocity. Unlike previous work on time to contact [9], our focal flow analysis is restricted to front-parallel scene patches, though experimental results suggest that useful depth can be obtained for some slanted planes as well (see Fig. 5).

Defocus. When many images are collected under a variety of calibrated camera settings, a search for the most-in-focus image will yield depth [10]. This approach is called depth from focus, and it is reliable but expensive in terms of time and images captured. When restricted to a few images, none of which are guaranteed to be in focus, a depth from defocus algorithm must be used [11]. This method is more difficult because the underlying texture is unknown: we cannot tell if the scene is a blurry picture of an oil painting or the sharp image of a watercolor, and without natural image priors both solutions are equally valid. To reduce ambiguity, most depth from defocus techniques require at least two exposures with substantially different blur kernels, controlled by internal camera actuation that changes the focal length or aperture diaphragm to manipulate the blur kernel [11–14]. The complexity of recovering depth depends on the blur kernels and the statistical image model that is used for inference. Depth performance improves when well-designed binary attenuation patterns are included in the aperture plane [15–17], and with appropriate inference, binary codes can even provide useful depth from a single exposure [18–20].

Focal flow is similar to depth from defocus in that it relies on focus changes over a small set of defocused images to reveal depth, and that it requires a specific blur kernel. However, both the implied hardware and the computation are different. Unlike multi-shot depth from defocus, our sensor does not require internal actuation, and unlike binary aperture codes, it employs a continuous radially symmetric filter. Most importantly, by observing differential changes in defocus, it replaces costly inference with a much simpler measurement algorithm.

Differential defocus with Gaussian blur was previously considered by Farid and Simmoncelli [21], who used it to derive a two-aperture capture sequence. We build on this work by proving the uniqueness of the Gaussian filter, and by exploiting differential motion to avoid aperture actuation.

Cue Combination. Our use of relative motion between scene and sensor means that in many settings, such as robotics or motion-based interfaces, this cue comes without an additional power cost. Previous efforts to combine camera/scene motion and defocus cues [22–27] require intensive computations, though they often account for motion blur which we ignore. Even when motion is known, equivalent to combining defocus with stereo, measuring depth still requires inference [28, 29]. The simplicity of focal flow provides an advantage in efficiency.

2 The Focal Flow Constraint

In differential optical flow, a pinhole camera views a Lambertian object with a temporally constant albedo pattern, here called texture and denoted $T:\mathbb {R}^2 \rightarrow [0,\infty )$. For now the texture is assumed to be differentiable, but this requirement will be relaxed later when deriving focal flow. For front-parallel planar objects, located at a time-varying offset (X, Y) and depth Z from the pinhole, the camera captures an all-in-focus image that varies in time t and pixel location (x, y) over a bounded patch S on a sensor located a distance $\mu _s$ from the pinhole. The intensity of this image $P:S \times \mathbb {R}\rightarrow [0,1]$ is a magnified and translated version of the texture, scaled by an exposure-dependent constant $\gamma$:

$$\begin{aligned} P(x,y,t) =&~ \gamma ~ T\left( \frac{Z(t)}{-\mu _s}x-X(t), ~ \frac{Z(t)}{-\mu _s}y-Y(t)\right) . \end{aligned}$$

(1)

It is well known that the ratios of the spatial and temporal derivatives of this image are independent of texture, and so can reveal information about the scene. A familiar formulation [7] provides optical flow $(\dot{x},\dot{y})$ from image derivatives:

$$\begin{aligned} 0 =&\begin{bmatrix} P_x&P_y \end{bmatrix} \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} + P_t, \end{aligned}$$

(2)

while following [6] to split the translation and magnification terms:

$$\begin{aligned} 0 =&\begin{bmatrix} P_x&P_y&(xP_x+yP_y) \end{bmatrix} \mathbf {u} + P_t, \end{aligned}$$

(3)

$$\begin{aligned} \mathbf {u} =&[u_1, u_2, u_3]^T = \left[ -\frac{\dot{X}\mu _s}{Z},-\frac{\dot{Y}\mu _s}{Z},-\frac{\dot{Z}}{Z}\right] ^T, \end{aligned}$$

(4)

provides texture-independent time to contact $\frac{Z}{\dot{Z}}=\frac{-1}{u_3}$ and direction of motion $\left( \!\frac{\dot{X}}{\dot{Z}},\frac{\dot{Y}}{\dot{Z}}\!\right) =\left( \frac{-u_1}{\mu _s u_3},\frac{-u_2}{\mu _s u_3}\!\right)$.

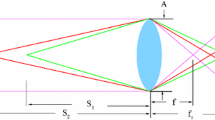
For focal flow, we replace the pinhole camera with a finite-aperture camera having an ideal thin lens and an attenuating filter in the aperture plane. We represent the spatial transmittance profile of the filter with the function $\kappa : \mathbb {R}^2 \rightarrow [0,1]$. We assume that this function is radially symmetric, so that this two-dimensional function of x and y can be written as a function of the single variable $r=\sqrt{x^2+y^2}$. However, we do not require smoothness, which allows for pillboxes and binary codes as well as continuous filters. For a front-parallel world plane at depth Z, the filter induces a blur kernel k on the image that is a “stretched” version of the aperture filter:

$$\begin{aligned} k(r;Z) =&\frac{1}{\sigma ^2(Z)}\kappa \left( \frac{r}{\sigma (Z)}\right) , \end{aligned}$$

(5)

where the magnification factor $\sigma$, illustrated in Fig. 1C, is determined by object depth, sensor distance, and in-focus depth $\mu _f$:

$$\begin{aligned} \sigma (Z) =&\left( \frac{1}{Z}-\frac{1}{\mu _f}\right) \mu _s. \end{aligned}$$

(6)

Denoting by $*$ a convolution in x and y, we can write the blurred image I as

$$\begin{aligned} I(x,y,t) =&k\left( \sqrt{x^2+y^2};Z(t)\right) *P(x,y,t). \end{aligned}$$

(7)

Unlike the pinhole image P, the ratios of the spatial and temporal derivatives of this defocus-blurred image I depend on texture. This is because the constant brightness constraint does not hold under defocus: pixel intensity changes both as image features move and also as patch contrast is reduced away from the focal plane. This difference, illustrated in Fig. 1, implies that any finite-aperture system for measuring optical flow will suffer a systematic error from defocus. Mathematically, this appears as an additive residual term on the time derivative, as shown in the following proposition.

Proposition

¹For an ideal thin lens camera and front-parallel planar scene,

$$\begin{aligned} I_x =&k_x *P, \end{aligned}$$

(8)

$$\begin{aligned} I_y =&k_y *P, \end{aligned}$$

(9)

$$\begin{aligned} I_t =&k_t *P + k *P_t \end{aligned}$$

(10)

$$\begin{aligned} =&-u_1 I_x - u_2 I_y - u_3(xI_x + yI_y) - R, \end{aligned}$$

(11)

where, denoting by $\kappa '$ the distributional derivative of $\kappa$,

$$\begin{aligned} R(x,y,t;P,\kappa ,Z,\dot{Z}) =&\frac{\dot{Z}}{Z-\mu _f}\frac{1}{\sigma ^2(Z)}\! \left( \! 2\kappa \!\left( \!\frac{r}{\sigma (Z)}\!\right) \!+\! \frac{r}{\sigma (Z)}\kappa '\left( \!\frac{r}{\sigma (Z)}\!\right) \!\right) \!*\!P. \end{aligned}$$

(12)

The time-varying residual image R(x, y, t) changes with depth, velocity, and camera design. It is troublesome because it also depends on the pinhole image P, which is not directly measured. Only the blurred image $I\!=\!k\!*\!P$ is available. This means that for almost all aperture filters, there is no way to express R using scene geometry and image information alone—it is inherently texture-dependent.

However, we observe that for a very specific aperture filter, this source of error can actually be transformed into a usable signal that resolves both depth and 3D velocity. For this to happen, the aperture filter must be paired with a particular linear image processing operation that, when combined with the filter, allows the decomposition of residual image R into a depth/velocity factor (analogous to $u_1$) and an accessible measurement (analogous to $I_x$). To formally identify such a filter and image operator, we seek triples $(M,\kappa ,v)$ of shift-invariant linear image operators M (like $\partial _x$ and $\partial _y$), aperture filters $\kappa$, and scalar depth/velocity factors v (analogous to $u_1$ and $u_2$) that satisfy, for any texture,

$$\begin{aligned} v(t) ~ M[I](x,y) =&R(x,y,t). \end{aligned}$$

(13)

We prove in the following theorem that there exists a unique family of such triples, comprised of Gaussian aperture filters and Laplacian image measurements. This leads directly to a simple sensor and algorithm that we prototype and evaluate in Sect. 4.

Theorem

Let $\kappa :\mathbb {R}^2\rightarrow [0,1]$ be radially symmetric, with $\kappa (r)$ and $r \kappa (r)$ Lebesgue integrable. For $v:\mathbb {R}\rightarrow \mathbb {R}$ and translation-invariant linear spatial operator M with finite support:

$$\begin{aligned}&v(t;Z,\dot{Z}) ~ M \left[ \frac{\kappa \left( \frac{\sqrt{x^2+y^2}}{\sigma (Z)}\right) }{\sigma ^2(Z)} *P(x,y,t)\right] = R(x,y,t;P,\kappa ,Z,\dot{Z}), \nonumber \\&\forall P:S \times \mathbb {R}\rightarrow [0,1],~~\forall Z \in \mathbb {R}^+,~~\forall \dot{Z} \in \mathbb {R},~~\forall (x,y,t)\in \mathbb {R}^3 \end{aligned}$$

(14)

if and only if, for aperture width and transmittance parameters $\Sigma , \alpha \in \mathbb {R}^+$ and measurement scaling parameter $\beta \in \{\mathbb {R}-0\}$,

$$\begin{aligned} \kappa (r) =&~\alpha ~e^{-\frac{r^2}{2 \Sigma ^2}}, \end{aligned}$$

(15)

$$\begin{aligned} M =&~\beta ~\nabla ^2,\end{aligned}$$

(16)

$$\begin{aligned} v(t;Z,\dot{Z}) =&~\frac{1}{\beta }~\frac{\dot{Z}(t)}{Z(t)}\left( \frac{\mu _f}{Z(t)}-1\right) \left( \frac{\Sigma \mu _s}{\mu _f}\right) ^2. \end{aligned}$$

(17)

This theorem states that, when the filter $\kappa (r)$ is Gaussian, the residual R is proportional to the image Laplacian $M[I]=I_{xx}+I_{yy}$ and is therefore directly observable. Moreover, the Gaussian is the only radially-symmetric aperture filter—out of a broad class of possibilities including pillboxes, binary codes, and smooth functions—that permits observation by a depth-blind linear operator.

Combining the proposition and theorem leads to a per-pixel linear constraint, analogous to those used in measuring optical flow or time to contact.

Corollary

For a camera with Gaussian point spread functions observing a front-parallel planar scene, the following constraint holds at each image pixel:

$$\begin{aligned} 0 =&\begin{bmatrix} I_x~&I_y~&(xI_x + yI_y) ~&(I_{xx} + I_{yy}) \end{bmatrix} \mathbf {v}+ I_t, \nonumber \\ \mathbf {v} =&[u_1,u_2,u_3,v]^T = \left[ -\frac{\dot{X}\mu _s}{Z},-\frac{\dot{Y}\mu _s}{Z},-\frac{\dot{Z}}{Z}, -\frac{\dot{Z}}{Z}\left( 1-\frac{\mu _f}{Z}\right) \left( \frac{\Sigma \mu _s}{\mu _f}\right) ^2\right] ^T . \end{aligned}$$

(18)

Holding this constraint over a generic image patch yields a system of linear equations that can be solved for $\mathbf {u}$ and v. In the presence of axial motion ($\dot{Z} \ne 0$) the new scalar factor v provides enough additional information to directly recover complete depth and velocity:

$$\begin{aligned} Z =&\frac{(\mu _s^2 \Sigma ^2 \mu _f)u_3}{(\mu _s^2 \Sigma ^2)u_3-(\mu _f^2){v}}, \end{aligned}$$

(19)

$$\begin{aligned} (\dot{X},\dot{Y},\dot{Z}) =&-\left( Z u_1/\mu _s,Z u_2/\mu _s,Z u_3\right) . \end{aligned}$$

(20)

This implies a simple patch-wise algorithm for measuring depth and velocity, about which we make a few notes. When an image patch is degenerate, meaning that the matrix having a row $[I_x,I_y,xI_x+yI_y,I_{xx}+I_{yy}]$ for each of the patch’s pixels is not full rank, partial scene information can often still be obtained. For example, a patch that contains a single-orientation texture and is subject to the classical aperture problem gives rise to ambiguities in the lateral velocity $(\dot{X},\dot{Y})$, but depth Z and axial velocity $\dot{Z}$ can still be determined. Separately, in the case of zero axial motion $(\dot{Z}=0)$ it follows that $u_3=v=0$, and the patch can only provide optical flow. Finally, note that unlike many depth from defocus methods, focal flow produces no side-of-focal-plane ambiguity.

The following proof draws heavily on the theory of distributions, for which we suggest [30] as a reference. Additional intuition may be gained from two alternate derivations of Eq. (18) that are provided in an associated technical report [31]. These alternate derivations are simpler because they begin by assuming a Gaussian filter instead of proving its uniqueness.

Proof

Because M is a translation-invariant linear operator with finite support, M[I] can be written as a convolution

$$\begin{aligned} M[I] =&m *I, \end{aligned}$$

(21)

with a compactly-supported distribution m. This compactness, along with the compactness of P (which we relax later but need for uniqueness), guarantees that the convolution theorem applies to $m *\kappa *P$. Then, with 2D spatial Fourier transforms denoted by $\mathcal {F}[f(r)] = \hat{f}(\hat{r})$, Eq. (14) can be written as

$$\begin{aligned} \hat{m}(\hat{r}) \hat{\kappa }(\sigma \hat{r})\hat{P} =&-\frac{\hat{r}}{w}\hat{\kappa }'(\sigma \hat{r})\hat{P}, \end{aligned}$$

(22)

$$\begin{aligned} w(t) =&\frac{Z-\mu _f}{\dot{Z}}v(t), \end{aligned}$$

(23)

which we require to hold for all textures by eliminating $\hat{P}$ terms. By assuming compactness of m and integrability of $\kappa$ and $r\kappa$, $\hat{m}$ is smooth and $\hat{\kappa }$ has a continuous first derivative, so the resulting differential equation in $\hat{\kappa }$ has solution

$$\begin{aligned} \hat{\kappa }(\sigma \hat{r}) \propto&e^{-{w}(t) \int _0^{\hat{r}} \frac{\hat{m}(\hat{s})}{\hat{s}}d\hat{s}}, \end{aligned}$$

(24)

which restricts the class of possible $\hat{m}$ and w to the form²

$$\begin{aligned} \hat{m} \propto&\hat{r}^{2n}, ~ w \propto \sigma ^{2n}, ~ n \in \mathbb {R}. \end{aligned}$$

(25)

These are Riesz kernels, with inverse Fourier transform

$$\begin{aligned} m(r;n) \propto {\left\{ \begin{array}{ll} \text {undefined}, &{}n \le -1\\ (\delta ''(x)\delta (y) + \delta (x)\delta ''(y))^{*n}, &{}n \in \{0,1,2,...\} \\ r^{-2(n-\lfloor |n| \rfloor )} *(\delta ''(x)\delta (y) + \delta (x)\delta ''(y))^{*\lfloor |n| \rfloor }, &{}n \in \mathbb {R}, \text {else}, \end{array}\right. } \end{aligned}$$

(26)

where starred exponents indicate repeated convolution. When n is not a nonnegative integer, the corresponding m is undefined or has noncompact support. When $n=0$, the aperture filter $\kappa$ is a pinhole, violating the finite transmittance assumption. Thus, the complete set of image operators M that can satisfy condition (14) are powers of the Laplacian: $M \in \{\beta (\nabla ^2)^n \mid n \in \mathbb {Z}^+,\beta \in \{\mathbb {R}-0\}\}$.

For the proportionality v between measurement M[I] and residual R, note from Eq. (25) that w takes a constant value under unit magnification $\sigma$. Calling this constant $\Sigma ^2$ so that $w=\Sigma ^2\sigma ^{2n}$, Eq. (23) produces v:

$$\begin{aligned} v(t;Z,\dot{Z}) = \dot{Z}\Sigma ^2\sigma ^{2n}/(\beta (Z-\mu _f)). \end{aligned}$$

(27)

Since $v/u_3$ is monotonic in depth, it resolves complete scene information for any n. For aperture filter $\kappa$ we take Eqs. (24, 25) under unit $\sigma$:

$$\begin{aligned} \kappa (r;n) =&\mathcal {F}^{-1}\left[ e^{-\Sigma ^2\hat{r}^{2n}} \right] , \end{aligned}$$

(28)

which corresponds to a Gaussian filter for $n=1$. For all $n \ge 2$, $\kappa (r;n)$ cannot describe a transmittance profile because it is negative for some r.³ Thus $n=1$, and M[k] is a rapidly decreasing function, so $m *k *P$ is well-defined for any bounded locally-integrable P, and the focal flow constraint holds regardless of the compactness of the texture’s support.    $\square$

3 Inherent Sensitivity

Due to the loss of image contrast as an object moves away from the focal plane, we expect the focal flow depth signal to be strongest for scene patches that are in focus or nearly in focus. This is similar to the expected performance of stereo or depth from defocus, for which depth accuracy degrades at large distances. In those cases, accuracy is enhanced by increasing the baseline or aperture size. In focal flow, focal settings play the analogous role.

Following Schechner and Kiryati in [34], we can describe the inherent sensitivity of all three depth cues. Recall that for a stereo system with baseline b and an inference algorithm that estimates disparity $\varDelta x$, depth is measured as

$$\begin{aligned} Z =&\frac{b \mu _s}{\varDelta x}, \end{aligned}$$

(29)

with first-order sensitivity to the disparity estimate

$$\begin{aligned} \left| \frac{dZ}{d(\varDelta x)}\right| =&\left| \frac{b \mu _s}{-(\varDelta x)^2}\right| = \frac{Z^2}{b \mu _s}. \end{aligned}$$

(30)

Similarly, for a depth from defocus sensor with aperture radius A and an algorithm that estimates blur radius $\tilde{A}$, the sensitivity of depth to error in $\tilde{A}$ is

$$\begin{aligned} Z =&\frac{\mu _f \mu _s A}{\mu _f \tilde{A} + \mu _s A}, \end{aligned}$$

(31)

$$\begin{aligned} \left| \frac{dZ}{d \tilde{A}}\right| =&\left| \frac{-\mu _f^2 \mu _s A}{(\mu _f\tilde{A} +\mu _s A)^2} \right| = \frac{Z^2}{A\mu _s}. \end{aligned}$$

(32)

These equations show a fundamental similarity between stereo and depth from defocus, in which the baseline and aperture size are analogous.

For a toy model of focal flow, we consider images of a sinusoidal texture blurred by a normalized Gaussian. We assume the texture has frequency $\omega _0$, unit amplitude, and arbitrary phase and orientation. Then, the image captured at time t has frequency $\omega$ and amplitude B, which are determined by depth:

$$\begin{aligned} \omega (t) =&Z\omega _0/\mu _s, \end{aligned}$$

(33)

$$\begin{aligned} B(t) =&\iint \frac{e^{-\frac{x^2}{4 \Sigma ^2 \sigma ^2}}}{4 \pi \Sigma ^2 \sigma ^2} \cos (\omega (t)x) dx dy = e^{-\Sigma ^2 \omega _0^2 \left( \frac{Z-\mu _f}{\mu _f}\right) ^2}. \end{aligned}$$

(34)

Depth can be measured from image amplitude, frequency, and their derivatives:

$$\begin{aligned} Z =&\frac{\mu _f}{1+\left( \frac{\mu _f}{\mu _s \Sigma }\right) ^2\frac{\dot{B}}{2 B \omega \dot{\omega }}}. \end{aligned}$$

(35)

When image quantities $(\omega , \dot{\omega }, B, \dot{B})$ are measured within error bounds $(\epsilon _{\omega }, \epsilon _{\dot{\omega }}, \epsilon _{B}, \epsilon _{\dot{B}})$, a simple propagation of uncertainty bounds the depth error $\epsilon _Z$:

$$\begin{aligned} \epsilon _Z \le&\sqrt{\left( \frac{\partial Z}{\partial \omega }\right) ^2\epsilon _{\omega }^2+ \left( \frac{\partial Z}{\partial \dot{\omega }}\right) ^2\epsilon _{\dot{\omega }}^2 + \left( \frac{\partial Z}{\partial B}\right) ^2\epsilon _{B}+\left( \frac{\partial Z}{\partial B_1}\right) ^2\epsilon _{\dot{B}}^2} \end{aligned}$$

(36)

$$\begin{aligned} =&\frac{Z|Z-\mu _f|}{\mu _f}\sqrt{\frac{\epsilon _\omega ^2}{\omega ^2}+\frac{\epsilon _{\dot{\omega }}^2}{\dot{\omega }^2} +\frac{\epsilon _B^2}{B^2}+\frac{\epsilon _{\dot{B}}^2}{\dot{B}^2}}. \end{aligned}$$

(37)

This combination of error terms suggests that accuracy in measuring either brightness or spatial frequency can be used to mitigate error in the other quantity. This presents a novel trade-off between bit depth and spatial resolution when selecting a photosensor.

Depending on the error model, the radicand in expression (37) could introduce additional scene dependencies, but in the simplest case, it is constant and focal flow is immediately comparable to stereo and depth from defocus. Just as the sensitivity of those measurements goes as depth squared, we see that focal flow measurements are sensitive to object distance from both the camera and the focal plane through the $Z|Z-\mu _f|$ term. The focal flow analogue to aperture size or baseline in this scenario is the ratio of focal depth to sensor distance.

4 Prototype and Evaluation of Non-idealities

In theory, when an ideal thin lens camera with an infinitely-wide Gaussian aperture filter observes a single moving, front-parallel, textured plane, there is a unique solution $\varvec{v}\in \mathbb {R}^4$ to the system of per-pixel linear focal flow constraints (Eq. (18)), and this uniquely resolves the scene depth $Z(\varvec{v})$ and velocity $(\dot{X},\dot{Y},\dot{Z})(\varvec{v})$ through Eqs. (19, 20). In practice, a physical instantiation of a focal flow sensor will deviate from the idealized model, and there will only be approximate solutions $\tilde{\varvec{v}}\in \mathbb {R}^4$ that can produce errors in depth and velocity.

We expect two main deviations from the idealized model. First, thick lenses have optical aberrations and a finite extent, making it impossible to create ideal Gaussian blur kernels that scale exactly with depth. Second, image derivatives must be approximated by finite differences between noisy photosensor values. We assess the impacts of both of these effects using the prototype in Fig. 2. Based on 1”-diameter optics, it includes an f=100 mm planar-convex lens, a monochromatic camera (Grasshopper GS3-U3-23S6M-C, Point Grey Research), and an adjustable-length lens tube. The aperture side of the sensor supports various configurations, including an adjustable aperture diaphragm and the optional inclusion of a Gaussian apodizing filter (NDYR20B, Thorlabs) adjacent to the planar face of the lens. A complete list of parts can be found in [31].

Fig. 2.

Prototype focal flow sensor. The configurable aperture has a variable diaphragm the optional inclusion of a Gaussian apodizing filter. An adjustable lens tube enables varying pairs of focal and sensor distances ($\mu _s,\mu _f$).

Measurement Algorithm. For all results, we produce depth and velocity measurements using three frames from a temporal sequence, $I(x,y,t_i), i\in \{1,2,3\}$. To emulate a lower-noise sensor, each frame is created as the average of ten shots from the camera, unless otherwise noted. We use temporal central differences, $I_t(x,y)\approx 1/2\left( I(x,y,t_3)-I(x,y,t_1)\right)$, and spatial difference kernels $D_x=(-1/2,0,1/2)$, $D_{xx}= D_x *D_x$, and likewise in y, convolved with the middle frame $I(x,y,t_2)$. To densely estimate the scene vectors $\varvec{v}(x,y)$, we aggregate the per-pixel linear constraints over a square window into the matrix equation $A\varvec{v}=\mathbf{b}$, and take the least-squares solution as the measurement for the central pixel. Similar to optical flow, this can be implemented efficiently by computing, storing, and inverting the normal equations $A^TA\varvec{v}=A^T\mathbf{b}$ at all pixels in parallel. A reference implementation is included in [31].

This measurement process requires knowing the image sensor’s principal point (the origin of the coordinate system for x and y in Eq. (18)). We set it to the central pixel during alignment. We also find that numerical stability is improved by pre-normalizing the spatial coordinates $x\leftarrow x/c, y\leftarrow y/c$ for some constant c (we use $c=10^4$). This pre-normalization and the use finite differences lead to depth and velocity values that, if computed naively with Eqs. (19, 20), are scaled by an unknown constant. We accommodate these and other non-idealities through the following off-line calibration procedure.

Calibration. Mapping a scene vector $\varvec{v}$ to depth and velocity requires only two calibrated values: the filter width parameter $\Sigma$, and sensor distance $\mu _s$ (which, along with the lens’ focal length f=100 mm, determines the object focal distance $\mu _f$). Since blur kernels often deviate substantially from Gaussians, we optimize the calibration parameters directly with respect to depth accuracy. We mount a textured plane on a high-precision translation stage in front of the sensor, carefully align it to be normal to the optical axis, and use images of many translations to optimize the parameters $\mu _s$ and $\Sigma$. Details are included in [31]. To ensure that the system generalizes over texture patterns and focal depths, all reported results use textures and sensor distances $\mu _s$ that differ from those used in calibration.

Calibration must be repeated when the aperture is reconfigured, such as when inserting an apodizing filter or adjusting the diaphragm. When the effective blur kernels change, so does the optimal effective width $\Sigma$. But for a fixed aperture, we find that the sensor distance $\mu _s$ can be adjusted without re-calibrating $\Sigma$.

Fig. 3.

Accuracy and working range. Top and middle rows: Estimated depth and speed versus true depth for two aperture settings: apodizing filter (top) and open diaphragm (middle). Solid black lines are true depth and speed. Insets are sample image and PSF. Colors are separate trials with different focal distances $\mu _f$, marked by dashed vertical lines. Depth interval for which depth error is less than $1\,\%$ of $\mu _f$ defines the working range. Bottom left: Sample PSFs, and working range versus focal distance, for aperture settings: (I) diaphragm $\varnothing 4.5$ mm, no filter; (II) diaphragm open, with filter; (III) diaphragm $\varnothing 8.5$ mm, no filter; (IV) diaphragm $\varnothing 25.4$ mm, no filter. Bottom right: Working range for distinct noise levels, controlled by number of averaged shots.

Results. Figures 3 and 4 show performance for different apertures and noise levels. Accuracy is determined using a textured front-parallel plane whose ground truth position and velocity are precisely controlled by a translation stage. In each case, the measurement algorithm is applied to a $201\times 201$ window around the image center. The top and middle rows of Fig. 3 compare the measured depth Z and speed $\Vert (\dot{X},\dot{Y},\dot{Z})\Vert$ to ground truth, indicated by solid black lines. Speed is measured in units of millimeter per video frame (mm/frame). Different colors in these plots represent experiments with different focus distances $\mu _f$, corresponding to different lengths of the adjustable lens tube. We show measurements taken both with an apodizing filter (and open diaphragm) and without it (with diaphragm closed to about $\varnothing 4.5$ mm). In both cases, the inset point spread functions reveal a deviation from the Gaussian ideal, but the approximate solutions to the linear constraint equations still provide useful depth information over ranges that are roughly centered at, and proportional to, the focus distances.

The bottom of Fig. 3 shows the effects that aperture configuration and noise level have on the working range, defined as the range of depths for which the absolute difference between the measured depth and the true depth is less than $1\,\%$ of the focus distance $\mu _f$. The prototype achieves a working range of more than 15 cm. Figure 4 shows both the measured speed and the measured 3D direction of a moving texture. Comprehensive results for different textures, aperture configurations, and noise levels can be found in [31].

Fig. 4.

Velocity. Measured depth, speed, and 3D direction $(\dot{X},\dot{Y},\dot{Z})/\Vert (\dot{X},\dot{Y},\dot{Z})\Vert$ versus true depth, with markers colored by true depth. Directions shown by orthographic projection to XY-plane, where the view direction is the origin. Ground truth is black lines for depth and speed, and white squares for direction. (Two ground truth directions result from remounting a translation stage to gain sufficient travel.)

Figure 5 shows full-field depths maps measured by the system. Each is obtained by applying the reconstruction algorithm in parallel to overlapping windows. We used $71\times 71$ windows for the top row and $241\times 241$ windows for the bottom. We do not use multiple window sizes or any form of spatial regularization; we simply apply the reconstruction algorithm to every window independently. Even using this simple approach, the depths map are consistent with the scene’s true shape, even when the shape is not front-parallel. The Matlab code used to generate these depth maps can be found in [31]. It executes in 6.5 s on a 2.93 GHz processor with Intel Xeon X5570 CPU.

Fig. 5.

Depth maps for two different scenes. From left to right: one frame from an input three-frame image sequence; per-pixel depth measured by independent focal flow reconstruction in overlapping square windows; and true scene shape for comparison.

5 Discussion

By combining blur and differential motion in a way that mitigates their individual weaknesses, focal flow enables a passive, monocular sensor that provides depth and 3D velocity from a simple, small-patch measurement algorithm. While the focal flow theory is developed using Gaussian blur kernels and front-parallel scene patches, we find in practice that it can provide useful scene information for a much broader class of aperture configurations, and some slanted scene planes.

The prototype described in this paper currently has some limitations. Its simple measurement algorithm uses naive derivative filters and performs independent measurement in every local patch. As such, it is overly sensitive to noise and requires high-contrast texture to be everywhere in the scene. Performance can likely be improved by including noise suppression and dynamical filtering that combines the available depth and velocity values. At the expense of additional computation, performance could also be improved by adapting techniques from optical flow and stereo, such as outlier-rejection, multi-scale reasoning, and spatial regularization that can interpolate depth in textureless regions.

Another way to extract depth with an unactuated, monocular sensor is single-shot depth from defocus with a binary coded aperture (e.g., [18, 19, 35]), where one explicitly deconvolves each image patch with a discrete set of per-depth blur kernels and selects the most “natural” result. Compared to focal flow, this provides a larger working range, but lower depth precision and a much greater computational burden. For example, a simulated comparison to [18] showed its working range to be at least four times larger, but its precision to be more than seven times lower and its computation time to be at least a hundred times greater [31]. The relative efficiency of focal flow suggests its suitability for small, low-power platforms, particularly those with well-defined working ranges and regular ambient motion, either from the platform or the scene.