1 Introduction

When designing a cryptographic cipher, security is the most important concern. Indeed, there exist a number of threats to be evaluated and it is advisable to build in a security margin large enough to withstand future attacks. By doing so, ciphers are usually large and often don’t fit on constrained platforms like smart cards or microprocessors. Furthermore, even if they do fit, the speed of the execution renders the cipher often impractical for most use cases. This has led to the advent of lightweight cryptography. In lightweight cryptography, the security constraints are usually relaxed in order to make smaller and faster ciphers. Naturally, the security of such ciphers is still of prime importance, but the implementation properties are also taken into proper consideration. In battery-powered devices, considering only the area or speed is not enough, since the lifetime of the battery is determined by the energy efficiency of the device. In the examination of lightweight ciphers, we can observe that many are realized as Substitution Permutation Networks (SPNs) where the substitution part is done by one or more Substitution boxes (S-boxes). Recent results show that in a number of such ciphers, the S-box is the most power hungry building block [1]. Therefore, this work focuses on the design of S-boxes for lightweight cryptography. To be more precise, we experiment with S-boxes of size \(4\times 4\) and \(5\times 5\) that are implementation-friendly while remaining with good cryptographic properties.

We emphasize that our approach is to generate power efficient and/or small S-boxes using methods that are as simple (i.e. computationally easy) as possible. The size of the search space containing all \(4 \times 4\) lookup tables is equal to \(2^{2^4 \times 4}=2^{64}\). Since we only consider bijections in the construction of S-boxes, the search space is reduced to 16! (\({\approx }2^{44}\)). Reducing the search space even further, considering only affine equivalent S-boxes of 16 optimal classes [2], would still result in a search space size larger than \(2^{35}\). Evaluating the power consumption of all S-boxes in the search space would consume too much time. This is even worse for \(5 \times 5\) S-boxes. Therefore, we advocate the use of heuristics for optimizing S-boxes for power/area efficiency and we offer the experimental results that support our choice.

Considering the design choices for ciphers that use S-boxes, there are three main scenarios. The first one is to use different S-boxes in the encryption and decryption process, which is done in e.g. [3]. This is less efficient for area as well as energy optimized ciphers, since it requires the implementation of two different S-boxes. From a heuristics perspective, this scenario would increase the search space size, because it requires the optimization of the area and/or power consumption of the combination of both the encryption and the decryption S-boxes. Therefore, we do not consider this option in our experiments. The second scenario is to use a cipher in counter mode or in a sponge construction; in that case, the inverse of the S-box is not needed. This scenario is good for area and energy efficiency as well as for the minimization of the search space size. Finally, the third scenario is to use involutive S-boxes, for which the S-box is the same as its inverse. This is the approach used for instance in the Midori [4] and Noekeon ciphers [5].

The contributions of this paper are as follows:

  1. 1.

    In this work, we concentrate on the selection mechanism of S-boxes with power/area efficiency as a goal. As far as we know, we are the first to conduct such investigation. Since power/area efficiency plays an important role in lightweight ciphers, we also concentrate only on the S-box dimension usually found in such constructs, namely, we experiment with \(4\times 4\) and \(5\times 5\) S-box sizes.

  2. 2.

    We experiment with several different design methods and we identify the advantages of each of the methods. As a result we obtain a number of power/area efficient S-boxes of which the best one has a more than two times smaller power consumption and an almost two times smaller area than the PRESENT S-box. Naturally, our S-boxes also fulfill relevant cryptographic properties as discussed in [2].

  3. 3.

    Besides the main contribution, we also analyze the power/area efficiency of a number of S-boxes used in modern lightweight ciphers.

We emphasize that the main goal of this paper is to present a methodology on the construction of power/area efficient S-boxes, and not to concentrate on the specific results or technology. In all experiments, we use the NANGATE 45 open cell library.

The paper is organized as follows. Section 2 gives an overview of related work in terms of lightweight cipher design and power/area evaluation/optimization. In Sect. 3, we discuss basic notions about power and energy as well as the relevant cryptographic properties of S-boxes. Section 4 presents the methodology we use for obtaining power/area efficient S-boxes and discusses the results. Finally, in Sect. 5, we end with a conclusion and possible future work.

2 Related Work

There exist a number of research studies on lightweight ciphers, two of the most prominent ones being the PRESENT [6] and PRINCE [7] ciphers. In the rest of this paper, we will also concentrate on the comparison with those two ciphers/S-boxes. However, we mention several other ciphers that are SPN constructions for which we evaluate the energy consumption of the S-boxes. Those ciphers are RECTANGLE [3], Klein [8], Noekeon [5], and Luffa [9].

From the energy perspective of lightweight ciphers, Batina et al. give a comprehensive study of the area, power, and energy considerations in a number of lightweight ciphers [10]. In their paper, the authors also show that area is not always correlated with the power and energy consumption. This result further justifies our approach that to find a power efficient S-box, one needs to consider the power and not only the area. Knežević et al. analyze lightweight ciphers from the latency perspective and they discuss trade-offs between latency on the one hand and area, power, and energy on the other hand [11].

Kerckhof et al. present an evaluation of several lightweight ciphers with a focus on the energy cost [12]. Next, Banik et al. study the energy consumption of 9 lightweight ciphers as well as the AES cipher [1]. The authors also develop a model that predicts the optimal value r at which the r-round unrolled architecture should have the best energy efficiency. Banik et al. propose the energy efficient cipher Midori that uses involutive S-boxes that are extremely power efficient [4]. We note that the smaller version of the cipher, Midori64, has been broken and the authors recommend to use an S-box different from the one used in Midori128, since that leads to another invariant subspace attack [13].

Besides those results, there exist a number of papers considering heuristics to evolve S-boxes with good cryptographic properties [14, 15], but we note that none of those papers consider the implementation properties of S-boxes.

3 Preliminaries

3.1 Power and Energy

The power consumption of a CMOS device is given by

$$\begin{aligned} P_{total}=P_{dynamic} + P_{static}. \end{aligned}$$
(1)

The dynamic power consumption originates from the switching activity of the circuit, while the static power consumption is caused by subthreshold currents and gate leakage. The static power consumption is constant over time and does not depend on the clock frequency or the switching activity. In older technology nodes the dynamic power consumption was dominant in the total power consumption and the static power consumption was negligible. By moving to smaller transistor dimensions and thinner gate oxide layers, subthreshold currents and gate tunneling currents have increased causing higher leakage currents. Therefore, with smaller technology nodes, the relative contribution of the static leakage power consumption has increased.

The dynamic energy relates to the dynamic power consumption as follows:

$$\begin{aligned} P_{dynamic} = E_{dynamic} \cdot f_{CLK}, \end{aligned}$$
(2)

where \(f_{CLK}\) is the clock frequency. The dynamic energy is given by

$$\begin{aligned} E_{dynamic}=\alpha \cdot C_{load} \cdot {V_{dd}}^{2}, \end{aligned}$$
(3)

where \(\alpha \) is the switching activity of the signal and \(C_{load}\) is the load capacitance.

3.2 Cryptographic Properties of S-Boxes

The inner product of vectors \({\varvec{a}} = (a_0, a_1, \ldots , a_{n-1})\) and \({\varvec{b}} = (b_0, b_1, \ldots , b_{n-1})\) is denoted as \({\varvec{a}} \cdot {\varvec{b}}\) and equals \({\varvec{a}}\cdot {\varvec{b}} = \oplus _{i=1}^{n} a_{i}b_{i}\). The addition modulo 2 is denoted as “\(\oplus \)”. The Hamming weight HW of a vector \({\varvec{a}}\), where \({\varvec{a}} \in \mathbb {F}_{2}^{n}\), is the number of non-zero positions in the vector.

An (n, m)-function is a function from n bits to m bits. It is called bijective if it takes every value of \(\mathbb {F}_{2}^{m}\) the same number of times, namely \(2^{n - m}\) [16]. Balanced (n, n)-functions are permutations on \(\mathbb {F}_{2}^{n}\).

The nonlinearity \(N_F\) of an (n, m)-function F is equal to the minimum nonlinearity of all non-zero linear combinations \({\varvec{b}}\cdot F\), with \({\varvec{b}} \not = 0\), of its coordinate functions \(f_{i}\) [16].

$$\begin{aligned} N_{F} = 2^{n - 1} - \frac{1}{2} \max _{\begin{array}{c} {{\varvec{a}} \in \mathbb {F}_{2}^{n}}\\ {{\varvec{v}} \in \mathbb {F}_{2}^{m*}} \end{array}} |W_{F} ({\varvec{a}}, {\varvec{v}})|. \end{aligned}$$
(4)

\(W_{F} ({\varvec{a}}, {\varvec{v}})\) is the Walsh-Hadamard transform of F:

$$\begin{aligned} W_{F} ({\varvec{a}}, {\varvec{v}}) = \sum \limits _{{\varvec{x}} \in \mathbb {F}_{2}^{n}} (-1)^{{\varvec{v}}\cdot F({\varvec{x}}) \oplus {\varvec{a}}\cdot {\varvec{x}}}. \end{aligned}$$
(5)

The nonlinearity \(N_{F}\) of any (n, n)-function F must satisfy the inequality [16]:

$$\begin{aligned} N_{F} \le 2^{n-1} - 2^{\frac{n-1}{2}}. \end{aligned}$$
(6)

An S-box F has fixed points if there exist \({\varvec{x}}\) such that \({\varvec{x}} = F({\varvec{x}})\) [17].

Let F be a function from \(\mathbb {F}_2^n\) into \(\mathbb {F}_2^n\) and \(a, b \in \mathbb {F}_2^n\). We denote:

$$\begin{aligned} D (a, b) = |\left\{ x \in \mathbb {F}_2^n : F(x+a)+F(x) =b\right\} |. \end{aligned}$$
(7)

The entry at the position (a, b) corresponds to the cardinality of D(a, b) and is denoted as \(\delta (a, b)\). The \(\delta \)-uniformity \(\delta _F\) is then defined as [18, 19]:

$$\begin{aligned} \delta _F = \max _{\begin{array}{c} a \ne 0, b \end{array}} \delta (a, b). \end{aligned}$$
(8)

To define the algebraic degree of an S-box, first we use the algebraic normal form (ANF) representation of a Boolean function f [20] represented by a polynomial in \(\mathbb {F}_{2} \left[ x_{0},\ldots , x_{n-1}\right] /(x_{0}^{2} - x_{0},\ldots , x_{n - 1}^{2} - x_{n - 1})\). ANF is a multivariate polynomial defined as:

$$\begin{aligned} f({\varvec{x}}) = \oplus _{\begin{array}{c} {\varvec{a}} \in \mathbb {F}_{2}^{n} \end{array}} h({\varvec{a}})\cdot {\varvec{x}}^{{\varvec{a}}}, \end{aligned}$$
(9)

where \(h({\varvec{a}})\) is defined by the Möbius inversion principle

$$\begin{aligned} h({\varvec{a}})= \oplus _{\begin{array}{c} {\varvec{x}} \preceq {\varvec{a}} \end{array}} f({\varvec{x}}), \text { for any } {\varvec{a}} \in \mathbb {F}_{2}^{n}. \end{aligned}$$
(10)

The algebraic degree \(deg_f\) of a Boolean function f is defined as the number of variables in the largest product term of the function’s ANF having a non-zero coefficient [20]:

$$\begin{aligned} deg_f = max (HW({\varvec{a}}): h({\varvec{a}}) = 1). \end{aligned}$$
(11)

The algebraic degree \(deg_F\) of an S-box F is the maximum algebraic degree of all non-zero linear combinations of the coordinate functions (i.e. component functions) of F [16]:

$$\begin{aligned} deg_F = \max _{\begin{array}{c} {{\varvec{b}} \in \mathbb {F}_{2}^{m*}}\\ {HW({\varvec{b}})=1} \end{array}} deg ({\varvec{b}} \cdot F). \end{aligned}$$
(12)

In the case of equality in Eq. (6), such functions are called almost bent (AB) functions [16]. When a function is differentially 2-uniform, it is called almost perfect nonlinear (APN) function [16]. Every AB function is also APN, but the other direction does not hold. AB functions exist only in an odd number of variables, while APN functions also exist for an even number of variables. Furthermore, the maximal algebraic degree of AB functions equals \((n+1)/2\) while for the inverse APN equals \(n-1\) [21].

Size \(\mathbf 4 \times \mathbf 4 \) . Leander and Poschmann define optimal 4-bit S-boxes as being bijective, with the minimal possible linearity (or, maximal possible nonlinearity) and with a minimal \(\delta \)-uniformity value. For optimal S-boxes, both \(N_F\) and the \(\delta \)-uniformity are equal to 4 [2].

Furthermore, Leander and Poschmann show that all optimal 4-bit S-boxes belong to 16 classes, i.e. all optimal S-boxes are affine equivalent to one of those classes [2]. For two S-boxes \(S_{a}\) and \(S_{b}\) to be equivalent, the following equation needs to hold:

$$\begin{aligned} S_a(x) = B(S_b(A(x) \oplus {\varvec{a}}))\oplus {\varvec{b}}, \end{aligned}$$
(13)

where A and B are invertible \(4\times 4\) matrices and \({\varvec{a}}, {\varvec{b}} \in \mathbb {F}_{2}^{4}\).

For PRESENT, S-boxes from the 16 classes mentioned in [2] are considered, but some lightweight ciphers use S-boxes with different cryptographic conditions. For instance, the authors of the PRINCE cipher impose several additional criteria on the S-box and therefore there are only 8 out of the 16 classes that are acceptable [7]. Alternatively, one can follow a different classification of S-boxes as for example given in [22].

Size \(\mathbf 5 \times \mathbf 5 \) . When considering \(5\times 5\) S-boxes, the cryptographic properties one can obtain differ with regards to the choice of the S-box. As a first example, we consider the Keccak S-box [23] for which both the nonlinearity and \(\delta \)-uniformity are equal to 8. Note that those values are relatively far from the optimal ones. Furthermore, the algebraic degree of Keccak is low, and it actually equals the minimal possible algebraic degree for a nonlinear function. However, the Keccak S-box has an extremely efficient hardware implementation. The S-box used in Ascon [24] is an affine transformation of the Keccak S-box in order to remove the fixed points and to increase the branch number value [25]. On the other hand, the PRIMATEs S-box [26] is based on an almost bent permutation, which means it has a nonlinearity equal to 12 and a \(\delta \)-uniformity equal to 2, while the algebraic degree is only 2.

4 Methodology and Results

4.1 Power Estimation

Before the optimization procedure, the working frequency is specified. To illustrate the methodology, we work with a clock frequency of 10 MHz. This is because the dynamic power and the cell leakage power have similar orders of magnitude for this frequency for the technology used in this paper. This enables us to optimize both shares of the power at the same time. Furthermore, for a fixed clock frequency and computation time, optimizing for energy is the same as optimizing for average power. We note that our methodology can be used for any other frequency. In this work, the power consumption of S-boxes is estimated by means of simulation.

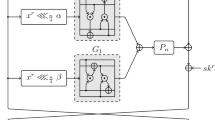
In the first step of our simulation setup, an S-box is generated in the style of a lookup table (LUT). A Matlab (R2014b) script is used to generate the HDL description of the S-box (Verilog file S-box.v). For logic synthesis, we use a standard cell approach using the NANGATE 45 open cell library (PDKv1_3_v2010_12). Synopsys Design Compiler (I-2013.12) is used to produce the gate-level netlist and the delay file (.sdf). The standard method for estimating the power consumption using the Synopsys tool chain is based on the random switching activity of the internal nodes. While this approach may be suitable for first-order estimation it does not give realistic application-specific data. In order to obtain a more realistic estimation, one needs to use a real test-bench to approximate the switching activity for each gate. For this purpose, we have developed a test-bench that goes through all possible \(n \times (n-1)\) input transitions of the S-box. Then, Modelsim SE PLUS 6.6d is used to simulate the wave file (.vcd) containing the switching activity of all nodes. This file is then converted to an activity file (.saif) using vcd2saif (D-2010.06-SP2). Finally, Design Compiler is used to estimate the power consumption. The obtained results are used as the fitness value for the optimization algorithm for both \(4\times 4\) and \(5\times 5\) S-box sizes. In Fig. 1, we depict our simulation setup in which the communication of our search strategies with the simulation part of the framework can be observed.

Fig. 1.
figure 1

Simulation setup for the generation/evaluation of S-boxes.

Full size image

4.2 \(4\times 4\) S-Boxes

The results for several commonly used \(4\times 4\) S-boxes are given in Table 1.

Table 1. Reference \(4\times 4\) S-boxes
Full size table

Random Search. As a first step in finding power/area optimized S-boxes, we run a simple random search to evaluate whether the optimization problem is trivial (disregarding the fact that randomly finding an optimal S-box is possible, but not trivial). We emphasize that this step serves only for comparison purposes. We create random S-boxes as permutations of values between 0 and \(2^n-1\) and check the results in terms of area and power. When evaluating only the optimal S-boxes, our results show that the power consumption is higher than 550 nW which makes this method quite inefficient when looking for power efficient S-boxes. In terms of area, the optimal S-boxes obtained through random search have an area larger than 20 GE.

Heuristics. Here, we improve the power/area of the S-boxes by using heuristics instead of random search. In order to do that, we investigate a population based metaheuristic algorithm called the Genetic Algorithm (GA). Although not widely used in the cryptographic community, we observe there are some papers in which GAs show good results for \(4\times 4\) S-boxes [28, 29].

In order to simplify the methodology as much as possible, we use a simple GA with a 3-tournament selection [30]. In a 3-tournament selection, three solutions are selected randomly and the worst one is discarded. From the remaining two solutions one offspring is created by the crossover operator. Each solution (i.e. individual) is represented as a permutation of values in the range \([0, 2^n-1]\). This representation avoids the necessity to look after the bijectivity property. We use well-known operators for permutation encoding, namely, the Toggle mutation and the Order crossover. In the Toggle mutation we randomly select two values and swap them. The Order crossover (OX) works by first randomly selecting two crossover points and copying everything between those two points from the first parent to the offspring. Then, starting from the second crossover point in the second parent, the unused numbers are copied in the order they appear in that parent [30]. The initial population is created uniformly at random and its size equals 100 individuals. We note that the computational complexity of the GA is negligible when compared with the evaluation cost, i.e. estimating the area or power consumption as further discussed later. As a stopping criterion, we use the number of evaluations without improvement, which is 30 generations in our case. Note that this algorithm also has the property of elitism, which means that the best solution will always remain intact in the population [30]. In order to better understand how GA works, we give a short pseudocode description:

figure a

In Fig. 2, we display one iteration of tournament selection, crossover and mutation (i.e., one generation of the GA). The numbers written next to the solutions represent the solutions’ fitness values. We note that we expect that similar results could be obtained with other heuristic techniques, like local search for instance. However, we opted to work with GAs since they use a population of individuals, which allows us to generate a number of solutions before sending the data for evaluation. Since the evaluation part is the most expensive one, it makes sense to run the power and area estimation at once for a whole population, while with local search, every evaluation would consist of only one individual. For further details about GAs, we refer the readers to [30].

Fig. 2.
figure 2

One generation of the GA.

Full size image

To evaluate the quality of each obtained S-box, we use a fitness function that consists of two parts. The first part checks the cryptographic properties of the S-box and only if all the criteria are met, it progresses to the second part where the power/area measurements are done. All S-boxes are ranked on the basis of their fitness where a higher value means an S-box is better. Therefore, since lower \(\delta \)-uniformity is better, we subtract \(\delta \) from a constant value. In summary, for the first part (cryptographic evaluation), the fitness function equals:

$$\begin{aligned} fitness = N_{F} + (2^m - \delta ). \end{aligned}$$
(14)

With this equation, we allow that our solutions have fixed points, but since we observe that the removal of fixed points can affect the power/area consumption, we also add that part to the fitness function. Since we work under the assumption that the smaller number of fixed points the better, we subtract the number of fixed points from the maximal possible number of fixed points:

$$\begin{aligned} fitness = N_{F} + (2^m - \delta ) + (2^m - nr\_fixed\_points). \end{aligned}$$
(15)

We note that we experimented with more complex fitness functions where we added weights to each parameter, but here we present the simplest version of fitness function that yields good results. Such simple fitness function has advantages that it is more intuitive and there is no need to tune the weights in it. To state it differently, for size \(4\times 4\), this fitness function is more than sufficient to find solutions with maximal nonlinearity and minimal \(\delta \)-uniformity (with or without fixed points). However, when working with size \(5 \times 5\), there are no weight factors for the fitness function that reach values as obtained in e.g., AB functions. To improve the cryptographic properties, we believe one should use a completely different fitness function considering not only the nonlinearity value, but also all the values present in the Walsh-Hadamard spectrum. Naturally, this holds also for sizes larger than \(5\times 5\). We leave this research direction for future work.

In the second part of the evaluation, only those S-boxes that have the maximal nonlinearity and the minimal \(\delta \)-uniformity are evaluated with regards to the power/area consumption. This means that all our solutions must have optimal cryptographic properties before the power/area estimation is performed. When evaluating power, we take into account both static power and dynamic power (i.e., we consider the sum of those two values). Naturally, this also means that the results could be somewhat different if only one power value is considered. Still, we believe our approach is the most general one, and we note that changing the fitness functions and consequently optimization process would be trivial. We also discuss the influence of the operators used on the obtained results. For instance, since the power consumption can change significantly with a single mutation operation, the question is how that influences the search process. It is not possible to give a definitive answer to this question, and for sure there will be a number of occasions in the evolution process where such a small change influences the fitness value significantly. However, from the other perspective, there will also be a number of building blocks (i.e., subsets of the solutions/permutations) that have a low power consumption and when combined also have a low power consumption. Because of that, the search process will eventually converge to better solutions, as evident from our results. In Table 2, we give results for the best evolved S-boxes, both for S-boxes with and without fixed points. Note that all S-boxes are optimal, so we do not add the cryptographic properties to the table. Furthermore, all mentioned S-boxes also have a maximal algebraic degree of 3. It is interesting to note that when optimizing with regards to the power consumption, we also found an S-box with smaller area than when optimizing for area (for the case without fixed points). A possible reason for such a result is that when considering power, there are more values one can obtain and therefore the search space is more fine grained. On average, our search process needed several hours to reach those solutions.

Table 2. Best evolved \(4\times 4\) S-boxes
Full size table

Involutive S-Boxes. The total number of involutions for an S-box of size \(n \times n\) equals [31]:

$$\begin{aligned} \#Involution = \sum _{i = 0}^{2^{n - 1}}\frac{2^n !}{(2^{n - 1} - i) ! 2^{2^{n - 1} - i}}. \end{aligned}$$
(16)

If we consider the \(4\times 4\) case, there are in total 462 067 736 involutive S-boxes. This search space can be exhaustively searched if we consider only relevant cryptographic properties, but when power/area estimation is necessary, it still represents a search space too large to be efficiently exhausted. In order to conduct this search, we implemented a recursive swap algorithm that traverses all possible involutions with a defined number of fixed points. We tested more than 250 000 involutive S-boxes that are optimal (i.e., with the best possible nonlinearity and \(\delta \)-uniformity values) and the best obtained result for area equals 13 GE. On the other hand, when considering power results, the best S-box has a dynamic power of 201.84 nW and a static leakage power of 271.48 nW. We note that when considering power results, we found two S-boxes with the same result and both of them are S-boxes with 4 fixed points. Finally, to put these results into perspective from the computational complexity point and with a conservative estimate of only 10 s per S-box power/area evaluation, we needed around 30 days of continuous computation to conduct this experiment.

Next, we concentrate only on involutive S-boxes with 4 and 6 fixed points that are optimal. There are in total 18 918 900 involutive S-boxes with 4 fixed points, and 7 567 560 involutive S-boxes with 6 fixed points. We opted to follow this line of research since for instance in Midori, both S-boxes have 4 fixed points, while 6 fixed points is the maximal number of fixed points we could find in \(4\times 4\) S-boxes that are optimal. Furthermore, we additionally prune the results in order to keep only those that have an algebraic degree equal to 3. For S-boxes with 4 fixed points, we investigate 30 000 optimal involutive S-boxes. The best result for area is 13 GE while the best result for power is an S-box with a dynamic power of 201.8418 nW and a leakage power of 255.1868 nW. For optimal involutive S-boxes with 6 fixed points, we evaluate 3 000 S-boxes. The best result for area is 15 GE and the best result for power is an S-box with a dynamic power of 223.3748 nW and a leakage power of 293.5608 nW. As can be seen, the best results are obtained for the search within optimal S-boxes with 4 fixed points. However, this search yields a somewhat larger (to be exact, 0.33 GE larger) S-box with a higher power consumption compared to the GA approach. As a future work, it would be interesting to run a heuristic search only within involutive S-boxes. However, we note that in that scenario, one would need to design custom heuristic initialization in order to seed the algorithm with only involutive S-boxes. Furthermore, in that scenario, custom-made crossover and mutation operators are also needed when only involutive S-boxes are produced. In order to give a better perspective to those results, we give the average results over 100 random involutions with 0 to 8 fixed points in Table 3. Note that those S-boxes are mostly not optimal.

Table 3. Random involutive \(4\times 4\) S-boxes
Full size table

4.3 \(5\times 5\) S-Boxes

We omit the random search results since our experiments show that this problem is too difficult and the obtained results are far from power/area efficient. Furthermore, randomly created S-boxes also have cryptographic properties far from those observed in literature. In Table 4, we give the results for area and power for several S-boxes used in literature as well as for an “APN S-box”, which is an S-box we generated with the multiplicative inverse function and irreducible polynomial \(x^5 + x^4 + x^3 + x^2 + 1\) [19].

Table 4. Reference \(5\times 5\) S-boxes
Full size table

Heuristics. We use heuristics in the same way as in the \(4\times 4\) case. We note that we are unable to obtain AB \(5\times 5\) S-boxes with heuristics, but we are able to find S-boxes with cryptographic properties similar or somewhat better than those in the Keccak S-box. All the presented S-boxes have a nonlinearity equal to 8, \(\delta \)-uniformity 6, and algebraic degree 4. The results are given in Table 5.

Table 5. Best evolved \(5\times 5\) S-boxes
Full size table

Affine Transformations. Since we are unable to find \(5\times 5\) S-boxes that have cryptographic properties closer to the optimal values (either AB or APN), we use the fact that affine transformations can change the power/area of an S-box. Therefore, we aim to optimize the affine transformation in order to reduce the area/power.

Recall from Eq. (13) the matrices A and B need to be invertible in \(\mathbb {F}_2\) and the number of such matrices equals:

$$\begin{aligned} GL = \prod _{i = 0}^{n - 1}(2^n - 2^i). \end{aligned}$$
(17)

For \(n = 4\) there are in total 20 160 invertible matrices. However, since there are two matrices and additionally two constants \(a, b \in \mathbb {F}_{2}^{n}\), the total number of combinations is \({\approx }2^{36}\). When calculating cryptographic properties, this number is within reach, but for implementation properties like power where the time necessary to calculate the results for a single \(4\times 4\) S-box is in the order of magnitude of 10 s, this task becomes impossible. Moreover, for the \(4\times 4\) size, there are 16 optimal classes, which means that we need to run such a search 16 times. For the \(5\times 5\) size, there are 9 999 360 invertible matrices and therefore, the total number of combinations equals \({\approx }2^{56}\).

Based on the aforesaid, we see that an exhaustive search is most often not a realistic option. Therefore, we need a faster way to obtain good results. To be able to do so, we again use the same genetic algorithms setting, only now the individuals are encoded as a set of genotypes of bitstring values. Each genotype represents one matrix or a constant as in Eq. (13). Each individual has four genotypes of which the first two represent matrices A and B and genotypes 3 and 4 represent constants a and b. For an easier visualization of the solutions, one can imagine genotypes A and B as row vectors of size \(n^2\) where the transformation to a matrix is done by splitting the vector in n rows of size n.

The fitness function we aim to minimize is:

$$\begin{aligned} fitness = Power. \end{aligned}$$
(18)

Since we know that affine transformations cannot change the cryptographic properties we consider here, we do not need to check them during the evolution. Here, we investigate 3 S-boxes: the Keccak S-box, the PRIMATEs S-box (AB), and our APN S-box. The results for the best obtained affine transformations with regards to power consumption are given in Table 6. Note that for the Keccak and PRIMATEs case our search did not reveal any better S-boxes that are affine equivalent to the original S-box. Still, our best S-box that is affine equivalent to Keccak has a significantly smaller area/power than for instance affine transformations of the Keccak S-box as used in the Ascon and ICEPOLE ciphers. We note that when we optimize the affine transformation for Keccak with the goal of improving the area, the best S-box we find has an area of 21 GE and is without fixed points (recall that Keccak has 2 fixed points) like those used in Ascon and ICEPOLE. For the “APN S-box” the result is quite improved. This shows it is not easy to find better S-boxes with respect to power efficiency, but also that the S-boxes in Keccak and PRIMATEs are also good candidates from the area/power perspective. Since “APN S-box” is an S-box we created with a randomly selected irreducible polynomial of degree 5, one could expect that the results for such S-box could be significantly improved and our analysis confirms that.

Table 6. Best evolved \(5\times 5\) S-boxes, affine transformations
Full size table

4.4 Discussion

When implementing an S-box, one can follow the encoder/decoder structure as presented in [33], but we note that that scheme is effective only on larger S-boxes, for example size \(8\times 8\). The extra cost to implement an encoder/decoder is cumbersome for \(4\times 4\) S-boxes both from the power and area perspective.

Therefore, we advocate here the usage of heuristics when generating S-boxes with good power/area properties. To put our solutions into an adequate perspective, we compare them with S-boxes that are used in a number of lightweight designs. As can be observed, the Midori S-boxes have the smallest power consumption as well as the smallest area when considering currently used S-boxes. However, when compared with the evolved S-boxes in this paper, we see that our S-box without fixed points, has the smallest area (12.67 GE) and the smallest power consumption except for the Midori \(Sb_0\) S-box where the difference is only 14 nW. As a matter of fact, our best evolved \(4\times 4\) S-box has a more than two times smaller power consumption than the PRESENT S-box while retaining the same nonlinearity and \(\delta \)-uniformity values as the PRESENT S-box. However, we emphasize that our evolved S-boxes are not involutive.

On the other side, we observe that the involutive S-boxes that have the smallest power consumption (both in our work and other work) have 4 fixed points. Indeed, both Midori S-boxes (432.75 nW and 581.17 nW) as well as the two involutive S-boxes found in our search (473.32 nW) represent the best results for power consumption when considering involutive S-boxes. Therefore, in scenarios where involutive S-boxes with an as small as possible power consumption are necessary, it seems to be prudent first to conduct an exhaustive search within involutive S-boxes with 4 fixed points. Still, we emphasize that such a comparison in not completely fair since the PRESENT S-box has branch number equal to 3, while our S-boxes has branch number 2. Naturally, this is expected since we did not include the branch number property into our optimization process. Indeed, obtaining a high branch number in our current setting, would be more a matter of luck than the optimization process itself. However, we note a number of currently used S-boxes also have branch numbers equal to 2 (e.g., Klein, Noekeon, Rectangle, Prince). Finally, adding the branch number to the objective function is trivial, and we plan to explore that direction in future work. Moreover, we see that our evolved S-boxes have smaller area and power consumption than the S-box used in Piccolo, which is an S-box known to be extremely efficient from both area/power perspectives. However, we note that the Piccolo S-box is not intended to be implemented as a lookup table, which makes a fair comparison somewhat difficult.

For the \(5\times 5\) size, we observe that the problem is much more difficult, but we offer two heuristic techniques to improve the results; one based on the direct evolution of solutions, and another one that looks for the best affine transformation of a certain S-box. There, we managed to find an S-box that is affine equivalent to the Keccak S-box, with slightly worse area/power results, but without fixed points. However, that S-box has better area/power properties than those used in the Ascon and ICEPOLE ciphers.

A possible drawback of our approach is that S-boxes could be also implemented in other ways and not only as lookup tables. This is also the reason why we do not include results for S-boxes larger than \(5\times 5\), since those S-boxes are too big to be implemented as lookup tables in most realistic scenarios. With our approach, there is no guarantee that a certain power efficient S-box in lookup table style will remain power efficient when implemented using some other technique, but our results suggest that this is most often the case. Still, we believe our approach is as fair as possible since our technique can always serve as a strong indicator of S-box behavior. Implementing S-boxes in another way would make the search even more difficult (and computationally complex) since then we do not only look for S-boxes with good properties (i.e., the first level of the search) but also for different implementation methods (can be considered as the second level of search).

From the scalability perspective, our technique shows good behavior. Indeed, the same technique given for the \(5\times 5\) size (i.e., affine transformation-based search) works good for larger sizes. Still, those results are more difficult to interpret since such sizes usually necessitate different styles of the implementation of S-boxes. All our experiments were conducted on a PC that has an i7 4720HQ processor and 8 GB of RAM. For all relevant sizes (\(4\times 4, 5\times 5\), and \(8\times 8\)) the evaluation cost of the implementation properties is dominant. For instance, for size \(4\times 4\), to test all relevant cryptographic properties of a single S-box we need around 4 ms, for size \(5\times 5\) we need 8 ms, and for size \(8\times 8\), we need around 15 ms. Even for the smallest size of \(4\times 4\), evaluating the power consumption takes more than 10 s.

Naturally, these results should be taken with care. We do not suggest just to use our S-box and replace some of the existing ones with it. Indeed, doing that without a proper cryptanalytic analysis could be devastating for the security of the cipher. Rather, we suggest to use S-boxes we created in some new designs that specifically target low power consumption and area. Since we concentrated here only on the S-box part, we cannot give any cryptanalysis results since our S-boxes are not intended to replace existing S-boxes in modern ciphers. Therefore, we give relevant cryptographic properties that can be used as a comparison with other S-boxes. Furthermore, we focus here on a small set of cryptographic properties of S-boxes, but if other criteria need to be fulfilled, our heuristic approach can easily be adjusted. Finally, we tested our approach with one library using all possible input transitions of the \(n\times n\) S-box to do the power estimation. Our method is easily transferable to other libraries and other ways of power estimation. We believe that such adaptability of our framework to different settings is the main advantage of our approach. Indeed, if a researcher needs to run experiments with different constraints, the running time of our approach coupled with good results makes a good choice.

5 Conclusions and Future Work

In this work, we focused on the power and area efficiency of S-boxes of small sizes, namely \(4\times 4\) and \(5\times 5\). First, we defined an objective experimental setting for testing the power/area efficiency and we conducted experiments based on several different approaches. The best results were obtained using the heuristic approach, for which our best S-box has a more than two times smaller power consumption than the PRESENT S-box. We emphasize that we do not recommend for instance to exchange the PRESENT S-box with this new one, but rather use the new S-box when designing new ciphers that are energy efficient. When further cryptographic constraints are imposed in the choice of an S-box, our heuristic approach can be readily adapted. We note that any automatic search strategy is only as good as the synthesis tool. Therefore, with a more powerful synthesis algorithm, our search strategy would also be more efficient.

As future work, we plan to investigate the possibility of finding one S-box that performs optimally when considering more cryptographic properties as well as both power and area over several implementation libraries and to use such an S-box in the design of a new cipher that is energy efficient.