Abstract
We give three fully homomoprhic encryption (FHE) schemes that are secure against non-adaptive chosen ciphertext attacks (CCA1). For the first two, we extend the generic transformation of Boneh, Canetti, Halevi and Katz to turn any multi-key identity-based FHE scheme into a CCA1-secure FHE scheme. We then show two instantiations of multi-key identity-based FHE: One from LWE in the random oracle model, and one from sub-exponentially secure indistinguishability obfuscation. Both constructions are compact with respect to the function evaluated homomorphically but not compact with respect to the number of ciphertext involved in the homomorphic evaluation. The third scheme uses succinct non-interactive arguments of knowledge (SNARKs) and is fully compact.
Research supported in part by DARPA and the U.S. Army Office under contract number W911NF-15-C-0226 and W911NF-15-C-0236, NSF CAREER Award CNS-1350619, NSF Grant CNS-1413964 (MACS: A Modular Approach to Computer Security, Israel Science Foundation grant, Alfred P. Sloan Research Fellowship, Microsoft Faculty Fellowship, NEC Corporation, a Steven and Renee Finn Career Development Chair from MIT, and a SIMONS Investigator Award Agreement Dated 6-5-12.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Fully homomorphic encryption (FHE) [RAD78, Gen09, BV11] is a powerful cryptographic primitive that allows anyone to compute on encrypted data without decrypting it, and without knowledge of the secret key. The basic security property considered for FHE is semantic security [GM84], also known as security against chosen plaintext attacks (CPA), where it is required that an adversary that has access to the public parameters cannot distinguish between ciphertexts that result from encrypting two adversarially chosen plaintexts. This should hold even though the public parameters allow for encrypting messages and for homomorphic evaluation of ciphertexts.
However, CPA security provides only a weak guarantee in settings where ciphertexts can be generated maliciously. Indeed, it is easy to come up (either intentionally or unintentionally) with CPA-secure encryption schemes where one can maliciously generate ciphertexts that completely compromise the security of the scheme. The same holds, of course, for CPA-secure FHE schemes, So, for instance, a client that sends a ciphertext \(c=Enc(x)\) along with a function f to a server, expecting to obtain a ciphertext \(c'=\text {HomEval}(f,c)\) that decrypts to f(x), may instead receive a maliciously formed ciphertext \(c''\) such that \(Dec(c'')\) will output the secret decryption key which allows the server to fully recover x. This is so even when using CPA-secure FHE, and even when x is much larger than both the decryption key and \(c''\). Such attacks can indeed be taken care of by adding verifiability mechanisms “at the protocol level” on top of plain CPA-secure FHE schemes. However, can we have FHE scheme that guarantee, in of themselves, security against malformed ciphertexts?
The golden standard of security for encryption schemes against malformed ciphertetxts is security against chosen ciphertext attacks, also called CCA security (see, e.g., [NY90, RS91, DDN91, CS98, Sah99] and more) which requires that semantic security holds even when the adversary gets to ask for decryption queries. CCA security comes in two flavors: the non-adaptive flavor, called CCA1 or lunchtime attack, where the adversary is limited to ask decryption queries before she receives the challenge ciphertext, and the adaptive, or CCA2 version, where she can continue asking decryption queries even after she receives the challenge ciphertext (as long as the decryption queries are different from the challenge ciphertext itself).
CCA2 security prevents any meaningful modification of a given ciphertext, and so appears to be in direct contradiction with homomorphism (althouth some works do manage to reconcile the two notions in a meaningful way, see e.g. [CKN03, BSW12]). However, CCA1 security, which does consider security in face of malformed ciphertexts, but only ones that were generated before the challenge ciphertext is given, does not appear to be in contratiction for homomorphism. Indeed, the Cramer-Shoup-lite [CS98] scheme is both CCA1-secure and additively homomorphic. Still, several works [LMSV10, ZPS12, DGM15] show CCA1 attacks against (leveled) FHE schemes.Footnote 1 Moreover, the key paradigm for constructing unleveled FHE schemes goes through Gentry’s bootstrapping theorem [Gen09], wherein one publishes a circular encryption of the secret key as part of the public evaluation key, an approach that by its very definition falls to a CCA1 attack.
Loftus et al. [LMSV10] give a leveled CCA1-secure FHE scheme under a highly non-standard “lattice-based knowledge assumption”. This state of affairs leads us to ask:
Can we construct CCA1-secure fully homomorphic encryption schemes under better-understood computational assumptions? Can they be unleveled? Can they be compact?
1.1 Our Results and Techniques
We answer the above question positively.
CCA1-Secure FHE from Multi-key Identity-Based FHE. Our starting point is the work of Boneh et al. [BCHK07] who showed that any (semantically secure) identity-based encryption scheme can be used to construct a chosen-ciphertext-secure encryption scheme. An encryption of a message m in their (CCA1) construction is simply an ID-based encryption of m under a randomly chosen identity. Namely, the public key of the scheme is the IBE master public key, and the encryptor chooses a fresh random \(\mathsf{id}\) every time, and outputs \(\mathsf {IBE}.\mathsf {Enc}(\mathsf {mpk},\mathsf{id},m)\). In a nutshell, CCA1-security of the scheme follows from the fact that an ID-based encryption under an identity \(\mathsf{id}^*\) is secure even given the secret keys for all identities \(\mathsf{id}\ne \mathsf{id}^*\).
A natural idea to get a CCA1 fully homomorphic encryption scheme is to start with an Id-based fully homomorphic encryption scheme. This runs into a difficulty since in an FHE scheme, one has to be able to homomorphically evaluate ciphertexts that come from different sources (encryptors) but all encrypted to the same person (i.e., encrypted under the same public key). When we use the [BCHK07] transformation, this translates to being able to compute on IBE ciphertexts that all use the same master public key, but different identities. This leads us to our first connection: we define the notion of a multi-key Id-based FHE (IBFHE) scheme, and show that being able to construct one directly gives us a CCA1-secure FHE scheme.
This immediately gives two constructions of leveled CCA1 FHE based on two prior constructions of leveled multi-key IBFHE. The first is a generic construction from leveled multi-key FHE and IBE due to Brakerski, Cash, Tsabary and Wee [BCTW16]. Their scheme is very simple: to encrypt, draw a key pair and encrypt using the multi-key FHE; also encrypt the secret key using IBE. The second construction is based on LWE in the random oracle model, due to Clear and McGoldrick [CM15]. See Sect. 3 for our adaptation of the proof of [BCHK07], and more information on these transformations.
Obfuscation Construction. Recently, [CLTV15] showed how to use indistinguishability obfuscation to build homomorphism into an encryption scheme by publishing an obfuscation of a program which decrypts a pair of ciphertexts, evaluates and re-encrypts. Crucial to the proof of security is the ability to switch the underlying encryption scheme to lossy mode so that the output of the program which behaves honestly is statistically close to the output of the program which ignores the inputs and outputs an encryption of 0. We use this same idea, though in our setting things are more complex as we need to have the program continue to output valid encryptions for all identities except for the challenge. This is our main construction and is presented in Sect. 4.
A Note on Compactness. Compactness in FHE requires that the complexity of decryption (and thus ciphertext size) does not grow too much with the complexity of the function being evaluated. This prevents trivial schemes where the evaluator simply sends the circuit to be evaluated to the decryptor who decrypts and then evaluates the circuit. The ciphertexts in all of the above mentioned schemes grow with the number of inputs to the circuit to be evaluated, but not with the complexity of the circuit. We refer to such schemes as compact w.r.t. circuit complexity and we stress that this is less ideal than true compactness. The generic construction inherently is only compact w.r.t. circuit size (even if the underlying multi-key FHE is truly compact). The LWE and IO based constructions are also only compact w.r.t. circuit complexity, though it is not clear that this is inherent. Obtaining a truly compact CCA1 FHE would represent progress in either case, and would be particularly important for the LWE scheme as this would improve other constructions which have used the multi-key FHE scheme of [CM15]. We note that in many use cases multiple inputs to the FHE can be “batched together” and encrypted with the same key in order to keep ciphertext growth small.
CCA1 FHE from Knowledge Assumptions. Naor and Yung [NY90] show how to go from CPA encryption to CCA1 encryption using non-interactive zero-knowledge proofs (NIZKs). The CCA1 ciphertext is simply a (pair of) CPA ciphertexts along with a NIZK proving correctness. We adopt this approach to the FHE setting. We replace the NIZK with a zero-knowledge succinct non-interactive argument of knowledge (zkSNARK) to preserve compactness since otherwise the proof length would grow with the circuit being evaluated. This construction is described in Sect. 5.
Another Approach to CCA1 FHE. In the appendix, we present a different approach to constructing CCA1-secure FHE through what we call a linear-algebraic encryption scheme, a variant of a single-key-secure functional encryption scheme for linear functions. Although this approach currently only works to obtain additive homomorphism, we present it in the appendix as a potential approach to obtain alternative constructions of CCA1-secure FHE.
2 CCA-Secure Fully Homomorphic Encryption
Definition 1
Let \(\mathcal {M}\), be a message space. A CCA1-secure fully homomorphic encryption scheme (CCA1 FHE) is a tuple of polynomial time algorithms \((\mathsf{Gen},\mathsf{Enc},\mathsf{Dec},\mathsf{Eval})\), defined as follows, which satisfy the correctness, compactness and security properties below.
-
 a randomized algorithm which outputs a public key, secret key pair \((\mathsf{pk},\mathsf{sk})\).
a randomized algorithm which outputs a public key, secret key pair \((\mathsf{pk},\mathsf{sk})\). -
 a randomized algorithm which outputs a ciphertext \(\mathsf{ct}\).
a randomized algorithm which outputs a ciphertext \(\mathsf{ct}\). -
 an algorithm which outputs a message \(\mu \in \mathcal {M}\).
an algorithm which outputs a message \(\mu \in \mathcal {M}\). -
 an algorithm which takes a collection of ciphertexts \(\{\mathsf{ct}_i\}\) and a circuit to be evaluated \(\mathcal {C}\) and outputs an evaluated ciphertext \(\mathsf{ct}_\mathsf{eval}\).
an algorithm which takes a collection of ciphertexts \(\{\mathsf{ct}_i\}\) and a circuit to be evaluated \(\mathcal {C}\) and outputs an evaluated ciphertext \(\mathsf{ct}_\mathsf{eval}\).
-
Correctness: For any \(\mu \in \mathcal {M}\), and whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}\bigl (1^\lambda \bigr )\),
$$\begin{aligned} \Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Enc}(\mu ,\mathsf{pk}),\mathsf{sk}\bigr )=\mu \Bigr ]=1-\mathsf{negl}. \end{aligned}$$ -
Homomorphic Correctness: For any \(\{\mu _i\}\in \mathcal {M}^{\mathsf{poly}(\lambda )}\), polynomially sized circuit \(\mathcal {C}\), and whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}\bigl (1^\lambda \bigr )\), \(\mathsf{ct}_i\leftarrow \mathsf{Enc}\bigl (\mu _i,\mathsf{pk}\bigr )\),
$$\begin{aligned} \Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Eval}\bigl (\{\mathsf{ct}_i\},\mathcal {C}\bigr ),\mathsf{sk}\bigr )=\mathcal {C}\bigl (\{\mu _i\}\bigr )\Bigr ]=1-\mathsf{negl}. \end{aligned}$$ -
Compactness: There exists a polynomial \(\mathsf{poly}(\cdot )\) st \(|\mathsf{ct}_\mathsf{eval}|\le \mathsf{poly}(\lambda )\) for all \(\mathsf{ct}_\mathsf{eval}\leftarrow \mathsf{Eval}\bigl (\{\mathsf{ct}_i\},\mathcal {C}\bigr )\). In particular, \(\mathsf{poly}(\cdot )\) is independent of the size, depth or number of inputs to \(\mathcal {C}\).
-
CCA1 Security: For any PPT adversary \(\mathcal {A}\), its chance of winning the following game against a challenger \(\mathcal {C}\) is at most \(1/2+\mathsf{negl}\).
-
1.
\(\mathcal {C}\) draws \({(\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}(1^\lambda )}\) and sends \(\mathsf{pk}\) to \(\mathcal {A}\).
-
2.
For \({\alpha =1,\ldots ,\mathsf{poly}}\):
-
\(\mathcal {A}\) sends \(\mathsf{ct}_\alpha \) to \(\mathcal {C}\);
-
\(\mathcal {C}\) computes \(\mu _\alpha =\mathsf{Dec}(\mathsf{ct}_\alpha ,\mathsf{sk})\) and returns \(\mu _\alpha \) to \(\mathcal {A}\).
-
-
3.
\(\mathcal {A}\) sends \(\mu _0,\mu _1\in \mathcal {M}\) to \(\mathcal {C}\).
-
4.
\(\mathcal {C}\) draws \(\mathsf{ct}^*\leftarrow \mathsf{Enc}(\mu _\mathsf{bit},\mathsf{pk})\) for a random \(\mathsf{bit}\in \{0,1\}\) and sends \(\mathsf{ct}^{*}\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(\mathsf{guess}\in \{0,1\}\) and wins if \(\mathsf{guess}=\mathsf{bit}\).
-
1.
Remark. The query ciphertexts \(\mathsf{ct}_\alpha \) above are chosen by the adversary and can be base ciphertexts, evaluated ciphertexts, or may be altogether malformed.
Remark. We say that a CCA1 FHE scheme is leveled if there exists a polynomial \(\ell =\ell (\lambda )\) such that homomorphic correctness only holds when \(\mathcal {C}\) has depth at most \(\ell \). Also, we say that a CCA1 FHE is compact wrt circuit complexity if a weaker compactness condition holds which allows \(|\mathsf{ct}_\mathsf{eval}|\) to grow with the number of inputs to \(\mathcal {C}\), but demands that it remain independent of the size and depth of \(\mathcal {C}\).
Remark. In general, evaluated ciphertexts are allowed to have a slightly different form from fresh ciphertexts, in which case evaluated ciphertexts are decrypted with a separate decryption algorithm \(\mathsf{EvalDec}\). For notational simplicity, we refrain from explicitly specifying \(\mathsf{EvalDec}\). For all the schemes in this paper, evaluated decryption is the same as ordinary decryption except for minor differences.
3 Multi-key Identity-Based FHE to CCA1 FHE
In this section, we define the notion of multi-key identity-based FHE (IBFHE), and show that it implies CCA1-secure FHE. The transformation preserves the homomorphic (i.e., leveled or full) and compactness properties of the multi-key IBFHE scheme. By applying this transformation on prior multi-key IBFHE schemes we obtain two constructions of CCA1 FHE. Neither construction is fully compact as in each construction, the evaluated ciphertext size grows with the number of inputs to the circuit. They are however compact wrt circuit complexity as evaluated ciphertext sizes are independent of the size or depth of the circuit being evaluated. In Sect. 3.3 we apply our transformation to a recent construction of [BCTW16] to obtain CCA1 FHE from any multi-key FHE and IBE. In Sect. 3.4 we apply our transformation to the construction of [CM15] to obtain leveled CCA1 FHE based on sub-exponential LWE in the random oracle model.
We point out that in both of these constructions, the ciphertext size grows only with the number of batches of inputs to be evaluated. In settings where the total number of users is small and the input to the circuits are known all at once, this growth can be easily controlled.
3.1 Multi-key IBFHE
Definition 2
Let \(\mathcal {M}\), \(\mathcal {ID}\) be message and identity spaces. A multi-key identity-based fully homomorphic encryption scheme is a tuple of polynomial time algorithms \(\bigl (\mathsf{Setup},\mathsf{Extract},\mathsf{Enc},\mathsf{Dec},\mathsf{Eval}\bigr )\), defined as follows, which satisfy the correctness and security properties below.
-
 : outputs the master key pair \((\mathsf{mpk},\mathsf{msk})\).
: outputs the master key pair \((\mathsf{mpk},\mathsf{msk})\). -
 : outputs a secret key \(\mathsf{sk}_\mathsf{id}\) for the identity \(\mathsf{id}\).
: outputs a secret key \(\mathsf{sk}_\mathsf{id}\) for the identity \(\mathsf{id}\). -
 : encrypts message \(\mu \) to identity \(\mathsf{id}\), outputting \((\mathsf{ct}_\mathsf{id},\mathsf{id})\).
: encrypts message \(\mu \) to identity \(\mathsf{id}\), outputting \((\mathsf{ct}_\mathsf{id},\mathsf{id})\). -
 : decrypts \(\mathsf{ct}_\mathsf{id}\) using \(\mathsf{sk}_\mathsf{id}\), outputting \(\mu \).
: decrypts \(\mathsf{ct}_\mathsf{id}\) using \(\mathsf{sk}_\mathsf{id}\), outputting \(\mu \). -
 : takes a family of ciphertexts and a circuit and outputs \(\bigl (\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval}\bigr )\).
: takes a family of ciphertexts and a circuit and outputs \(\bigl (\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval}\bigr )\).
-
Correctness: For any \(\mu \in \mathcal {M}\), \(\mathsf{id}\in \mathcal {ID}\), and whp over \((\mathsf{mpk},\mathsf{msk})\leftarrow \mathsf{Setup}\bigl (1^\lambda \bigr )\), \(\mathsf{sk}_\mathsf{id}\leftarrow \mathsf{Extract}(\mathsf{id},\mathsf{msk})\),
$$\begin{aligned} \Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Enc}(\mu ,\mathsf{id},\mathsf{mpk}\bigr ),\mathsf{sk}_\mathsf{id}\bigr )=\mu \Bigr ]=1-\mathsf{negl}. \end{aligned}$$ -
Homomorphic Correctness: For any \(\{\mu _i\}\in \mathcal {M}^{\mathsf{poly}(\lambda )}\), \(\{\mathsf{id}_i\}\in \mathcal {ID}^{\mathsf{poly}(\lambda )}\), circuit \(\mathcal {C}\), and with high probability over \((\mathsf{mpk},\mathsf{msk})\leftarrow \mathsf{Setup}\bigl (1^\lambda \bigr )\), \(\mathsf{sk}_i\leftarrow \mathsf{Extract}(\mathsf{id}_i,\mathsf{msk})\), \(\mathsf{ct}_i\leftarrow \mathsf{Enc}\bigl (\mu _i,\mathsf{id}_i,\mathsf{mpk}\bigr )\),
$$\begin{aligned} \Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Eval}\bigl (\{(\mathsf{ct}_i,\mathsf{id}_i)\},\mathcal {C}\bigr ),\mathsf{sk}_\mathsf{eval}\bigr )\bigr )=\mathcal {C}\bigl (\{\mu _i\}\bigr )\Bigr ]=1-\mathsf{negl}, \end{aligned}$$where \(\mathsf{sk}_\mathsf{eval}\leftarrow \mathsf{Extract}(\mathsf{id}_\mathsf{eval},\mathsf{msk})\).
-
Compactness: There exists a polynomial \(\mathsf{poly}(\cdot )\) st \(|\mathsf{id}_\mathsf{eval}|,|\mathsf{ct}_\mathsf{eval}|\le \mathsf{poly}(\lambda )\) for all evaluated \((\mathsf{id}_\mathsf{eval},\mathsf{ct}_\mathsf{eval})\leftarrow \mathsf{Eval}\bigl (\{\mathsf{id}_i,\mathsf{ct}_i\},\mathcal {C}\bigr )\). In particular, \(\mathsf{poly}(\cdot )\) is independent of the size, depth or number of inputs to \(\mathcal {C}\).
-
Selective Security for Random Identities: For any PPT adversary \(\mathcal {A}\), its chance of winning the following game against a challenger \(\mathcal {C}\) is at most \(1/2+\mathsf{negl}\).
-
1.
\(\mathcal {C}\) draws \(\mathsf{id}^*\leftarrow \mathcal {ID}\) and \((\mathsf{mpk},\mathsf{msk})\leftarrow \mathsf{Setup}(1^\lambda )\) and sends \(\mathsf{mpk}\) to \(\mathcal {A}\).
-
2.
For \(\alpha =1,\ldots ,\mathsf{poly}\):
-
\(\mathcal {A}\) sends \(\mathsf{id}_\alpha \) to \(\mathcal {C}\);
-
if \(\mathsf{id}_\alpha =\mathsf{id}^*\), the game ends and \(\mathcal {A}\) loses; if \(\mathsf{id}_\alpha =\mathsf{id}_\beta \) for \(\beta <\alpha \), \(\mathcal {C}\) returns \(\mathsf{sk}_\beta \); otherwise \(\mathcal {C}\) draws \(\mathsf{sk}_\alpha \leftarrow \mathsf{Extract}(\mathsf{id}_\alpha ,\mathsf{msk})\), sends \(\mathsf{sk}_\alpha \) to \(\mathcal {A}\) and stores \((\mathsf{id}_\alpha ,\mathsf{sk}_\alpha )\).
-
-
3.
\(\mathcal {A}\) sends \(\mu _0,\mu _1\in \mathcal {M}\) to \(\mathcal {C}\).
-
4.
\(\mathcal {C}\) draws \(\mathsf{ct}^*\leftarrow \mathsf{Enc}(\mu _b,\mathsf{id}^*,\mathsf{mpk})\) for a random \(b\in \{0,1\}\) and sends \(\mathsf{ct}^*\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(b'\in \{0,1\}\) and wins if \(b'=b\).
-
1.
Remark. A stronger version of security allows \(\mathcal {A}\) to specify the identity \(\mathsf{id}^*\) he wishes to attack after seeing \(\mathsf{mpk}\) and the \(\mathsf{sk}_\alpha \). Additionally, we could allow \(\mathcal {A}\) to ask another round of identity queries after receiving the challenge ciphertext (provided he does not ask \(\mathsf{id}^{*}\)). We use the above notion as it is sufficient for CCA1 FHE.
Remark. As with CCA1 FHE, we consider relaxations of the above definition where homomorphic correctness is only required to hold for circuits whose depth is at most some polynomial \(\ell =\ell (\lambda )\). We call such schemes leveled. Similarly, we consider relaxations of compactness where \(|\mathsf{id}_\mathsf{eval}|\) and \(|\mathsf{ct}_\mathsf{eval}|\) may grow polynomially with the number of inputs to \(\mathcal {C}\), but remain otherwise independent of the complexity of \(\mathcal {C}\).
3.2 CCA1 FHE from Multi-key IBFHE
Let \(\mathcal {E}\) be a multi-key IBFHE scheme. Our CCA1 FHE scheme is as follows.
-
 : Output \((\mathsf{pk},\mathsf{sk})=(\mathsf{mpk},\mathsf{msk})\leftarrow \mathcal {E}.\mathsf{Setup}\bigl (1^\lambda \bigr )\).
: Output \((\mathsf{pk},\mathsf{sk})=(\mathsf{mpk},\mathsf{msk})\leftarrow \mathcal {E}.\mathsf{Setup}\bigl (1^\lambda \bigr )\). -
 : Draw \(\mathsf{id}\leftarrow \mathcal {ID}\) and \(\mathsf{ct}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl (\mu ,\mathsf{id},\mathsf{mpk}\bigr )\). Output \(\mathsf{ct}=(\mathsf{ct}_\mathsf{id},\mathsf{id})\).
: Draw \(\mathsf{id}\leftarrow \mathcal {ID}\) and \(\mathsf{ct}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl (\mu ,\mathsf{id},\mathsf{mpk}\bigr )\). Output \(\mathsf{ct}=(\mathsf{ct}_\mathsf{id},\mathsf{id})\). -
 : Parse \(\mathsf{ct}=(\mathcal {E}.\mathsf{ct},\mathsf{id})\). Draw \(\mathsf{sk}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Extract}(\mathsf{id},\mathsf{msk})\), output \(\mu \leftarrow \mathcal {E}.\mathsf{Dec}(\mathsf{ct}_\mathsf{id},\mathsf{id},\mathsf{sk}_\mathsf{id})\).
: Parse \(\mathsf{ct}=(\mathcal {E}.\mathsf{ct},\mathsf{id})\). Draw \(\mathsf{sk}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Extract}(\mathsf{id},\mathsf{msk})\), output \(\mu \leftarrow \mathcal {E}.\mathsf{Dec}(\mathsf{ct}_\mathsf{id},\mathsf{id},\mathsf{sk}_\mathsf{id})\). -
 : Parse \(\mathsf{ct}_i=(\mathcal {E}.\mathsf{ct}_i,\mathsf{id}_i)\), output \(\mathsf{ct}_\mathsf{eval}=(\mathcal {E}.\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval})\leftarrow \mathcal {E}.\mathsf{Eval}\bigl (\{(\mathcal {E}.\mathsf{ct}_i,\mathsf{id}_i)\},\mathcal {C}\bigr )\).
: Parse \(\mathsf{ct}_i=(\mathcal {E}.\mathsf{ct}_i,\mathsf{id}_i)\), output \(\mathsf{ct}_\mathsf{eval}=(\mathcal {E}.\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval})\leftarrow \mathcal {E}.\mathsf{Eval}\bigl (\{(\mathcal {E}.\mathsf{ct}_i,\mathsf{id}_i)\},\mathcal {C}\bigr )\).
Lemma 1
The above scheme is a CCA1-secure FHE scheme.
Proof
Correctness and homomorphic correctness follow immediately from the same properties of \(\mathcal {E}\). CCA1 security follows from the security of \(\mathcal {E}\) via the proof from [BCHK07]. We sketch this proof for completeness. The idea is to use an adversary \(\mathcal {A}\) who wins the CCA1 game to construct \(\mathcal {B}\) who wins the selective IBE security game against a challenger \(\mathcal {C}\). This \(\mathcal {B}\) receives \(\mathsf{mpk}\) which he forwards to \(\mathcal {A}\). Each time \(\mathcal {A}\) asks a ciphertext query \(\mathsf{ct}_\alpha \), \(\mathcal {B}\) asks \(\mathcal {C}\) for secret keys for the identity in \(\mathsf{ct}_\alpha \) so he can decrypt them for \(\mathcal {A}\). As \(\mathsf{id}^*\) is random, the chance that some \(\mathsf{id}_\alpha =\mathsf{id}^*\) is negligible. When \(\mathcal {A}\) sends \((\mu _0,\mu _1)\), \(\mathcal {B}\) forwards it to \(\mathcal {C}\) and receives \(\mathsf{ct}^*\). \(\mathcal {B}\) sends \((\mathsf{id}^*,\mathsf{ct}^*)\) to \(\mathcal {A}\), and forwards \(\mathcal {A}\)’s guess to \(\mathcal {C}\). \(\mathcal {B}\) wins the IBE security game if and only if \(\mathcal {A}\) wins the CCA1 game.
3.3 Generic Instantiation of Multi-key IBFHE
In a recent work, Brakerski et al. [BCTW16] give a generic construction of a multi-key, attribute-based fully homomorphic encryption scheme from a multi-key FHE and an ABE scheme. Their scheme is very simple: to encrypt, draw a key pair and encrypt using the multi-key FHE; also encrypt the secret key using ABE. Their transformation applies in our setting as well to give a generic construction of multi-key IBFHE from multi-key FHE and IBE. The scheme is only compact wrt circuit complexity. We omit the definitions of multi-key FHE and IBE as they are analogous to our definition of multi-key IBFHE with proper relaxations. We refer the reader to [MW16, GPV08] for definitions of these primitives.
 : Let \((\mathsf{MK.Gen},\mathsf{MK.Enc},\mathsf{MK.Dec},\mathsf{MK.Eval})\) be a multi-key FHE scheme, and let \((\mathsf{IBE.Setup},\mathsf{IBE.Extract},\mathsf{IBE.Enc},\mathsf{IBE.Dec})\) be an IBE scheme.
: Let \((\mathsf{MK.Gen},\mathsf{MK.Enc},\mathsf{MK.Dec},\mathsf{MK.Eval})\) be a multi-key FHE scheme, and let \((\mathsf{IBE.Setup},\mathsf{IBE.Extract},\mathsf{IBE.Enc},\mathsf{IBE.Dec})\) be an IBE scheme.
 : Draw and output \((\mathsf{mpk},\mathsf{msk})\leftarrow \mathsf{IBE.Setup}\).
: Draw and output \((\mathsf{mpk},\mathsf{msk})\leftarrow \mathsf{IBE.Setup}\).
 : Draw and output \(\mathsf{sk}_\mathsf{id}\leftarrow \mathsf{IBE.Extract}(\mathsf{id},\mathsf{msk})\).
: Draw and output \(\mathsf{sk}_\mathsf{id}\leftarrow \mathsf{IBE.Extract}(\mathsf{id},\mathsf{msk})\).
 : Draw \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{MK.Gen}(1^\lambda )\), \(\mathsf{ct}_1\leftarrow \mathsf{MK.Enc}(\mu ,\mathsf{pk})\) and \(\mathsf{ct}_2\leftarrow \mathsf{IBE.Enc}(\mathsf{sk},\mathsf{id},\mathsf{mpk})\). Output \((\mathsf{id},\mathsf{ct}_\mathsf{id})\) where \(\mathsf{ct}_\mathsf{id}=(\mathsf{ct}_1,\mathsf{ct}_2)\).
: Draw \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{MK.Gen}(1^\lambda )\), \(\mathsf{ct}_1\leftarrow \mathsf{MK.Enc}(\mu ,\mathsf{pk})\) and \(\mathsf{ct}_2\leftarrow \mathsf{IBE.Enc}(\mathsf{sk},\mathsf{id},\mathsf{mpk})\). Output \((\mathsf{id},\mathsf{ct}_\mathsf{id})\) where \(\mathsf{ct}_\mathsf{id}=(\mathsf{ct}_1,\mathsf{ct}_2)\).
 : Parse \(\mathsf{ct}_\mathsf{id}=(\mathsf{ct}_1,\mathsf{ct}_2)\). Compute \(\mathsf{sk}=\mathsf{IBE.Dec}(\mathsf{ct}_2,\mathsf{id},\mathsf{sk}_\mathsf{id})\), output \(\mathsf{MK.Dec}(\mathsf{ct}_1,\mathsf{sk})\).
: Parse \(\mathsf{ct}_\mathsf{id}=(\mathsf{ct}_1,\mathsf{ct}_2)\). Compute \(\mathsf{sk}=\mathsf{IBE.Dec}(\mathsf{ct}_2,\mathsf{id},\mathsf{sk}_\mathsf{id})\), output \(\mathsf{MK.Dec}(\mathsf{ct}_1,\mathsf{sk})\).
 : Set \(\mathsf{id}_\mathsf{eval}=\{\mathsf{id}_i\}\). Parse \(\mathsf{ct}_i=(\mathsf{ct}_{i,1},\mathsf{ct}_{i,2})\). Draw multi-key evaluation \(\mathsf{ct}_{\mathsf{eval},1}\leftarrow \mathsf{MK.Eval}\bigl (\{\mathsf{ct}_{i,1}\},\mathcal {C}\bigr )\), and set \(\mathsf{ct}_{\mathsf{eval},2}=\{\mathsf{ct}_{i,2}\}\). Set \(\mathsf{ct}_\mathsf{eval}=(\mathsf{ct}_\mathsf{eval,1},\mathsf{ct}_\mathsf{eval,2})\) and output \((\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval})\).
: Set \(\mathsf{id}_\mathsf{eval}=\{\mathsf{id}_i\}\). Parse \(\mathsf{ct}_i=(\mathsf{ct}_{i,1},\mathsf{ct}_{i,2})\). Draw multi-key evaluation \(\mathsf{ct}_{\mathsf{eval},1}\leftarrow \mathsf{MK.Eval}\bigl (\{\mathsf{ct}_{i,1}\},\mathcal {C}\bigr )\), and set \(\mathsf{ct}_{\mathsf{eval},2}=\{\mathsf{ct}_{i,2}\}\). Set \(\mathsf{ct}_\mathsf{eval}=(\mathsf{ct}_\mathsf{eval,1},\mathsf{ct}_\mathsf{eval,2})\) and output \((\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval})\).
Lemma 2
If \(\mathsf{MK}\) and \(\mathsf{IBE}\) are multi-key FHE and IBE schemes, respectively and \(\mathsf{MK}\) is compact wrt circuit complexity, then the above scheme is a multi-key IBFHE scheme which is compact wrt circuit complexity.
Remark. The second component of the evaluated ciphertext \(\mathsf{ct}_\mathsf{eval}\) is the concatenation of the encryptions of all of the secret keys from the \(\mathsf{MK}\) ciphertexts. Therefore, the above multi-key IBFHE scheme is only compact wrt circuit complexity even if \(\mathsf{MK}\) is fully compact. Moreover, if \(\mathsf{MK}\) is a leveled multi-key FHE scheme then the resulting scheme is also leveled.
Remark. In the above scheme, evaluated identities are collections of identities: \(\mathsf{id}_\mathsf{eval}=\{\mathsf{id}_i\}\). We define \(\mathsf{Extract}\) to work on such inputs: \(\mathsf{Extract}(\mathsf{id}_\mathsf{eval},\mathsf{msk})=\{\mathsf{sk}_i\}\) where \(\mathsf{sk}_i\leftarrow \mathsf{Extract}(\mathsf{id}_i,\mathsf{msk})\).
Proof
(Proof Sketch). Correctness follows immediately from correctness of \(\mathsf{MK}\) and \(\mathsf{IBE}\). Security follows from security of \(\mathsf{IBE}\) to change the \(\mathsf{IBE}\) portion of the challenge ciphertext to an encryption of 0 instead of \(\mathsf{sk}\) and then the security of \(\mathsf{MK}\) to say that \(\mathcal {A}\) cannot distinguish encryptions of \(\mu _0\) from \(\mu _1\).
Combining Lemma 2 with Lemma 1 we get the following.
Theorem 1
If there exists a multi-key FHE scheme which is compact wrt circuit complexity and an IBE scheme with selective security for random identities then there is a CCA1 FHE scheme which is compact wrt circuit complexity. If the multi-key FHE scheme is leveled, then the resulting CCA1 FHE scheme is also.
3.4 Multi-key IBFHE from LWE and ROs
Clear and McGoldrick [CM15] construct multi-key IBFHE (under the name “multi-identity IBFHE”) from learning with errors in the random oracle model. Like the generic construction above, their scheme is only compact wrt circuit complexity, as their evaluated ciphertexts grow in size with the number of inputs to the circuit. However, unlike the generic construction, their ciphertext growth is dominated by the ciphertext growth in the multi-key FHE. In other words, the failure of their scheme to be fully compact is due only to the failure of current multi-key FHE scheme to be fully compact. Combining the main theorem of [CM15] with Lemma 1 we get the following.
Theorem 2
Assuming sub-exponential LWE, there is a leveled CCA1 FHE scheme in the random oracle model which is compact wrt circuit complexity. The size of the evaluated ciphertexts in the scheme is \(S\cdot \mathsf {poly}(\lambda ,\log |\mathcal {C}|,\ell \) where S is the number of inputs to \(\mathcal {C}\), the circuit being evaluated, and \(\ell \ge \text {Depth}(\mathcal {C})\) is the maximum allowable depth for which homomorphic correctness still holds.
4 Instantiation from IO and Lossy Encryption
In this section, we construct a multi-key IBFHE from a sub-exponentially secure indistinguishability obfuscation (IO) and sub-exponentially secure lossy encryption. The latter primitive can be instantiated from standard assumptions, e.g., the decisional Diffie-Hellman (DDH) assumption. The multi-key IBFHE scheme in this section is fully compact and unleveled. The following lemma combined with Lemma 1 gives compact, non-leveled CCA1 FHE.
Lemma 3
Assuming sub-exponential IO and sub-exponential hardness of DDH, there is a compact, non-leveled multi-key IBFHE scheme.
In order to prove Lemma 3, we abstract an intermediate notion of encryption that we call tag-puncturable encryption. We then show that a tag-puncturable encryption scheme, together with IO, implies a multi-key IBFHE scheme, and finish up with showing a construction of tag-puncturable encryption from IO and additively homomorphic lossy encryption.
4.1 Tag-Puncturable Encryption
Definition 3
Let \(\mathcal {M}\), \(\mathcal {TAG}\) be message and tag spaces where \(\mathcal {M}\) is an abelian group. Let \(\mathsf{BAD}:\mathcal {TAG}\rightarrow \{U:U\subset \mathcal {TAG}\}\) be such that \(|\mathsf{BAD}(\mathsf{tag})|\le \mathsf{B}_{\max }\) for some parameter \(\mathsf{B}_{\max }\). Let \(\varepsilon >0\). A \((\mathsf{BAD},\mathsf{B}_\mathsf{max},\varepsilon )\)–tag-puncturable, additively homomorphic encryption scheme is a tuple \(\bigl (\mathsf{Gen},\mathsf{Punc.Gen},\mathsf{Enc},\mathsf{Dec},\mathsf{Add}\bigr )\) of polytime algorithms, defined as follows, which satisfy the properties below.
-
 : outputs the key pair \((\mathsf{pk},\mathsf{sk})\).
: outputs the key pair \((\mathsf{pk},\mathsf{sk})\). -
 : outputs the keys \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\).
: outputs the keys \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\). -
 : encrypts \(\mu \) to \(\mathsf{tag}\), outputting ciphertext \(\mathsf{ct}_\mathsf{tag}\).
: encrypts \(\mu \) to \(\mathsf{tag}\), outputting ciphertext \(\mathsf{ct}_\mathsf{tag}\). -
 : outputs message \(\mu \).
: outputs message \(\mu \). -
 : outputs a homomorphically evaluated ciphertext \(\mathsf{ct}_\mathsf{add}\).
: outputs a homomorphically evaluated ciphertext \(\mathsf{ct}_\mathsf{add}\).
-
Correctness: For any \(\mu \in \mathcal {M}\), \(\mathsf{tag}\in \mathcal {TAG}\), and whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}\bigl (1^\lambda \bigr )\),
$$\Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Enc}(\mu ,\mathsf{tag},\mathsf{pk}\bigr ),\mathsf{tag},\mathsf{sk}\bigr )=\mu \Bigr ]=1.$$ -
Homomorphic Correctness: For any \(\{\mu _i\}\in \mathcal {M}^k\), \(\mathsf{tag}\in \mathcal {TAG}\), and whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}\bigl (1^\lambda \bigr )\), and \(\mathsf{ct}_i\leftarrow \mathsf{Enc}\bigl (\mu _i,\mathsf{tag},\mathsf{pk}\bigr )\),
$$\Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Add}(\{\mathsf{ct}_i\},\mathsf{tag}),\mathsf{tag},\mathsf{sk}\bigr )=\mu _1+\cdots +\mu _k\Bigr ]=1.$$ -
Key Indistinguishability: This property comes in two parts. First, for any \(\mathsf{tag}^*\in \mathcal {TAG}\), \(\big \{(\mathsf{pk},\mathsf{sk}):(\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\leftarrow \mathsf{Punc.Gen}(\mathsf{tag}^*)\big \}\) is distributed identically to \(\mathsf{Gen}(1^\lambda )\).
Secondly, for all PPT \(\mathcal {A}\),
$$ \Big |\mathrm{Pr}_{\mathsf{Punc.Gen}(\mathsf{tag}^*)}\bigl (\mathcal {A}(\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})=1\bigr )-\mathrm{Pr}_{\mathsf{Punc.Gen}(\mathsf{tag}^*)}\bigl (\mathcal {A}(\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})=1\bigr )\Big |\le \varepsilon . $$(We remark that an alternate exposition could completely do away with \(\mathsf{Gen}\) and simply refer to \(\mathsf{Punc.Gen}\) for both the “real” public keys and punctured ones. We choose to keep \(\mathsf{Gen}\) around for familiarity.)
-
Punctured Key Utility: For every \(\mathsf{tag}^*\in \mathcal {TAG}\), and with high probability over \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\leftarrow \mathsf{Punc.Gen}(\mathsf{tag}^*)\), we have:
-
Lossiness with Bad Keys: For all \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\), and \(\mu _0,\mu _1\in \mathcal {M}\),
$$\mathsf{Enc}(\mu _0,\mathsf{tag},\mathsf{pk}_{\mathsf{tag}^*})\approx _\mathsf{s}\mathsf{Enc}(\mu _1,\mathsf{tag},\mathsf{pk}_{\mathsf{tag}^*}).$$ -
Correctness with Good Keys: For all \(\mathsf{tag}\notin \mathsf{BAD}_{\mathsf{tag}^*}\), and \(\mu \in \mathcal {M}\),
$$\mathsf{Dec}\bigl (\mathsf{Enc}(\mu ,\mathsf{tag},\mathsf{pk}_{\mathsf{tag}^*}\bigr ),\mathsf{tag},\mathsf{sk}_{\mathsf{tag}^{*}}\bigr )=\mu .$$
-
4.2 Multi-key IBFHE from Tag-Puncturable Encryption
The key ideas in this construction here borrow from recent works Canetti et al. [CLTV15] and Dodis et al. [DHRW16].
-
 : \(\mathsf{L}_\mathsf{max}=\lambda ^{\omega (1)}\) is an upper bound on the number of levels, \(\varepsilon >0\) such that \(\varepsilon \cdot \mathsf{L}_\mathsf{max}=\mathsf{negl}\); let \(\mathcal {E}\) be a \((\mathsf{L}_\mathsf{max},\varepsilon )\)–tag-puncturable additively homomorphic encryption scheme with tag space \(\mathcal {E}.\mathcal {TAG}=\mathcal {ID}\times [\mathsf{L}_\mathsf{max}]\), and for any \(\mathsf{tag}^*=(\mathsf{id}^*,\mathsf{L}^*)\in \mathcal {E}.\mathcal {TAG}\), define the bad set \(\mathsf{BAD}_{\mathsf{tag}^*}=\{(\mathsf{id}^*,\mathsf{L}):\mathsf{L}\ge \mathsf{L}^*\}\). Let the message space of \(\mathcal {E}\) be \(\mathcal {E}.\mathcal {TAG}\times \mathcal {M}\) where \(\mathcal {M}\) is the message space of our multi-key IBFHE. Assume \(\mathcal {M}\) is a ring. Also assume that the homomorphism of \(\mathcal {E}\) is only over the second coordinate of the message. Let \(\mathsf{pi}\mathcal {O}\) be an \(\epsilon \)-secure PIO scheme.
: \(\mathsf{L}_\mathsf{max}=\lambda ^{\omega (1)}\) is an upper bound on the number of levels, \(\varepsilon >0\) such that \(\varepsilon \cdot \mathsf{L}_\mathsf{max}=\mathsf{negl}\); let \(\mathcal {E}\) be a \((\mathsf{L}_\mathsf{max},\varepsilon )\)–tag-puncturable additively homomorphic encryption scheme with tag space \(\mathcal {E}.\mathcal {TAG}=\mathcal {ID}\times [\mathsf{L}_\mathsf{max}]\), and for any \(\mathsf{tag}^*=(\mathsf{id}^*,\mathsf{L}^*)\in \mathcal {E}.\mathcal {TAG}\), define the bad set \(\mathsf{BAD}_{\mathsf{tag}^*}=\{(\mathsf{id}^*,\mathsf{L}):\mathsf{L}\ge \mathsf{L}^*\}\). Let the message space of \(\mathcal {E}\) be \(\mathcal {E}.\mathcal {TAG}\times \mathcal {M}\) where \(\mathcal {M}\) is the message space of our multi-key IBFHE. Assume \(\mathcal {M}\) is a ring. Also assume that the homomorphism of \(\mathcal {E}\) is only over the second coordinate of the message. Let \(\mathsf{pi}\mathcal {O}\) be an \(\epsilon \)-secure PIO scheme. -
 : Draw \((\mathsf{pk},\mathsf{sk})\leftarrow \mathcal {E}.\mathsf{Gen}\bigl (1^\lambda \bigr )\). Also, let \(\mathsf{P}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]\) and \(\mathsf{P}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\) be the following probabilistic programs:
: Draw \((\mathsf{pk},\mathsf{sk})\leftarrow \mathcal {E}.\mathsf{Gen}\bigl (1^\lambda \bigr )\). Also, let \(\mathsf{P}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]\) and \(\mathsf{P}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\) be the following probabilistic programs:-
\((\mathsf{pk},\mathsf{sk})\) is hardwired into both; both take inputs \((\mathsf{tag},\mathsf{ct}),(\mathsf{tag}',\mathsf{ct}')\in \mathcal {E}.\mathcal {TAG}\times \mathcal {E}.\mathcal {CT}\);
-
both compute \((\mathsf{id},\mathsf{L},\mu )=\mathcal {E}.\mathsf{Dec}(\mathsf{ct},\mathsf{tag},\mathsf{sk})\) and \((\mathsf{id}',\mathsf{L}',\mu ')=\mathcal {E}.\mathsf{Dec}(\mathsf{ct}',\mathsf{tag}',\mathsf{sk})\), if either decryption is not of this form, or if \(\mathsf{tag}\ne (\mathsf{id},\mathsf{L})\) or \(\mathsf{tag}'\ne (\mathsf{id}',\mathsf{L}')\), or if either of \(\mathsf{L}\) or \(\mathsf{L}'\) is \(\ge \mathsf{L}_\mathsf{max}\), output \(\bot \);
-
now the programs differ:
-
 let \(\eta ,\eta '\in \mathcal {M}\) be random st \(\eta +\eta '=\mu \cdot \mu '\), draw $$\mathsf{ct}_\mathsf{out}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id},\mathsf{L}+1,\eta ),\mathsf{tag},\mathsf{pk}\bigr )\text { and }\mathsf{ct}'_\mathsf{out}\leftarrow \mathcal {E}.\ \mathsf{Enc}\bigl ((\mathsf{id}',\mathsf{L}'+1,\eta '),\mathsf{tag}',\mathsf{pk}\bigr );$$
let \(\eta ,\eta '\in \mathcal {M}\) be random st \(\eta +\eta '=\mu \cdot \mu '\), draw $$\mathsf{ct}_\mathsf{out}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id},\mathsf{L}+1,\eta ),\mathsf{tag},\mathsf{pk}\bigr )\text { and }\mathsf{ct}'_\mathsf{out}\leftarrow \mathcal {E}.\ \mathsf{Enc}\bigl ((\mathsf{id}',\mathsf{L}'+1,\eta '),\mathsf{tag}',\mathsf{pk}\bigr );$$output \(\bigl ((\mathsf{id},\mathsf{L}+1,\mathsf{ct}_\mathsf{out}),(\mathsf{id}',\mathsf{L}'+1,\mathsf{ct}'_\mathsf{out})\bigr )\); \(\mathcal {E}\)-encryptions to tags \((\mathsf{id},\mathsf{L}+1)\), \((\mathsf{id}',\mathsf{L}'+1)\), respectively.
-
 let \(\mathsf{id}_\mathsf{out}=\mathsf{id}\oplus \mathsf{id}'\), \(\mathsf{L}_\mathsf{out}=\max \{\mathsf{L},\mathsf{L}'\}+1\) and \(\mathsf{tag}_\mathsf{out}=(\mathsf{id}_\mathsf{out},\mathsf{L}_\mathsf{out})\). Draw \(\mathsf{ct}_\mathsf{out}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id}_\mathsf{out},\mathsf{L}_\mathsf{out},\mu +\mu '),\mathsf{tag}_\mathsf{out},\mathsf{pk}\bigr )\); output \((\mathsf{tag}_\mathsf{out},\mathsf{ct}_\mathsf{out})\).
let \(\mathsf{id}_\mathsf{out}=\mathsf{id}\oplus \mathsf{id}'\), \(\mathsf{L}_\mathsf{out}=\max \{\mathsf{L},\mathsf{L}'\}+1\) and \(\mathsf{tag}_\mathsf{out}=(\mathsf{id}_\mathsf{out},\mathsf{L}_\mathsf{out})\). Draw \(\mathsf{ct}_\mathsf{out}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id}_\mathsf{out},\mathsf{L}_\mathsf{out},\mu +\mu '),\mathsf{tag}_\mathsf{out},\mathsf{pk}\bigr )\); output \((\mathsf{tag}_\mathsf{out},\mathsf{ct}_\mathsf{out})\).
-
Let \(\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]=\mathsf{pi}\mathcal {O}\bigl (\mathsf{P}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]\bigr )\) and \(\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]=\mathsf{pi}\mathcal {O}\bigl (\mathsf{P}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\bigr )\). Set \(\mathsf{msk}=\mathsf{sk}\) and \({\textsf {mpk}}=\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}],\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\bigr )\).
-
-
 : Parse \(\textsf {msk}=\textsf {sk}\). Let \(\mathsf{P}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\) be the deterministic program:
: Parse \(\textsf {msk}=\textsf {sk}\). Let \(\mathsf{P}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\) be the deterministic program:-
\(\mathsf{id}\) and \(\mathsf{sk}\) are hardwired, take input \(\mathsf{ct}\in \mathcal {E}.\mathcal {CT}\);
-
compute \((\mathsf{id},\mathsf{L},\mu )=\mathcal {E}.\mathsf{Dec}(\mathsf{ct},\mathsf{id},\mathsf{sk})\), if the decryption is not of this form, or if \(\mathsf{L}>\mathsf{L}_\mathsf{max}\), output \(\bot \); otherwise output \(\mu \).
Let \(\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]=\mathsf{i}\mathcal {O}\bigl (\mathsf{P}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\bigr )\). Output \(\mathsf{sk}_\mathsf{id}=\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\).
-
-
 : Parse \({\mathsf {mpk}}=\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}],\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\bigr )\), set \(\mathsf{tag}=(\mathsf{id},0)\), \(\mathsf{msg}=(\mathsf{id},0,\mu )\); draw \(\mathsf{ct}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Enc}(\mathsf{msg},\mathsf{tag},\mathsf{pk})\), and output \((\mathsf{ct}_\mathsf{id},\mathsf{id})\).
: Parse \({\mathsf {mpk}}=\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}],\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\bigr )\), set \(\mathsf{tag}=(\mathsf{id},0)\), \(\mathsf{msg}=(\mathsf{id},0,\mu )\); draw \(\mathsf{ct}_\mathsf{id}\leftarrow \mathcal {E}.\mathsf{Enc}(\mathsf{msg},\mathsf{tag},\mathsf{pk})\), and output \((\mathsf{ct}_\mathsf{id},\mathsf{id})\). -
 : Parse \(\mathsf{sk}_\mathsf{id}=\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\), output \(\mu =\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}](\mathsf{ct}_\mathsf{id})\).
: Parse \(\mathsf{sk}_\mathsf{id}=\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}]\), output \(\mu =\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}](\mathsf{ct}_\mathsf{id})\). -
 : Parse \({\textsf {mpk}}=\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval},\mathcal {O}_\mathsf{comb}\bigr )\) and write \(\mathcal {C}\) as an algebraic circuit, organized so that each layer consists either entirely of addition gates or entirely of multiplication gates.
: Parse \({\textsf {mpk}}=\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval},\mathcal {O}_\mathsf{comb}\bigr )\) and write \(\mathcal {C}\) as an algebraic circuit, organized so that each layer consists either entirely of addition gates or entirely of multiplication gates.-
1.
Evaluate \(\mathcal {C}\) a la GMW: For \(i,j=1,\dots ,t\), define ciphertext \(\mathsf{ct}^i_j\) by \(\mathsf{ct}^i_i=\mathsf{ct}_i\) and \(\mathsf{ct}^i_j\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id}_j,0,0),(\mathsf{id}_j,0),\mathsf{pk}\bigr )\) for \(i\ne j\). This defines a set of ciphertexts \(\{\mathsf{ct}^i_j\}_j\) for each input wire i, where for each j, \(\mathsf{ct}^i_j\) is an \(\mathcal {E}\)–ciphertext to \(\mathsf{tag}_{j,0}=(\mathsf{id}_j,0)\). Consider a gate of \(\mathcal {C}\) with input wires (u, v) and output wire w. Assume by induction that we have ciphertext families \(\{\mathsf{ct}^u_j\}_j\) and \(\{\mathsf{ct}^v_j\}_j\), where \(\mathsf{ct}^u_j\) and \(\mathsf{ct}^v_j\) are \(\mathcal {E}\)–ciphertexts for \(\mathsf{tag}_{j,\mathsf{L}}=(\mathsf{id}_j,\mathsf{L})\), we describe how to construct \(\{\mathsf{ct}^w_j\}_j\).
-
Addition Gate: Set \(\mathsf{ct}^w_j=\mathcal {E}.\mathsf{Add}(\mathsf{ct}^u_j,\mathsf{ct}^v_j,\mathsf{tag}_{j,\mathsf{L}})\), so \(\mathsf{ct}^w_j\) is an \(\mathcal {E}\)–ciphertext to \(\mathsf{tag}_{j,\mathsf{L}}\).
-
Multiplication Gate: For \(i,j=1,\dots ,t\), draw
$$\bigl (\mathsf{id}_i,\mathsf{L}+1,\mathsf{CT}^u_{i,j}\bigr ),\bigl (\mathsf{id}_j,\mathsf{L}+1,\mathsf{CT}^v_{j,i}\bigr )\leftarrow \mathcal {O}_\mathsf{eval}\bigl ((\mathsf{id}_i,\mathsf{L},\mathsf{ct}^u_i),(\mathsf{id}_j,\mathsf{L},\mathsf{ct}^v_j)\bigr ).$$Note that \(\mathsf{CT}^u_{j,i}\) and \(\mathsf{CT}^v_{i,j}\) are both \(\mathcal {E}\)–ciphertexts to \(\mathsf{tag}_{j,\mathsf{L}+1}\). Set
$$\mathsf{ct}_j^w=\mathcal {E}.\mathsf{Add}\bigl (\{\mathsf{CT}^u_{j,i}\}_i,\{\mathsf{CT}^v_{i,j}\}_i,\mathsf{tag}_{j,\mathsf{L}+1}\bigr ).$$
After all gates of \(\mathcal {C}\) have been computed as above we have \((\mathsf{id}_1,\dots ,\mathsf{id}_t,\mathsf{ct}^\mathsf{out}_1,\dots ,\mathsf{ct}^\mathsf{out}_t)\) where \(\{\mathsf{ct}^\mathsf{out}_j\}_j\) is the ciphertext family for the output wire of \(\mathcal {C}\). Note \(\mathsf{ct}^\mathsf{out}_j\) is an \(\mathcal {E}\)-ciphertext to \(\mathsf{tag}_{j,\mathsf{L}_\mathsf{depth}}\) where \(\mathsf{L}_\mathsf{depth}\) is the multiplicative depth of \(\mathcal {C}\).
-
-
2.
Combine output ciphertexts: Initialize \(\mathsf{tag}_\mathsf{eval}=(\mathsf{id}_1,\mathsf{L}_\mathsf{depth})\) and \(\mathsf{ct}_\mathsf{eval}=\mathsf{ct}^\mathsf{out}_1\). For \(j=2,\dots ,t\):
-
draw \((\mathsf{tag}_\mathsf{eval},\mathsf{ct}_\mathsf{eval})\leftarrow \mathcal {O}_\mathsf{comb}\bigl ((\mathsf{tag}_\mathsf{eval},\mathsf{ct}_\mathsf{eval}),(\mathsf{tag}_{j,\mathsf{L}_\mathsf{depth}},\mathsf{ct}^\mathsf{out}_j)\bigr )\);
-
parse \(\mathsf{tag}_\mathsf{eval}=(\mathsf{id}_\mathsf{eval},\mathsf{L}_\mathsf{eval})\); output \((\mathsf{ct}_\mathsf{eval},\mathsf{id}_\mathsf{eval})\). Note \(\mathsf{ct}_\mathsf{eval}\) is an \(\mathcal {E}\)-ciphertext to \(\mathsf{tag}_\mathsf{eval}\), where \(\mathsf{id}_\mathsf{eval}=\bigoplus _i\mathsf{id}_i\), and \(\mathsf{L}_\mathsf{eval}=\mathsf{L}_\mathsf{depth}+t-1\ll \mathsf{L}_\mathsf{max}\).
-
-
1.
Lemma 4
The above scheme is a multi-key identity-based FHE assuming the existence of sub-exponential \(\mathsf{i}\mathcal {O}\) and that \(\mathcal {E}\) is a \((\mathsf{L}_\mathsf{max},\varepsilon )\)–tag-puncturable additively homomorphic encryption scheme.
4.3 Proof of Lemma 4
- Correctness: :
-
This follows from the correctness of \(\mathcal {E}\) and \(\mathsf{i}\mathcal {O}\). For any \(\mu \in \{0,1\}\), \(\mathsf{id}\in \mathcal {ID}\), whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathcal {E}.\mathsf{Gen}(1^\lambda )\), and \(\mathsf{ct}\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id},0,\mu ),(\mathsf{id},0),\mathsf{pk}\bigr )\), \(\mathcal {E}.\mathsf{Dec}\bigl (\mathsf{ct},(\mathsf{id},0),\mathsf{sk}\bigr )=(\mathsf{id},0,\mu )\), and so \(\mathcal {O}_\mathsf{dec}[\mathsf{id},\mathsf{sk}](\mathsf{ct})=\mu \).
- Homomorphic Correctness: :
-
For any \(\{\mu _i\}\in \mathcal {M}^t\), \(\{\mathsf{id}_i\}\in \mathcal {ID}^t\), circuit \(\mathcal {C}\), we show that for any wire w at (multiplicative) level \(\mathsf{L}\), the ciphertexts \(\{\mathsf{ct}^w_j\}_j\) satisfy \(\mu ^w=\sum _j\mathcal {E}.\mathsf{Dec}\bigl (\mathsf{ct}^w_j,\mathsf{tag}_{j,\mathsf{L}},\mathsf{sk}\bigr )\). Homomorphic correctness then follows from correctness of \(\mathsf{pi}\mathcal {O}\). This equality holds for the input wires by construction. Assume it is true for \(\{\mathsf{ct}^u_j\}\) and \(\{\mathsf{ct}^v_j\}\), the ciphertexts for wires u and v which are the input wires to a gate of \(\mathcal {C}\) with output wire w. If the gate is addition then we have
$$\begin{aligned} \sum _j\mathcal {E}.\mathsf{Dec}\bigl (\mathsf{ct}^w_j,\mathsf{tag}_{j,\mathsf{L}},\mathsf{sk}\bigr )= & {} \sum _j\mathcal {E}.\mathsf{Dec}\bigl (\mathcal {E}.\mathsf{Add}(\mathsf{ct}^u_j,\mathsf{ct}^v_j,\mathsf{tag}_{j,\mathsf{L}}),\mathsf{tag}_{j,\mathsf{L}},\mathsf{sk}\bigr )\bigr )\\= & {} \sum _j\mu ^u_j+\mu ^v_j=\mu ^u+\mu ^v=\mu ^w. \end{aligned}$$If the gate is multiplication then we have
$$\begin{aligned}&\!\!\!\!\!\sum _j\mathcal {E}.\mathsf{Dec}\bigl (\mathsf{ct}^w_j,\mathsf{tag}_{j,\mathsf{L}},\mathsf{sk}\bigr )\!=\! \sum _j\mathcal {E}.\mathsf{Dec}\bigl (\mathcal {E}.\mathsf{Add}\bigl (\{\mathsf{CT}^u_{j,i}\}_i,\{\mathsf{CT}^v_{i,j}\}_i,\mathsf{tag}_{j,\mathsf{L}+1}\bigr ),\mathsf{tag}_{j,\mathsf{L}+1},\mathsf{sk}\bigr )\\&\quad = \sum _{i,j}\eta _{i,j}^u+\eta _{i,j}^v=\sum _{i,j}\mu ^u_i\cdot \mu ^v_j=\mu ^u\cdot \mu ^v=\mu ^w. \end{aligned}$$ - Security: :
-
We show that for any PPT \(\mathcal {A}\), its chance of winning the selective IBE security game for random identities is at most \(1/2+\mathsf{negl}\). We use a hybrid argument.
Hybrid \(\mathsf{H}_0\) : The IBE security game.
-
1.
\(\mathcal {C}\) draws \(\mathsf{id}^*\leftarrow \mathcal {E}.\mathcal {ID}\) and \((\mathsf{pk},\mathsf{sk})\leftarrow \mathcal {E}.\mathsf{Gen}(1^\lambda )\), computes the obfuscated programs \(\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]\), \(\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\) and sends \(\bigl (\mathsf{pk},\mathcal {O}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}],\mathcal {O}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\bigr )\) to \(\mathcal {A}\).
-
2.
For \(\alpha =1,\dots ,\mathsf{poly}(\lambda )\):
-
\(\mathcal {A}\) sends \(\mathsf{id}_\alpha \) to \(\mathcal {C}\);
-
if \(\mathsf{id}_\alpha =\mathsf{id}^*\), the game ends \(\mathcal {A}\) loses; if \(\mathsf{id}_\alpha =\mathsf{id}_\beta \) for \(\beta <\alpha \), \(\mathcal {C}\) sends \(\mathsf{sk}_\beta \);
-
otherwise, \(\mathcal {C}\) sends \(\mathsf{sk}_\alpha =\mathcal {O}_\mathsf{dec}[\mathsf{id}_\alpha ,\mathsf{sk}]\) to \(\mathcal {A}\), and records \((\mathsf{id}_\alpha ,\mathsf{sk}_\alpha )\).
-
-
3.
\(\mathcal {A}\) sends \(\mu _0,\mu _1\in \mathcal {M}\) to \(\mathcal {C}\).
-
4.
\(\mathcal {C}\) chooses \(\mathsf{bit}\leftarrow \{0,1\}\), \(\mathsf{ct}^*\leftarrow \mathcal {E}.\mathsf{Enc}\bigl ((\mathsf{id}^*,0,\mu _\mathsf{bit}),(\mathsf{id}^*,0),\mathsf{pk}\bigr )\), and sends \(\mathsf{ct}^*\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(\mathsf{guess}\in \{0,1\}\) and wins if \(\mathsf{guess}=\mathsf{bit}\).
Hybrid \(\mathsf{H}_1\) : This is the same as \(\mathsf{H}_0\) except that \(\mathcal {C}\) draws \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\leftarrow \mathcal {E}.\mathsf{Punc.Gen}(\mathsf{tag}^*)\), in step 1, where \(\mathsf{tag}^*=(\mathsf{id}^*,\mathsf{L}_\mathsf{max})\). \(\mathcal {C}\) still sends \(\mathsf{pk}\) in step 1 and uses \(\mathsf{sk}\) in all obfuscations. The following claim holds because \((\mathsf{pk},\mathsf{sk})\) output by \(\mathcal {E}.\mathsf{Punc.Gen}(\mathsf{tag}^*)\) are distributed identically to \(\mathcal {E}.\mathsf{Gen}(1^\lambda )\), by key indistinguishability of \(\mathcal {E}\).
Claim 1
For any (unbounded) \(\mathcal {A}\), \(\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_0\bigr )=\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_1\bigr )\).
Hybrid \(\mathsf{H}_2\) : This is the same as \(\mathsf{H}_1\) except that \(\mathcal {C}\) now uses \(\mathsf{sk}_{\mathsf{tag}^*}\), \(\mathsf{tag}^*=(\mathsf{id}^*,\mathsf{L}_\mathsf{max})\) in all obfuscations instead of \(\mathsf{sk}\). Note that \(\mathsf{P}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}]\) (resp. \(\mathsf{P}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}]\)) is functionally equivalent to \(\mathsf{P}_\mathsf{eval}[\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*}]\) (resp. \(\mathsf{P}_\mathsf{comb}[\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*}]\)), as \(\mathsf{BAD}_{\mathsf{tag}^*}=\{(\mathsf{id}^*,\mathsf{L}_\mathsf{max})\}\) and neither program ever decrypts at level \(\mathsf{L}_\mathsf{max}\). Moreover, since \(\mathcal {A}\) does not query \(\mathsf{id}_\alpha =\mathsf{id}^*\) whp, \(\mathsf{P}_\mathsf{dec}[\mathsf{id}_\alpha ,\mathsf{sk}]\) is functionally equivalent to \(\mathsf{P}_\mathsf{dec}[\mathsf{id}_\alpha ,\mathsf{sk}_{\mathsf{tag}^*}]\). The claim follows from the security of \(\mathsf{i}\mathcal {O}\).
Claim 2
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_1\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_2\bigr )\Big |=\mathsf{negl}\).
Hybrid \(\mathsf{H}_3\) : This is the same as \(\mathsf{H}_2\) except that \(\mathcal {C}\) uses \(\mathsf{sk}_{\mathsf{tag}^*}\) where \(\mathsf{tag}^*=(\mathsf{id}^*,0)\) in all obfuscations instead of \((\mathsf{id}^*,\mathsf{L}_\mathsf{max})\). The following claim is more involved than the others, requiring a few sub-hybrids. We prove it below.
Claim 3
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_2\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_3\bigr )\Big |=\mathsf{negl}\).
Hybrid \(\mathsf{H}_4\) : This is the same as \(\mathsf{H}_3\) except that \(\mathcal {C}\) uses \((\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\) where \(\mathsf{tag}^*=(\mathsf{id}^*,0)\), instead of \((\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})\). Indistinguishability follows from key-indistinguishability of \(\mathcal {E}\). As \(\mathsf{pk}_{\mathsf{tag}^*}\) is lossy, even an unbounded adversary cannot have noticeable advantage in this hybrid’s game. This completes our proof of security.
Claim 4
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_3\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_4\bigr )\Big |=\mathsf{negl}\).
Claim 5
For any (unbounded) \(\mathcal {A}\), \(\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_4\bigr )\le 1/2+\mathsf{negl}\).
Proof
(Proof of Claim 3 ). Recall we must argue that \(\mathsf{H}_2\) and \(\mathsf{H}_3\) are indistinguishable, where the only difference is that \(\mathcal {C}\) uses \((\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})\) where in \(\mathsf{H}_2\), \(\mathsf{tag}^*=(\mathsf{id}^*,\mathsf{L}_\mathsf{max})\) and in \(\mathsf{H}_3\), \(\mathsf{tag}^*=(\mathsf{id}^*,0)\). Let \(\mathsf{H}_{3,i}\) be the game where \(\mathcal {C}\) uses \(\mathsf{tag}^*=(\mathsf{id}^*,i)\), so that \(\mathsf{H}_{3,0}=\mathsf{H}_3\) and \(\mathsf{H}_{3,\mathsf{L}_\mathsf{max}}=\mathsf{H}_2\). We prove that \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{H}_{3, i}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{H}_{3, i-1}\bigr )\Big |\le 4\varepsilon \) for each \(i=1,\dots ,\mathsf{L}_\mathsf{max}\), from which it follows that \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{H}_2\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{H}_3\bigr )\Big |\le 4\varepsilon \cdot \mathsf{L}_\mathsf{max}=\mathsf{negl}\).
Let \(\mathsf{G}_0=\mathsf{H}_{3,i}\) and let \(\mathsf{G}_1\) be the same as \(\mathsf{G}_0\) except that \(\mathcal {C}\) uses \((\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\) in the obfuscations \(\mathcal {O}_\mathsf{eval}\) and \(\mathcal {O}_\mathsf{comb}\) instead of \((\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})\). The key-indistinguishability of \(\mathcal {E}\) implies that for all PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_0\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_1\bigr )\Big |\le \varepsilon \).
Let \(\mathsf{G}_2\) be the same as \(\mathsf{G}_1\) except we change \(\mathsf{P}_\mathsf{eval}\) and \(\mathsf{P}_\mathsf{comb}\) so that instead of outputting an encryption of an evaluated value under the tag \((\mathsf{id}^*,j)\) for \(j\ge i\), they just output encryptions of 0. As \(\mathsf{pk}_{(\mathsf{id}^*,j)}\) is lossy, the output distributions of \(\mathsf{P}_\mathsf{eval}\) and \(\mathsf{P}_\mathsf{comb}\) in \(\mathsf{G}_2\) are statistically close to those in \(\mathsf{G}_1\). The security of \(\mathsf{pi}\mathcal {O}\) ensures that for all PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_1\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_2\bigr )\Big |\le \varepsilon \).
Let \(\mathsf{G}_3\) be the same as \(\mathsf{G}_2\) except that \(\mathcal {C}\) uses \((\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})\) where \(\mathsf{tag}^*=(\mathsf{id}^*,i)\) instead of \((\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\), but \(\mathsf{P}_\mathsf{eval}\) and \(\mathsf{P}_\mathsf{comb}\) still encrypt 0 instead of valid messages to tags \((\mathsf{id}^*,j)\) with \(j\ge i\). The key-indistinguishability of \(\mathcal {E}\) again gives \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_2\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_3\bigr )\Big |\le \varepsilon \) for all PPT \(\mathcal {A}\).
Finally, let \(\mathsf{G}_4\) be the same as \(\mathsf{G}_3\) except that \(\mathcal {C}\) uses \((\mathsf{pk},\mathsf{sk}_{\mathsf{tag}^*})\) where \(\mathsf{tag}^*=(\mathsf{id}^*,i-1)\) instead of \((\mathsf{id}^*,i)\). Since neither obfuscation ever decrypts ciphertexts with tag \((\mathsf{id}^*,i)\), program functionality does not change. Security of \(\mathsf{pi}\mathcal {O}\) gives \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_3\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\text { wins }\mathsf{G}_4\bigr )\Big |\le \varepsilon \) for all PPT \(\mathcal {A}\). \(\mathsf{G}_4=\mathsf{H}_{3,i-1}\) so the result follows.
4.4 Statistical Trapdoor Encryption
In order to instantiate our tag-puncturable encryption used in the previous section, we start from a statistical trapdoor encryption scheme, defined below. This was also the starting point for the \(\mathsf{pi}\mathcal {O}\)–based construction of FHE from [CLTV15], who note that any lossy encryption scheme implies statistical trapdoor encryption. Our construction also has the property that if the statistical trapdoor scheme is additively homomorphic then so will be the resulting tag-puncturable scheme. We can therefore use a DDH-based additively homomorphic, lossy encryption scheme as our starting point.
Definition 4
An \(\varepsilon \)–statistical trapdoor encryption scheme is a tuple of polytime algorithms \(\bigl (\mathsf{Gen},\mathsf{Enc},\mathsf{Dec},\mathsf{tGen}\bigr )\) such that \((\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})\) is a semantically secure encryption scheme and additionally \(\mathsf{tGen}\bigl (1^\lambda \bigr )\) outputs a trapdoor public key \(\mathsf{pk}^*\) such that
-
for any \(\mu _0,\mu _1\in \mathcal {M}\) and whp over \(\mathsf{pk}^*\leftarrow \mathsf{tGen}(1^\lambda )\),
$$\{\mathsf{Enc}(\mu _0,\mathsf{pk}^*)\}\approx _\mathsf{s}\{\mathsf{Enc}(\mu _1,\mathsf{pk}^*)\};$$ -
for all PPT \(\mathcal {A}\),
$$\Big |\mathrm{Pr}_{\mathsf{Gen}(1^\lambda )}\bigl (\mathcal {A}(\mathsf{pk})=1\bigr )-\mathrm{Pr}_{\mathsf{tGen}(1^\lambda )}\bigl (\mathcal {A}(\mathsf{pk}^*)=1\bigr )\Big |\le \varepsilon .$$
4.5 From Statistical Trapdoor Encryption to Tag-Puncturable Encryption
-
 : Let \(\mathcal {E}\) be a statistical trapdoor encryption scheme. Let \(\mathsf{pi}\mathcal {O}\) be a piO scheme and \(\mathcal {F}\) be a puncturable PRF.
: Let \(\mathcal {E}\) be a statistical trapdoor encryption scheme. Let \(\mathsf{pi}\mathcal {O}\) be a piO scheme and \(\mathcal {F}\) be a puncturable PRF. -
 : Sample a PRF key K and set \(\mathsf{sk}= K\). Let \(\mathsf{P}_\mathsf{gen}[K]\) be the probabilistic program:
: Sample a PRF key K and set \(\mathsf{sk}= K\). Let \(\mathsf{P}_\mathsf{gen}[K]\) be the probabilistic program:-
K is hardwired, take input \(\mathsf{tag}\in \mathcal {TAG}\);
-
computes \((\mathsf{pk}_{\mathsf{tag}}, \mathsf{sk}_{\mathsf{tag}}) = \mathcal {E}.\mathsf{Gen}(1^{\lambda }; \mathcal {F}_{K}(\mathsf{tag}))\);
-
outputs \(\mathsf{pk}_{\mathsf{tag}}\).
Set \(\mathsf{pk}= \mathsf{pi}\mathcal {O}\bigl (P_\mathsf{gen}[K]\bigr ) = \mathcal {O}_\mathsf{gen}[K]\). Output \((\mathsf{pk},\mathsf{sk})\).
-
-
 : Parse \(\mathsf{pk}=\mathcal {O}_\mathsf{gen}\). Compute \(\mathsf{pk}_{\mathsf{tag}} = \mathcal {O}_\mathsf{gen}(\mathsf{tag})\) and output \(\mathsf{ct}_\mathsf{tag}\leftarrow \mathcal {E}.\mathsf{Enc}(\mu , \mathsf{pk}_{\mathsf{tag}})\).
: Parse \(\mathsf{pk}=\mathcal {O}_\mathsf{gen}\). Compute \(\mathsf{pk}_{\mathsf{tag}} = \mathcal {O}_\mathsf{gen}(\mathsf{tag})\) and output \(\mathsf{ct}_\mathsf{tag}\leftarrow \mathcal {E}.\mathsf{Enc}(\mu , \mathsf{pk}_{\mathsf{tag}})\). -
 : Compute \((\mathsf{pk}_{\mathsf{tag}}, \mathsf{sk}_{\mathsf{tag}}) = \mathcal {E}.\mathsf{Gen}\bigl (1^{\lambda };\mathcal {F}_K(\mathsf{tag})\bigr )\), output \(\mu = \mathcal {E}.\mathsf{Dec}(\mathsf{ct}_{\mathsf{tag}}, \mathsf{sk}_{\mathsf{tag}})\).
: Compute \((\mathsf{pk}_{\mathsf{tag}}, \mathsf{sk}_{\mathsf{tag}}) = \mathcal {E}.\mathsf{Gen}\bigl (1^{\lambda };\mathcal {F}_K(\mathsf{tag})\bigr )\), output \(\mu = \mathcal {E}.\mathsf{Dec}(\mathsf{ct}_{\mathsf{tag}}, \mathsf{sk}_{\mathsf{tag}})\). -
 : Sample a PRF key K set \(\mathsf{sk}= K\), and \(\mathsf{pk}=\mathcal {O}_\mathsf{gen}[K]=\mathsf{pi}\mathcal {O}\bigl (\mathsf{P}_\mathsf{gen}[K]\bigr )\), as in \(\mathsf{Gen}\). Additionally, let \(K_{\mathsf{tag}^*}\) be K punctured at all \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\) and set \(\mathsf{sk}_{\mathsf{tag}^*}=K_{\mathsf{tag}^*}\). Finally, let \(\mathsf{P}^*_\mathsf{gen}[K_{\mathsf{tag}^*}]\) be the probabilistic program:
: Sample a PRF key K set \(\mathsf{sk}= K\), and \(\mathsf{pk}=\mathcal {O}_\mathsf{gen}[K]=\mathsf{pi}\mathcal {O}\bigl (\mathsf{P}_\mathsf{gen}[K]\bigr )\), as in \(\mathsf{Gen}\). Additionally, let \(K_{\mathsf{tag}^*}\) be K punctured at all \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\) and set \(\mathsf{sk}_{\mathsf{tag}^*}=K_{\mathsf{tag}^*}\). Finally, let \(\mathsf{P}^*_\mathsf{gen}[K_{\mathsf{tag}^*}]\) be the probabilistic program:-
\(K_{\mathsf{tag}^*}\) is hardwired, take input \(\mathsf{tag}\in \mathcal {TAG}\);
-
if \(\mathsf{tag}\notin \mathsf{BAD}_{\mathsf{tag}^*}\), compute \((\mathsf{pk}_\mathsf{tag},\mathsf{sk}_\mathsf{tag})=\mathcal {E}.\mathsf{Gen}\bigl (1^\lambda ;\mathcal {F}_{K_{\mathsf{tag}^*}}(\mathsf{tag})\bigr )\);
-
if \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\), sample \(\mathsf{pk}^*\leftarrow \mathcal {E}.\mathsf{tGen}(1^\lambda )\)
-
output either \(\mathsf{pk}_\mathsf{tag}\) in the first case, or \(\mathsf{pk}^*\) in the second.
Output the data \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})=(\mathcal {O}_\mathsf{gen},K,\mathcal {O}^*_\mathsf{gen},K_{\mathsf{tag}^*})\) where \(\mathcal {O}^*_\mathsf{gen}=\mathsf{pi}\mathcal {O}\bigl (\mathsf{P}_\mathsf{gen}^*[K_{\mathsf{tag}^*}]\bigr )\).
-
Lemma 5
The above scheme is a tag-puncturable encryption scheme assuming that \(\mathcal {E}\) is an \(\varepsilon \)–statistical trapdoor encryption scheme and that sub-exponential \(\mathsf{i}\mathcal {O}\) exists.
Proof
Correctness follows immediately from correctness of \(\mathcal {E}\) and \(\mathsf{pi}\mathcal {O}\). The above scheme clearly satisfies the required punctured key utility properties as \(\mathsf{Enc}(\mu ,\mathsf{tag},\mathsf{pk}_{\mathsf{tag}^*})\) is lossy if and only if \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\) and \(\mathsf{pi}\mathcal {O}\) is correct. We now prove key-indistinguishability through a hybrid argument.
Hybrid \(\mathsf{H}_0\) : This is the distribution \((\mathsf{pk}, \mathsf{sk}_{\mathsf{tag}^*})\) where \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\leftarrow \mathsf{Punc.Gen}(\mathsf{tag}^*)\).
Hybrid \(\mathsf{H}_1\) : This is the distribution \((\mathsf{pk}', \mathsf{sk}_{\mathsf{tag}^*})\) where \(\mathsf{pk}' = \mathsf{pi}\mathcal {O}(\mathsf{P}'_\mathsf{gen}[K_{\mathsf{tag}^*}])\) and \(\mathsf{P}'_\mathsf{gen}[K_{\mathsf{tag}^*}]\) be the probabilistic program:
-
\(K_{\mathsf{tag}^*}\) is hardwired, take input \(\mathsf{tag}\in \mathcal {TAG}\);
-
if \(\mathsf{tag}\notin \mathsf{BAD}_{\mathsf{tag}^*}\), compute \((\mathsf{pk}_\mathsf{tag},\mathsf{sk}_\mathsf{tag})=\mathcal {E}.\mathsf{Gen}\bigl (1^\lambda ;\mathcal {F}_{K_{\mathsf{tag}^*}}(\mathsf{tag})\bigr )\);
-
if \(\mathsf{tag}\in \mathsf{BAD}_{\mathsf{tag}^*}\), sample \((\mathsf{pk}_\mathsf{tag},\mathsf{sk}_\mathsf{tag})=\mathcal {E}.\mathsf{Gen}\bigl (1^\lambda ;r\bigr )\) where r is sampled at random
-
output \(\mathsf{pk}_\mathsf{tag}\).
The following claim holds because from the security of the puncturable PRF, even in the presence of the punctured key \(K_{\mathsf{tag}^*} = \mathsf{sk}_{\mathsf{tag}^*}\), the output distributions of the programs \(\mathsf{P}_\mathsf{gen}[K]\) and \(\mathsf{P}'_\mathsf{gen}[K_{\mathsf{tag}^*}]\) are close, and hence, the security of \(\mathsf{pi}\mathcal {O}\) implies that the obfuscations of the programs are also indistinguishable even given the punctured key.
Claim 6
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_0\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_1\bigr )\Big |=\mathsf{negl}\).
Hybrid \(\mathsf{H}_2\) : This is the distribution \((\mathsf{pk}_{\mathsf{tag}^*}, \mathsf{sk}_{\mathsf{tag}^*})\) where \((\mathsf{pk},\mathsf{sk},\mathsf{pk}_{\mathsf{tag}^*},\mathsf{sk}_{\mathsf{tag}^*})\leftarrow \mathsf{Punc.Gen}(\mathsf{tag}^*)\).
The following claim holds because from the key-indistinguishability of \(\mathcal {E}\), the output distributions of the programs \(\mathsf{P}'_\mathsf{gen}[K]\) and \(\mathsf{P}^*_\mathsf{gen}[K_{\mathsf{tag}^*}]\) are close (the constrained key is not relevant here and hence security holds even in its presence), and hence, the security of \(\mathsf{pi}\mathcal {O}\) implies that the obfuscations of the programs are also indistinguishable (even given the punctured key).
Claim 7
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_1\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_2\bigr )\Big |=\mathsf{negl}\).
This completes the proof of key-indistinguishability.
5 CCA1 FHE from Knowledge Assumptions
Naor and Yung [NY90] show how to go from CPA encryption to CCA1 encryption using non-interactive zero-knowledge proofs (NIZKs). The CCA1 ciphertext is simply a (pair of) CPA ciphertexts along with a NIZK proving correctness. In this section we adopt this approach to the FHE setting. Applying this transformation directly results in a non-compact CCA1 FHE scheme even if the underlying CPA FHE scheme is compact as the proof length grows with the complexity of the circuit being evaluated. Thus we replace the NIZK with a zero-knowledge succinct non-interactive argument of knowledge (zkSNARK) to preserve compactness (argument of knowledge will be important in our proof of security). The zkSNARKs we use in our scheme are defined in [BCCT13, BCC+14] and constructed from knowledge assumptions. In Sect. 5.1 we formally define the zkSNARK primitive we will use, and in Sect. 5.2 we give our scheme based on them.
5.1 Zero-Knowledge SNARKs
Definition 5
Let \(\mathsf{L}\) be a language in \(\mathsf{NP}\). A zero-knowledge succinct non-interactive argument of knowledge (zkSNARK) for \(\mathsf{L}\) is a tuple of algorithms \((\mathsf{Setup},\mathsf{Gen},\mathsf{Prove},\mathsf{Verify})\), defined as follows, which satisfy the correctness, succinctness, proof of knowledge, and zero-knowledge properties below.
-
\(\underline{\mathsf{Setup}\bigl (1^\lambda \bigr )}\) : is executed by a trusted third party and outputs \(\mathsf{crs}\in \{0,1\}^{\mathsf{poly}(\lambda )}\).
-
\(\underline{\mathsf{Gen}\bigl (1^\lambda \bigr )}\) : is executed by the verifier and outputs a reference string \(\sigma \in \{0,1\}^{\mathsf{poly}(\lambda )}\).
-
\(\underline{\mathsf{Prove}\bigl ((\mathsf{crs},\sigma );x;w\bigr )}\) : is executed by the prover and outputs a proof \(\pi \) certifying \((x,w)\in \mathsf{L}\).
-
\(\underline{\mathsf{Verify}\bigl ((\mathsf{crs},\sigma );x;\pi \bigr )}\) : is executed by the verifier and outputs 1 or 0 according to whether \(\mathsf{V}\) accepts or rejects \(\mathsf{P}\)’s proof.
- Correctness: :
-
If \((x,w)\in \mathsf{L}\) then for any \((\mathsf{crs},\sigma )\leftarrow \mathsf{Setup}(1^\lambda )\times \mathsf{Gen}(1^\lambda )\),
$$\Pr \Bigl [\mathsf{Verify}\bigl ((\mathsf{crs},\sigma );x;\mathsf{Prove}((\mathsf{crs},\sigma );x;w)\bigr )=1\Bigr ]=1.$$ - Succinctness: :
-
The length of the proof \(\pi \) output by \(\mathsf{Prove}\) and the running time of \(\mathsf{Verify}\) are bounded by \(p(\lambda +|x|)\) where \(p(\cdot )\) is a polynomial which does not depend on the language \(\mathsf{L}\).
- Proof of Knowledge: :
-
For all PPT cheating provers \(\mathsf{Prove}^*\) who output \((x,\pi )\) on input \((\mathsf{crs},\sigma )\), there exists a PPT extractor \(\mathsf{E}_{\mathsf{Prove}^*}\) such that with high probability over \((\mathsf{crs},\sigma )\leftarrow \mathsf{Setup}(1^\lambda )\times \mathsf{Gen}(1^\lambda )\),
$$ \Pr \Bigl [\mathsf{Verify}\bigl ((\mathsf{crs},\sigma );\mathsf{Prove}^*(\mathsf{crs},\sigma )\bigr )=1\text { } \& \text { }\mathsf{E}_{\mathsf{Prove}^*}(\mathsf{crs},\sigma )=(x,w)\notin \mathsf{L}\Bigr ]=\mathsf{negl}.$$ - Zero Knowledge: :
-
For all PPT cheating verifiers \(\mathsf{Verify}^*\) who output an adversarial reference string \(\sigma ^*\), there exists a simulator \(\mathsf{S}\) such that for all PPT distinguishers \(\mathsf{D}\), and all \((x,w)\in \mathsf{L}\),
$$\bigg |\mathrm{Pr}_{\pi \leftarrow \mathsf{Prove}(\mathsf{crs},\sigma ^*,x,w)}\Bigl [\mathsf{D}(\pi )=1\Bigr ]-\mathrm{Pr}_{\pi \leftarrow \mathsf{S}(\mathsf{Verify}^*,\mathsf{crs},x)}\Bigl [\mathsf{D}(\pi )=1\Bigr ]\bigg |=\mathsf{negl}.$$
Remark. The zkSNARKs defined above are publicly verifiable; one could (and often does) consider a weaker designated verifier variant, where \(\mathsf{Gen}(1^\lambda )\) outputs \((\sigma ,\tau )\) where \(\sigma \) is a public reference string as above and \(\tau \) is a private verification tag, known only to the verifier. Our use of publicly verifiable zkSNARKS is for convenience; our construction could be made to work using designated verifier zkSNARKs using techniques of [BCCT12]. zkSNARKS can be constructed from a variety of non-standard assumptions including knowledge assumptions and extractable CRHF [BCCT12, BCCT13, BCC+14].
5.2 The Scheme
 : Let \((\mathsf{G}_\mathsf{fhe},\mathsf{E}_\mathsf{fhe},\mathsf{D}_\mathsf{fhe},\mathsf{Ev}_\mathsf{fhe})\) be an FHE scheme, and let \((\mathsf{S}_\mathsf{snark},\mathsf{G}_\mathsf{snark},\mathsf{P}_\mathsf{snark},\mathsf{V}_\mathsf{snark})\) be a zkSNARK.
: Let \((\mathsf{G}_\mathsf{fhe},\mathsf{E}_\mathsf{fhe},\mathsf{D}_\mathsf{fhe},\mathsf{Ev}_\mathsf{fhe})\) be an FHE scheme, and let \((\mathsf{S}_\mathsf{snark},\mathsf{G}_\mathsf{snark},\mathsf{P}_\mathsf{snark},\mathsf{V}_\mathsf{snark})\) be a zkSNARK.
 : Draw \((\mathsf{pk}_0,\mathsf{sk}_0),(\mathsf{pk}_1,\mathsf{sk}_1)\leftarrow \mathsf{G}_\mathsf{fhe}(1^\lambda )\), and \((\mathsf{crs},\sigma )\leftarrow \mathsf{S}_\mathsf{snark}(1^\lambda )\times \mathsf{G}_\mathsf{snark}(1^\lambda )\). Output \((\mathsf{pk},\mathsf{sk})=\bigl ((\mathsf{pk}_0,\mathsf{pk}_1,\mathsf{crs},\sigma ),(\mathsf{sk}_0,\mathsf{sk}_1)\bigr )\).
: Draw \((\mathsf{pk}_0,\mathsf{sk}_0),(\mathsf{pk}_1,\mathsf{sk}_1)\leftarrow \mathsf{G}_\mathsf{fhe}(1^\lambda )\), and \((\mathsf{crs},\sigma )\leftarrow \mathsf{S}_\mathsf{snark}(1^\lambda )\times \mathsf{G}_\mathsf{snark}(1^\lambda )\). Output \((\mathsf{pk},\mathsf{sk})=\bigl ((\mathsf{pk}_0,\mathsf{pk}_1,\mathsf{crs},\sigma ),(\mathsf{sk}_0,\mathsf{sk}_1)\bigr )\).
 : For \(\alpha =0,1\), draw \(\omega _\alpha \leftarrow \$\) and set \(\mathsf{ct}^\alpha =\mathsf{E}_\mathsf{fhe}(\mu ,\mathsf{pk}_\alpha ;\omega _\alpha )\) for \(\alpha =0,1\). Also draw \(\pi \leftarrow \mathsf{P}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}^0,\mathsf{ct}^1);(\mu ,\omega _0,\omega _1)\bigr )\), a proof for the statement:
: For \(\alpha =0,1\), draw \(\omega _\alpha \leftarrow \$\) and set \(\mathsf{ct}^\alpha =\mathsf{E}_\mathsf{fhe}(\mu ,\mathsf{pk}_\alpha ;\omega _\alpha )\) for \(\alpha =0,1\). Also draw \(\pi \leftarrow \mathsf{P}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}^0,\mathsf{ct}^1);(\mu ,\omega _0,\omega _1)\bigr )\), a proof for the statement:
Output \(\mathsf{ct}=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\).
 : Parse \(\mathsf{ct}=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\), and \(\mathsf{sk}=(\mathsf{sk}_0,\mathsf{sk}_1)\). If \(\mathsf{V}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}^0,\mathsf{ct}^1);\pi \bigr )=1\), output \(\mathsf{D}_\mathsf{fhe}(\mathsf{ct}^0,\mathsf{sk}_0)\), otherwise output \(\bot \).
: Parse \(\mathsf{ct}=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\), and \(\mathsf{sk}=(\mathsf{sk}_0,\mathsf{sk}_1)\). If \(\mathsf{V}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}^0,\mathsf{ct}^1);\pi \bigr )=1\), output \(\mathsf{D}_\mathsf{fhe}(\mathsf{ct}^0,\mathsf{sk}_0)\), otherwise output \(\bot \).
 : Parse \(\mathsf{ct}_i=(\mathsf{ct}_i^0,\mathsf{ct}_i^1,\pi _i)\). For \(\alpha =0,1\), draw \(\omega '_\alpha \leftarrow \$\) set \(\mathsf{ct}_\mathsf{eval}^\alpha =\mathsf{Ev}_\mathsf{fhe}\bigl (\{\mathsf{ct}_i^\alpha \},\mathcal {C};\omega '_\alpha \bigr )\). Also draw \(\pi _\mathsf{eval}\leftarrow \mathsf{P}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}_\mathsf{eval}^0,\mathsf{ct}_\mathsf{eval}^1);(\{\mathsf{ct}_i^0\},\{\mathsf{ct}_i^1\},\{\pi _i\},\mathcal {C},\omega '_0,\omega '_1)\bigr )\), a proof for:
: Parse \(\mathsf{ct}_i=(\mathsf{ct}_i^0,\mathsf{ct}_i^1,\pi _i)\). For \(\alpha =0,1\), draw \(\omega '_\alpha \leftarrow \$\) set \(\mathsf{ct}_\mathsf{eval}^\alpha =\mathsf{Ev}_\mathsf{fhe}\bigl (\{\mathsf{ct}_i^\alpha \},\mathcal {C};\omega '_\alpha \bigr )\). Also draw \(\pi _\mathsf{eval}\leftarrow \mathsf{P}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}_\mathsf{eval}^0,\mathsf{ct}_\mathsf{eval}^1);(\{\mathsf{ct}_i^0\},\{\mathsf{ct}_i^1\},\{\pi _i\},\mathcal {C},\omega '_0,\omega '_1)\bigr )\), a proof for:
Output \(\mathsf{ct}_\mathsf{eval}=(\mathsf{ct}_\mathsf{eval}^0,\mathsf{ct}_\mathsf{eval}^1,\pi _\mathsf{eval})\).
Theorem 3
If \((\mathsf{G}_\mathsf{fhe},\mathsf{E}_\mathsf{fhe},\mathsf{D}_\mathsf{fhe},\mathsf{Ev}_\mathsf{fhe})\) is an FHE scheme, and \((\mathsf{S}_\mathsf{snark},\mathsf{G}_\mathsf{snark},\mathsf{P}_\mathsf{snark},\mathsf{V}_\mathsf{snark})\) is a zkSNARK then the above scheme is CCA1 FHE.
Proof
(Proof Sketch). We use essentially the same hybrid argument as [NY90].
Hybrid \(\mathsf{H}^0_0\) : The CCA1 security game where \(\mathcal {C}\) chooses \(\mathsf{bit}=0\).
-
1.
\(\mathcal {C}\) draws \((\mathsf{pk}_0,\mathsf{sk}_0),(\mathsf{pk}_1,\mathsf{sk}_1)\leftarrow \mathsf{G}_\mathsf{fhe}(1^\lambda )\) and \((\mathsf{crs},\sigma )\leftarrow \mathsf{S}_\mathsf{snark}(1^\lambda )\times \mathsf{G}_\mathsf{snark}(1^\lambda )\), and sends \(\mathsf{pk}=(\mathsf{pk}_0,\mathsf{pk}_1,\mathsf{crs},\sigma )\) to \(\mathcal {A}\), and holds \(\mathsf{sk}=(\mathsf{sk}_0,\mathsf{sk}_1)\) for later use.
-
2.
For \(\beta =1,\dots ,\mathsf{poly}(\lambda )\):
-
\(\mathcal {A}\) sends \(\mathsf{ct}_\beta =(\mathsf{ct}_\beta ^0,\mathsf{ct}_\beta ^1,\pi _\beta )\) to \(\mathcal {C}\).
-
\(\mathcal {C}\) returns \(\mathsf{Dec}(\mathsf{ct}_\beta ,\mathsf{sk})\) to \(\mathcal {A}\). This involves checking \(\mathsf{V}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}_\beta ^0,\mathsf{ct}_\beta ^1);\pi _\beta \bigr )=1\), and outputting \(\mathsf{D}_\mathsf{fhe}(\mathsf{ct}_\beta ^0,\mathsf{sk}_0)\).
-
-
3.
\(\mathcal {A}\) chooses \((\mu _0,\mu _1)\leftarrow \mathcal {M}\) and sends \((\mu _0,\mu _1)\) to \(\mathcal {C}\).
-
4.
\(\mathcal {C}\) draws \(\omega _\alpha \leftarrow \$\) and sets \(\mathsf{ct}^\alpha =\mathsf{E}_\mathsf{fhe}(\mu _0,\mathsf{pk}_\alpha ;\omega _\alpha )\) for \(\alpha =0,1\). Furthermore, \(\mathcal {C}\) draws a certificate \(\pi \leftarrow \mathsf{P}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}^0,\mathsf{ct}^1);(\mu _0,\omega _0,\omega _1)\bigr )\), sets \(\mathsf{ct}^*=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\) and sends \(\mathsf{ct}^*\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(\mathsf{guess}\in \{0,1\}\) and wins if \(\mathsf{guess}=0\).
Hybrid \(\mathsf{H}^0_1\) : This is the same as \(\mathsf{H}^0_0\) except for the way \(\mathcal {A}\)’s queries are answered. Each time \(\mathcal {A}\) sends \((\mathsf{ct}_\beta ^0,\mathsf{ct}_\beta ^1,\pi _\beta )\), \(\mathcal {C}\) verifies \(\pi _\beta \) as usual: if \(\mathsf{V}_\mathsf{snark}\bigl ((\mathsf{crs},\sigma );(\mathsf{ct}_\beta ^0,\mathsf{ct}_\beta ^1);\pi _\beta )=0\), \(\mathcal {C}\) returns \(\bot \). However, in addition, \(\mathcal {C}\) computes \(\mu _\beta ^\alpha =\mathsf{D}_\mathsf{fhe}(\mathsf{ct}_\beta ^\alpha ,\mathsf{sk}_\alpha )\) for \(\alpha =0,1\) and checks that \(\mu _\beta ^0=\mu _\beta ^1\). If not, \(\mathcal {C}\) aborts and \(\mathcal {A}\) wins the game. Otherwise, \(\mathcal {C}\) returns \(\mu _\beta ^0\) as usual.
Claim 8
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A} \ {wins} \ \mathsf{H_0^0}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_1^0}\bigr )\Big |=\mathsf{negl}\).
Proof
(Proof Sketch). This follows immediately from the proof of knowledge of the zkSNARK.
Hybrid \(\mathsf{H}_2^0\) : This is the same as \(\mathsf{H}^0_1\) except that \(\mathcal {C}\) simulates the proof \(\pi \) in the challenge ciphertext. Specifically, \(\mathcal {C}\) produces \(\mathsf{ct}^*\) by drawing \(\mathsf{ct}^\alpha \leftarrow \mathsf{E}_\mathsf{fhe}(\mu _\mathsf{bit},\mathsf{pk}_\alpha )\) as usual, but draws \(\pi \leftarrow \mathsf{S}\bigl (\mathcal {A},(\mathsf{crs},\sigma ),(\mathsf{ct}^0,\mathsf{ct}^1)\bigr )\) instead of from \(\mathsf{P}_\mathsf{snark}(\cdot )\) as in \(\mathsf{H}_1\).
Claim 9
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H^0_1}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H^0_2}\bigr )\Big |=\mathsf{negl}\).
Proof
(Proof Sketch). This follows immediately from the zero knowledge of the zkSNARK.
Hybrid \(\mathsf{H}^{0,1}_2\) : This is the same as \(\mathsf{H}^0_2\) except for the way \(\mathcal {C}\) produces \(\mathsf{ct}^*\). This time, \(\mathcal {C}\) draws ciphertexts \(\mathsf{ct}^\alpha \leftarrow \mathsf{E}_\mathsf{fhe}(\mu _\alpha ,\mathsf{pk}_\alpha )\) for \(\alpha =0,1\) as well as a simulated \(\pi \), and sends \(\mathsf{ct}^*=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\).
Claim 10
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_2^0}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_2^{0,1}}\bigr )\Big |=\mathsf{negl}\).
Proof
(Proof Sketch). This follows immediately from the semantic security of the underlying FHE scheme.
Hybrid \(\mathsf{H}^{0,1}_3\) : This is the same as \(\mathsf{H}^{0,1}_2\) except that now \(\mathcal {C}\) answers ciphertext queries by sending \(\mu _\beta ^1\) instead of \(\mu _\beta ^0\). This game is identical to \(\mathsf{H}^{0,1}_2\) because of the equality check performed during decryption.
Claim 11
For any (unbounded) \(\mathcal {A}\), \(\mathrm{Pr}_{}\bigl (\mathcal {A} \ {wins}\ \mathsf{H_2^{0,1}}\bigr )=\mathrm{Pr}_{}\bigl (\mathcal {A} \ {wins}\ \mathsf{H_3^{0,1}}\bigr )\).
Hybrid \(\mathsf{H}^{1,1}_{3}\) : This is the same as \(\mathsf{H}^{0,1}_3\) except for the way \(\mathcal {C}\) produces \(\mathsf{ct}^*\). Now, \(\mathcal {C}\) draws \(\mathsf{ct}^\alpha \leftarrow \mathsf{E}_\mathsf{fhe}(\mu _1,\mathsf{pk}_\alpha )\) for \(\alpha =0,1\) and simulates \(\pi \) as usual. \(\mathcal {C}\) sends \(\mathsf{ct}^*=(\mathsf{ct}^0,\mathsf{ct}^1,\pi )\).
Claim 12
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A} \ {wins}\ \mathsf{H_3^{0,1}}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A} \ {wins}\ \mathsf{H_3^{1,1}}\bigr )\Big |=\mathsf{negl}\).
Proof
(Proof Sketch). This follows immediately from the semantic security of the underlying FHE scheme.
Hybrid \(\mathsf{H}^1_2\) : This is the same as \(\mathsf{H}^{1,1}_3\) except that \(\mathcal {C}\) answers ciphertext queries by sending \(\mu _\beta ^0\) again instead of \(\mu _\beta ^1\). This game is identical to \(\mathsf{H}^{1,1}_3\) because of the equality check performed during decryption.
Claim 13
For any (unbounded) \(\mathcal {A}\), \(\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_2^1}\bigr )=\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_3^{1,1}}\bigr )\).
We now complete the argument by going from \(\mathsf{H}_2^1\) to \(\mathsf{H}_0^1\) in reverse just as we went from \(\mathsf{H}_0^0\) to \(\mathsf{H}_0^2\). The next claim follows, and completes the proof of Theorem 3.
Claim 14
For any PPT \(\mathcal {A}\), \(\Big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_0^0}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H_0^1}\bigr )\Big |=\mathsf{negl}\).
Notes
- 1.
A leveled FHE scheme is one that permits evaluation of circuits of a-priori bounded polynomial depth on encrypted data. In contrast, a pure FHE scheme is one that permits evaluation of circuits of any depth.
References
Bitansky, N., Canetti, R., Chiesa, A., Goldwasser, S., Lin, H., Rubinstein, A., Tromer, E.: The hunting of the SNARK. IACR Cryptology ePrint, Archive 2014:580 (2014)
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In: Goldwasser [Gol12], pp. 326–349
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: Recursive composition and bootstrapping for SNARKS and proof-carrying data. In: Symposium on Theory of Computing Conference, STOC 2013, Palo Alto, CA, USA, pp. 111–120, June 1–4 2013 (2013)
Boneh, D., Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. SIAM J. Comput. 36(5), 1301–1328 (2007)
Brakerski, Z., Cash, D., Tsabary, R., Wee, H.: Targeted homomorphic attribute based encryption. Manuscript (2016)
Boneh, D., Segev, G., Waters, B.: Targeted malleability: homomorphic encryption for restricted computations. In: Goldwasser [Gol12], pp. 350–366
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: Ostrovsky, R. (ed.) FOCS, pp. 97–106. Piscataway, IEEE (2011). Invited to SIAM Journal on Computing
Canetti, R., Krawczyk, H., Nielsen, J.B.: Relaxing chosen-ciphertext security. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 565–582. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45146-4_33
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_19
Clear, M., McGoldrick, C.: Multi-identity and multi-key leveled FHE from learning with errors. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 630–656. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_31
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). doi:10.1007/BFb0055717
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Koutsougeras, C., Vitter, J.S. (eds.) Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, pp. 542–552. ACM, New York (1991)
Dahab, R., Galbraith, S., Morais, E.: Adaptive key recovery attacks on NTRU-based somewhat homomorphic encryption schemes. In: Lehmann, A., Wolf, S. (eds.) ICITS 2015. LNCS, vol. 9063, pp. 283–296. Springer, Heidelberg (2015). doi:10.1007/978-3-319-17470-9_17
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. IACR Cryptology ePrint Archive 2016:272 (2016)
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC, pp. 169–178 (2009)
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Goldwasser, S. (ed.): Innovations in Theoretical Computer Science 2012, Cambridge, MA, USA, 8–10 January 2012. ACM (2012)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, British Columbia, Canada, pp. 197–206, 17–20 May 2008
Loftus, J., May, A., Smart, N.P., Vercauteren, F.: On CCA-secure fully homomorphic encryption. IACR Cryptology ePrint Archive 2010:560 (2010)
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_26
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: Ortiz, H., (ed.) Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, Baltimore, Maryland, USA, 13–17 May 1990, pp. 427–437. ACM (1990)
Rivest, R., Adleman, L. Dertouzos, M.: On data banks and privacy homomorphisms. In: Foundations of Secure Computation, pp. 169–177. Academic Press (1978)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). doi:10.1007/3-540-46766-1_35
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: 40th Annual Symposium on Foundations of Computer Science, FOCS 1999, New York, NY, USA, 17–18 October 1999, pp. 543–553. IEEE Computer Society (1999)
Zhang, Z., Plantard, T., Susilo, W.: On the CCA-1 security of somewhat homomorphic encryption over the integers. In: Ryan, M.D., Smyth, B., Wang, G. (eds.) ISPEC 2012. LNCS, vol. 7232, pp. 353–368. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29101-2_24
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Linear Algebraic Encryption
In this section we define linear algebraic encryption, LAE, as an intermediate type of encryption with which to instantiate CCA. Roughly speaking, a LAE scheme is an encryption scheme whose plaintext space \(\mathcal {M}\) is a finite field, and which supports \(\mathcal {M}\)–linear operations on ciphertexts. If one encrypts \(\mathbf{v}\in \mathcal {M}^k\), coordinate by coordinate obtaining ciphertexts \(\{\mathsf{ct}_i\}_{i=1,\dots ,k}\), then for any linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \), one can compute evaluated ciphertexts \(\{\mathsf{ct}_j'\}_{j=1,\dots ,\ell }\leftarrow \mathsf{Eval}\bigl (\{\mathsf{ct}_i\},\varphi \bigr )\) which decrypt, using evaluated secret keys \(\{\mathsf{sk}_j'\}\leftarrow \mathsf{KeyEval}\bigl (\{\mathsf{sk}_i\},\varphi \bigr )\), to \(\varphi (\mathbf{v})\in \mathcal {M}^\ell \). Syntactically, this puts LAE very close to functional encryption for linear circuits; the correctness and security properties are essentially the same. LAE, however, also requires soundness. Specifically, it must be that evaluating ciphertexts and decrypting is the same as decrypting and evaluating plaintexts even for adversarially chosen ciphertexts. This will be crucial to obtain CCA security. We now define LAE formally.
Definition 6
(Linear Algebraic Encryption). Let \(\mathcal {M}\), \(\mathcal {CT}\), \(\mathcal {PK}\), and \(\mathcal {SK}\) represent the message, ciphertext, public key, and secret key spaces of the scheme, respectively; let \(\mathcal {M}\) be a finite field. A linear algebraic encryption scheme is a tuple \(\bigl (\mathsf{Gen},\mathsf{Enc},\mathsf{Dec},\mathsf{CTEval},\mathsf{SKEval},\mathsf{EvalDec}\bigr )\) of polytime algorithms, defined as follows, which satisfy the correctness, soundness and security properties below.
-
 : takes security parameter \(\lambda \), \(k\in \mathbb {Z}\) and outputs \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathcal {PK}^k\times \mathcal {SK}^k\). The algorithms below all also take \((1^\lambda ,1^k)\) as implied inputs.
: takes security parameter \(\lambda \), \(k\in \mathbb {Z}\) and outputs \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathcal {PK}^k\times \mathcal {SK}^k\). The algorithms below all also take \((1^\lambda ,1^k)\) as implied inputs. -
 : is a randomized algorithm which takes \(\bigl (\{\mathsf{msg}_i\},\{\mathsf{pk}_i\}\bigr )\in \mathcal {M}^k\times \mathcal {PK}^k\) and outputs ciphertexts \(\{\mathsf{ct}_i\}\in \mathcal {CT}^k\).
: is a randomized algorithm which takes \(\bigl (\{\mathsf{msg}_i\},\{\mathsf{pk}_i\}\bigr )\in \mathcal {M}^k\times \mathcal {PK}^k\) and outputs ciphertexts \(\{\mathsf{ct}_i\}\in \mathcal {CT}^k\). -
 : takes \(\bigl (\{\mathsf{ct}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathcal {CT}^k\times \mathcal {SK}^k\) and outputs \(\{\mathsf{msg}_i\}\in \mathcal {M}^k\).
: takes \(\bigl (\{\mathsf{ct}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathcal {CT}^k\times \mathcal {SK}^k\) and outputs \(\{\mathsf{msg}_i\}\in \mathcal {M}^k\). -
 : takes \(\{\mathsf{ct}_i\}\in \mathcal {CT}^k\), linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and outputs \(\{\mathsf{ct}'_j\}\in \mathcal {CT}^\ell \).
: takes \(\{\mathsf{ct}_i\}\in \mathcal {CT}^k\), linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and outputs \(\{\mathsf{ct}'_j\}\in \mathcal {CT}^\ell \). -
 : takes \(\{\mathsf{sk}_i\}\in \mathcal {SK}^k\), a linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and outputs \(\{\mathsf{sk}'_j\}\in \mathcal {SK}^\ell \).
: takes \(\{\mathsf{sk}_i\}\in \mathcal {SK}^k\), a linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and outputs \(\{\mathsf{sk}'_j\}\in \mathcal {SK}^\ell \). -
 : takes \(\bigl (\{\mathsf{ct}'_j\},\{\mathsf{sk}'_j\}\bigr )\in \mathcal {CT}^\ell \times \mathcal {SK}^\ell \) and outputs \(\{\mathsf{msg}'_j\}\in \mathcal {M}^\ell \).
: takes \(\bigl (\{\mathsf{ct}'_j\},\{\mathsf{sk}'_j\}\bigr )\in \mathcal {CT}^\ell \times \mathcal {SK}^\ell \) and outputs \(\{\mathsf{msg}'_j\}\in \mathcal {M}^\ell \).
-
Correctness: For any \(\{\mathsf{msg}_i\} \in \mathcal {M}^{k}\), and whp over \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr ) \mathop {\leftarrow }\limits ^{\$}\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\),
$$\Pr \Bigl [\mathsf{Dec}\bigl (\mathsf{Enc}(\{\mathsf{msg}_i\},\{\mathsf{pk}_i\}\bigr ),\{\mathsf{sk}_i\}\bigr )=\{\mathsf{msg}_i\}\Bigr ]=1-\mathsf{negl}.$$ -
Soundness: For any \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and whp over \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr ) \mathop {\leftarrow }\limits ^{\$}\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\), for any (potentially malformed) ciphertexts \(\{\mathsf{ct}_i\} \in \mathcal {CT}^k\), the following distributions are statistically close:
-
draw \(\{\mathsf{msg}_i\}\leftarrow \mathsf{Dec}\bigl (\{\mathsf{ct}_i\},\{\mathsf{sk}_i\}\bigr )\), output \(\varphi \bigl (\{\mathsf{msg}_i\}\bigr )\);
-
draw \(\{\mathsf{ct}_j'\}\leftarrow \mathsf{CTEval}\bigl (\{\mathsf{ct}_i\},\varphi \bigr )\), \(\{\mathsf{sk}_j'\}\leftarrow \mathsf{SKEval}\bigl (\{\mathsf{sk}_i\},\varphi \bigr )\), output \(\mathsf{EvalDec}\bigl (\{\mathsf{ct}_j'\},\{\mathsf{sk}_j'\}\bigr )\).
-
-
Security: For any PPT adversary \(\mathcal {A}\), its chance of winning the following game against a challenger \(\mathcal {C}\) is at most \(1/2+\mathsf{negl}\).
-
1.
\(\mathcal {A}\) sends \((k,\ell ,\varphi )\) to \(\mathcal {C}\) where \(k = \mathsf{poly}(\lambda )\), \(\ell <k\) and \(\varphi : \mathcal {M}^k\rightarrow \mathcal {M}^\ell \) is a linear map.
-
2.
\(\mathcal {C}\) draws \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr ) \mathop {\leftarrow }\limits ^{\$}\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\), \(\{\mathsf{sk}'_j\} \leftarrow \mathsf{SKEval}\bigl (\{\mathsf{sk}_i\},\varphi \bigr )\), and sends \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_j'\}\bigr )\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) chooses \(\{\mathsf{msg}^0_i\},\{\mathsf{msg}^1_i\}\in \mathcal {M}^k\) st \(\varphi \bigl (\{\mathsf{msg}_i^0\}\bigr )=\varphi \bigl (\{\mathsf{msg}_i^1\}\bigr )\), and sends \(\bigl (\{\mathsf{msg}^0_i\},\{\mathsf{msg}_i^1\}\bigr )\) to \(\mathcal {C}\). \(\mathcal {C}\) draws \(b\leftarrow \{0,1\}\), \(\{\mathsf{ct}^*_i\}\leftarrow \mathsf{Enc}\bigl (\{\mathsf{msg}_i^b\},\{\mathsf{pk}_i\}\bigr )\) and sends \(\{\mathsf{ct}_i^*\}\) to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) sends a bit \(b' \in \{0,1\}\) to \(\mathcal {C}\) and wins if \(b=b'\).
-
1.
Remark 1. If a LAE scheme is such that every tuple in \(\mathcal {CT}^k\) is a valid encryption of some message vector in \(\mathcal {M}^k\), then perfect correctness implies soundness.
Remark 2. It is possible to define versions of the above security game where \(\mathcal {A}\) gets to choose \(\varphi \) after receiving \(\{\mathsf{pk}_i\}\), or in an adaptive, coordinate-by-coordinate fashion. We use the above simple version as it is already sufficient for CCA2 encryption.
1.1 A.1 Adding Homomorphism
Definition 7
(Additively Homomorphic LAE). Let \(\mathsf{LAE}\) be a LAE scheme. We say that \(\mathsf{LAE}\) is additively homomorphic if there exists a PPT algorithm \(\mathsf{Add}\) which satisfies the properties below. Let \(m,m'\in \mathcal {M}\) be arbitrary and \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}(1^\lambda )\).
-
 : Given \(\mathsf{ct}=\mathsf{Enc}(m,\mathsf{pk})\) and \(\mathsf{ct}'=\mathsf{Enc}(m',\mathsf{pk})\), output \(\mathsf{ct}+\mathsf{ct}'\) which satisfies \(\mathsf{Dec}(\mathsf{ct}+\mathsf{ct}',\mathsf{sk})=m+m'\).
: Given \(\mathsf{ct}=\mathsf{Enc}(m,\mathsf{pk})\) and \(\mathsf{ct}'=\mathsf{Enc}(m',\mathsf{pk})\), output \(\mathsf{ct}+\mathsf{ct}'\) which satisfies \(\mathsf{Dec}(\mathsf{ct}+\mathsf{ct}',\mathsf{sk})=m+m'\).
Remark. Though the definition of homomorphic LAE only requires homomorphic additions on single ciphertexts, it extends coordinate-wise to give homomorphic addition on ciphertext vectors. We also have soundness.
Claim 15
(Homomorphic Soundness). For any (possibly malformed) ciphertexts \(\mathsf{ct},\mathsf{ct}'\in \mathcal {CT}^k\) and whp over \((\mathsf{pk},\mathsf{sk})\leftarrow \mathsf{Gen}(1^\lambda ,1^k)\) we have that for any linear \(\varphi :\mathbb {Z}_q^k\rightarrow \mathbb {Z}_q^\ell \), if \(\mathsf{sk}_\varphi =\mathsf{SKEval}(\mathsf{sk},\varphi )\) then
Proof
Let \(\mathbf{v}=\mathsf{EvalDec}\bigl (\mathsf{CTEval}(\mathsf{ct},\varphi ),\mathsf{sk}_\varphi \bigr )\) and \(\mathbf{v}'=\mathsf{EvalDec}\bigl (\mathsf{CTEval}(\mathsf{ct}',\varphi ),\mathsf{sk}_\varphi \bigr )\). We have
using soundness of \(\mathsf{LAE}\), additive homomorphism and linearity of \(\varphi \).
1.2 A.2 Additively Homomorphic CCA1 Encryption from LAE
-
 : Let \(\mathsf{LAE}\), be an additively homomorphic LAE scheme with message space \(\mathcal {M}=\mathbb {Z}_q\) for a large prime \(q=\lambda ^{\omega (1)}\).
: Let \(\mathsf{LAE}\), be an additively homomorphic LAE scheme with message space \(\mathcal {M}=\mathbb {Z}_q\) for a large prime \(q=\lambda ^{\omega (1)}\). -
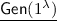 : Draw \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )_{i=1,\dots ,5}\leftarrow \mathsf{LAE.Gen}\bigl (1^\lambda ,1^5\bigr )\). Output \((\mathsf{pk},\mathsf{sk})=\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\).
: Draw \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )_{i=1,\dots ,5}\leftarrow \mathsf{LAE.Gen}\bigl (1^\lambda ,1^5\bigr )\). Output \((\mathsf{pk},\mathsf{sk})=\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\). -
 : Choose random \(r,s\leftarrow \mathbb {Z}_q\), and compute ciphertexts \(\{\mathsf{ct}_i\}\leftarrow \mathsf{LAE.Enc}\bigl (\mathbf{v},\{\mathsf{pk}_i\}\bigr )\), where \(\mathbf{v}=(m-r-s,r,s,0,0)\in \mathbb {Z}_q^5\). Output \(\mathsf{ct}=\{\mathsf{ct}_i\}\).
: Choose random \(r,s\leftarrow \mathbb {Z}_q\), and compute ciphertexts \(\{\mathsf{ct}_i\}\leftarrow \mathsf{LAE.Enc}\bigl (\mathbf{v},\{\mathsf{pk}_i\}\bigr )\), where \(\mathbf{v}=(m-r-s,r,s,0,0)\in \mathbb {Z}_q^5\). Output \(\mathsf{ct}=\{\mathsf{ct}_i\}\). -
 : Given \(\mathsf{ct}=\{\mathsf{ct}_i\}\) and \(\mathsf{ct}'=\{\mathsf{ct}'_i\}\), output \(\mathsf{ct}+\mathsf{ct}'=\{\mathsf{ct}_i+\mathsf{ct}_i'\}\) where \(+\) denotes the ciphertext addition of \(\mathsf{LAE}\).
: Given \(\mathsf{ct}=\{\mathsf{ct}_i\}\) and \(\mathsf{ct}'=\{\mathsf{ct}'_i\}\), output \(\mathsf{ct}+\mathsf{ct}'=\{\mathsf{ct}_i+\mathsf{ct}_i'\}\) where \(+\) denotes the ciphertext addition of \(\mathsf{LAE}\). -
 : Parse \(\mathsf{ct}=\{\mathsf{ct}_i\}\). Compute \(\mathbf{v}=\mathsf{LAE.Dec}\bigl (\{\mathsf{ct}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathbb {Z}^5\). If \(v_4=v_5=0\), output \(v_1+v_2+v_3\), otherwise output \(\bot \).
: Parse \(\mathsf{ct}=\{\mathsf{ct}_i\}\). Compute \(\mathbf{v}=\mathsf{LAE.Dec}\bigl (\{\mathsf{ct}_i\},\{\mathsf{sk}_i\}\bigr )\in \mathbb {Z}^5\). If \(v_4=v_5=0\), output \(v_1+v_2+v_3\), otherwise output \(\bot \).
Theorem 4
The above scheme is an additively homomorphic CCA1 encryption scheme.
Correctness and homomorphic correctness follow immediately from the same properties of \(\mathsf{LAE}\). To prove security, we use a hybrid argument.
Hybrid \(\mathsf{H}_0^\mathsf{bit}\) : The CCA1 Game
-
1.
\(\mathcal {C}\) draws \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\leftarrow \mathsf{LAE.Gen}(1^\lambda ,1^5)\) and sends \(\{\mathsf{pk}_i\}\) to \(\mathcal {A}\).
-
2.
For \(\alpha =1,\dots ,\mathsf{poly}(\lambda )\):
-
\(\mathcal {A}\) sends a ciphertext \(\mathsf{ct}_\alpha \) to \(\mathcal {C}\);
-
\(\mathcal {C}\) computes \(\mathbf{v}_\alpha =\mathsf{LAE.Dec}\bigl (\mathsf{ct}_\alpha ,\{\mathsf{sk}_i\}\bigr )\), checks that \(v_{\alpha ,4}=v_{\alpha ,5}=0\), if not \(\mathcal {C}\) returns \(\bot \); if so sends \(v_{\alpha ,1}+v_{\alpha ,2}+v_{\alpha ,3}\) to \(\mathcal {A}\).
-
-
3.
\(\mathcal {A}\) sends two messages \(m_0,m_1\in \mathbb {Z}_q\) to \(\mathcal {C}\).
-
4.
\(\mathcal {C}\) sets \(m^*=m_\mathsf{bit}\), draws \(\mathsf{ct}^*\leftarrow \mathsf{Enc}\bigl (m^*,\{\mathsf{pk}_i\}\bigr )\) and returns \(\mathsf{ct}^*\) to \(\mathcal {A}\).
-
5.
\(\mathcal {A}\) outputs \(\mathsf{guess}\in \{0,1\}\) and wins if \(\mathsf{guess}=\mathsf{bit}\).
Hybrid \(\mathsf{H}_1^\mathsf{bit}\) : This is the same as \(\mathsf{H}_0^\mathsf{bit}\) except for the way \(\mathcal {C}\) answers ciphertexts \(\mathsf{ct}_\alpha \). In step 1, in addition to \(\bigl (\{\mathsf{pk}_i\},\{\mathsf{sk}_i\}\bigr )\leftarrow \mathsf{LAE.Gen}(1^\lambda ,1^5)\) \(\mathcal {C}\) chooses random linear \(\varphi :\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q\) such that \(\varphi (H)=0\) where \(H=\{\mathbf{v}\in \mathbb {Z}_q^5:v_4=v_5=0\}\). Also, let \(\varphi _\mathsf{eval}:\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q\) be a random linear map of the form \(\varphi _\mathsf{eval}(\mathbf{v})=v_1+v_2+v_3+av_4+bv_5\) for random \(a,b\in \mathbb {Z}_q\). \(\mathcal {C}\) computes \(\mathbf{v}_\alpha =\mathsf{LAE.Dec}\bigl (\mathsf{ct}_\alpha ,\{\mathsf{sk}_i\}\bigr )\), as usual. If \(\varphi (\mathbf{v}_\alpha )=0\), \(\mathcal {C}\) returns \(\varphi _\mathsf{eval}(\mathbf{v}_\alpha )\), otherwise \(\bot \).
Claim 16
For any (computationally unbounded) adversary \(\mathcal {A}\) and \(\mathsf{bit}\in \{0,1\}\),
Proof
(Proof Sketch). Note \(\mathsf{H}_1^\mathsf{bit}\) is identical to \(\mathsf{H}_0^\mathsf{bit}\) except that in \(\mathsf{H}_0^\mathsf{bit}\), \(\mathcal {C}\) checks that \(\mathbf{v}_\alpha \in H\), while in \(\mathsf{H}_1^\mathsf{bit}\), \(\mathcal {C}\) checks that \(\varphi (\mathbf{v}_\alpha )=0\). As \(\varphi :\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q\) is random such that \(\varphi (H)=0\), for any \(\mathbf{v}_\alpha \notin H\), \(\mathrm{Pr}_{\varphi }[\varphi (\mathbf{v}_\alpha )=0]=1/q=\mathsf{negl}(\lambda )\). Claim 16 follows from the union bound over the polynomially many query ciphertexts.
Hybrid \(\mathsf{H}_2^\mathsf{bit}\) : This is the same as \(\mathsf{H}_1^\mathsf{bit}\) except that instead of computing decryptions honestly \(\mathbf{v}_\alpha =\mathsf{LAE.Dec}\bigl (\mathsf{ct}_\alpha ,\{\mathsf{sk}_i\}\bigr )\) and checking \(\varphi (\mathbf{v}_\alpha )=0\), \(\mathcal {C}\) computes \(\mathsf{ct}'=\mathsf{LAE.CTEval}\bigl (\{\mathsf{ct}_i\},(\varphi ,\varphi _\mathsf{eval})\bigr )\), and evaluated decryption \((v,w)=\mathsf{LAE.EvalDec}(\mathsf{ct}',\mathsf{sk}')\), where \(\mathsf{sk}'=\mathsf{LAE.SKEval}\bigl (\{\mathsf{sk}_i\},(\varphi ,\varphi _\mathsf{eval})\bigr )\), and \((\varphi ,\varphi _\mathsf{eval}):\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q^2\) is the linear map \(\mathbf{v}\mapsto \bigl (\varphi (\mathbf{v}),\varphi _\mathsf{eval}(\mathbf{v})\bigr )\). If \(v=0\) \(\mathcal {C}\) returns w, otherwise \(\bot \). The claim follows immediately from the soundness of \(\mathsf{LAE}\).
Claim 17
For any (computationally unbounded) adversary \(\mathcal {A}\) and \(\mathsf{bit}\in \{0,1\}\),
Hybrid \(\mathsf{H}_3^\mathsf{bit}\) : This is the same as \(\mathsf{H}_2^\mathsf{bit}\) except for the way the challenge ciphertext is produced. Upon receiving \((m_0,m_1)\) from \(\mathcal {A}\), \(\mathcal {C}\) chooses a random \(\mathbf{v}^*\in \mathbb {Z}_q^5\) such that \(v^*_1+v^*_2+v^*_3=m_\mathsf{bit}\) and \(\varphi (\mathbf{v}^*)=0\). \(\mathcal {C}\) draws \(\mathsf{ct}^*\leftarrow \mathsf{LAE.Enc}\bigl (\mathbf{v}^*,\{\mathsf{pk}_i\}\bigr )\), and sends \(\mathsf{ct}^*\) to \(\mathcal {A}\).
Claim 18
For any PPT \(\mathcal {A}\) and \(\mathsf{bit}\in \{0,1\}\), \(\big |\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_2^\mathsf{bit}\bigr )-\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_3^\mathsf{bit}\bigr )\big |=\mathsf{negl}(\lambda )\).
Proof
(Proof Sketch.). Let \(\mathcal {A}\) be a PPT adversary who distinguishes between \(\mathsf{H}_2^\mathsf{bit}\) and \(\mathsf{H}_3^\mathsf{bit}\) with noticeable advantage, we construct \(\mathcal {B}\) who breaks the security of the LAE scheme. \(\mathcal {B}\) chooses \(\varphi \) as above and sends \((\varphi ,\varphi _\mathsf{eval})\) to \(\mathcal {C}\) and receives \(\{\mathsf{pk}_i\},\mathsf{sk}'\) from \(\mathcal {C}\), and forwards \(\{\mathsf{pk}_i\}\) to \(\mathcal {A}\). Every time \(\mathcal {A}\) asks a query \(\mathsf{ct}_\alpha \), \(\mathcal {B}\) uses \(\mathsf{sk}'\) to decrypt the evaluated ciphertext like in both games. Upon receiving \((m_0,m_1)\) from \(\mathcal {A}\), \(\mathcal {B}\) chooses \(\mathbf{v}_0,\mathbf{v}_1\) such that \(\varphi _\mathsf{eval}(\mathbf{v}_0)=\varphi _\mathsf{eval}(\mathbf{v}_1)=m_\mathsf{bit}\), \(\mathbf{v}_0\in H\) and \(\mathbf{v}_1\) is otherwise random such that \(\varphi (\mathbf{v}_1)=0\). \(\mathcal {B}\) sends \((\mathbf{v}_0,\mathbf{v}_1)\) to \(\mathcal {C}\) and receives \(\mathsf{ct}^*\), which he forwards to \(\mathcal {A}\). \(\mathcal {B}\) forwards \(\mathcal {A}\)’s guess back to \(\mathcal {C}\). It is clear that \(\mathcal {B}\) wins if and only if \(\mathcal {A}\) guesses correctly between \(\mathsf{H}_2^\mathsf{bit}\) or \(\mathsf{H}_3^\mathsf{bit}\).
Claim 19
For any \(\mathcal {A}\), \(\mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_3^0\bigr ) = \mathrm{Pr}_{}\bigl (\mathcal {A}\ {wins}\ \mathsf{H}_3^1\bigr )\).
Proof
(Proof Sketch). Consider the random process specified by \(m\in \mathbb {Z}_q\): (1) choose random \(\varphi :\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q\) such that \(\varphi (H)=0\) and \(a,b\leftarrow \mathbb {Z}_q\), defining \(\varphi _\mathsf{eval}:\mathbb {Z}_q^5\rightarrow \mathbb {Z}_q\) (2) choose and output random \(\mathbf{v}\in \mathbb {Z}_q^5\) such that \(\varphi (\mathbf{v})=0\) and \(\varphi _\mathsf{eval}(\mathbf{v})=m\). The randomness of \(\varphi \) and \(\varphi _\mathsf{eval}\) ensures that the output of this process is identically distributed for all \(m\in \mathbb {Z}_q\), so \(\mathsf{H}_3^0\) and \(\mathsf{H}_3^1\) are identical.
B Instantiating Homomorphic LAE from DDH
In this section, we describe instantiations of linear algebraic encryption schemes from the Decisional Diffie-Hellman (DDH) assumption. The idea is to use El-Gamal encryption under different public keys but using the same randomness in order to enable the linear homomorphism we need. We describe the scheme below. The system is designed for small message spaces such as \(\mathcal {M} = \{0, 1\}\).
-
\(\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\) takes security parameter \(\lambda \), \(k\in \mathbb {Z}\). It chooses a group \(\mathbb {G}\) of order q, where q is a prime of length \(\mathsf{poly}(\lambda )\), along with a generator g of \(\mathbb {G}\). Next, it samples k random values \(\alpha _{i} \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_{q}\), \(i \in [k]\). Finally, it sets and outputs \(\mathsf{pk}= \bigl (\mathbb {G}, g, q, \{\mathsf{pk}_i\}\bigr )\) and \(\mathsf{sk}= \bigl (\{\mathsf{sk}_i\}\bigr )\), where \(\mathsf{sk}_{i} = \alpha _{i}\) and \(\mathsf{pk}_{i} = g^{\alpha _{i}}\).
-
\(\mathsf{Enc}\bigl (\{\mathsf{msg}_i\}, \mathsf{pk}\bigr )\) is a randomized algorithm which takes k messages \(\mathsf{msg}_{i}\), \(i \in [k]\) and the public key \(\mathsf{pk}\). It first chooses a random value \(r \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_{q}\). It outputs \(\mathsf{ct}= \bigl (g^{r}, \{\mathsf{ct}_i\}\bigr )\) where \(\mathsf{ct}_{i} = \mathsf{pk}_{i}^{r}g^{\mathsf{msg}_{i}}\).
-
\(\mathsf{Dec}\bigl (\mathsf{ct},\mathsf{sk}\bigr )\) takes a ciphertext \(\mathsf{ct}= \bigl (g^{r}, \{\mathsf{ct}_i\}\bigr )\) and the secret key \(\mathsf{sk}\) and outputs \(\{\mathsf{msg}_i\}\) where for each \(i \in [k]\),
$$\mathsf{msg}_{i} = \text {dLog}_{g}\left( \frac{\mathsf{ct}_{i}}{(g^{r})^{\mathsf{sk}_{i}}}\right) $$where \(\text {dLog}_{g}(\cdot )\) denotes computing the discrete logarithm with respect to g.
-
\(\mathsf{CTEval}\bigl (\{\mathsf{ct}_i\},\varphi \bigr )\) takes a ciphertext \(\mathsf{ct}= \bigl (g^{r}, \{\mathsf{ct}_i\}\bigr )\) and linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \). Let \(\varphi ^{\times }\) denote the map which replaces addition in \(\varphi \) with multiplication and multiplication in \(\varphi \) with exponentiation. More formally, suppose
$$\varphi (x) = \left\{ \sum \limits _{i \in [k]}\varphi _{i, j}x_{i}\right\} _{j \in [\ell ]}$$Define
$$\varphi ^{\times }(x) = \left\{ \prod \limits _{i \in [k]}x_{i}^{\varphi _{i, j}}\right\} _{j \in [\ell ]}$$The algorithm outputs \(\mathsf{ct}' = g^{r}, \{\mathsf{ct}'_j\}_{j \in [\ell ]} = \varphi ^{\times }(\{\mathsf{ct}_i\})\).
-
\(\mathsf{KeyEval}\bigl (\{\mathsf{sk}_i\},\varphi \bigr )\) takes the secret key \(\mathsf{sk}\), a linear map \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \) and outputs \(\mathsf{sk}' = \{\mathsf{sk}'_j\}_{j \in [\ell ]} = \varphi (\mathsf{sk})\).
-
\(\mathsf{EvalDec}\bigl (\mathsf{ct}',\mathsf{sk}'\bigr )\) takes an evaluated ciphertext \(\mathsf{ct}' = g^{r}, \{\mathsf{ct}'_j\}\) and an evaluated secret key \(\mathsf{sk}' = \{\mathsf{sk}'_j\}\) outputs \(\{\mathsf{msg}'_j\}\) where for each \(j \in [\ell ]\),
$$\mathsf{msg}'_{j} = \text {dLog}_{g}\left( \frac{\mathsf{ct}'_{j}}{(g^{r})^{\mathsf{sk}'_{j}}}\right) $$where \(\text {dLog}_{g}(\cdot )\) denotes computing the discrete logarithm with respect to g.
Correctness and Soundness. The scheme is perfectly correct and sound. For any \(\{\mathsf{msg}_i\} \in \mathcal {M}^{k}\) and \((\mathsf{pk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{\$}\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\),
For any \(\varphi :\mathcal {M}^k\rightarrow \mathcal {M}^\ell \), \((\mathsf{pk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{\$}\mathsf{Gen}\bigl (1^\lambda ,1^k\bigr )\) and any (potentially malformed) ciphertexts \(\mathsf{ct}\),
Security. Security of the scheme is based on the security of the El-Gamal cryptosystem and hence the Decisional Diffie-Hellman (DDH) assumption. We prove here security for the case that \(k = 2\) and \(\ell = 1\) and note that the proof inductively generalizes for larger k and \(\ell \).
Suppose there exists a PPT adversary \(\mathcal {A}\) who can break the security of the LA encryption scheme with \(k = 2\) and \(\ell = 1\). We now construct a PPT adversary \(\mathcal {B}\) who breaks the semantic security of the El-Gamal encryption scheme with the same advantage. Since we know that under the DDH assumption, the latter advantage is negligible, so is the former.
\(\mathcal {B}\) runs using \(\mathcal {A}\) as follows. Let \(\mathcal {C}\) denote the challenger of the El-Gamal encryption scheme. \(\mathcal {A}\) sends \((k = 2,\ell = 1,\varphi )\) to \(\mathcal {B}\) where \(\varphi : \mathcal {M}^k\rightarrow \mathcal {M}^\ell \) is a linear map. Let \(\varphi = [\varphi _{1}, \varphi _{2}]\). \(\mathcal {B}\) also receives the public key \(\mathsf{pk}_{\textsf {EG}} = \bigl (\mathbb {G}, g, q, h_{1}\bigr )\) from \(\mathcal {C}\), where \(h = g^{\alpha _{1}}\) for some \(\alpha _{1} \in \mathbb {Z}_{q}\) unknown to \(\mathcal {B}\). \(\mathcal {B}\) then samples a random \(\alpha \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_{q}\) and computes
Note that this implicitly sets \(h_{2} = g^{\alpha _{2}}\), where \(\phi ([\alpha _{1}, \alpha _{2}]^{T}) = \alpha \). \(\mathcal {B}\) sets \(\mathsf{pk}= \bigl (\mathbb {G}, g, q, \{\mathsf{pk}_i\}\bigr )\) and \(\mathsf{sk}' = \alpha \), where \(\mathsf{pk}_{i} = h_{i}\), and sends \(\bigl (\mathsf{pk},\mathsf{sk}'\bigr )\) to \(\mathcal {A}\). \(\mathcal {A}\) chooses \(\{\mathsf{msg}^0_i\},\{\mathsf{msg}^1_i\}\in \mathcal {M}^k\) such that \(\varphi \bigl (\{\mathsf{msg}_i^0\}\bigr )=\varphi \bigl (\{\mathsf{msg}_i^1\}\bigr ) = M\) (say), and sends \(\bigl (\{\mathsf{msg}^0_i\},\{\mathsf{msg}_i^1\}\bigr )\) to \(\mathcal {B}\). \(\mathcal {B}\) forwards the messages \(\bigl (\mathsf{msg}^0_1,\mathsf{msg}_1^1\bigr )\) to \(\mathcal {C}\). \(\mathcal {C}\) draws \(b\leftarrow \{0,1\}\), \(r \mathop {\leftarrow }\limits ^{\$}\mathbb {Z}_{q}\) and computes \(\mathsf{ct}_{\textsf {EG}} = \bigl (g^{r}, \mathsf{ct}^*_1 = h_{1}^{r}g^{\mathsf{msg}_1^b}\bigr )\) and sends \(\mathsf{ct}_{\textsf {EG}}\) to \(\mathcal {B}\). \(\mathcal {B}\) constructs \(\mathsf{ct}_{2}^{*}\) as follows. We have that
\(\mathcal {B}\) computes
Note that this implicitly sets \(\mathsf{ct}_{2}^{*} = h_{2}^{r}g^{\mathsf{msg}_2^b}\). \(\mathcal {B}\) then sends \(\mathsf{ct}^{*} = \bigl (g^{r}, \{\mathsf{ct}_i^{*}\}\bigr )\) to \(\mathcal {A}\). \(\mathcal {A}\) sends a bit \(b' \in \{0,1\}\) to \(\mathcal {B}\) which \(\mathcal {B}\) forwards to \(\mathcal {C}\). Note that the implicit bit chosen by \(\mathcal {B}\) in the game against \(\mathcal {A}\) is b and hence \(\mathcal {B}\) succeeds with the same probability as \(\mathcal {A}\). This completes the proof.
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Canetti, R., Raghuraman, S., Richelson, S., Vaikuntanathan, V. (2017). Chosen-Ciphertext Secure Fully Homomorphic Encryption. In: Fehr, S. (eds) Public-Key Cryptography – PKC 2017. PKC 2017. Lecture Notes in Computer Science(), vol 10175. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54388-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-662-54388-7_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54387-0
Online ISBN: 978-3-662-54388-7
eBook Packages: Computer ScienceComputer Science (R0)


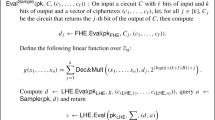


 a randomized algorithm which outputs a public key, secret key pair
a randomized algorithm which outputs a public key, secret key pair  a randomized algorithm which outputs a ciphertext
a randomized algorithm which outputs a ciphertext  an algorithm which outputs a message
an algorithm which outputs a message  an algorithm which takes a collection of ciphertexts
an algorithm which takes a collection of ciphertexts  : outputs the master key pair
: outputs the master key pair  : outputs a secret key
: outputs a secret key  : encrypts message
: encrypts message  : decrypts
: decrypts  : takes a family of ciphertexts and a circuit and outputs
: takes a family of ciphertexts and a circuit and outputs  : Output
: Output  : Draw
: Draw  : Parse
: Parse  : Parse
: Parse  : outputs the key pair
: outputs the key pair  : outputs the keys
: outputs the keys  : encrypts
: encrypts  : outputs message
: outputs message  : outputs a homomorphically evaluated ciphertext
: outputs a homomorphically evaluated ciphertext  :
:  : Draw
: Draw  let
let  let
let  : Parse
: Parse  : Parse
: Parse  : Parse
: Parse  : Parse
: Parse  : Let
: Let  : Sample a PRF key K and set
: Sample a PRF key K and set  : Parse
: Parse  : Compute
: Compute  : Sample a PRF key K set
: Sample a PRF key K set  : takes security parameter
: takes security parameter  : is a randomized algorithm which takes
: is a randomized algorithm which takes  : takes
: takes  : takes
: takes  : takes
: takes  : takes
: takes  : Given
: Given  : Let
: Let 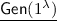 : Draw
: Draw  : Choose random
: Choose random  : Given
: Given  : Parse
: Parse 