Abstract
Strings play a central role in JavaScript and similar scripting languages. Owing to dynamic features such as the eval function and dynamic property access, precise string analysis is a prerequisite for automated reasoning about practically any kind of runtime property. Although the literature presents a considerable number of abstract domains for capturing and representing specific aspects of strings, we are not aware of tools that allow flexible combination of string abstract domains. Indeed, support for string analysis is often confined to a single, dedicated string domain. In this paper we describe a framework that allows us to combine multiple string abstract domains for the analysis of JavaScript programs. It is implemented as an extension of SAFE, an open-source static analysis tool. We investigate different combinations of abstract domains that capture various aspects of strings. Our evaluation suggests that a combination of a few, simple abstract domains suffice to outperform the precision of state-of-the-art static analysis tools for JavaScript.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
JavaScript is a highly dynamic and flexible language. Flexibility has a price: features such as dynamic property access and code execution, prototype-based inheritance, profligate coercion, and reflection combine to make the static analysis of JavaScript very challenging.Footnote 1
Precise reasoning about strings is especially critical in JavaScript analysis. A coarse treatment of string values, and in particular of property names, may result in an inefficient and less than useful analysis. For example, consider the dynamic access obj[x] for property name x of object obj. Since the value of x can be unknown (or difficult to know) at compile time, a rough static analysis may approximate x with the set of all possible string values. This can lead to a dramatic loss of precision (and, consequently, of efficiency) since obj[x] would point to any property of obj and any property of its prototype.
In this paper we consider static analysis of string values by means of abstract interpretation [8], a well-known theory of reasoning with approximations. Informally, each JavaScript string is approximated by an abstract counterpart, an “abstract” string. The abstract values used for abstracting a “concrete” string constitute a string abstract domain, or just string domain.
State-of-the-art JavaScript static analysers such as TAJS [11], JSAI [13], and SAFE [15] use similar, yet slightly different, abstract domains for representing string values. However, each commits to one single string domain defined ad hoc for JavaScript analysis. The precision of such JavaScript-specific domains is often limited, e.g., for most of the web applications relying on the well-known jQuery library [12], owing to the inherently dynamic nature of such libraries. On the other hand, the literature contains proposals for a large variety of general-purpose string domains [6, 7, 14, 16, 17].
Here we describe a usable and open-source tool which implements and integrates several string domains. The tool is built on top of SAFE and we refer to it as \(\text {SAFE}_{\mathsf {str}}\). It allows a user to use combinations of different string domains for the analysis of JavaScript programs. Analysis with \(\text {SAFE}_{\mathsf {str}}\) is not limited to a single specific string domain but allows arbitrary combination of string domains. This is useful, since a large number of string abstract domains have been proposed. It facilitates experiments with different combinations and investigation into the (complementary) advantages of different domains.
We have validated the performance of \(\text {SAFE}_{\mathsf {str}}\) on different JavaScript programs, most of which rely on the jQuery library. Our experiments suggest that the use of a single domain often leads to a severe loss of precision, whereas a suitable combination of relatively simple string domains can match, and sometimes outperform the precision of state-of-the-art JavaScript analysers.
The contributions of this paper are:
-
a detailed discussion of state-of-the-art string domains, useful also in contexts beyond JavaScript, that we have integrated into \(\text {SAFE}_{\mathsf {str}}\);
-
a description of \(\text {SAFE}_{\mathsf {str}}\), a major extension and re-engineering of SAFE which enables the tuning of different string abstract domains;
-
an empirical evaluation of \(\text {SAFE}_{\mathsf {str}}\) on different JavaScript benchmarks that shows the impact and the benefits of combining string domains.
Paper Structure. Section 2 recapitulates string analysis concepts and gives examples. Section 3 discusses a range of string domains we have implemented and evaluated. Section 4 describes \(\text {SAFE}_{\mathsf {str}}\). Section 5 reports on the experimental results. Section 6 discusses related work and Sect. 7 concludes.
2 Preliminaries
JavaScript is a high-level, dynamic, and untyped language. It has been standardised in the ECMAScript language specification [10]. The flexibility of JavaScript is a double-edged sword that might surprise the user with unexpected behaviours.
Consider the snippet of code in Fig. 1. The value of variable res will be the string  . This is due to the coercion of numbers to strings for property access, including not only digits but also special literals. For instance, the numerical expressions 1/0 and Math.pow(2, 1024) both evaluate to the Infinity string literal, while 0/0 turns into the string NaN.
. This is due to the coercion of numbers to strings for property access, including not only digits but also special literals. For instance, the numerical expressions 1/0 and Math.pow(2, 1024) both evaluate to the Infinity string literal, while 0/0 turns into the string NaN.
In this case, the value of res can be statically determined since all the accesses to the properties of obj are known at compile time. Unfortunately, as we shall see, this is not always the case.
Example 1
Consider Fig. 2(left). The call to lookup returns the value of property \(\mathtt {0}^n\mathtt {123}\) of object obj (that we assumed defined somewhere in the code) where \(n = \max \{0, \texttt {N} - 3\}\) and \(\texttt {N}\) is a value unknown at compile time (it may be a random-generated number or an input value provided by the user). This function might encode the lookup to a dictionary where the keys are numbers of at least \(\texttt {N}\) digits. A precise string analysis should be able to infer that \(\texttt {x} = \mathtt {0}^n\mathtt {123}\). Unfortunately, static analysis often results in over-approximations and thus imprecision, so it is possible that a sound analysis says that \(\texttt {x}\) can be any string and therefore the function lookup(obj, x) points to any of the properties of obj, including all the properties of the prototype hierarchy of obj. \(\square \)
Example 2
Dynamic writes can be even nastier, since JavaScript enables to override properties dynamically. Consider the code in Fig. 2 (right) which acts analogously to lookup. The update function might encode the update of a value in a dictionary where the input key is padded to length \(\texttt {N}\) with \(n = \max \{0, \texttt {N} - 3\}\) leading zeros. In this case \(\mathtt {obj}[\mathtt {0}^n\mathtt {123}]\) is set to value "foo". If the analysis can not say anything about \(\texttt {x}\), we have a situation where any property of object obj (including special property __proto__) can be overwritten by "foo". In our example, this raises a false alarm that a coarse analysis cannot avoid. \(\square \)
For the static analysis of string-manipulation we take advantage of the abstract interpretation framework [8].
Let \(\varSigma \) be the set of characters allowed in JavaScript. We define the concrete domain as the lattice \(\langle \mathcal {P}(\varSigma ^*), \subseteq , \emptyset , \varSigma ^*, \cap , \cup \rangle \) where \(\varSigma ^*\) is the set of all the strings of \(\varSigma \), \(\mathcal {P}(\varSigma ^*)\) is its powerset, and \(\subseteq , \emptyset \), \(\cap \), and \(\cup \) have the usual set-theoretic meanings. We define a string (abstract) domain as a lattice \(\langle \mathcal {S}, \sqsubseteq , \bot , \top , \sqcap , \sqcup \rangle \) where each abstract string \(\hat{s} \in \mathcal {S} \) denotes a set of concrete strings \(\gamma (\hat{s}) \in \mathcal {P}(\varSigma ^*)\) via a concretisation function \(\gamma \) such that \(\hat{s} \sqsubseteq \hat{s}' \Rightarrow \gamma (\hat{s}) \subseteq \gamma (\hat{s}')\). Hence \(\sqsubseteq \) captures the relation “is at least as precise as” on \(\mathcal {S}\).
Often we require that \(\gamma \) has a (lower) adjoint \(\alpha : \mathcal {P}(\varSigma ^*) \rightarrow \mathcal {S} \), the so-called abstraction function.Footnote 2 In this case, every k-ary “concrete operation” \(f : \mathcal {P}(\varSigma ^*)^k \rightarrow \mathcal {P}(\varSigma ^*)\) has a unique optimal counterpart on \(\mathcal {S} \), namely the “abstract operation” \(\hat{f}\) such that \(\hat{f}(\hat{s_1}, \dots , \hat{s_k}) = (\alpha \circ f)(\gamma (\hat{s_1}), \dots , \gamma (\hat{s_k}))\).
Now suppose we have \(n \ge 1\) string abstract domains \(\langle \mathcal {S} _i, \sqsubseteq _i, \bot _i, \top _i, \sqcap _i, \sqcup _i \rangle \), each abstracting the concrete domain \(\mathcal {P}(\varSigma ^*)\). We can define their direct product as a structure \(\langle \mathcal {S}, \sqsubseteq , \bot , \top , \sqcap , \sqcup \rangle \) such that:
-
\(\mathcal {S} = \mathcal {S} _1 \times \cdots \times \mathcal {S} _n\)
-
\((\hat{s}_1, \ldots , \hat{s}_n) \sqsubseteq (\hat{s}'_1, \ldots , \hat{s}'_n) \iff \hat{s}_1 \sqsubseteq _1 \hat{s}'_1 \wedge \ldots \wedge \hat{s}_n \sqsubseteq _n \hat{s}'_n\)
-
\(\bot = (\bot _1, \ldots , \bot _n)\) and \(\top = (\top _1, \ldots , \top _n)\)
-
\((\hat{s}_1, \ldots , \hat{s}_n) \sqcap (\hat{s}'_1, \ldots , \hat{s}'_n) = (\hat{s}_1 \sqcap _1 \hat{s}'_1, \ldots , \hat{s}_n \sqcap _n \hat{s}'_n)\)
-
\((\hat{s}_1, \ldots , \hat{s}_n) \sqcup (\hat{s}'_1, \ldots , \hat{s}'_n) = (\hat{s}_1 \sqcup _1 \hat{s}'_1, \ldots , \hat{s}_n \sqcup _n \hat{s}'_n)\)
-
\(\gamma (\hat{s}_1, \dots , \hat{s}_n) = \bigcap _{i = 1}^n \gamma _i(\hat{s}_i)\) and \(\alpha (S) = (\alpha _1(S), \dots , \alpha _n(S))\)
The direct product simply captures an analysis which acts componentwise on the Cartesian product \(\mathcal {S} _1 \times \cdots \times \mathcal {S} _n\). A drawback of the direct product is that \(\gamma \) may not be injective, even if all of \(\gamma _1,\ldots ,\gamma _n\) are. This may give rise to a not optimal, but still sound, precision of the analysis.
3 String Domains
This section summarises the string domains we have integrated in \(\text {SAFE}_{\mathsf {str}}\). We show how they behave in analysis of the programs from Fig. 2, assuming that lookup(obj, "123") is called after update(obj, "123", "foo") on an initially empty object obj, in a context where N has an unknown value.
3.1 The String Set and Constant String Domains
The String Set (\(\mathcal {SS}_k\)) enables precise representation of at most \(k \ge 1\) concrete strings. Formally, \(\mathcal {SS}_k = \{\top _{\mathcal {SS}_k}\} \cup \{S \in \mathcal {P}(\varSigma ^*) \mid |S| \le k \}\) and the lattice operations \(\sqsubseteq _{\mathcal {SS}_k}, \sqcap _{\mathcal {SS}_k}, \sqcup _{\mathcal {SS}_k}\) correspond to \(\subseteq , \cap , \cup \) respectively (\(\bot _{\mathcal {SS}_k} = \emptyset \)).
The concretisation function is: \(\gamma _\mathcal {CS} (S) = S\), if \(S \ne \top _{\!\mathcal {SS}_k}\); \(\varSigma ^*\) otherwise. The abstraction function is: \(\alpha _\mathcal {CS} (S) = S\), if \(|S| \le k\); \(\top _{\!\mathcal {SS}_k}\) otherwise. The abstract concatenation is \(S \odot _{\mathcal {SS}_k} S' = \{s \cdot s' \mid s \in S, s' \in S' \}\). If the set resulting from an abstract operation exceeds k strings, \(\top _{\mathcal {SS}_k}\) is returned.
One instance of \(\mathcal {SS}_k\) is the Constant String (\(\mathcal {CS}\)) domain, which is able to represents a single concrete string exactly (i.e., \(\mathcal {CS} = \mathcal {S} \mathcal {S} _1\)). Despite the limited expressive power, this domain is commonly used, as pointed out in [16].
The \(\mathcal {SS}_k \) domain is clearly more expressive than \(\mathcal {CS} \), and for some analysis a well picked value of k can be enough for achieving high precision. Unfortunately, when analysing loops with an unknown number of iterations, it is often no more expressive. This is the case of the update function of Fig. 2, where the abstract value of variable x becomes \(\top \) and thus string "foo" might potentially be assigned to any property of obj. As a consequence, lookup(obj, "123") returns not only "foo" but also all the properties of the prototype of obj.
3.2 The Character Inclusion Domain
The Character Inclusion (\(\mathcal {CI} \)) domain tracks the characters occurring in a string. Each abstract string has the form \([L, U] = \{X \in \mathcal {P}(\varSigma ) \mid L \subseteq X \subseteq U\}\). The lower bound L contains the characters that must occur in the concrete string(s), while the upper bound U represents the characters that may appear.
Formally, \(\mathcal {CI} = \{\bot _\mathcal {CI} \} \cup \{[L, U] \mid L, U \in \mathcal {P}(\varSigma ), L \subseteq U \}\) and \([L, U] \sqsubseteq _\mathcal {CI} [L', U'] \iff L' \subseteq L \wedge U \subseteq U'\). The meet operation is \([L, U] \sqcap _\mathcal {CI} [L', U'] = [L \cup L', U \cap U']\) while the join is \([L, U] \sqcup _\mathcal {CI} [L', U'] = [L \cap L', U \cup U']\).
Let \( chars : \varSigma ^* \rightarrow \mathcal {P}(\varSigma )\) return the set of characters occurring in a string. The abstraction function is \(\alpha _\mathcal {CI} (S) = [\bigcap {C_S}, \bigcup {C_S}]\), where \(C_S = \{ chars (w) \mid w \in S\}\), while \(\gamma _\mathcal {CI} ([L, U]) = \{w \in \varSigma ^* \mid L \subseteq chars (w) \subseteq U \}\). Abstract concatenation is \([L,U] \odot _\mathcal {CI} [L',U'] = [L \cup L', U \cup U']\).
This domain completely ignores the structure of the concrete strings it approximates. But, \(\mathcal {CI}\) is in general computationally cheap and sometimes provides very useful information. For example, for the update function in Fig. 2 we have that \(\alpha _\mathcal {CI} (\mathtt {x}) = [\{\mathtt {1, 2, 3}\}, \{\mathtt {0, 1, 2, 3} \}]\). This information is enough to avoid the assignment of \(\alpha _\mathcal {CI} (\texttt {"foo"})\) to all the properties of obj and to restrict the (string) return value of the lookup function to \(\alpha _\mathcal {CI} (\texttt {"foo"}) = [\{\mathtt {f,o}\}, \{\mathtt {f,o}\}]\).Footnote 3
3.3 The Prefix-Suffix Domain
An element of the Prefix-Suffix (\(\mathcal {PS} \)) domain is a pair \(\langle p, s \rangle \in \varSigma ^* \times \varSigma ^*\), corresponding to all the concrete strings that start as p and end as s. The domain is \(\mathcal {PS} = \{\bot _\mathcal {PS} \} \cup (\varSigma ^* \times \varSigma ^*)\). Let \( lcp (S)\) (respectively \( lcs (S)\)) be the longest common prefix (suffix) of a set of strings S. Then \(\langle p, s \rangle \sqsubseteq _\mathcal {PS} \langle p', s' \rangle \iff lcp (\{p, p'\}) = p' \wedge lcs (\{s, s'\}) = s'\), the join is \(\langle p, s \rangle \sqcup _\mathcal {PS} \langle p', s' \rangle = \langle lcp \{p, p'\}, lcs \{s, s'\} \rangle \), and the meet \(\sqcap _\mathcal {PS} \) is naturally induced by \(\sqsubseteq _\mathcal {PS} \).
Abstraction is defined by \(\alpha _\mathcal {PS} (S) = \langle lcp (S), lcs (S) \rangle \) while concretisation is \(\gamma (\langle p,s \rangle ) = \{p \cdot w \mid w \in \varSigma ^*\} \cap \{w \cdot s \mid w \in \varSigma ^*\}\). The abstract concatenation is \(\langle p, s \rangle \odot _\mathcal {PS} \langle p', s' \rangle = \langle p, s' \rangle \).
The \(\mathcal {PS}\) domain can not keep track of concrete strings. Nonetheless, as for \(\mathcal {CI}\), this domain is able to increase the precision of \(\mathcal {SS}_k \). Indeed, for the update function we have that \(\alpha _\mathcal {PS} (\mathtt {x}) = \langle \epsilon , \mathtt {123} \rangle \) which allows to restrict the string return value of the lookup function to \(\alpha _\mathcal {PS} (\texttt {"foo"}) = \langle \texttt {"foo"},\texttt {"foo"} \rangle \).
3.4 The String Hash Domain
The String Hash (\(\mathcal {SH}\)) domain was proposed by Madsen and Andreasen [16]. For some fixed integer range \(U = [0, b]\) and hash function \(h: \varSigma ^* \rightarrow U\), a concrete string s is mapped into a “bucket” of U according to the sum of the character codes of s, i.e., \(\alpha (S) = \bigcup _{s \in S} h(\varSigma _{c \in chars (s)} I(c))\) where \(I : \varSigma \rightarrow \mathbb {N}\) maps a character of alphabet \(\varSigma \) to the corresponding code (e.g., ASCII or Unicode). The concretisation function is \(\gamma _\mathcal {SH} (X) = \{s \in \varSigma ^* \mid h(\varSigma _{c \in chars (s)} I(c)) \in X \}\).
The abstract concatenation requires the hash function to be distributive. A linear-time implementation is possible (see [16] for details). This is one of the main strengths of \(\mathcal {SH}\), together with its ability to infer string disequality: if \(\alpha _\mathcal {SH} (s) \sqcap _\mathcal {SH} \alpha _\mathcal {SH} (s') = \emptyset \) then we can safely conclude that \(s \ne s'\).
Unfortunately, \(\mathcal {SH}\) can display slow convergence when analysing loops (in the worst case we may generate all elements of U before reaching a fixed point) and its precision appears limited. As with \(\mathcal {CS}\) and \(\mathcal {SS}_k\), this domain loses all information when analysing the programs in Fig. 2.
3.5 JavaScript-Specific Domains
The string domains we have seen so far are “general-purpose”, rather than tailored for specific applications. We now discuss three simple domains, \(\mathcal {UO} \), \(\mathcal {NO} \), and \(\mathcal {NS} \), that constitute the bases for the string domains of the TAJS, SAFE, and JSAI static analysers. Although easily extensible to other languages, these domains are in fact JavaScript-specific.
The Unsigned-or-Other \((\mathcal {UO})\) domain used by TAJS (see Fig. 3) discriminates between strings representing an unsigned integer and all the other JavaScript strings. TAJS uses this domain to better analyse array indexing. Note that if we concatenate two unsigned integers we do not necessarily get a valid unsigned integer since we might exceed the maximum unsigned integer \(2^{32} - 1\). Also, if we concatenate an unsigned i with a string x we can still have i if \(x = \epsilon \). However, concatenating two non-unsigned always results in a non-unsigned.
The Number-or-Other (\(\mathcal {NO}\)) domain used by SAFE (see Fig. 4) is very similar to \(\mathcal {UO}\): the only difference is that it discriminates between numeric strings and other strings. Literals like −3, 0.1, or NaN are considered numeric strings. In this case the concatenation is even more imprecise: we can get a numeric string by concatenating two non-numeric strings (e.g., "N" and "aN").
The Number-Special-or-other (\(\mathcal {NS}\)) domain used by JSAI (see Fig. 5) generalises \(\mathcal {NO}\) by also distinguishing special JavaScript strings.Footnote 4 Concatenating a special string with another special string or a numeric string always results in an “\( Other \)” string, i.e., a string neither special nor numeric. Concatenating a special string with \( Other \) always results in a non-numeric string.
Although these domains are useful to capture specific aspects of JavaScript they have little meaning when used stand-alone. In the next section we show how TAJS, SAFE, and JSAI combine them with the \(\mathcal {CS} \) and \(\mathcal {SS}_k \) lattices.
3.6 The TAJS, SAFE and JSAI Domains
The string domains adopted by TAJS, SAFE, and JSAI are built respectively on top of the \(\mathcal {UO}\), \(\mathcal {NO}\), and \(\mathcal {NS}\) domains from Sect. 3.5 in combination with the \(\mathcal {CS}\) and \(\mathcal {SS}_k\) domains from Sect. 3.1. The \(\mathcal {TJ} \) domain used by TAJS is shown in Fig. 3. First, the analysis is conducted with the constant domain \(\mathcal {CS}\). Then, when there is more than one constant string to track, \(\mathcal {TJ} \) falls back to the \(\mathcal {UO} \) domain trying to discriminate if all such strings are definitely unsigned or definitely not unsigned integers. If such a distinction is not possible (e.g., \(\texttt {-1} \sqcup _\mathcal {TJ} \texttt {1}\)) then \(\top _\mathcal {TJ} \) is returned.
The \(\mathcal {SF} \) domain used by SAFE (Fig. 4) uses a similar logic. The difference is that the analysis is conducted with the string set domain \(\mathcal {SS}_k\) (for a certain value of \(k \ge 1\)) and then, when we have more than k constant strings to track, it falls back to the \(\mathcal {NO} \) domain trying to discriminate if such strings are numeric or not. This is not a generalisation of \(\mathcal {TJ} \): indeed, let us suppose \(k = 2\) and \(S = \{\texttt {foo}, \texttt {bar}, \texttt {-1}\}\). We have \(\alpha _\mathcal {SF} (S) = \top _\mathcal {SF} \) and thus \(\gamma _\mathcal {SF} (\alpha _\mathcal {SF} (S)) = \varSigma ^*\). Instead, \(\alpha _\mathcal {TJ} (S) = NotUnsigned \) so \(\gamma _\mathcal {TJ} (\alpha _\mathcal {TJ} (S)) = \varSigma ^* \setminus \{\texttt {0}, \dots , \texttt {4294967295}\}\).
Being built on top of \(\mathcal {SS}_k \), \(\mathcal {SF} \) is also parametric. When the set size is not specified, we will assume \(k = 1\) (which is the default value in SAFE).
The \(\mathcal {JS} \) domain used by JSAI (Fig. 5) acts analogously to \(\mathcal {SF} \). However, like \(\mathcal {TJ} \), a single constant string is tracked instead of a set of k strings. When we have more than one constant string to track, the \(\mathcal {JS} \) domain falls back to the \(\mathcal {NS} \) domain (which actually generalises \(\mathcal {NO} \), so we can say that \(\mathcal {JS} \) generalises \(\mathcal {SF} \) if and only if \(k = 1\) for the \(\mathcal {SS}_k \) domain of \(\mathcal {SF} \)).
Even if not strictly comparable, \(\mathcal {TJ}\), \(\mathcal {SF}\) and \(\mathcal {JS}\) are very similar. Their JavaScript-driven nature is however not helpful for analysing the programs in Fig. 2. Indeed, when we call update(obj,"123", "foo") we have that the abstract value of property x at the end of the loop is \(\top \) for both \(\mathcal {TJ} \) and \(\mathcal {SF} \) (as seen in Sect. 3.5, they lose all the information when concatenating two numbers) while \(\alpha _\mathcal {JS} (\texttt {x}) = NotSpecial \). However, this information is not enough to prevent the return of all the properties of obj and its prototypes (except for those corresponding to the special strings) when lookup(obj, "123") is called.
3.7 Direct Products and the Hybrid Domain
So far we have seen several string domains, some general, some JavaScript specific. We observed that each has its strengths and weaknesses. A natural extension is to combine different string domains into a single, compound string domain that generalises them in order to improve the precision of the analysis.
In Sect. 2 we introduced the direct product \(\mathcal {S} = \mathcal {S} _1 \times \dots \times \mathcal {S} _n\) for systematically composing n string domains. We can thus apply this definition for combining the string domains we have seen so far. Clearly, while the precision of \(\mathcal {S} \) is never lower than for a component domain \(\mathcal {S} _i\), it may be the case that the direct product does not bring any benefit. For instance, \(\mathcal {SH} \times \mathcal {TJ} \times \mathcal {SF} \times \mathcal {JS} \) is not beneficial for analysing the Examples 1 and 2. Conversely, \(\mathcal {CI} \times \mathcal {PS} \) significantly increases the precision: if we consider \(\alpha (\texttt {x})\) as the abstraction of property x of Examples 1 and 2 we have \(\alpha (\texttt {x}) = (\alpha _\mathcal {CI} (\texttt {x}), \alpha _\mathcal {PS} (\texttt {x})) = ([\{\texttt {1,2,3}\}, \{\texttt {0,1,2,3}\}], \langle \epsilon ,\texttt {123} \rangle )\), so by definition the corresponding concretisation is \(\gamma (\alpha (\texttt {x})) = \gamma _\mathcal {CI} (\alpha _\mathcal {CI} (\texttt {x}))\ \cap \ \gamma _\mathcal {PS} (\alpha _\mathcal {PS} (\texttt {x})) = \{ x \cdot \texttt {123} \mid x \in \{\texttt {0,1,2,3}\}^* \}\).
The Hybrid (\(\mathcal {HY} \)) string domain [16] is defined as the product of character inclusion, string set, and string hash: \(\mathcal {HY} = \mathcal {CI} \times \mathcal {SS}_k \times \mathcal {SH} \). This domain appears to perform well, so we consider it in our evaluation of Sect. 5.
As mentioned in Sect. 2, the systematic combination via direct product does not always reach the optimal precision. For example, at first it may appear that \(\mathcal {SF} = \mathcal {SS}_k \times \mathcal {NO} \) but this is not the case, as the following example shows.
Example 3
Consider the following JavaScript statement, where E is unknown:

If we approximate x with \(\mathcal {S} \mathcal {S} _1 \times \mathcal {NO} \) we have  after the statement. Conversely, even if the default \(\mathcal {SF}\) domain can not represent the set {0,01}, it can infer from it that x is a \( Number \). \(\square \)
after the statement. Conversely, even if the default \(\mathcal {SF}\) domain can not represent the set {0,01}, it can infer from it that x is a \( Number \). \(\square \)
To avoid these precision leaks when combining different domains, the reduced product [4, 9] has been introduced as a refinement of the direct product.
Figure 6 concludes the section with a diagram summarising the string domains we have encountered so far. There is an upward edge between domain \(\mathcal {S} \) and domain \(\mathcal {S} '\) if and only if \(\mathcal {S} \) is never less precise than \(\mathcal {S} '\).
4 Implementation
We now describe \(\text {SAFE}_{\mathsf {str}}\), the extension of the SAFE tool in which we have implemented all the string domains discussed in Sect. 3.
SAFE [15] is a static analyser for ECMAScript developed for the JavaScript community. We chose it as a starting point for our analyser because it is open-source, under active development, exhaustively implements the DOM semantics, and utilises loop-sensitive analysis.
The execution flow of SAFE is structured into three main parts. First, the input JavaScript program is parsed and translated into a simplified Abstract Syntax Tree (AST). Then, the AST is translated into an Intermediate Representation (IR). Finally, the IR is used to build the Control Flow Graph (CFG). The CFG is the best representation for tracing control flows of a program, and in fact is used by SAFE to perform a type-based analysis of JavaScript programs. SAFE is implemented in Scala (with some modules written in Java).
The static analysis performed by SAFE relies on the string abstract domain described in Sect. 3.6 to model primitive JavaScript strings as well as for the lookup and update of properties in abstract JavaScript objects. The user can tune the size k of the underlying \(\mathcal {SS}_k \) domain, but can not choose among other string domains. We therefore re-engineered and extended this tool to enable the user to combine all the domains described in Sect. 3. The resulting tool, \(\text {SAFE}_{\mathsf {str}}\), is a major extension of SAFE with improved usability, flexibility, and—as we shall see in Sect. 5—precision of the static analysis.
Table 1 lists the Scala classes that we have implemented in \(\text {SAFE}_{\mathsf {str}}\). The AbsString represents the base class, from which every other string domain inherits. AbsString has methods for the lattice operations (e.g., \(\sqcup \), \(\sqcap \), \(\sqsubseteq \)), for the abstraction/concretisation functions \(\alpha \) and \(\gamma \), for abstracting string operations (e.g., concatenation, trimming, slicing) and for general utility (e.g., toString or equals). Each class that implements a string domain must be a subclass of AbsString, and possibly overrides its methods.
The new design of \(\text {SAFE}_{\mathsf {str}}\) is suitable for combining different string domains. An important novelty is the AbsStringProd class—which is itself a subclass of AbsString—that allows the user to systematically combine an arbitrary collection of AbsString classes. AbsStringProd can be specialised for refining the direct product of different string domains (see Example 3). For example, the \(\mathcal {TJ}\), \(\mathcal {SF}\), and \(\mathcal {JS}\) domains are now specialised subclasses of AbsStringProd since they actually combine other basic domains (as shown in Figs. 3, 4, and 5). Furthermore, the \(\mathcal {HY}\) domain does not need to be implemented at all: it is enough to define it as an AbsStringProd object consisting of AbsStringCharIncl, AbsStringSet, and AbsStringHash domains.
We implemented the string domains in \(\text {SAFE}_{\mathsf {str}}\) trying to be as un-intrusive as possible and to preserve the original structure of SAFE. In this we faced a number of design choices. For instance, SAFE analysis is not sound unless the target string domain is able to keep track of a single, concrete string. With \(\text {SAFE}_{\mathsf {str}}\) it is trivial to ensure this by just adding (via direct product) a new constituent domain like \(\mathcal {CS}\) or \(\mathcal {SS}_k\). Another crucial point for SAFE analysis is the ability to distinguish whether an abstract string is definitely numeric or not numeric. Again, with \(\text {SAFE}_{\mathsf {str}}\) it is easy to enrich a given domain by composing it with \(\mathcal {NO}\) or \(\mathcal {NS}\) for discriminating numeric strings.
The \(\text {SAFE}_{\mathsf {str}}\) tool can be imported into a Scala application or used as a stand-alone analyser from the command line. Notably, the user can choose and configure the string domains for an analysis run via command line options. \(\text {SAFE}_{\mathsf {str}}\) is open-source and can be downloaded from https://git.io/vPH9w.
5 Evaluation
In this section we evaluate the string domains that we implemented in \(\text {SAFE}_{\mathsf {str}}\). The default configuration for \(\text {SAFE}_{\mathsf {str}}\) tries to be as precise as possible. In particular, like SAFE, it uses a loop-sensitive analysis with a context-depth of 10 (see [18] for more details). While \(\text {SAFE}_{\mathsf {str}}\) diverged from the version of SAFE in [17], we tried to resemble the evaluation environment as closely as possible.
We evaluated \(\text {SAFE}_{\mathsf {str}}\) on two benchmark sets from the literature:Footnote 5
-
jQuery, a set of 61 JavaScript programs from a jQuery tutorialFootnote 6. All the programs of this benchmark, adopted also in [17], use jQuery version 1.7.0 without any modification.
-
Jsai, a set of 11 JavaScript sources made available with the JSAI tool [13]. Because of their JSAI-specific modelling, we made some minor modifications to conform with \(\text {SAFE}_{\mathsf {str}}\). Seven programs of Jsai are Firefox browser add-ons, while the remaining four come from the linq.js project.Footnote 7
We stress that the goal of the evaluation is not to assess the performance of different analysis tools. Rather, our focus is on evaluating (the composition of) different string domains within the \(\text {SAFE}_{\mathsf {str}}\) environment. Note that we are comparing the implementation of TAJS and JSAI domains in \(\text {SAFE}_{\mathsf {str}}\), not the TAJS and JSAI tools themselves. A direct comparison with such tools is impracticable since a fair measurement of their performance requires knowledge, and modification, of their internals.
Measuring the precision within a complex static analysis framework like SAFE is inherently difficult. Simple metrics, such as runtime of the analysis or reachable program states provide glib information at best. To measure the overall performance we adopted three metrics—used in [17] and, with modifications, in [18]—that count ‘how much imprecision’ occurs during the static analysis. In more detail, the metrics are:
-
Multiple dereference \(\mathbf {(}\textsf {MD}\mathbf {):}\) The number of program points where dereferencing an abstract object leads to more than one object value.
-
Multiple call \(\mathbf {(}\textsf {MC}\mathbf {):}\) The number of program points where dereferencing an abstract function object leads to more than one function.
-
Non-concrete property access \(\mathbf {(}\textsf {PR}\mathbf {):}\) The number of program points where an object property is accessed with a non-concrete abstract string, i.e., with an abstract string representing an infinite set of concrete strings.
Static analysis of non-trivial programs often involves the handling of failures and timeouts. In particular, owing to the dynamic nature of JavaScript, a lack of static boundaries like types or modules can cause the imprecision to spread explosively, causing the analysis to become infeasible or its results to be unusable.
We devised a mechanism to possibly terminate the analysis early, thus avoiding getting stuck in a non-meaningful analysis. We use empirically determined bounds to trigger an “imprecision stop”, e.g., when the number of possible call targets for a function encountered during analysis becomes greater than 20.Footnote 8
Unfortunately, since \(\mathsf {MD}\), \(\mathsf {MC}\), and \(\mathsf {PR}\) do not have a reasonable upper bound, choosing a “penalty value” for these metrics when the analysis fails is not trivial. To overcome this problem, inspired by the MiniZinc Challenge [20], we defined a scoring system where we compare pairs of domains on each benchmark program.
Let \(\mathbb {P}\) be a benchmark set of programs and \(\mathbb {D}\) a collection of string domains. For each program \(P \in \mathbb {P}\) and each domain \(\mathcal {S} \in \mathbb {D}\) we define the imprecision index of \(\mathcal {S} \) on P as: \( IMP _\mathcal {S} (P) = \mathsf {MD} _\mathcal {S} (P) + \mathsf {MC} _\mathcal {S} (P) + \mathsf {PR} _\mathcal {S} (P)\), if the analysis of P using domain \(\mathcal {S} \) terminates normally; \( IMP _\mathcal {S} (P) = \infty \) if the imprecision stop is triggered. Given two distinct domains \(\mathcal {S} \) and \(\mathcal {S} '\) we define a scoring function:
Finally, the overall score of the domain \(\mathcal {S} \) on benchmark \(\mathbb {P}\) is the sum of each \( Score _\mathcal {S} (P, \mathcal {S} ')\) value, for each \(P \in \mathbb {P}\) and for each \(\mathcal {S} \in \mathbb {D}\) such that \(\mathcal {S} \ne \mathcal {S} '\).
We analysed all the domains depicted in Fig. 6. As mentioned in Sect. 4, because of the internal design of SAFE (which we did not want to modify), the static analysis in \(\text {SAFE}_{\mathsf {str}}\) needs a string abstract domain able to track (at least) a single constant string. For each \(\mathcal {S} \in \{\mathcal {PS}, \mathcal {CI}, \mathcal {SH}, \mathcal {NO}, \mathcal {NS}, \mathcal {JS} \}\) we therefore evaluated the domain extension \(\overline{\mathcal {S}} = \mathcal {S} \times \mathcal {CS} \) instead of \(\mathcal {S} \). Note that this did not require any additional effort, since \(\text {SAFE}_{\mathsf {str}}\) allows the user to specify the preferred domain combination on the command line.
Similarly, instead of the original TAJS domain \(\mathcal {TJ} \) we actually considered \(\mathcal {TJ} ^* = \mathcal {TJ} \times \mathcal {NO} \). This is because the underlying \(\mathcal {UO} \) domain allows to discriminate only strings representing unsigned integers, but can not deal with numeric strings in general (e.g., floats or negative numbers). Since SAFE’s design relies heavily on the distinction between numeric and other strings, the \(\mathcal {TJ} \) domain is inevitably penalised when used by \(\text {SAFE}_{\mathsf {str}}\). This is arguably due to the SAFE structure, and not necessarily a weakness of TAJS. Thus, we took advantage of \(\text {SAFE}_{\mathsf {str}}\) for automatically combining \(\mathcal {TJ} \) with \(\mathcal {NO} \).
In addition, we evaluated the \( All \) baseline, i.e., the direct product of all the implemented domains, and a new hybrid domain, namely \(\mathcal {HY} ^* = \mathcal {CI} \times \mathcal {NO} \times \mathcal {SS}_k \). That is, we replace the more complex \(\mathcal {SH}\) domain of \(\mathcal {HY}\) by the simpler \(\mathcal {NO}\). For \(\mathcal {HY} ^*\), as well as for \(\mathcal {SS}_k\), we used the default set size of the \(\mathcal {HY}\) domain, \(k = 3\). For \(\mathcal {SF}\) we instead used the default set size of SAFE, \(k = 1\). As we shall see, the difference turned out to be irrelevant.
Table 2a shows the overall performance of the string domains. All is the union of jQuery and Jsai, thus consisting of 61 + 11 = 72 programs.Footnote 9
The “Score” column summarises the overall score of each domain. We note that \(\mathcal {HY} ^*\) has the same performance as \( All \). Hence, at least for our benchmarks, it sufficient to combine three simple domains, namely \(\mathcal {CI}\), \(\mathcal {NO}\), and \(\mathcal {SS}_k\), to reach the same precision as the combination of all the domains. However, if we consider such domains independently the precision is far lower and often results in imprecision stops (especially for jQuery, see the bottommost row of Table 2a). This shows the potential of combining different string domains.
The \(\mathcal {HY} ^*\) domain outperforms \(\mathcal {HY}\). Why is replacing the String Hash domain by the Numeric-or-Other domain advantageous? In our context, \(\mathcal {SH}\) appears to be unfruitful, but the \(\mathcal {NO}\) domain is essential for detecting (non-)numeric strings. While that other \(\mathcal {HY} ^*\) component, \(\mathcal {CI}\), can be helpful in this regard (as noticed in Sect. 3.2), it is often not enough. For example, let x be a variable representing a string in \(S = \{\texttt {-1,0,1}\}\). Its abstraction is \(\alpha _\mathcal {CI} (S) = [\emptyset , \{\texttt {-},\texttt {0},\texttt {1}\}]\), but this does not suffice to state that x is a number (e.g., the string - belongs to \(\alpha _\mathcal {CI} (S)\) but it is not a number). However, \(\alpha _\mathcal {NO} (S) = Number \).
The benefits of \(\mathcal {NO}\) are noticeable especially for the Jsai benchmark, while for jQuery, \(\mathcal {CI}\) remains important. \(\mathcal {CI}\) never causes a loss of precision in abstract concatenation, and this is very important, especially when concatenating an unknown string (as often happens when generating the jQuery.expando property). Overall, \(\mathcal {HY} ^*\) scores better than \(\mathcal {HY}\) and \(\mathcal {CI}\) for 40 programs (31 of jQuery and 9 of Jsai) and is never worse than any other domain.
The \(\mathcal {HY}\) domain is better than \(\mathcal {CI}\) for only seven programs of jQuery. This is the only benefit that \(\mathcal {S} \mathcal {S} _3\) has brought to the analysis, compared to the constant domain \(\mathcal {CS}\). We tried to investigate this aspect further, by performing a sensitivity analysis on the k parameter of \(\mathcal {SS}_k \) for all the domains we implemented, varying \(k \in \{8, 16, 32, 64, 128\}\). No improvement was observed for larger k.
If we look at the domains used by TAJS, SAFE, and JSAI, we observe a substantial equivalence. They are all very effective on the Jsai benchmark, but they have rather poor performance for the problems of jQuery. We believe that this happens because these domains fail when concatenation involves an unknown string. Note that, in spite of Example 3 highlighting their difference, \(\mathcal {SF}\) and \(\overline{\mathcal {NO}} = \mathcal {NO} \times \mathcal {CS} \) have identical performance. Similarly, \(\mathcal {JS}\) and \(\overline{\mathcal {NS}}\) perform equally well.
Looking at the bottom of the table, apart from the aforementioned \(\mathcal {SH}\), \(\mathcal {SS}_k\) and \(\mathcal {UO}\), we see that \(\mathcal {PS}\) too has a rather poor performance. This was somewhat unexpected, considering the benefits seen in Examples 1 and 2. One explanation is that \(\mathcal {PS}\) is less precise than \(\mathcal {CI}\) when joining different abstract strings, and it loses all the information about the ‘inner’ structure of the string. A curious drawback of \(\mathcal {PS}\) is that abstracting the empty string means losing all information, since \(\alpha _\mathcal {PS} (\epsilon ) = \langle \epsilon , \epsilon \rangle = \top _\mathcal {PS} \).
The “Fails” column of Table 2 shows, in percentage, the number of times the analysis failed due to imprecision stops or timeouts. Again in this case we see the advantage of combining the string domains. For example, while the analysis using the TAJS, SAFE, or JSAI domains often fail, the \(\mathcal {HY} ^*\) domain we introduced significantly improve on them (in particular for jQuery benchmark). Nevertheless, even for \(\mathcal {HY} ^*\) we still notice a remarkable number of cases (about 44%) where the analysis fails. This calls for further investigation.
Although in this work we are more concerned in the precision of the analysis, it is clear that also efficiency plays an important role. Table 2b reports the average analysis time, where we assign a penalty of \(T = 600\) seconds when the analysis fails. We see that in this case \(\mathcal {HY} ^*\) slightly outperforms the combination of all the domains. This is due to its lighter composition (only three domains). On average, the analysis with \(\mathcal {HY} ^*\) takes about 100 seconds less than analysing programs with the TAJS, SAFE, or JSAI domains.
Let us finally compare our evaluation with that of [16]. In that work, 12 string domains (including \(\mathcal {HY}\), referred as \(\mathcal {H}\) in the paper) are proposed and compared. We note that, while the dynamic analysis evaluation of [16] is exhaustive, the static analysis evaluation is limited: it is performed on only 10 JavaScript programs (for which sources are not available) and \(\mathcal {HY}\) is only compared against the constant domain \(\mathcal {CS}\) (which is inherently less precise than \(\mathcal {HY}\)). The more comprehensive evaluation we provide in this paper in part confirms the good intuition of [16] of including the \(\mathcal {CI}\) domain within a collection of other domains.
6 Related Work
Our work has taken the SAFE framework [15] as inspiration and starting point. There are other well-engineered mature analysis frameworks such as TAJS [11], WALA [19], and JSAI [13]. We chose SAFE because of its conformance with the latest ECMAScript standard, formal specification, loop-sensitivity [18], accessibility, and active development (SAFE 2.0 was released in October 2016).
The number of (string) abstract domains that have been proposed is surprisingly large. In [1, 2] the configurable program analysis (CPA) and the dynamic precision adjustment (CPA+) frameworks are introduced to make the analysis configurable and possibly improve its precision.
Many of the domains we have evaluated were discussed by Madsen and Andreasen [16] who cover 12 string domains, half of which were new. Costantini et al. [5, 7] discuss two domains whose product amounts to \(\mathcal {PS}\), the \(\mathcal {CI}\) domain, and two additional (rather more complex) string domains. In the context of Java analysis, Choi et al. [3] have used restricted regular expressions as an abstract domain. Sets of strings are approximated by sets of “regular string expressions”. Such expressions are liberally defined and allow for nesting of Kleene stars. However, regular expressions of the form \(r^*\) cannot be juxtaposed. So while \(a^* a b^*\) is a valid regular string expression, \(a a^* b^*\) is not, and the latter, should it arise, will effectively be “flattened” into the coarser \(a (a+b)^*\). Excessive nesting of stars is curbed through widening, which similarly flattens expressions at a certain star-depth.
Park et al. [17] use a stricter variant of this idea, with a more clearly defined string abstract domain. Here sets of strings are approximated by sets of “atomic” regular expressions. A regular expression is atomic (over alphabet \(\varSigma = \{a_1,\ldots ,a_n\}\)) iff it can be generated by the grammar

Quotes indicate that \(\epsilon \) and \(\varSigma ^*\) are not meta-symbols, but terminals. This abstract domain is more restrictive than that of Choi et al. [3]. What is gained by this is faster analysis, and in particular tractability of the inclusion relation.
The number and richness of different string abstract domains provides a rich seam for experimental work and comparative evaluation. In spite of that, the number of systematic studies is very limited. An exception is the work by Madsen and Andreasen [16] which, in the static analysis evaluation, compares the precision of \(\mathcal {HY} \)-based analysis against \(\mathcal {CS} \).
7 Conclusion
We have presented \(\text {SAFE}_{\mathsf {str}}\), an extension of the SAFE JavaScript static analysis tool. \(\text {SAFE}_{\mathsf {str}}\) provides support for a number of string analysis domains, as well as for analysis using arbitrary combinations of these domains. Precise string analysis is of paramount importance in a programming language like JavaScript, because almost any other kind of analysis relies heavily on the quality of string analysis to aid it; without precise string analysis, control and data flow information is weak; for example, field access becomes ambiguous. The required precision is ultimately achieved through the combination of a variety of string domains, each capturing some relevant aspect of strings and, accordingly, the literature is replete with proposals for string abstract domains.
We have used \(\text {SAFE}_{\mathsf {str}}\) to conduct the first systematic comparison of a broad range of such string abstract domains for the static analysis of JavaScript programs. We have measured precision and analysis time over two established benchmark sets. The results suggest that there is little value in maintaining string sets (elements of \(\mathcal {SS}_k\)) of cardinality \(k > 3\); and that the relatively simple combination \(\mathcal {CI} \times \mathcal {NO} \times CS\) achieves higher precision than the various combinations proposed elsewhere—in fact, for our sets of benchmarks, it achieves as high precision as the combination of all of the string domains we have studied.
Future work will focus on the evaluation, and the combination, of new domains over new benchmarks. In particular, we wish to compare the use of direct products with reduced products [9] of string abstract domains.
Notes
- 1.
In JavaScript, an object is a map that associates property names to values. The prototype of an object is instead the object from which it inherits (possibly recursively) methods and properties. Each object has a property named
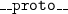 (standardized in ECMAScript6, even if deprecated) which points to its prototype.
(standardized in ECMAScript6, even if deprecated) which points to its prototype. - 2.
In this case \(\alpha \) and \(\gamma \) form a Galois connection, i.e., \(\alpha (S) \sqsubseteq \hat{s} \iff S \subseteq \gamma (\hat{s})\).
- 3.
This is actually the only possible string value. However, SAFE also tracks possible non-string results (such as the special value undefined).
- 4.
Namely, length, concat, join, pop, push, shift, sort, splice, reverse, valueOf, toString, indexOf, lastIndexOf, constructor, isPrototypeOf, toLocaleString, hasOwnProperty, and propertyIsEnumerable.
- 5.
All the benchmarks and the scripts we used are available at https://git.io/vPH9w.
- 6.
- 7.
- 8.
We noticed that imprecision stops only occurred in the analysis of jQuery.
- 9.
We have run all the experiments with a timeout of \(T = 600\) seconds on Ubuntu 15.10 machines with 16 GB of RAM and 2.60 GHz CPU.
References
Beyer, D., Henzinger, T.A., Théoduloz, G.: Configurable software verification: concretizing the convergence of model checking and program analysis. In: Damm, W., Hermanns, H. (eds.) CAV 2007. LNCS, vol. 4590, pp. 504–518. Springer, Heidelberg (2007). doi:10.1007/978-3-540-73368-3_51
Beyer, D., Henzinger, T.A., Théoduloz, G.: Program analysis with dynamic precision adjustment. In: 23rd IEEE/ACM International Conference on Automated Software Engineering (ASE 2008), pp. 29–38 (2008)
Choi, T.-H., Lee, O., Kim, H., Doh, K.-G.: A practical string analyzer by the widening approach. In: Kobayashi, N. (ed.) APLAS 2006. LNCS, vol. 4279, pp. 374–388. Springer, Heidelberg (2006). doi:10.1007/11924661_23
Cortesi, A., Costantini, G., Ferrara, P.: A survey on product operators in abstract interpretation. In: Semantics, Abstract Interpretation, and Reasoning About Programs: Essays Dedicated to David A. Schmidt on the Occasion of his Sixtieth Birthday, pp. 325–336 (2013)
Costantini, G.: Lexical and numerical domains for abstract interpretation. Ph.D. thesis, Università Ca’ Foscara Di Venezia (2014)
Costantini, G., Ferrara, P., Cortesi, A.: Static analysis of string values. In: Qin, S., Qiu, Z. (eds.) ICFEM 2011. LNCS, vol. 6991, pp. 505–521. Springer, Heidelberg (2011). doi:10.1007/978-3-642-24559-6_34
Costantini, G., Ferrara, P., Cortesi, A.: A suite of abstract domains for static analysis of string values. Softw. Pract. Exp. 45(2), 245–287 (2015)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Proceedings of the Fourth ACM Symposium on Principles of Programming Languages, pp. 238–252. ACM Publication (1977)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: Proceedings of the Sixth Annual ACM Symposium on Principles of Programming Languages, pp. 269–282. ACM Publication (1979)
ECMAScript 2016 language specification. http://www.ecma-international.org/publications/files/ECMA-ST/Ecma-262.pdf
Jensen, S.H., Møller, A., Thiemann, P.: Type analysis for JavaScript. In: Palsberg, J., Su, Z. (eds.) SAS 2009. LNCS, vol. 5673, pp. 238–255. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03237-0_17
jQuery JavaScript library. https://jquery.com/
Kashyap, V., Dewey, K., Kuefner, E.A., Wagner, J., Gibbons, K., Sarracino, J., Wiedermann, B., Hardekopf, B.: JSAI: A static analysis platform for JavaScript. In: Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, pp. 121–132. ACM Publication (2014)
Kim, S.-W., Chin, W., Park, J., Kim, J., Ryu, S.: Inferring grammatical summaries of string values. In: Garrigue, J. (ed.) APLAS 2014. LNCS, vol. 8858, pp. 372–391. Springer, Cham (2014). doi:10.1007/978-3-319-12736-1_20
Lee, H., Won, S., Jin, J., Cho, J., Ryu, S.: SAFE: formal specification and implementation of a scalable analysis framework for ECMAScript. In: Proceedings of the 19th International Workshop on Foundations of Object-Oriented Languages (FOOL 2012) (2012)
Madsen, M., Andreasen, E.: String analysis for dynamic field access. In: Cohen, A. (ed.) CC 2014. LNCS, vol. 8409, pp. 197–217. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54807-9_12
Park, C., Im, H., Ryu, S.: Precise and scalable static analysis of jQuery using a regular expression domain. In: Proceedings of the 12th Symposium on Dynamic Languages, DLS 2016, Amsterdam, The Netherlands, 1 November 2016, pp. 25–36 (2016)
Park, C., Ryu, S.: Scalable and precise static analysis of JavaScript applications via loop-sensitivity. In: Boyland, J.T. (ed.) Proceedings of the 29th European Conference on Object-Oriented Programming (ECOOP 2015), Leibniz International Proceedings in Informatics, pp. 735–756. Dagstuhl Publishing (2015)
Sridharan, M., Dolby, J., Chandra, S., Schäfer, M., Tip, F.: Correlation tracking for points-to analysis of JavaScript. In: Noble, J. (ed.) ECOOP 2012. LNCS, vol. 7313, pp. 435–458. Springer, Heidelberg (2012). doi:10.1007/978-3-642-31057-7_20
Stuckey, P.J., Feydy, T., Schutt, A., Tack, G., Fischer, J.: The MiniZinc challenge 2008–2013. AI Mag. 35(2), 55–60 (2014)
Acknowledgements
This work is supported by the Australian Research Council (ARC) through Linkage Project Grant LP140100437.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Amadini, R. et al. (2017). Combining String Abstract Domains for JavaScript Analysis: An Evaluation. In: Legay, A., Margaria, T. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2017. Lecture Notes in Computer Science(), vol 10205. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54577-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-54577-5_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54576-8
Online ISBN: 978-3-662-54577-5
eBook Packages: Computer ScienceComputer Science (R0)











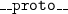 (standardized in ECMAScript6, even if deprecated) which points to its prototype.
(standardized in ECMAScript6, even if deprecated) which points to its prototype.