Fractional differential models in finite viscoelasticity

Summary

A new class of constitutive models is derived for viscoelastic media with finite strains. The models employ the so-called fractional derivatives of tensor functions.

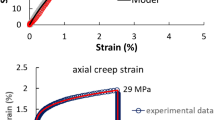
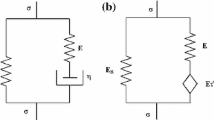
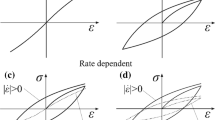
We introduce fractional derivatives for an objective tensor which satisfies some natural assumptions. Afterwards, we construct fractional differential analogs of the Kelvin-Voigt, Maxwell, and Maxwell-Weichert constitutive models. The models are verified by comparison with experimental data for viscoelastic solids and fluids. We consider uniaxial tension of a bar and radial oscillations of a thick-walled spherical shell made of the fractional Kelvin-Voigt incompressible material. Explicit solutions to these problems are derived and compared with experimental data for styrene butadiene rubber and synthetic rubber. It is shown that the fractional Kelvin-Voigt model provides excellent prediction of experimental data. For uniaxial tension of a bar and simple shear of an infinite layer made of the fractional Maxwell compressible material, we develop explicit solutions and compare them with experimental data for polyisobutylene specimens. It is shown that the fractional Maxwell model ensures fair agreement between experimental data and results of numerical simulation. This model allows the number of adjustable parameters to be reduced significantly compared with other models which ensure the same level of accuracy in the prediction of experimental data.