Skip to main content
SpringerLink
Log in

A numerical method for fractional integral with applications

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

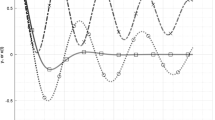
A new numerical method for the fractional integral that only stores part history data is presented, and its discretization error is estimated. The method can be used to solve the integro-differential equation including fractional integral or fractional derivative in a long history. The difficulty of storing all history data is overcome and the error can be controlled. As application, motion equations governing the dynamical behavior of a viscoelastic Timoshenko beam with fractional derivative constitutive relation are given. The dynamical response of the beam subjected to a periodic excitation is studied by using the separation variables method. Then the new numerical method is used to solve a class of weakly singular Volterra integro-differential equations which are applied to describe the dynamical behavior of viscoelastic beams with fractional derivative constitutive relations. The analytical and unmerical results are compared. It is found that they are very close.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ross B.A Brief History and Exposition of the Fundamental Theory of Fractional Calculus [M]. Lecture Notes in Math, Vol457, New York: Springer-Verlag, 1975,40–130.

    Google Scholar 

  2. Samko S G, Kilbas A A, Marichev O L.Fractional Integrals and Derivatives: Theory and Application [M]. New York: Gordon and Breach Science Publishers, 1993,24–56, 120–140.

    Google Scholar 

  3. Gemant A. On fractional differences [J].Phil Mag, 1938,25(1):92–96.

    Google Scholar 

  4. Delbosco D, Rodino L. Existence and uniqueness for a nonlinear fractional differential equation [J].J Math Anal Appl, 1996,204(4):609–625.

    Article  MATH  MathSciNet  Google Scholar 

  5. Koeller R C. Applications of the fractional calculus to the theory of viscoelasticity [J].J Appl Mech, 1984,51(2):294–298.

    Article  MathSciNet  Google Scholar 

  6. Bagley R L, Torvik P J. On the fractional calculus model of viscoelasticity behavior [J].J Rheology, 1986,30(1):133–155.

    Article  MATH  Google Scholar 

  7. Rossikhin Y A, Shitikova M V. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solid [J].Appl Mech Rev, 1997,50(1):15–67.

    Article  MathSciNet  Google Scholar 

  8. Enelund M, Mahler L, Runesson K,et al. Formulation and integration of the standard linear viscoelastic solid with fractional order rate laws [J].Int J Solids Strut, 1999,36(18):2417–2442.

    Article  MATH  Google Scholar 

  9. Enelund M, Olsson P. Damping described by fading memory—analysis and application to fractional derivative models [J].Int J Solids Strut, 1999,36(5):939–970.

    Article  MATH  MathSciNet  Google Scholar 

  10. Argyris J. Chaotic vibrations of a nonlinear viscoelastic beam [J].Chaos Solitons Fractals, 1996,7(1):151–163.

    Article  Google Scholar 

  11. CHENG Chang-jun, ZHANG Neng-hui. Chaos and hyperchaos motion of viscoelastic rectangular plates under a transverse periodic load [J].Acta Mechanica Sinica, 1998,30(6):690–699. (in Chinese)

    MathSciNet  Google Scholar 

  12. Akoz Y, Kadioglu F. The mixed finite element method for the quasi-static and dynamic analysis of viscoelastic Timoshenko beams [J].Int J Numer Mech Engng, 1999,44(5):1909–1932.

    Article  Google Scholar 

  13. Suire G, Cederbaum G. Periodic and chaotic behavior of viscoelastic nonlinear (elastica) bars under harmonic excitations [J].Int J Mech Sci, 1995,37(2):753–772.

    Article  MATH  Google Scholar 

  14. CHEN Li-qun, CHENG Chang-jun. Dynamical behavior of nonlinear viscoelastic beams [J].Applied Mathematics and Mechanics (English Edition), 2000,21(9):995–1001.

    Google Scholar 

  15. Atkinson K E.An Introduction to Numerical Analysis [M]. London: John Wiley & Sons, 1978, 120–128.

    Google Scholar 

  16. Timoshenko S, Gere J.Mechanics of Materials [M]. Nostrand Reinhold Company, 1972.

  17. Makris N. Three-dimensional constitutive viscoelastic law with fractional order time derivatives [J].J Rheology, 1997,41(5):1007–1020.

    Article  Google Scholar 

  18. LIU Yan-zhu, CHEN Wen-liang, CHEN Li-qun.Mechanics of Vibrations [M]. Beijing: Advanced Educational Press, 1998,143–147. (in Chinese)

    Google Scholar 

  19. YANG Ting-qing.Viscoelastic Mechanics [M]. Wuhan: Huazhong University of Science and Technology Press, 1990,55–102. (in Chinese)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, 200072, Shanghai, P. R. China

    Zhu Zheng-you & Cheng Chang-jun

  2. Department of Mathematics, Shanghai University, 200436, Shanghai, P. R. China

    Zhu Zheng-you

  3. Department of Mechanics, Shanghai University, 200436, Shanghai, P. R. China

    Cheng Chang-jun

  4. Shanghai Supercomputer Center, 201203, Shanghai, P. R. China

    Li Gen-guo

Authors
  1. Zhu Zheng-you
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Gen-guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cheng Chang-jun
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Contributed by Cupheng Chang-jun

Foundation items: the National Natural Science Foundation of China (60273048); the Science Foundation of Shanghai Municipal Commission of Education (99A01); the Science Foundation of Shanghai Municipal Commission of Sicences and Technology (98JC14032)

Biographies: Zuphu Zheng-you (1937-), Professor Lupi Gen-guo (1969-), Doctor

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zheng-you, Z., Gen-guo, L. & Chang-jun, C. A numerical method for fractional integral with applications. Appl Math Mech 24, 373–384 (2003). https://doi.org/10.1007/BF02439616

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02439616

Key words

Chinese library classification

2000 MR subject classification

Search

Navigation