Abstract
Suppose that N is a prime number greater than 19 and that P is a point on the modular curve X 0(N) whose image in J o(N) (under the standard embedding ι: X 0(N)→J 0(N)) has finite order. In [2], Coleman-Kaskel-Ribet conjecture that either P is a hyperelliptic branch point of X 0(N) (so that N∈{23,29,31,41,47,59,71}) or else that ι(P) lies in the cuspidal subgroup C of J 0(N). That article suggests a strategy for the proof: assuming that P is not a hyperelliptic branch point of X 0(N), one should show for each prime number ℓ that the ℓ-primary part of ι(P) lies in C. In [2], the strategy is implemented under a variety of hypotheses but little is proved for the primes ℓ=2 and ℓ=3. Here I prove the desired statement for ℓ=2 whenever N is prime to the discriminant of the ring End J 0(N). This supplementary hypothesis, while annoying, seems to be a mild one; according to W.A. Stein of Berkeley, California, in the range N<5021, it is false only in case N=389.
The author’s research was partially supported by National Science Foundation contract #DMS 96 22801.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
N. Boston, H. W. Lenstra, Jr., and K. A. Ribet, Quotients of group rings arising from two-dimensional representations, C. R. Acad. Sci. Paris Sér. I Math. 312 (1991), 323–328.
R. Coleman, B. Kaskel, and K. Ribet, Torsion points on X 0 (N), Contemporary Math. (to appear).
J. A. Csirik, The Galois structure of J 0 (N)[I] (to appear).
P. Deligne and M. Rapoport, Les schémas de modules de courbes elliptiques, Lecture Notes in Math., vol. 349, Springer-Verlag, Berlin and New York, 1973, pp. 143–316.
E. De Shalit, A note on the Shimura subgroup of J 0 (p), Journal of Number Theory 46 (1994), 100–107.
A. Grothendieck, SGA 7 I, Exposé IX, Lecture Notes in Math., vol. 288, Springer-Verlag, Berlin and New York, 1972, pp. 313–523.
B. Kaskel, The adelic representation associated to X 0(37), Ph. D. thesis, UC Berkeley, May, 1996.
S. Lang and H. Trotter, Frobenius distributions in GL2-extensions, Lecture Notes in Math., vol. 504, Springer-Verlag, Berlin and New York, 1976.
B. Mazur, Modular curves and the Eisenstein ideal, Publ. Math. IHES 47 (1977), 33–186.
B. Mazur, Rational isogenies of prime degree, Invent. Math. 44 (1978), 129–162.
A. Ogg, Hyperelliptic modular curves, Bull. Soc. Math. France 102 (1974), 449–462.
A. Ogg, Automorphismes de courbes modulaires, Sém. Delange-Pisot-Poitou (1974/1975, exposé 7).
M. Raynaud, Courbes sur une variété abélienne et points de torsion, Invent. Math. 71 (1983), 207–233.
K. A. Ribet, On modular representations of
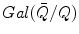 arising from modular forms, Invent. Math. 100 (1990), 431–476.
arising from modular forms, Invent. Math. 100 (1990), 431–476.K. A. Ribet, Report on mod ℓ representations of
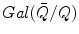 , Proceedings of Symposia in Pure Mathematics 55 (2) (1994), 639–676.
, Proceedings of Symposia in Pure Mathematics 55 (2) (1994), 639–676.K. A. Ribet, Images of semistable Galois representations, Pacific Journal of Math. 81 (1997), 277–297.
J.-P. Serre, Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.
J.-P. Serre, Sur les représentations modulaires de degré 2 de
 , Duke Math. J. 54 (1987), 179–230.
, Duke Math. J. 54 (1987), 179–230.G. Shimura, A reciprocity law in non-solvable extensions, Journal für die reine und angewandte Mathematik 221 (1966), 209–220.
J. Tate, The non-existence of certain Galois extensions of Q unramified outside 2, Contemporary Mathematics 174 (1994), 153–156.
L. C. Washington, Introduction to cyclotomic fields, Graduate Texts in Math., vol. 83 (second edition), Springer-Verlag, Berlin-Heidelberg-New York, 1997.
Author information
Authors and Affiliations
Editor information
Additional information
To Barry Mazur, for his 60th birthday
Rights and permissions
Copyright information
© 1999 Springer-Verlag
About this chapter
Cite this chapter
Ribet, K.A. (1999). Torsion points on J 0(N) and Galois representations. In: Viola, C. (eds) Arithmetic Theory of Elliptic Curves. Lecture Notes in Mathematics, vol 1716. Springer, Berlin, Heidelberg. https://doi.org/10.1007/BFb0093454
Download citation
DOI: https://doi.org/10.1007/BFb0093454
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-66546-5
Online ISBN: 978-3-540-48160-7
eBook Packages: Springer Book Archive


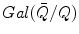 arising from modular forms, Invent. Math. 100 (1990), 431–476.
arising from modular forms, Invent. Math. 100 (1990), 431–476.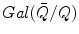 , Proceedings of Symposia in Pure Mathematics 55 (2) (1994), 639–676.
, Proceedings of Symposia in Pure Mathematics 55 (2) (1994), 639–676. , Duke Math. J. 54 (1987), 179–230.
, Duke Math. J. 54 (1987), 179–230.