Abstract
In this work, we are interested in the differential geometry of surfaces in simply isotropic \({\mathbb {I}}^3\) and pseudo-isotropic \({\mathbb {I}}_{\mathrm {p}}^3\) spaces, which consists of the study of \({\mathbb {R}}^3\) equipped with a degenerate metric such as \(\mathrm {d}s^2=\mathrm {d}x^2\pm \mathrm {d}y^2\). The investigation is based on previous results in the simply isotropic space (Pavković in Glas Mat Ser III 15:149–152, 1980; Rad JAZU 450:129–137, 1990), which point to the possibility of introducing an isotropic Gauss map taking values on a unit sphere of parabolic type and of defining a shape operator from it, whose determinant and trace give the known relative Gaussian and mean curvatures, respectively. Based on the isotropic Gauss map, a new notion of connection is also introduced, the relative connection (r-connection, for short). We show that the new curvature tensor in both \({\mathbb {I}}^3\) and \({\mathbb {I}}_{\mathrm {p}}^3\) does not vanish identically and is directly related to the relative Gaussian curvature. We also compute the Gauss and Codazzi–Mainardi equations for the r-connection and show that r-geodesics on spheres of parabolic type are obtained via intersections with planes passing through their center (focus). Finally, we show that admissible pseudo-isotropic surfaces are timelike and that their shape operator may fail to be diagonalizable, in analogy to Lorentzian geometry. We also prove that the only totally umbilical surfaces in \({\mathbb {I}}_{\mathrm {p}}^3\) are planes and spheres of parabolic type and that, in contrast to the r-connection, the curvature tensor associated with the isotropic Levi-Civita connection vanishes identically for any pseudo-isotropic surface, as also happens in simply isotropic space.
Similar content being viewed by others
Notes
The index z is here to emphasize that z is the isotropic (degenerate) direction.
Observe that the center P is not uniquely defined since any other point Q with the same top view as P, i.e., \({\tilde{Q}}={\tilde{P}}\), is also a center.
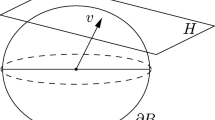
Indeed, if \((x^*,y^*,z^*)\in \varPi _{a,b}\cap S\), then from \(-ax^*-bx^*=p/2-[(x^*)^2+(y^*)^2]/2p\) we find \((x^*-ap)^2+(y^*-bp)^2=p^2(1+a^2+b^2)\).
Indeed, if \((x^*,y^*,z^*)\in \varPi _{a,b}\cap S\), then from \(-ax^*+bx^*=p/2-[(x^*)^2-(y^*)^2]/2p\) we find \((x^*-ap)^2-(y^*-bp)^2=p^2(1+a^2-b^2)\).
References
Aydin, M.E.: Constant curvature surfaces in a pseudo-isotropic space. Tamkang J. Math. 49, 221–233 (2018)
Aydin, M.E., Ergut, M.: Isotropic geometry of graph surfaces associated with product production functions in economics. Tamkang J. Math. 47, 433–443 (2016)
Aydin, M.E., Ergut, M.: Affine translation surfaces in the isotropic 3-space. Int. Electron. J. Geom. 10, 21–30 (2017)
Aydin, M.E., Mihai, A.: Ruled surfaces generated by elliptic cylindrical curves in the isotropic space. Georgian Math. J. (2017). https://doi.org/10.1515/gmj-2017-0044
Brauner, H.: Geometrie des zweifach isotropen Raumes. I. Bewegungen und kugeltreue Transformationen. J. Reine Angew. Math 224, 118–146 (1966)
Chen, B.Y., Decu, S., Verstraelen, L.: Notes on isotropic geometry of production models. Kragujevac J. Math. 38, 23–33 (2014)
Da Silva, L.C.B.: Rotation minimizing frames and spherical curves in simply isotropic and pseudo-isotropic 3-spaces (To appear in Tamkang J. Math.). arXiv:1707.06321
Giering, O.: Vorlesungen über höhere Geometrie. Vieweg, Wiesbaden (1982)
Husty, M., Röschel, O.: On a particular class of cyclides in isotropic respectively pseudoisotropic space. Colloquia Math. Soc. Janos Bolayai 46, 531–557 (1984)
Koenderink, J., van Doorn, A.: Image processing done right. Comput Vis ECCV 2002, 158–172 (2002)
Lense, J.: Über isotrope Mannigfaltigkeiten. Math. Ann. 116, 297–309 (1939)
Liu, H., Yu, Y.: Affine translation surfaces in Euclidean 3-space. Proc. Jpn Acad., Ser. A 89, 111–113 (2013)
López, R.: Differential geometry of curves and surfaces in Lorentz-Minkowski space. Int. Electron. J. Geom. 7, 44–107 (2015)
Mészáros, F.: Klassifikationstheorie der verallgemeinerten Zykliden 4. Ordnung in pseudoisotropen Raum. Math. Pannonica 18, 299–323 (2007)
Pavković, B.: An interpretation of the relative curvatures for surfaces in the isotropic space. Glas. Mat. Ser. III 15, 149–152 (1980)
Pavković, B.: Relative differential geometry of surfaces in isotropic space. Rad JAZU 450, 129–137 (1990)
Pottmann, H., Grohs, P., Mitra, N.J.: Laguerre minimal surfaces, isotropic geometry and linear elasticity. Adv. Comput. Math. 31, 391–419 (2009)
Pottmann, H., Opitz, K.: Curvature analysis and visualization for functions defined on Euclidean spaces or surfaces. Comput. Aided Geom. Des. 11, 655–674 (1994)
Sachs, H.: Ebene Isotrope Geometrie. Vieweg, Braunschweig/Wiesbaden (1987)
Sachs, H.: Parabolische Schiebzykliden des einfach isotropen Raumes. Geom. Dedicata 31, 301–320 (1989)
Sachs, H.: Isotrope Geometrie des Raumes. Vieweg, Braunschweig/Wiesbaden (1990)
Strubecker, K.: Beiträge zur Geometrie des isotropen Raumes. J. Reine Angew. Math. 178, 135–173 (1938)
Strubecker, K.: Die Geometrie des isotropen Raumes und einige ihrer Anwendungen. Jahresber. Dtsch. Math.-Ver. 48, 236–257 (1938)
Strubecker, K.: Differentialgeometrie des isotropen Raumes, I. Theorie der Raumkurven. Sitzungsber. Akad. Wiss. Wien. Math.-Naturw. Kl., IIa 150, 1–53 (1941)
Strubecker, K.: Differentialgeometrie des isotropen Raumes, II. Die Flächen konstanter Relativkrümmung \(K=rt - s^{2}\). Math. Z 47, 743–777 (1942)
Strubecker, K.: Differentialgeometrie des isotropen Raumes. III. Flächentheorie. Math. Z. 48, 369–427 (1942)
Vogel, W.O.: Über lineare Zusammenhänge in singulären Riemannschen Räumen. Arch. Math. 16, 106–116 (1965)
Acknowledgements
The author would like to thank M. E. Aydin (Firat University) for useful discussions and the Departamento de Matemática, Universidade Federal de Pernambuco (Recife, Brazil), where this research initiated when da Silva was a temporary lecturer.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
da Silva, L.C.B. The geometry of Gauss map and shape operator in simply isotropic and pseudo-isotropic spaces. J. Geom. 110, 31 (2019). https://doi.org/10.1007/s00022-019-0488-9
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00022-019-0488-9