Radial expansion preserves hyperbolic convexity and radial contraction preserves spherical convexity

Abstract

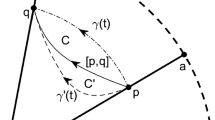
On a flat plane, convexity of a set is preserved by both radial expansion and contraction of the set about any point inside it. Using the Poincaré disk model of hyperbolic geometry, we prove that radial expansion of a hyperbolic convex set about a point inside it always preserves hyperbolic convexity. Using stereographic projection of a sphere, we prove that radial contraction of a spherical convex set about a point inside it, such that the initial set is contained in the closed hemisphere centred at that point, always preserves spherical convexity.

Appendix

Lemma 1

Let $f(x) = \tanh ^{-1}\left( \frac{1}{k_1\coth (u_1x) + k_2\coth (u_2x)}\right)$. If $k_1,k_2 > 0,k_1 + k_2 \geqslant 1$ and $u_1,u_2 > 0$, then f(x) is concave, that is, $f''(x) \leqslant 0$ for all $x > 0$.

Proof

For convenience, denote $p_i \equiv \coth (u_ix)$. Note that $p_i \geqslant 1$ for all $x \geqslant 0$ and $p_i' \equiv u_i(1-p_i^2)$. Then

$$\begin{aligned} f'(x)&= \frac{f_1(x)}{f_2(x)}, \end{aligned}$$

where

$$\begin{aligned} f_1(x)&= k_1u_1(p_1^2-1) + k_2u_2(p_2^2-1),\\ f_2(x)&= (k_1p_1 + k_2p_2)^2-1. \end{aligned}$$

Note that $f_1(x), f_2(x) > 0$ for all $x > 0$. Next,

$$\begin{aligned} f''(x)&= \frac{f_1'(x)f_2(x)-f_1(x)f_2'(x)}{f_2(x)^2}, \end{aligned}$$

where

$$\begin{aligned} f_1'(x)&= -2(k_1u_1^2p_1(p_1^2-1) + k_2u_2^2p_2(p_2^2-1)),\\ f_2'(x)&= -2(k_1p_1+k_2p_2)f_1(x). \end{aligned}$$

Note that $f_1'(x), f_2'(x) \leqslant 0$ for all $x > 0$. The denominator $f_2(x)^2$ is non-negative. We show that the numerator $f_1'(x)f_2(x)-f_1(x)f_2'(x)$ is non-positive. Using the Cauchy-Schwarz inequality, we have

$$\begin{aligned} f_1(x)^2&= \left( u_1\sqrt{k_1p_1(p_1^2-1)} \cdot \sqrt{k_1(p_1 - p_1^{-1})} + u_2\sqrt{k_2p_2(p_2^2-1)}\cdot \sqrt{k_2(p_2-p_2^{-1})}\right) ^2\\&\leqslant (k_1u_1^2p_1(p_1^2-1) + k_2u_2^2p_2(p_2^2-1))(k_1(p_1-p_1^{-1})+k_2(p_2-p_2^{-1}))\\&= -\frac{f_1'(x)}{2}(k_1(p_1-p_1^{-1})+k_2(p_2-p_2^{-1})). \end{aligned}$$

Substituting the above inequality in $f_1'(x)f_2(x)-f_1(x)f_2'(x)$, we get

$$\begin{aligned}&f_1'(x)f_2(x)-f_1(x)f_2'(x)\nonumber \\&\ \ = f_1'(x)f_2(x)+2(k_1p_1+k_2p_2)f_1(x)^2 \nonumber \\&\ \ \leqslant f_1'(x)(f_2(x)-(k_1p_1+k_2p_2)(k_1(p_1-p_1^{-1})+k_2(p_2-p_2^{-1}))) \nonumber \\&\ \ = f_1'(x)((k_1p_1+k_2p_2)^2 - 1 - (k_1p_1+k_2p_2)(k_1(p_1-p_1^{-1})+k_2(p_2-p_2^{-1}))) \nonumber \\&\ \ = f_1'(x)(k_1^2+k_2^2+k_1k_2(p_1p_2^{-1}+p_2p_1^{-1})- 1) \nonumber \\&\ \ \leqslant f_1'(x)((k_1+k_2)^2- 1)\nonumber \\&\ \ \leqslant 0. \end{aligned}$$

(19)

Inequality (19) follows from the facts that $f_1'(x) \leqslant 0$ and $p_1p_2^{-1}+p_2p_1^{-1} \geqslant 2$ for all $x > 0$. The last inequality follows from $f_1'(x) \leqslant 0$ and $(k_1+k_2)^2 \geqslant 1$. $\square$

Lemma 2

Let $f(x) = \tan ^{-1}\left( \frac{1}{k_1\cot (u_1x) + k_2\cot (u_2x)}\right)$. If $k_1,k_2 > 0, k_1+k_2\geqslant 1$, and $u_1,u_2 > 0$, then f(x) is convex, that is, $f''(x) \geqslant 0$ for all $x \in (0,x^*]$ where $x^* = \frac{\pi }{2}\min (u_1^{-1},u_2^{-1})$.

Proof

For convenience, denote $p_i \equiv \cot (u_ix)$. Note that $p_i \geqslant 0$ for all $x \in (0,x^*]$ and $p_i' \equiv -u_i(1+p_i^2)$. Then

$$\begin{aligned} f'(x)&= \frac{f_1(x)}{f_2(x)}, \end{aligned}$$

where,

$$\begin{aligned} f_1(x)&= k_1u_1(1+p_1^2) + k_2u_2(1+p_2^2), \\ f_2(x)&= (k_1p_1 + k_2p_2)^2+1. \end{aligned}$$

Note that $f_1(x), f_2(x) > 0$ for all $x \in (0,x^*]$. Next,

$$\begin{aligned} f''(x)&= \frac{f_1'(x)f_2(x) - f_1(x)f_2'(x)}{f_2(x)^2}, \end{aligned}$$

where

$$\begin{aligned} f_1'(x)&= -2\left( k_1u_1^2p_1(1+p_1^2) + k_2u_2^2p_2(1+p_2^2)\right) , \nonumber \\ f_2'(x)&= -2(k_1p_1+k_2p_2)f_1(x). \end{aligned}$$

(20)

Note that $f_1'(x), f_2'(x) \leqslant 0$ for all $x \in (0,x^*]$. The denominator $f_2(x)^2$ is positive, so we will show that the numerator $f_1'(x)f_2(x) - f_1(x)f_2'(x)$ is also positive for all $x \in (0,x^*]$. First we show that

$$\begin{aligned} f_1'(x)\left( k_1\sqrt{p_1^2+1} + k_2\sqrt{p_2^2+1}\right) ^2 - f_1(x)f_2'(x) \geqslant 0. \end{aligned}$$

(21)

Using the Cauchy-Schwarz inequality, we have

$$\begin{aligned}&\left( k_1\sqrt{p_1^2+1} + k_2\sqrt{p_2^2+1}\right) ^2 \\&\ \ = \left( \sqrt{k_1u_1(p_1^2+1)}\cdot \sqrt{k_1u_1^{-1}} + \sqrt{k_2u_2(p_2^2+1)}\cdot \sqrt{k_2u_2^{-1}}\right) ^2 \\&\ \ \leqslant (k_1u_1(p_1^2+1) + k_2u_2(p_2^2+1))(k_1u_1^{-1}+k_2u_2^{-1}) \\&\ \ = f_1(x)(k_1u_1^{-1}+k_2u_2^{-1}). \end{aligned}$$

Using the above inequality and Eq. (20) in Eq. (21), we get

$$\begin{aligned}&f_1'(x)\left( k_1\sqrt{p_1^2+1} + k_2\sqrt{p_2^2+1}\right) ^2 - f_1(x)f_2'(x)\nonumber \\&\ \ \geqslant f_1'(x)f_1(x)(k_1u_1^{-1}+k_2u_2^{-1}) - f_1(x)f_2'(x) \end{aligned}$$

(22)

$$\begin{aligned}&\ \ = f_1'(x)f_1(x)(k_1u_1^{-1}+k_2u_2^{-1}) + 2(k_1p_1+k_2p_2)f_1(x)^2\nonumber \\&\ \ = f_1(x)(f_1'(x)(k_1u_1^{-1}+k_2u_2^{-1}) + 2(k_1p_1+k_2p_2)f_1(x))\nonumber \\&\ \ = 2f_1(x)\left[ \frac{k_1k_2}{u_1u_2}\left( u_1p_1-u_2p_2\right) \left( u_2^2(1+p_2^2) - u_1^2(1+p_1^2)\right) \right] \nonumber \\&\ \ \geqslant 0 \end{aligned}$$

(23)

as required. We used the fact that $f_1'(x) \leqslant 0$ to obtain (22). Equation (23) follows by substitution. Since $x \in (0,x^*]$, we have $u_ix \leqslant \pi /2$. Also, note that $f_1(x),k_1,k_2,u_1,u_2 > 0$. Then the last inequality follows from the fact that $\alpha \cot (k\alpha )$ is decreasing in $\alpha$ and $\alpha ^2(1+\cot (k\alpha )^2)$ is increasing in $\alpha$ for all $\alpha$ such that $\alpha > 0$ and $k\alpha \in (0,\pi /2]$, so that either both terms in the product $\left( u_1p_1-u_2p_2\right) \left( u_2^2(1+p_2^2) - u_1^2(1+p_1^2)\right)$ are non-positive or both non-negative.

Finally, we substitute (21) in $f_1'(x)f_2(x) - f_1(x)f_2'(x)$, to get

$$\begin{aligned}&f_1'(x)f_2(x) - f_1(x)f_2'(x)\nonumber \\&\ \ \geqslant f_1'(x)f_2(x) - f_1'(x)\left( k_1\sqrt{p_1^2+1} + k_2\sqrt{p_2^2+1}\right) ^2\nonumber \\&\ \ = -f_1'(x)\left[ -f_2(x) + \left( k_1\sqrt{p_1^2+1} + k_2\sqrt{p_2^2+1}\right) ^2\right] \nonumber \\&\ \ = -f_1'(x)\left[ \left( k_1\sqrt{p_1^2+1}+k_2\sqrt{p_2^2+1}\right) ^2 - (k_1p_1+k_2p_2)^2-1\right] \nonumber \\&\ \ = -f_1'(x)\left[ k_1^2+k_2^2+2k_1k_2\left( \sqrt{p_1^2+1}\sqrt{p_2^2+1}-p_1p_2\right) - 1\right] \nonumber \\&\ \ \geqslant -f_1'(x)(k_1^2+k_2^2+2k_1k_2 - 1) \nonumber \\&\ \ = -f_1'(x)((k_1+k_2)^2 - 1)\nonumber \\&\ \ \geqslant 0. \end{aligned}$$

(24)

We used the fact that $\sqrt{a^2+1}\sqrt{b^2+1}-ab \geqslant 1$ to obtain (24). $\square$