Abstract
Affine rotation surfaces, which appear in the context of affine differential geometry, are generalizations of surfaces of revolution. These affine rotation surfaces can be classified into three different families: elliptic, hyperbolic and parabolic. In this paper we investigate some properties of algebraic parabolic affine rotation surfaces, i.e. parabolic affine rotation surfaces that are algebraic, generalizing some previous results on algebraic affine rotation surfaces of elliptic type (classical surfaces of revolution) and hyperbolic type (hyperbolic surfaces of revolution). In particular, we characterize these surfaces in terms of the structure of their implicit equation, we describe the structure of the form of highest degree defining an algebraic parabolic affine rotation surface, and we prove that these surfaces can have either one, or two, or infinitely many axes of affine rotation. Additionally, we characterize the surfaces with more than one parabolic axis.





Similar content being viewed by others
References
Alcázar, J.G., Goldman, R.: Finding the axis of revolution of an algebraic surface of revolution. IEEE Trans. Vis. Comput. Graph. 22(9), 2082–2093 (2016)
Alcázar, J.G., Goldman, R., Hermoso, C.: Algebraic surfaces invariant under scissor shears. Graph. Models 87, 23–34 (2016)
Alcázar, J.G., Goldman, R.: Detecting when an implicit equation or a rational parametrization defines a conical or cylindrical surface, or a surface of revolution. IEEE Trans. Vis. Comput. Graph. 23(12), 2550–2559 (2017)
Lee, I.C.: On generalized affine rotation surfaces. RM 27, 63–76 (1995)
Manhart, F.: Surfaces with affine rotational symmetry and flat affine metric in \({\mathbb{R}}^3\). Studia Sci. Math. Hungar. 40, 397–406 (2003)
Manhart, F.: Affine rotational surfaces with vanishing affine curvature. J. Geom. 80, 166–178 (2004)
Nomizu, K., Sasaki, T.: Affine Differential Geometry. Cambridge University Press, Cambridge (1994)
Schirokow, P., Schirokow, A.: Affine Differential Geometrie. B.G. Teubner, Leipzig (1962)
Su, B.: Affine moulding surfaces and affine surfaces of revolution. Tohoku Math. J. 5, 185–210 (1928)
Süss, W.: Ein affingeometrisches Gegenstück zu den Rotationsflächen. Math. Ann. 98, 684–696 (1928)
Vrs̆ek, J., Làvic̆ka, M.: Determining surfaces of revolution from their implicit equations. J. Comput. Appl. Math. 290, 125–135 (2014)
Yang, Y., Yu, Y., Liu, H.: Centroaffine geometry of equiaffine rotation surfaces in \({\mathbb{R}}^3\). J. Math. Anal. Appl. 414, 46–60 (2014)
Acknowledgements
The authors are grateful to the reviewer, whose observations allowed us to improve an earlier version of the paper, and correct an initially incorrect statement. Juan G. Alcázar is partially supported by FEDER/Spanish Ministerio de Ciencia, Innovación y Universidades-Agencia Estatal de Investigación/MTM2017-88796-P (Symbolic Computation: new challenges in Algebra and Geometry together with its applications), and is a member of the Research Group asynacs (Ref. ccee2011/r34).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix I: The cones \(y^2-2xz-wx^2=0\)
Appendix I: The cones \(y^2-2xz-wx^2=0\)
The matrix associated with the quadratic form \(y^2-2xz-wx^2\) is
The eigenvalues of the matrix \(\mathbf{P}\) are
Observe that \(\lambda _2\cdot \lambda _3=-1\), therefore \(\lambda _2\) and \(\lambda _3\) are never zero. Furthermore, if \(w\ne 0\) then \(\lambda _i\ne 1\) for \(i=2,3\); also, \(\lambda _2=\lambda _3\) iff \(w^2+4=0\), i.e. \(w=\pm 2i\), where \(i^2=-1\). Now we distinguish the following three cases:
- (1)
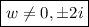 The matrix \(\mathbf{P}\) has three distinct, eigenvalues, so \(\mathbf{P}\) is diagonalizable and \(y^2-2xz-wx^2=0\) defines a cone that is not a surface of revolution. Since \(\lambda _2\cdot \lambda _3=-1\), \(\lambda _2\) and \(\lambda _3\) have opposite signs, so \(y^2-2xz-wx^2=0\) defines a real cone iff w is real. Furthermore, in that case we get an elliptic cone. The eigenvector associated with \(\lambda =1\) is (0, 1, 0), which defines one of the symmetry axes of the cone. The eigenvectors associated with the other two eigenvalues are parallel to the xz-plane.
The matrix \(\mathbf{P}\) has three distinct, eigenvalues, so \(\mathbf{P}\) is diagonalizable and \(y^2-2xz-wx^2=0\) defines a cone that is not a surface of revolution. Since \(\lambda _2\cdot \lambda _3=-1\), \(\lambda _2\) and \(\lambda _3\) have opposite signs, so \(y^2-2xz-wx^2=0\) defines a real cone iff w is real. Furthermore, in that case we get an elliptic cone. The eigenvector associated with \(\lambda =1\) is (0, 1, 0), which defines one of the symmetry axes of the cone. The eigenvectors associated with the other two eigenvalues are parallel to the xz-plane. - (2)
 The matrix \(\mathbf{P}\) has only two distinct eigenvalues, \(\lambda _1=1\) (simple) and \(\lambda _2=\mp i\) (double), but \(\mathbf{P}\) is not diagonalizable. The eigenvector associated with \(\lambda =1\) is (0, 1, 0).
The matrix \(\mathbf{P}\) has only two distinct eigenvalues, \(\lambda _1=1\) (simple) and \(\lambda _2=\mp i\) (double), but \(\mathbf{P}\) is not diagonalizable. The eigenvector associated with \(\lambda =1\) is (0, 1, 0). - (3)
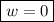 The matrix \(\mathbf{P}\) has only two distinct eigenvalues, \(\lambda _1=1\) (double) and \(\lambda _2=-1\) (simple). The matrix \(\mathbf{P}\) is diagonalizable, so \(y^2-2xz=0\) defines a real cone of revolution about the line through the origin in the direction of the eigenvector associated with \(\lambda _2=-1\), namely (1, 0, 1). Notice that the axis of revolution of this cone forms an angle of \(\frac{\pi }{4}\) with both the x-axis and the z-axis.
The matrix \(\mathbf{P}\) has only two distinct eigenvalues, \(\lambda _1=1\) (double) and \(\lambda _2=-1\) (simple). The matrix \(\mathbf{P}\) is diagonalizable, so \(y^2-2xz=0\) defines a real cone of revolution about the line through the origin in the direction of the eigenvector associated with \(\lambda _2=-1\), namely (1, 0, 1). Notice that the axis of revolution of this cone forms an angle of \(\frac{\pi }{4}\) with both the x-axis and the z-axis.
Rights and permissions
About this article
Cite this article
Alcázar, J.G., Goldman, R. Algebraic affine rotation surfaces of parabolic type. J. Geom. 110, 46 (2019). https://doi.org/10.1007/s00022-019-0500-4
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00022-019-0500-4



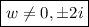 The matrix
The matrix  The matrix
The matrix 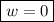 The matrix
The matrix