Skip to main content
SpringerLink
Log in

The Fermat–Torricelli theorem in convex geometry

  • Published:
Journal of Geometry Aims and scope Submit manuscript

Abstract

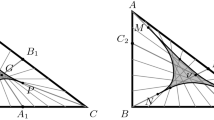
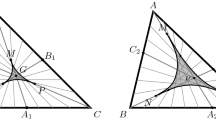
This paper studies a generalization of the Euclidean triangle, the generalized deltoid, which we believe to be the right one for convex geometry. To illustrate the process, our main result shows that the generalized deltoid satisfies a convex generalization of the Fermat–Torricelli theorem. A point that minimizes the sum of distances to the vertices of a triangle (Fermat–Torricelli point) is the same as one through which pass three equiangular affine diameters (Fermat–Ceder point). A generalized deltoid is a triangle whose sides are disjoint, outwardly-looking arcs of convex curves. The Fermat–Torricelli theorem in convex geometry extends the Fermat–Ceder point of a triangle to a Fermat–Ceder point of a generalized deltoid. As an application, we show that the Fermat–Ceder points for the continuous families of affine diameters, area-bisecting lines, and perimeter-bisecting lines are unique for every triangle, and non-unique for every pentagon. In the case of quadrilaterals, the uniqueness of the Fermat–Ceder point for affine diameters holds precisely for all non-trapezoids, the one for the Fermat–Ceder point for area-bisecting lines holds for all quadrilaterals, and the one for the Fermat–Ceder point for perimeter-bisecting lines is open.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Bajaj, C.: The algebraic degree of geometric optimization problems. Discrete Comput. Geom. 3(2), 177–191 (1988)

    MathSciNet  MATH  Google Scholar 

  2. Bárány, I., Blagojević, P., Szücs, A.: Equipartitioning by a convex 3-fan. Adv. Math. 223(2), 579–593 (2010)

    MathSciNet  MATH  Google Scholar 

  3. Bárány, I., Hug, D., Schneider, R.: Affine diameters of convex bodies. Proc. Am. Math. Soc. 144(2), 797–812 (2016)

    MathSciNet  MATH  Google Scholar 

  4. Bárány, I., Matoušek, J.: Simultaneous partitions of measures by k-fans. Discrete Comput. Geom. 25(3), 317–334 (2001)

    MathSciNet  MATH  Google Scholar 

  5. Benítez, C., Fernández, M., Soriano, M.L.: Location of the Fermat–Torricelli medians of three points. Trans. Am. Math. Soc. 354(12), 5027–5038 (2002)

    MathSciNet  MATH  Google Scholar 

  6. Bereg, S.: Equipartitions of measures by 2-fans. Discrete Comput. Geom. 34(1), 87–96 (2005)

    MathSciNet  MATH  Google Scholar 

  7. Berele, A., Catoiu, S.: The perimeter sixpartite center of a triangle. J. Geom. 108(3), 861–868 (2017)

    MathSciNet  MATH  Google Scholar 

  8. Berele, A., Catoiu, S.: Bisecting the perimeter of a triangle. Math. Mag. 91(2), 121–133 (2018)

    MathSciNet  MATH  Google Scholar 

  9. Berele, A., Catoiu, S.: Nonuniqueness of sixpartite points. Am. Math. Mon. 125(7), 638–642 (2018)

    MathSciNet  MATH  Google Scholar 

  10. Berele, A., Catoiu, S.: Bisecting envelopes of convex polygons, preprint.

  11. Blagojević, P., Ziegler, G.: Convex equipartitions via equivariant obstruction theory. Isr. J. Math. 200(1), 49–77 (2014)

    MathSciNet  MATH  Google Scholar 

  12. Blaschke, W.: Aufgaben 540 und 541. Arch. Math. Phys. 26, 65 (1917)

    Google Scholar 

  13. Boltyanski, V., Martini, H., Soltan, V.: Geometric Methods and Optimization Problems, vol. 4. Combinatorial Optimization, Kluwer Academic Publishers, Dordrecht (1999)

  14. Breen, M.: The dimension of the kernel of a planar set. Pac. J. Math. 82(1), 15–21 (1979)

    MathSciNet  MATH  Google Scholar 

  15. Breen, M.: A quantitative version of Krasnosel’skii’s theorem in \(R^2\). Pac. J. Math. 91, 31–37 (1980)

  16. Breen, M.: A Krasnosel’skiĭ-type theorem for points of local nonconvexity. Proc. Am. Math. Soc. 85(2), 261–266 (1982)

    MATH  Google Scholar 

  17. Breen, M.: Clear visibility and the dimension of kernels of starshaped sets. Proc. Am. Math. Soc. 85(3), 414–418 (1982)

    MathSciNet  MATH  Google Scholar 

  18. Buck, R.C., Buck, Ellen F.: Equipartition of convex sets. Math. Mag. 22(4), 195–198 (1949)

    MathSciNet  Google Scholar 

  19. Ceder, J.G.: Generalized sixpartite problems. Bol. Soc. Mat. Mex. (2). 9, 28–32 (1964)

    MathSciNet  MATH  Google Scholar 

  20. Ceder, J.G.: On outwardly simple line families. Can. J. Math. 16, 1–11 (1964)

    MathSciNet  MATH  Google Scholar 

  21. Cieslik, D.: Steiner Minimal Trees, Nonconvex Optimization and Its Applications, vol. 23. Kluwer Academic Publishers, Dordrecht (1998)

    MATH  Google Scholar 

  22. Cieslik, D.: The Fermat–Steiner–Weber problem in Minkowski spaces. Optimization 19(4), 485–489 (1988)

    MathSciNet  MATH  Google Scholar 

  23. Cockayne, E.J., Melzak, Z.A.: Euclidean constructibility in graph-minimization problems. Math. Mag. 42, 206–208 (1969)

    MathSciNet  MATH  Google Scholar 

  24. Courant, R., Robbins, H.: What Is Mathematics?. Oxford University Press, New York (1941)

    MATH  Google Scholar 

  25. Dalla, L.: A note on the Fermat–Torricelli point of a d-simplex. J. Geom. 70(1–2), 38–43 (2001)

    MathSciNet  MATH  Google Scholar 

  26. Dunn, J.A., Pretty, J.E.: Halving a triangle. Math. Gaz. 56(396), 105–108 (1972)

    MATH  Google Scholar 

  27. Durier, R., Michelot, C.: Geometrical properties of the Fermat–Weber problem. Eur. J. Oper. Res. 20, 332–343 (1985)

    MathSciNet  MATH  Google Scholar 

  28. Eggleston, H.G.: Some properties of triangles as extremal convex curves. J. Lond. Math. Soc. 28, 32–36 (1953)

    MathSciNet  MATH  Google Scholar 

  29. Eggleston, H.G.: Problems in Euclidean Space: Aplications of Convexity, V edn. International Series of Monographs on Pure and Applied Mathematics, New York, Pergamon Press (1957)

  30. Eggleston, H.G.: Convexity, vol. 47. Cambridge Tracts in Mathematics and Mathematical Physics, Cambridge University Press, New York (1958)

  31. Erdös, P., Vincze, I.: On the approximation of convex, closed plane curves by multifocal ellipses. J. Appl. Probab. Spec. 19A, 89–96 (1982)

    MathSciNet  MATH  Google Scholar 

  32. Falconer, K.J.: The dimension of the kernel of a compact starshaped set. Bull. Lond. Math. Soc. 9, 313–316 (1977)

    MathSciNet  MATH  Google Scholar 

  33. Gilbert, E.N., Pollack, H.O.: Steiner minimal trees. SIAM J. Appl. Math. 16, 1–29 (1968)

    MathSciNet  MATH  Google Scholar 

  34. Gross, C., Strempel, T.-K.: On generalizations of conics and on a generalization of the Fermat–Torricelli problem. Am. Math. Mon. 105(8), 732–743 (1998)

    MathSciNet  MATH  Google Scholar 

  35. Grünbaum, B.: Partitions of mass-distributions and of convex bodies by hyperplanes. Pac. J. Math. 10, 1257–1261 (1960)

    MathSciNet  MATH  Google Scholar 

  36. Grünbaum, B.: Measures of symmetry for convex sets. In: Proceedings of Symposium Pure Math., Vol. VII, pp. 233–270. Providence, RI: Amer. Math. Soc. (1963)

  37. Grünbaum, B.: Continuous families of curves. Can. Math. J. 18, 529–537 (1966)

    MathSciNet  MATH  Google Scholar 

  38. Guàrdia, R., Hurtado, F.: On the equipartition of plane convex bodies and convex polygons. J. Geom. 83, 32–45 (2005)

    MathSciNet  MATH  Google Scholar 

  39. Hajja, M., Martini, H., Spirova, M.: On converses of Napoleon’s theorem and a modified shape function. Beiträge Algebra Geom. 47(2), 363–383 (2006)

    MathSciNet  MATH  Google Scholar 

  40. Hajja, M., Martini, H., Spirova, M.: New extensions of Napoleon’s theorem to higher dimensions. Beiträge Algebra Geom. 49(1), 253–264 (2008)

    MathSciNet  MATH  Google Scholar 

  41. Hammer, P.C.: The centroid of a convex body. Proc. Am. Math. Soc. 2, 522–525 (1951)

    MathSciNet  MATH  Google Scholar 

  42. Hammer, P.C.: Convex bodies associated with a convex body. Proc. Am. Math. Soc. 2, 781–793 (1951)

    MathSciNet  MATH  Google Scholar 

  43. Hammer, P.C.: Diameters of convex bodies. Proc. Am. Math. Soc. 5, 304–306 (1954)

    MathSciNet  MATH  Google Scholar 

  44. Hammer, P.C., Sobczyk, A.: Planar line families I. Proc. Am. Math. Soc. 4, 226–233 (1953)

    MathSciNet  MATH  Google Scholar 

  45. Hammer, P.C., Sobczyk, A.: Planar line families II. Proc. Am. Math. Soc. 4, 341–349 (1953)

    MathSciNet  MATH  Google Scholar 

  46. Honsberger, R.: Mathematical gems I. Dolciani Mathematical Expositions no 1. Mathematical Association of America, Buffalo, NY (1973)

    Google Scholar 

  47. Klee, V.: The critical set of a convex body. Am. J. Math. 75, 178–188 (1953)

    MathSciNet  MATH  Google Scholar 

  48. Kuhn, H.W.: “Steiner’s” problem revisited. Studies in Optimization, pp. 52–70. Studies in Math., Vol. 10. Washington, DC: Mathematical Association of America (1974)

  49. Kupitz, Y.S., Martini, H.: The Fermat–Torricelli point and isosceles tetrahedra. J. Geom. 49(1–2), 150–162 (1994)

    MathSciNet  MATH  Google Scholar 

  50. Kupitz, Y.S., Martini, H.: Geometric aspects of the generalized Fermat-Torricelli problem. Intuitive Geometry (Budapest, 1995), pp. 55–127. Bolyai Soc. Math. Stud., Vol. 6. Budapest: János Bolyai Math. Soc. (1997)

  51. Kupitz, Y.S., Martini, H., Spirova, M.: The Fermat–Torricelli problem, part I: a discrete gradient-method approach. J. Optim. Theory Appl. 158(2), 305–327 (2013)

    MathSciNet  MATH  Google Scholar 

  52. Lockwood, E.H.: (1967) A book of curves. New York: Cambridge University Press. Reprinted (2007)

  53. Martini, H., Montejano, L., Oliveros, D.: Bodies with Constant Width. An Introduction to Convex Geometry with Applications. Birkhäuser/Springer, Cham (2019)

    MATH  Google Scholar 

  54. Martini, H., Nguyen, M.H., Soltan, V.P.: On Eggleston’s theorem about affine diameters. Mathematika 37(1), 81–84 (1990)

    MathSciNet  MATH  Google Scholar 

  55. Martini, H., Swanepoel, K.J., Weiss, G.: The Fermat–Torricelli problem in normed planes and spaces. J. Optim. Theory Appl. 115(2), 283–314 (2002)

    MathSciNet  MATH  Google Scholar 

  56. Martini, H., Weissbach, B.: Napoleon’s theorem with weights in n-space. Geom. Dedic. 74(2), 213–223 (1999)

    MathSciNet  MATH  Google Scholar 

  57. Mehlhos, S.: Simple counter-examples for the unsolvability of the Fermat and Steiner–Weber problem by compass and ruler. Beiträge Algebra Geom. 41(1), 151–158 (2000)

    MathSciNet  MATH  Google Scholar 

  58. Mordukhovich, B., Nam, N.N.: Applications of variational analysis to a generalized Fermat–Torricelli problem. J. Optim. Theory Appl. 148(3), 431–454 (2011)

    MathSciNet  MATH  Google Scholar 

  59. Neumann, B.H.: On some affine invariants of closed convex regions. J. Lond. Math. Soc. 14, 262–272 (1939)

    MathSciNet  MATH  Google Scholar 

  60. Neumann, B.H.: On invariant of plane regions and mass distributions. J. Lond. Math. Soc. 20, 226–237 (1945)

    MathSciNet  MATH  Google Scholar 

  61. Schneider, R.: Convex Bodies: The Brunn–Minkowski Theory, vol. 151. Encyclopedia of Mathematics and its Applications, Cambridge University Press, Cambridge (2014)

  62. Soltan, V.: Affine diameters of convex bodies—a survey. Expo. Math. 23(1), 47–63 (2005)

    MathSciNet  MATH  Google Scholar 

  63. Stavrakas, Nick M.: The dimension of the convex kernel and points of local nonconvexity. Proc. Am. Math. Soc. 34, 222–224 (1972)

    MathSciNet  MATH  Google Scholar 

  64. Steiger, W., Szegedy, M., Zhao, J.: Six-way equipartitioning by three lines in the plane. In: Proceedings of the 22nd Canadian Conference on Computational Geometry, Winnipeg, August (2010)

  65. Süss, W.: Über eine Affininvariante von Eibereichen. Arch. Math. (Basel) 1, 127–128 (1948/49)

  66. Tan, T.V.: An extension of the Fermat–Torricelli problem. J. Optim. Theory Appl. 146, 735–744 (2010)

    MathSciNet  MATH  Google Scholar 

  67. Toth, G.: Asymmetry of convex sets with isolated extreme points. Proc. Am. Math. Soc. 137(1), 287–295 (2009)

    MathSciNet  MATH  Google Scholar 

  68. Toth, G.: On the structure of convex sets with symmetries. Geom. Dedic. 143, 69–80 (2009)

    MathSciNet  MATH  Google Scholar 

  69. Toth, G.: Measures of Symmetry for Convex Sets and Stability. Universitext, Springer, Cham (2015)

    MATH  Google Scholar 

  70. Yaglom, I. M., Boltyanskii, V.G.: Convex Figures. (Kelly, P. J., Walton, L. F., trans.) New York: Holt, Rinehart and Winston (1960)

  71. Yates, R.C.: A Handbook on Curves and Their Properties. J. W. Edwards, Ann Arbor, MI (1947)

    Google Scholar 

  72. Zamfirescu, T.: On planar continuous families of curves. Can. J. Math. 21, 513–530 (1969)

    MathSciNet  MATH  Google Scholar 

  73. Zindler, K.: Ueber konvexe Gebilde, I. Monatsh. Math. 30, 87–102 (1920)

    MathSciNet  MATH  Google Scholar 

  74. Zindler, K.: Ueber konvexe Gebilde, II. Monatsh. Math. 31, 25–56 (1921)

    MATH  Google Scholar 

  75. Zindler, K.: Ueber konvexe Gebilde, III. Monatsh. Math. 32, 107–138 (1922)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referee for his careful reading and suggestions for improvement. We are grateful to Horst Martini for his proof reading of an earlier version of the manuscript, his generosity and valuable insight. In addition, we thank Marilyn Breen, Paul Goodey, Rolf Schneider and Tudor Zamfirescu for their support.

Author information

Authors and Affiliations

  1. Deparment of Mathematics, DePaul University, Chicago, IL, 60614, USA

    Allan Berele & Stefan Catoiu

Authors
  1. Allan Berele
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stefan Catoiu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stefan Catoiu.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest in regards to this submission.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Berele, A., Catoiu, S. The Fermat–Torricelli theorem in convex geometry. J. Geom. 111, 22 (2020). https://doi.org/10.1007/s00022-020-00535-6

Download citation

  • Received:

  • Revised:

  • Published:

  • DOI: https://doi.org/10.1007/s00022-020-00535-6

Keywords

Mathematics Subject Classification

Search

Navigation