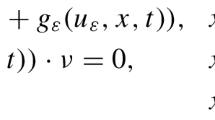Abstract
This paper deals with the Neumann boundary value problem for the system
in a smooth bounded domain \({\Omega\subset{\mathbb{R}}^n}\) \({(n\geq1)}\), where the functions D(u) and S(u) are supposed to be smooth satisfying \({D(u)\geq Mu^{-\alpha}}\) and \({S(u)\leq Mu^{\beta}}\) with M > 0, \({\alpha\in{\mathbb{R}}}\) and \({\beta\in{\mathbb{R}}}\) for all \({u\geq1}\), and the logistic source f(u) is smooth fulfilling \({f(0)\geq0}\) as well as \({f(u)\leq a-\mu u^{\gamma}}\) with \({a\geq0}\), \({\mu > 0}\) and \({\gamma\geq1}\) for all \({u\geq0}\). It is shown that if
then for sufficiently smooth initial data, the problem possesses a unique global classical solution which is uniformly bounded.
Similar content being viewed by others
References
Cao X.: Boundedness in a quasilinear parabolic–parabolic Keller–Segel system with logistic source. J. Math. Anal. Appl. 412, 181–188 (2014)
Cieślak T., Stinner C.: Finite-time blowup and global-in-time unbounded solutions to a parabolic–parabolic quasilinear Keller–Segel system in higher dimensions. J. Differ. Equ. 252, 5832–5851 (2012)
Cieślak T., Stinner C.: Finite-time blowup in a supercritical quasilinear parabolic–parabolic Keller–Segel system in dimension 2. Acta Appl. Math. 129, 135–146 (2014)
Cieślak T., Stinner C.: New critical exponents in a fully parabolic quasilinear Keller–Segel system and applications to volume filling models. J. Differ. Equ. 258, 2080–2113 (2015)
Hillen T., Painter K.: Global existence for a parabolic chemotaxis model with prevention of overcrowding. Adv. Appl. Math. 26, 280–301 (2001)
Horstmann D., Wang G.: Blow-up in a chemotaxis model without symmetry assumptions. Eur. J. Appl. Math. 12, 159–177 (2001)
Horstmann D., Winkler M.: Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215, 52–107 (2005)
Ishida S., Seki K., Yokota T.: Boundedness in quasilinear Keller–Segel systems of parabolic–parabolic type on non-convex bounded domains. J. Differ. Equ. 256, 2993–3010 (2014)
Keller E.F., Segel L.A.: Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26, 399–415 (1970)
Lankeit J.: Eventual smoothness and asymptotics in a three-dimensional chemotaxis system with logistic source. J. Differ. Equ. 258, 1158–1191 (2015)
Li X., Xiang Z.: Boundedness in quasilinear Keller–Segel equations with nonlinear sensitivity and logistic source. Discrete Contin. Dyn. Syst. 35, 3503–3531 (2015)
Mizoguchi N., Souplet P.: Nondegeneracy of blow-up points for the parabolic Keller–Segel system. Ann. Inst. H. Poincaré Anal. Non Linéaire 31, 851–875 (2014)
Nagai T., Senba T., Yoshida K.: Application of the Trudinger–Moser inequality to a parabolic system of chemotaxis. Funkcial. Ekvac. 40, 411–433 (1997)
Nakaguchi E., Osaki K.: Global existence of solutions to a parabolic–parabolic system for chemotaxis with weak degradation. Nonlinear Anal. 74, 286–297 (2011)
Nakaguchi E., Osaki K.: Global solutions and exponential attractors of a parabolic–parabolic system for chemotaxis with subquadratic degradation. Discrete Contin. Dyn. Syst. Ser. B 18, 2627–2646 (2013)
Osaki K., Tsujikawa T., Yagi A., Mimura M.: Exponential attractor for a chemotaxis-growth system of equations. Nonlinear Anal. 51, 119–144 (2002)
Osaki K., Yagi A.: Finite dimensional attractor for one-dimensional Keller–Segel equations. Funkcial. Ekvac. 44, 441–469 (2001)
Painter K.J., Hillen T.: Volume-filling and quorum-sensing in models for chemosensitive movement. Can. Appl. Math. Q. 10, 501–543 (2002)
Quittner, P., Souplet, P.: Superlinear parabolic problems. Birkhäuser advanced texts: Basler Lehrbücher. [Birkhäuser advanced texts: Basel textbooks], Birkhäuser Verlag, Basel (2007). Blow-up, global existence and steady states
Senba T., Suzuki T.: Parabolic system of chemotaxis: blowup in a finite and the infinite time. Methods Appl. Anal. 8, 349–367 (2001) IMS Workshop on Reaction–Diffusion Systems (Shatin, 1999)
Tao Y., Winkler M.: Boundedness in a quasilinear parabolic–parabolic Keller–Segel system with subcritical sensitivity. J. Differ. Equ. 252, 692–715 (2012)
Wang L., Li Y., Mu C.: Boundedness in a parabolic–parabolic quasilinear chemotaxis system with logistic source. Discrete Contin. Dyn. Syst. 34, 789–802 (2014)
Winkler M.: Boundedness in the higher-dimensional parabolic–parabolic chemotaxis system with logistic source. Commun. Partial Differ. Equ. 35, 1516–1537 (2010)
Winkler M.: Does a ‘volume-filling effect’ always prevent chemotactic collapse?. Math. Methods Appl. Sci. 33, 12–24 (2010)
Winkler M.: Blow-up in a higher-dimensional chemotaxis system despite logistic growth restriction. J. Math. Anal. Appl. 384, 261–272 (2011)
Winkler M.: Finite-time blow-up in the higher-dimensional parabolic–parabolic Keller–Segel system. J. Math. Pures Appl. (9) 100, 748–767 (2013)
Winkler M.: Global asymptotic stability of constant equilibria in a fully parabolic chemotaxis system with strong logistic dampening. J. Differ. Equ. 257, 1056–1077 (2014)
Winkler M., Djie K.C.: Boundedness and finite-time collapse in a chemotaxis system with volume-filling effect. Nonlinear Anal. 72, 1044–1064 (2010)
Xiang T.: Boundedness and global existence in the higher-dimensional parabolic–parabolic chemotaxis system with/without growth source. J. Differ. Equ. 258, 4275–4323 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
The study was supported in part by National Natural Science Foundation of China (No. 11171063). The first author is also supported by the Scientific Research Foundation of Graduate School of Southeast University (No. YBJJ1445) and the Key Technologies R&D Program of Henan Province (No. 132102110120).
Rights and permissions
About this article
Cite this article
Zhang, Q., Li, Y. Boundedness in a quasilinear fully parabolic Keller–Segel system with logistic source. Z. Angew. Math. Phys. 66, 2473–2484 (2015). https://doi.org/10.1007/s00033-015-0532-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00033-015-0532-z