Optimum structure to carry a uniform load between pinned supports

Abstract

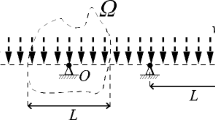
Since the time of Huygens in the 17th century it has been believed that, if the weight of the structural members themselves are negligible in comparison to the applied load, the optimum structure to carry a uniformly distributed load between pinned supports will take the form of a parabolic arch rib (or, equivalently, a suspended cable). In this study, numerical layout optimization techniques are used to demonstrate that when a standard material with equal tension and compressive strength is involved, a simple parabolic arch rib is not the true optimum structure. Instead, a considerably more complex structural form, comprising a central parabolic section and networks of truss bars in the haunch regions, is found to possess a lower structural volume.

Appendix: Extrapolation of numerically computed data to estimate volume for infinite nodal density

In a recent review article Rozvany (2009) observes that ‘Most of the authors in numerical topology optimization simply compare their solutions visually with the exact optimal truss topology and are satisfied with a vague resemblance’. He goes on to suggest that a rigorous verification approach should comprise the following steps:

• 1 For a given set of constraints, derive numerically the optimal topology for various numbers of elements.

• 2 Calculate the structural volume (weight) for each solution.

• 3 Extrapolate the volume (weight) value for infinite number of elements.

• 4 Compare this extrapolated value with that calculated analytically for the exact benchmarks.

These steps have been applied to the numerical data presented in Fig. 6.⁴ These data appear to follow a relation of the form:

$$ V_{n_x} = V_{\infty}+kn_x^{-{\alpha}} \label{eqn:extrapolate} $$

(9)

where $V_{n_x}$ is the numerically computed optimal volume for n _x equally spaced nodal divisions across the span, V _∞ is the volume when n _x → ∞, and k and α are positive constants.

Fig. 6

Computed volume vs. nodal refinement (for 100σ ⁺ = σ − = 1 and σ ⁺ = σ − = 1 cases)

Using (9), a non-linear least-squares approach was used to find best-fit values for V _∞, k and α. The resulting trend lines and values for V _∞ are shown in Fig. 6.