Stacking sequence optimization with genetic algorithm using a two-level approximation

Abstract

We propose a new method for laminate stacking sequence optimization based on a two-level approximation and genetic algorithm (GA), and establish an optimization model including continuous size variables (thicknesses of plies) and discrete variables (0/1 variables that represent the existence of each ply). To solve this problem, a first-level approximate problem is constructed using the branched multipoint approximate (BMA) function. Since mixed-variables are involved in the first-level approximate problem, a new optimization strategy is introduced. The discrete variables are optimized through the GA. When calculating the fitness of each member in the population of GA, a second-level approximate problem that can be solved by the dual method is established to obtain the optimal thicknesses corresponding to the each given ply orientation sequence. The two-level approximation genetic algorithm optimization is performed starting from a ground laminate structure, which could include relatively arbitrarily discrete set of angles. The method is first applied to cylindrical laminate design examples to demonstrate its efficiency and accuracy compared with known methods. The capacity of the optimization strategy to solve more complex problems is then demonstrated using a design example. With the presented method, the stacking sequence in analytical tools can be directly taken as design variables and no intermediate variables need be adopted.

1 Introduction

Because of their high strength-to-weight and high stiffness-to-weight ratios, composite materials have been widely used in structures in the aerospace industry over recent decades. Laminated composite materials are usually fabricated from unidirectional plies of a given thickness with fiber orientations limited to a small set of angles, for example $0^{\circ }, +45^{\circ }, -45^{\circ }$ and $90^{\circ }$. Designing such laminates for various strength and stiffness requirements involves an integer-programming problem for selecting the best number of plies of each orientation, and then determining an optimal stacking sequence. An extensive review of the topic can be found in recent paper by Ghiasi et al. (2009, 2010) and the earlier paper by Venkataraman and Haftka (1999). It showed that two main scenarios are classified: constant stiffness (the stacking sequence is uniform for the entire structure) and variable stiffness (material distribution and fiber orientation might change over the structural domain). With lower design and manufacturing costs involved, constant stiffness design is widely used in engineering and is also the focus of this paper.

For constant stiffness design problems, many composite structure optimization codes use ply thickness as a design variable with a fixed stacking sequence and perform continuous optimization. Examples are PANDA2 (Bushnell 1987), ANSYS (Giger and Ermanni 2005), Msc. Nastran (Taskinoglu and Sahin 2011), and Altair OptiStruct (Zhou et al. 2010). The continuous solution is then rounded to an integer number of plies. Because of the ease of implementation, this method has been applied to solve practical problems (Yuan et al. 2006). However, the approach is greatly affected by the pre-fixed stacking sequence, which yields sub-optimal designs.

For optimizing the stacking sequence of a laminated composite with discrete variables, GAs have been the most popular method (Venkataraman and Haftka 1999). Unfortunately, one major shortcoming of GAs is their high computational cost for the large number of objective and constraint evaluations. For this reason, several modifications to GAs have been proposed, such as parallel computing (Henderson 1994; Punch et al. 1994; Kere and Lento 2005), multi-level optimization (Punch et al. 1994), approximation methods for function evaluation (Liu et al. 1998; Gantovnik et al. 2002; Todoroki and Ishikawa 2004), as well as a combination of these methods (Park et al. 2008). Among these methods, the approximation concepts like response surface methods have been widely employed to reduce the computational cost. However, the cost of constructing the response surface becomes prohibitive as the number of design variables increases. To reduce the number of design variables used in the construction of the response surface, lamination parameters were employed as intermediate variables (Todoroki and Ishikawa 2004), which is independent to the number of layers and leads to great computational saving.

Based on lamination parameters, two–step approaches were proposed and refined by several authors (Yamazaki 1996; IJsselmuiden et al. 2009; Irisarri et al. 2011). The first step takes lamination parameters as continuous design variables to search for the optimal stiffness and thickness of the laminate. The stacking sequence of each laminate is then searched with GA based on structural approximations in the second step. This reduces the number of design variables considerably and allows easy use of approximation for changes in the stacking sequence. However, for most analytical tools, stacking sequences are required as input data whereas lamination parameters cannot be input directly.

In the present study, aiming at reducing the computational cost and implementing the stacking sequence optimization with general FE programs directly, a method incorporating a two-level approximation and GA is constructed. The original optimization strategy was proposed by Dong and Huang (2004) in solving truss topology optimization problem, which showed that the optimal solutions could be reached after an extremely few structural analyses. Considering the similarity between stacking sequence optimization problem and truss topology optimization problem, in which both discrete topology variables and continuous size variables are involved, we introduce the optimization strategy into solving the stacking sequence optimization problem. In order to increase the approximation accuracy, a branched multipoint approximation (BMA) proposed by Huang and Xia (1995) is adopted to establish the first-level approximation problem. The new method is applied to weight minimization problems of a composite cylinder and a composite cone-cylinder, for which the computational cost is demonstrated at the level of optimization calculations with only continuous variables.

2 Problem formulation

In the present study, the optimization model is established based on a ground stacking sequence. The ground stacking sequence and the number of layers are relatively arbitrary, which means the ply angle has been given before the calculation and the corresponding discrete {0, 1} will decide the ply should be retained or not. Besides the discrete {0, 1} variable, there is a thickness variable for each layer. The thickness variables seem redundant, however, from lots of calculations, the results of models with thickness variables are much better than models without thickness variables, which will be shown in section 4.1. The thickness variables optimization which will be solved in the second level approximation could help to approach the optimal stiffness. Based on the ground laminate sequence, the optimization problem can be formulated as follows:

$$ \left\{ \begin{array}{lll} Min & f(\boldsymbol{X}) & \\ s.t. & g_{j} (\boldsymbol{X})\le 0 & j=1,\cdots m \\ & \alpha_{i} x_{i}^{L} +(1-\alpha_{i} )x_{i}^{b} \le x_{i} & i=1,\cdots n \\ & x_{i} \le \alpha_{i} x_{i}^{U} +(1-\alpha_{i} )x_{i}^{b} & \\ & \alpha_{i} =0\quad \;or\;\quad \alpha_{i} =1 & \\ \end{array} \right.,$$

(1)

where X is the vector of ply thickness variables, $\boldsymbol {\alpha }$ is the vector of discrete 0/1 variables which represent the existence of each ply, n denotes the total number of plies in the ground structure, m is the number of constraints, f(X) is the objective function, $g_{j}$(X) is the j-th constraint function, $x_{i}^{U}$ and $x_{i}^{L}$ are the upper and lower bounds on the i-th thickness variable, respectively, and $x_{i}^{b}$ is a very small value $\left (\mathrm {usually}\,0.01x_{i}^{L}\right )$ used to represent the thickness of a removed ply. For instance, when the ground laminate is $[(0/\pm 45/90)_{12}/0/45]_{s}$, the total number of plies is 100 and by considering symmetric laminate there are 50 thickness variables $\left (X=\{x_{1},x_{2},{\ldots },x_{50}\}^{T}\right )$ and 50 discrete variables $\left (\alpha =\{\alpha _{1},\alpha _{2},{\ldots },\alpha _{50}\}^{T}\right )$.

3 Optimization algorithm

3.1 The first-level approximate problem with BMA function

Investigating the former work (Huang and Xia 1995), it can be seen that an explicit approximate function $g_{j}^{(p)} (X)$ was formed based on multipoint aproximation (MA) in structural optimization problems. In fact, MA is a wighted representation of the Taylor expansions with respect to intermediate variables $y_{i} =x_{i}^{r}$. MA is shown to be of higher quality as it is used for cross-sectional size optimization, but it becomes singular and no longer effective if the design variable $x_{k\thinspace }$approaches to zero or is substituted by a user-defined very small value $x_{k}^{b}$, which could happen when the k-th ply is removed in laminate stacking sequence optimization. For example, if $x_{i}\to 0$ and $r < 0$, then $x_{i}^{r}\to \infty$. So MA cannot be used for laminate stacking sequence optimization.

To solve this problem, a modified MA (MMA) method was proposed by Dong and Huang (2004), which is a weighted representation of the Taylor expansions with respect to intermediate variables $y_{i}=e^{-rxi}$. MMA is still effective even if some variables are removed and substituted by a small value, i.e., $x_{k}=x_{k}^{b}$. However, the approxination accuracy of MA is generally better than MMA for complex constraint functions approximation with continuous variables. For this reason, BMA was proposed by Huang et al. (2006), which integrates MA and MMA as one function with two branches for conditions when the corresponding variable exsits or is absent respectively. Here, BMA is a piecewise function with two branches for conditions when the corresponding ply exsits or is absent respectively.

Therefore, to solve problem (1), a series of first-level approximate problems are established using BMA.

In the p-th stage, the first-level approximate problems can be stated as below:

$$ \left\{ \begin{array}{lll} Min & f^{(p)}(\boldsymbol{X}) & \\ s.t. & g_{_{j} }^{(p)} (\boldsymbol{X})\le 0 & j=1,\cdots J_{1}\\ & \alpha_{i} x_{i(p)}^{L} +(1-\alpha_{i} )x_{i}^{b} \le x_{i} & i=1,\cdots n \\ & x_{i} \le \alpha_{i} x_{i(p)}^{U} +(1-\alpha_{i} )x_{i}^{b}& \\ & \alpha_{i} =0\;\;\mathrm{or}\;\;\alpha_{i} =1 & \end{array}\right., $$

(2)

$$ x_{i(p)}^{U} =\min \left\{ {x_{i}^{U} ,\widetilde{x}_{i(p)}^{U} } \right\},$$

(3)

$$ x_{i(p)}^{L} =\max \left\{ {x_{i}^{L} ,\widetilde{x}_{i(p)}^{L} } \right\}, $$

(4)

where $\widetilde {x}_{i(p)}^{U}$ and $\widetilde {x}_{i(p)}^{L}$ are the move limits of $x_{i}$ at the p-th stage. $f^{(p)}$(X) is the p-th approximate objective function created using the BMA function with the information of the primal function f(X) and its derivatives at multiple known points. If the objective is to minimize the weight of the structure, f(X) is explicit and approximating f(X) is not necessary because the weight of laminates is in proportion of the thickness of each ply. $J_{1}$ is the number of active constraints of the original problem (1), and $g_{j}^{(p)}(X)$ represents the j-th approximate constraint function created by using BMA function at the p-th stage. The form of $f^{(p)}$(X) and $g_{j}^{(p)}(X)$ is as follows:

$$ w^{(p)}(\boldsymbol{X})=\sum\limits_{t=1}^{H} {\left\{ {w(\boldsymbol{X}_{t} )+\sum\limits_{i=1}^{n} {\widetilde{w}_{i,t} (\boldsymbol{X})} } \right\}} h_{t} (\boldsymbol{X}), $$

(5)

where

$$ \widetilde{w}_{i,t} (X)=\left\{ \begin{array}{lll} \dfrac{1}{r_{o,t}}\dfrac{\partial w(X_{t})}{\partial x_{i}}x_{it}^{1-r_{o,t}}\left({x_{i}^{r_{o,t}}-x_{it}^{r_{o,t}}}\right)&if&\alpha_{i} =1\\ [15pt] \dfrac{1}{r_{m,t}}\dfrac{\partial w(X_{t})}{\partial x_{i}}\left({1-e^{-r_{m,t}(x_{i}-x_{it})}}\right)&if&\alpha_{i}=0\\ \end{array}\right., $$

(6)

$$ h_{t} (X)=\frac{\overline h_{t} (X)}{\sum\limits_{l=1}^{H} {\overline h_{l} (X)} },\quad t=1,\cdots H, $$

(7)

$$ \overline h_{l} (X)=\prod\limits_{{\begin{array}{*{20}c} {s=1} \\ {s\ne l} \\ \end{array} }}^{H} {(X-X_{s} )^{T}(X-X_{s} )}. $$

(8)

In (5)–(8), $w^{(p)}$(X) represents the objective function $f^{(p)}$(X) or the constraint function $g_{j}^{(p)}(X)$, X $_{t}$ is the t-th known point, and H is the number of points to be counted, bounded above by $H_{\max }$. When the number of known points is larger than $H_{\max }$, only the last $H_{\max }$ points obtained are counted in (5)–(8). w(X $_{t}$) and $\partial w$(X $_{t})$/$\partial x_{i}$ are the function values and partial derivatives of w(X) at X $_{t}$, and $h_{t}$(X) is the weighted function. The exponents $r_{o,t\thinspace }$ and $r_{m,t}$ ($t= 1,{\ldots },H$), are adaptive parameters used to control the non-linearity of the approximation, and can be obtained from the following equations:

$$ \left\{ \begin{array}{*{20}c} Min &\sqrt{\sum\limits_{k=1}^{H}{\left\{{w(X_{k} )-w(X_{t})-\sum\limits_{i=1}^{n}{\widetilde{w}_{i,t}(X_{t})}}\right\}^{2}}}\\ s.t.& r_{o}^{L} \le r_{o,t} \le r_{o}^{U} ,r_{m}^{L} \le r_{m,t} \le r_{m}^{U} ,\quad t=1,\cdots ,H\\ \end{array},\right. $$

(9)

where $r_{o}^{L}$, $r_{o}^{U}$, $r_{m}^{L}$ and $r_{m}^{U}$ are the lower and upper bounds on $r_{o,t\thinspace }$ and $r_{m,t}$, respectively. If there is only one known point, $r_{o,t\thinspace }$ and $r_{m,t\thinspace }$ are assigned the initial values $r_{o,t0}$ and $r_{m,t0}$, respectively. In this paper, $r_{o,t0\thinspace }=-1$, $r_{m,t0\thinspace }= 3.5$, $r_{o}^{L} =-5$, $r_{o}^{U} =5$, $r_{m}^{L} =-5$ and $r_{m}^{U} =5$.

It should be noted that a ply is not deleted when its related discrete variable becomes zero, but is substituted by a special ply with a very small thickness. Thus, the objective function and structural constraint functions are still differentiable with respect to the ply thickness variables, which can be approximated by multipoint approximation.

In the first-level approximate problems, the objective function and constraint functions are made explicit by using the BMA function. Since the first-level approximate problem (2) is an optimization problem with both continuous and discrete variables, it cannot be solved by normal mathematical programming methods. If GA is used to solve this problem directly and the continuous and discrete variables are encoded simultaneously, the scale of the design variables and the computational resources required will become huge. Thus a new optimization strategy is proposed. The discrete variables representing the existence of plies are optimized through a GA and the thicknesses of existed plies are optimized using the dual method, which could significantly reduce the gene code length in the GA and improve the optimization efficiency and accuracy.

3.2 Discrete variables (0/1 variables) optimization with GA

• (1) GA code

Considering that the laminate is symmetrical, one string of genes is used to represent half of the laminate. The existence of each ply is indicated by a 0 or 1, with 0 representing that the ply is removed and 1 representing that the ply is kept. Thus the gene can be written as $s=\alpha _{1}\alpha _{2}...\alpha _{n}$, where $\alpha _{i}$ is a discrete 0/1 variable which represents the existence of each ply in the original problem (1). The string is the classical binary representation.

• (2) Generation of the initial population

Since we have no knowledge of how to choose the initial members at the first/initial calling of GA, the initial population of designs can be generated randomly. Once the optimal members of the population have been obtained, the initial population of next generation is generated according to the elite of former generations of the GA. That is to say, from the second calling of the GA, the initial population consists of three parts: 1) the optimal members of former generations; 2) members generated from those in 1) by making $\alpha _{i}$ approach 0 with a greater probability if the corresponding optimal thickness is less than 1.5 times the single ply thickness; 3) members generated randomly. Here, we use N to denote the number of members in the population.

• (3) Fitness function

The GA is used to solve unconstrained maximization problems, so a constrained minimization problem using an exterior penalty function is established as follows:

$$F_{1} =\phi^{n_{c} }\left[ {f(X^{\ast})+R\sum\limits_{j=1}^{J_{2}}{\left({\max\left\{{g_{j}(X^{\ast}),0} \right\}}\right)^{q}} } \right], $$

(10)

where $n_{c}$ is the number of stacks violating the limitation that the number of continuous plies with the same ply angle must be less than 4 (the number of plies adjacent to the mid-plane of the laminate must be less than 2); $\phi = (10/9)^{0.5}$ is the penalty parameter for this manufacturing constraint (Soremekun et al. 1995), which means the value of $F_{1}$ will be penalized when the number of stacks with the same ply angle exceed 4; R is the penalty factor, which is multiplied by an increasing rate $r(r > 1),q$ denotes the penalty exponent (normally 1–5, 1 is recommended), and f(X*) and $g_{j}$(X*) are the objective value and constraint values with respect to the optimal thicknesses of given stacking sequences, obtained from (16). The composite function can be then appended to the objective function $F_{2}$, which is to be maximized as:

$$ F_{2} =\left( {1-\frac{F_{1} -\min (F_{1} )}{\max (F_{1} )-\min (F_{1} )}} \right)^{s}, $$

(11)

where s is the exponent of normalization (1–3, 2 is recommended). In addition, to prevent too many copies of members with high fitness, which would induce premature convergence, a parameter $P_{p}$ is given to the fitness function to control the maximum number of copies of each member. We take $P_{p}=2$ in the present study. Finally, the fitness function is defined as:

$$ Fitness=aF_{2} +b $$

(12)

$$ a=\left\{ \begin{array}{cc} avg(F_{2})/\left[avg(F_{2})-\min\left(F_{2}\right)\right]&(P_{p} -1)\min \left(F_{2}\right)\le P_{p} avg(F_{2})-\max (F_{2})\\ [4pt] (P_{p}-1)avg(F_{2})/\left[\max \left(F_{2}\right)-avg(F_{2})\right]& \mathrm{other}\\ \end{array}\right. $$

(13)

$$ b=\left\{ \begin{array}{cc} -a\min (F_{2})&(P_{p}-1)\min \left(F_{2}\right)\le P_{p} avg(F_{2})-\max (F_{2})\\ [4pt] (1-a)avg(F_{2})& \mathrm{other}\\ \end{array}\right. $$

(14)

It can be seen that to calculate the fitness of each member in a population, further sizing optimization is needed to obtain the optimal thicknesses corresponding to a given ply orientation sequence, which is solved by the internal sizing optimization in Section 3.3. Fitnesses that have been calculated are stored in a database to shorten the computational time for optimizing the same genetic code.

• (4) Reproduction operator

The simulated roulette wheel selection method (Goldberg 1989) is applied to select parents for reproduction in the present work. The selection probability $P_{i}$ of a member, shown in (15) in the population is in proportion to its current fitness. Members with high fitness will produce more offspring, while members with low fitness may be eliminated in this process.

$$P_{i} ={Fitness_{i} } \mathord{\left/ {\vphantom {{Fitness_{i} } {\sum\limits_{j=1}^{N} {Fitness_{j} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j=1}^{N} {Fitness_{j} } } $$

(15)

In (15), $Fitness_{i}$ is the fitness of the i-th member, and $P_{i}$ is the selection probability of this member.

Firstly, according to $P_{i}$, we divide the wheel into a number of sectors equal to the number of members in the population (N). The proportion of each sector area out of the total wheel area corresponds to the fitness of each member. We then spin the wheel N times to simulate roulette. Each time the pointer stops at a sector the corresponding member is selected.

• (5) Crossover operator

A one-point crossover method is used. Firstly, two members are selected randomly from the population after the reproduction operation. A random number between 0 and 1 is then drawn to determine whether the crossover is to be executed. If the number is smaller than the crossover probability $P_{c}$, the crossover operator is executed, and the pair of genes is swapped at a randomly chosen point. Otherwise, the two members are reproduced directly to the child population. This process is repeated until the size of the child population is equal to the size of the parent population.

• (6) Mutation operator

A simple mutation method is used as the mutation operator. For each member in the population after the crossover operation, we switch a 0 to a 1 or vice versa if the number randomly generated is smaller than the mutation probability $P_{m}$. Otherwise, the code in a gene is kept unchanged.

3.3 Size optimization for fitness calculation

After a ply orientation sequence is given for each member by the GA, the discrete variables in the first-level approximate problem (2) are fixed. Moreover, the sizing variables of the members whose corresponding discrete variables are zero will not change and can be removed. Additionally, the deleted plies and related constraints $g_{j}^{(p)} (X)$ will not exist. The retained constraints will be further selected through temporal deletion techniques. Finally, the internal sizing optimization problem can be simplified to:

$$\left\{ \begin{array}{lll} Min& \widetilde{f}\left({\widetilde{X}}\right)=f^{(p)}\left(X\right)& \\ s.t.& \widetilde{g}_{j}\left({\widetilde{X}}\right)=g_{j}^{(p)} \left(X\right)\le 0 & j=1,\cdots ,J_{2}\\ & \overline x_{i(p)}^{L} \le \widetilde{x}_{i} \le \overline x_{i(p)}^{U}&i=1,\cdots ,I\\ \end{array}\right., $$

(16)

$$ \left\{ \begin{array}{ll} \widetilde{x}_{i}& \alpha_{k} =1\\ x_{k}^{b}& \alpha_{k} =0\\ \end{array} \quad (k=1,\cdots ,n)\right., $$

(17)

where X is the vector of the remaining ply thickness variables, I is the number of remaining variables, $\bar {{x}}_{i(p)}^{U}$ and $\bar {{x}}_{i(p)}^{L}$ are the upper and lower bounds on the i-th remaining variable at the p-th stage, $g_{j}$(X) is the retained constraint, $J_{2}$ is the number of retained constraints, and $\widetilde {f}(X)$ is the structure weight for the given ply orientation sequence.

Problem (16) is an explicit optimization problem with continuous variables only, but it is still difficult to solve the problem due to its complicated nonlinearity. Since the number of thickness variables in the first-level problem (16) is usually much more than the number of active constraints, it is reasonable to use the dual method to efficiently solve the problem. Thus a second-level approximate problem that can be solved by the dual method is established to approach the optimum of the first-level approximate problem (16).

3.4 The second-level approximate problem

For common use, the objective function and the constraint functions in the first-level approximate problem (16) are expanded into linear Taylor series in the variable space X and its reciprocal variable space, respectively, then the second-level approximate problem is formed. In the k-th step, the approximate problem can be stated as:

$$ \left\{ \begin{array}{lll} Min & f^{(k)}\left(\widetilde{X}\right)=\widetilde{f}\left(\widetilde{X}_{(k)}\right)+\sum\limits_{i=1}^{I} {\dfrac{\partial \widetilde{f}\left(\widetilde{X}_{(k)}\right)}{\partial \tilde{x}_{i}}\left(\tilde{x}_{i}-\tilde{x}_{i(k)}\right)}& \\ s.t. & g_{j}^{(k)} \left( {\widetilde{X}}\right)=\widetilde{g}_{j} \left({\widetilde{X}_{(k)}}\right)-\sum\limits_{i=1}^{I} {\tilde{x}_{i(k)}^{2} \dfrac{\partial \widetilde{g}_{j} \left({\widetilde{X}_{(k)}}\right)}{\partial \tilde{x}_{i} }\left({\frac{1}{\tilde{x}_{i}}-\frac{1}{\tilde{x}_{i(k)}}}\right)} \le 0 & j=1,\cdots ,J_{2},\\ & \overline x_{i(k)}^{L} \le \tilde{x}_{i} \le \overline{x}_{i(k)}^{U} &i=1,\cdots ,I\\ \end{array}\right. $$

(18)

$$\overline x_{i(k)}^{U} =\min \left\{ {x_{i(p)}^{U} ,\widetilde{x}_{i(k)}^{U} } \right\}, $$

(19)

$$ \overline x_{i(k)}^{L} =\max \left\{ {x_{i(p)}^{L} ,\widetilde{x}_{i(k)}^{L} } \right\}, $$

(20)

where $f^{(k)}$ ${\tilde{\mathit{X}}}$ is the objective function at the k-th step, $g_{j}^{(k)} (X)$ ${\tilde{X}}$ is the constraint function, $\widetilde {x}_{i(k)}^{U}$ and $\widetilde {x}_{i(k)}^{L}$ are the move limits of $x_{i\thinspace }$at the k-th step, and $\overline x_{i(k)}^{U}$ and $\overline x_{i(k)}^{L}$ are the upper and lower bounds on $x_{i\thinspace }$ at the k-th step.

The dual problem for the approximate problem (18) can be stated as follows:

$$\left\{\begin{array}{ll} Max \;\; l(\lambda )=\mathop{\min}\limits_{\tilde{{X}}\in R\left(\tilde{{X}}\right)}\left[{f^{(k)}\left({\widetilde{X}} \right)+\sum\limits_{j=1}^{J_{2} } {\lambda_{j}\widetilde{g}_{j} \left({\widetilde{X}}\right)}}\right]\\ s.t. \quad \lambda_{j} \ge 0,\quad j=1,\cdots , J_{2}\end{array}\right.,$$

(21)

where $R({\widetilde {X}})=\left \{{\widetilde {x}_{i} \left | {\overline x_{i(k)}^{L} } \right .\le \widetilde {x}_{i} \le \overline x _{i(k)}^{U} ,\;i=1,\;\cdots ,\;I} \right \}$. The relationship between the design variables and the dual variables can be established as follows:

$$ \widetilde{x}_{i} =\left\{ \begin{array}{cc} \overline x_{i(k)}^{L}& \overline x_{i} <\overline x_{i(k)}^{L}\\ \overline x_{i}&\overline x_{i(k)}^{L} \le \overline x_{i} \le \overline x_{i(k)}^{U}\\ \overline x_{i(k)}^{U}& \overline x_{i} >\overline x_{i(k)}^{U} \end{array} \quad i=1,\cdots ,n \right., $$

(22)

where

$$ \overline x_{i} =\left\{ {{\begin{array}{*{20}c} {\sqrt {x_{i}^{\prime} } } \hfill & {x_{i}^{\prime} \ge 0} \hfill \\ 0 \hfill & {x_{i}^{\prime} <0} \hfill \\ \end{array} }} \right. $$

(23)

and

$$ x_{i}^{\prime}=-\dfrac{\sum\limits_{j=1}^{J_{2} } {\lambda_{j} \widetilde{x}_{i(k)}^{2} \dfrac{\partial g_{j} \left({\widetilde{X}_{(k)} } \right)}{\partial \widetilde{x}_{i} }} }{\dfrac{\partial f\left( {\widetilde{X}_{(k)}} \right)}{\partial \widetilde{x}_{i} }}. $$

(24)

After finding the optimal design variables (X and $\boldsymbol {\alpha }$), the thickness variables X need to be rounded to make them integer multiples of the ply thickness, and plies corresponding to a discrete variable of 0 are deleted.

3.5 The sensitivity analysis

The sensitivities of objective function and constraint functions with respect to the thickness variables in the first-level approximation problem are derived from the results of commercial finite element program Nastran sol 200, in which semianalytical method is used. Within the second-level approximation problems, only the sensitivities of objective function (weight) are needed, which are equal to the area × density of each layer.

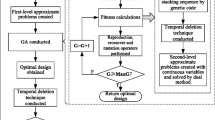
3.6 Flow chart and convergence criteria

The flow chart of the optimum algorithm is organized as shown in Fig. 1. The structural analysis within the procedure is implemented by Natran. In the end of the optimization procedure, the thickness variables will be rounded to the nearest integer and the layers with thickness of 0.01 t will be removed.

Fig. 1

Flow chart of the optimization algorithm

Within the optimization calculation procedure, there are three positions need to evaluate convergence. The convergence criteria in these positions are applied as follow.

• 1) First-level approximation problem convergence evaluation

There are three conditions involved.

$$\mathrm{a}.\quad \left|\left(f^{(p)}(\mathbf{X})-f^{(p-1)}(\mathbf{X})\right)\left/\right.f^{(p)}(\mathbf{X})\right|<DELTA1 $$

(25)

$$\mathrm{or}\;\sqrt{\sum\limits_{i=1}^{n}\left({x_{i(p)}-x_{i({p-1})}}\right)^{2}}<DELTAX $$

(26)

$$ \mathrm{b}.\quad Max\left\{g_{1}^{p}(\mathbf{X}),g_{2}^{p}(\mathbf{X}),\cdots ,g_{J_{1}}^{p}(\mathbf{X})\right\}\le DELTAC $$

(27)

$$ \mathrm{c}.\quad p\le LPMAX1 $$

(28)

Where DELTA1, DELTAX and DELTAC are convergence control parameters, and LPMAX1 is the maximum iteration number of the first-level approximation problem. To evaluate the convergence, condition a, b & c should be satisfied simultaneously.

• 2) Second-level approximation problem convergence evaluation

Three conditions are involved.

$$\mathrm{a}.\quad \left|f^{(k)}(\mathbf{X})-f^{\left(k-1\right)}(\mathbf{X})\right|\mathord{\left/\right.{f^{(k)}}\le DELTA} $$

(29)

$$ \mathrm{b}.\quad \left|{f^{( k )}({\mathbf{X}})-f^{\left( {k-1} \right)}(\mathbf{X})} \right|<DELTA $$

(30)

$$ \mathrm{c}.\quad k\ge NMAX1 $$

(31)

where DELTA and NMAX1 are the convergence precision and maximum iteration number of the second-level approximation problem. When any one of the three conditions is satisfied, the second-level approximation problem is converged. In the present work, $D\hspace *{-.7pt}E\hspace *{-.7pt}L\hspace *{-.7pt}T\hspace *{-.7pt}A\hspace *{-.7pt}1=0.001$, $D\hspace *{-.7pt}E\hspace *{-.7pt}L\hspace *{-.7pt}T\hspace *{-.7pt}A\hspace *{-.7pt}X=0.001$, $D\hspace *{-.7pt}E\hspace *{-.7pt}L\hspace *{-.7pt}T\hspace *{-.7pt}A\hspace *{-.7pt}C=0.005$, $L\hspace *{-.7pt}P\hspace *{-.7pt}M\hspace *{-.7pt}A\hspace *{-.7pt}X\hspace *{-.7pt}1=20$, $D\hspace *{-.7pt}E\hspace *{-.7pt}L\hspace *{-.7pt}T\hspace *{-.7pt}A=0.001$, $N\hspace *{-.7pt}M\hspace *{-.7pt}A\hspace *{-.7pt}X\hspace *{-.7pt}1=10$.

• 3) Convergence evaluation of GA

When the number of total evolution generations is larger than the maximum number of generations, the GA iterations will stop.

4 Numerical examples

Two numerical examples are presented to illustrate the capabilities of the optimization procedure. The calculations are conducted in a computer with CPU3.30 GHz/ RAM8.00G.

4.1 Example 1

Consider a composite cylinder with a radius of 100 mm and a length of 400 mm. One end of the cylinder is fixed. The composite material properties are: Young’s modulus in two directions $E_{1}=128$ Gpa, $E_{2}=13$ Gpa; shear modulus $G_{12}=6.4$ Gpa; Poisson’s ratio $\nu _{12}=0.3$; ply thickness $t=0.127$ mm; density $\rho =1600$ kg/m$^{3}$. The stacking sequence for the cylinder is symmetric, and the 0° fiber direction is along the longitudinal direction of the cylinder. The objective is to minimize the weight of the cylinder. The constraint is $f_{1}\ge 492.93$ Hz, where $f_{1}$ is the first-order frequency of the cylinder. Due to the restrictions on the manufacturing process, which is that the thickness of one layer could not be lower than t, the lower and upper bounds on ply thickness are set as $x_{i}^{L}=t$ and $x_{i}^{U}=4t$, and the thickness of a removed ply is $x_{i}^{b}=0.01t$. The upper bound on the number of known points is $H_{\max }=5$.

Eight optimization cases were conducted. In each case, the optimization without thickness variables, which means there is only first-level approximation and GA involved in the optimization procedure, was also implemented to verify the necessity of thickness variables. The number of layers in the ground laminates is given from 30 to 100 to test the optimum searching capability of the present optimization strategy. The optimum stacking sequence will be affected by optimization control parameters, such as the number of members in the population N, the maximum number of generations MaxG, the crossover probability $P_{c}$, the mutation probability $P_{m}$, and the maximum delete percentage FITP. The optimization control parameters of the selected results are listed in Table 1, the initial penalty factor is $R=0.05$, and the increasing rate is $r=2$.

The optimization results are shown in Table 2. The value of weights and frequencies listed in Table 2 are actual weights and frequencies obtained from the finite element program Nastran. The results of Ref. (Wang 2008) and Ref. (Tang et al. 2004) are also shown as comparison. The algorithm performance is also evaluated with the reliability in researching the best solution. Taking the case 1 as an instance, we assume that feasible designs with layers less than 18 (the number of layer of the best known design is 16) are acceptable and we denote them as practical optima. The reliability is 80 % with 10 structural analyses on average through 200 tests.

Table 1 The optimization control parameters of studied cases

Table 2 Optimization results

From the results listed in Table 2, it can be seen that the present optimization procedure is able to find relatively good stacking sequences which are close to the results in published literatures. Starting from different ground stacking sequences, which are varied from 30 layers to 100 layers, the present optimization procedure can all approach practical optima efficiently. Comparing the results of that with thickness variables (a) and that without thickness variables (b) for the studied cases, the weight of (b) is higher than that of (a), and the iterations of (b) is less than that of (a), which means that the second-level approximation can help the GA to approach the optimum and avoid to convergence prematurely at local optimums. In addition, it showed that relatively low number of iterations were needed in each case, and the computational time are all less than 100 s, which showed that the computational expense of the present optimization procedure is not too sensitive to the number of design variables. The iteration history of structural weight in case 1, 6 and 8 during the optimization process is shown in Table 3.

Table 3 The iteration history of structural weight (unit:Kg)

4.2 Example 2

The composite cone-cylinder structure shown in Fig. 2 consists of two composite parts: the conic part and the cylindrical part. The dimensions are: $\mathrm {r}=60$ mm, $\mathrm {R}=100$ mm, $\mathrm {a}=100$ mm, $\mathrm {b}=200$ mm. The two ends of the structure are fixed, and the outer surfaces are under a pressure of 0.3 Mpa. The material is same as that in Example 1. The stacking sequence for this structure is symmetric, and the 0° fiber direction is along the longitudinal direction of the cone and cylinder. The objective is to minimize the structural weight. The first constraint is $\lambda _{1}\ge 6$, where $\lambda _{1}$ is the critical buckling factor of the structure. The second constraint is $f_{1}\ge 1700$ Hz, where $f_{1}$ is the first-order frequency of the structure.

Fig. 2

Dimensions of cone-cylinder structure

In composite materials, it is usually required that the number of $+45^{\circ }$ plies equals to the number of $-45^{\circ }$ plies, which is called the balanced constraint. In the present work, the balanced constraint is enforced by linking the thickness variables of adjacent $+45^{\circ }$ and $-45^{\circ }$ plies. Two kinds of calculation are investigated: (1) considering the balanced constraint (BC); (2) not considering the balanced constraint (NBC). The optimization parameters are: $x_{i}^{L}=t$, $x_{i}^{U}=4t$, $x_{i}^{b}=0.01t$, $H_{\max }=5$, $R=0.05$, $r=2$. N, MaxG, $P_{c}$, and $P_{m}$ are different in studied cases for results comparison.

Table 4 gives three groups of results with varied ground stacking sequences: 1) 40 layers in both conic and cylindrical part; 2) 60 layers in both conic and cylindrical part; 3) 60 layers in conic part and 100 layers in cylindrical part. It can be seen that the optimization calculations can converge to the optimal results from different ground stacking sequences with a small number of iterations. Comparing the results of BC and NBC, it showed that the structural weight of BC in three groups are a little lower than that of NBC, which might be caused by fewer variables in BC than that in NBC. It also showed that present procedure can conduct stacking sequence optimization problem with multiple parts. The iteration history of structural weight in the group 1 and 3 during the optimization process is shown in Table 5. The values of the final weight in Table 5 are a little higher than that in Table 4, which is caused by the results rounding.

Table 4 Optimal stacking sequence of composite cone-cylinder structure

Table 5 The iteration history of structural weight (unit:Kg)

5 Conclusions

An efficient stacking sequence optimization strategy for composite structures is presented in this paper. This strategy is based on a two-level multi-point approximation and GA. The procedure starts with a ground stacking sequence and both continuous size variables (thicknesses of plies) and discrete variables (0/1 variables that represent the existence of each ply) are included. The genetic solver is run to deal with the discrete variables based on the first-level approximation, and the fitness calculation of each member is obtained by solving a second-level approximation problem for thickness variables optimization. The structural and sensitivity analyses are only required before constructing first-level approximate problem. The data of the critical responses and their gradients in each iteration must be stored for the next iteration. This procedure only requires a very small part of computational time. The numerical tests demonstrate that the present method can rapidly and in a stable manner reach the solution under a given 0.1 % weight precision. The effectiveness of the method is comparable with up-to-date existing methods (Irisarri et al. 2011), but the stacking sequence in analytical tools can be directly taken as design variables and no intermediate variables need be adopted. The extension of this work to the general case with stress constraints is currently under investigation.