Skip to main content
SpringerLink
Log in

Projection-based two-phase minimum and maximum length scale control in topology optimization

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

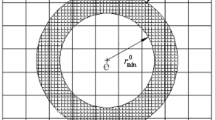
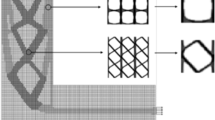
Length scale control in topology optimization is an important area of research with direct implications on numerical stability and solution manufacturability. Projection-based algorithms for continuum topology optimization have received considerable attention in recent years due to their ability to control minimum length scale in a flexible and computationally efficient manner. In this paper, we propose a new projection-based algorithm that embeds minimum length scale control on two material phases (e.g., solid and void) as well as optional maximum length scale on one material phase (e.g., solid or void) into the projection methodology used for material distribution approaches to topology optimization. The proposed algorithms are demonstrated on benchmark problems and are shown to satisfy the length scale constraints imposed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Allaire G, Jouve F, Michailidis G (2016) Thickness control in structural optimization via a level set method. Struct Multidiscip Optim 53(6):1349–1382

    Article  MathSciNet  Google Scholar 

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202

    Article  Google Scholar 

  • Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69(9–10):635–654

    MATH  Google Scholar 

  • Borrvall T (2001) Topology optimization of elastic continua using restriction. Arch Comput Meth Eng 8 (4):351–385

    Article  MathSciNet  Google Scholar 

  • Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(9):2143–2158

    Article  MathSciNet  Google Scholar 

  • Bruns TE, Tortorelli DA (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Methods Appl Mech Eng 190(26):3443–3459

    Article  Google Scholar 

  • Carstensen JV, Guest JK (2014) New projection methods for two-phase minimum and maximum length scale control in topology optimization. In: 15th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Atlanta, pp 1–11

  • Clausen A, Aage N, Sigmund O (2016) Exploiting additive manufacturing infill in topology optimization for improved buckling load. Engineering 2(2):250–257

    Article  Google Scholar 

  • Diaz A, Sigmund O (1995) Checkerboard patterns in layout optimization. Struct Multidiscip Optim 10 (1):40–45

    Article  Google Scholar 

  • Gaynor AT, Guest JK (2014) Topology optimization for additive manufacturing: considering maximum overhang constraint. In: Proceedings of the 15th AIAA/ISSMO multidisciplinary analysis and optimization conference, Atlanta, pp 1–8

  • Gaynor AT, Guest JK (2016) Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design. Struct Multidiscip Optim 54(5):1157–1172

    Article  MathSciNet  Google Scholar 

  • Gaynor AT, Meisel NA, Williams CB, Guest JK (2014) Multiple-material topology optimization of compliant mechanisms created via polyjet three-dimensional printing. J Manuf Sci Eng 136(6):061015–1–061015–10

    Article  Google Scholar 

  • Guest JK (2009a) Imposing maximum length scale in topology optimization. Struct Multidiscip Optim 37 (5):463–473

    Article  MathSciNet  Google Scholar 

  • Guest JK (2009b) Topology optimization with multiple phase projection. Comput Methods Appl Mech Eng 199(1):123–135

    Article  MathSciNet  Google Scholar 

  • Guest JK (2015) Optimizing the layout of discrete objects in structures and materials: a projection-based topology optimization approach. Comput Methods Appl Mech Eng 283:330–351

    Article  Google Scholar 

  • Guest JK, Smith Genut LC (2010) Reducing dimensionality in topology optimization using adaptive design variable fields. Int J Numer Methods Eng 81(8):1019–1045

    MATH  Google Scholar 

  • Guest JK, Zhu M (2012) Casting and milling restrictions in topology optimization via projection-based algorithms. In: ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, pp 913–920

  • Guest JK, Prévost JH, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238– 254

    Article  MathSciNet  Google Scholar 

  • Guest JK, Asadpoure A, Ha S-H (2011) Eliminating beta-continuation from heaviside projection and density filter algorithms. Struct Multidiscip Optim 44(4):443–453

    Article  MathSciNet  Google Scholar 

  • Guo X, Zhang W, Zong W (2014) An explicit length scale control approach in simp-based topology optimization. Comput Methods Appl Mech Eng 282:71–86

    Article  MathSciNet  Google Scholar 

  • Ha S-H, Guest JK (2014) Optimizing inclusion shapes and patterns in periodic materials using discrete object projection. Struct Multidiscip Optim 50(1):65–80

    Article  Google Scholar 

  • Langelaar M (2017) An additive manufacturing filter for topology optimization of print-ready designs. Struct Multidiscip Optim 55(3):871–883

    Article  MathSciNet  Google Scholar 

  • Lazarov BS, Wang F (2017) Maximum length scale in density based topology optimization. Comput Methods Appl Mech Eng 318:826–844

    Article  MathSciNet  Google Scholar 

  • Petersson J, Sigmund O (1998) Slope constrained topology optimization. Int J Numer Methods Eng 41 (8):1427–1434

    Article  MathSciNet  Google Scholar 

  • Poulsen TA (2003) A new scheme for imposing a minimum length scale in topology optimization. Int J Numer Methods Eng 57(6):741–760

    Article  MathSciNet  Google Scholar 

  • Qian X (2017) Undercut and overhang angle control in topology optimization: a density gradient based integral approach. Int J Numer Methods Eng 111(3):247–272

    Article  MathSciNet  Google Scholar 

  • Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidiscip Optim 33(4–5):401–424

    Article  Google Scholar 

  • Sigmund O (2009) Manufacturing tolerant topology optimization. Acta Mech Sinica 25(5):227–239

    Article  Google Scholar 

  • Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Multidiscip Optim 16(1):68–75

    Article  Google Scholar 

  • Sigmund O, Torquato S (1997) Design of materials with extreme thermal expansion using a three-phase topology optimization method. J Mech Phys Solids 45(6):1037–1067

    Article  MathSciNet  Google Scholar 

  • Stolpe M, Svanberg K (2001) An alternative interpolation scheme for minimum compliance topology optimization. Struct Multidiscip Optim 22(2):116–124

    Article  Google Scholar 

  • Svanberg K (1987) The method of moving asymptotes: a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    Article  MathSciNet  Google Scholar 

  • Tootkaboni M, Asadpoure A, Guest J K (2012) Topology optimization of continuum structures under uncertainty—a polynomial chaos approach. Comput Methods Appl Mech Eng 201:263–275

    Article  MathSciNet  Google Scholar 

  • Wang F, Lazarov B S, Sigmund O (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidiscip Optim 43(6):767–784

    Article  Google Scholar 

  • Watts S, Tortorelli DA (2017) Optimality of thermal expansion bounds in three dimensions. Extreme Mech Lett 12:97–100

    Article  Google Scholar 

  • Wu J, Aage N, Westermann R, Sigmund O (2018) Infill optimization for additive manufacturing—pproaching bone-like porous structures. IEEE Trans Vis Comput Graph 24(2):1127–1140

    Article  Google Scholar 

  • Xu S, Cai Y, Cheng G (2010) Volume preserving nonlinear density filter based on heaviside functions. Struct Multidiscip Optim 41(4):495–505

    Article  MathSciNet  Google Scholar 

  • Yan S, Wang F, Sigmund O (2018) On the non-optimality of tree structures for heat conduction. Int J Heat Mass Transf 122:660–680

    Article  Google Scholar 

  • Zhou M, Lazarov BS, Wang F, Sigmund O (2015) Minimum length scale in topology optimization by geometric constraints. Comput Methods Appl Mech Eng 293:266–282

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work was supported by the US National Science Foundation under Award Number 1400394. Any opinions, findings, and conclusions or recommendations expressed in this article are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Author information

Author notes

  1. Josephine V. Carstensen

    Present address: Department of Civil and Environmental Engineering, Department of Architecture, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA, 02139, USA

Authors and Affiliations

  1. Department of Civil Engineering, Johns Hopkins University, 3400 N Charles St, Baltimore, MD, 21218, USA

    Josephine V. Carstensen & James K. Guest

Authors
  1. Josephine V. Carstensen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James K. Guest
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Josephine V. Carstensen.

Additional information

Responsible Editor: Ole Sigmund

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carstensen, J.V., Guest, J.K. Projection-based two-phase minimum and maximum length scale control in topology optimization. Struct Multidisc Optim 58, 1845–1860 (2018). https://doi.org/10.1007/s00158-018-2066-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-018-2066-4

Keywords

Search

Navigation