Giant star seismology

Abstract

The internal properties of stars in the red-giant phase undergo significant changes on relatively short timescales. Long near-uninterrupted high-precision photometric timeseries observations from dedicated space missions such as CoRoT and Kepler have provided seismic inferences of the global and internal properties of a large number of evolved stars, including red giants. These inferences are confronted with predictions from theoretical models to improve our understanding of stellar structure and evolution. Our knowledge and understanding of red giants have indeed increased tremendously using these seismic inferences, and we anticipate that more information is still hidden in the data. Unraveling this will further improve our understanding of stellar evolution. This will also have significant impact on our knowledge of the Milky Way Galaxy as well as on exo-planet host stars. The latter is important for our understanding of the formation and structure of planetary systems.

1 Introduction

Stars are bodies formed by baryonic mass. They are an important source of electromagnetic radiation in the universe allowing for studies of many phenomena, from distant galaxies to the interstellar medium and extra-solar planets. However, due to their opacity it is not trivial to study the internal structure of stars (Eddington 1926). The only way to probe and study the internal stellar structure directly is through global stellar oscillations. Many stars across the Hertzsprung–Russell (HR) diagram oscillate (driven by different mechanisms), which allows for in-depth studies of stars and stellar evolution.

1.1 History

Asteroseismology, the study of global properties of stars and their internal structure through their global intrinsic oscillations, is already more than a century old. An early remarkable result was obtained for Cepheids revealing the period–luminosity relation (Leavitt and Pickering 1912), which played an important role in measuring distances of galaxies and star clusters and ultimately the expansion of the universe. Observations of pulsators which display large (photometric) variations have been ongoing ever since. These stars include, among others, Cepheids, high amplitude $\delta$ Scuti stars, RR Lyrae stars, white dwarfs and Miras. An early result for which asteroseismic observations and stellar modelling were inconsistent was presented by Petersen (1973) on double-mode Cepheids. He showed that stellar masses inferred from the periods and period ratios were inconsistent with the location of the stars in the HR diagram as predicted by stellar evolution models. This problem motivated a revision of stellar opacity tables which led to very good agreement between the models and the observations (e.g., Moskalik et al. 1992). Despite the long-term research on such bright large amplitude oscillators there are still open questions concerning their oscillations (e.g., Blazkho effect, Blažko 1907) and internal properties. For recent reviews on classical oscillators, see, e.g., Balona (2010), Handler (2013) and Szabó et al. (2015) and references therein.

Lower-amplitude oscillations were not detected for several more decades. In the 1960s, oscillations were first discovered in the Sun (Leighton et al. 1962). Subsequent observations provided details of the solar interior and constraints for general stellar modelling beyond that previously possible (Christensen-Dalsgaard et al. 1996; Christensen-Dalsgaard 2002). Seismology was pivotal in the solar neutrino problem (Bahcall 1972; Trimble and Reines 1973) and confirmed that the solution lies within particle physics (Elsworth et al. 1990a). Through sensitive neutrino detections, McDonald et al. (2001) later showed that low-energy neutrinos do indeed change flavour. The Nobel Prize 2015 for physics was awarded for this discovery. Unfortunately, our understanding of the Sun remains incomplete. The ‘new solar abundances’ (Asplund 2005; Asplund et al. 2009) result in a solar structure that deviates much further from that obtained from the oscillations (Bahcall et al. 2005; Guzik 2008; Basu and Antia 2008, 2013) as compared with the ‘old solar abundances’ (Grevesse and Noels 1993; Grevesse and Sauval 1998). Additionally, the 11-year solar activity cycle discovered by Schwabe (1843) and visible in the solar oscillations (Elsworth et al. 1990b; Howe et al. 2002; Hathaway 2015) is not fully understood. This includes dynamo processes involving interaction between rotation and convection, restructuring the magnetic field between the toroidal and poloidal components, in a manner that is yet to be resolved. This also gives rise to surface manifestations such as sunspots when flux tubes break through the solar surface (e.g., Charbonneau 2014; Cameron and Schüssler 2015). Additionally, the reasons for the long solar minimum between cycle 23 and 24 are still subject of discussion (Basu et al. 2012; Basu 2013; Jiang et al. 2015). Furthermore, oscillations sensitive to the activity suggest the presence of a 2-year cycle in addition to the 11-year cycle (Broomhall et al. 2012) which is yet to be understood.

The road to the detection of low-amplitude oscillations in stars other than the Sun was paved by radial-velocity measurements—much like the variations used to discover pulsations in the Sun. Ground-based spectroscopic surveys first identified excess oscillation power in Arcturus (Smith et al. 1987) and Procyon (Brown et al. 1991) as well as the first evidence for individual modes in $\eta$ Bootis (Kjeldsen et al. 1995, 2003), $\alpha$ Centauri A (Bouchy and Carrier 2001), $\xi$ Hydrae (Frandsen et al. 2002) and $\mu$ Her (Bonanno et al. 2008). These seminal discoveries relied on single-site spectroscopic programs and inspired longer multi-site spectroscopic campaigns on nearby bright stars, such as $\alpha$ Cen A (Bedding et al. 2004; Butler et al. 2004) and B (Carrier and Bourban 2003; Kjeldsen et al. 2005), $\beta$ Hydrae (Bedding et al. 2007), $\nu$ Indi (Carrier et al. 2007), $\eta$ Serpentis (De Ridder et al. 2006) and Procyon (Hekker et al. 2008; Arentoft et al. 2008; Bedding et al. 2010b). Complementary photometric multi-site campaigns were also pursued (Stello et al. 2006a, 2007) and although both strategies revealed detailed oscillation patterns, they were yet unable to fully constrain the internal structure of the stars (Miglio and Montalbán 2005; Huber et al. 2011a).

Space-based instruments contributed to the progression of the field, with the star-tracker of the WIRE (Wide field InfraRed Explorer) mission (Buzasi 2002; Stello et al. 2008) and the Hubble Space Telescope (Gilliland 2008) both detecting low-amplitude oscillations in other stars. Soon after, the era of dedicated photometric space-based missions heralded a revolution for asteroseismology. Observations with the MOST mission (Microvariability and Oscillations of STars; Matthews et al. 2000) have contributed significantly to the revolution of red-giant asteroseismology (Barban et al. 2007; Kallinger et al. 2008a, b) and our understanding of classical pulsators such as $\delta$ Scuti stars (Casey et al. 2013), Slowly Pulsating B stars (SPB; Aerts et al. 2006; Jerzykiewicz et al. 2013) and rapidly oscillating Ap stars (Huber et al. 2008; Gruberbauer et al. 2011), as well as other pulsators such as pre-main sequence stars (Zwintz et al. 2013) and Wolf–Rayet stars (David-Uraz et al. 2012). CoRoT (Convection, Rotation and planetary Transits; Baglin et al. 2006) and Kepler (Borucki et al. 2008) have contributed greatly to the detection of pulsations in, and understanding of, many different kinds of stars such as massive stars (Belkacem et al. 2009; Degroote et al. 2010; Kurtz et al. 2015), RR Lyrae stars (Kolenberg et al. 2010) and sub-dwarf B stars (Østensen et al. 2014). Additionally, many break-through results have been reported on low-amplitude oscillations in Sun-like stars, subgiants and red-giant stars [see recent reviews by Chaplin and Miglio (2013), Hekker (2013), Mosser and Miglio (2016) and references therein].

1.2 Observations of stellar oscillations

Oscillations can be determined from timeseries data of either intensity variations or radial-velocity (RV) variations. Intensity variations reflect the brightness variations of a star induced by stellar oscillations. RV variations reveal the outward and inward movement of the stellar surface due to stellar oscillations through a Doppler shift of the spectrum. Part of a timeseries of intensity variations of a red-giant star observed with the Kepler space telescope is shown in the top panel of Fig. 1.

There are significant differences between intensity and RV variation measurements in the sense of their sensitivity to other intrinsic stellar features. For example, granulation (the visible effect of convection at a star’s surface) has higher amplitude in intensity variations than in RV variations, relative to the oscillations. Additionally, stars other than the Sun can be observed only in integrated light, causing cancellation effects that differ between intensity and RV observations. Since solar-like oscillations are mainly in the radial direction, RV observations with the projection onto the line of sight have a reduced sensitivity to the oscillations near the limb, increasing the response to modes of slightly higher degree and hence the diagnostic potential, compared with intensity observations.

Fig. 1

A 20-day long subset of a Kepler photometric timeseries (or light curve) of a red-giant star (KIC 9145955, top panel) and the Fourier power spectrum of the same star using a 1060-day long dataset (bottom panel). Note that for the Fourier power spectrum only the frequency range in which oscillations occur is shown here

To extract oscillation frequencies the timeseries data are most commonly transformed to frequency space by a Fourier transform. The resulting Fourier power spectrum reveals the oscillation frequencies as sharp peaks. An example of a Fourier power spectrum of a red-giant star observed with the Kepler space telescope is shown in the bottom panel of Fig. 1.

In this review we will discuss the internal structure and structure changes of subgiants and red giants including AGB stars in more detail (Sect. 2). These stars oscillate with intrinsically damped oscillations stochastically excited by convection in the outer layers of the stars, i.e., some of the convective energy is converted into energy of eigenmodes of the star. Consequently, these oscillations allow for observational investigations of internal stellar structure. As such oscillations are present in the Sun, they are referred to as solar-like oscillations. Solar-like oscillations are expected to be present in all stars with turbulent outer layers. In Sect. 3 we discuss the diagnostics that can be obtained from timeseries data and Fourier power spectra. An overview of stellar pulsation theory is presented in Sect. 4. We highlight ground-breaking results from the past years in Sect. 5. Finally, we discuss some promising prospects of asteroseismology and stellar structure of giants in Sect. 6.

2 Giant star evolution

Here we provide an overview of the internal structures of low- to intermediate-mass stars (roughly 0.8–10 $\hbox {M}_{\odot }$) in their respective evolutionary stages. We discuss the low-mass stars and intermediate-mass stars separately. Low-mass stars are those stars that ignite helium in the core under degenerate conditions. This occurs in stars with masses between $\sim$0.48 $\hbox {M}_{\odot }$ and $\sim$2 $\hbox {M}_{\odot }$. The lower limit is defined by the lower limit of the critical mass needed to ignite helium, while the upper limit depends on the chemical composition of the stars. If mass loss is small enough, and time long enough, all low-mass stars will go through the giant phases discussed below. At the current age of the universe ($\sim$14 Gyr) only stars with $M>0.8\,\mathrm{M}_\odot$ will have reached these late stages of evolution, unless substantial mass transfer in a binary system has taken place. Intermediate-mass stars are stars that do not develop a degenerate core and have a more gentle onset of core-helium burning. These stars range in mass between $\sim$2 $\hbox {M}_{\odot }$ and 8–10 $\hbox {M}_{\odot }$ depending on metallicity (Kippenhahn et al. 2012). For stars with degenerate cores the helium-core mass at ignition is the same, while this decreases for more massive stars without degenerate cores (see Fig. 2). To illustrate the internal structure changes of low- and intermediate-mass stars we show the paths of a $1~\hbox {M}_{\odot }$ and a $3~\hbox {M}_{\odot }$ model in the Herzsprung–Russel diagram (Fig. 3) and so-called Kippenhahn diagrams of these models in Figs. 4 and 5.

The description provided here is aimed to provide an insight into the many internal structure changes that a giant star undergoes. For a more complete picture and details of stellar evolution we refer the reader to Kippenhahn et al. (2012).

Fig. 2

Helium core mass at ignition vs. stellar mass for stellar models of solar metallicity computed with the MESA stellar evolution code (Paxton et al. 2011)

Fig. 3

Herzsprung–Russell diagram of a 1 $\hbox {M}_{\odot }$ and a 3 $\hbox {M}_{\odot }$ model. The insets show the “bump” of the 1 $\hbox {M}_{\odot }$ model (see Sect. 2.1.2) and the helium core burning phase for the 3 $\hbox {M}_{\odot }$ model (see Sect. 2.2.4). The models are computed using the MESA stellar evolution code (Paxton et al. 2011) with solar metallicity. The letters indicate different phases of evolution: A zero-age main-sequence; B $'$ core hydrogen mass fraction $\approx 0.05$, B start of thick shell burning; C maximum extent of thick shell (in mass); D start of thin shell burning; E maximum bump luminosity; F minimum bump luminosity; G tip of the red-giant branch; H end of helium-core burning, and correspond to the letters indicated in Figs. 4 and 5

Fig. 4

Kippenhahn diagram of a 1 $\hbox {M}_{\odot }$ model shown in Fig. 3. Regions where convection takes place are hatched. Regions where nuclear burning produces more than $10 \,\mathrm{erg\,g^{-1}\,s^{-1}}$ are shown in grey for hydrogen burning and in red in case of helium burning. The right panel shows a zoom of the late stages of evolution. The letters at the top indicate different stages of evolution corresponding to the phases indicated in Fig. 3

Fig. 5

Kippenhahn diagram of a 3 $\hbox {M}_{\odot }$ model as shown in Fig. 3. Regions where convection takes place are hatched. Regions where nuclear burning produces more than $10 \,\mathrm{erg\,g^{-1}\,s^{-1}}$ are shown in grey for hydrogen burning and in red in case of helium burning. The central panel shows a zoom of the subgiant and red-giant branch. The right panel shows a zoom of the late stages of evolution.The letters at the top indicate different stages of evolution corresponding to the phases indicated in Fig. 3

2.1 Low-mass stars ($M \lesssim 2~\hbox {M}_{\odot }$)

2.1.1 End of hydrogen core burning phase: end of main sequence

For stars with masses below 1–1.5 $\hbox {M}_{\odot }$ (depending on chemical composition) hydrogen (H) in the central regions fuse to helium via proton–proton (pp) chains under conditions of radiative energy transport. Conversely, stars with masses above this range develop a convective core on the main-sequence, with the CNO (Carbon–Nitrogen–Oxygen) catalytic reactions predominately responsible for the conversion of H into $^4$He. CNO burning takes place at higher temperatures (T) than proton–proton interactions. Additionally, the energy production ($\epsilon$) of CNO burning is more temperature-dependent than that of proton–proton chains ($\epsilon _\mathrm{CNO} \sim T^{17}$ vs. $\epsilon _\mathrm{pp} \sim T^4$; Iliadis 2007). The respective conditions in the core significantly impact the structure and evolution at the end of the main sequence and, therefore, the two regimes, i.e., stars with radiative cores and convective cores on the main sequence, are discussed separately.

Stars with radiative cores For stars with a radiative core the fusion of H to $^4$He is predominantly enacted via the pp chains. The increase in the mean molecular weight ($\mu$) resulting from hydrogen fusion affects hydrostatic equilibrium. To sustain pressure support to the overlying layers of the star the core must contract. This increases the temperature in the inner parts of the star, leading to an increase in the efficacy of energy transport and hence in the luminosity ($\sim$0.7% increase in brightness every 100 Myr in a 1 $\hbox {M}_{\odot }$ star). This is matched by a corresponding increase in the energy generation.

The gradual depletion of H from the radiative core generates a smooth transition to a chemically inhomogeneous structure with hydrogen burning in an extended shell around a growing inert degenerate helium core. Complete depletion of hydrogen in the centre marks the end of the main-sequence and the transition to the hydrogen shell burning phase.

Stars with convective cores There is a physical limit to which energy can be transported by radiation. The Schwarzschild criterion (Schwarzschild 1906) states that if the temperature gradient inside a star is too steep, convection will take over as the primary means of energy transport. In addition to efficient energy transport, the associated bulk mass motions of convection ensure that the composition of any convective region is well mixed. In a more formal sense convection is activated once the radiative temperature gradient exceeds the adiabatic temperature gradient (Schwarzschild 1906).

The Schwarzschild criterion defines the likely regimes in stellar interiors in which convection will develop. The first regime is where there is a large energy flux, the second where the stellar material is opaque to photons (such as in ionization regions of abundant elements) and energy transfer by radiation is, therefore, inefficient. In stars with $M \gtrsim 1.1$ $\hbox {M}_{\odot }$ the central conditions are sufficient for the activation of the CNO cycle, reactions that are highly temperature dependent. A consequence for these stars is that the burning region becomes ever more centrally concentrated, and the large energy flux and steep temperature gradient drive a convective core.

An alternative to the Schwarzschild criterion is the condition derived by Ledoux (1947) which, in addition to the temperature gradients, takes into account the spatial variation of the mean molecular weight. In some stars, particularly those with $M \gtrsim 2.25$ $\hbox {M}_{\odot }$, a composition gradient may develop outside the shrinking (Ledoux) convective core. Application of the Schwarzschild criterion would render this region convectively unstable; however, according to Ledoux, the presence of a molecular weight gradient can have a stabilizing effect. The true behaviour of material in the stellar interior under these circumstances remains unclear (Gabriel et al. 2014). However, in stellar evolution codes some form of slow (slow compared to convection) mixing is applied in these regions in order to match various observational constraints (see, e.g., Lattanzio 1983; Langer et al. 1985). This slow mixing process can also be referred to as semi-convection.

In stars below $\sim$ 2$\,\mathrm{M}_\odot$ with a convective core, the core grows for most of the main-sequence lifetime. This is caused by the increasing contribution to the energy production from the highly temperature-sensitive CNO cycle, as oxygen is gradually converted to nitrogen in parts of the cycle. A further extension of the mixed core can be caused by material that approaches the boundary of stability with momentum and overshoots into the radiative layer. This process, convective-core overshoot, extends the burning region and brings in fresh H-rich fuel prolonging the main-sequence evolution. As with a radiative core the decrease in hydrogen abundance with nuclear burning and the resulting increase in $\mu$ cause an increase in luminosity. However, with a convective core this depletion takes place uniformly in an extended region. When hydrogen is nearly depleted in this region ($X_\mathrm{core} \approx 0.05$, B$'$ in Fig. 3) the star contracts to maintain the energy production. This contraction leads to an increase in effective temperature ($T_\mathrm{eff}$) and luminosity ($\mathcal L$) until hydrogen is completely depleted in the centre (the “hook” in the Hertzsprung–Russell diagram: B$'$-B in the 3$\hbox {M}_{\odot }$ track in Fig. 3). At this point the central burning and convection cease abruptly. This is the end of the main-sequence phase.

2.1.2 Hydrogen shell burning phase: subgiants and red-giant branch stars

Subgiants Without the central nuclear reactions the star must find an alternative way to generate energy to compensate for the energy loss from the core. The star turns to another available source of energy in core contraction and the corresponding release of gravitational potential energy. For stars with $M \lesssim 1.1$ $\hbox {M}_{\odot }$ the central density is large enough that electron degeneracy dominates and provides significant pressure support. Therefore, low-mass stars can remain in thermal and hydrostatic equilibrium with a degenerate, isothermal core as they smoothly transition to hydrogen-shell burning. As a consequence the contraction phase and transition to giant is gradual and the timescale much longer compared with the higher-mass counterparts (see Sect. 2.2.2). Shell burning is initially in the form of an extended burning region outside the core. Slowly, the core mass increases as the ashes of hydrogen-shell burning are deposited on the He core. As the core is degenerate this corresponds to a reduction in radius, accompanied by an expansion of the envelope. The boundary where contraction changes to expansion is located near the hydrogen-burning shell. This behaviour is typical of a more general exchange in evolving stellar models between contraction and expansion at shell-burning sources, referred to as the mirror principle.

The shell-burning region, dominated by the CNO cycle, is confined to increasingly narrow mass. The envelope expands and cools while the star evolves from the main sequence towards the Hayashi line. The Hayashi line is the locus in the Herzsprung Russell diagram of fully convective stars, where a star cannot decrease its temperature further (otherwise it cannot maintain hydrostatic equilibrium). Thus, upon approaching the Hayashi line further increase of the radius causes an increase in luminosity. A large convective region develops in the envelope due to the increased photospheric opacity at lower temperatures (contribution from H$^-$ ions). The star is now on the red-giant branch, just on the hot side of the Hayashi line with a large convective envelope on top of a small radiative core.

Red-giant branch stars On the red-giant branch, H-burning ashes are deposited on the degenerate core as the shell burns and moves outwards. Due to the degenerate conditions an increase in mass results in contraction and heating of the inert helium core. This also heats the hydrogen-burning shell, which reacts to the higher temperatures by compressing the burning region and increasing the energy generation. The density contrast becomes so large that the envelope and core are essentially decoupled. Therefore, the hydrogen burning in the shell is completely determined by the properties of the helium core and not by the envelope. Hence, the luminosity of the star is now related to the mass of the inert degenerate helium core and does no longer depend on the total mass of the star. Therefore, stars with the same core mass, but a spread in total mass, follow the same path in the Hertzsprung–Russell diagram.

First dredge-up The convective envelope penetrates deep into the star to the regions where the chemical composition has been altered by nuclear processes that took place during the main sequence. The processed material is then subsequently transported to the surface. This is the first “dredge-up” phase, i.e., chemical elements from deeper layers are dredged up towards the surface of the stars: for example, the $^{12}$C/$^{13}$C ratios are lowered. The convective region reaches a maximum depth in mass and recedes because of the advance of the hydrogen-burning shell, leaving behind a chemical (mean molecular weight) discontinuity.

Bump The hydrogen shell, in which burning takes place, moves gradually outwards (in mass) while the helium-core mass steadily increases. In a simplified picture the luminosity decreases when the hydrogen-burning shell reaches the chemical discontinuity left behind by the deepest extent of the convective envelope due to the decrease in the mean molecular weight at the chemical discontinuity, causing the luminosity to decrease again following $\mathcal {L}\propto \mu ^7M_\mathrm{core}^7$ (Refsdal and Weigert 1970). After this the core mass keeps increasing at constant $\mu$ causing a resumption of the increase in the luminosity.

In fact, the situation is more complex with the luminosity beginning to decrease prior to the shell burning through the discontinuity. As discussed by Christensen-Dalsgaard (2015) the reason is that the decrease in $\mu$ above the discontinuity starts affecting the hydrostatic structure, and hence the temperature, within and above the hydrogen-burning shell before it reaches the discontinuity. This causes the decrease in the luminosity. This zig-zag in the evolution path is the so-called RGB-bump (see right inset in Fig. 3). The bump is visible for stars up to about 2.2 $\hbox {M}_{\odot }$ as an over-density of stars in stellar clusters at the bump luminosity. For more massive stars helium-core burning starts before the hydrogen-burning shell approaches the composition discontinuity left behind by the first dredge-up. In these cases a bump-like structure is not present on the red-giant branch.

High-luminosity red-giant branch stars The process on the RGB continues till the core reaches a temperature of $\sim$10$^8$ K (at a core mass of $\sim$0.45 $\hbox {M}_{\odot }$) at which helium is ignited in a thermal run-away process. This is the so-called helium flash. We note here that additional mixing processes, such as thermohaline mixing (e.g., Eggleton et al. 2006, 2008; Charbonnel and Zahn 2007; Charbonnel and Lagarde 2010; Angelou et al. 2011, 2012), are necessary to include in models of stars ascending the red-giant branch to match the observed chemical compositions of these stars.

2.1.3 Onset of helium burning: He-flash

At a temperature of $\sim$10$^8$ K in the inert helium core, helium fusion can be ignited in a triple-alpha process.¹ In the highly degenerate core the pressure does not depend on the temperature and hence there is no thermostatic control to expand and cool the core. The onset of (unstable) burning in these degenerate conditions results in a thermal runaway process creating for a very short time (of order a few hours!) an enormous overproduction of nuclear energy. This energy is absorbed by the expansion of non-degenerate layers outside the degenerate core and does not reach the stellar surface.

The onset of helium fusion takes place at the location of maximum temperature. The temperature is generally at its maximum in a concentric shell around the centre of the degenerate core due to gravo-thermal energy and neutrino losses. Stellar models predict that the first main helium flash is followed by a series of sub-flashes. Each subsequent sub-flash is located closer to the centre such that eventually the degeneracy in the centre is completely lifted and the star is back in equilibrium with helium burning in a convective core. As neither the energy of the flash, nor the energy of the subflashes reaches the stellar surface, the existence of sub-flashes in real stars is not observationally confirmed, i.e., they could be artefacts of stellar models.

2.1.4 Helium core burning phase: red clump

The star has now two sources of energy generation: hydrogen burning in a shell around the core producing helium, while in the core helium is consumed to produce carbon and oxygen. Due to the expansion and accompanying decrease in density and temperature of the hydrogen-burning shell after the helium flash it generates less energy (this is, however, still the main source of energy generation in the star). Therefore, the luminosity decreases while the core expands and the envelope contracts (mirror principle, see Sect. 2.1.2). The star is back in equilibrium and settles in the red clump.

All stars that have gone through a helium flash have very similar core masses and hence very similar luminosities on the horizontal branch. Therefore, all stars that go through a He-flash end up at a very similar spot in the Herzsprung–Russell diagram, with only some dependence on $T_\mathrm{eff}$ owing to their total masses (with lower masses being slightly hotter) and composition (stars with higher contents of heavier elements are cooler).

Properties of the convective core The helium core burning stars have a central convective core that becomes enriched in carbon and oxygen during helium burning. The opacity in the temperature–density regime present in the core is dominated by free–free transitions and increases with increasing carbon and oxygen abundance. This causes an increase in the radiative temperature gradient in the core leading to a discontinuity in the radiative temperature gradient at the boundary between the convective core and the radiative envelope. In models with no mixing beyond the convective core the nuclear burning gives rise to an increasing composition discontinuity at the edge of the core. Convective overshoot and/or semiconvection increases the size of the core and, depending on the implementation, may lead to a smooth composition profile or further discontinuities in composition (see Constantino et al. 2015 for an overview of these processes). As discussed in Sects. 4.2.4 and 4.2.5 the detailed properties of the composition profile can have a strong effect on the behaviour of the oscillations of the star. Towards the end of the central helium burning sudden mixing in the models between the carbon-oxygen-rich core and the overlying helium-rich layers may occur at the edge of the core. This leads to an abrupt increase in the helium content of the core and a loop in the Herzsprung–Russell diagram. These are so-called breathing pulses. The occurrence and appearance of these breathing pulses in stellar models depend on the criterion used for convection and may only be an artefact of the way convection is included in models and may not be present in real stars.

After some time helium is exhausted in the convective core and the star will undergo some rapid evolution towards a shell-burning phase with burning taking place in a helium shell and hydrogen shell surrounding the core. This phase of evolution is the asymptotic giant branch (AGB).

2.1.5 Helium and hydrogen shell burning phase: asymptotic giant branch

In the low-mass regime, the asymptotic giant branch is characterized by an inert carbon–oxygen core surrounded by two burning shells of which the helium shell is thermally unstable. In this phase a star is again moving in the Herzsprung–Russell diagram towards the Hayashi line and at the same time increasing its luminosity and radius. In the early AGB (E-AGB) phase hydrogen is burning outwards and the temperature in this shell drops. Consequently, the hydrogen-burning shell supplies only a small fraction of the energy for some time. However, as the temperature in the hydrogen shell increases again in between thermal pulses (see below) burning is recovered and dominates the energy production.

Thermal pulses As the star ascends the asymptotic giant branch, the helium-burning shell narrows while providing most of the energy to the stellar surface. Eventually the helium-burning shell advances in mass towards the hydrogen-burning shell, and their separation, the inter-shell region, becomes too narrow. This, along with the high-temperature dependence of the helium-burning reactions, results in a thermal runaway and the onset of the thermally pulsing (TP) AGB phase.

The thermally pulsing AGB phase is characterized by long periods of quiescent hydrogen-shell burning, followed by instabilities of the helium-burning shell (Schwarzschild and Härm 1965; Weigert 1966). Each instability or ‘helium-shell flash’ grows in amplitude for the first 5–10 pulses before approaching a maximum in helium luminosity. As per Iben (1981) we describe the TP-AGB cycle by four distinct phases:

• On phase: the sudden deposition of energy from the shell flash drives an inter-shell convection/burning zone cycling the products of the triple-alpha process into the region below the hydrogen shell.

• Power down phase: although the carbon-oxygen core is highly electron degenerate the shell-flash instability occurs in a non-degenerate region of the stellar interior. The energy generated by the flash helps drive expansion of the star and thereby extinguishing the hydrogen-burning shell. The flash is able to generate luminosities of the order 10$^7$ or 10$^8$ solar luminosities. However, due to the expansion this increase in luminosity is not manifested at the surface.

• Third dredge-up²: As the star expands and cools, convection is able to penetrate beyond the hydrogen-burning shell into regions homogenised by the inter-shell convection zone. Hence the products of He burning are mixed into the envelope where they can be observed at the stellar surface.

• The inter-pulse phase: eventually the helium-burning luminosity drops below the surface luminosity and the outer regions can once more contract. The hydrogen shell can reignite where it provides most of the luminosity until once again the interior conditions arise for a successive helium-shell instability. The inter-pulse phase lasts for $\approx$10$^4$ years.

Third dredge-up Third dredge-up plays an important role in the chemical enrichment of the galaxy. The significant amount of carbon produced in these stars and brought to the stellar surface is in some cases able to raise the C/O abundance ratio to become larger than unity. In addition TP-AGB stars have been identified as a site of the s-process nucleosynthesis,³ which is responsible for the production of half of the elements beyond iron. Through efficient mass-loss processes these elements are expelled into the interstellar medium.

Post-thermally-pulsing AGB phaseAt some point, the envelope mass is insufficient to allow TP to continue. When the envelope mass drops below about a few ($\sim$5) per cent of the total mass, the envelope contracts and shell burning extinguishes: the star becomes a white dwarf. This is the post-AGB phase. The number of thermal pulses the star experiences and the final white dwarf mass depend on the competition between mass loss and core growth in the AGB phase. For extensive reviews of the AGB stars we refer to Iben and Renzini (1983), Herwig (2005) and Karakas and Lattanzio (2014).

2.2 Intermediate-mass stars ($M\sim 2{-}10~\hbox {M}_{\odot }$)

2.2.1 End of hydrogen core burning phase: end of main sequence

Intermediate-mass stars have a convective core on the main sequence and show the same behaviour as low-mass stars with a convective core as described in Sect. 2.1.1.

2.2.2 Hydrogen shell-burning phase: subgiants and red-giant branch stars

After a short resettling at the end of the main sequence, hydrogen-shell burning intensifies in the region around the core. As for the low-mass star, this shell burning steepens the hydrogen profile at the edge of the He-core leading to a narrowing of the burning shell when the lower hydrogen tail has been consumed. The core contraction and envelope expansion below and above the shell burning layer, respectively, (mirror principle) increase the radius of the star.

Hertzsprung gap

In intermediate-mass stars the core is non-degenerate following central hydrogen exhaustion. Schönberg and Chandrasekhar (1942) demonstrated that there is a maximum relative core mass that an isothermal, non-degenerate core can have whilst maintaining hydrostatic and thermal equilibrium and deriving all its energy from a nuclear burning shell source. Without electron degeneracy to supply additional pressure support, contraction on a Kelvin–Helmholtz timescale will develop when the core mass exceeds this Schönberg–Chandrasekhar limit, so that the star can maintain equilibrium between the energy it generates in the interior and that which it loses at the surface. Whether stars in the intermediate-mass range reach the Schönberg–Chandrasekhar limit depends on their hydrogen-exhausted core mass. This mass depends on the amount of overshoot the convective core experienced on the main sequence. Upon reaching the Schönberg–Chandrasekhar limit, stars cross the Hertzsprung–Russell diagram rapidly and move onto the red-giant branch. The fast timescales involved in this phase of evolution leads to a dearth of intermediate-mass stars observed in this region of the HR diagram: the so-called Hertzsprung gap.

At the bottom of the red-giant branch, intermediate-mass stars develop a deep outer convective region to transport energy more efficiently and prevent the star from cooling beyond the Hayashi line. This deepening of the convective envelope causes a change in the surface chemical composition due to the first dredge-up (Sect. 2.1.2). At the same time the core continues to contract and heat. When the core temperature has increased to about $10^8$ K, helium is ignited. We note that the bump (Sect. 2.1.2) is only present on the red-giant branch for stars with masses roughly below 2.2 $\hbox {M}_{\odot }$. More massive stars ignite helium before the hydrogen-burning shell reaches the chemical discontinuity left behind by the first dredge-up.

2.2.3 Onset of helium burning: non-degenerate ignition

In the non-degenerate regime, the luminosity at which helium ignites is a monotonically increasing function of the core mass. Because the pressure and temperature are related, the thermostatic feedback allows intermediate mass stars to gently ignite helium in their core.

2.2.4 Helium core burning phase: secondary clump

Stars in the secondary clump have two sources of burning. Firstly, helium burning that produces carbon and oxygen is present in the core. Like the CNO reactions, energy production via the triple-alpha process is highly temperature dependent. The reactions are concentrated towards the centre and give rise to a convective core. Burning proceeds quiescently with the core growing as a function of time. Secondly, hydrogen burning is taking place in a shell around the core. The latter provides most of the total energy output as a rather small release of nuclear energy is sufficient in the core to compensate for the energy loss from the core and prevent the core from contracting. As the core masses of these stars can be different when they ignite helium, these stars do not “clump” as the red-clump stars. Instead they form the secondary clump at lower luminosities and effective temperatures. Additionally these stars loop through the red-giant region during central helium burning [see left inset in the HR diagram (Fig. 3), where the stars leave the Hayashi line to become hotter and subsequently move back towards the Hayashi line]. The temperature range that the loops cover increases with increasing stellar mass. The cause of these loops lies in the chemical composition profile in the central regions of stars that had a convective core on the main-sequence.

2.2.5 Helium and hydrogen shell burning phase: asymptotic giant branch

When helium burning terminates in the core the burning continues in two shells around the inert carbon–oxygen core. For stars with masses of 4–8 $\hbox {M}_{\odot }$ the hydrogen shell is at best barely active. This allows the convective envelope to penetrate down reaching layers through which the hydrogen shell has burned (similar as for low-mass stars on the red-giant branch). This so-called second dredge-up brings processed material that is generated by helium and hydrogen burning such as carbon, oxygen, nitrogen and helium to the surface. For all stars that do not ignite carbon in their core, the AGB proceeds in roughly the same fashion as for low-mass stars (see also Sect. 2.1.5). They experience episodic thermal pulses and efficient mass loss until they lose most of their envelope and become a white dwarf. However, their s-process nucleosythesis will differ greatly depending on stellar mass.

2.3 Why do stars become giants?

The description written above represents our current understanding of stellar evolution based on stellar models and observations. However, the reason why stars become red giants is actually not understood. The mirror phenomenon mentioned before seems to play an essential role in stars to become a red giant. However, it is not understood what physical mechanism(s) drive the mirror nor what other physical mechanisms are essential in a star to become a giant.

A number of studies have investigated the question ‘Why do stars become giants?’ proposing reasons related to central gravitational field (Hoppner and Weigert 1973; Weiss 1983), the effective equation of state (Eggleton and Cannon 1991; Eggleton et al. 1998), gravothermal instability in the core (Iben 1993), thermal instabilities in the stellar envelope (Renzini et al. 1992) and mean molecular weight gradient (Stancliffe et al. 2009). Some of these studies have been met with fierce opposition whilst others have devised conditions that were later shown to be necessary but not sufficient in all stars. Currently, it is clear that a strong gravitational field and a mean molecular weight gradient play an important role (Stancliffe et al. 2009) in stars for them to become a giant. For an extensive overview regarding the literature addressing ‘Why do stars become giants?’ we refer the reader to Sugimoto and Fujimoto (2000), while Faulkner (2005) provided a detailed analytical investigation inspired by the scientific legacy of Fred Hoyle.

2.4 Rotation

In the description of the internal structure of stars provided here, rotation has not been taken into account. However, it is plausible that all stars rotate as the clouds of gas and dust that they are formed from contain angular momentum. For slowly rotating stars it is generally assumed that second-order effects can be neglected and that the hydrostatic structure of the star is not affected. For low-mass stars on the main sequence and more evolved stars this will generally be the case. Intermediate-mass stars on and shortly after the main sequence may, however, be faster rotators before they slow down under the influence of magnetic braking. The rotation can have a strong impact on the thermal structure and radiative transfer, possibly inducing meridional flows and instabilities affecting mixing processes. Additionally, the shape of the star may become aspherical. Work on including rotation in stellar structure models has been performed by for example Palacios et al. (2006), Eggenberger et al. (2010), Eggenberger et al. (2012), based on earlier work by Zahn (1992). A critical issue is the treatment of the evolution of the internal angular velocity, including transport of angular momentum, which currently fails to reproduce the seismically inferred internal rotation (see Sect. 5.5). One of the main conclusions for red-giant stars so far is that rotationally induced mixing and meridional circulation do not provide enough mixing of chemicals to explain the abundance anomalies observed around the bump luminosity of globular clusters (see also Sect. 6). For a detailed analysis of the evolution of rotating stars, see Maeder (2009).

3 Seismic diagnostics

Seismic diagnostics are by definition obtained from a signal that varies over time. In the context of oscillating stars, timeseries data (see top panel of Fig. 1) are most often taken from photometric fluxes or radial velocities (see Sect. 1). Some stellar parameters can be directly determined from the timeseries data. However, most seismic diagnostics are obtained from a Fourier transform (Figs. 1, 6, 7) of the timeseries data.

Important characteristics of the timeseries data are the total length or timespan of the data (T) and the typical time sampling ($\delta t$). These translate in Fourier space in the frequency resolution $\delta \nu =1/T$, and the highest frequency at which one can reliably obtain results, i.e., the Nyquist frequency $\nu _\mathrm{Nyq} = 1/(2\delta t)$. The Nyquist frequency is a hard limit for evenly sampled timeseries. However, astrophysical datasets are usually not exactly evenly sampled, which allows for measurements with higher frequencies, so-called super-Nyquist determinations (Murphy et al. 2013). It was shown by Eyer and Bartholdi (1999) that in cases of serious oversampling or undersampling the Nyquist frequency can be derived as $\nu _\mathrm{Nyq} = 1/(2p)$ with p being the greatest common divisor of all differences between consecutive observation times. In practise a realistic estimate of $\nu _\mathrm{Nyq}$ in the case of unevenly sampled data is to use the inverse of twice the median of all time differences between two consecutive measurements in the entire timeseries (Aerts et al. 2010).

The power in Fourier transforms is commonly normalized using Parseval’s theorem. This theorem states that the integral of the square of a function is equal to the integral of the square of its transform, i.e., the total power in the Fourier transform is equal to the total of the squared flux variations (for intensity) in the timeseries. Alternatively, Fourier transforms can be normalized using ‘peak-scaling’ in which the Fourier transform is normalized to recover the full sine-amplitude of an injected signal. The power can either be computed per bin, i.e., the frequency resolution, or per frequency unit. In the latter case it is the power density that is shown which has the advantage that its value does not depend on the frequency resolution.

The fact that integration times of the observations are not infinitely short causes apodization $\eta _a$. This affects the power at all frequencies with the largest impact close to the Nyquist frequency. The apodization can be accounted for by multiplying the power by $\eta _a^2$, where $\eta _a^2$ is defined as⁴:

$$\begin{aligned} \eta _a^2= \mathrm{sinc}^2 \left[ \pi /2\left( \frac{\nu }{\nu _\mathrm{Nyq}}\right) \right] . \end{aligned}$$

(1)

Gaps in the timeseries data impact on features in the power spectrum. This window function, i.e., the pattern of observations and gaps, causes alias frequencies (or sidelobes) to occur at $n(1/T_\mathrm{gap})$, with n an integer and $T_\mathrm{gap}$ the typical time between gaps (for instance, one day for ground-based single-site observations).

When the data quality between the observations varies significantly, such as can happen with ground-based spectroscopic (multi-site) campaigns, one can opt to compute a weighted Fourier transform. This weighting can be performed to optimize the noise level, but also to optimize the window function and reduce the sidelobes caused by gaps (Arentoft et al. 2009).

For a crash course on data analysis in asteroseismology including the statistics and uncertainties of timeseries data we refer the reader to Appourchaux (2014).

3.1 Variance and typical timescale in timeseries data

For stars with a convective outer layer, such as low-mass dwarfs, subgiants and red giants, the variations in the flux are dominated by granulation and oscillations. As both granulation, i.e., visible pattern of convection, and oscillations depend on surface gravity it has been possible to calibrate relations between the variance in the flux and surface gravity (Hekker et al. 2012; Bastien et al. 2013) as well as between the typical timescales present in the timeseries data and surface gravity (Kallinger et al. 2016).

3.2 Background signal in Fourier spectrum

For stars with a convective outer layer a frequency-dependent background signal is present in the Fourier spectrum. This background consists of stellar intrinsic phenomena including activity features, such as spots and flares that are observable features of magnetic fields, rotation and granulation. In addition to the intrinsic stellar background signal an observed power spectrum also includes white noise and instrumental effects. These instrumental effects may include, for instance, degrading of CCDs, but also incidental cosmic ray hits or telescope jitter.

All these features together form a background on top of which the oscillation modes are visible as relatively narrow peaks. This background can be fitted with the following function (e.g., Harvey 1985; Kallinger et al. 2014):

$$\begin{aligned} P(\nu )=P'_n+\eta _a(\nu )^2\sum _i \frac{ a_i^2/b_i}{1+(\nu /b_i)^{c_i}}, \end{aligned}$$

(2)

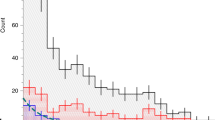
where $P'_n$ is the white noise; $a_i$, $c_i$ and $b_{i}$ are for the i-th background component the rms amplitude, exponent, and the frequency at which the power of the component is equal to half its value at zero frequency (the characteristic frequency), respectively. The factor $\eta _a^2$ is the apodization defined in Eq. (1). The exponent $c_{i}$ provides a measure of the temporal correlation of the signal and determines the slope of the decay of the background in Fourier space (Mathur et al. 2011b). The number of functions (i) needed depends on the presence of activity, (super)granulation, or faculae (bright spots) on the star. Based on state-of the-art data, a two-component fit is in most cases necessary and sufficient (Karoff et al. 2013; Kallinger et al. 2014). An example of a background fit is shown in Fig. 6.

Fig. 6

Fourier power density spectrum of a red giant (KIC 9145955) in log-log space. The solid red line shows the background fit with the different background components shown with dashed lines. The white-noise level is indicated with a dotted-dashed line

3.3 Oscillation signal

Oscillations establish themselves as a series of relatively narrow peaks on top of the background described in the previous subsection. The oscillations are confined to a limited range in frequency. Within this frequency range the individual modes of stochastic oscillations have a Lorentzian shape with a width that represents the lifetime of the mode and a height determined by the intrinsic amplitude of the mode and geometrical effects. In the limit of infinite lifetime, i.e., an oscillation that appears coherent over the timespan of the observations, the mode is unresolved and takes the form of a sinc$^2$ function (see footnote 4) in power. Each oscillation mode is characterized by its quantum numbers: radial order n, related to the number of nodes in the radial direction (cf. Sect. 4.2.1); degree l, the number of nodal lines on the surface and azimuthal order m, the number of nodal lines crossing the stellar equator. The frequencies, width and amplitudes of the individual modes as well as the overall shape of, and patterns in, the oscillation power excess have valuable diagnostic power. Here, we first discuss the global features of the oscillation power excess, i.e., single measures that provide a diagnostic. We subsequently provide more details regarding the individual frequencies and the diagnostics that can be extracted from them.

In red giants all non-radial modes have a mixed character, with a gravity-mode behaviour (buoyancy is the restoring force) in the core and an acoustic behaviour (pressure is the restoring force) in the envelope. Observationally, the acoustic behaviour is most prominent, and we first discuss the related observed properties. Afterwards we consider the more profound aspects of the star that are revealed by the mixed nature of the modes.

Fig. 7

Oscillations in the background-corrected power density spectrum of KIC 9145955. The numbers indicate the degree (l) of the modes (see Sect. 3.4). The red dashed curve shows a heavily (triangular) smoothed power spectrum indicating the power excess envelope of the oscillations. The amplitude of the smoothed power spectrum is enhanced for visual purposes

3.3.1 Frequency of maximum oscillation power ($\nu _\mathrm{max}$)

All solar-like oscillations in a star form together a bell-shaped power excess above the granulation and background signal centred around a specific frequency (see Fig. 7, where the amplitude of the power excess envelope is enhanced for visual purposes). This specific frequency is often referred to as frequency of maximum oscillation power or $\nu _\mathrm{max}$. This frequency has been linked empirically to the acoustic cut-off frequency

$$\begin{aligned} \nu _\mathrm{ac}=\frac{c}{4\pi H_p} \end{aligned}$$

(3)

(Lamb 1932, using the approximation for an isothermal atmosphere); here c is the adiabatic sound speed and $H_p$ is the pressure scale height. (See Eq. (25) and subsequent text for a theoretical explanation of the acoustic cut-off frequency.) It can be shown that $\nu _\mathrm{max}$ provides a direct measure of the surface gravity (g) when the effective temperature ($T_\mathrm{eff}$) is known (e.g., Brown et al. 1991; Kjeldsen and Bedding 1995):

$$\begin{aligned} \nu _\mathrm{max} \propto \frac{g}{\sqrt{T_\mathrm{eff}}} \propto \frac{M}{R^2\sqrt{T_\mathrm{eff}}}, \end{aligned}$$

(4)

with M and R the stellar mass and radius, respectively. A theoretical basis for this relation has been investigated by Belkacem et al. (2011) and is discussed further in Sect. 4.3.

The value of $\nu _\mathrm{max}$ can be estimated as the centroid of a Gaussian fit to the oscillation power excess (Kallinger et al. 2012). Alternatively, one can use the peak of the oscillation power excess in the smoothed power spectrum (Huber et al. 2009) or the first moment of the area under the smoothed power envelope (Hekker et al. 2010b). All these methods use slightly different, but equally valid, definitions of $\nu _\mathrm{max}$ and therefore can provide different values. Comparisons between values obtained with different methods show that this difference is generally within a few per cent (Hekker et al. 2011, 2012; Verner et al. 2011).

As stated above, for high-precision data such as the Kepler timeseries the main sources of the signal in the timeseries data are the granulation and the oscillations. The amplitudes of these signals are correlated with $\nu _\mathrm{max}$, and, therefore, the frequency of maximum oscillation power can also be directly estimated from the variance in the timeseries (Hekker et al. 2012).

3.3.2 Frequency pattern

Following asymptotic theory (Tassoul 1980, and Sect. 4.1), acoustic oscillation modes (pressure as restoring force) of solar-like oscillators follow a distinct pattern:

$$\begin{aligned} \nu _{n\,l} \simeq \Delta \nu \left( n+\frac{l}{2}+\epsilon \right) -d_{n\,l} , \end{aligned}$$

(5)

with $\nu$ cyclic oscillation frequency, $\Delta \nu$ large frequency separation (Sect. 3.3.3), $\epsilon$ a phase term (Sect. 3.3.4) and $d_{nl}$ a small correction to the leading order asymptotics, which is zero for $l = 0$.

Based on the asymptotic expression, Mosser et al. (2011b) developed the universal pattern for red-giant spectra, according to which all parameters are assumed to be a function of $\Delta \nu$. This is equivalent to assuming that the underlying physics of the parameters varies as a function of the global stellar parameters. The universal pattern has the following form to describe pure acoustic modes (Mosser et al. 2011b, 2012a):

$$\begin{aligned} \nu _{n_p\,l}=\left( n_p +\frac{l}{2}+\epsilon (\Delta \nu )-\hat{d}_{l}(\Delta \nu )+\frac{\alpha (\Delta \nu )}{2}[n_p-n_\mathrm{max}]^2\right) \Delta \nu , \end{aligned}$$

(6)

where $n_\mathrm{max}=\nu _\mathrm{max}/\Delta \nu$. The phase term $\epsilon$ and non-radial correction $\hat{d}_{l}$, with $\hat{d}_0 = 0$, are described by scaling laws of the form $A+B\log \Delta \nu$ (Mosser et al. 2010). The second-order term (or curvature) in the asymptotic expression is represented by the parameter $\alpha = 0.015 \Delta \nu ^{-0.32}$ (Mosser et al. 2012a).

The reason for the universal behaviour of red giants is not yet fully understood, as the asymptotic approximation is fundamentally related to the behaviour of the solution of the oscillation equations near the singularity at $r=0$ (Gough 1986b, 1993, and Sect. 4.2.3). In the case of red giants the conditions in the central region of the star are considerably different compared with the conditions in main-sequence stars (Sect. 4.2.3). Nevertheless, it seems that the asymptotic approximation and the universal pattern provide reasonable results for both models and observations. Only for the very luminous and expanded red giants close to the tip of the RGB the universality does not hold (Stello et al. 2014). For modes with low radial orders the dipole mode is located closer to the neighbouring quadrupole mode, providing a regular pattern of three modes together instead of a pattern of a cluster of two modes together (the 0–2 pair) alternating with one (dipole) mode.

3.3.3 Large frequency separation

The large frequency separation $\Delta \nu$ is the separation between modes of the same degree and consecutive radial orders. $\Delta \nu$ is proportional to the inverse of the acoustic diameter, i.e., the sound travel time across a stellar diameter. Furthermore, it can be shown that $\Delta \nu$ is a direct probe of the mean density ($\overline{\rho }$) of the star (Ulrich 1986):

$$\begin{aligned} \Delta \nu = \nu _{n\,l} - \nu _{n-1\,l} = \left( 2 \int _0^R \frac{\mathrm{d}r}{c} \right) ^{-1} \propto \sqrt{\frac{M}{R^3}} \propto \sqrt{ \overline{\rho }} , \end{aligned}$$

(7)

with r the distance to the centre of the star, see also Eq. (31).

The near-regular pattern of the large frequency separation can be measured in a global sense from the autocorrelation of a power spectrum (e.g., Huber et al. 2009), the power spectrum of a power spectrum (e.g., Hekker et al. 2010b) or the mathematically equivalent autocorrelation of the timeseries (EACF, Mosser and Appourchaux 2009) with a cosine filter or Hanning function with a full-width at half maximum (FWHM) of the order of the FWHM of the power excess. Additionally, Mosser et al. (2011b) have used the universal pattern (Sect. 3.3.2) in which the known patterns in the power spectrum are used to compute templates which are convolved with observed power spectra to determine $\Delta \nu$. Furthermore, the large frequency separation can be obtained from fits to individual frequencies (Kallinger et al. 2010), from pair-wise differences, or from a linear fit of the frequencies versus their radial order. It has been shown that the different determinations are consistent within their uncertainties and definitions (e.g., Verner et al. 2011; Hekker et al. 2011, 2012). Nevertheless, some biases depending on the number of radial orders that were used in the analysis have been identified (Hekker et al. 2012).

A convenient way to represent the power spectrum of solar-like oscillators is in an échelle diagram (Grec et al. 1983), as shown for a subgiant star in Fig. 8. This is obtained by dividing the frequency spectrum into segments of length $\Delta \nu$ and stacking the segments. According to Eq. (5) this should lead to roughly vertical sequences of points corresponding to different degrees. As shown in the figure this is satisfied for modes of degree $l = 0$ and 2; for $l = 1$ the presence of mixed modes (see Sects. 3.4.1, 4.2, 5.4) causes departures from the simple behaviour.

Fig. 8

Échelle diagram of KIC 11395018 showing the frequencies (black points) as determined by Mathur et al. (2011a): modes with $l = 0$, $l = 1$ and $l = 2$ are indicated with circles, triangles and squares, respectively. For reference, a grey-scale map showing the power spectrum (smoothed to 1 $\upmu$Hz resolution) is included in the background. The fits made to the $l = 0$ and $l = 2$ modes are shown by red lines. The values of $\Delta \nu$ and $\delta \nu _{02}$ (at $\nu _\mathrm{max}$) and the relationship $\Delta \nu (\epsilon -1)$, i.e., the absolute position of the $l = 0$ ridge, are indicated by the blue arrows, as labelled. Image reproduced with permission from White et al. (2011), copyright by AAS

We stress here that the actual separation between the frequencies of adjacent modes of the same degree varies as a function of frequency due to stellar internal structure properties, as also reflected by Eq. (6) and discussed further by Mosser et al. (2013b) and in Sect. 4.1. Structure variations that happen on scales that are comparable with or shorter than the oscillation wavelength, i.e., a glitch, cause a damped sinusoidal modulation in the frequencies (see for more details Sects. 3.4.5 and 4.2.4). Structure changes that take place over longer scales cause a gradual change, or curvature, in the large frequency separation. Therefore, the value of the large frequency separation may change depending on the frequency range that is taken into account.

3.3.4 Phase term ($\epsilon$)

The asymptotic relation for acoustic modes (Eq. 5) also contains a phase term $\epsilon$. This phase term is a dimensionless offset of the radial modes in an échelle diagram (see Fig. 8). Its value is correlated with the determination of $\Delta \nu$. The value of $\epsilon$ can be determined from the universal pattern in which it is considered to be a function of $\Delta \nu$. Additionally, a (weighted⁵) least-squares fit to the radial ($l = 0$) frequencies to simultaneously determine $\Delta \nu$ and $\epsilon$ can be performed. These global methods average over the variation of $\epsilon$ with frequency. Additionally, a ‘local’ $\epsilon$ can be determined by only including the three central radial orders around $\nu _\mathrm{max}$ in the analysis (Kallinger et al. 2012).

The inferred value of $\epsilon$ is generally between 0.5 and 1.5, with a potential ‘offset’ of $\pm 1$. This ‘offset’ only reflects the observational limitations in that the radial order n cannot be measured independently and is not an offset of the actual value of $\epsilon$.

The main diagnostic power of the global phase term lies in the mode identification of the different ridges in the échelle diagram for stochastic oscillators with short mode lifetimes. In these cases the width of the oscillation signals in the Fourier space does not allow to resolve the small frequency separation (see next subsection) between the $l=0$ and $l=2$ modes and hence the $l=1$ and $l=0,2$ ridges have very similar characteristics. In these cases $\epsilon$, i.e., the location of the radial modes in an échelle diagram, can be used to identify the ridges correctly (White et al. 2012).

The ‘local’ phase term can be used to distinguish between different evolutionary phases (Kallinger et al. 2012). This is caused by the fact that the differences in the core cause differences in the thermodynamic state of the envelope, which results in a different location of the second helium-ionisation zone for stars with an inert helium core compared with stars with helium-core burning. The location of the second helium-ionisation zone leaves a trace in small oscillatory deviations in the frequencies (see Sects. 3.4.5 and 4.2.4 on glitches). This causes a difference in the ‘local’ phase term for stars in different evolutionary phases (Christensen-Dalsgaard et al. 2014).

3.3.5 Small frequency separation ($\delta \nu _{02}$ and $\delta \nu _{13}$)

A typical separation in frequency exists between odd- and even-degree modes. This is the so-called small frequency separation that can be approximated asymptotically, for main-sequence stars, by (e.g., Gough 1986b, see also Eq. 32):

$$\begin{aligned} \delta \nu _{l\,l+2}(n)=\nu _{n\,l}-\nu _{n-1\,l+2} \simeq -(4l+6)\frac{\Delta \nu }{4\pi ^2 \nu _{n\,l}}\int _0^R\frac{\mathrm{d} c}{\mathrm{d} r}\frac{\mathrm{d} r}{r}. \; \end{aligned}$$

(8)

This parameter is generally measured from frequency differences between observed individual frequencies. Equation (8) depends on the sound-speed gradient, which depends on the composition. Hence, $\delta \nu _{l\,l+2}(n)$ provides a measure of the helium content in the core of main-sequence stars, and with that $\delta \nu _{l\,l+2}(n)$ is a diagnostic of stellar age (Christensen-Dalsgaard 1984; Ulrich 1986; Christensen-Dalsgaard 1988). It was noted by Huber et al. (2010) from early Kepler observations, that for more evolved stars (subgiants and giants) the small frequency separation between modes of degree 0 and 2 essentially scales as $\Delta \nu$. This is due to the fact that these stars have a highly concentrated core such that the inner turning point of the pressure-mode cavity lies outside the compact core. Therefore, this small separation does not provide a measure of the helium content in the core and hence is no longer an age diagnostic.

3.3.6 Small frequency separation ($\delta \nu _{01}$)

In a Fourier spectrum dipole modes are located approximately mid-way between radial modes as per Eq. (5). The offset from the midpoint between the radial modes and the frequency of the dipole mode can be computed from a three-point difference⁶ and indicated as $\delta \nu _{0\,1}$:

$$\begin{aligned} \delta \nu _{0\,1}(n)=0.5(\nu _{n\,0}-2\nu _{n\,1}+\nu _{n+1\,0}). \end{aligned}$$

(9)

In main-sequence stars $\delta \nu _{0\,1}$ is known to be sensitive to the central physical conditions. For red giants this is not the case. It has been shown that for red giants $\delta \nu _{0\,1}$ is correlated with the distance between the $l=1$ turning point and the bottom of the convective envelope. The value of $\delta \nu _{0\,1}$ takes small and negative values for stars ascending and descending the RGB where the turning points of acoustic $l=1$ modes are well within the convective envelope. Stars in the He-core burning phase have a shallower convective envelope and the turning points of $l=1$ modes are in the radiative region and $\delta \nu _{0\,1}$ generally takes positive values (Montalbán et al. 2010). As shown in Sect. 4.2.5 (Figs. 32, 33) the evanescent region between the buoyancy and acoustic cavities is smaller in a red-clump star compared with a RGB star. This leads to a stronger coupling between modes in a red-clump star increasing the spread in the modes, which most likely leads to less regular behaviour of $\delta \nu _{0\,1}$ in clump stars compared with RGB stars. Hence, the value of $\delta \nu _{0\,1}$ and the regularity of the acoustic dipole spectrum can be used as a diagnostic to distinguish between different evolutionary phases (Montalbán et al. 2010). We note here that most of the work on $\delta \nu _{0\,1}$ for red giants was performed before the discovery of the fact that all non-radial modes are to some extent mixed modes. Hence, this influence was not taken into account.

3.3.7 Period spacing ($\Delta \varPi$)

As mentioned above, non-radial modes in red giants all involve aspects of gravity-mode behaviour. To analyse the relevant properties we note that an asymptotic approximation (see Sect. 4.1) reveals that gravity modes of a given degree appear with near constant separation in period, the so-called period spacing $\Delta \varPi$, as reflected in the asymptotic behaviour of their periods $\varPi _{n,l}$:

$$\begin{aligned} \varPi _{n,l} = {\varPi _0 \over \sqrt{l(l+1)}} (n + \epsilon _\mathrm{g} +1/2) , \end{aligned}$$

(10)

with

$$\begin{aligned} \varPi _0 = 2 \pi ^2 \left( \int _{r_1}^{r_2} N {\mathrm{d}r \over r} \right) ^{-1} , \end{aligned}$$

(11)

where N is the Brunt–Väisälä frequency (Eq. 24), $r_1$ and $r_2$ the turning points of the gravity-mode cavity and $\epsilon _\mathrm{g}$ is a phase accounting for the behaviour near the turning points. This defines the period spacing:

$$\begin{aligned} \Delta \varPi _l = \varPi _0/\sqrt{l(l+1)}. \end{aligned}$$

(12)

Based on the regular nature, one can use similar techniques to determine the period spacing as used to determine $\Delta \nu$ (power spectrum of the power spectrum, auto-correlations and differences between modes with consecutive order, see Sect. 3.3.3), but now in period space and centred on regions where dipole (or quadrupole) modes are expected. It is, however, important to account for the fact that in solar-like oscillators no pure gravity modes can be observed, but only modes that have mixed gravity-pressure nature (see also Sects. 3.4 and 4.2 for more details about mixed modes). Due to this mixed nature the regular spacing in period deviates from the asymptotically predicted value of ‘pure’ gravity oscillation modes in the vicinity of ‘pure’ pressure modes. The observed period spacing follows, in general, a predictable pattern for each acoustic radial order with an empirically determined Lorentzian shape (Mosser et al. 2011b, 2012c, and Sect. 4.2.3).

Fig. 9

Two period échelle diagrams with different density of $l = 1$ modes for a $1 \,\mathrm{M}_\odot$ red-giant model are shown (for details of the model, see Datta et al. 2015). The red points connected with the light grey lines are $l = 1$ modes and the horizontal dotted lines represent the frequencies of the radial modes. The blue dashed line shows the g-mode period spacing of high-order g modes. The top panel shows the period échelle diagram for all the $l = 1$ modes in a frequency range spanning 7 radial orders, with $\Delta \varPi = 73.28$ s. The lower panel shows the period échelle diagram for only a subset of the most p-dominated $l = 1$ modes in a smaller frequency range consisting of 5 radial orders with $\Delta \varPi = 73.26$ s. Image reproduced with permission from Datta et al. (2015), copyright by the authors

The underlying period spacing can be determined from the modulated observed period spacing using a period échelle diagram (see Fig. 9). In this diagram the period spacing can be obtained by aligning the g-dominated modes surrounded in a roughly symmetric way by the p-dominated modes (Bedding et al. 2011; Mosser et al. 2012c; Datta et al. 2015). The patterns in the period échelle diagram can also be described by an analytical expression based on the coupling between the gravity and acoustic cavity as derived by Mosser et al. (2012c) (see also Sect. 4.2.3):

$$\begin{aligned} \nu =\nu _{n_p,l}+\frac{\Delta \nu }{\pi }\arctan \left[ q\tan \pi \left( \frac{1}{\Delta \varPi _l\nu }-\epsilon _g\right) \right] , \end{aligned}$$

(13)

where q is the coupling strength. This is set to $q=0$ for no coupling and $q=1$ indicates maximum coupling. The period spacing and coupling strength can be determined in an iterative manner, when assuming $\epsilon _g$ is a fixed value (often zero, i.e., the pattern is assumed symmetric). Note that Buysschaert et al. (2016) have employed Eq. (13) while leaving $\epsilon _g$ also as a free parameter. They find that although $\epsilon _g$ remains ill-defined, its determination improves the determination of the period spacing.

An alternative way to determine period spacing and to constrain the evanescent region between the p and g cavities (and thus coupling strength q) is through the inertia ratio of dipole and radial modes (see Sect. 4.2). Benomar et al. (2014) for the first time estimated mode inertias observationally from the measurements of mixed mode characteristics. The mode inertia ratio could develop to be a diagnostic that can potentially provide strong constraints on the stellar structure.

Recently, Mosser et al. (2015) and Vrard et al. (2016) have proposed a way to stretch the period Fourier spectrum to remove the modulation due to the coupling between the pressure and gravity modes and obtain the regular underlying period spacing in a direct manner.

The period spacing provides a strong diagnostic on the central regions of the star. It can be used to distinguish between stars in different evolutionary phases, most notably between red giants with an inert He-core and red giants with He-core burning (Bedding et al. 2011; Mosser et al. 2011a, 2014). Furthermore, small deviations from the regular period spacing pattern can reveal localised stellar structure changes such as the chemical discontinuity due to the first dredge-up (Cunha et al. 2015, and Sect. 4.2.4).

3.4 Individual oscillation modes

Individual oscillation modes in stochastic oscillations are characterized by their mode frequency $\nu _\mathrm{central}$, line width $\varGamma$ and height H. A resolved oscillation mode, i.e., a mode with a lifetime that is at least $\sim$10 times shorter than the timespan of the timeseries data (Hekker et al. 2010a) can be modelled by a Lorentzian profile in the power spectrum $P(\nu )$:

$$\begin{aligned} P(\nu )=\frac{H}{\displaystyle {1+\left( \frac{2(\nu -\nu _\mathrm{central})}{\varGamma }\right) ^2}}. \end{aligned}$$

(14)

The mode lifetime $t_\mathrm{damp}$ is directly related to the mode line width through $\varGamma =1/(\pi t_\mathrm{damp})$. The mode height and width are highly correlated and relate through the root-mean-square flux amplitude $A=\sqrt{\pi H\varGamma /2}$ (e.g., Chaplin et al. 2005) which is the area underneath the profile. Hence the amplitude is a more robust parameter. The amplitude of the modes contains information on the excitation and damping of the oscillations (see, e.g., Houdek 2012; Samadi et al. 2012, and Sect. 4.3). However, the visibility of the modes is a combination of the intrinsic amplitude and geometrical effects, i.e., cancellation of some of the signal due to the fact that only integrated light from the visible part of stars can be observed. In case the oscillations are not resolved (lifetime longer than the timespan of the timeseries data) they are often approximated with a sinc function (see footnote 4) in which case the amplitude is $A=\sqrt{2H\delta \nu }$, where $\delta \nu$ is the frequency resolution. In intermediate cases where the modes are partly resolved a mixture of the resolved and unresolved description has to be applied (see Sect. 4.3.2).

3.4.1 Mixed modes

Radial modes are always pure acoustic modes with pressure as the restoring force. Non-radial modes in red giants, however, always have a mixed nature, i.e., are mixed modes, for which buoyancy acts as restoring force in the deep interior of the star and pressure acts as restoring force in the outer layers of the star. In other words a mixed mode is a single mode with different behaviour in the different regions. Frequencies of mixed modes are shifted compared with pure acoustic or gravity modes by an amount depending on the coupling strength between the two (gravity and pressure) oscillation cavities (e.g., Deheuvels and Michel 2010; Hekker and Mazumdar 2014, and Sect. 4.2).

Mixed modes [and hence period spacings (Sect. 3.3.7)] are mostly observed in dipole ($l=1$) modes as for these modes the coupling between the pressure- and gravity-mode cavities is stronger (narrower evanescent zone between the cavities, see Fig. 12) and also because the period spacings are larger due to the dependence on $\sqrt{l(l+1)}$ (see Eq. 10), and thus better resolved.

In case there are only a few mixed modes present in, for instance, subgiants, Deheuvels and Michel (2010, 2011) showed that $l=1$ avoided crossings in subgiant stars involve more than two modes and induce a characteristic distortion in the $l=1$ ridge in the échelle diagram (see Fig. 16). This can be used to constrain stellar models. Deheuvels and Michel (2011) have done so by matching the observed large frequency separation and frequency of the avoided crossing with values obtained from models. This results in a precise age estimate given the mass and physics of the models.

Following the analysis by Deheuvels and Michel (2011), Bedding (2012) introduced a powerful tool for analysing these mixed modes. He showed that by replicating the échelle diagram horizontally the full structure of the avoided crossings can be displayed. Benomar et al. (2012) subsequently used this to develop a method to fit the avoided crossings and determine the minimum separation between the two branches as a measure of the coupling strength (see Sect. 4.2.2). This provides a useful diagnostics of the stellar mass for subgiant stars.

3.4.2 Mode identification

The degree l of the observed individual frequencies can be obtained from the known pattern of the stochastic oscillation (Sect. 3.3.2) through an échelle diagram (Fig. 8), where the ridges of radial and quadrupole modes are close together with the dipole ridge appearing at about a 0.5$\Delta \nu$ offset. In case the mode lifetimes are very short the radial modes can be so broad that they overlap the quadrupole modes. In that case the phase term ($\epsilon$) can be useful to distinguish the odd and even ridge (Sect. 3.3.4). The (acoustic) radial order $n_p$ can be estimated from Eq. (5), i.e., from the ratio of the frequency of the mode over the large frequency separation bearing in mind that n is an integer and that the phase term $\epsilon$ takes values between 0.5 and 1.5. Note that for mixed modes the total radial order n consists of the nodes in the acoustic cavity $n_p$ as defined here and the nodes in the buoyancy cavity. The buoyancy radial order $n_g$ is indicated by definition with a negative number and can take large values (see also Sect. 4.2.1 and Fig. 18).

Mode identification can also be performed from spectroscopic data. Red- or blue-shifted parts of the surface of a star leave traces in the shape of a spectral line profile. Over the course of the pulsation the blue- and red-shifted parts change and hence the line-profile shape changes. Therefore, the amplitude and phase of the line-profile variations at a particular frequency are fundamentally different for radial and non-radial oscillation modes. This technique has mainly been developed for stars with coherent oscillations (Zima et al. 2004; Zima 2008), but also proved useful for providing evidence for the presence of non-radial oscillations in red giants (Hekker et al. 2006; Hekker and Aerts 2010).

3.4.3 Surface effect

Due to incomplete modelling of the convective outer layers of stars and the strong non-adiabatic behaviour of the oscillations in the superficial layers there is an offset between modelled and observed frequencies, the so-called surface effect. This offset is a function of frequency, but independent of degree at least for the Sun. Using the solar offset Kjeldsen et al. (2008) proposed a widely used power–law correction that can be applied to other stars. An alternative procedure is to directly scale the solar offset on a suitable frequency scale (e.g., Christensen-Dalsgaard 2012b). Additionally, Aerts et al. (2010) have shown that due to their larger amplitudes in the inner regions and hence larger inertia (cf. Eq. 38), mixed modes in subgiants are less sensitive to the incorrect modelling of the non-adiabatic outer layers, and hence the solar calibrated offset needs to be adapted. Ball and Gizon (2014), based on Gough (1990), have developed a correction based on mode inertia. So far this method has only been tested for observations of the Sun and solar-like stars as well as for models of different mass and metallicity covering a significant portion of the HR diagram from the main-sequence to red giants for models with $T_\mathrm{eff} < 6500$ K (Schmitt and Basu 2015). In their work Schmitt and Basu (2015) concluded that the two-term model proposed by Ball and Gizon (2014) works much better than other models across a large portion of the HR diagram, including the red giants.

For main-sequence stars it is possible to reduce the influence of the near-surface region by using frequency-separation ratios such as

$$\begin{aligned} r_{0\,2}=\frac{\nu _{n\,0}-\nu _{n-1\,2}}{\nu _{n\,1}-\nu _{n-1\,1}}, \end{aligned}$$

(15)

which are essentially independent of the near-surface problems (e.g., Roxburgh and Vorontsov 2003; Roxburgh 2005). As for the small frequency separations ($\delta \nu _{02}$, Sect. 3.3.5) the usefulness of the frequency-separation ratios for red-giant stars is limited due to the universality of the frequency patterns (e.g., Huber et al. 2010). Additionally, in giants all non-radial modes are mixed modes, which have different sensitivities to the surface effect.

3.4.4 Rotational splitting

Rotation splits the non-radial modes into $2l+1$ single modes of different azimuthal orders m. These incorporate modes travelling with the rotational direction (prograde modes) and in the opposite direction (retrograde modes) in addition to the original mode unperturbed by rotation, i.e., in cyclic frequency (see also Eq. (124) given in angular frequency):

$$\begin{aligned} \nu _{n\,l\,m}=\nu _{n\,l\,0}+m\delta \nu _{n\,l\,m}. \end{aligned}$$

(16)

In cases of slow rotation, which is in general the case for subgiants and red-giant stars, the assumption of symmetric splittings is often valid. The relative heights or visibility of the different azimuthal orders in a multiplet are indicative of the inclination angle with respect to the rotation axis at which we view the system (Gizon and Solanki 2003). When viewing the system pole on, only the $m=0$ mode is visible, while for an equator-on system all modes with even $l - m$ are visible. A rotationally split mode can be fitted with a set of Lorentzian functions:

$$\begin{aligned} P(\nu _{n\,l})=\sum _{m=-l}^l\frac{\varPsi _{l\,m}(i)H}{\displaystyle {1+\left( \frac{2(\nu -\nu _{n\,l\,0}-m\delta \nu _{n\,l\,m})}{\varGamma }\right) ^2}}, \end{aligned}$$

(17)

where $\varPsi _{l\,m}(i)$ is the visibility of the mode which depends on the inclination angle (i) and $\delta \nu _{n\,l\,m}$ is the rotational splitting. Here we assumed that all modes in a multiplet are excited to the same intrinsic average height, as may be reasonable for stochastically excited modes observed for a long time compared with the lifetime of the modes. To detect the average rotational splitting one can also use the fact that the rotational splitting is approximately symmetric in slow rotators and apply, for instance, the EACF (autocorrelation of the timeseries, Mosser et al. 2011b) with a very narrow Hanning filter in the range of a non-radial rotationally split modes.

It has been shown that the rotational splitting of modes with mixed character (i.e., all non-radial modes in red-giant stars) is a function of the mixed character (Beck et al. 2012; Mosser et al. 2012b; Goupil et al. 2013, and Sect. 4.4). Hence the rotational splitting of mixed modes is a diagnostic to probe the radial internal rotation profile.

3.4.5 Glitches

Information on specific transition regions in a star, such as the boundaries of convective zones or ionization zones of helium or hydrogen, can be obtained from the fact that, at such boundaries, the properties of the star change on a scale substantially smaller than the local wavelength of the oscillations (e.g.,Vorontsov 1988; Gough 1990, and Sect. 4.2.4). These sharp features (also called glitches) cause oscillatory variations in the frequencies with respect to the pattern described in Eq. (5), or the corresponding pattern satisfied by mixed modes (cf. Eq. 13). The period of the variation depends on the location of the feature, while the amplitude depends on the detailed properties of the feature. Note that the diagnostic use of glitches can be done completely independent of stellar models.

For acoustic modes the oscillatory behaviour due to glitches can be measured in frequency differences ($\Delta \nu$) but more often in second differences, and can be described by a damped oscillator:

$$\begin{aligned} \Delta _2\nu _{n\,l} \equiv \nu _{n-1\,l}-2\nu _{n\,l}+\nu _{n+1\,l}=c_0\nu _{n\,l} e^{-c_2\nu _{n\,l}^2}\sin {(4\pi \nu _{n\,l}\tau _\mathrm{gl}+2\phi _\mathrm{gl})} \end{aligned}$$

(18)

in the case of the glitch due to the He II ionisation zone, where $c_0$ indicates the amplitude of the oscillation and $c_2$ a characteristic width of the e-folding time of the damped oscillator. Here $\tau _\mathrm{gl}$ is the acoustic depth, i.e., the sound travel time between the surface and the glitch, and $\phi _\mathrm{gl}$ is a constant that accounts for the phase. Equation (18) was derived by Houdek and Gough (2007) and applied in various forms by e.g., Miglio et al. (2010), Mazumdar et al. (2014), Broomhall et al. (2014) and Verma et al. (2014). In addition to the intrinsic limits of the sharpness of the glitch compared with the local wavelength of the oscillation mode (see Sect. 4.2.4), the observational data also provide natural limits. The depth in the star at which a glitch can be measured depends on the frequency range covered by the oscillations, i.e., the largest period in Eq. (18) that can be measured, while the minimum period is defined by the resolution of the measured frequencies. From these limitations we find that the bottom of the convection zone is located too deep in red giants to be measured. Furthermore, the helium I and hydrogen ionisation zones are located close to the surface, which make them very challenging to measure.

For mixed modes the effects of buoyancy glitches are described by Cunha et al. (2015) and in Sect. 4.2.4. However, no solid observational results on such effects have been presented so far.

3.5 Scaling relations and grid-based modelling

The scaling relations Eqs. (4) and (7) can be used to obtain the mean density and surface gravity of stars exhibiting solar-like oscillations (and from that stellar mass and radius) in a direct manner, i.e., so-called direct method. These scaling relations are exceptionally good given that these relations do not account for metallicity differences, nor do they account for any knowledge we have about stellar evolution. To take account of this knowledge, it is also possible to compare the observables {$\Delta \nu , \nu _\mathrm{max}, T_\mathrm{eff}, \mathrm {[Fe/H]}, \pi$, $\mathcal L$} or a subset thereof with a grid of models; here $\mathrm {[Fe/H]}$ is metallicity, $\pi$ is parallax and $\mathcal L$ is luminosity. In this so-called grid-based modelling one does account for knowledge of stellar structure and evolution, as well as metallicity. However, in case the scaling relations are used to determine $\Delta \nu$ and $\nu _\mathrm{max}$ from the models suitable reference values (with uncertainties) to which one scales have to be adopted. Alternatively, one can compute individual frequencies for the models and derive $\Delta \nu$ from that.

Reference values Both the direct method and grid-based modelling are based on the scaling relations (Eqs. 4, 7) which assume that the scaling is valid in a consistent way between the reference and the observed star. Often reference values based on the Sun are used; however, this may not be correct for stars with different properties, such as a different metallicity or rotation rate, or stars in different evolution phases, as their stellar internal structures are different. This has indeed been confirmed by White et al. (2011) for stars with different metallicities along the main-sequence and just beyond that. Mosser et al. (2013b) proposed new reference values based on relations derived using results obtained using the universal pattern (Mosser et al. 2011b). It is currently unclear whether these newly derived reference values are also valid when other methods are used to derive $\Delta \nu$ and $\nu _\mathrm{max}$. For instance, Hekker et al. (2013) failed to confirm the relations quantitatively using stellar models. Furthermore, Miglio et al. (2012) showed that the difference in internal temperature structure (hence sound speed) between RGB and RC stars has a significant impact on the scaling relations. Therefore, they applied a correction for red-clump stars in the open clusters NGC 6719 and NGC 6819 based on the masses of the RGB stars in the respective clusters and theoretical models. Subsequently, Christensen-Dalsgaard et al. (2014) showed that the difference in the variation of the phase term $\epsilon$ (see Sect. 3.3.4) with frequency between RC and RGB stars is related to differences in the thermodynamic state of the convection zone. This supports the findings of Miglio et al. (2012) that RC and RGB stars have internal structures that are significantly different, which calls for corrections to the scaling relations. Recently, Guggenberger et al. (2016) proposed a new reference function for the $\Delta \nu$ scaling relation (Eq. 7) that accounts for metallicity differences and is applicable for stars on the main sequence up till past the RGB bump on the red-giant branch. Additionally, Sharma et al. (2016) and Serrenelli et al. (in preparation) devised methods to apply a correction between $\Delta \nu$ scaling and $\Delta \nu$ from frequencies in model calculations.

3.6 ‘Boutique’ modelling

Oscillation frequencies can be compared with stellar models to infer the internal stellar structure. This is often done on a star by star basis, hence ‘boutique’ or ‘detailed’ modelling. This modelling can be done in both a forward and an inverse approach.

Forward modelling In forward modelling the observed frequencies and stellar parameters such as $\log g$, $T_\mathrm{eff}$, [Fe/H] are matched with stellar models. This is mostly done using $\chi ^2$ minimisation either in a direct manner or through singular value decomposition (SVD) (e.g., Brown et al. 1994). In this procedure the surface term is accounted for by one of the prescriptions mentioned above (Kjeldsen et al. 2008; Ball and Gizon 2014) or by using the frequency-separation ratios (Roxburgh and Vorontsov 2003; Roxburgh 2005). Detailed descriptions of the different methods currently applied can be found in the appendix of Chaplin et al. (2013), Ballard et al. (2014), Silva Aguirre et al. (2015) and references therein.

Inverse modelling An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system. For stars the individual frequencies can be used to obtain information about the internal structure of stars. An inverse problem is, however, by nature ill-posed, and many frequencies probing the star to different depths are needed to obtain meaningful results. Most commonly inversions have been used to study the stellar rotation at different depths in the stars (e.g., Deheuvels et al. 2012, 2014; Di Mauro et al. 2016). It is, however, in principle also possible to perform structure inversions. These have been very powerful in determining the internal structure of the Sun (e.g., Gough et al. 1996, and references therein). For other stars the lack of observed frequencies probing the star to different depths has precluded detailed structure inversions. However, inversion techniques have been used in asteroseismic analyses to constrain specific properties of stars (e.g.,Reese et al. 2012; Buldgen et al. 2016). For a complete overview of stellar inversions we refer to Basu (2014, 2016).

4 Theory of stellar pulsations

The general theory of stellar pulsations has been presented in considerable detail by, for example, Unno et al. (1989) and Aerts et al. (2010). However, oscillations of evolved stars present special properties which are important for the understanding of the observations. Thus, here we provide some background which is useful in the interpretation of the observations of the oscillations of such stars, relating the frequencies and other aspects of the oscillations to the properties of the stars.

We are dealing with low-amplitude oscillations, which can be regarded as small perturbations to the equilibrium structure. Formally, these can be described using linearized perturbation analysis of the general equations of hydrodynamics. An important result concerns the geometrical properties of the modes of spherically symmetric stars. For the modes that are relevant the properties can be described by spherical harmonics $Y_l^m(\theta , \phi ) = P_l^m(\cos \theta ) \mathrm{e}^{\mathrm{i}m \phi }$ as functions of co-latitude $\theta$ and longitude $\phi$; here $P_l^m$ is a Legendre function, characterized by the degree l and the azimuthal order m (see Sect. 3.3 for a definition). The time dependence of a mode is conveniently written as $\mathrm{e}^{- \mathrm{i}\omega t}$ where $\omega$ is the angular frequency, which is in general complex. The displacement vector can be written, as a function of position $\varvec{r}$ and time t,

$$\begin{aligned} \varvec{\delta }\varvec{r}(\varvec{r}, t) = \mathrm{Re}\left\{ \left[ \xi _r(r) Y_l^m \varvec{a}_r + \xi _\mathrm{h}(r) \left( {\partial Y_l^m \over \partial \theta } \varvec{a}_\theta + {1 \over \sin \theta } {\partial Y_l^m \over \partial \phi } \varvec{a}_\phi \right) \right] \mathrm{e}^{- \mathrm{i}\omega t} \right\} \; , \end{aligned}$$

(19)

where $\mathrm{Re}$ denotes the real part, $\xi _r$ and $\xi _\mathrm{h}$ are the radial- and horizontal-displacement amplitude functions that depend only on the distance r to the centre, and $\varvec{a}_r$, $\varvec{a}_\theta$ and $\varvec{a}_\phi$ are unit vectors in a spherical polar coordinate system. Other oscillating variables, such as the pressure perturbation, vary as the real part of $Y_l^m(\theta , \phi ) \mathrm{e}^{-\mathrm{i}\omega t}$. We can separate the frequency into real and imaginary parts as $\omega = \omega _\mathrm{r} + \mathrm{i}\omega _\mathrm{i}$. Then the dependence of the oscillations on longitude $\phi$ and time t is essentially

$$\begin{aligned} \cos (m \phi - \omega _\mathrm{r} t) \mathrm{e}^{\omega _\mathrm{i} t} . \end{aligned}$$

(20)

Unless $m = 0$ this describes a wave running in the $\phi$ direction, growing or decaying with time depending on whether $\omega _\mathrm{i}$ is positive or negative. In much of the following we consider adiabatic oscillations where processes causing excitation or damping are neglected. Then the frequency $\omega$ is real and we ignore the distinction between $\omega$ and $\omega _\mathrm{r}$. We note that observed oscillations are typically discussed in terms of the cyclic frequency $\nu = \omega _\mathrm{r}/2 \pi$, as done in the previous sections. However, for the theoretical analysis it is more convenient to use the angular frequency $\omega$.

After this separation of variables we are left with differential equations that depend just on r. Combined with suitable boundary conditions, this is a relatively straightforward numerical problem, which determines the frequencies $\omega$ as eigenvalues. However, the physical treatment of the near-surface layers still suffers from substantial uncertainties, particularly when the mode energetics is taken into account (see Sect. 3.4.3).

To evaluate the diagnostic potential of solar-like oscillations in giant stars and interpret the inferences that are made, an understanding of the properties of the oscillations is required. Moreover, these properties are fascinating in their own right. A full utilization of the observed data requires detailed comparison of the observed frequencies, and other properties, with computations for stellar models. However, a great deal of insight as well as powerful diagnostics can be obtained from asymptotic analyses of the oscillations, to which we turn next.

4.1 Asymptotic theory

We first concentrate on the oscillation frequencies and overall properties of the eigenfunctions, assuming the oscillations to be adiabatic. Solar-like oscillations are generally of high radial order, such that the eigenfunctions mostly vary on a scale much shorter than the scale of variation of the equilibrium structure. In this case the analysis of the behaviour of the modes and their relation to stellar structure in terms of their asymptotic properties is extremely informative; some effects of rapid variations in the model structure, and hence departures from the asymptotic behaviour, are discussed in Sect. 4.2.4. Also, owing to the high radial order it is common to ignore the perturbation to the gravitational potential, in the so-called Cowling approximation (Cowling 1941). We return to the limitations of this approximation towards the end of Sect. 4.1.

The Cowling approximation reduces the equations of adiabatic oscillations to a second-order system, greatly simplifying the analysis. The equations are often expressed in the form

$$\begin{aligned} {\mathrm{d}^2 X \over \mathrm{d}r^2} = - K X , \end{aligned}$$

(21)

for suitable choices of the dependent variable X and the function K. The choice of X and K may depend on the specific properties that are being investigated. A convenient formulation was derived by Gough (Deubner and Gough 1984; Gough 1993) based on an analysis by Lamb (1932). Here $X = c^2 \rho ^{1/2} \mathrm{div}\,\varvec{\delta }\varvec{r}$, where c is the adiabatic sound speed and $\rho$ is density. The corresponding approximation to K is

$$\begin{aligned} K = {1 \over c^2} \left[ S_l^2 \left( {N^2 \over \omega ^2} - 1\right) + \omega ^2 - \omega _\mathrm{c}^2 \right] , \end{aligned}$$

(22)

which is determined by three characteristic frequencies of the star:

• The Lamb frequency $S_l$, with

  $$\begin{aligned} S_l^2 = {l(l+1) c^2 \over r^2} . \end{aligned}$$

  (23)

  The Lamb frequency is a local characteristic frequency of horizontally propagating sound waves with a wavenumber $k_\mathrm{h} = \sqrt{l(l+1)}/r$.

• The buoyancy frequency (or Brunt–Väisälä frequency) N,

  $$\begin{aligned} N^2 = g \left( {1 \over \varGamma _1} {\mathrm{d}\ln p \over \mathrm{d}r} - {\mathrm{d}\ln \rho \over \mathrm{d}r} \right) , \end{aligned}$$

  (24)

  where g is the local gravitational acceleration, p is pressure and $\varGamma _1 = (\partial \ln p/\partial \ln \rho )_\mathrm{ad}$, the derivative being for an adiabatic process; note that $N^2$ is negative in convectively unstable regions. The Brunt–Väisälä frequency is the local frequency of internal gravity waves of short horizontal wavelength.

• The acoustic cut-off frequency $\omega _\mathrm{c}$,

  $$\begin{aligned} \omega _\mathrm{c}^2 = {c^2 \over 4 H^2} \left( 1 - 2 {\mathrm{d}H \over \mathrm{d}r} \right) , \end{aligned}$$

  (25)

  where $H = - (\mathrm{d}\ln \rho / \mathrm{d}r)^{-1}$ is the density scale height. The acoustic cut-off frequency arises from the inability of modes to propagate when their vertical wavelength is too long compared with the scale of the density variation in the equilibrium structure. This leads to reflection of the waves. We note that since $\omega _\mathrm{c}^2$ depends on the second derivative of density (see the definition of density scale height and Eq. 25), it varies rapidly in the region of substantial superadiabaticity just below the surface, as shown in the right-hand panel of Fig. 10. On the other hand, in the nearly isothermal atmosphere $H \simeq H_p$ is essentially constant, and $\omega _c^2 \simeq c^2 /(4 H^2)$. Thus $\omega _\mathrm{c}/2 \pi$ reduces to $\nu _\mathrm{ac}$ (cf. Eq. 3).

Fig. 10

Characteristic frequencies for a model of the Sun, expressed in terms of cyclic frequencies, as functions of fractional radius. The solid line shows the buoyancy frequency $N/2 \pi$ (cf. Eq. 24), the dashed lines show the Lamb frequencies $S_l/2\pi$ for $l = 1$ and 2 (cf. Eq. 23) with $S_1/2\pi$ having lower values than $S_2/2\pi$, and the dot-dashed line shows the acoustic cut-off frequency $\omega _\mathrm{c}/2 \pi$ (cf. Eq. 25). The horizontal dotted line indicates an estimate of the frequency of maximum oscillation power $\nu _\mathrm{max}$ (cf. Eq. 26), with the blue part marking the p-mode cavity for $l = 1$. The right-hand panel shows an expanded view of the near-surface region

According to Eqs. (21) and (22) the behaviour of the oscillations is determined by the dependence of the characteristic frequencies on position. This is illustrated in Fig. 10 for a model approximating the present Sun. To characterize the location of typical frequencies of solar-like oscillations the horizontal line shows the estimated frequency $\nu _\mathrm{max}$ of maximum oscillation power, obtained as

$$\begin{aligned} \nu _\mathrm{max} = 0.6 \nu _\mathrm{ac} , \end{aligned}$$

(26)

where $\nu _\mathrm{ac}$ is the isothermal acoustic cut-off frequency (cf. Eq. 3); in the Sun $\nu _\mathrm{max} \simeq 3150~\upmu \mathrm{Hz}$. At this frequency $\omega \gg N$ except in the atmosphere, reducing Eq. (22) to $K \simeq c^{-2}(\omega ^2 - S_l^2 - \omega _c^2)$. The corresponding modes are acoustic modes, or p modes, where pressure is the restoring force. In the region where $K > 0$ the solution X oscillates as a function of r (see Eq. 21), whereas X behaves locally exponentially where $K < 0$. For acoustic oscillations the oscillatory region, also known as the p-mode cavity, extends from the surface to a distance $r_\mathrm{t}$ from the centre, approximately given by $\omega \simeq S_l$, or

$$\begin{aligned} {\omega \over \sqrt{l(l+1)}} = {c(r_\mathrm{t}) \over r_\mathrm{t}} . \end{aligned}$$

(27)

Physically this corresponds to total internal reflection of the oscillations, described as a superposition of sound waves. The upper turning point $R_\mathrm{t}$ is where $\omega \simeq \omega _\mathrm{c}(R_\mathrm{t})$, which is satisfied just below the photosphere at high frequency and somewhat deeper at lower frequency (see right panel of Fig. 10). Waves with frequencies exceeding the acoustic cut-off frequency in the atmosphere are free to travel outwards in the atmosphere, resulting in strong damping.

A more quantitative analysis of Eq. (21) can be carried out using JWKB theory (see Gough 2007). In general, this results in an eigenvalue condition on $\omega$ given by

$$\begin{aligned} \int _{r_1}^{r_2} K^{1/2} \mathrm{d}r = (k - 1 / 2) \pi , \end{aligned}$$

(28)

for integer k, where $r_1$ and $r_2$ are adjacent turning points at which $K = 0$, such that $K > 0$ between $r_1$ and $r_2$. In the present case, for predominantly acoustic modes in main-sequence stars, this leads to

$$\begin{aligned} \omega \int _{r_\mathrm{t}}^{R_\mathrm{t}} \left( 1 - {\omega _\mathrm{c}^2 \over \omega ^2} - {S_l^2 \over \omega ^2} \right) ^{1/2} {\mathrm{d}r \over c} \simeq (k - 1/2)\pi . \end{aligned}$$

(29)

For low-degree modes, $r_\mathrm{t}$ is close to the centre in main-sequence stars. Equation (29) can be reduced to

$$\begin{aligned} \nu _{n l} \simeq \Delta \nu \left( n+\frac{l}{2}+\epsilon \right) -d_{n l} , \end{aligned}$$

(30)

using an expansion around $r = 0$ as well as near the surface (Gough 1986a, 1993). For main-sequence stars k can in general be related directly to the radial order n of the mode which was, therefore, used instead of k in Eq. (30). For evolved stars the definition of mode order is more complex; we return to this in Sect. 4.2.1. Equation (30) is the basis for the different frequency separations

$$\begin{aligned} \Delta \nu= & {} \nu _{n l} - \nu _{n-1\,l} \simeq \left( 2 \int _0^R \frac{\mathrm{d}r}{c} \right) ^{-1} , \end{aligned}$$

(31)

$$\begin{aligned} \delta \nu _{l\,l+2} (n)= & {} \nu _{n l}-\nu _{n-1\,l+2} \simeq -(4l+6)\frac{\Delta \nu }{4\pi ^2 \nu _{n l}}\int _0^R\frac{\mathrm{d} c}{\mathrm{d} r}\frac{\mathrm{d} r}{r} , \end{aligned}$$

(32)

and the phase term $\epsilon$. As discussed in Sects. 3.3.3–3.3.6 these quantities provide important diagnostics of stars based on their acoustic oscillations.⁷ From homology scaling $c^2 \propto M/R$. It follows from Eq. (31) that $\Delta \nu$, and hence from the leading-order first term in Eq. (30) $\nu _{nl}$, scale as

$$\begin{aligned} \nu _{nl} \propto \Delta \nu \propto \sqrt{\frac{M}{R^3}} \propto \sqrt{ \bar{\rho }} . \end{aligned}$$

(33)

From Eq. (23) it follows that the same scaling applies to $S_l$.

Fig. 11

Evolution track of a $1.3 \,\mathrm{M}_\odot$ star, from Jiang and Christensen-Dalsgaard (2014). The models $\mathrm{M_{SG}}$ and $\mathrm{M_{RG}}$ which are analysed below are marked by diamonds, and the segment corresponding to Fig. 13 is indicated in red

To investigate the changes in oscillation properties as a star evolves from the main sequence through the subgiant phase to the red-giant branch we consider a $1.3 \,\mathrm{M}_\odot$ evolution sequence from Jiang and Christensen-Dalsgaard (2014). The evolution in the HR diagram is illustrated in Fig. 11. The behaviour of the Lamb frequency remains similar as the star evolves, apart from the scaling with $\bar{\rho }^{1/2}$. However, the behaviour of the Brunt–Väisälä frequency is very different for red-giant models compared with main-sequence models. This can be seen by approximating $N^2$ as

$$\begin{aligned} N^2 \simeq {g^2 \rho \over p} ( \nabla _\mathrm{ad} - \nabla + \nabla _\mu ) , \end{aligned}$$

(34)

where $\nabla = \mathrm{d}\ln T / \mathrm{d}\ln p$, $\nabla _\mathrm{ad}$ is its adiabatic value and $\nabla _\mu = \mathrm{d}\ln \mu / \mathrm{d}\ln p$, with $\mu$ being the mean molecular weight. In a red giant with a compact core g reaches very high values in the deep interior of the star and so, therefore, does N. This is illustrated in Fig. 12 (note the logarithmic abscissa). Given the larger radius, both $S_l$ and $\nu _\mathrm{max}$ are substantially reduced. However, the most dramatic difference compared with Fig. 10 is the very large value of N in the core. Additional features in N are caused by the composition discontinuity at $r \simeq 0.09 R$ left behind after the first dredge-up (see Sect. 2.1.2) and local maximum at $r \simeq 0.005 R$ arising from the steep abundance gradient in the hydrogen-burning shell. Note also the very deep convective envelope, where N is imaginary and hence not shown.

Fig. 12

Characteristic frequencies for a red-giant model with mass $1.3\,\,\mathrm{M}_\odot$ and radius $6.2\,\,\mathrm{R}_\odot$ (Model $\mathrm{M_{RG}}$ in Fig. 11); a–d mark the turning points for $l = 1$ (cf. the analysis in Sect. 4.2.3) at the frequency indicated by the dotted line (cf. Eq. 26), with the red and blue parts marking, respectively, the g-mode and p-mode cavities for $l = 1$. See caption to Fig. 10 for the meaning of the different linestyles

For ascending-branch red-giant models such as the one shown in Fig. 12, there are two regions where $K >0$, leading to an oscillatory behaviour of the eigenfunctions, i.e., with $\omega > S_l, N$ or $\omega < S_l,N$. Of these, the outer region ($\omega > S_l, N$) corresponds essentially to the p-mode cavity in main-sequence stars discussed above. Modes trapped in this region, with the eigenfunction decreasing exponentially below it, satisfy Eq. (29). We note, however, that the analysis leading to the asymptotic approximation for low-degree modes cannot immediately be transferred to more evolved stars, given that the lower turning points lie outside the compact core (see also Sect. 4.2.3). Even so, both model computations and observations show that the acoustic modes of red giants satisfy a relation very similar to Eq. (30), i.e., the ‘universal pattern’. This was discussed in Sect. 3.3.2, where departures from this pattern were also mentioned. Indeed, Dziembowski (2012) found from stellar models that for the most luminous red-giant branch stars the dipolar mode frequencies are shifted substantially relative to the location at the mid-point between the neighbouring radial-mode frequencies which is predicted by the leading-order term in Eq. (29). This was confirmed observationally by Stello et al. (2014).

The inner oscillatory region ($\omega < S_l, N$) is in the core of the model, where the frequency is below the Brunt–Väisälä frequency. Modes trapped in this g-mode cavity are standing internal gravity waves, g modes, where buoyancy is the restoring force. Their frequencies may be estimated from Eq. (28), with $r_1$ and $r_2$ being approximately the points where $\omega = N$. Approximating K by assuming that $\omega \ll S_l$ and neglecting $\omega _c$ we obtain

$$\begin{aligned} \sqrt{l(l+1)}\int _{r_1}^{r_2} \left( {N^2 \over \omega ^2} - 1 \right) ^{1/2} \mathrm{d}r \simeq (k - 1/2) \pi . \end{aligned}$$

(35)

In most of the region $\omega \ll N$. With a correction for the behaviour near the turning points we can, therefore, approximate this further. We obtain a relation for the period $\varPi = 2 \pi / \omega$:

$$\begin{aligned} \varPi _{k\,l} = {\varPi _0 \over \sqrt{l(l+1)}} (k + \epsilon _\mathrm{g} +1/2) , \end{aligned}$$

(36)

where

$$\begin{aligned} \varPi _0 = 2 \pi ^2 \left( \int _{r_1}^{r_2} N {\mathrm{d}r \over r} \right) ^{-1} , \end{aligned}$$

(37)

and $\epsilon _\mathrm{g}$ is a phase term accounting for the behaviour near the turning points.⁸ Thus for modes trapped in the core of the model we obtain oscillations with uniformly spaced periods. These periods increase with increasing k, and with a spacing $\varPi _{k+1\,l} - \varPi _{k\,l} \simeq \Delta \varPi _l = \varPi _0 /\sqrt{l(l+1)}$ which depends on the degree of the modes. The diagnostic power of the period spacing is summarized in Sect. 3.3.7. As discussed in Sect. 4.2.1 g modes are by convention assigned negative radial orders $n_\mathrm{g}$, with frequency tending to zero as $n_\mathrm{g}$ tends to $- \infty$. Thus at least in simple cases of a pure g-mode spectrum k in Eq. (37) can be identified with $|n_\mathrm{g}|$. We return to a more complete discussion of mode order in Sect. 4.2.1 and beyond.

The preceding discussion was based on assuming the Cowling approximation, reducing to two the order of the equations of adiabatic pulsations. Dziembowski (2012) pointed out, however, that this approximation is questionable for dipolar modes (with $l = 1$). Here the perturbation to the gravitational potential gives rise to a slowly varying component of the solution which may have a significant effect on the properties of the modes. Takata (2005) and Takata (2006) provided the basis for a more complete analysis of these modes by introducing a change of variables that reduces the full oscillation equations for $l = 1$ to a second-order system, facilitating the asymptotic analysis. A detailed asymptotic analysis in this case was carried out by Takata (2016a) and supplemented by a more physical analysis, of broader applicability, by Takata (2016b). Qualitatively the new analyses are broadly consistent with earlier work on which we focus here. However, they contribute greatly to an understanding of the properties of the oscillations and the detailed diagnostic potential of the observed oscillation properties. Thus Takata’s results will undoubtedly play a major role in the further development of the field.

In the analysis leading to Eqs. (29) and (35) we assumed that the modes were completely trapped in the corresponding regions, i.e., acoustic modes with pressure as the restoring force (p modes) in the outer part of the star and gravity (g) modes with buoyancy as the restoring force in the core. However, it is clear from Fig. 12 that the evanescent region separating the two trapping regions is quite thin, particularly for $l = 1$ modes. This leads to substantial coupling between the two regions and hence generally to a mixed character of the modes. These mixed modes are responsible for the diagnostic richness of the solar-like oscillations in evolved stars. We discuss this in the following subsection.

4.2 Mixed modes

The first to consider non-radial mixed modes in highly evolved stars was likely Dziembowski (1971), who analysed the oscillations of Cepheid-type stars. Dziembowski noted that the huge values of the buoyancy frequency in the core of such stars meant that even at high frequencies the modes behaved as standing internal gravity waves in the inner parts of the star. Dziembowski carried out an asymptotic analysis of these properties. This was subsequently followed by a detailed investigation concerning the effects of non-adiabatic properties of the modes by Dziembowski (1977). Scuflaire (1974) analysed the oscillation properties of polytropes of high polytropic index and hence centrally condensed models. Scuflaire similarly noticed the mixed character of the modes and may have been the first to use explicitly the term ‘mixed modes’. Osaki (1975) followed the evolution of mixed modes in a massive main-sequence model. He noticed the effect of the increasing frequencies of the gravity waves in the core that led to the characteristic behaviour of the model frequencies with age (see Fig. 13).

Fig. 13

Evolution of frequencies for a $1.3 \,\mathrm{M}_\odot$ stellar model, from the beginning of the subgiant phase through the early red-giant phase (marked by the red part of the line in Fig. 11; see Sect. 2.1.2). The frequencies have been scaled by $(R/R_0)^{3/2}$, where $R_0$ is the ZAMS radius, to correct for the evolution with mean density of the acoustic-mode frequencies (cf. Eq. 7). The heavy long-dashed line shows an estimate of $\nu _\mathrm{max}$ (cf. Eq. 26), similarly scaled. The dashed lines show radial modes while the solid lines show dipolar modes, exhibiting avoided crossings first mentioned by Aizenman et al. (1977). The lower panel shows a small part, marked by a red rectangle, of the upper panel, to illustrate the behaviour in more detail. Adapted from Jiang and Christensen-Dalsgaard (2014)

The overall evolution of the frequencies of mixed modes is illustrated in Fig. 13, showing results for a $1.3 \,\mathrm{M}_\odot$ evolution sequence extending from just after central hydrogen exhaustion to the early part of the red-giant ascent (cf. Fig. 11). To eliminate the dependence of the acoustic-mode frequencies on stellar radius the frequencies have been scaled with $(R/R_0)^{3/2}$ (cf. Eq. 7), where $R_0$ is the zero-age main-sequence radius, such that the modes following the acoustic scaling relation, Eq. (33), appear with constant frequency. This is approximately the case for the radial modes (dashed lines in Fig. 13), and for $l = 1$ (solid lines in Fig. 13) for those modes that are predominantly of acoustic nature. However, there is clearly a second class of modes with scaled frequencies increasing with age. These modes are predominantly of g-mode character. Their frequencies increase with age following the strong increase in the buoyancy frequency caused by the contraction of the core (cf. Eq. 34). Where the frequency of such a mode meets an acoustically dominated mode the frequencies do not cross but approach quite closely. This is followed by an exchange of mode character such that the mode previously of g-mode nature becomes predominantly acoustic and vice versa. This behaviour was first noticed for evolving stars by Osaki (1975). It was also investigated by Aizenman et al. (1977), who were probably the first to use the term ‘avoided crossing’⁹ to describe it in astrophysics. Note, however, that similar phenomena have wide applicability to cases of coupled oscillations, including in atomic physics. An early illustrative analysis was provided by Neuman and Wigner (1929).

Even though the actual frequencies do not cross it is sometimes useful to relate them to fictitious uncoupled gravity and acoustic modes. These are the so-called ‘$\gamma$’ and ‘$\pi$’ modes, respectively, that do cross (see Aizenman et al. 1977). As discussed below the behaviour of the actual modes can then be analysed by introducing coupling between these fictitious modes. This also allows the definition of the numbers $N_\pi$ and $N_\gamma$ that represent the number of $\pi$ and $\gamma$ modes in the relevant frequency interval, e.g., corresponding to the range of radial modes (e.g., Benomar et al. 2013). In the earlier phases of evolution $N_\gamma \ll N_\pi$, whereas on the red-giant branch (towards the right edge of Fig. 13) $N_\pi \ll N_\gamma$. This variation in the overall structure of the oscillation spectrum has a major effect on the observed Fourier spectra (see Fig. 7).

To characterize the relative contributions of the different regions of the star to a mixed mode, a useful quantity is normalized inertia E. This is defined by

$$\begin{aligned} E = {\int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V \over M |\varvec{\delta }\varvec{r}|_\mathrm{phot}^2 } , \end{aligned}$$

(38)

where the integral is over the volume of the star, and the normalization uses the average squared photospheric displacement. In addition to E we also consider mode mass $M_\mathrm{mode} = M E$, where M is the mass of the star. These quantities are defined such that the average kinetic energy of the oscillation is

$$\begin{aligned} E_\mathrm{kin} = {1 \over 2} M_\mathrm{mode} V_\mathrm{rms}^2 , \end{aligned}$$

(39)

where $V_\mathrm{rms}$ is the average photospheric velocity. For p-dominated modes E is largely a function of frequency. This frequency dependence is determined by the depth of the upper turning point $R_\mathrm{t}$ and hence the decrease in amplitude of the eigenfunction between the oscillatory region below $R_\mathrm{t}$ and the surface. The value of E can be much larger for g-dominated modes, with a considerable amplitude in the gravity-wave propagating region in the deep interior, than for p-dominated modes. This is conveniently characterized by the scaled inertia

$$\begin{aligned} Q = {E \over \bar{E}_0(\omega )} , \end{aligned}$$

(40)

where $\bar{E}_0(\omega )$ is the radial (purely acoustic) mode inertia at the frequency of the mode considered.

For the analysis of red-giant oscillations it is convenient to consider the fraction of the mode inertia that comes from the inner parts of the star relative to the total mode inertia. Following Goupil et al. (2013) we introduce

$$\begin{aligned} \zeta = {E_\mathrm{core} \over E} , \end{aligned}$$

(41)

where $E_\mathrm{core}$ is defined as in Eq. (38) but restricting the integral to the region where $\omega < N, S_l$. Evidently $\zeta$ is small for modes trapped in the envelope, whereas $\zeta$ is close to one for modes trapped in the core. We also note that, as a rough approximation,

$$\begin{aligned} \zeta \simeq 1 - Q^{-1} , \end{aligned}$$

(42)

assuming that the envelope contribution to the inertia is similar to the inertia of a radial mode with the same frequency.¹⁰

For the practical evaluation and later analysis we note that the inertia can be expressed in terms of the displacement vector (cf. Eq. 19) as

$$\begin{aligned} E = {4 \pi \int _0^R [\xi _r(r)^2 + l(l+1) \xi _\mathrm{h}(r)^2] \rho r^2 \mathrm{d}r \over M [\xi _r(R_\mathrm{phot})^2 + l(l+1) \xi _\mathrm{h}(R_\mathrm{phot})^2]} , \end{aligned}$$

(43)

where $R_\mathrm{phot}$ is the photospheric radius.

4.2.1 Mode order

The mixed nature of the modes precludes a simple identification of the radial order of a mode based on the number of nodes. Using an earlier analysis by Eckart (1960), Scuflaire (1974) and Osaki (1975) independently proposed a scheme plotting the eigenfunction in a suitable phase diagram, e.g., in terms of $(\xi _r, \xi _\mathrm{h})$; the radial order is determined by counting the zero-crossings of $\xi _r$ with a positive or negative sign depending on whether the curve crosses the axis in the counter-clockwise or clockwise direction in the phase diagram. These zero-crossings are associated with the regions in the star where the mode has a p-mode or a g-mode character, respectively. If the number of counter-clockwise crossings is $\hat{n}_\mathrm{p}$ and the number of clockwise crossings is $|\hat{n}_\mathrm{g}|$,¹¹ with $\hat{n}_\mathrm{g} < 0$, the mode order is

$$\begin{aligned} n = \hat{n}_\mathrm{p} + \hat{n}_\mathrm{g} . \end{aligned}$$

(44)

When the perturbation to the gravitational potential is neglected this defines a mode order that is not changed for a given mode as the star evolves, even though its dominant physical character may change. For modes of degree $l \ge 2$ this property has also been found to be satisfied for solutions of the full equations of adiabatic oscillation. On the other hand, an application of the Eckart scheme to dipolar modes ($l = 1$) leads to a poorly defined mode order for evolved models (Lee 1985; Guenther 1991) or centrally condensed polytropes (Christensen-Dalsgaard and Mullan 1994). It was shown by Takata (2005) and Takata (2006) that a relation satisfied by the eigenfunctions of dipolar modes allows the definition of a scheme for the determination of mode order that is well-defined and invariant under evolution. As in Eq. (44) this is characterized by contributions $\hat{n}_\mathrm{p}$ and $\hat{n}_\mathrm{g}$ from the p-mode and g-mode dominated parts of the star. We use this in the later discussion of dipolar modes. Together with the original scheme proposed by Scuflaire (1974) and Osaki (1975) this defines mode orders that are invariant under evolution. Thus the order is unchanged when following a given mode as the star evolves in Fig. 13.

Formally, modes with positive n may be classified as p modes and modes with negative n as g modes. This classification largely corresponds to the physical nature of the modes for unevolved stars. However, as discussed below the non-radial mixed modes develop a large number of nodes in the g-mode propagation region as the star evolves on the red-giant branch and hence typically have a large negative value of $\hat{n}_\mathrm{g}$. Thus for such stars all relevant modes have negative n, and other properties of the modes must be used to characterize their physical nature. In any case, it should be kept in mind that the radial order defined here is a purely theoretical concept, although very useful in characterizing the oscillation modes of a given stellar model.

4.2.2 Subgiant stars

Fig. 14

Characteristic frequencies for the $1.3 \,\mathrm{M}_\odot$ subgiant model $\mathrm{M_{SG}}$ in Fig. 11, of age 4.293 Gyr and with $T_\mathrm{eff} = 5887.8\,$K. The red arrow marks the peak in the buoyancy frequency arising from the hydrogen-burning shell. See captions to Figs. 10 and 12 for the meaning of the linestyles

Fig. 15

Evolution of frequencies and mode inertias as a function of age (upper abscissa) and effective temperature (lower abscissa), for a $1.3 \,\mathrm{M}_\odot$ evolution sequence (cf. Fig. 11), including the model $\mathrm{M_{SG}}$ illustrated in Fig. 14. Dashed lines show modes with $l = 0$, and solid lines show modes with $l = 1$ (left) and $l = 2$ (right). The lower panels show the evolution of the inertia for the modes identified by triangles and squares in the upper panels, as well as a neighbouring radial mode (dashed line); note that the right-hand panel uses a logarithmic ordinate scale. The vertical dotted line in the top panels marks the model corresponding to the échelle diagram in Fig. 16

As a star evolves, the first g-dominated mixed modes start to be observable in subgiants. This provides a useful illustration of the properties of mixed modes. The characteristic frequencies for a subgiant model are shown in Fig. 14. This model has a helium core of radius 0.022R, containing 5% of the star’s mass. The behaviour of the acoustic frequencies differs little from those of a main-sequence model. However, the compact core and resulting high gravitational acceleration give rise to a high peak in the buoyancy frequency in the core, augmented by the sharp composition gradient in the hydrogen-burning shell. Therefore, at the indicated typical oscillation frequency (horizontal dotted line in Fig. 14) there are two trapping regions. The increase in the core buoyancy frequency with age leads to avoided crossings when following the evolution of the modes with age. This is illustrated in the top left panel of Fig. 15, which shows the behaviour of radial and dipolar modes. The resulting changes in the character of the modes in terms of the mode inertia for two of the dipolar modes, compared with a neighbouring radial mode, are shown in the lower left panel of Fig. 15. As long as the dipolar modes are predominantly acoustic their inertia is very similar to that of the radial mode. As a mode undergoes an avoided crossing and takes on a substantial g-mode character its inertia increases. At the next avoided crossing its inertia decreases again and the mode returns to an acoustic character, exchanging character with the next mode. At the point of closest approach the inertias of the two modes are very similar.

Figure 14 shows that for dipolar modes the evanescent region is relatively thin. This leads to strong coupling between the two oscillatory regions, a relatively large minimum separation during the avoided crossings, and a rather modest increase in the mode inertia when the modes are most g-mode like. This should be contrasted with the case of quadrupolar modes, shown in the right panels of Fig. 15. Here the evanescent region is considerably thicker, the coupling consequently weaker and the avoided crossings very sharp. Also, the inertia increases very rapidly as a mode takes on predominantly g-mode character. This shows that in any given model it is unlikely to find a mode that is not either predominantly p- or g-dominated.

The diagnostic potential of mixed modes in subgiant stars was discussed in Sect. 3.4.1.

Fig. 16

Top échelle diagram plotted with $\Delta \nu = 51.6~\upmu \mathrm{Hz}$, for the $1.3 \,\mathrm{M}_\odot$ subgiant model $\mathrm{M_{SG}}$, illustrated in Fig. 14 and marked with a vertical dotted line in Fig. 15, of age 4.293 Gyr and with $T_\mathrm{eff} = 5887.8\,$K. Modes with $l = 0$ are shown as circles, $l = 1$ as triangles, $l = 2$ as squares and $l = 3$ as diamonds. The size of the symbols is proportional to $Q^{-1/2}$ (cf. Eq. 40), providing a rough estimate of mode amplitude relative to a radial mode of the same frequency (cf. Eq. 118). For four quadrupolar modes very small symbols have been replaced by ‘+’. Dipolar modes are connected with dotted lines to highlight the effects of an avoided crossing; the two dipolar modes at the centre of an avoided crossing in Fig. 15 are shown with red triangles. Bottom for comparison we also show an échelle diagram for the observed low-degree observations of the Sun (Chaplin et al. 2002, $\Delta \nu =135.4$ $\upmu$Hz)

The presence of mixed modes causes departures from the asymptotic behaviour of pure acoustic modes, as illustrated in the échelle diagram in the top panel of Fig. 16; for comparison the bottom panel shows the corresponding diagram for the purely acoustic modes in the Sun. In the case of subgiant models the density of g-dominated modes is relatively low (i.e., $N_\gamma \ll N_\pi$; see above), and each avoided crossing effectively adds another mode to the frequency spectrum. The resulting changes in the oscillation spectrum were analysed by Deheuvels and Michel (2010) based on a simple physical model of coupled oscillators. They considered the coupling between a single $\gamma$ mode and several $\pi$ modes.¹² The effect on the distribution of peaks in the échelle diagram is illustrated in Fig. 16 for the model marked by a vertical dotted line in Fig. 15. At high frequency the dipolar modes have not yet been affected by g-mode mixing, and the behaviour corresponds to the purely acoustic case. However, as shown in Fig. 15 there is a pair of mixed dipolar modes with nearly the same inertia at a frequency around $930~\upmu \mathrm{Hz}$. These are visible as a pair of modes on either side of the $l = 1$ ridge in Fig. 16. At lower frequency essentially all the dipolar modes show an effect of the avoided crossings, as also argued by Deheuvels and Michel (2010).

For $l = 2$ the right-hand panels of Fig. 15 also indicate the presence of g-dominated modes. However, for these the scaled inertias $Q_{n\,l}$ are so high that they would not be visible with the proposed scaling of symbol size in Fig. 16. Therefore, they are indicated by plusses. As discussed above the high scaled inertias of mixed $l=2$ modes are a consequence of the much weaker coupling between the buoyancy and acoustic cavities for quadrupole modes. Only mixed quadrupole modes with frequencies close to the pure acoustic $l=2$ mode can reach observable amplitudes and could thus be detected. However, such modes would be difficult to identify observationally, except if a clear pair of closely spaced modes is detected.

Fig. 17

Mode inertia for the red-giant model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The upper panel shows the inertia (cf. Eq. 38) as a function of frequency for modes of degree $l = 0$ (circles, connected by a solid line), $l = 1$ (triangles, connected by a dashed line) and $l = 2$ (squares, connected by a dot-dashed line). The lower panel shows the normalized inertia (cf. Eq. 40) for $l = 1$ and 2

Fig. 18

Integrands $\mathcal{I}$ for the mode inertia E (cf. Eq. 38), defined such that $E = \int _0^R \mathcal{I}\mathrm{d}\ln r$, for modes with $l = 1$ in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The red dashed line shows the p-dominated mode with frequency $84.3~\upmu \mathrm{Hz}$ and the black solid line the g-dominated mode with frequency $79.1~\upmu \mathrm{Hz}$. The modes are marked as red diamonds in Fig. 21

4.2.3 Ascending-branch red giants

As a star evolves up the red-giant branch its internal structure and hence its oscillation spectrum change dramatically. As an example of an ascending-branch star we consider the most evolved stellar model in Fig. 13, which is indicated with the upper diamond in Fig. 11. The properties of the modes of this model in terms of the mode inertia and scaled mode inertia (cf. Eqs. 38 and 40) are shown in Fig. 17. The $l = 1$ and 2 modes form a very dense spectrum with inertias typically exceeding the inertia of the neighbouring acoustic modes by several orders of magnitude. These high-inertia modes are buoyancy-dominated modes that are predominantly trapped in the g-mode cavity in the deep interior of the star. Additionally, there are acoustic resonances where one or more modes have inertias close to the radial-mode inertia. This is particularly visible in the bottom panel of Fig. 17, where low scaled inertia $Q_{n\,l}$ indicates the modes that have largest amplitude in the p-mode cavity.

To further illustrate the properties of the modes, Fig. 18 shows the integrands of the inertia for the most p-dominated and the most g-dominated dipolar modes with a frequency near $80~\upmu \mathrm{Hz}$. There is clear similarity in shape between the two curves;¹³ the main difference is in the behaviour in the evanescent region near $r/R = 0.1$, where the eigenfunction increases with depth for the g-dominated mode (black curve) and decreases with depth for the p-dominated mode (red curve). As a result, the region beneath 0.1R contributes 99.5% to the inertia of the g-dominated mode, while for the most p-dominated mode 63% of the inertia comes from the g-mode cavity. Hence, even for p-dominated modes the contribution from the g-mode cavity is significant. Additionally, Fig. 18 illustrates the extremely rapid variation of the eigenfunction that results from the high buoyancy frequency in the g-mode cavity. This rapid variation becomes even more extreme in more evolved red giants where the eigenfunctions may have thousands of nodes in the deep interior. This places severe requirements on the numerical techniques used to compute these modes. Techniques that explicitly take such rapid variations into account have indeed been developed (Gabriel and Noels 1976; Townsend and Teitler 2013).

Pressure-dominated modes The acoustic resonances of non-radial modes together with the radial modes satisfy a frequency pattern similar to the asymptotic behaviour of acoustic modes in main-sequence stars (cf. Eq. 30). This is evident in the échelle diagram shown in Fig. 19 where in particular the $l = 0$ and 2 modes have a behaviour very similar to what is seen in the solar case (cf. bottom panel of Fig. 16). In addition to these p-dominated modes a few additional $l = 2$ modes are visible with the chosen scaling. For $l = 1$ the pattern is more complicated, i.e., several mixed modes are visible per acoustic-mode order. Nevertheless, a dominant set of modes still follows the asymptotic expression.

Fig. 19

Échelle diagram for the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. See the caption to Fig. 16 for the meaning of symbols and symbol sizes

This regular pattern is a universal feature of observed (and modelled) red-giant oscillations (Mosser et al. 2011b, and Sect. 3.3.2). However, the reason that the asymptotic relation holds is not entirely clear. The analysis leading to Eq. (30) is fundamentally related to the behaviour of the solution of the oscillation equations near the singularity at $r = 0$ (see also Gough 1986a, 1993). However, in the case of red giants the properties of the acoustic resonances are determined by the requirement that the solution decrease with increasing depth in the evanescent region (see also Fig. 18). Here conditions are very different from the conditions in the central regions of a main-sequence star. Despite these different conditions the universal pattern seems to hold. A better physical understanding of this behaviour of the frequency pattern of the acoustically dominated modes may lead to additional diagnostic potential of the observations.

Fig. 20

Period spacing for $l = 1$ modes, as a function of frequency, in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The heavy dashed line shows the asymptotic period spacing $\varPi _0/\sqrt{2}$ (cf. Eqs. 36 and 37). For clarity we do not show the individual modes

Fig. 21

Frequency as a function of scaled mode inertia Q (left), period spacing (centre) and period modulo period spacing ($\Delta \varPi _1 = 75.4~\mathrm{s}$), i.e., period échelle diagram (right) for $l = 1$ modes in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The red diamonds mark the modes illustrated in Fig. 18 or, in the central panel, the period spacings between those marked modes and the adjacent mode with higher period

Gravity-dominated modes The properties of gravity-dominated modes are to a large extent determined by the structure of the core. Hence, these oscillations have a large potential for the study of the internal structure of red giants. It was found by Beck et al. (2011) that the observed spectrum of a red giant shows additional peaks which were identified as coming from mixed modes with a stronger g-dominated component (see Fig. 1). The behaviour of these mixed modes is dominated by the g-mode asymptotic relation, Eq. (36). According to this relation the gravity modes are uniformly spaced in period. This is illustrated by Fig. 20 showing the period spacing $\varPi _{n\,l} - \varPi _{n+1\,l}$ for $l = 1$, as a function of frequency. At relatively low frequency there are modes with nearly constant spacing, while the spacing shows a characteristic decrease around the more p-dominated modes. The actual period spacing is in excellent agreement, particularly at low frequency, with the asymptotic period spacing marked by the horizontal dashed line. Thus observations of low-frequency g-dominated modes provide a direct measure of the integral of the buoyancy frequency in the core of the star.

The fact that several dipolar mixed modes are visible in the vicinity of the acoustically dominated modes, as observed by Beck et al. (2011), might indeed have been expected from the rough amplitude scaling in an échelle diagram such as shown in Fig. 19. In fact, as discussed in Sect. 4.3, even fully g-dominated modes may have sufficient visibility to be observed in very long time series, such as those that were obtained by Kepler’s nominal 4-year mission. An example is shown in fig. 1b of Stello et al. (2013a) for a red-clump star.

Following Bedding et al. (2011) we introduced period échelle diagrams in Sect. 3.3.7, based on the uniform period spacing of g-dominated modes. Figure 21 shows such a diagram for a part of the modes shown in Fig. 20. For comparison we also show the scaled mode inertia and the period spacing. Gravity-dominated modes with high inertia fall approximately on a vertical line in the period échelle diagram. This is as expected from the asymptotic behaviour. Around this vertical line departures are visible near the acoustic resonances. It may be noticed that the variations near the resonances are qualitatively similar to the variations induced by g-dominated modes in the frequency échelle diagram for a subgiant star (cf. Fig. 16).

Coupling of buoyancy and acoustic cavities Asymptotic analysis of the mixed modes in red giants must take into account the coupling between the buoyancy and acoustic cavities. A full analysis of this problem has been carried out by Shibahashi (1979) (see also Unno et al. 1989).¹⁴ The analysis is based on simplified equations of the form given in Eq. (21), and has been implemented for the red-giant case by Goupil (private communication) and Mosser et al. (2012c). Shibahashi showed that continuous matching of the solutions between the two cavities leads to the resonance condition

$$\begin{aligned} \cot \left( \int _{r_\mathrm{a}}^{r_\mathrm{b}} K^{1/2} \mathrm{d}r - \phi _\mathrm{g} \right) \tan \left( \int _{r_\mathrm{c}}^{r_\mathrm{d}} K^{1/2} \mathrm{d}r - \phi _\mathrm{p} \right) = q , \end{aligned}$$

(45)

implicitly determining the eigenfrequencies. In Eq. (45) $r_\mathrm{a}$, $r_\mathrm{b}$, $r_\mathrm{c}$ and $r_\mathrm{d} \simeq R$ are the four turning points where K changes sign (cf. Fig. 12), and $\phi _\mathrm{g}$ and $\phi _\mathrm{p}$ are phases depending on the properties of the turning points. Additionally,

$$\begin{aligned} q = {1 \over 4} \exp \left( -2 \int _{r_\mathrm{b}}^{r_\mathrm{c}} |K|^{1/2} \mathrm{d}r \right) \end{aligned}$$

(46)

is a measure of the strength of the coupling between the two cavities.

Takata (2016b) carried out a very illuminating physical analysis of the properties of mixed modes in terms of the reflection and transmission of waves at the evanescent region, with a more rigorous analysis for dipolar modes provided by Takata (2016a). He pointed out that Eq. (46) is only valid in the case of weak coupling and provided expressions of more general validity. In particular, with strong coupling the value of q may substantially exceed the upper limit of 1 / 4 indicated by Eq. (46). However, the resonance condition, Eq. (45), on which the following discussion is largely based, remains valid.

To analyse Eq. (45) it is convenient to introduce

$$\begin{aligned} \theta _\mathrm{g} = \int _{r_\mathrm{a}}^{r_\mathrm{b}} K^{1/2} \mathrm{d}r - \phi _\mathrm{g} , \quad \theta _\mathrm{p} = \int _{r_\mathrm{c}}^{r_\mathrm{d}} K^{1/2} \mathrm{d}r - \phi _\mathrm{p} \end{aligned}$$

(47)

(e.g., Unno et al. 1989; Mosser et al. 2012c), so that the equation becomes

$$\begin{aligned} \tan \theta _\mathrm{p} \cot \theta _\mathrm{g} = q . \end{aligned}$$

(48)

We approximate K by $K \simeq l(l+1) r^{-2} \, N^2/\omega ^2$ in the buoyancy cavity, $[r_\mathrm{a}, r_\mathrm{b}]$ and by $K \simeq \omega ^2 / c^2$ in the acoustic cavity, $[r_\mathrm{c}, r_\mathrm{d}]$. Then we obtain

$$\begin{aligned} \theta _\mathrm{p} \simeq \omega / \omega _\mathrm{p} - \phi _\mathrm{p} , \quad \theta _\mathrm{g} \simeq \omega _\mathrm{g} / \omega - \phi _\mathrm{g} , \end{aligned}$$

(49)

where

$$\begin{aligned} \omega _\mathrm{p} = \left( \int _{r_\mathrm{c}}^{r_\mathrm{d}} {\mathrm{d}r \over c} \right) ^{-1} \simeq 2 \Delta \nu \end{aligned}$$

(50)

(cf. Eq. 31) and

$$\begin{aligned} \omega _\mathrm{g} = \sqrt{l(l+1)} \int _{r_\mathrm{a}}^{r_\mathrm{b}} {N \over r} \mathrm{d}r \simeq {2 \pi ^2 \over \Delta \varPi _l} \; \end{aligned}$$

(51)

(cf. Eq. 37). In Eq. (50) we neglected the small contribution to $\Delta \nu$ from the core region.

To interpret Eq. (48) we first consider the uncoupled case, i.e., $q = 0$. This should in principle yield Eqs. (30) and (36) for the uncoupled $\pi$ and $\gamma$ modes, respectively. In the uncoupled case Eq. (48) has one set of solutions with $\tan \theta _\mathrm{p} = 0$, or, equivalently,

$$\begin{aligned} \nu = {\omega \over 2 \pi } \simeq \Delta \nu (n_\mathrm{p} + \epsilon _\mathrm{p}) \end{aligned}$$

(52)

for integer $n_\mathrm{p}$, and $\epsilon _\mathrm{p} = \phi _\mathrm{p}/\pi$. This indeed superficially recovers the leading-order term in the acoustic-mode asymptotic relation (30) for the uncoupled $\pi$ modes, although with $\phi _\mathrm{p}$ and $\epsilon _\mathrm{p}$ being independent of l. In contrast, the observed and computed p-dominated frequencies satisfy Eq. (30) which includes an l dependence. However, the analysis leading to Eq. (52) neglected the dependence on l of K in the acoustic cavity and the detailed behaviour near the lower turning point $r_\mathrm{c}$. To compensate for this we simply replace $\epsilon _\mathrm{p}$ by $\epsilon _{\mathrm{p}\,l}$ (and similarly for $\phi _\mathrm{p}$) with $\epsilon _{\mathrm{p}\,l} = \epsilon _\mathrm{p\,0} + l/2$, such that we recover Eq. (30). A full understanding of the universal pattern (Eq. 6) requires a more complete analysis extending the one leading to Eq. (45), which has so far not been carried out. However, it was pointed out by Mosser et al. (2012c, 2015), Deheuvels et al. (2015) that expressing $\theta _\mathrm{p}$ as

$$\begin{aligned} \theta _\mathrm{p} = {\pi \over \Delta \nu } \left( \nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)}\right) , \end{aligned}$$

(53)

in terms of purely acoustic frequencies $\nu _{n_\mathrm{p}\,l}^\mathrm{(p)}$, such as the universal acoustic-mode pattern, Eq. (6), allows the use of a more complete description of the location of the acoustic resonances than provided by Eq. (52).

The second set of solutions for an uncoupled ($q=0$) case satisfy $\cot \theta _\mathrm{g} = 0$ or, equivalently,

$$\begin{aligned} \varPi = {2 \pi \over \omega } = \Delta \varPi _l ( |n_\mathrm{g}| + \epsilon _\mathrm{g} + 1/2) , \end{aligned}$$

(54)

where $n_\mathrm{g}$ is an integer and $\epsilon _\mathrm{g} = \phi _\mathrm{g}/\pi$. In accordance with the discussion in Sect. 4.2.1 we have chosen $n_\mathrm{g} < 0$, using $n_\mathrm{g}$ rather than $\hat{n}_\mathrm{g}$ in this asymptotic expression. We discuss the relation between $n_\mathrm{g}$ and $\hat{n}_\mathrm{g}$ below. In this case we indeed recover Eq. (36), defining the uncoupled $\gamma$ modes. Corresponding to Eq. (53), we express $\theta _\mathrm{g}$ as

$$\begin{aligned} \theta _\mathrm{g} \equiv {\omega _\mathrm{g} \over \omega } - \phi _\mathrm{g} \simeq \pi \left( {1 \over \Delta \varPi _l \nu } - \epsilon _\mathrm{g} \right) = {\pi \over \Delta \varPi _l} \left( {1 \over \nu } - {1 \over \nu _{n_\mathrm{g}\,l}^\mathrm{(g)}} \right) + {\pi \over 2} , \end{aligned}$$

(55)

where we introduced the uncoupled g-mode frequency as per Eq. (54):

$$\begin{aligned} \nu _{n_\mathrm{g}\,l}^\mathrm{(g)} = \left[ \Delta \varPi _l ( |n_\mathrm{g}| + \epsilon _\mathrm{g} + 1/2)\right] ^{-1} . \end{aligned}$$

(56)

We note that, in the last equalities in Eqs. (53) and (55), we ignored the contributions $n_\mathrm{p} \pi$ and $|n_\mathrm{g}| \pi$ which have no effect in Eq. (48).

To analyse the coupled case, i.e., Eq. (48), Mosser et al. (2012c) rewrote it by moving the g-mode-related part to the right-hand side as $\tan \theta _\mathrm{g}$, using Eqs. (53) and (55) and taking the inverse tangent, to obtain

$$\begin{aligned} \nu = \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} + {\Delta \nu \over \pi } \arctan \left[ q \tan \pi \left( {1 \over \Delta \varPi _l \nu } - \epsilon _\mathrm{g} \right) \right] . \end{aligned}$$

(57)

This provides an implicit equation for $\nu$, which can be determined iteratively, given the other parameters of the equation. Also, it provides the basis for determining these parameters through fits to observed frequencies. As discussed in Sects. 3.3.7 and 5.4 this results in powerful diagnostics for stellar structure and evolution.

The detailed relation between the numerical order n and its components $\hat{n}_\mathrm{p}$ and $\hat{n}_\mathrm{g}$ (cf. Sect. 4.2.1) and the asymptotic indices $n_\mathrm{p}$ and $n_\mathrm{g}$ has apparently not been fully explored. Passing through an acoustic resonance $\nu = \nu _{n_\mathrm{p}\,l}^\mathrm{(p)}$ is associated with the increase by one in the number of nodes in the p-mode region of the star, and hence with an increase by one in $\hat{n}_\mathrm{p}$. In fact it seems that we can identify $\hat{n}_\mathrm{p}$ with $n_\mathrm{p}$ for the acoustically-dominated modes. Similarly, there is a close relation between $\hat{n}_\mathrm{g}$ and $n_\mathrm{g}$ characterizing the asymptotic properties of the g-dominated modes, at least for stars on the ascending red-giant branch. The situation is probably more complicated in more complex stars, possibly with several separate regions of g-mode propagation and/or buoyancy glitches (see also Sects. 4.2.4 and 4.2.5).

As noted by Mosser et al. (2012c) a useful quantity is the estimate of the number of g-dominated modes associated with a given acoustic resonance, which can be obtained as

$$\begin{aligned} \mathcal{N}= {\Delta \nu \over \Delta \varPi _l {\nu _{n_\mathrm{p}\,l}^\mathrm{(p)}}^2} . \end{aligned}$$

(58)

Adding the mode at the acoustic resonance the total number of modes in a $\Delta \nu$ interval around the resonance is $\mathcal{N}+ 1$.

An alternative way to analyse Eq. (48) was proposed by Christensen-Dalsgaard (2012a)¹⁵ and developed further by Jiang and Christensen-Dalsgaard (2014). They rewrote Eq. (48) as

$$\begin{aligned} \sin \theta _\mathrm{p} \cos \theta _\mathrm{g} - q \cos \theta _\mathrm{p} \sin \theta _\mathrm{g} =0 . \end{aligned}$$

(59)

This can be rewritten as

$$\begin{aligned} \cos [\omega _\mathrm{g} / \omega + \varPhi (\omega ) - \phi _\mathrm{g}] = 0 \; , \end{aligned}$$

(60)

where $\varPhi$ satisfies

$$\begin{aligned} \tan \varPhi = q \cot \theta _\mathrm{p} = q \cot \left[ {\pi \over \Delta \nu } \left( \nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} \right) \right] . \end{aligned}$$

(61)

By choosing the appropriate integer multiples of $\pi$ we can define $\varPhi$ as a continuous function of $\omega$. Thus the eigenfrequencies satisfy

$$\begin{aligned} \omega _\mathrm{g}/\omega + \varPhi (\omega ) - \phi _\mathrm{g} = (k + 1/2) \pi , \end{aligned}$$

(62)

for integer k, or equivalently

$$\begin{aligned} \varPsi (\nu ) \equiv {1 \over \Delta \varPi _l \nu } + \pi ^{-1} \varPhi (2 \pi \nu ) - \epsilon _\mathrm{g} -1/2 = k . \end{aligned}$$

(63)

The function $\varPhi$ is illustrated in Fig. 22. To understand its properties it is convenient to rewrite Eq. (61) as $\varPhi = \arctan [ q \cot \pi (\nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)})/\Delta \nu ]$.¹⁶ The value of q is typically relatively small. Therefore, for most frequencies $\varPhi$ is close to a multiple of $\pi$. This is illustrated by the dotted lines in Fig. 22. However, near the acoustic resonances, where $\nu \simeq \nu _{n_\mathrm{p}\,l}^\mathrm{(p)}$, the argument to $\arctan$ goes through a singularity. This leads to the rapid variation of $\varPhi$.

We note that Eq. (63) provides an alternative way to determine the frequencies of mixed modes, given $\Delta \nu , \nu _{n_\mathrm{p}\,l}^\mathrm{(p)}, q, \Delta \varPi _l$ and $\epsilon _\mathrm{g}$: $\varPhi$ can be directly computed from Eq. (61), defining $\varPsi$ as a function of frequency from Eq. (63); the frequencies of the mixed modes are then simply obtained as those values where $\varPsi$ takes on consecutive integer values. This is numerically straightforward, given that $\varPsi$ is a monotonic function of $\nu$, and relates the frequencies directly to the mode order in the integer k.

Fig. 22

The effective phase $\varPhi$ (cf. Eq. 61) as a function of frequency for $l = 1$, in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The horizontal dotted lines indicate multiples of $\pi$. Here we used $\theta _\mathrm{p} = \pi (\nu / \Delta \nu - \epsilon _{\mathrm{p}\,l})$, with $\Delta \nu = 9.32~\upmu \mathrm{Hz}$ and $\epsilon _{\mathrm{p}\,l} = 1.528$

In Eq. (63) increasing k leads to decreasing frequency, corresponding to decreasing n, where n is the numerical mode order introduced in Sect. 4.2.1; also, $\varPhi$ is only defined from Eq. (61) to within an integer multiple of $\pi$. It appears that this can be chosen such that $k = -n$. This reflects the fact that Eq. (63) defines the complete spectrum of mixed modes for the given degree.

The behaviour of $\varPhi$ near the resonances is directly related to the variation in the period spacing (cf. Fig. 20). Writing Eq. (63) as

$$\begin{aligned} \varPi _{n\,l} = \Delta \varPi _l [ k + \epsilon _\mathrm{g} + 1/2 - \pi ^{-1} \varPhi (2 \pi \nu _{n\,l}) ] , \end{aligned}$$

(64)

with $\nu _{n\,l} = 1/\varPi _{n\,l}$, and making a Taylor expansion of $\varPhi (2 \pi \nu _{k+1}) - \varPhi (2 \pi \nu _{k})$ we obtain

$$\begin{aligned} \varPi _{n\,l} - \varPi _{n+1\,l} \simeq \Delta \varPi _l \left( 1 - {2 \Delta \varPi _l \over \varPi _{n\,l}^2} {\mathrm{d}\varPhi \over \mathrm{d}\omega } \right) ^{-1} . \end{aligned}$$

(65)

Thus for the g-dominated modes, where $\varPhi$ is nearly constant, we recover $\Delta \varPi _l$. At the same time the period spacing decreases near the acoustic resonances (note that $\mathrm{d}\varPhi /\mathrm{d}\omega < 0$). Jiang and Christensen-Dalsgaard (2014) presented an approximation to Eq. (65) and discussed the use of this to estimate q from the variation in the period spacings.

The quality of the asymptotic fit derived above (Eq. 63) is illustrated in Fig. 23 for model $\mathrm{M_{RG}}$ in Fig. 11. For the g-dominated modes the relative differences between the computed and asymptotic frequencies are less than $10^{-4}$. The relative difference increases to $5 \times 10^{-4}$ for frequencies undergoing acoustic resonances. However, these differences have a far stronger effect on the period spacings.

Fig. 23

Period échelle diagram for $l = 1$, in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. Here a frequency range encompassing two pressure-dominated modes is shown. The numerically computed periods are shown by a solid line with plus symbols. The solution from Eq. (63), based on $\varPhi$ as shown in Fig. 22, is depicted by a dashed line and diamonds

The coupling constant q depends on the properties of the evanescent region and hence in principle provides further diagnostics of the stellar interior. This is reflected by Eq. (46) that was already obtained by Shibahashi (1979). The values of q determined from Eq. (46) and from fits to numerical frequencies were compared by Jiang and Christensen-Dalsgaard (2014), who found substantial differences between these values. This appears in part to be due to the neglect of the perturbation to the gravitational potential in the asymptotic analysis, and could, for dipolar modes, be avoided by using the formulation of Takata (2006) which avoids this approximation. Furthermore, the approximation to Eq. (65) by Jiang and Christensen-Dalsgaard (2014) neglects potential singularities, particularly in the evanescent region. These effects require further analysis. Finally, as mentioned above, Takata (2016a, b) showed that Eq. (46) is only valid for weak coupling, which may not be appropriate in the cases considered by Jiang and Christensen-Dalsgaard (2014).

From an observational point of view Mosser et al. (2012c) determined coupling strengths for a substantial number of red-giant and clump stars observed with Kepler; they noted that clump stars showed larger values of q than did the red giants, in many cases exceeding the upper limit of 0.25 predicted by Eq. (46). A very large number of Kepler targets was analysed by Mosser et al. (2017b), providing a detailed overview of the dependence of q on stellar parameters.

The phase $\epsilon _\mathrm{g}$ in principle provides further information about stellar structure, particularly the regions at the turning points of the g-mode cavity. Buysschaert et al. (2016) carried out fits to data for three red giants obtained by Kepler, including a variable $\epsilon _\mathrm{g}$ as one of the fitted parameters (see Sect. 3.3.7). They found that $\epsilon _\mathrm{g}$ was only weakly constrained by the observations; however, allowing $\epsilon _\mathrm{g}$ to vary resulted in a clearer definition of the values of the period spacing and its uncertainty obtained in the fit. From a theoretical point of view, Takata (2016a) provided some insight into the dependence of $\epsilon _\mathrm{g}$ on the properties of the model. These issues also deserve further studies.

Asymptotic properties of mode inertia It is instructive to consider the asymptotic properties of the mode inertia, in particular the relative contribution $\zeta$ from the core (cf. Eq. 41). The value of $\zeta$ is closely related to the effects of rotation on the oscillation frequencies and the damping of the modes. The following is based on the detailed analysis by Shibahashi (1979, S79), which was further developed by Goupil et al. (2013) and Deheuvels et al. (2015).

S79 expressed the asymptotic analysis in terms of two functions v(r) and w(r) related to $\xi _r$ and $\xi _\mathrm{h}$ by

$$\begin{aligned} v= & {} \rho ^{1/2} c r \left( \left| 1 - {S_l^2 \over \omega ^2} \right| \right) ^{-1/2} \xi _r \nonumber \\ w= & {} \rho ^{1/2} \omega r^2 \left( \left| {N^2 \over \omega ^2} -1\right| \right) ^{-1/2} \xi _\mathrm{h} . \end{aligned}$$

(66)

In the outer parts of the star the modes are predominantly acoustic, with $|\xi _r| \gg |\xi _\mathrm{h}|$. In this case the integral for the inertia (Eq. 43) is dominated by the term in $\xi _r$. From the asymptotic expression for v (Eq. (28) of S79, applied in the acoustic outer region) we here obtain

$$\begin{aligned} \xi _r \simeq C \rho ^{-1/2} c^{-1/2} \omega ^{-1/2} r^{-1} \cos \left( \int _r^R K^{1/2} \mathrm{d}r - \phi _\mathrm{p}^\prime \right) , \end{aligned}$$

(67)

where C is a normalization constant and $\phi _\mathrm{p}^\prime$ is a phase. As noted above, we use the definition of K given in footnote 14. As in the derivation of Eq. (50), we neglected $S_l^2/\omega ^2$ in the amplitude function in Eq. (66) compared with 1, which is a good approximation except close to the turning point $r_\mathrm{c}$. Using the same approximation, we obtain from Eq. (67) the contribution of the outer parts of the star to the numerator in Eq. (43)

$$\begin{aligned} I_\mathrm{p} = \int _{r_\mathrm{c}}^R \xi _r^2 \rho r^2 \mathrm{d}r \simeq C^2 \omega ^{-1} \int _0^{\tau _\mathrm{c}} \cos ^2(\omega \tau - \phi _\mathrm{p}^\prime ) \mathrm{d}\tau , \end{aligned}$$

(68)

where

$$\begin{aligned} \tau = \int _r^R {\mathrm{d}r \over c} \end{aligned}$$

(69)

is the acoustic depth, and $\tau _\mathrm{c}$ is the acoustic depth of the turning point $r_\mathrm{c}$. For a mode of high acoustic order the integral over $\cos ^2$ can be replaced by $1/2 \, \tau _\mathrm{c}$. Using Eq. (50) we obtain

$$\begin{aligned} I_\mathrm{p} \simeq {1 \over 4} C^2 {1 \over \omega \Delta \nu } . \end{aligned}$$

(70)

In the inner parts of the star the mode is buoyancy dominated, with $|\xi _\mathrm{h}| \gg |\xi _r|$. Here, the inertia integral is dominated by the term in $\xi _\mathrm{h}$. In this case the relevant asymptotic solution, from the relevant expression for w (Eq. (29) of S79, in the g-mode cavity) is

$$\begin{aligned} \xi _\mathrm{h} \simeq A \rho ^{-1/2} \omega ^{-3/2} r^{-3/2} L^{-1/2} N^{1/2} \sin \left( \int _{r_\mathrm{a}}^r K^{1/2} \mathrm{d}r - \phi _\mathrm{g}^\prime \right) , \end{aligned}$$

(71)

where $L^2 = l(l+1)$, A is a normalization constant and $\phi _\mathrm{g}^\prime$ is a phase. As in the derivation of Eq. (51) we neglected 1 compared with $N^2 / \omega ^2$. From Eq. (71) we then obtain for the contribution of the g-mode region to the numerator in Eq. (43)

$$\begin{aligned} I_\mathrm{g} = L^2 \int _{r_\mathrm{a}}^{r_\mathrm{b}} \xi _\mathrm{h}^2 \rho r^2 \mathrm{d}r \simeq A^2 \omega ^{-3} L \int _0^{r_\mathrm{b}} N \sin ^2 \left( {L \over \omega } \int _0^r N {\mathrm{d}r' \over r'} - \phi _\mathrm{g}^\prime \right) {\mathrm{d}r \over r} , \end{aligned}$$

(72)

where we extended the integrals to $r = 0$. It should be noticed that the amplitude of the integrand scales like N, when integrating with respect to $\ln r$. This is indeed confirmed by comparing the integrand shown in Fig. 18 with the buoyancy frequency in Fig. 12. Introducing the buoyancy radius

$$\begin{aligned} \upsilon = \int _0^r N {\mathrm{d}r \over r} \end{aligned}$$

(73)

we obtain

$$\begin{aligned} I_\mathrm{g} \simeq A^2 \omega ^{-3} L \int _0^{\upsilon _\mathrm{b}} \sin ^2 \left( {L \over \omega } \upsilon - \phi _\mathrm{g}^\prime \right) \mathrm{d}\upsilon \simeq {1 \over 2} A^2 \omega ^{-3} L \upsilon _\mathrm{b} , \end{aligned}$$

(74)

where $\upsilon _\mathrm{b}$ is the buoyancy radius of the turning point $r_\mathrm{b}$, and replacing as before the integral over $\sin ^2$ by $1/2 \, \upsilon _\mathrm{b}$. Using Eq. (51) yields

$$\begin{aligned} I_\mathrm{g} \simeq A^2 {\pi ^2 \over \Delta \varPi _l \omega ^3} . \end{aligned}$$

(75)

Finally, by combining Eqs. (70) and (75), we obtain

$$\begin{aligned} {I_\mathrm{p} \over I_\mathrm{g}} \simeq {C^2 \over A^2} {\Delta \varPi _l \nu ^2 \over \Delta \nu } . \end{aligned}$$

(76)

To complete the analysis we need the ratio C / A between the amplitudes of the eigenfunctions in Eqs. (67) and (71). This ratio is determined by the coupling across the evanescent region, $[r_\mathrm{b}, r_\mathrm{c}]$. From Eq. (30) of S79, and using the dispersion relation (Eq. 48), it can be shown that

$$\begin{aligned} {C \over A} = q^{-1/2} {\cos \theta _\mathrm{g} \over \cos \theta _\mathrm{p}} . \end{aligned}$$

(77)

Thus

$$\begin{aligned} {I_\mathrm{p} \over I_\mathrm{g}} \simeq q^{-1} {\cos ^2 \theta _\mathrm{g} \over \cos ^2 \theta _\mathrm{p}} {\Delta \varPi _l \nu ^2 \over \Delta \nu } , \end{aligned}$$

(78)

or, using Eqs. (53) and (55),

$$\begin{aligned} {I_\mathrm{p} \over I_\mathrm{g}} \simeq q^{-1} {\Delta \varPi _l \nu ^2 \over \Delta \nu } {\displaystyle \cos ^2 \left[ \pi \left( {1 \over \Delta \varPi _l \nu } - \epsilon _\mathrm{g} \right) \right] \over \displaystyle \cos ^2 \left[ { \pi ( \nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} ) \over \Delta \nu } \right] } . \end{aligned}$$

(79)

It follows that the fractional contribution of the g-mode region to the inertia is obtained as

$$\begin{aligned} \zeta\simeq & {} {I_\mathrm{g} \over I_\mathrm{p} + I_\mathrm{g}} = \left( 1 + {I_\mathrm{p} \over I_\mathrm{g}} \right) ^{-1} \nonumber \\\simeq & {} \left\{ 1 + q^{-1} {\Delta \varPi _l \nu ^2 \over \Delta \nu } {\displaystyle \cos ^2 \left[ \pi \left( {1 \over \Delta \varPi _l \nu } - \epsilon _\mathrm{g} \right) \right] \over \displaystyle \cos ^2 \left[ { \pi ( \nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} ) \over \Delta \nu } \right] } \right\} ^{-1} \equiv \zeta _\mathrm{as} \; \end{aligned}$$

(80)

(Deheuvels et al. 2015). They also demonstrated that $\zeta _\mathrm{as}$ provides a remarkably good fit to the numerically computed $\zeta$. By using Eq. (48) this can be further simplified as

$$\begin{aligned} \zeta _\mathrm{as} = \left\{ 1 + q {\Delta \varPi _l \nu ^2 \over \Delta \nu } {1 \over \displaystyle q^2 + (1 - q^2) \sin ^2 \left[ { \pi ( \nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} ) \over \Delta \nu } \right] } \right\} ^{-1} . \end{aligned}$$

(81)

Mosser et al. (2015) pointed out that Eq. (81) shows a very interesting relation between $\zeta$ and the actual period spacing between mixed modes. To see this, we return to Eq. (65). Differentiating Eq. (61) we obtain

$$\begin{aligned} {\mathrm{d}\varPhi \over \mathrm{d}\omega }= & {} - q \omega _\mathrm{p}^{-1} {1 \over (q^2 \cot ^2 \theta _\mathrm{p} + 1) \sin ^2\theta _\mathrm{p}} \nonumber \\= & {} - q \omega _\mathrm{p}^{-1} {1 \over q^2 + (1 - q^2) \sin ^2\theta _\mathrm{p}} . \end{aligned}$$

(82)

Substituting this into Eq. (65), using Eqs. (50) and (53), yields

$$\begin{aligned} \varPi _{n\,l} - \varPi _{n+1\,l} \simeq \zeta _\mathrm{as} \Delta \varPi _l , \end{aligned}$$

(83)

with $\zeta _\mathrm{as}$ given by Eq. (81). This is the result obtained by Mosser et al. (2015). Equation (83) is satisfied to high accuracy by computed values of $\zeta$ and period spacing for red-giant models. As an example, Fig. 24 shows part of the period spacing from Fig. 20, but including also $\zeta \Delta \varPi _1$, with $\zeta$ computed from the numerical eigenfunctions.

Fig. 24

Enlargement of the period spacing for $l = 1$ modes, as a function of frequency, shown in Fig. 20, in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The heavy dashed line shows the asymptotic period spacing $\Delta \varPi _1 = \varPi _0/\sqrt{2}$, and the red dotted line and symbols show $\zeta \Delta \varPi _1$ (cf. Eq. 83), where $\zeta$ was obtained from the numerically computed eigenfunctions

We note that the derivation of $\zeta _\mathrm{as}$, and hence the relation in Eq. (83), assumes the validity of the comparatively simple asymptotics employed by Shibahashi (1979), which requires a slow variation of the equilibrium quantities. This approximation is not valid in the case of sharp features in the buoyancy frequency, such as is the case for Model 1a of Cunha et al. (2015) (see also Fig. 30). In these cases the more complex analysis of Cunha et al. would be required.

From Eq. (83) Mosser et al. (2015) and Vrard et al. (2016) noted that the properties of $\zeta _\mathrm{as}$ (or $\zeta$)¹⁷ are largely controlled by the properties of the acoustic resonances, with little dependence on the period spacing. As a result they were able to develop a technique for determining $\zeta$ from the observations in the vicinity of the acoustic resonances. Given $\zeta$, they introduced a stretching function $\mathcal{P}(\nu )$ ¹⁸ by

$$\begin{aligned} \mathrm{d}\mathcal{P}(\nu ) = - {1 \over \zeta } {\mathrm{d}\nu \over \nu ^2} , \end{aligned}$$

(84)

and the stretched periods $\tilde{\varPi }_{nl} = \mathcal{P}(\nu _{nl})$. Replacing $\zeta$ by $\zeta _\mathrm{as}$ and relating $\zeta _\mathrm{as}^{-1}$ to $\mathrm{d}\varPhi / \mathrm{d}\omega$ using Eqs. (81) and (82) yield

$$\begin{aligned} \mathrm{d}\mathcal{P}(\nu ) = \left( - {1 \over \nu ^2} + {\Delta \varPi _l \over \pi } {\mathrm{d}\varPhi \over \mathrm{d}\nu } \right) \mathrm{d}\nu , \end{aligned}$$

(85)

or, with suitable choice of integration constant,

$$\begin{aligned} \mathcal{P}= {1 \over \nu } + {\Delta \varPi _l \over \pi } \varPhi = \Delta \varPi _l \left[ \varPsi (\nu ) + \epsilon _\mathrm{g} + 1/2 \right] , \end{aligned}$$

(86)

using the definition of $\varPsi$ in Eq. (63). From Eq. (63) it follows that the stretched periods of the modes satisfy

$$\begin{aligned} \tilde{\varPi }_{n\,l} = \Delta \varPi _l (k + \epsilon _\mathrm{g} + 1/2) . \end{aligned}$$

(87)

Thus we formally recover the relation (54) for the uncoupled g modes. However, this relation is now valid for all modes. As shown by Mosser et al. (2015) this greatly simplifies the period échelle diagram when expressed in terms of the stretched period. This is illustrated in Fig. 25; as suggested by Eq. (87) all modes fall essentially on a straight line.

Fig. 25

Left period échelle diagram with $\Delta \varPi _1 = 75.4~\mathrm{s}$ for $l = 1$ modes, in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$, as also shown in the right panel of Fig. 21. Right period échelle diagram using stretched periods $\tilde{\varPi }$, with $\Delta \varPi _1 = 75.6~\mathrm{s}$. The red diamonds mark the modes illustrated in Fig. 18

Vrard et al. (2016) developed the stretching technique into an automated method for analysing the red-giant mixed-mode spectra of large samples of stars; this is particularly powerful in dealing with the complications of rotational splitting. We return to this in Sect. 4.4.

4.2.4 Effects of glitches

Much of the preceding discussion of the properties of red-giant oscillations was based on the asymptotic properties of the modes. This conveniently allows characterizing the oscillation spectrum by a relatively small number of parameters, such as $\Delta \nu$, $\Delta \varPi _1$, etc. However, the asymptotic approximation also indicates a limitation of the diagnostic potential of the observations, as far as the detailed internal properties of the stars are concerned. It should be kept in mind that the asymptotic analysis is based on the assumption that the underlying stellar structure varies on a scale that is long compared with the local wavelength of the oscillations. Structure features on a smaller scale introduce perturbations to the frequencies which may provide diagnostics about these structures. This was pointed out in the case of p modes in the Sun by Gough (1990), who noted that at the base of the convection zone in normal solar models the second derivative of the sound speed is discontinuous. In addition, the relatively rapid variation of $\varGamma _1$, and hence the sound speed, in the second helium ionization zone may also cause departures from the asymptotic behaviour. Vorontsov et al. (1991) used the signature of helium ionization in observed solar frequencies to infer the solar envelope helium abundance. Such features in the sound speed were denoted acoustic glitches by Gough (2002). Similarly, sharp features in the buoyancy frequency (buoyancy glitches Cunha et al. 2015) may affect g-dominated modes.

Fig. 26

Top panel gradient of sound speed with respect to acoustic depth $\tau$ (cf. Eq. 69) in the red-giant model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. Lower panel scaled displacement eigenfunction, on arbitrary scale, for a radial mode with frequency $\nu = 98.1~\upmu \mathrm{Hz}$ in the same model. The lower abscissa shows acoustic depth and the upper abscissa the corresponding relative distance to the centre

The base of the convective envelope in red giants is typically too deep to induce a significant effect on the p-dominated modes (Miglio et al. 2010). An example of the acoustic glitch associated with the helium ionization zone in a red-giant star is illustrated in Fig. 26, showing the derivative of sound speed in terms of acoustic depth $\tau$ (cf. Eq. 69). Here the dominant feature is the dip in $\mathrm{d}c /\mathrm{d}\tau$ near $\tau = 1.5 \times 10^4 \, \mathrm{s}$ which is associated with the second helium ionization zone. For comparison the lower panel shows the scaled displacement eigenfunction of a radial mode of frequency $98.1~\upmu \mathrm{Hz}$, with a variation at the helium feature which is substantially slower than the structural variation. Thus the helium dip does act as an acoustic glitch.

Fig. 27

Second frequency differences (cf. Eq. 89) in the model illustrated in Fig. 26 for $l = 0$ (circles) and the most acoustically dominated modes with $l = 1$ (triangles) and $l = 2$ (squares). For clarity modes of degree 0 and 2 are connected by a dotted line

Gough (1990) showed that the effect of an acoustic glitch is to introduce a variation $\delta \nu ^\mathrm{(gl)}$ of the form

$$\begin{aligned} \delta \nu ^\mathrm{(gl)} \propto \sin (4 \pi \nu \tau _\mathrm{gl} + 2 \phi _\mathrm{gl}) \; \end{aligned}$$

(88)

(see also Eq. 18), where $\tau _\mathrm{gl}$ is the acoustic depth of the glitch and $\phi _\mathrm{gl}$ is a phase. Thus at fixed $\tau _\mathrm{gl}$ we expect an oscillatory behaviour of $\delta \nu ^\mathrm{(gl)}$ as a function of cyclic frequency, with a period of around $(2 \tau _\mathrm{gl})^{-1}$. Gough (1990) furthermore proposed isolating the effect of the glitch from other possible slower variations of the frequencies with radial order by considering second differences at fixed l,

$$\begin{aligned} \Delta _2 \nu _{n\,l} = \nu _{n-1\,l} - 2 \nu _{n\,l} + \nu _{n+1\,l} \; . \end{aligned}$$

(89)

This is illustrated in Fig. 27 for the same model as shown in Fig. 26. The effect of the helium glitch is only relevant for the acoustic properties of the modes, and hence we have selected just those modes with $l = 1$ and 2 with the lowest inertia in each radial-mode frequency interval; modes with degree 0 and 2 are connected by a dotted line. The figure shows the expected oscillatory behaviour, although modes with $l = 1$ that are more strongly affected by the mixed nature show some scatter around the general trend and hence have not been connected. The period of the oscillation is roughly consistent with the acoustic depth of the glitch. The amplitude of the oscillation depends on the strength of the glitch, which is determined by the magnitude of the variation in $\varGamma _1$ and hence provides a diagnostic of the helium abundance in the convective envelope of the star. With increasing frequency the local wavelength of the eigenfunction gets shorter, making the glitch appear less sharp and hence reducing the amplitude of the variation in the second difference (see also Sect. 3.4.5).

Houdek and Gough (2007) carried out a detailed analysis of the effects of the acoustic glitches in the first and second helium ionization zones and the base of the convective envelope in the Sun. This led to an expression already summarized in Eq. (18). They noted the importance of a proper definition of the acoustic surface, i.e., the zero point of the acoustic depth, in the interpretation of the analysis of acoustic glitches. The potential uncertainty involved in the definition of the acoustic surface, and the effects of the near-surface errors in stellar modelling (cf. Sect. 3.4.3), can in principle be avoided by converting the acoustic depth to an acoustic distance from the centre (e.g., Ballot et al. 2004); this uses the fact that the asymptotic large frequency separation $\Delta \nu$ is related to the total acoustic radius of the star (cf. Eq. 31). In practice the acoustic depth of a feature and the large frequency separation may respond differently to the near-surface uncertainties, in particular since $\Delta \nu$ is typically determined from a suitable fit or average over the observed modes.

Buoyancy glitches, i.e., sharp features in the buoyancy frequency, are of great potential interest owing to their sensitivity to the composition structure. Analysis of buoyancy glitches caused by the composition discontinuities established through gravitational settling has played a major role in the study of white-dwarf oscillations as important diagnostics of the internal structure of the stars (e.g., Winget et al. 1994). Additionally, in a detailed analysis Miglio et al. (2008) demonstrated the diagnostic potential of the buoyancy glitch at the edge of convective cores in more massive main-sequence pulsators, leading to oscillations with mode order in the period spacings of high-order g modes. Evidence for this behaviour was found by Degroote et al. (2010) in a slowly pulsating B star observed by CoRoT, indicating effects of processes smoothing the composition gradient at the edge of the core. Thus it is of great interest to consider the potential for studies of buoyancy glitches in evolved stars.

Fig. 28

Buoyancy frequency in $1 \,\mathrm{M}_\odot$ model with a radius of $9.7 \,\mathrm{R}_\odot$ and an effective temperature of $4439 \, \mathrm{K}$ (adapted from Cunha et al. 2015)

Fig. 29

Top panel Buoyancy frequency in the core of the model illustrated in Fig. 28 (Cunha et al. 2015). Bottom panel scaled horizontal displacement (on arbitrary scale) for a mode in this model with $l = 1$, $\nu = 43.41~\upmu \mathrm{Hz}$

Figure 12 shows the presence of potential glitches in the buoyancy frequency in red-giant models. These were analysed in considerable detail by Cunha et al. (2015), including an asymptotic analysis of the effect of a discontinuity in composition and a resulting singularity in the buoyancy frequency (cf. Eq. 34). Here we discuss aspects of these issues using as an example a model corresponding to Model 1a of Cunha et al. (2015), but with a density discontinuity at the base of the dredge-up region. The buoyancy frequency for this model is shown in Fig. 28. The model is in a somewhat later evolutionary stage, just before the red-giant ‘bump’, than the model shown in Fig. 12. Here the convective envelope has retracted in mass since the maximal extent of the first dredge-up (see Sect. 2.1.2), leaving behind a composition and density discontinuity within the g-mode propagation region, here shown as a sharp spike in N at $r/R \simeq 0.02$. This is obviously a glitch.¹⁹ The second relatively sharp feature is associated with the hydrogen-burning shell. As illustrated in Fig. 29 this is not a glitch, however, since the eigenfunction varies extremely rapidly in this region. This is an immediate consequence of the asymptotic behaviour in Eq. (71), according to which the local radial wave number scales as N / r and hence becomes very large at the peak in the buoyancy frequency.

Fig. 30

Period spacings for modes with $l = 1$, in a $1 \,\mathrm{M}_\odot$ model at the bump, with buoyancy glitch (adapted from Cunha et al. 2015). The red dotted line shows $\zeta \Delta \varPi _{1,\mathrm{as}}$. The lower panel provides a blow-up of the region near the asymptotic period spacing

The analysis by Cunha et al. (2015) shows that, for a pure g mode, the presence of a buoyancy glitch gives rise to an oscillatory behaviour such as was found by, e.g., Miglio et al. (2008), with a period depending on the location of the glitch within the g-mode cavity. Taking into account also the mixed nature of the modes, with the coupling to the p-mode behaviour, leads to a complex variation in the frequencies and the period spacings, as illustrated in Fig. 30.²⁰ The presence of a glitch clearly invalidates the derivation of the asymptotic relation in Eq. (83) between $\zeta$ and the period spacing, as also illustrated in Fig. 30. This shows a very interesting diagnostic potential for the characterization of the chemical profile left by the dredge-up in red giants just below the bump; however, since the effects are subtle a more detailed analysis is required to ascertain whether the effect can reliably be isolated in the existing data. Cunha et al. (2015) proposed a diagnostic of the irregularity of the period spacings, based on a Fourier transform of period spacing as a function of period, which in the model results provides a strong indication of glitch effects. This also demonstrated that the effects in red-giant models are closely linked to the red-giant bump.

As discussed in the next section buoyancy glitches play a dominant role in the oscillation spectrum of core helium-burning stars.

4.2.5 Stars on the red clump

A major early realization in the analysis of space-based asteroseismic observations of evolved stars was that there is a sharp distinction between stars on the ascending red-giant branch, with hydrogen fusion around the helium core, and stars in the red clump where in addition there is helium fusion near the centre (Bedding et al. 2011; Mosser et al. 2011a) (see also Sect. 3.3.7). The g-mode period spacing is substantially smaller in the red giants than in clump stars. This is a straightforward consequence of the difference in the internal structure between these different stars (at fixed surface radius, say), given the asymptotic expression for the period spacing, Eq. (37), and the expression for the buoyancy frequency, Eq. (34). The core helium-burning stars have a convective core (see Figs. 4, 5), which restricts the g-mode cavity and contributes to reducing the integral over the buoyancy frequency in Eq. (37), hence increasing the asymptotic period spacing (e.g., Christensen-Dalsgaard 2014). In addition, with ignition of helium burning the core expands, reducing the local gravitational acceleration and hence the buoyancy frequency (cf. Eq. 34), further increasing the period spacing.

Fig. 31

Helium abundance as a function of fractional radius in a model in the core helium-burning phase, with initial mass $1.5 \,\mathrm{M}_\odot$, radius $12.2 \,\mathrm{R}_\odot$ and effective temperature $4648\,\mathrm{K}$

To illustrate these effects we consider models discussed by Christensen-Dalsgaard et al. (2014). The evolution sequence, extending from the pre-main sequence through the central helium-burning phase, was computed with the GARSTEC code (Weiss and Schlattl 2008). This includes full treatment of the helium flash and the subsequent sub-flashes (see Sect. 2.1.3). The resulting helium abundance profile Y in a model with initial mass $1.5 \,\mathrm{M}_\odot$ near the end of central helium burning is illustrated in Fig. 31. The region of constant Y inside $0.0015\, R$ is convective. As discussed in Sect. 2.1.4 a discontinuity in Y, and hence in density, may be established at the edge of the convective core. In the rest of the helium core the smaller steps in composition reflect the convective mixing associated with the initial helium flash and the sub-flashes.

Fig. 32

The solid curve shows the buoyancy frequency in the core helium-burning model illustrated in Fig. 31. For comparison, the dashed curve shows the buoyancy frequency in a red-giant model on the same $1.5 \,\mathrm{M}_\odot$ initial mass evolution sequence, with a radius of $12.0 \,\mathrm{R}_\odot$ and effective temperature $4532 \,\mathrm{K}$. The solid and dashed green lines show the Lamb frequency $S_{\!1}$ for the clump and red-giant models, respectively. The dotted lines indicate the frequencies $\nu _\mathrm{max}$ of maximum oscillation power (cf. Eq. 26), with the red and blue parts marking, respectively, the g-mode and p-mode cavities for $l = 1$; for clarity the g- and p-mode cavities are also shown, respectively, by the red and blue bars above the plot, for the red-giant (RGB) and clump (RC) models

The buoyancy frequency of this model is illustrated in Fig. 32 and compared with that of a red-giant model of the same initial mass and approximately the same radius and slightly lower effective temperature. This immediately shows the two effects mentioned above: the presence of a convective core and the lower general level of the buoyancy frequency in the core helium-burning model. As a result the asymptotic dipolar period spacing in the core helium-burning model is $\Delta \varPi _1 = 244.2 \, \mathrm{s}$ while in the red-giant model $\Delta \varPi _1 = 56.9 \, \mathrm{s}$. This is the effect found by Bedding et al. (2011) and Mosser et al. (2011a) and extensively used since then to characterize evolved stars (e.g., Stello et al. 2013b; Mosser et al. 2014, see Fig. 47).

Fig. 33

Frequency échelle diagrams for the red-giant (top) and clump (bottom) models illustrated in Fig. 32. In the red-giant model $\Delta \nu = 3.845~\upmu \mathrm{Hz}$, and in the clump model $\Delta \nu = 3.870~\upmu \mathrm{Hz}$. For clarity the frequencies have been shifted by $\nu _0 =0.4~\upmu \mathrm{Hz}$ in both panels. Circles, triangles and squares show modes of degree 0, 1 and 2, respectively. As in Fig. 16 the symbol size for the non-radial modes have been scaled with $Q^{-1/2}$, where Q is the inertia ratio (Eq. 40), providing a rough indication of the expected amplitude of the modes. The dipolar modes with lowest inertia in each radial-mode frequency interval are shown in red in the bottom panel

A second clear difference between the red-giant and clump models in Fig. 32 is the extent of the evanescent region between the buoyancy and acoustic cavities, which is much smaller in the clump than in the red-giant model, leading to a stronger coupling. The effect of this is illustrated in frequency échelle diagrams in Fig. 33 where, as in Fig. 16, the symbol size provides an indication of the expected amplitude of the modes. It is evident that the stronger coupling in the clump model leads to a much broader spread of modes, particularly for $l = 1$. This is probably the reason for the less regular behaviour of the dipolar mode separations found by Montalbán et al. (2010) who identified the most acoustic modes as those modes having the smallest inertia in a given radial-mode interval (see also Sect. 3.3.6). To illustrate this, these modes are shown in red in Fig. 33.

Fig. 34

Dipolar period spacings derived from the differences in the periods of the computed modes (solid line) in the core helium-burning model illustrated in Fig. 31. The horizontal dashed line shows the asymptotic period spacing $\Delta \varPi _1$; the red dotted line shows the period spacing $\zeta \Delta \varPi _1$ predicted from the comparatively simple asymptotic analysis in Sect. 4.2.3 (cf. Eq. 83), although using $\zeta$ computed from the numerical eigenfunctions

The diagnostics of clump stars has so far predominantly been based on the observed and asymptotically calculated period spacings. However, the actual behaviour of the model frequencies is rather more complicated, owing to the composition discontinuities and resulting spikes in the buoyancy frequency, also visible in Fig. 32. These act as glitches and lead to partial reflection of the g modes. The specific behaviour depends strongly on fine details of the model calculation, such as whether diffusion (numerical or physical) is included and whether the composition profile and buoyancy frequency are properly resolved in the numerical computations. Figure 34 shows the computed dipolar period spacings in the core helium-burning model in Fig. 32, compared with the asymptotic period spacing and the period spacing expected from the asymptotics in Eq. (83), but using the numerically computed $\zeta$. The computed period spacing is clearly related to the expected behaviour in this case, reflecting the location of the acoustic resonances shown by $\zeta$, but with substantial variations caused by the glitches in the buoyancy frequency.²¹

To illustrate further the sensitivity of the clump-model oscillations to details of the model structure we consider two models with initial mass $1 \,\mathrm{M}_\odot$ computed with the LPCODE (Althaus et al. 2005). Their helium-abundance profiles Y are illustrated in Fig. 35. The models only differ in the sharp decrease in Y caused by the off-centre onset of the helium flash and the associated convective mixing. In one model this is essentially discontinuous, whereas in the second model the composition has been slightly smoothed by diffusion. The resulting buoyancy frequencies in the vicinity of this glitch are shown in Fig. 36, which also shows the scaled horizontal displacement for a dipolar mode in the ‘sharp’ model. For the model with the sharp helium profile this variation in the buoyancy frequency is clearly a glitch. For the slightly smoothed model the scales of the buoyancy frequency and the eigenfunction are comparable, and hence one may expect a smaller effect of the local model structure.²²

Fig. 35

Helium abundance as a function of fractional radius in two models in the core helium-burning phase, with initial mass $1.0 \,\mathrm{M}_\odot$, radius $12 \,\mathrm{R}_\odot$ and effective temperature $4699\,\mathrm{K}$. The inset shows the region near the sharp decrease in Y at $r/R \simeq 0.0047$ caused by convection associated with the helium flash at the start of helium burning. One model (solid) has a composition discontinuity, whereas in the second model (dashed) this has been slightly smoothed by diffusion. (Models courtesy of Marcelo Miguel Miller Bertolami)

Fig. 36

Top panel Buoyancy frequency in the vicinity of the sharp decrease in the helium abundance in the models illustrated in Fig. 35. For the nearly discontinuous helium profile the buoyancy frequency is essentially a delta function (solid line). The buoyancy frequency for the slightly smoothed model is shown by a dashed line. Bottom panel scaled horizontal displacement (on arbitrary scale) for a mode in the model with the nearly discontinuous helium profile, with $l = 1$, $\nu = 19.9~\upmu \mathrm{Hz}$. (Models courtesy of Marcelo Miguel Miller Bertolami)

Fig. 37

Dipolar period spacings derived from the differences in the periods of the computed modes (solid line) in the core helium-burning models illustrated in Fig. 35. The top panel shows results for the model with a sharp helium profile from the onset of the helium flash, while the lower panel is for the model with a slightly smoothed profile. The horizontal dashed lines show the asymptotic period spacing $\Delta \varPi _1$, while the red dotted lines show $\zeta \Delta \varPi _1$ (see caption to Fig. 34). (Models courtesy of Marcelo Miguel Miller Bertolami)

This is indeed confirmed by the dipolar period spacings shown in Fig. 37. For the ‘sharp’ model the period spacings vary wildly, with little indication of the effects of the acoustic resonances, as reflected by the period spacing expected from asymptotics (cf. Eq. 83) shown by the dotted red curve. In the slightly smoothed model (bottom panel) the variations in the period spacing are less dramatic and there are some indications of the decreases in the period spacing expected from the asymptotic behaviour, shown by the red dotted curve. However, even in this case a proper analysis of the variation in the period spacing, and a determination of its asymptotic value, would be difficult.

The behaviour of the internal structure during the phases of the helium flash and sub-flashes was analysed by Bildsten et al. (2012). They found strong changes in the asymptotic period spacing and the coupling between the buoyancy and acoustic propagation regions, noting that this may provide opportunities for the detailed diagnostics of this evolution phase. Even though it is brief, the large number of clump stars for which oscillation data are available from Kepler may make it realistic that at least a few stars are in this phase; interestingly, Mosser et al. (2014) do in fact identify several such stars in their $(\Delta \nu , \Delta \varPi _1)$ diagram (see Fig. 47). Cunha et al. (2015) pointed out that the expansion of the helium core at the onset of helium burning compresses the hydrogen-burning shell, so that it acts as a buoyancy glitch during this phase (unlike on the red-giant branch; cf. Fig. 29). This would add to the diagnostic potential of the observed oscillations. We note, however, that the early helium-burning model considered by Cunha et al. (2015) did not have discontinuities in the composition and hence did not suffer from the strong glitch effects illustrated in Fig. 37.

Constantino et al. (2015) carried out an extensive analysis of the oscillation properties of stars in the clump phase, varying also convective-core overshoot and other mixing processes at the edge of the convective core. This clearly showed the very rich pulsational behaviour that may be found in these stars. An interesting issue raised was the relation to the g-mode oscillations of the core helium-burning subdwarf B stars which essentially correspond to the naked core of the clump stars (e.g., Østensen et al. 2014). Constantino et al. also addressed the fact that computed asymptotic period spacings for clump models tend to be lower than the observed spacings (see also Fig. 47). A possible solution, although perhaps with limited physical justification, would be the effect of what Constantino et al. call the ‘maximum-overshoot’ scheme. Similarly, Bossini et al. (2015) considered various mixing schemes at the edge of the helium-burning convective core and their effects on the period spacing. They also pointed out that combining observed period spacings with the location of the so-called AGB bump in stellar clusters, resulting from non-monotonic luminosity evolution at the onset of helium shell burning (see Sect. 2.1.5), would provide further observational constraints on these mixing processes. Further studies are certainly needed on the apparent discrepancies between the theoretically predicted detailed properties and the observations, and of the consequences for the interpretation of the observations in terms of simple diagnostics such as the asymptotic period spacing.

4.3 Energetics of stellar oscillations

It is generally accepted that solar-like oscillations, including those in the Sun, are intrinsically damped (but see Xiong and Deng 2007) and excited stochastically by the near-surface convection whose near-sonic speed makes the gas motions efficient in generating acoustic noise (Stein 1968). This is confirmed by analysis of the statistical properties of the variations in solar-oscillation amplitudes (Chaplin et al. 1997),²³ which follow the pattern expected from stochastic excitation (Kumar et al. 1988; Chang and Gough 1998). Also, there is a striking similarity of the variation of amplitudes with frequency from the main sequence to red-giant branch, apart from the scaling of the frequency of maximum power with surface gravity (e.g., De Ridder et al. 2009; Stello et al. 2010). Furthermore, there is strong evidence that the variability seen in very evolved stars represents an extension of the red-giant solar-like oscillations (Dziembowski and Soszyński 2010; Mosser et al. 2013a). This possibly includes semiregular variables, where analysis of up to century-long series of amateur observations has revealed statistical properties matching those of solar-like oscillations (Christensen-Dalsgaard et al. 2001). A concise review of energetics of red-giant oscillations was provided by Dupret and Belkacem (2012).

The general theory of stochastic forcing of a damped oscillator was described by Batchelor (1953). It was applied to the analysis of observed solar modes by Christensen-Dalsgaard et al. (1989). The resulting average power spectrum of a single mode, with angular frequency $\omega _0$ and damping rate $\eta = - \omega _\mathrm{i}$ (cf. Eq. 20), has the form

$$\begin{aligned} P(\omega ) \simeq {1 \over 4 \omega _0^2} {P_\mathrm{f} (\omega ) \over (\omega - \omega _0)^2 + \eta ^2} , \end{aligned}$$

(90)

where $P_\mathrm{f}$ is the average power spectrum of the forcing function, which varies relatively slowly with frequency. Consequently the spectrum is a Lorentzian with a full width at half maximum in angular frequency of $2 \eta$; in terms of cyclic frequency the full width at half maximum is

$$\begin{aligned} \varGamma = {\eta \over \pi } . \end{aligned}$$

(91)

Measurement of the width of the observed peaks, therefore, provides a measure of the damping rates of the modes (see also Sect. 3.4, in particular Eq. 14). In addition to the damping rate it is convenient to characterize the damping by the mode damping time $t_\mathrm{damp}$, defined by the time required to reduce the mode amplitude by a factor e and given by

$$\begin{aligned} t_\mathrm{damp} = \eta ^{-1} . \end{aligned}$$

(92)

4.3.1 Properties of the damping rate

To study the energetics of the modes the full set of non-adiabatic equations must be solved. These include also perturbations to the energy transport and the energy equation and result in a determination of the complex frequency $\omega = \omega _\mathrm{r} + \mathrm{i}\omega _\mathrm{i}$ as an eigenvalue, and hence the damping rate $\eta = - \omega _\mathrm{i}$. However, to analyse $\eta$ it is convenient to express it in terms of the work integral (e.g., Baker and Kippenhahn 1962; Cox 1967, see also Aerts et al. 2010). Considering just perturbations to thermodynamic quantities the result is

$$\begin{aligned} \eta = \eta _\mathrm{gas} = - {1 \over 2 \omega _\mathrm{r}^2} {\displaystyle \mathrm{Re} \left[ \int _V {\delta \rho ^* \over \rho } (\varGamma _3 - 1) \delta (\rho \varepsilon - \mathrm{div}\,\varvec{F}) \mathrm{d}V \right] \over \int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} , \end{aligned}$$

(93)

where $\varepsilon$ is the rate of energy generation per unit mass, $\varvec{F}$ is the flux of energy, $\varGamma _3 - 1 = (\partial \ln T / \partial \ln \rho )_\mathrm{ad}$ and the star indicates the complex conjugate; also, $\delta$ denotes the Lagrangian perturbation, i.e., the perturbation following the motion (see also footnote 24). The integral in the numerator of Eq. (93) reflects the operation of a heat engine, with $\delta \rho$ defining compression, and $\delta (\rho \varepsilon - \mathrm{div}\,\varvec{F})$ defining heating. If the integral is positive, $\omega _\mathrm{i}$ is positive and the mode is excited. However, in the case discussed here of solar-like oscillations the integrated effect is negative and the mode is damped.

Equation (93) is generally valid, including for fully non-adiabatic solutions. A major source of uncertainty in the calculation of the work integral is the treatment of the perturbations to the convective contribution to the flux, particularly near the surface. An additional complication in the near-surface region is the effect of turbulent pressure $p_\mathrm{t}$ which makes a significant contribution to the total pressure in the outermost parts of the convection zone and hence also affects the pulsations. As a consequence, the full expression of the damping rate becomes

$$\begin{aligned} \eta = \eta _\mathrm{gas} + \eta _\mathrm{t} , \end{aligned}$$

(94)

where $\eta _\mathrm{gas}$ is given by Eq. (93) and

$$\begin{aligned} \eta _\mathrm{t} = {1 \over 2 \omega _\mathrm{r}} {\displaystyle \mathrm{Im} \left( \int _V {\delta \rho ^* \over \rho } \delta p_\mathrm{t} \mathrm{d}V \right) \over \int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} \end{aligned}$$

(95)

(e.g., Balmforth 1992a; Houdek and Dupret 2015), Im denoting the imaginary part. We return to these convective effects below.

In much of the star where the oscillations are essentially adiabatic, the contribution to the work integral can be estimated from the quasi-adiabatic approximation, calculating all terms from the adiabatic eigenfunctions. In red giants a potentially substantial contribution to the damping comes from the buoyancy-dominated region in the core, where the very high radial order of the g-mode behaviour causes a strong diffusive damping. In the outer parts of the star, on the other hand, the contributions to the damping are dominated by the near-surface layers, where the properties of the oscillations are independent of degree. To analyse this it is, therefore, convenient to separate the work integral into contributions from the core and the envelope. We introduce

$$\begin{aligned} \mathcal{D}= - {1 \over 2 \omega _\mathrm{r}^2} \mathrm{Re} \left[ {\delta \rho ^* \over \rho } (\varGamma _3 - 1) \delta (\rho \varepsilon - \mathrm{div}\,\varvec{F}) \right] + {1 \over 2 \omega _\mathrm{r}} \mathrm{Im} \left( {\delta \rho ^* \over \rho } \delta p_\mathrm{t} \right) , \end{aligned}$$

(96)

such that the full expression for the work integral can be written

$$\begin{aligned} \eta = { \int _V \mathcal{D}\mathrm{d}V \over \int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} = { \int _\mathrm{env} \mathcal{D}\mathrm{d}V \over \int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} + { \int _\mathrm{core} \mathcal{D}\mathrm{d}V \over \int _V \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} . \end{aligned}$$

(97)

Here, as in the determination of $\zeta$ (Eq. 41), we have separated the star into the envelope and the core, the latter being defined as the region where $\omega < N, S_l$. In the envelope contribution we can replace $\mathcal{D}$ by the function $\bar{\mathcal{D}}_0$ for radial modes, interpolated to the frequency of the mode considered. Also, the denominator is closely related to the mode inertia (Eq. 38); using this we replace the denominator in the first term by Q times the corresponding integral for radial modes, similarly interpolated, where Q is the scaled inertia (Eq. 40). Thus the first term becomes $Q^{-1} \bar{\eta }_0$, where $\bar{\eta }_0$ is the interpolated damping rate for radial modes. In the second term we replace the denominator by an integral just over the core, using Eq. (41). Thus we finally obtain the full damping rate as

$$\begin{aligned} \eta = Q^{-1} \bar{\eta }_0 + \zeta { \int _\mathrm{core} \mathcal{D}\mathrm{d}V \over \int _\mathrm{core} \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} \equiv Q^{-1} \bar{\eta }_0 + \zeta \eta _\mathrm{core} \end{aligned}$$

(98)

(see also Grosjean et al. 2014). As discussed below, $\bar{\eta }_0$ can be obtained from solving the full non-adiabatic equations for radial oscillations. However, we first consider the estimate of the second term from the asymptotic properties of the eigenfunction.

In the core there is no contribution to $\mathcal{D}$ from the turbulent pressure. For simplicity we neglect the term in the energy generation in Eq. (96), and we assume that the flux is purely radiative. Also, in the core we can use the quasi-adiabatic approximation, so that the eigenfunctions are real, and no complex conjugate is needed, and we replace $(\varGamma _3 - 1)\delta \rho /\rho$ by $\delta T/T$. Thus we obtain, for the contribution from the core in Eq. (98),

$$\begin{aligned} \eta _\mathrm{core} = {1 \over 2 \omega _\mathrm{r}^2 } { \displaystyle \int _\mathrm{core} {\delta T \over T} \delta (\mathrm{div}\,\varvec{F}) \mathrm{d}V \over \int _\mathrm{core} \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V} . \end{aligned}$$

(99)

The flux is obtained as

$$\begin{aligned} \varvec{F}= - {4 a \tilde{c} T^4 \over 3 \kappa \rho } \nabla \ln T \equiv -\mathcal{K}\nabla \ln T , \end{aligned}$$

(100)

defining the conductivity $\mathcal{K}$; here a is the radiation density constant, $\tilde{c}$ is the speed of light and $\kappa$ is the opacity. In $\delta (\mathrm{div}\,\varvec{F})$ the radial component of $\varvec{F}$ dominates, since it involves the second derivative of the rapidly varying eigenfunction. Thus, we neglect the tangential component of the flux and obtain, using also the neglect of the nuclear term,

$$\begin{aligned} \delta ( \mathrm{div}\,\varvec{F}) = {\mathcal{L}\over 4 \pi r^2} {\mathrm{d}\over \mathrm{d}r} \left( {\delta \mathcal{L}\over \mathcal{L}} \right) , \end{aligned}$$

(101)

where $\mathcal{L}= 4 \pi r^2 F_r$ is the luminosity, $F_r$ being the radial component of the flux. Here, using Eq. (100),

$$\begin{aligned} {\delta \mathcal{L}\over \mathcal{L}} = 2 {\xi _r \over r} + {\delta F_r \over F_r} = 2 {\xi _r \over r} + {\delta \mathcal{K}\over \mathcal{K}} + {1 \over \mathrm{d}\ln T/\mathrm{d}r} \delta \left( {\mathrm{d}\ln T \over \mathrm{d}r}\right) , \end{aligned}$$

(102)

or, expanding the last term²⁴

$$\begin{aligned} {\delta \mathcal{L}\over \mathcal{L}} = 2 {\xi _r \over r} + {\delta \mathcal{K}\over \mathcal{K}} - {\mathrm{d}\xi _r \over \mathrm{d}r} + {1 \over \mathrm{d}\ln T/\mathrm{d}r} {\mathrm{d}\over \mathrm{d}r} \left( {\delta T \over T}\right) . \end{aligned}$$

(103)

In the asymptotic analysis of this equation for the extreme g-mode behaviour in the core we follow Godart et al. (2009) (see also Dziembowski 1977). From the oscillation equations it may be shown that

$$\begin{aligned} \left| {p' \over \xi _r \mathrm{d}p/\mathrm{d}r} \right| = \mathcal{O}(\omega /S_l) \ll 1 , \end{aligned}$$

(104)

and hence, according to footnote 24,

$$\begin{aligned} {\delta p \over p} \simeq \xi _r {\mathrm{d}\ln p \over \mathrm{d}r} . \end{aligned}$$

(105)

It follows that $\delta p /p$ is small compared with terms involving derivatives of $\xi _r$ and, given the quasi-adiabatic approximation, the same is true of $\delta \rho /\rho$ and $\delta T/T$. From the equation of continuity,

$$\begin{aligned} {\delta \rho \over \rho } = - \mathrm{div}\,(\varvec{\delta }\varvec{r}) = - {1 \over r^2} {\mathrm{d}\over \mathrm{d}r} (r^2 \xi _r) + {l(l+1) \over r^2} \xi _\mathrm{h} , \end{aligned}$$

(106)

it then follows that

$$\begin{aligned} {\mathrm{d}\xi _r \over \mathrm{d}r} \simeq l(l+1) {\xi _\mathrm{h} \over r} , \end{aligned}$$

(107)

where in addition we neglected $2 \xi _r/r$ compared with $\mathrm{d}\xi _r / \mathrm{d}r$. In Eq. (103) $2 \xi _r/r$ and $\delta \mathcal{K}/\mathcal{K}= \mathcal{O}(\delta p/p)$ can be neglected compared with $\mathrm{d}\xi _r/\mathrm{d}r$. Using also

$$\begin{aligned} {\delta T \over T} = \nabla _\mathrm{ad} {\delta p \over p} \end{aligned}$$

(108)

and Eqs. (105) and (107) we obtain

$$\begin{aligned} {\delta \mathcal{L}\over \mathcal{L}} \simeq {1 \over \mathrm{d}\ln T/\mathrm{d}r} \nabla _\mathrm{ad} {\mathrm{d}\xi _r \over \mathrm{d}r} {\mathrm{d}\ln p \over \mathrm{d}r} - {\mathrm{d}\xi _r \over \mathrm{d}r} \simeq \left( {\nabla _\mathrm{ad} \over \nabla } - 1 \right) l(l+1) {\xi _h \over r} . \end{aligned}$$

(109)

Using Eqs. (101), (105), (108) and the equation of hydrostatic support we can finally write the numerator in Eq. (99) as

$$\begin{aligned} \int _\mathrm{core} {\delta T \over T} \delta (\mathrm{div}\,\varvec{F}) \mathrm{d}V = - \int _\mathrm{core} \nabla _\mathrm{ad} \xi _r {g \rho \over p} \left( {\nabla _\mathrm{ad} \over \nabla } - 1 \right) l(l+1) {1 \over r} {\mathrm{d}\xi _h \over \mathrm{d}r} \mathcal{L}\mathrm{d}r . \end{aligned}$$

(110)

To approximate the integrand in Eq. (110) we use the g-mode asymptotic eigenfunction in Eq. (71). From Eq. (107) we furthermore have, to leading order,

$$\begin{aligned} {1 \over r} {\mathrm{d}\xi _\mathrm{h} \over \mathrm{d}r} \simeq L^{-2} {\mathrm{d}^2 \xi _r \over \mathrm{d}r^2} \simeq -L^{-2} K \xi _r , \end{aligned}$$

(111)

where again we introduced $L^2 = l(l+1)$. Here we used that, to leading order, $\xi _r$ satisfies an equation of the form in Eq. (21); in the g-mode cavity K can be approximated by

$$\begin{aligned} K \simeq {L^2 \over r^2} \left( {N^2 \over \omega ^2} - 1 \right) \; . \end{aligned}$$

(112)

Differentiating Eq. (71), Eq. (111) also yields

$$\begin{aligned} \xi _r \simeq -A \rho ^{-1/2} \omega _\mathrm{r}^{-1/2} r^{-3/2} L^{1/2} N^{-1/2} \cos \left( \int _{r_\mathrm{a}}^r K^{1/2} \mathrm{d}r - \phi _\mathrm{g}^\prime \right) . \end{aligned}$$

(113)

Thus the integrand in Eq. (110) becomes

$$\begin{aligned} - A^2 \omega _\mathrm{r}^{-3} L^3 \nabla _\mathrm{ad} \left( {\nabla _\mathrm{ad} \over \nabla } - 1 \right) {g \over p} N r^{-5} \mathcal{L}\cos ^2 \left( \int _{r_\mathrm{a}}^r K^{1/2} \mathrm{d}r - \phi _\mathrm{g}^\prime \right) . \end{aligned}$$

(114)

The integral in the denominator of Eq. (99) is evaluated essentially as in Eq. (72), yielding

$$\begin{aligned} \int _\mathrm{core} \rho |\varvec{\delta }\varvec{r}|^2 \mathrm{d}V \simeq 4 \pi A^2 \omega ^{-3} L \int _0^{r_\mathrm{b}} N \sin ^2 \left( {L \over \omega } \int _0^r N {\mathrm{d}r' \over r'} - \phi _\mathrm{g}^\prime \right) {\mathrm{d}r \over r} . \end{aligned}$$

(115)

Thus we finally obtain, replacing $\cos ^2$ and $\sin ^2$ by their average values 1 / 2,

$$\begin{aligned} \eta _\mathrm{core} \simeq {L^2 \over 8 \pi \omega _\mathrm{r}^2} {\displaystyle \int _\mathrm{core} \nabla _\mathrm{ad} \left( {\nabla _\mathrm{ad} \over \nabla } - 1 \right) {N g \over p r^4} \mathcal{L}\mathrm{d}r/r \over \int _\mathrm{core} N \mathrm{d}r /r } . \end{aligned}$$

(116)

Fig. 38

Mode damping time $t_\mathrm{damp} = 1/\eta _\mathrm{core}$ corresponding to the asymptotic core damping rate (Eq. 116), evaluated at the frequency $\nu _\mathrm{max}$ of maximum oscillation power estimated as in Eq. (26). The results were obtained for a $1 \,\mathrm{M}_\odot$ evolution sequence and are shown against surface radius (lower abscissa) and luminosity (upper abscissa) in solar units, for $l = 1$ (solid) and $l = 2$ (dashed)

As a star evolves up the red-giant branch, increasing the luminosity and the mass of the core, the core gravitational acceleration and buoyancy frequency increase. According to Eq. (116) these effects all contribute to increasing the core damping rate. This is illustrated in Fig. 38, showing the corresponding damping time in a $1 \,\mathrm{M}_\odot$ evolution sequence. On the low red-giant branch the core damping is small and unlikely to affect the observed properties of the modes, while around the bump, clearly reflected in the figure, the core damping rate has increased to a level where the corresponding damping time is comparable with or smaller than the duration of the nominal Kepler mission, such that significant effects can be expected (see also Fig. 41 below).

Returning to the near-surface contributions to the damping of the modes, a full non-adiabatic treatment of the oscillations is required, taking into account the pulsation-induced perturbations to the convective properties. These issues were discussed in detail by Houdek and Dupret (2015). Time-dependent generalizations of mixing-length theory were developed by Unno (1967) and Gough (1977b, based on earlier work in 1965), while Xiong (1977) used a Reynolds-stress model to treat convection in pulsating stars.

Unno’s theory was further developed by Gabriel (1996) and Grigahcène et al. (2005). With a suitable adjustment of parameters it provides a relatively reasonable fit to the detailed observations of solar oscillation linewidths (Dupret et al. 2006). This was subsequently used in the analysis of red-giant mode energetics by Dupret et al. (2009) and Grosjean et al. (2014).

Gough’s theory was generalized to included nonlocal effects by Balmforth (1992a), based on an analysis by Gough (1977a). Specifically, local mixing-length theory implicitly makes the assumption that the relevant convective scales are much smaller than the scale of variation of stellar structure, whereas in fact the typical mixing-length scale is of order a pressure scale height. The nonlocal analysis involves an average over the extent of the motion of convective eddies and over the ensemble of eddies at any given location; this also gives rise to limited convective overshoot and circumvents mathematical problems that occur in a fully local convection formulation when consistently including turbulent pressure in the equation of hydrostatic support. The theory has so far only been developed for radial oscillations; however, given that the relevant effects are concentrated in the superficial layers of the stars, the results are expected to be representative also for non-radial oscillations of low degree, at least in the frequency range of solar-like oscillations. With suitable, and plausible, choice of parameters characterizing the nonlocality this formulation results in oscillation line widths in reasonable agreement with solar observations (e.g., Balmforth 1992a; Houdek et al. 2001; Chaplin et al. 2005).

Fig. 39

Mode damping times $t_\mathrm{damp} = 1/\eta$ in the $7 \,\mathrm{R}_\odot$ red-giant model from the $1 \,\mathrm{M}_\odot$ sequence illustrated in Fig. 38. The dotted curve shows radial-mode damping times computed using a nonlocal time-dependent convection formulation (Houdek et al. 1999), and the solid ($l = 1$) and dashed ($l = 2$) curves show the results of combining the radial-mode damping rates with the asymptotic estimate (Eq. 116), as in Eq. (98). The vertical dot-dashed line marks an estimate of the frequency $\nu _\mathrm{max}$ of maximum oscillation power (cf. Eq. 26). (Radial-mode damping rate courtesy Günter Houdek.)

Given the fully non-adiabatic results for radial modes, including the effects of turbulent pressure, we can estimate the damping times of the mixed modes by combining the radial-mode damping rate²⁵ with the asymptotic treatment of the damping in the core (cf. Eq. 98). An example is shown in Fig. 39, for a fairly low-luminosity $1 \,\mathrm{M}_\odot$ red giant. Here we obtained $\bar{\eta }_0$ using the Gough (1977b) and Balmforth (1992a) nonlocal treatment of the perturbations to the convective properties, as described by Houdek et al. (1999). We note that the acoustic-mode lifetimes are a factor 2–3 larger than those found by Grosjean et al. (2014) and hence in substantially better agreement with observations (Huber et al. 2010; Corsaro et al. 2015a, Handberg et al. submitted). Comparison with Fig. 38 indicates that in this case the near-surface damping dominates near $\nu = \nu _\mathrm{max}$, even for the most g-dominated modes.

4.3.2 Mode excitation

Stochastically excited mode amplitudes were first estimated by Goldreich and Keeley (1977). Their results were used by Christensen-Dalsgaard and Frandsen (1983b) in a first estimate of the expected mode amplitudes of stochastically excited oscillations across the HR diagram. This was later summarized by Kjeldsen and Bedding (1995) in a widely used relation according to which the mode amplitudes roughly scale as $\mathcal{L}/M$. In particular, it was already then clear that evolved stars were expected to have higher oscillation amplitudes, as has certainly been confirmed observationally.

The stochastic energy input from convection is driven by turbulent Reynolds stresses and entropy fluctuations, their relative importance depending on the detailed assumptions made in the calculation (e.g., Balmforth 1992b; Goldreich et al. 1994; Samadi and Goupil 2001; Samadi et al. 2003; Chaplin et al. 2005). However, regardless of these details the dominant contributions come from the near-surface layers where convection is most vigorous. Here the local properties of the oscillations are essentially independent of the degree of the mode, at least for the low-degree modes that are relevant in distant stars, and the rate of energy input is consequently a function of frequency but not degree. It may be shown (e.g., Chaplin et al. 2005) that the resulting mean square amplitude can be expressed as

$$\begin{aligned} \langle A^2\rangle \simeq {1 \over E \eta } {\mathcal{F}(\omega ) \over E} \; , \end{aligned}$$

(117)

where $\mathcal{F}$ is the rate of energy input. The details of this expression, including the precise form of $\mathcal{F}(\omega )$, depend on the observed quantity represented by A (see also Sect. 1.2). However, since the ratio between the physical amplitudes of different observable oscillation properties is generally a function of frequency this does not change the form of the equation. From Eq. (117) the rate of energy input can be determined from $\eta \langle A^2 \rangle$, with $\eta$ determined from the observed line width and the mode inertia obtained from computed eigenfunctions. In this manner Stein and Nordlund (2001) showed a remarkable agreement between the predictions from three-dimensional simulations of convection and radial-velocity observations of solar oscillations. Also, Jacoutot et al. (2008) used such a comparison to constrain the detailed properties of their simulations of solar convection. A similar analysis based on the results from Kepler, including for red giants, would clearly be very interesting. Samadi et al. (2007) compared the rate of energy input obtained from hydrodynamical simulations with the results obtained for mixing-length based models. The analysis was extended to red giants by Samadi et al. (2012), comparing the results with CoRoT observations analysed by Baudin et al. (2011). They noted the importance of the proper conversion of the predicted velocity amplitudes to the photometric data, such as obtained by CoRoT.

As discussed above, the properties of $\eta$ can be understood in terms of the work integral, Eq. (93). Here (and in the expression for the contribution $\eta _\mathrm{t}$ from the turbulent pressure, Eq. 95) the denominator essentially corresponds to the normalized mode inertia E, apart from the normalization with the surface displacement (cf. Eq. 38). Near the surface the integrands in the numerators of Eqs. (93) and (95) depend only on frequency. Thus if the contribution from the core to the work integral can be neglected, $E \eta$ is just a function of frequency. Consequently, $\langle A^2 \rangle \propto E^{-1}$, and the amplitude of a general non-radial mode, relative to a radial mode of the same frequency, scales as

$$\begin{aligned} \langle A^2 \rangle = Q^{-1} \langle \bar{A}_0^2 \rangle \end{aligned}$$

(118)

(cf. Eq. 40), where $\langle \bar{A}_0^2 \rangle$ is the radial-mode amplitude, interpolated to the frequency of the mode considered. However, in the mixed modes in red giants the contribution $\eta _\mathrm{core}$ from the damping in the core can be very significant and must be taken into account. Using Eqs. (40) and (98) we obtain

$$\begin{aligned} \langle A^2\rangle\simeq & {} {1 \over Q \bar{E}_0(\omega ) [ Q^{-1} \bar{\eta }_0 + \zeta \eta _\mathrm{core}]} {\mathcal{F}(\omega ) \over Q \bar{E}_0(\omega ) } \nonumber \\\simeq & {} {1 \over 1 + Q \zeta \eta _\mathrm{core}/\bar{\eta }_0} Q^{-1} {1 \over \bar{E}_0(\omega ) \bar{\eta }_0} {\mathcal{F}(\omega ) \over \bar{E}_0(\omega ) } \nonumber \\\simeq & {} {1 \over 1 + (Q - 1) \eta _\mathrm{core}/\bar{\eta }_0} Q^{-1} \langle \bar{A}_0^2\rangle ; \end{aligned}$$

(119)

here, despite the caveat in footnote 10, we used Eq. (42) to replace $Q \zeta$ by $Q-1$, with sufficient accuracy for the present purpose.

In terms of the observed oscillation power spectrum $\langle A^2 \rangle$ corresponds to the area under a Lorentzian peak (cf. Eq. 90). Of more relevance to the interpretation of the observations is the peak height H, related to $\langle A^2 \rangle$ by

$$\begin{aligned} H = {2 \over \eta } \langle A^2 \rangle \end{aligned}$$

(120)

(see Baudin et al. 2005; Chaplin et al. 2005, and Sect. 3.4). Relating as in Eq. (119) the peak height to the peak height $\bar{H}_0$ of radial modes, interpolated to the relevant frequency, we obtain

$$\begin{aligned} H \simeq {1 \over [1 + (Q - 1) \eta _\mathrm{core}/\bar{\eta }_0]^2} \bar{H}_0 . \end{aligned}$$

(121)

In particular, in the lower part of the red-giant branch the core damping is small compared with the envelope contribution (cf. Fig. 38) and hence can be neglected; consequently the peak heights of all mixed modes are predicted to be comparable to the peak height of the adjacent radial modes, in clear contradiction to the observations.

In an important breakthrough in the interpretation of the observations of red-giant oscillations it was noted by Dupret et al. (2009) that the origin of this discrepancy was the assumption that all peaks have a Lorentzian profile, leading to Eq. (120). In fact, this is only strictly true if the oscillations are observed for an infinite period. For observations over a finite period $T_\mathrm{obs}$ the line profile is a combination of a Lorentzian and a $\mathrm{sinc}^2$ function (cf. footnote 4). The broader peaks result in a reduction in H, at the given $\langle A^2 \rangle$, and a behaviour that is qualitatively consistent with the observations. This analysis was extended, including a more detailed comparison with the observations, by Grosjean et al. (2014).

Fletcher et al. (2006) showed that the transition between unresolved and fully resolved peaks can be approximated by replacing Eq. (120) by

$$\begin{aligned} H = {2 \over \eta + 2/T_\mathrm{obs}} \langle A^2 \rangle . \end{aligned}$$

(122)

As a result, Eq. (121) is replaced by

$$\begin{aligned} H \simeq {1 + 2 \bar{t}_{\mathrm{damp},0}/T_\mathrm{obs} \over [1 + (Q - 1) \eta _\mathrm{core}/\bar{\eta }_0] [1 + (Q - 1) \eta _\mathrm{core}/\bar{\eta }_0+2 Q \bar{t}_{\mathrm{damp},0}/T_\mathrm{obs}]} \bar{H}_0 , \end{aligned}$$

(123)

where we introduced the interpolated radial-mode damping time $\bar{t}_{\mathrm{damp},0} = 1/\bar{\eta }_0$ and peak height $\bar{H}_0$. For observations extending over 100–1000 days, as was the case for CoRoT and the nominal Kepler mission, typically $\bar{t}_{\mathrm{damp},0} \ll T_\mathrm{obs}$ and the correction in the numerator in Eq. (123) can be neglected. However, the same is not true of the corresponding term in the denominator for the more g-dominated mixed modes, with Q much larger than 1 (cf. Fig. 17), whose heights are, therefore, reduced. A further reduction can clearly come from the core damping, represented by $\eta _\mathrm{core}$. It seems probably that this reduction of peak height is the reason that Frandsen et al. (2002) only identified the radial modes in 30-day observations of $\xi$ Hydrae, since even the acoustically dominated dipolar modes have a somewhat higher inertia than the neighbouring radial modes.

Fig. 40

Simulated power spectra for the model illustrated in Fig. 39, for observing times of 100 days (top) and 1000 days (bottom). The combined power density is shown with the black curve, while the red, blue and green curves show the contributions from modes with degree $l = 0$, 1 and 2

To illustrate these effects Fig. 40 shows a simplified modelling of power density spectra, for the $1 \,\mathrm{M}_\odot$, $7 \,\mathrm{R}_\odot$ model illustrated in Fig. 39, based on the damping times shown there. Here we have approximated $\bar{H}_0$ by a Gaussian centred on the estimated $\nu _\mathrm{max} \simeq 68~\upmu \mathrm{Hz}$ and with a maximum of 1. The total power is calculated as the sum over the modes of degree $l = 0 - 2$, each mode represented by a Lorentzian with the width corrected for the finite observing time, as implicit in Eq. (122), and a height given by Eq. (123). In the top panel, for $T_\mathrm{obs} = 100 \, \mathrm{days}$, most mixed modes have a strongly reduced height, owing to the relatively short observing time, although some mixed dipolar modes may in principle be visible. At high frequency the peaks are very substantially broadened by the short mode lifetimes (cf. Fig. 39). With $T_\mathrm{obs} = 1000 \, \mathrm{days}$, shown in the lower panel, most dipolar mixed modes are excited to substantial heights, and hence one might expect to detect an almost complete dipolar spectrum, at least at moderate and high frequency. However, at low frequency the dipolar modes are strongly suppressed by the increase in the damping rate (note that, according to Eq. (116), $\eta _\mathrm{core} \propto \nu ^{-2}$) and in particular the small damping rate compared with $2/T_\mathrm{obs}$. For $l = 2$ the suppression of the peak height, except for the most acoustic modes, is far higher owing to the larger values of Q, and very few if any mixed modes are predicted to be visible.

Fig. 41

Simulated power density, in $\mathrm{m^2 \, s^{-2} ~\upmu Hz^{-1}}$, for models in a $1.5 \,\mathrm{M}_\odot$ evolution sequence with radii $5.2 \,\mathrm{R}_\odot$ (top), $7.3 \,\mathrm{R}_\odot$ (middle) and $11.9 \,\mathrm{R}_\odot$ (bottom). Image reproduced with permission from Grosjean et al. (2014), copyright by ESO

The strong increase in the damping rates as the star moves up the red-giant branch (cf. Fig. 38) has a dramatic effect on the predicted power density spectra; this is illustrated in Fig. 41 taken from Grosjean et al. (2014), for a $1.5 \,\mathrm{M}_\odot$ evolution sequence here assuming $T_\mathrm{obs} = 360 \, \mathrm{days}$.²⁶ For the $5.2 \,\mathrm{R}_\odot$ model all dipolar mixed modes are visible. When R reaches $7.3 \,\mathrm{R}_\odot$ the heights of the dipolar mixed modes are substantially reduced, although many modes would still be expected to be visible. Finally, at a radius of $11.9 \,\mathrm{R}_\odot$, just below the bump, the mixed modes are no longer visible. Although further investigations along these lines, matching also the observed linewidths, are needed, this clearly indicates a serious limitation on the diagnostic possibilities for very evolved stars.

At even higher luminosity, the damping in the g-mode cavity becomes so strong that gravity waves are damped before being reflected from the centre, essentially eliminating the g-dominated mixed modes. In this case the remaining p-dominated oscillation spectrum can be computed for just the envelope model, applying boundary conditions at the edge of the g-mode cavity which select those waves that propagate towards the centre (Dziembowski 1977; Osaki 1977; Van Hoolst et al. 1998; Dziembowski et al. 2001; Dziembowski 2012). It was noted by Dziembowski (2012) that towards the tip of the red-giant branch the resulting loss of wave energy to the core becomes essentially negligible.

As shown by Eqs. (119) and (123) the mode amplitudes and peak heights of the mixed modes depend strongly on the mode inertia, in units of the radial-mode inertia. It was pointed out by Benomar et al. (2014) that this provides an opportunity to use the observed amplitudes or peak heights as diagnostics of the stellar interior, supplementing the information obtained from the frequencies. In particular, given the sensitivity of $\zeta$, and equivalently Q, on the coupling strength q (cf. Eq. 81) this may provide information about the evanescent region between the acoustic- and gravity-mode cavities. These possibilities should be further explored, given the extended data available from Kepler.

The original amplitude scaling relation with $\mathcal{L}/M$ proposed by Kjeldsen and Bedding (1995), and the analysis carried out in this section, strictly speaking only apply to the amplitudes observed in radial velocity, which are directly related to the mode energy; furthermore, for comparison with observations, the predicted amplitudes should be referred to the effective height in the atmosphere where the radial-velocity observations are carried out, requiring modelling of the oscillation eigenfunctions in the atmosphere. We also note that, as discussed briefly in the opening paragraph of Sect. 3.4, the observed amplitudes depend on the mode visibility, determined by the geometric cancellation across the stellar disk, which has not been taken into account here. Predicting photometric amplitudes requires the ratio between the intensity variations, in the appropriate wavelength band, and the velocity amplitudes (e.g., Houdek 2006, 2009; Samadi et al. 2013; Grosjean et al. 2014) which, as noted by Kjeldsen and Bedding (1995), depends on the effective temperature. Analyses of observed amplitudes have typically started from the $\mathcal{L}/M$ scaling but introduced different exponents and included the dependence on $T_\mathrm{eff}$ (e.g., Huber et al. 2011b; Corsaro et al. 2013). However, there is still a very substantial potential for more detailed comparisons between observed and modelled amplitudes and linewidths.

4.4 Rotation

A striking result of the early analysis of red-giant observations from Kepler was the detection by Beck et al. (2012) of rotational splitting of the observed frequencies, leading to a first inference of the internal rotation of a red-giant star. Extensive results are now available for both red-giant and clump stars (e.g., Mosser et al. 2012b; Deheuvels et al. 2015; Vrard et al. 2016). Strikingly, the inferred core rotation of red giants is far slower than would be expected from models of angular-momentum evolution (e.g., Eggenberger et al. 2012; Marques et al. 2013; Cantiello et al. 2014, see Sect. 5.5) . Here we discuss the effects of rotation on the stellar oscillation frequencies.

For evolved stars it is generally assumed that rotation is so slow that second-order effects of rotation, including the centrifugal acceleration, can be neglected. Then in particular the hydrostatic structure of the star is not affected. The oscillation frequencies are affected by advection of the pattern of waves propagating in the azimuthal direction, such that the frequencies of prograde waves (travelling in the direction of rotation) increase and frequencies of retrograde waves decrease. In addition, the oscillations are affected locally by the Coriolis force in a frame rotating with the star. The result is the first-order rotational splitting, with the frequencies given by

$$\begin{aligned} \omega _{nlm} = \omega _{nl0} + m \delta \omega _{nlm} \; \end{aligned}$$

(124)

(see also Sect. 3.4.4).

We cannot assume that stars rotate as a solid body. Hence the rotational splitting measures an average over the internal rotation rate, determined by the properties of the mode. For simplicity we only consider the case of the so-called shellular rotation where the angular frequency $\varOmega = \varOmega (r)$ only depends on the distance to the centre. Then $\delta \omega _{nlm}$ does not depend on m, and we can express it as

$$\begin{aligned} \delta \omega _{nl} = \int _0^R K_{nl}(r) \varOmega (r) \mathrm{d}r , \end{aligned}$$

(125)

where the rotational kernel $K_{nl}$ is given by

$$\begin{aligned} K_{nl}(r) = {\left[ \xi _r^2 + l(l+1) \xi _\mathrm{h}^2 - 2 \xi _r \xi _\mathrm{h} - \xi _\mathrm{h}^2 \right] r^2 \rho \over \int _0^R \left[ \xi _r^2 + l(l+1) \xi _\mathrm{h}^2 \right] r^2 \rho \mathrm{d}r} . \end{aligned}$$

(126)

Here the first two terms provide a weighted average of $\varOmega$ and correspond to the advection, while the last two terms arise from the Coriolis force. It is common also to consider

$$\begin{aligned} \beta _{nl} = \int _0^R K_{nl}(r) \mathrm{d}r , \end{aligned}$$

(127)

such that for uniform rotation $\delta \omega _{nl} = \beta _{nl} \varOmega$. For acoustic modes with $|\xi _r| \gg |\xi _\mathrm{h}|$ we can neglect the last two terms in the numerator of $K_{nl}$, so that $\beta _{nl} \simeq 1$. For general rotation we obtain in this case

$$\begin{aligned} \delta \omega _{nl} \simeq \langle \varOmega \rangle , \end{aligned}$$

(128)

i.e., an average angular velocity weighted by the local contribution to the inertia. For high-order g modes, on the other hand, with $|\xi _\mathrm{h}| \gg |\xi _r|$ we can neglect the terms in $\xi _r$ to obtain

$$\begin{aligned} \beta _{nl} \simeq 1 - {1 \over l(l+1) } ; \end{aligned}$$

(129)

in particular, for dipolar modes, with $l = 1$, we obtain $\beta _{n1} \simeq 1/2$.

To analyse the rotational splitting for red giants, we follow Goupil et al. (2013) and use the asymptotic description of the mode inertia discussed in Sect. 4.2.3. For simplicity, we suppress the subscript ‘nl’ in the following. Neglecting the term in $\xi _r \xi _\mathrm{h}$ in Eq. (126) and using Eqs. (80) and (129), $\beta$ may be approximated by

$$\begin{aligned} \beta \simeq {[1 - (l(l+1))^{-1}] I_\mathrm{g} + I_\mathrm{p} \over I_\mathrm{p} + I_\mathrm{g} } = [1 - (l(l+1))^{-1}] \zeta + (1 - \zeta ) = \beta _\mathrm{core} + \beta _\mathrm{env} ; \end{aligned}$$

(130)

here the contributions to $\beta$ from the core and the envelope are

$$\begin{aligned} \beta _\mathrm{core} = \int _\mathrm{core} K_{}(r) \mathrm{d}r \simeq [1 - (l(l+1))^{-1}] \zeta \end{aligned}$$

(131)

and

$$\begin{aligned} \beta _\mathrm{env} = \int _\mathrm{env} K_{}(r) \mathrm{d}r \simeq 1 - \zeta . \end{aligned}$$

(132)

We furthermore introduce the average kernel-weighted core and envelope angular velocities:

$$\begin{aligned} \langle \varOmega \rangle _\mathrm{core} = {\int _\mathrm{core} \varOmega (r) K_{}(r) \mathrm{d}r \over \int _\mathrm{core} K_{}(r) \mathrm{d}r } \end{aligned}$$

(133)

and

$$\begin{aligned} \langle \varOmega \rangle _\mathrm{env} = {\int _\mathrm{env} \varOmega (r) K_{}(r) \mathrm{d}r \over \int _\mathrm{env} K_{}(r) \mathrm{d}r } . \end{aligned}$$

(134)

These averages formally depend on the mode; however, the dependence on at least the mode order is weak, given the asymptotic description of the modes and assuming that $\varOmega (r)$ varies smoothly with r on the scale of the eigenfunctions. With these definitions we obtain

$$\begin{aligned} \delta \omega = \beta _\mathrm{core} \langle \varOmega \rangle _\mathrm{core} + \beta _\mathrm{env} \langle \varOmega \rangle _\mathrm{env} \simeq \langle \varOmega \rangle _\mathrm{core} \{ [ 1 - (l(l+1))^{-1}] \zeta + (1 - \zeta ) \mathcal{R}\} , \end{aligned}$$

(135)

where $\mathcal{R}= \langle \varOmega \rangle _\mathrm{env}/\langle \varOmega \rangle _\mathrm{core}$. Writing the splitting $\delta \nu = \delta \omega / 2 \pi$ in terms of cyclic frequency and specializing to $l = 1$, we finally obtain

$$\begin{aligned} \delta \nu = \delta \nu _\mathrm{max} [(1 - 2 \mathcal{R}) \zeta + 2 \mathcal{R}] \end{aligned}$$

(136)

(Goupil et al. 2013), where $\delta \nu _\mathrm{max} = \langle \varOmega \rangle _\mathrm{core}/4 \pi$, assuming that the core is rotating substantially faster that the envelope, so that the maximum splitting occurs for the g-dominated modes with $\zeta \simeq 1$. Thus we find that the splitting varies linearly with $\zeta$. This is illustrated for a stellar model in Fig. 42; from the coefficients of the linear fit the core and envelope rotation can be determined with very good precision: the relative errors in the inferred $\langle \varOmega \rangle _\mathrm{core}$ and $\langle \varOmega \rangle _\mathrm{env}$ are 0.6 and 6%, respectively.

Fig. 42

Computed rotational splittings as functions of $\zeta$ for dipole modes, with $l = 1$, in the red-giant model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. An angular velocity was imposed with $\varOmega = 4.98 \times 10^{-6} \,\mathrm{s}^{-1}$ in the core, corresponding to a rotation period of 15 days, $\varOmega = 3.02 \times 10^{-7} \,\mathrm{s}^{-1}$ in the envelope and a narrow transition at the hydrogen-burning shell, with $r = 0.09 R$. All modes with frequency above $0.4 \nu _\mathrm{ac}$ were included. We note the expected linear dependence (cf. Eq. 136). The dashed line shows a uniformly weighted linear least-squares fit to the results

In analyses of observed power spectra Mosser et al. (2012c) and Mosser et al. (2012b) assumed that the envelope contribution to the splitting could be neglected, corresponding to taking $\mathcal{R}= 0$, and applied an empirically based approximation to the splitting, which can be expressed as $\delta \nu = \zeta _\mathrm{Mosser} \delta \nu _\mathrm{max}$, where

$$\begin{aligned} \zeta _\mathrm{Mosser} = 1 - {\lambda \over \displaystyle 1 + \left( {\nu - \nu _{n_\mathrm{p}\,l}^\mathrm{(p)} \over \gamma \Delta \nu } \right) ^2} , \end{aligned}$$

(137)

where $\lambda$ and $\gamma$ are empirically determined parameters.²⁷ An expression of this form can in fact be obtained from the full asymptotic expression for $\zeta$, Eq. (81), by expanding the inverse, assuming that $\zeta$ is close to 1, and expanding $\sin ^2$ on the assumption that $\nu$ is close to $\nu _{n_\mathrm{p}\,l}^\mathrm{(p)}$. A similar functional form, based on a Lorentzian departure from the asymptotic period spacing, was used by Stello (2012) in the analysis of computed period spacings.

Fig. 43

Normalized partial kernel integrals for the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. The modes illustrated are $l = 1, \nu = 79.09~\upmu \mathrm{Hz}$ (g-dominated; blue, solid), $l = 1, \nu = 84.33~\upmu \mathrm{Hz}$ (p-dominated, blue, dashed), $l = 2, \nu = 82.19~\upmu \mathrm{Hz}$ (g-dominated, red, dot-dashed), $l = 2, \nu = 87.42~\upmu \mathrm{Hz}$ (p-dominated, red, triple-dot-dashed). The right-hand panel shows details near the surface. The vertical dotted line marks the base of the convective envelope

The relative contribution to the rotational splittings of the different parts of the star can also be illustrated by the partial integrals of the kernels (see Beck et al. 2012, supplementary material). These are shown in Fig. 43 for selected p- and g-dominated modes with $l = 1$ and 2 in a $1.3 \,\mathrm{M}_\odot$ red-giant model, normalized such that the surface values are one. This shows that even for the p-dominated modes a substantial contribution to the splitting comes from the radiative core, particularly for $l = 1$. This is related to the fact that $\zeta$ even for these modes is substantially bigger than 0. Given that generally $\mathcal{R}\ll 1$ for red giants, this makes it difficult to determine the envelope rotation rate; observations of rotational splittings for modes with $l = 2$ or, even better, $l = 3$ would be very helpful.

Fig. 44

Stretched period échelle diagrams for rotationally split dipolar modes in the model $\mathrm{M_{RG}}$ in Fig. 11 $(1.3 \,\mathrm{M}_\odot \, , \; 6.2 \,\mathrm{R}_\odot )$. In the left-hand panel slow rotation, with an angular velocity 5 times smaller than in Fig. 42, was assumed, while the right-hand panel used the same angular velocity as in Fig. 42. Plusses show modes with $m = 0$ and diamonds the rotationally split modes with $m = \pm 1$. The red diamonds mark the modes illustrated in Fig. 18

The analysis of rotationally split modes in red giants is complicated by the possible overlap between neighbouring multiplets in the mixed-mode spectrum, when $\delta \nu _\mathrm{max} \sim \nu ^2 \Delta \varPi$. Even so, Mosser et al. (2012b) succeeded in determining the rotational splitting in a large number of stars, including cases of overlap, by identifying the pattern of rotationally split components using the approximation in Eq. (137). As pointed out by Mosser et al. (2015) the analysis is greatly simplified by using the stretching with the function $\mathcal{P}$ introduced by Eq. (84). We first note that, according to Eq. (136), the frequencies of the rotationally split modes can be approximated by

$$\begin{aligned} \nu _{nlm} \simeq \nu _{nl0} + m \zeta \delta \nu _\mathrm{max} , \end{aligned}$$

(138)

where for simplicity we neglected the envelope contribution and hence assumed that $\mathcal{R}\simeq 0$. From this it follows, using also that $\mathcal{P}$ is defined as a function of frequency, that the rotationally split modes for a given m are approximately uniformly spaced in stretched period $\mathcal{P}(\nu _{nlm})$, with a period spacing given by

$$\begin{aligned} \Delta \varPi _{lm} \simeq \Delta \varPi _l\left( 1 - 2 m \langle \zeta \rangle {\delta \nu _\mathrm{max} \over \nu } \right) , \end{aligned}$$

(139)

where $\langle \zeta \rangle$ is a suitable average of $\zeta$. In a period échelle diagram based on the stretched periods this corresponds of a sequence of modes on a line inclined relative to the modes with $m = 0$. Two examples of this are shown in Fig. 44, for $l = 1$ and two different rotation rates. We note that in the right-hand panel the rotational splitting in terms of period is around 62 s, i.e., comparable with the period spacing of 75 s and hence leading to a complex structure of the power spectrum. Even so, the structure of the rotationally split modes can be unambiguously identified in the stretched period échelle diagram.

Mosser et al. (2015) argued that $\langle \zeta \rangle$ can be represented by $\mathcal{N}(\nu )/[\mathcal{N}(\nu ) + 1]$ where $\mathcal{N}$ measures the number of gravity modes in a $\Delta \nu$-wide interval around $\nu$ (see Eq. 58). Assuming also that the modes considered have frequencies close to the frequency $\nu _\mathrm{max}$ of maximum oscillation power they obtain for the period spacings

$$\begin{aligned} \Delta \varPi _{lm} \simeq \Delta \varPi _l(1 - m x_\mathrm{rot}) , \end{aligned}$$

(140)

where

$$\begin{aligned} x_\mathrm{rot} = 2 {\mathcal{N}(\nu _\mathrm{max}) \over \mathcal{N}(\nu _\mathrm{max}) +1} {\delta \nu _\mathrm{max} \over \nu _\mathrm{max}} . \end{aligned}$$

(141)

As a complication in the treatment of red-giant rotational splitting it was noted by Ouazzani et al. (2013) that the core rotation may be so rapid that the perturbation analysis discussed here is inadequate. In such cases, Ouazzani et al. demonstrated that a two-dimensional solution of the oscillation equations is required, involving coupling between components of different degrees. A complication in these cases is also that properties of the eigenfunctions, in particular the mode inertia, can vary substantially between the different components of the multiplet.

5 Groundbreaking results

Asteroseismology of red-giant stars has been very successful over the past decade with many publications and ground-breaking results. We anticipate that this will continue in the decade(s) to come (see next section). In this section we discuss results that we think have been seminal for the field.

Early observations and interpretations of oscillations in very large red giants such as Arcturus (Merline 1995) and $\alpha$ UMa (Buzasi et al. 2000; Dziembowski et al. 2001) have already been conducted during the last century and the beginning of this century. Following these discoveries, the study of solar-like oscillations in red-giant stars all along the red-giant and horizontal branch (Sects. 2.1.2, 2.1.4) has effectively started with the spectroscopic campaigns in which $\xi$ Hydrae (Frandsen et al. 2002), $\epsilon$ Ophiuchi (De Ridder et al. 2006) and $\eta$ Serpentis (Barban et al. 2004) were observed. In these observations oscillation power excesses exhibiting a regular pattern of oscillation modes were observed unambiguously for the first time for early red giants. These discoveries led to many questions concerning, e.g., whether non-radial oscillation modes would be observable or damped in the core or what the typical lifetime of the stochastically excited and damped modes would be. Data from the dedicated photometric space missions MOST (Microvariability and Oscillations of STars; Matthews et al. 2000), CoRoT (Convection Rotation and planetary Transits; Baglin et al. 2006) and Kepler (Borucki et al. 2008) have been vital in answering these and subsequent questions.

5.1 Non-radial oscillation modes

The theoretical work by Dziembowski et al. (2001) for $\alpha$ UMa showed that high up on the red-giant branch non-radial modes are strongly damped in the core. Extrapolating from this result, it was initially thought that non-radial modes would be strongly damped in the cores of stars all along the red-giant branch (Christensen-Dalsgaard 2004). However, this was contradicted by observations. Firstly, Hekker et al. (2006) claimed the detection of non-radial modes in red-giant stars. For this claim they analysed the moments of the cross-correlation functions (CCFs) of the spectra of $\xi$ Hydrae, $\epsilon$ Ophiuchi and $\eta$ Serpentis taken during the previously mentioned spectroscopic campaigns (see Sect. 3.4 for this diagnostic). The variations in the moments as a function of frequency were inconsistent with radial modes, and hence Hekker et al. (2006) concluded that these oscillations are non-radial. This was subsequently followed by a similar claim based on MOST data of $\epsilon$ Ophiuchi (Kallinger et al. 2008a), where the authors extracted frequencies of non-radial modes from the power spectrum. These claims were finally unambiguously confirmed using CoRoT data (De Ridder et al. 2009). The CoRoT data showed that the oscillations in red giants form a regular pattern similar to that seen for the Sun. This includes oscillation modes with significant amplitudes at the expected locations of dipole ($l=1$) and quadrupole ($l=2$) modes. Hence, these observations confirmed that non-radial modes reach observable heights at the surface of red-giant stars (see Fig. 45 taken from De Ridder et al. 2009). At the same time, the presence of non-radial modes with observable amplitudes at the stellar surface for stars along the red-giant and horizontal branch could be confirmed theoretically by Dupret et al. (2009, see also Sect. 4.3).

Fig. 45

Left Power density spectrum of the red giant CoRoT-101034881 showing a frequency pattern with a regular spacing. Right échelle diagram of the modes shown in the left panel showing ‘ridges’ related to radial and non-radial modes. Image reproduced with permission from De Ridder et al. (2009), copyright by Macmillan

5.2 Mode lifetimes

The mode lifetimes of the individual oscillation frequencies (see Fig. 39) are tied to the excitation and damping of the modes. From the first observations of $\xi$ Hydrae the lifetimes and amplitudes of the oscillation modes were examined by, e.g., Houdek and Gough (2002) and Stello et al. (2006b). Houdek and Gough (2002) reproduced the amplitudes tolerably well with their computations of a stochastic excitation model in which they used a non-local time-dependent generalisation of the mixing-length formulation of Gough (1977b). Subsequently, Stello et al. (2006b) estimated the mode lifetime for $\xi$ Hydrae from the scatter of the measured frequencies about a regular pattern. With this method Stello et al. (2006b) found a substantially shorter mode lifetime than Houdek and Gough (2002). Data from the CoRoT space mission were again seminal in showing that lifetimes of oscillation modes can vary from tens of days to of order one hundred days (see narrow peaks in the left panel of Fig. 45; De Ridder et al. 2009).

Although the physics responsible for the damping mechanism is not yet fully understood (see also Sect. 4.3), the mode lifetime ($\tau \propto 1/\varGamma$, with $\varGamma$ indicating the FWHM mode linewidth) follows a trend with temperature (see Fig. 46 and Chaplin et al. 2009; Baudin et al. 2011; Corsaro et al. 2012, 2015a, and references therein). Interestingly, there seems to be a steeper temperature gradient for the hotter main-sequence stars than for the cooler red-giant stars, whose origin is yet to be explained.

Fig. 46

Linewidths ($\varGamma$) of the $l=0$ ridge plotted against $T_\mathrm{eff}$ for the stars of NGC 6791 (red circles) and NGC 6819 (green squares). Red-giant-branch stars (RGB) are indicated with filled symbols and red-clump stars (RC) with open symbols (see legend). Also shown are measured linewidths for main-sequence and subgiant field stars (blue diamonds) from Appourchaux et al. (2012). The fit to the main-sequence and subgiant stars taken from Appourchaux et al. (2012) is also shown (dot-dashed blue line). The dashed black line shows an exponential fit to all stars. Image reproduced with permission from Corsaro et al. (2012), copyright by AAS

Fig. 47

Dipolar period spacing $\Delta \varPi _{1}$ as a function of the frequency spacing $\Delta \nu$. Top the seismic proxy for the stellar mass is indicated by the colour code. The evolutionary states are indicated by S (subgiants), R (RGB), f (helium subflash stage), C (red clump), p2 (pre secondary clump), 2 (secondary clump), and A (stars leaving the red clump moving toward the AGB). The error boxes on the right side indicate the mean uncertainties, as a function of $\Delta \varPi _{1}$, for stars on the RGB; for clump stars, uncertainties are indicated on the left side. Dotted lines indicate the boundaries between evolutionary stages. We note that only Mosser et al. (2014) have so far claimed evidence of stars with sub-flashes (f); these assignments have not been assessed nor dismissed by other work. Bottom zoom in the red-clump region. Image reproduced with permission from Mosser et al. (2014), copyright by ESO

5.3 Glitches

The first evidence for the helium glitch in a red-giant star was found using CoRoT data by Miglio et al. (2010), who pointed out that the properties of the glitch could be used as additional seismic diagnostics in the global characterization of the star. Broomhall et al. (2014) made an extensive analysis of the effects of the helium glitch in red-giant models. They noted the difficulty in obtaining meaningful inferences of the helium abundance, given the limited number of modes available for the analysis. Encouraging results were obtained by Corsaro et al. (2015b) for 18 low-luminosity red giants observed for the full Kepler mission; they showed that the formulation derived by Houdek and Gough (2007) gave an excellent fit to the observed glitch signatures and obtained relatively precise determinations of the amplitude and acoustic depth of the glitch signal. Vrard et al. (2015) analysed a large sample of Kepler red giants and found interesting differences in the glitch properties of red-giant-branch and clump stars. This may be related to the difference found by Kallinger et al. (2012) between these two evolutionary stages in the phase term $\epsilon$ (cf. Sect. 3.3.4), which appears to be caused by differences in the ionization behaviour of helium (Christensen-Dalsgaard et al. 2014).

5.4 Mixed modes

A first mention of dense and/or irregular frequency patterns in the solar-like oscillations of red giants was made by Hekker et al. (2009). These authors already indicated that this could be explained by the fact that the observed oscillations are influenced by their behaviour in both the p-mode and g-mode cavity. Kepler observations were needed to resolve these modes and identify that non-radial modes in red-giant stars are mixed modes (Bedding et al. 2010a), i.e. they propagate in both the outer acoustic cavity as well as in the inner buoyancy cavity. Results on mixed modes for stars observed by both CoRoT and Kepler have been presented by, e.g., Beck et al. (2011), Bedding et al. (2011), Mosser et al. (2011a) and Mosser et al. (2014). The detection of mixed modes in timeseries data from the Kepler mission for a few hundred stars showed that the period spacing between the mixed modes is a direct measure of whether a star is in the hydrogen shell burning phase or also burning helium in the core (Bedding et al. 2011; Mosser et al. 2011a). Subsequently, Mosser et al. (2014) used the combined period spacing and large frequency separation to also identify stars in short evolutionary phases such as the helium subflash stage, pre-secondary clump stars and stars leaving the red clump moving towards the AGB (see Fig. 47). The differences in the period spacings between stars with an inert helium core and stars with core-helium fusion are in part attributed to the presence of a convective core in stars with helium-core fusion (Christensen-Dalsgaard et al. 2014, see also Sect. 4.2.5).

Fig. 48

Rotational splitting $\delta \nu _\mathrm{rot}$ as a function of large frequency separation $\Delta \nu$ in log-log scale. RGB stars are indicated with crosses, red-clump stars are indicated with triangles and secondary-clump stars are indicated with squares. All symbols are colour coded by the mass estimate from asteroseismic parameters (see colour bar). The mean uncertainties in $\delta \nu _\mathrm{rot}$ are indicated by the vertical bars on the right. The horizontal dotted line indicates the frequency resolution. The dashed (dotted-dashed) line shows the confusion limit with mixed modes in RGB (RC) stars. Image reproduced with permission from Mosser et al. (2012b), copyright by ESO

Fig. 49

Evolution of the average core rotation period as a function of stellar radius for different assumptions of angular momentum transport in a 1.5 $\hbox {M}_{\odot }$ model initially rotating at 50 km s$^{-1}$. Models without angular momentum transport (green), including transport of angular momentum due to rotational instabilities (purple) and accounting for magnetic torques in radiative regions (red, Tayler-Spruit magnetic fields) are shown. The star symbols indicate the locations of KIC8366239 and KIC5006817 as derived using the maximum observed splitting of their mixed modes (Beck et al. 2012, 2014). Dashed lines indicate a linear fit to the different curves during the early RGB. The vertical dotted line shows the location of H-core exhaustion (TAMS, terminal-age main sequence). The red dotted line shows the evolution of core rotational period for a model where the resulting Tayler-Spruit diffusion coefficient has been multiplied by a factor of 100. Stars in the red giant sample of Mosser et al. (2012b) with $R < 7.5$ R$_{\odot }$ are shown as black dots. The best fit to the core rotation of the sample Mosser et al. (2012b) is also shown as a dashed blue line. Image reproduced with permission from Cantiello et al. (2014), copyright by AAS

5.5 Radial differential rotation

Using the fact that different mixed modes probe different radial regions in stars, Beck et al. (2012) investigated the mixed modes for rotational splittings. They found that rotational splittings show different behaviour depending on whether the rotationally-split modes are pressure dominated or gravity dominated. Qualitative comparison with models revealed that subgiants and red-giant stars ascending the red-giant branch exhibit radial differential rotation with the core rotating faster than the surface (Beck et al. 2012; Deheuvels et al. 2012). Deheuvels et al. (2014) showed that the core of stars in the subgiant phase spins up before reaching the base of the RGB and subsequently spins down on the RGB (Mosser et al. 2012b, see their Fig. 9) due to efficient transport of angular momentum (AM) from the core to the envelope the origin of which is still unknown. At the same time Mosser et al. (2012a) also found an important slow down for red-clump stars compared with the red-giant-branch stars (see Fig. 48). Deheuvels et al. (2012), Deheuvels et al. (2014) and Di Mauro et al. (2016) subsequently performed rotational inversions to investigate the radial rotation profiles. They showed that the core rotation rate can be determined with only a weak model dependence. Additionally, an upper limit for the surface rotation could be obtained.

Interestingly, from a theoretical point of view the observed core rotation cannot be explained. Current models include transport of angular momentum due to rotationally induced instabilities and circulations as well as magnetic fields in radial zones (generated by the Tayler-Spruit dynamo; Tayler 1973; Spruit 1999) and internal gravity waves. However, these models over-predict the core rotation rate by about one order of magnitude (e.g., Eggenberger et al. 2012; Marques et al. 2013; Fuller et al. 2014; Cantiello et al. 2014), as illustrated in Fig. 49. This leads to the conclusion that an additional angular momentum transport process must be operating that is currently not included in the models. Belkacem et al. (2015a) and Belkacem et al. (2015b) investigated the efficiency of mixed modes in extracting angular momentum from the innermost regions of subgiants and red giants. They concluded that for evolved red giants, mixed modes are sufficiently efficient to balance and exceed the effect of the core contraction, in particular in the hydrogen-burning shell. However, this is not the case for subgiants and early red giants.

5.6 Suppressed dipole modes

For a small subset of stars the dipole ($l=1$) modes seem to be suppressed, i.e. they have a low height or visibility ($V^2$, i.e. amount of integrated power compared with that of the radial modes) in the power spectrum. This was first flagged by Mosser et al. (2012a) and followed by a detailed investigation for a single star by García et al. (2014). These authors concluded that the low visibility cannot be explained by damping effects nor by a fast-rotating core. Recently, Fuller et al. (2015) showed in a theoretical study that a high magnetic field in the stellar core, i.e. a magnetic greenhouse effect, would induce low mode visibilities. In parallel, Stello et al. (2016a) showed that there is agreement between the observed and simulated visibilities of the suppressed oscillation modes and that this lends evidence for the presence of a high magnetic field in the cores of the red giants with suppressed dipole modes. Further support for this model follows from the fact that the suppressed modes are only found in stars with masses above ${\sim } 1.1 \,\mathrm{M}_\odot$, i.e., stars that in the main-sequence phase would have had a convective core which could have given rise to a dynamo-generated field in the core. Figure 50 shows a schematic diagram of the magnetic greenhouse scenario as well as a comparison of the predicted visibilities from this scenario with observed visibilities of dipole modes as a function of stellar mass. Subsequently, Stello et al. (2016b) also investigated the suppression of quadrupole and octupole modes. They found that mode suppression weakens for higher-degree modes with a reduction in the quadrupole mode visibility of up to 49% and no detectable suppression in octuple modes. This is consistent with predictions based on the theory of the magnetic greenhouse effect (Fuller et al. 2015) applied to these higher-degree modes. Recently, Mosser et al. (2017a) analysed a sub-sample of red giants with suppressed modes, characterized by having high signal-to-noise ratio, and showed that in these cases the suppressed dipole modes are mixed modes, with a character similar to that of modes in stars with no suppression. Therefore, in this case a mechanism that only partially damps the oscillations without affecting the basic frequency structure, is implied. On this basis Mosser et al. (2017a) questioned the scenario of Fuller et al. (2015). However, it remains to be seen whether the magnetic mechanism, perhaps with suitable modifications, is consistent with these observations.

Fig. 50

Left Average visibility of each star vs. $\nu _\mathrm{max}$, which correlates closely with surface gravity (shown on the top axis) for stars with masses ranging from 0.9 to 2.1 (top to bottom and colour scale). Stellar mass has a formal $1\sigma$ uncertainty of 10%. Stars evolve from right to left in the diagrams, corresponding roughly with the beginning of the red-giant phase to the red-giant luminosity bump. The solid black line shows the theoretical predicted dipole-mode suppression for $1.1\hbox {M}_{\odot }$, $1.3\hbox {M}_{\odot }$, 1.5$\hbox {M}_{\odot }$, 1.7$\hbox {M}_{\odot }$ and 1.9$\hbox {M}_{\odot }$ (top to bottom panels) and a radial-mode lifetime of 20 days. The fiducial dotted lines separate normal and dipole-suppressed stars. Image reproduced with permission from Stello et al. (2016a), copyright by AAAS. Right Schematic representation of the magnetic greenhouse effect. Acoustic waves excited in the envelope couple to gravity waves in the radiative core. In the presence of a magnetic field in the core, the gravity waves are scattered at regions of high field strength. Because the field cannot be spherically symmetric, the waves are scattered to high angular degree and become trapped within the core, where they eventually dissipate (dashed wave with arrow). Image reproduced with permission from Fuller et al. (2015), copyright by Macmillan

5.7 Galactic archaeology

The large number of dwarfs and intrinsically bright red-giant stars for which accurate stellar parameters are now becoming available from asteroseismology has added a new dimension to the field of Galactic archaeology, i.e., the study of the formation and evolution of the Milky Way by reconstructing its past from its current constituents. The first study using asteroseismic data to probe the galactic disk was performed on a set of about 800 CoRoT stars. This study showed qualitative agreement between the models and observations, but also flagged differences in $\nu _\mathrm{max}$ distributions (Miglio et al. 2009). This was subsequently followed by a population synthesis study using asteroseismic data of about 500 dwarfs observed with Kepler. Again the models and observations were in qualitative agreement, although there were differences present in the mass distributions (Chaplin et al. 2011).

These early investigations have initiated major collaborations between asteroseismic experts and experts in galactic astronomy to combine the efforts of large spectroscopic surveys (see Feltzing 2016, for an overview of the ongoing spectroscopic surveys and the requirements for them) with the asteroseismic measurements. These collaborations have among others led to improvements in red giant spectroscopy (Pinsonneault et al. 2014; Ren et al. 2016; Valentini et al. 2016); to improved estimates of distances and extinctions (Rodrigues et al. 2014); to a direct measurement of a vertical age gradient in the Milky Way (Casagrande et al. 2016); as well as to the detection of $\alpha$-rich young stars, i.e., stars that are young according to their asteroseismic measures and old based on their chemical abundance of $\alpha$ elements (Chiappini et al. 2015; Martig et al. 2015). First studies investigating these young $\alpha$-rich stars hint towards these stars being blue stragglers (Yong et al. 2016; Jofré et al. 2016).

5.8 Extra-solar planets

The photometric timeseries obtained by the CoRoT and Kepler space instruments are suitable for both exoplanet studies and asteroseismology. The combination of both has been the basis of many ground-breaking planet discoveries (e.g., Carter et al. 2012; Barclay et al. 2013; Campante et al. 2015). Transiting exoplanets leave larger signatures in the timeseries data when orbiting a smaller star, hence one may expect an observational bias against stars with larger radii. Nevertheless, it is possible to detect transiting planets around early red giants. Huber et al. (2013) detected a planetary system consisting of two transiting planets around a low-luminosity red giant. Using the rotationally split (mixed) oscillation modes (Sect. 3.4.4) they also found that the spin axis of the star is not aligned with the orbital axis of the two planets. This could only be explained by a third wide companion, which has indeed been detected (Otor et al. 2016). Studies like the one by Huber et al. are essential to unravel planet formation scenarios.

6 Future

The wealth of data obtained by the photometric space missions CoRoT (Baglin et al. 2006), Kepler (Borucki et al. 2008) and K2 (Howell et al. 2014) is currently being explored. Exploiting these as well as data from future complementary (space) telescopes such as TESS (Ricker et al. 2014), PLATO (Rauer et al. 2014) and the ground-based SONG network (Grundahl et al. 2014) will be essential to study many of the questions that are still open in stellar structure and evolution of giant stars exhibiting solar-like oscillations. These questions include, but are not limited to convection, rotation, (core) overshoot, additional mixing and stellar ages. We discuss these in some detail here.

Convection and surface effects Deep in stars convection leads to a temperature stratification that is essentially adiabatic. Near the surface, where the convective transport is less efficient, a substantially superadiabatic region is present. In stellar models this is typically described with some form of a mixing-length approach (e.g., Böhm-Vitense 1958; Canuto and Mazzitelli 1991). To take the next step forward it is important to improve the models to take convection properly into account. Very promising efforts are in progress to perform 3D hydrodynamical simulations of the atmosphere and near-surface part of the interior in which convection is realistically modelled (see for instance Trampedach et al. 2014a, b; Magic and Weiss 2016). The results of the simulations can be used in stellar modelling through a calibration of parameters of simpler formulations, such as the mixing length (Salaris and Cassisi 2015). Alternatively, the outer layers of the model can be replaced by suitably averaged versions of the simulations, interpolated to the parameters of the star.

The inadequate modelling of the structure of the outermost layers is an important contribution to the frequency dependent offset between the model frequencies and observed frequencies, i.e., the surface effect. As discussed in Sect. 3.4 several approaches exist to mitigate this, although these all require adjustments on a star by star basis. Thus a better theoretical understanding of these effects is highly desirable. Replacing the outer layers of the model by an averaged 3D simulation goes some way towards reducing these effects (Rosenthal et al. 1999; Robinson et al. 2003; Sonoi et al. 2015; Ball et al. 2016). An additional contribution comes from non-adiabatic effects and the influence of turbulent pressure which are typically ignored in the modelling. Interestingly, combining 3D simulations with a non-local treatment of time-dependent convection and non-adiabaticity very substantially improves the agreement between observed and modelled solar oscillation frequencies (Houdek et al. 2017).

Rotation The current stellar models cannot reproduce the core rotation rates observed using rotationally split mixed modes (see Sect. 5.5). In these models transport of angular momentum due to rotationally induced instability and circulation, as well as magnetic fields in radiative zones generated by the Tayler-Spruit dynamo are included (Cantiello et al. 2014). The fact that these models can still not match the observations is most likely due to missing physics in the models. Observations of (radially differential) rotation in stars across the HR diagram may provide indications of what additional physical effects play a role. Additionally, the impact on red-giant models of the recent results by van Saders et al. (2016) and Metcalfe et al. (2016) regarding rotation in main-sequence stars and subgiants may need to be investigated. van Saders et al. (2016) showed that the effective loss of angular momentum ceases above a critical Rossby number (Ro):

$$\begin{aligned} \mathrm {Ro} = \frac{\text {rotation}\,\,\text {period}}{\text {convective}\,\,\text {turn-over}\,\,\text {time}} \approx 2.1. \end{aligned}$$

(142)

Subsequently, Metcalfe et al. (2016) aimed to explain the underlying reasons for this by proposing a scenario implying a change in the character of differential rotation that ultimately disrupts the large-scale organisation of the magnetic field in solar-type stars. This process begins at Ro $\approx$ 1, where the rotation period becomes comparable to the convective turn-over time. Metcalfe et al. (2016) speculated that this may lead to an accelerated decrease in the surface area of spots while the star goes through a rapid phase of magnetic evolution while crossing the Vaughan–Preston gap (Vaughan and Preston 1980). Due to the changes in magnetic topology during this fast phase of magnetic evolution stars reach Ro $\approx$ 2 where magnetic breaking operates with a dramatically reduced efficiency (van Saders et al. 2016). Although this scenario is still speculative the proposed changes in the rotation of main-sequence stars may impact the rotation profiles of red giants.

Finally, in terms of observations of the envelope rotation rate it will be of importance to measure rotational splittings of p-dominated $l=2$ and $l=3$ modes (see Sects. 3.4.4 and 4.4) as these have larger sensitivity to the surface layers (see red triple-dot-dashed line in Fig. 43). Radial-velocity observations are more sensitive to these higher-degree modes and hence SONG could play a major role in this.

Additional mixing The standard theory of stellar evolution fails to explain abundance anomalies observed in stars ascending the red-giant branch. Spectroscopic studies showed that when stars reach the bump (see Sect. 2.1.2) a drop in the surface carbon isotopic ratio, lithium and carbon abundances is present, while nitrogen increases slightly (e.g., Gilroy and Brown 1991; Tautvaisiene et al. 2013). This is not seen in standard stellar models and provides evidence that an extra-mixing process should occur when low-mass stars reach the bump (e.g., Lagarde et al. 2015, for a study into the effects of rotation-induced mixing using both asteroseismic and spectroscopic constraints).

Asteroseismic measurements of the strength and locations of boundaries between radiative and convective regions that are observable as glitches (see Sects. 3.4.5 and 4.2.4) could be very important to determine the strength, location and efficiency of the additional mixing that needs to be added to the models to match both the observed stellar internal structure and the observed chemical yields.

Core overshoot In models the edge of a convective core can be described by different criteria (Sect. 2.1.1). Whether semi-convection exists or another form of slow mixing is present can currently not be directly constrained from observations (Constantino et al. 2015, 2016). With the mixed modes it is possible to probe the stellar core (e.g., Bedding et al. 2011; Mosser et al. 2014); model investigations show that there are prospects to investigate sharp features around the core (Cunha et al. 2015), and this will be essential in constraining the properties of the edge of a convective core. Such glitch analysis (Sects. 3.4.5, 4.2.4) based on mixed modes may be the only source of direct observational evidence that can be obtained for the region where core overshoot may take place. A full exploitation of the archival data from Kepler may provide these observational constraints on the core overshoot processes.

Suppressed dipole modes As described in Sect. 5.6 for a fraction of the observed red-giant stars the dipole modes are suppressed. Currently there exists one scenario (Fuller et al. 2015) to explain the presence of these suppressed dipole modes. For this scenario, the predictions are consistent with observations (Stello et al. 2016a, see also Fig. 50), although it was questioned by Mosser et al. (2017a). However, the presence of large magnetic fields in the core can currently not be tested directly, while further theoretical elaboration of the magnetic model is required (e.g., Cantiello et al. 2016). Hence, it is hard to confirm or reject this scenario at the moment. In this respect, it may be interesting if other scenarios that can be confirmed/rejected or correlations with other stellar parameters can be established.

Ages There is no observable that is sensitive to age and age only (Soderblom 2010), so all measures of stellar ages are either empirical (with a model dependent calibration) or model dependent. Hence, any improvement in the models and/or matching the data with models by mitigating the surface effect will influence the age determinations of stars. This is particularly relevant for evolved stars as uncertainties in earlier evolution phases accumulate. Despite these limitations, it may be possible to find combinations of (asteroseismic) observables that are more sensitive to age and to improve age estimates using asteroseismology.

Red-clump stars Red-clump stars are both from an observational as well as from a modelling point of view not well understood. Red-clump models carry information from the main-sequence stellar structure. Even a small change in the stellar structure at the main sequence can lead to significant differences in terms of effective temperature, luminosity and internal structure after the onset of helium-core burning. Additionally, the subflashes that are predicted to occur at the onset of helium-core burning for low-mass stars with degenerate cores (see Sect. 2.1.3) leave sharp features in the model internal structure. This results in a very irregular pattern of frequencies and period spacings for stars entering the red clump (Constantino et al. 2015, see also Sect. 4.2.5). Information on the reality and nature of the subflashes from observations will be essential to better understand the red-clump models. This may be obtained from stars that are descending the red-giant branch after helium ignition. However, this is challenging as this is a very short phase in evolution, reducing the probability that any observed star is in that phase. Additionally, stars already in the red clump may provide the observational evidence for the presence of the flashes. However, from an observational point of view, the combination of period spacings, rotational splittings and noise that seems to be present in the observed power density spectra make it very difficult to disentangle all individual oscillation modes. Hence, observational evidence of regularity or irregularity is still awaiting for many of these stars. We anticipate that with the long timeseries of Kepler data it will be possible to disentangle these observational features, but a detailed mining of the data with tailor-made tools will be required. The future for asteroseismology of giant stars with solar-like oscillations looks very promising. In addition to the wealth of archival data there are two new space missions planned which will again provide complementary data in terms of nearly all-sky coverage with TESS and brighter stars with PLATO. Additionally, the Stellar Oscillations Network Group (SONG) has one node fully operational and one node in development. SONG provides spectroscopic data from the ground, which will be valuable to study higher degree modes, as well as stars with long periods. These observational data together with improved 1-D and 3-D models are bound to improve significantly our knowledge of stellar structure and evolution of giant stars over the next decade(s).