From tolerance allocation to tolerance-cost optimization: a comprehensive literature review

Abstract

It is widely acknowledged that the allocation of part tolerances is a highly responsible task due to the complex repercussions on both product quality and cost. As a consequence, since its beginnings in the 1960s, least-cost tolerance allocation using optimization techniques, i.e. tolerance-cost optimization, was continuously in focus of numerous research activities. Nowadays, increasing cost and quality pressure, availability of real manufacturing data driven by Industry 4.0 technologies, and rising computational power result in a continuously growing interest in tolerance-cost optimization in both research and industry. However, inconsistent terminology and the lack of a classification of the various relevant aspects is an obstacle for the application of tolerance-cost optimization approaches. There is no literature comprehensively and clearly summarizing the current state of the art and illustrating the relevant key aspects. Motivated to overcome this drawback, this article provides a comprehensive as well as detailed overview of the broad research field in tolerance-cost optimization for both beginners and experts. To facilitate the first steps for readers who are less familiar with the topic, the paper initially outlines the fundamentals of tolerance-cost optimization including its basic idea, elementary terminology and mathematical formulation. These fundamentals serve as a basis for a subsequent detailed discussion of the key elements with focus on the different characteristics concerning the optimization problem, tolerance-cost model, technical system model and the tolerance analysis model. These aspects are gathered and summarized in a structured mind map, which equips the reader with a comprehensive graphical overview of all the various facets and aspects of tolerance-cost optimization. Beside this, the paper gives a retrospect of the past fifty years of research in tolerance cost-optimization, considering 290 relevant publications. Based thereon, current issues and future research needs in tolerance-cost optimization were identified.

1 Motivation

Despite the continuous improvements of manufacturing and measurement, geometrical deviations are unavoidable due to manufacturing and measurement imperfections [1]. These deviations, however, mainly influence the quality of mechanical products throughout their entire product life cycle [2, 3]. In order to limit the unintentional part deviations, the designer specifies and allocates tolerances to ensure the fulfillment of specified quality requirements. In this regard, tolerance allocation is a key task in design engineering and associated with high responsibility for product functionality as well as for profitability.

In general, tolerances are allocated on the basis of experimental data, previous drawings and expertise [4]. In this context, manual approaches are common to check and assign the tolerance values on a trial-and-error basis [5,6,7,8]. In doing so, the resulting manufacturing costs are mostly neglected or merely indirectly considered by qualitative thumb rules like “the lower the tolerance the higher the cost of manufacturing” [4]. Moreover, traditional tolerance allocation methods require extensive time and effort [4] and do not lead to a least-cost tolerance design due to their unsystematic procedure and the lack of considering quantitative (tolerance-) cost information [5].

For a more efficient and sophisticated tolerance allocation considering both quality and cost issues, various methods for optimal tolerance allocation using optimization techniques, i.e. tolerance-cost optimization, steadily evolved since its beginnings in the mid-twentieth century [9]. Especially in times of rising cost and quality awareness and the availability of manufacturing data in a digitalized, highly computerized production, it is seen as an important key element in industry [10,11,12,13] to bridge the gap between manufacturing and design [14] and to create a balance between manufacturing costs and quality [15].

However, the complexity of tolerance-cost optimization with its interdisciplinary elements is currently an obstacle for its profitable implementation and application in the industry [5]. In comparison with tolerance analysis, it is regarded as complex and challenging [5, 16].

Despite the broad field of related domains, the number of publications reflecting the state-of the art is limited. Existing review articles, e.g. [9, 17,18,19,20,21], indeed address the relevant topics in a suitable and illustrative manner but are either not up-to-date or focus merely on certain specific aspects. However, a comprehensive review of tolerance-cost optimization is missing so far.

With the aim to close this gap, the following review article gives a comprehensive overview of tolerance-cost optimization and discusses the relevant topics in detail. In doing so, the different aspects of manufacturing, tolerancing, optimization and their interrelations are illustrated using a car disk brake system as a case study of industrial complexity (see Fig. 1).

Fig. 1

Case study: car disk brake system [22]

The article is subdivided into three major parts: Firstly, Section 2 illustrates the role of tolerance allocation in the design process and presents the basic idea and the mathematical description of tolerance-cost optimization. Based on these fundamentals, Section 3 discusses the different aspects in detail. While Section 3 initially summarizes and categorizes all relevant aspects in a comprehensive mind map, the subsequent Sections 3.1–3.4 present the various details of tolerance-cost optimization and their interrelations. After that, Section 4.1 gives a comprehensive review of the last five decades of research in the field of tolerance-cost optimization. For this purpose, an extensive literature review of 290 research articles serves as a basis for discussing the current and future trends and to identify future research needs in Section 4.2. Finally, Section 5 summarizes the article.

2 Fundamentals of tolerance allocation and tolerance-cost optimization

The following section equips the reader with the fundamentals of tolerance allocation and tolerance-cost optimization and is particularly tailored to interested researchers and practitioners who are less experienced in these topics. As a consequence, experienced readers may skip this section and straightly continue with Section 3.

2.1 The role of tolerancing in design engineering

A successful development of high-quality products necessitates the fulfillment of requirements of a wide variety of interest groups. Consequently, conflicts of interests and competing objectives dominate and shape the product development process [23]. When detailing the product design in the different phases of the design engineering process, a balance must be created between the conflicting objectives, especially between quality and cost, to increase productivity [24, 25]. Motivated by this need, Taguchi proposed a three-step approach for a successful assignment of the nominal design parameter values and tolerances [24, 25] (see Fig. 2).

Fig. 2

Off-line quality control in design engineering according to Taguchi: system design, parameter design, tolerance design

Firstly, the system design is used to define the product configuration by applying different methods for the identification, evaluation and selection of solutions with respect to product robustness [24, 25]. Secondly, the nominal values for the design parameters are determined in the parameter design [25]. Thirdly, the tolerance design is intended to assure product quality by limiting the deviation of the geometry from nominal [24, 25]. In doing so, first general ideas are systematically turned into conceptual solutions and finally into the documented detailed product design.

2.1.1 Robust design

All these early and late phases of the design engineering process are accompanied by the paradigm of robust design [26, 27], i.e. improving the robustness of a system in terms of quality, reliability and costs [28]. Focusing on this global aim, a huge number of robust design techniques for system, parameter and tolerance design are used to reduce the sensitivity of design parameters of a system under uncertainties [9, 24, 29]. In tolerance design, this aspect is mainly incorporated by a concurrent optimization of dimensions and tolerances to achieve a so-called robust tolerance design at minimum cost [30, 31]. In doing so, numerous authors adopt the basic idea of Taguchi’s quality loss and integrate this aspect in tolerance design (see Section 3.2.2) [9]. These approaches take into account that any deviation from the target value results in an additional loss for the customer [32,33,34].

2.1.2 Tolerance design for manufacturing

Besides the important aspects from design, tolerance design has to consider numerous manufacturing issues to enable a profitable fabrication of quality products. Process planning is often seen as the missing link between design and manufacturing [35] that can help to bring the manufacturing concerns into the design process (see Fig. 2) [36]. While the design tolerances t are assigned with focus on the requirements of a mechanical assembly or a component in use, the machine or process tolerances δ are required to create a process plan for part manufacturing [17]. Therefore, the design tolerances are the result of a sequence of machining tolerances realized by a sequence of different machining operations (see Fig. 3).

Fig. 3

Car brake disk: manufacturing and design tolerances in comparison freely adapted from [9]

Traditionally, the specification and allocation of design and process tolerances are done by two separated divisions, by design and manufacturing [37, 38]. Door by door, methods supporting the assignment of manufacturing tolerances have concurrently evolved over the years. Therefore, tolerance transfer plays an important role as it attempts to convert the design tolerances into a production plan by using tolerance analysis and synthesis methods [39]. Thereby, a tolerance chart is used as a graphical representation of the process plan and serves as a basis to control the dimensions of a workpiece with its tolerances [40,41,42,43]. The tolerance chart balancing techniques aim to widen the tolerances without violating the blueprint specifications using both qualitative and quantitative cost information [44]. In its beginnings, these methods were associated with a great deal of manual effort and their usage was mainly experience-driven [43, 45, 46]. By successively computerizing them, they nowadays play an important role in computer-aided process planning (CAPP) [17, 47,48,49]. Huge effort was incurred to create mathematical models for tolerance chart allocation and solving them using optimization algorithms [39].

2.1.3 Concurrent tolerance design

For a long period of time, this separated view of design and manufacturing was quite common [50]. Pushed by the revolutionary stream of concurrent and simultaneous engineering, the machine tolerances were steadily integrated in the framework of tolerance design [17, 46, 51]. By linking both disciplines, various aspects of process planning, such as multi-station manufacturing processes, stock removal allowance, tolerance charting, process scheduling and tolerance-cost models including process parameters and machine accuracy, can simultaneously be considered [14, 51,52,53,54,55]. Such integrated approaches intend to better link design and manufacturing by transferring the relevant elements from process planning into tolerance design. In doing so, numerous information and aspects from manufacturing and inspection have to be incorporated in tolerance design. Due to this, tolerancing plays a responsible and decisive key role in the product development process.

2.2 Important issues in tolerancing

Tolerances are primarily assigned to control the inevitable part deviations and their effects on the total product quality [1, 56]. However, a proper assignment of part tolerances is a demanding task necessitating a number of different tolerancing activities (see Fig. 4) [56].

Fig. 4

Classification of tolerance specification, allocation, analysis, synthesis and optimization according to [56]

Initially, the product requirements must be translated into a set of geometrical requirements which are subsequently decomposed from product to assembly and part level. In doing so, essential features, often called key characteristics (KC), are identified. They significantly influence the fulfillment of the product requirements if they vary from nominal [57].

Afterwards, the tolerance specification is used to define the tolerance types for all relevant features in compliance with current tolerancing standards addressing the qualitative issues of tolerancing [58, 59]. Based on the tolerance specification, an appropriate value for each tolerance has to be assigned in the subsequent step of tolerance allocation (see Section 2.3). The initially allocated tolerances serve as a basis for the tolerance analysis which helps to study the effects of the part deviations and to check the fulfillment of the predefined quality objectives [39, 60].

In contrast to tolerance analysis, tolerance synthesis starts with the requirements of the KCs and identifies suitable tolerance values as well as tolerance types by considering the results of iterative tolerance specification, tolerance allocation and tolerance analysis in a common synthesis step (see Fig. 4) [61].

Driven by the demands of high-quality products, tolerance optimization aims to achieve an optimal tolerance allocation by selecting a set of tolerance values while the tolerance specification is fixed [39]. The usage of optimization techniques helps to identify the best tolerance values in terms of quality [9].

Challenging enough, the tolerance engineer is also responsible for the resultant costs caused by the assigned tolerances. For this purpose, tolerance-cost optimization plays an important role since it covers both quantitative quality and cost information to realize an optimal tolerance allocation [12].

2.3 Tolerance allocation

As highlighted, tolerance allocation corresponds to assigning and distributing the tolerance values among the parts of an assembly [59, 62]. In general, tolerances are primarily assigned for functionality mostly based on expertise or empirical data. In doing so, the cost aspect is neglected or only indirectly taken into account [63]. As a consequence, tolerances are typically chosen tighter as necessary to ensure product quality [64]. This leads to high-quality products but also to higher manufacturing costs [63, 65]. The identification of a valid set of tolerance values creating a balance between quality and cost is a challenging task. In order to solve this conflict (see Fig. 5), three main questions must be answered [66]:

• 1. ”How good does the product have to be?”

• 2. ”What can be done to improve the quality of the product?”

• 3. ”What is the most profitable action to take?”

Fig. 5

Quality-cost conflict in tolerance allocation according to [67]

With the aim to answer these questions, various methods have been developed over the last decades:

2.3.1 Traditional methods

Numerous approaches of tolerance allocation date back to a time where computer technology was either not available at all or their capability was strongly limited. Besides graphical approaches [68, 69], several analytical methods have emerged in those years, e.g. equal scaling by the same tolerance or same influence method or proportional scaling by using different weighting factors [70,71,72,73]. However, these methods are often based on rough rules of thumb [72, 74] and do not consider any quantitative cost information [21, 72]. As a consequence, their applicability is strongly limited and they are not sufficient for defining a tolerance design that withstands the quality and cost pressure in modern product development. Consequently, they are mostly used for a preliminary tolerance assignment in early design stages [21, 74] serving as a basis for subsequent optimization procedures today.

2.3.2 Manual, iterative application of tolerance analysis

In contrast, the iterative application of tolerance analysis is more common to check and assign the tolerance values on a trial-and-error basis [6, 8, 75]. Beginning with guessed or purposely assigned tolerances, the designer analyzes the design for the current tolerances and checks if the quality requirements are met. If the current allocation fails, tighter tolerances have to be assigned. Otherwise, wider tolerances leading to reduced manufacturing costs can be chosen [76]. Hence, the additional use of sensitivity analyses helps to identify the relevant tolerances by determining the contribution of each tolerance to the KC [77, 78]. Afterwards, the most relevant tolerances are manually adapted. This manual re-allocation step is repeated until the tolerance expert is satisfied with the current solution [78]. Despite its usability, this approach is very time-consuming [75] and leads to non-optimal solutions since there is no quantitative cost information taken into account [78].

2.3.3 Quality engineering methods

Alternatively, quality engineering and statistical methods are applied to solve the tolerance-cost conflict [18] since they are regarded as practicable for complex mechanical assemblies [39, 79] and they convey process knowledge [80]. Hence, different methods of design of experiments (DOE) in combination with analyses of variance (ANOVA) are used to identify an optimal tolerance design [18, 81,82,83]. However, these approaches are not universally applicable and do not necessarily lead to optimal results.

2.4 Tolerance-cost optimization

To overcome the drawbacks of the previously discussed approaches, the tolerance allocation problem can be formulated as a mathematical optimization problem and solved with the aid of deterministic and stochastic optimization algorithms [9]. In contrast to the open loop structure of the manual, repetitive application of tolerance analysis [84], the tolerance re-allocation is automatically performed within the optimization process considering both quality and cost information quantitatively [12]. Using the example of the brake disk, the tolerance values of the individual components are thus optimally chosen to both assure the braking performance and to achieve a cost-efficient tolerance design by considering the relations between the assigned tolerances and the resultant manufacturing costs.

Not least due to its great potential, the usage of optimization techniques for tolerance allocation has arisen the interest of a great number of research activities over the last years. As a consequence, several terms for tolerance-cost optimization were coined and synonymously used in literature. In addition to the term tolerance(-cost) optimization [12, 85,86,87], any combination of the terms optimum [38, 88,89,90], (cost-) optimal [91,92,93,94,95], minimum cost [64, 76, 96, 97] or least-cost [98,99,100,101,102] and a more or less interchangeable term for tolerance allocation [98, 99, 103, 104], such as tolerance assignment [76, 88, 105,106,107], tolerance selection [38, 63, 86, 108, 109], tolerance allotment [91, 110,111,112], tolerance distribution [62, 72, 113], tolerance synthesis [89, 90, 114, 115] or tolerance design [6, 93, 110, 116, 117], is used. Since first applications in the 1960s, tolerance-cost optimization has successively evolved and is the preferred approach for (cost-) optimal tolerance allocation today.

2.4.1 Basic idea

Since the type of tolerance-cost optimization and its implementation strongly depends on its objective [18], it can be interpreted in different ways. In most cases, however, it aims to minimize the manufacturing costs C_sum (objective) while ensuring the fulfillment of the quality requirements by keeping the lower and/or upper specification limits for the KCs to $Q_{\min \limits }$ (constraint) [39, 98].

Therefore, the optimizer has to identify an optimal combination of tolerances ${t}=[t_{i},\dots ,t_{I}]^{\text {T}}$. The design variables t_i define the design space which is constrained by the lower $t_{i,\min \limits }$ and upper boundaries $t_{i,\max \limits }$ in compliance with the manufacturing process limits. Mathematically spoken, least-cost tolerance-cost optimization corresponds in its most simple way to a single-objective optimization [9, 99]:

$$ \begin{array}{l l r } \displaystyle \text{Minimize} \qquad \quad & C_{\text{sum}}({t})& \textit{(objective)},\\ \displaystyle \text{subject\ to:}\qquad \quad & \hat{Q}({t}) \geq Q_{\min} & \textit{(constraint)}, \\ \displaystyle & \multicolumn{2}{l}{t_{i,\min} \leq t_{i} \leq t_{i,\max} ~\forall~i=1,\dots,I.} \end{array} $$

(1)

For the sake of completeness, it must be mentioned that, besides the popular least-cost tolerance-cost optimization, best-quality tolerance cost-optimization by maximizing the quality $\hat {Q}(t)$ without exceeding a predefined cost limit $C_{\max \limits }$ has been reported [118]. Therefore, objective and constraint are reversed leading to an optimization problem of maximize $\hat {Q}( {t})$ subject to $C_{\text {sum}}( {t}) \leq C_{\max \limits }$ and $t_{i,\min \limits } \leq t_{i} \leq t_{i,\max \limits } ~\forall ~i=1,\dots ,I.$.

For both optimization problem formulations, the detailed optimization procedure for solving the tolerance-cost problem is mostly shaped by the chosen optimization algorithm with its individual settings to handle the relevant design variables, objectives and constraints. Nevertheless, the basic workflow for tolerance-cost optimization can generally be represented by Fig. 6.

Fig. 6

General workflow of tolerance-cost optimization according to [12]

The optimization process starts with a combination of initial tolerances t_init [12]. The costs for the current tolerance assignment are estimated via a cost analysis based on a tolerance-cost model which links the allocated tolerances and the resulting manufacturing costs [12]. Hence, the relationships between the costs and each tolerance t_i are described by a tolerance-cost function C_i(t_i) and together they form the tolerance-cost model C_sum(t) [9]. In addition to the cost analysis, tolerance analysis using worst-case and statistical approaches intends to analyze the system for the currently allocated tolerances [12]. The results verify whether the resultant product quality $\hat {Q}( {t})$ meets the requirements and the current tolerance assignment provides a feasible solution [12]. Afterwards, both information of cost and quality are used to evaluate the current solution. Based on this information, a new set of tolerances is selected for the subsequent evaluation in terms of quality and cost by further tolerance and cost analyses [12]. In doing so, the optimization algorithm successively adapts the tolerance values t_i in each iteration considering the previous optimization results until a predefined termination criterion is met and the optimal tolerance values t_opt are identified [12].

In summary, tolerance-cost optimization covers all methods that aim to identify an optimal set of tolerances with focus on cost and quality using optimization techniques. This implies that the cost aspect is covered by at least one objective or one constraint.

3 A comprehensive overview of tolerance-cost optimization

Based on the fundamentals illustrated in Section 2, the subsequent Sections 3.1–3.4 provide a deeper insight into tolerance-cost optimization. In doing so, an extensive literature review was carried out to obtain a comprehensive overview on the complex and interdisciplinary topic. The literature study has shown that tremendous work has already been done in the past leading to a continuous evolution over the years. However, the different perspectives and the inconsistent terminology make it difficult to identify the main aspects and the interrelations of the various publications.

With the aim to structure the different findings and to create a common, fundamental understanding, the gathered information was categorized into four key elements, viz. the optimization problem, tolerance-cost model, technical system model and tolerance analysis model with its respective categories. As a result, Figs. 7 and 8 present a comprehensive mind map illustrating tolerance-cost optimization at a glance and guiding the reader through the sections without losing track.

Fig. 7

Holistic overview of tolerance-cost optimization with its key elements and characteristics—part 1

Fig. 8

Holistic overview of tolerance-cost optimization with its key elements and characteristics—part 2

This classification additionally intends to assist the tolerance engineer in analyzing and characterizing a given or newly defined optimization problem. For researchers, the mind map serves as a useful basis to position their work in the overall context of tolerance-cost optimization. Thus, it facilitates to identify current research needs and the novelty of their publications since it is easier to find related work and the interrelations between the different categories.

Even though the proposed classification does not claim to be all-embracing, it takes the most relevant aspects of tolerance-cost optimization of mechanical systems into account. Since the linking of the information is essential to understand the interrelations between the different aspects and terms and to obtain a global understanding of the method, the individual elements are consequently described with respect to the other key elements. Relevant sources are referenced at the respective text passages, however, they are limited to a representative selection for reasons of traceability.

3.1 Optimization problem

Optimization generally corresponds to the search of an optimal combination of the design variables X optimizing, i.e. minimizing or maximizing, a given objective function f(X). Equality l_j(X) and inequality conditions g_j(X) constrain the design space by defining regions of infeasibility (see Fig. 9) [119]:

$$ \text{Find } \boldsymbol{X} = [x_{1},x_{2},\dots,x_{I}]^{\text{T}} \ \text{ which minimizes } \ f(\boldsymbol{X}), $$

(2)

subject to

$$ g_{j} (\boldsymbol{X}) \leq 0,\qquad \forall~j=1,\dots,J, $$

(3)

$$ l_{k} (\boldsymbol{X}) = 0,\qquad\forall~k=1,\dots,K. $$

(4)

Fig. 9

Two-dimensional design space of function f(X) = f(x₁,x₂) constrained by the inequality condition g₁(X)

The design space is further limited by upper and lower boundaries of the design variables [119]:

$$ x_{i,lb} \leq x_{i} \leq x_{i,ub} \qquad\forall~i=1,\dots,I. $$

(5)

In tolerance-cost optimization it is the most challenging task to adapt the basic formulation of the optimization problem in Eqs. 2–5 to the given tolerance-cost problem. Therefore, the aforementioned aspects have to be interpreted from the perspective of tolerancing.

3.1.1 Objective(s)

The objective serves as the criterion to which the design is optimized and is described by a function of the design variables [119]. In tolerance-cost optimization, the choice of the objective function depends on the users global aim and intent [18].

In general, the total costs caused by the allocated tolerances are in focus of tolerance-cost optimization and are thus forming the objective(s) (see Eq. 1). Hence, the costs can either be expressed by the manufacturing costs, by the quality loss, or by both in context of robust tolerance design. In doing so, the tolerance-cost model serves as the objective function. In quality-driven or best-quality tolerance-cost optimization, the objective function predicts the resultant quality by a suitable quality metric, e.g. the manufacturing yield or the process capability (see Section 3.4.5) using the information of the tolerance analysis model.

The type of the objective function significantly influences the choice of the optimization algorithm and its results (see Fig. 7). Linear objective functions are in general easy to solve, but they are insufficient to describe most of real engineering problems. In tolerance-cost optimization, most objective functions are nonlinear (see Section 3.2.1 or Section 3.2.2). By linearization, the initially nonlinear objectives get easier to compute but the results are less accurate due to approximation errors. Instead of simplifying the functions, it is more expedient to apply and enhance powerful algorithms to identify the global optimum of the objectives.

If multiple objectives are concurrently optimized, multiobjective algorithms are required to identify the best combinations of the different conflicting objectives [119]:

$$ f(\boldsymbol{X}) = [f_{1} , f_{2},\dots,f_{m}]^{\text{T}}. $$

(6)

Alternatively, multiple objectives are frequently reduced to a single-objective problem and optimized by one linear, weighted objective function [119]:

$$ f(\boldsymbol{X}) = w_{1}\cdot f_{1}(\boldsymbol{X}) + w_{2}\cdot f_{2}(\boldsymbol{X})+{\dots} + w_{m}\cdot f_{m}(\boldsymbol{X}). $$

(7)

3.1.2 Design variables

The main design variables in tolerance-cost optimization are the tolerances t. The tolerances are in general considered uncorrelated, i.e. independent from each other (see Fig. 7). However, there are also approaches to consider the correlations of the tolerances within the optimization, which is especially relevant in the context of selective assembly [7, 120].

The boundaries for the tolerances are defined by the precision limits of the respective manufacturing machines (see Section 3.2.1). Although the limits do mostly not necessarily have to be set, it makes sense to limit the design space to only technically feasible solutions to minimize the computing time [121]. In addition, the nominal dimensions in combined parameter and tolerance design are considered as design variables [109, 122, 123].

Tolerances are mostly considered as continuous design variables. The restriction to a number of fixed tolerances using discrete tolerance-cost functions necessitates to consider the tolerances as discrete variables in the optimization process. If both discrete and continuous design parameters form the design vector, the problem is called a mixed-discrete problem and makes the optimization more challenging [119].

The complexity further increases with the number of design variables since it leads to a more noisy and multi-dimensional solution surface [121]. A previous reduction of the number of variables to the relevant parameters influencing cost and quality is useful to shrink the dimensionality of the design space [124].

3.1.3 Constraints

In general, the tolerance-cost optimization problem is constrained by at least one inequality condition. It primarily depends on the objective of the optimization if the fulfillment of a quality or a cost limit is expressed by a set of constraints (see Eq. 1). The optimization problem is further extended by additional constraints to consider specific aspects, such as machining and process capacities [125, 126] or stock removal allowance [17].

There are different ways to deal with these constraints within the optimization (see Fig. 7). Using a direct approach, the information of a current solution is only used if all conditions are fulfilled without exception, otherwise it is directly discarded [127]. Thus, this approach leads to slow and inefficient procedures [127]. In contrast, the Lagrange multiplier method transform the constrained in an unconstrained optimization problem using optimality conditions, whereas the penalty method extends the objective function by adding further terms that penalize non-compliance with the conditions [127].

While the penalty and direct approach is independent from the type of the constraints, the mathematical formulation of the Lagrange multipliers can be a challenging task to consider the numerous linear and particularly nonlinear constraints (see Fig. 7) [127]. The realization of these closed-form approaches requires advanced computational and mathematical skills [127].

Not least due to their easier implementation [127], the penalty method in combination with stochastic algorithms is often preferred to the usage of Lagrange multipliers for tolerance-cost optimization.

3.1.4 Optimization algorithms

A number of optimization algorithms has evolved over the years and can be classified into deterministic and stochastic algorithms (see Fig. 7) [128]. Traditional optimization algorithms are generally deterministic since they deliver the same results in different optimization runs [128, 129]. Thus, most of these mathematical programming methods are based on the gradients of both objective function and constraints [128].

Numerous researchers proved the suitability of deterministic optimization techniques, e.g. linear programming [50, 72], nonlinear programming [14, 105, 130, 131] or integer-programming [63, 132] to solve most basic tolerance allocation problems [9]. However, they reach their limits when tolerance-cost optimization becomes more complex through:

• Sophisticated cost functions [133],

• Sampling techniques in tolerance analysis [12, 91],

• Interrelated key characteristics [134, 135],

• Alternative process selection and stock removal allowance [133, 136, 137],

• Process precision limits and non-overlapping cost curves [133, 135] and

• Discrete design variables [135].

As a consequence, more powerful, derivative-free algorithms are required that can problem-independently be applied and do not force the user to oversimplify the optimization problem [39, 138, 139]. Therefore, stochastic algorithms are a suitable alternative to explore the whole, severely constrained design space and to reach the global optimum for multidimensional and -modal problems by the means of trial and error [128, 129, 139]

Despite the randomness of the identified solutions in different runs, most researchers nowadays preferably apply but also enhance both single- and multiobjective, stochastic optimization algorithms for optimal tolerance allocation (see Section 4.1).

Besides well-established algorithms, such as simulated annealing (SA) [3, 66, 134], genetic algorithm (GA) [92, 137, 138, 140], (multiobjective) differential evolution [122, 141, 142], non-dominated sorting genetic algorithm II [143,144,145], (multiobjective) particle swarm optimization (PSO) [95, 146,147,148] and ant colony algorithm [123], more uncommon algorithms, such as imperial competitive algorithm [149], self-organizing migration algorithm [150], artificial immune algorithm [151], seeker optimization algorithm [152], bat algorithm [153], artificial bee algorithm [154], cuckoo search [155] or teaching-learning based algorithm [156, 157], are used for tolerance-cost optimization. Moreover, hybrid algorithms, a combination of a stochastic and a deterministic or another stochastic optimization algorithm, are studied to improve the optimization results [158,159,160,161].

In doing so, numerous publications focus on tolerance-cost optimization with the aim to benchmark a newly developed or modified algorithm with other stochastic or deterministic algorithms. Thus, they do not study the different tolerance and cost aspects in detail. However, these studies are often less useful since the results are highly dependent on the algorithm-specific settings which have to be chosen individually. A reasonable choice of one or more termination criteria, such as a maximum number of iterations, total computing time or the achievement of a predefined quality of result, is essential for the identification of the global tolerance-cost optimum (see Fig. 7). Therefore, researchers strive to develop user-friendly algorithms with a small number of required settings to ensure the applicability and reproducibility of the optimization [156, 157].

3.2 Tolerance-cost model

The main benefit of tolerance-cost optimization compared with other allocation methods lies in the usage of quantitative information about the relation of cost and tolerance (see Section 2.3). For this purpose, a tolerance-cost model is needed to represent the relations between cost and tolerance for several processes and process sequences [72] and thus is a key element in tolerance-cost optimization (see Fig. 7).

Driven by the aim to model these relationships as realistically as possible, tolerance-cost models try to include all relevant cost drivers and their contribution to the resulting manufacturing costs as a function of the assigned tolerances [162].

In addition to their direct impact on the internal manufacturing costs, tolerance allocation further influences numerous internal and external costs incurred in the entire product life cycle [3]. Tolerance-cost models thus cover a wide range of different cost aspects (see Fig. 7), such as costs for assembly and tooling [163, 164], inspection [66, 165], scrap [166], rework [167], rejection [167, 168] maintenance and service [169, 170] or ecological and social costs [171,172,173]. Their modelling is however complicated by the fact that many costs are not directly measurable [174, 175]. The identification of the costs caused by intangible quality losses, e.g. by decreasing customers’ satisfaction or loyalty [174], is challenging, especially since quality loss changes over the product lifetime by product degradation [175, 176].

Although the establishment of a practical tolerance-cost model is a tedious and not easy task [14, 177], its efforts are rewarding [43] and seen as a decisive competitive advantage [178] in industrial mass production.

3.2.1 Manufacturing costs

The availability of quality empirical tolerance-cost data is an essential prerequisite for the establishment of a reliable tolerance-cost model [107, 178]. Therefore, most studies in literature are based on approximative data from charts and tables published in a small number of textbooks and publications [179,180,181,182,183]. Not least for reasons of industrial confidentiality, the amount of available manufacturing data is strongly limited which is critically recognized in literature [9, 18]. In any case, the general suitability of the tolerance-cost data is restricted since the information is tailored to the manufacturing of specific features by installed and available machines and tools for the different processes [70, 184]. Consequently, the data must fit to the given case to ensure reliable optimization results [178].

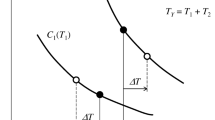
The empirical data serves as a basis to identify the correlation between tolerance and cost [177, 178]. In literature, the terms tolerance-cost (or cost-tolerance) curve, function, relationship or relation are synonymously used for the correlation of the cost C_i and the tolerance t_i or δ_i (see Fig. 10).

Fig. 10

Tolerance-cost function for a single process based on [185]

The tolerance-cost curve consists of several constant and variable cost elements. The fix costs, e.g. for material, are constant and independent from the chosen tolerance [185]. Nevertheless, they can be of importance in tolerance-cost optimization when selecting the minimum-cost machine from a number of machine alternatives. The machining costs vary with tolerance since the manufacturing of more accurate parts requires more precise tools or additional manufacturing operations, adjustment of the processing parameters, e.g. lower process rate, or particular care of the manufacturer [167, 185]. Furthermore, tighter tolerances increase the number of parts to be reworked, cause higher inspection costs to ensure their measureability and lead to a higher number of scrap parts and costs [185].

Depending on the data, different types of regression functions are suitable to derive continuous tolerance-cost function with acceptable fitting errors [45, 75, 177]. As a consequence, a number of traditional- and non-traditional, linear and nonlinear functions were presented in literature over the years (see Fig. 7) [9, 178]. The most relevant and frequently used functions in literature [178] can suitably be described by a generalized tolerance-cost function according to [144]:

$$ C_{i}(t_{i})=a_{i}+b_{i}\cdot e^{-m\cdot t_{i}}\cdot t_{i}^{-k}. $$

(8)

Thus, a number of linear and non-linear tolerance-cost functions with two up to four parameters can be expressed by the proper determination of the coefficients m,k (see Table 1).

Table 1 Excerpt of common tolerance-cost functions in literature with its coefficients according to Eq. 8 and the resulting function

Combinations of these approaches, e.g. the linear and the exponential function

$$ C=a+{b_{1}}\cdot t+\frac{b_{2}}{e^{t}} $$

(9)

or the reciprocal power and the exponential function

$$ C=a+\frac{b_{1}}{t^{c_{1}}}+\frac{b_{2}}{e^{c_{2}\cdot t}}, $$

(10)

as well as third- and higher-order polynomial functions

$$ C=a+b\cdot t+c\cdot t^{2}+d\cdot t^{3}+\dots $$

(11)

are occasionally used to reduce model uncertainty [75].

However, a proper application of analytical functions requires a reasonable selection of the model type and determination of the coefficients with respect to the given data [54, 145, 186]. Motivated to overcome this limitation, advanced approaches based on fuzzy and artificial neural networks [141, 145, 162, 177, 187, 188] have been developed to establish tolerance-cost functions without predefining the form of the curve by choosing a specific function [162].

Nevertheless, analytical functions with less coefficients are often preferred because they are easier to optimize, especially if gradient-based optimization algorithms are applied [75, 178, 188]. Exponential and polynomial functions and more sophisticated models, in contrast, approximate the curves with a higher accuracy [75, 189] but the objective function becomes more complex to be solved by optimization.

Moreover, discrete data is directly used in tolerance-cost optimization to avoid uncertainty from the choice of model type and its coefficients [186]. In addition to manufacturing, discrete tolerance-cost functions are used to address external supply in combination with alternative supplier selection [190, 191] or make-or-buy decisions (see Fig. 11a) [192]. However, besides the great amount of data, optimization algorithms handling discrete variables are required to solve the optimization problem correctly [38].

Fig. 11

Tolerance-cost model: a mapping of manufacturing costs using tolerance-cost functions and external supply with discrete tolerance classes, b gaps and overlapping areas

Traditionally, the tolerance-cost function is a function of dimensional and rarely of geometrical tolerances [193]. Alternative approaches substitute the tolerance as an input by the variance [104], process procession [194] or process capability indices [92, 195] to enhance the informative value of the tolerance-cost curves. This enables the consideration of further important aspects from serial production, e.g. discontinuous cost functions with a sharp increase in costs through a 100%-inspection if a specified process capability limit is not fulfilled [13].

However, most of the aforementioned aspects are not rigorously considered if the tolerance-cost models are just a means to an end. Thus, tolerance-cost functions and its parameters are often only arbitrarily chosen in literature, neglecting relevant manufacturing issues [178].

Since a number of tolerances is optimally allocated in tolerance-cost optimization, at least one tolerance-cost function is needed for each individual tolerance t_i to define the total tolerance-cost model [64, 101]:

$$ \begin{array}{@{}lccl} C_{\text{sum}}({\boldsymbol{t}}) = {\sum}_{i=1}^{I} C_{\text{i}}(t_{i}), \\ t_{i,\min} \leq t_{i} \leq t_{i,\max}. \end{array} $$

(12)

So far, Eq. 12 is valid if only one machine per tolerance t_i is available. However, the selection of a cost-optimal machine realized by the most cost-effective machine alternative j is of particular importance in the industrial manufacturing environment (see Fig. 11a) [196, 197]. Mathematically spoken, the tolerance-cost model considering alternative process selection is defined as:

$$ \begin{array}{@{}lccl} C_{\text{sum}}({t}) = {\sum}_{i=1}^{I}{\sum}_{j=1}^{J_{i}}x_{ij}\cdot C_{ij}(t_{\text{i}}),\\ {\sum}_{j=1}^{J_{i}}x_{ij}=1 \quad\text{with: } x_{\text{ij}} \in \{0;1\},\\ t_{ij,\min} \leq t_{ij} \leq t_{ij,\max}, \end{array} $$

(13)

while the selection parameter x_ij is used to choose a production machine/process to realize the tolerance t_i [63, 109]. Achieving a least-cost design, the minimum-cost machine is selected with the aid of a total minimum-cost curve of all machines with respect to their individual process limits$t_{ij,\min \limits }$ and $t_{ij,\max \limits }$ [36, 100] or the usage of mixed-discrete optimization techniques [117]. Besides the number of tolerances and available process alternatives, tolerance-cost optimization is further complicated by regions of non-overlapping, non-feasible solutions in the total tolerance-cost model (see Fig. 11b) [17, 99].

For a single-stage process, the design tolerance t corresponds to the process tolerance δ. In reality, multiple manufacturing steps are generally needed to realize the design tolerance t_i and the manufacturing costs for the sequence of multi-stage processes are considered by one tolerance-cost curve [50, 198]. Optimizing both design and manufacturing tolerances simultaneously, the tolerance-cost model of Eq. 13 further extends to:

$$ \begin{array}{@{}l} C_{\text{sum}}({\delta}) = {\sum}_{i=1}^{I}{\sum}_{j=1}^{J_{i}}{\sum}_{k=1}^{K_{ij}}x_{ijk}\cdot C_{ijk}(\delta_{\text{ijk}}),\\ {\sum}_{k=1}^{K_{ij}}x_{ijk}=1 \quad\text{with: } x_{\text{ijk}} \in \{0;1\},\\ \delta_{ijk,\min} \leq \delta_{ijk} \leq \delta_{ijk,\max}, \end{array} $$

(14)

while the machine selection parameter x_ijk is used to choose the best production machine k for each process j to realize the tolerance δ_ij [17].

3.2.2 Quality loss

Traditionally, it is assumed that as long as deviations from the target value of a KC are within predefined limits, they do not influence the customers’ awareness of quality [16]. In doing so, the quality loss for the customer is neglected since non-optimal products are perceived as products of same quality [16]. Only non-conformance is assumed to be critical and is considered in tolerance-cost optimization in terms of scrap or rework costs (see Fig. 12a). However, Taguchi’s basic idea of quality loss provoke a paradigm shift in the perception of quality. Any deviation from the optimum target value is noticed by the customer as a loss of quality (see Fig. 12b) [32].

Fig. 12

Customer’s perception of quality: a equally good quality vs. b loss of quality based on [16]

As a consequence, product quality can only be improved by incorporating the customer into optimal tolerance allocation [16, 32]. As a result, the quality loss has successively been integrated in the framework of tolerance-cost optimization over the years–in literature often discussed under the term of robust tolerance design. Hence, quality loss can most easily be described by a symmetrical, quadratic quality loss function:

$$ L(Y) = k\cdot(Y-m)^{2} $$

(15)

to estimate the monetary loss L in dependence of the systems response Y and its target value m [16]. The quality loss coefficient k must be assigned with respect to the given case. However, the identification of suitable quality loss coefficients can be crucial since the quality perception is both customer- and product-specific [16, 32]. Driven by the global aim of a realistic representation of the mostly intangible loss of quality, numerous analytical functions for the symmetrical and asymmetrical nominal-the-best, smaller-the-betterlarger-the-better case have been developed and integrated in least-cost tolerance-cost optimization (see Fig. 7) [33, 34, 53, 170, 175, 176, 199,200,201,202,203,204,205,206,207,208]. The quality loss functions were further adapted to different probability distributions, e.g. to the folded normal [209], trapezoid and triangular [210] or Weibull probability distribution [199] or alternatively expressed by fuzzy modelling [192, 211,212,213].

However, by additionally incorporating the customers’ expectation of quality into the optimization framework, the cost-quality dilemma is further intensified [214] since a balance between the manufacturing costs and quality loss must be struck [32]. Consequently, this leads to the fact that two conflicting objectives are concurrently optimized in least-cost tolerance-cost optimization. Either they are previously weighted and considered in one single-objective function [34, 126, 215] or they are optimized by multiobjective optimization algorithms creating a set of non-dominated solutions (see Section 3.1.1) [143]. Multiple, interrelated KCs thus function as dependent objectives and their correlations have to be considered in optimization [15, 216, 217].

3.3 Technical system model

Since it is the global aim to optimally allocate the tolerances for a newly or (re-)designed product, the representation of the technical system with its individual components is an important issue in the tolerance-cost optimization process (see Fig. 8). In general, any system under variations, which have a significant influence on the system behaviour and have to be limited by suitable tolerances, can be optimized. The size and complexity of the technical systems range from small assemblies with a manageable number of components and tolerances up to whole assemblies with multiple parts and sub-assemblies. Besides the optimization of mechanical systems, products of other disciplines are also in focus, such as electrical networks [76, 84, 88, 116, 218, 219], optical devices [220, 221] or chemical and pharmaceutical processes [222,223,224,225]. Therefore, the relevant key characteristics are often non-geometrical (see Section 3.3.1) and the tolerances are allocated to non-geometrical parameters (see Section 3.3.8). The subsequent discussion is however limited to mechanical systems.

With the aim to analyze the system of interest, it must be represented by a suitable model. By making assumptions, simplifications and neglectibilities the system becomes manageable in tolerance analysis. Therefore, the decision of the right level of detail to model a realistic system behaviour can become a challenging task since it influences the optimization process with respect to computation time and quality of results.

3.3.1 Key characteristics

Although technical systems primarily serve to fulfill a function in use, they must meet a number of different quality requirements. Therefore, the requirements are converted into geometrical requirements and expressed by a set of (functional) key characteristics (F)KC as measures of quality (see Section 2.2) [57].

The geometrical (F)KC, also known as assembly response function [60], is mathematically expressed by a geometrical measure. In addition, the effect of geometrical part deviations can directly be mapped on non-geometrical KCs by a function of tolerances but also of additional variables such as nominal dimensions and non-geometrical parameters (see Section 3.3.8). In the case of the car brake, the angle of the brake disk and the brake pads function as a geometrical key characteristic, while the performance of the system could further be described by the brake potential as a function of the brake angle [189].

The quantification of the KC is generally a complex task [19, 226] since it requires a good product expertise [227] or the correlations of part deviations and the resulting quality are simply not directly known (see Section 3.4) [228]. Hence, it is necessary to derive the KC functions by gathering information from simulations and experiments and transforming them in mathematical functions and surrogate models.

Moreover, it is quite common to further differ between linear and nonlinear KC functions (see Fig. 8). The type has a significant influence on the choice of the tolerance analysis model with its different aspects (see Section 3.4) and the definition of the optimization problem in combination with the selection of a suitable optimization algorithm (see Section 3.1).

In this context, increasing product complexity leads to the fact that multiple KCs represent the total quality of a product in accordance with the KC-flowdown [57, 229]. Depending on the correlation of the KCs (see Fig. 8), they can either be called simple, since they are independent from each other, or they are interrelated, because they are or connected by mutual elements and can conflict [9, 72, 73, 229]. As exemplarily illustrated in Fig. 13, the gaps between the brake disk and the pads Y₁ and Y₂ are interrelated by the distance of the brake disk X₄:

$$ Y_{1}={X_{4}}- (X_{1}+X_{2}+X_{3})\\ $$

(16)

$$ Y_{2}=X_{7}-({X_{4}}+X_{5}+X_{6}) $$

(17)

Fig. 13

Car brake system: interrelated key characteristics

Although existing design methods help to create a robust design by de- and uncoupling the KCs [230], they cannot completely be eliminated [229] and have to be considered in tolerance-cost optimization. As a consequence, the number of KCs and their correlation mainly influence the optimization problem and its solution procedure, especially the handling of multiple constraints in terms of establishing non-iterative, closed-form solutions by Lagrange multipliers [15, 65, 99, 231,232,233,234] and their proper consideration in tolerance evaluation and scrap rate estimation [235]. Over the years, various publications addressed the integration of multiple FKCs in the framework of tolerance-cost optimization, e.g. [15, 65, 99, 231,232,233,234,235,236,237,238].

3.3.2 Dimensionality

In order to model the technical system, the dimensionality of the system is decisive for a realistic tolerance analysis (see Fig. 8) [39]. If the KC can be described by a linear tolerance chain to consider only dimensional tolerances, it is sufficient to reduce the problem to a 1D-problem. The tolerance analysis of nonlinear KCs and geometrical tolerances often require a geometrical 2D- or even 3D-model [39, 239]. As a consequence, the dimensionality influences the tolerance analysis approach with its mathematical model (see Section 3.4.3) and the optimization process. However, it always depends on the effects to be considered and the dimensionality that has to be chosen as a compromise of model accuracy and computational effort.

3.3.3 Assembly type

In mechanical engineering, the development of a technical system generally corresponds to the process of designing an assembly consisting of various parts contributing to the overall system functionality. With respect to how the parts are assembled, systems can be classified into two different types [229]. The assembly process of a Type-1-assembly is typically part-driven since the system is exact constraint by the pre-fabricated mates positioning the different parts with respect to the others [229]. Focusing on the car brake from Fig. 1, the disk is put on the wheel hub which locates the disk by its mates [229]. In contrast, the assembly of a Type-2-assembly, e.g. a car door, requires fixtures for firstly defining the positions of the individual parts with the help of locators by temporarily locking the open degrees of freedom [229]. Secondly, the positions of the parts are fixed by joining the parts together by a joining operation such as welding, riveting or clinching [229].

As a consequence, the KC deviation of an Type-1-assembly is a direct result of the individual part deviations, whereas the total assembly process with its multiple, additional deviations mainly contributes to the overall deviation of the KC of a Type-2-assembly [229]. Several multi-station assembly steps with different manufacturing processes are required for the process-driven assembly of even small systems. Thus, the in-process deviations flow like a stream of variations over the different assembly stations [240]. Hence, tolerance-cost optimization of Type-2-assemblies is strongly related to the optimal selection of process parameters, optimal fixture layout design and the optimization of assembly and joining sequences for the realization of over-constrained systems of numerous compliant parts [18, 144, 164, 169, 241,242,243,244].

Accordingly, the focus of tolerance-cost optimization literature strongly depends on the assembly type of interest (see Fig. 8). Thus, an initial classification of the type is helpful to identify the scope and to make clear which aspects are most relevant.

3.3.4 Structural behaviour

In general, technical systems are often assumed to be rigid in tolerancing. Even if the compliance influences the KCs, which is especially relevant for Type-2-assemblies consisting of multiple, compliant sheet parts (see Section 3.3.3), this fact is often neglected in tolerance-cost optimization. Although several authors strive to integrate compliance in tolerance-cost optimization, especially in context of process-oriented tolerance-optimization [241, 244,245,246,247], mostly just simple cases are considered whose structural behaviour is approximated by simple analytical equation. If the system gets more complex, the use of finite element simulation in combination with meta modelling methods is favoured, primarily for reasons of computing time [246, 248,249,250]. Thereby, non-geometrical influence parameters play an important role and the tolerance expert has to identify, if their variations influence the compliance and thus the functionality of the system or if they can be assumed to be constant (see Section 3.3.8) [250].

3.3.5 Statical determinacy

The basic principle of a clear and robust design is to create an isostatic, exact constraint system ensuring a robust and predictable product functionality. Thus, each degree of freedom should exactly be constrained once [251]. Structured procedures based on screw theory [229] or so-called Schlussartenmatrizen [252] prevent the designer to mistakenly break this basic rule [229] prior to the parameter and tolerance design.

In reality, there are different reasons to consciously deviate from an exact constraint design. With the primary goal to increase system rigidity parts are often redundantly constrained several times by multiple fixing thus leading to over-constrained or also called hyperstatic systems [229, 253]. Thus, thermal or mechanical influences lead to stress and non-negligible part deformations significantly influencing the KCs [229]. As a consequence, additional information of finite element analysis is needed for the prediction of the geometrical part variations [229].

Fig. 14

Car brake system: time-variant KC for a system in motion

Besides, gaps between parts are purposefully added for function or used as clearances to ensure assemblability [229, 254]. In doing so, the system becomes under-constrained since some degrees of freedom are left open and thus the positions and orientations of individual parts in an assembly are not exactly defined [229]. Additional information is thus needed to compensate the uncertainty of part positions and to make the problem evaluable in tolerance analysis. Therefore, the unknown part locations can either be modelled probabilistic or deterministic by considering forces from assembly or gravity or identifying worst-case positions with the aid of additional optimization approaches [254,255,256,257,258,259].

Studies on tolerance analysis of statically indeterminate assemblies are gaining more importance in the last years, whereas their findings are just rarely transferred to tolerance-cost optimization [260] and mostly neglected. The fact that the status of constraintness can change under variation and over time [229] further complicates the analysis and optimization of these systems.

3.3.6 Mobility of systems

Besides static systems, systems in motion have arisen the interest of various research activities (see Fig. 8) [98, 118, 122, 234, 261,262,263,264,265]. If the total movement behaviour or parts of a defined motion of a kinematic system are relevant for its functionality, such as for the accuracy of motion over a period of time [98], the KCs are optimized as function of time for a whole motion with respect to a discrete time step i (see Section 3.3.7). Thus, the KCs are analyzed for each time step i and the time-variant results are evaluated according to a predefined quality criterion (see Section 3.4.5) within each optimization step (see Fig. 6) [98, 234]. However, depending on the type of the KCs and the system behaviour, the analysis can often be reduced to one discrete point in time. If selected positions of a time-dependent system are of interest, e.g. the initial or the final position of a mechanism, it is sufficient to only consider these points in time in the tolerance analysis to reduce the computation time. Moreover, dynamic aspects such as inertia can be considered by coupling tolerance-cost optimization with multi-body simulations to describe the dynamic system behaviour under motion [122, 266].

3.3.7 Time dependency

If the status of system changes over time, the time-variant KCs are described by a function of time τ and are solved for a number of time steps I to ensure the quality fulfillment for a predefined time period [98, 118]:

$$ {\hat{Q}}(\tau) =[\hat{Q}(\tau_{1}),\dots,\hat{Q}(\tau_{I})]^{\text{T}} ~ \forall~Y_{i}~ \text{with}~i=1,{\dots} I . $$

(18)

As exemplarily shown in Fig. 14, the angle γ between the brake disk and the brake pads influencing the clining pressure of the brake disk is analyzed for a whole rotation to consider the radial run-out and wobbling of the disk discretized by I time steps.

However, the I-times evaluation of the KCs in each optimization results in long computation times, especially for the application of sampling-based tolerance analysis and stochastic optimization algorithms (see Sections 3.1.4 and 3.4.4). Thus, the identification of the critical points in time are decisive for the evaluation of the quality of the product. Besides systems in motion (see Section 3.3.6), the consideration of short-time and long-time variant effects, such as wear or part deformations by varying loads, require a time-variant description of the KCs to cover the entire lifetime of a product [98].

3.3.8 Influences

In addition to the nominal geometrical parameters and its tolerances, non-geometrical internal and external influences on the KCs can also be in focus (see Fig. 8), such as temperature, forces, torques, gravity, loads or material properties, e.g. density, modulus of elasticity or thermal expansion coefficient [5, 98, 267,268,269,270]. Thus, it is a critical task to asses which influence parameters are relevant and have to be considered within the tolerance-cost optimization and to what extent. However, it is always case-specific and depends on the type of technical system and its purpose of use. In the case of the car brake system, the material properties for example strongly influences the braking performance in addition to the geometry.

In doing so, these parameters can be considered as constant or variable to be additionally optimized, also under the presence of uncertainty in context of robust tolerance design [98, 268]. Thereby, their effects on the KCs are either described by elementary analytical equations, e.g. the linear thermal expansion law, or derived from the results of experiments and simulations, which are often indirectly integrated in the KCs by surrogate models to reduce the computational effort [98, 267, 271, 272].

3.4 Tolerance analysis model

Tolerance analysis plays an important role in tolerance-cost optimization since it is used to analyze the technical system under variation (see Section 3.3) and to check the fulfillment of the requirements defined by the KCs (see Section 3.3.1). Thus, the efficiency and the results of the optimization strongly depend on the tolerance analysis model with its subsequently discussed aspects (see Fig. 8) [273].

3.4.1 Tolerance specification

As shown in Fig. 4, tolerance-cost optimization is based on a predefined tolerance specification [58]. Therefore, structured procedures as well as software tools assist the designer in the correct specification of dimensional and geometrical tolerances according to the current standards of ISO and ASME [58, 274,275,276]. Even if tolerance specification and analysis frequently address both geometrical and dimensional tolerances (GD&Ts), tolerance-cost optimization is mostly limited to dimensional tolerances (see Section 4.1).

3.4.2 Concurrent tolerance design

The general objective of optimal tolerance allocation differs from its application in design or manufacturing (see Section 2.1). The designer allocates design tolerances to the final part geometry features ensuring product functionality, whereas the manufacturer deals with the issue how to realize the defined design tolerances in manufacturing [4, 46]. Accordingly, each design tolerance has to be transformed in a set of manufacturing tolerances for a sequence of process operations [277]. In doing so, tolerances are sequentially defined for a different reason, for product functionality or for manufacturability [17].

In context of concurrent tolerance-cost optimization, both disciplines are combined and the design tolerance is considered as a sum of individual machine tolerances under the consideration of a sufficient stock removal allowance [17].

In doing so, the basic idea of tolerance balancing is integrated in the tolerance-cost optimization framework and manufacturing tolerances are optimally allocated with respect to product functionality [3].

Besides, the optimization of tolerance values for non-geometrical parameters, e.g. for temperature or loads, is addressed in robust tolerance design (see Section 3.3.8) [277].

3.4.3 Mathematical model

The representation of the individual part deviations within their limiting tolerance ranges is a key element in tolerancing since it serves as a basis to predict their influence on the KCs [226, 278]. In general, tolerance-cost optimization is not restricted to a specific mathematical model (see Fig. 8). However, it influences the tolerance analysis procedure and thus indirectly the optimization process in terms of its results and computing times. As a consequence, the tolerance expert should thoroughly choose the mathematical model with respect to the given technical system model and reasonable assumptions.

In most cases, vector loops with comparatively low computing times are sufficient for the optimization of simple, rigid assemblies with few components and dimensional tolerances. If commercial CAT-software is integrated in the optimization framework (see Section 3.4.4), the representation of the geometrical deviations are mostly represented by variational models based on the nominal CAD-model geometry [78, 198, 279, 280]. Besides, the application of polytopes [281] and torsor models [282,283,284] can occasionally be found in literature.

3.4.4 Tolerance evaluation

Tailored to the specific academic and industrial needs, a variety of worst-case and statistical approaches for tolerance evaluation have been developed over the years [60, 226, 285] (see Fig. 8). Especially in the early years of tolerance-cost optimization, worst-case approaches were quite popular to ensure a 100%-fit of the specification limits [96, 101, 102, 105]. Despite their unrealistic claim of a full acceptance [64, 71], they are still used since most designers are familiar with the easily applicable approach [60, 82]. Since the computational effort is similar to the most statistical methods but lead to tighter tolerances and consequently to higher manufacturing costs, they are increasingly losing importance. Rather, they are sensibly used for an initial estimation today [82].

Statistical approaches mitigate this unrealistic claim of a worst-case scenario by accepting a small percentage of non-conformance [286]. In doing so, the probability of each part deviation within their associated tolerances are considered in tolerance analysis [71, 286]. A number of statistical approaches were established for tolerancing and are frequently applied in tolerance-cost optimization, e.g. the root sum square method [32, 99, 137, 287], different variants of estimated mean shift methods [142, 207, 288, 289] and the Hasofer Lind reliability index [38, 85] (see Fig. 8).

Especially in times when deterministic optimization techniques were preferred, numerous authors studied the handling of the constraints by Lagrange multipliers with respect to the different approaches for tolerance analysis [45, 64, 101, 131, 234]. However, in most modern articles, the decision for a specific method is not made consciously but rather randomly in context of tolerance-cost optimization. Their integration in tolerance-cost optimization became scientifically less interesting with the emergence of stochastic optimization algorithms.

Besides, the usage of sampling techniques for statistical tolerance analysis is quite popular, especially in industry. Since they do not need to linearize KC functions and can consider any distribution [285], they are problem-independently applicable [290] and reflect a more realistic interpretation of part manufacturing and assembly [18, 194]. Driven by these benefits, sampling-based tolerance analysis software has successively been developed and was consequently integrated in the optimization framework, e.g. Sigmund^®; [291] eMTolMate^®; [279], RD&T [173, 292,293,294], VisVSA^®; [30, 78] and 3DCS^®; [249, 295, 296]. However, the principle of randomness leads to a noisy, non-deterministic system response which complicates the application of gradient-based optimization algorithms [297,298,299]. More sophisticated approaches are required to estimate the gradient information [131, 273, 297, 298, 300]. Therefore, stochastic optimization algorithms are preferably applied to overcome this problem since they do not need any gradient information and can properly handle the stochastic inputs (see Section 3.1.4). In this context, the Monte Carlo sampling, e.g. applied in [78, 118, 235, 260, 301] is frequently chosen for tolerance-cost optimization while alternatives, e.g. the Latin hypercube sampling [12, 302] or the Hammersley sequence sampling [222], are just rarely addressed. Thereby, the increasing computer powers enable the handling of huge sample sizes n which are necessary to get a reliable prediction of the probabilistic system response [12]. As a consequence, the function for each KC must be evaluated n-times in every iteration (see Fig. 6). Consequently, the usage of the computationally intensive sampling techniques with suitable large sampling sizes in combination with stochastic optimization algorithms require comparatively large time effort for the optimization approach [62, 70, 106]. Thus, optimization with increasing sample sizes over the optimization progress reduces the computational effort while achieving reliable results [155, 260].

Fig. 15

Conformance and non-conformance defined by the upper and lower specification limits

3.4.5 Quality metric

After the application of an tolerance evaluation technique, its results are assessed by a suitable quality metric to check if the assigned tolerances can fulfill the predefined quality requirements (see Fig. 8). The choice of quality metric depends on the chosen evaluation technique in combination with the definition of quality [12].

Using sampling techniques, the system response Y is calculated for all individual samples. As exemplarily shown in Fig. 15, the resultant probability distribution serves as the basis to determine the yield as the number of samples, which are in the acceptance range between the lower and upper specification limits LSL and USL [12]. Thus, the yield is decreased by the non-conform samples failing the specification limits [12]. The non-conformance ratez is thus expressed in parts-per-million in accordance with the philosophy of Six Sigma [303].

Even if the terms non-conformance rate [144, 260], scrap rate [12, 98], defect rate [304, 305] or rejection rate [88, 94] are not exactly synonymous, they are often used simultaneously in this context to define the percentage of samples which do not lie within the specification limits. The yield is calculated by the integral over the probability distribution ϱ. Subsequently, the non-conformance rate $\hat {z}$ is compared with the specified, maximum conformance rate $z_{\max \limits }$ and functions as a constraint in least-cost tolerance-cost optimization [12, 118]:

$$ \hat{z}({t})= 1-{\int}_{LSL}^{USL} \varrho (Y({{t}}))\ dx \leq z_{\max}. $$

(19)

If the distribution type ϱ is known, the cumulative frequency distribution can be used to calculate or rather predict the resultant (non-)conformance rate $\hat {z}$ [12]. Otherwise, distribution-independent estimation procedures are required [12]. Thus, the choice of a suitable estimation technique in combination with the sample size is decisive to avoid over- as well as underestimations of the (non-)conformance rate since they cause the allocation of either unnecessary tight or unacceptable wide tolerances [12].

In contrast to sampling techniques, convolution-based approaches are tailored to an idealized distribution of the resultant KC. The root sum square equation, for instance, assumes that the KC corresponds to a centred standard normal distribution. Thus, it determines the tolerance range T_RSS for a 99,73% yield ($\widehat {=} \pm 3 \sigma$) [285, 303]. In doing so, the conformance rate is indirectly checked by comparing the evaluated tolerance range T_RSS with the specified acceptable assembly toleranceT_{RSS, max} = USL −LSL [285]:

$$ T_{\text{RSS}}=\sqrt{\sum\limits_{i=1}^{I} \left( \frac{\partial f}{\partial X_{i}}\right) {t_{i}}^{2}} \leq T_{\text{RSS, max}}. $$

(20)

In accordance with statistical process control for series production, capability indices are also used to measure the quality fulfillment [195, 269, 279]. In context of robust tolerance design, the variance serves as a measure for the sensitivity of the system [80, 306].

3.5 Computer-aided systems for tolerance-cost optimization

Besides the development of the method, several authors concentrated on the integration of tolerance-cost optimization in the virtual product development environment using the functionalities of CAD-systems for product geometry representation and extending their functional scope [113, 283, 307,308,309,310]. In comparison with CAT-software for tolerance analysis, the integration of additional optimization modules and information basis of manufacturing knowledge are essential to assist the designer in the (semi-)automatic process of tolerance-cost optimization [46, 134, 197, 308, 311,312,313,314]. Hence, specific expert systems were developed for optimal tolerance allocation with the aim to cope with the complexity and to provide applicable, efficient and user-friendly software tools avoiding simulation code to be written [46, 76, 134, 197, 313, 315]. However, commercial stand-alone software programs for tolerance-cost optimization are not established yet. In most cases, suitable CAT-software modules are combined with optimization tools (see Section 3.4.4).

Fig. 16

Tolerance-cost optimization through the ages: number of publications focusing on tolerance-cost optimization from 1970 to 2019

4 Tolerance-cost optimization through the ages

Already in the early years of tolerancing, the impact of tolerances on quality and cost was addressed by optimal tolerance allocation. Traditional approaches were gradually substituted by optimization-based methods from the middle of the twentieth century up to modern days. Thus, the interest in tolerance-cost optimization has steadily grown and is reflected in the number of current research activities (see Fig. 16). A review on more than fifty years of research in the field of tolerance-cost optimization is presented in the following and serves as a basis to identify current drawbacks and future trends.

Fig. 17

Tolerance-cost optimization through the ages: a historical review on distinctive aspects from 1970 to 2019: a applied optimization algorithms, b consideration of manufacturing tolerances, c incorporation of quality loss, d dimensionality of studied systems, e type of tolerances, f applied tolerance evaluation methods

4.1 Historical development

Driven by the efforts and findings of numerous research activities, the method has constantly evolved over the years. While at the beginning, its fundamentals were studied, current research activities can make use of them and focus on specific partial aspects of the key elements (see Section 3). As a consequence, the tolerance-cost models are further enhanced, the technical system can be modelled and analyzed in a more realistic way and the optimization procedures are improved in terms of efficiency, accuracy and applicability. With the aim to represent the change and development through the ages, 290 publications were studied and analyzed with respect to the key elements of Figs. 7 and 8. Therefore, the subsequent discussion focuses on a selection of the most relevant categories and their change over the years which is illustrated in Fig. 17. A detailed list of the considered publications can be found in the Appendix in Table 2. The assigned keywords emphasizes the main focus of the individual contributions.

Optimization algorithms

In early years, the existing optimization techniques forced to oversimplify the optimization problems. Until the end of the twentieth century, mainly deterministic optimization algorithms were used. Mostly they are just valid to a very limited extent since their application require in-depth knowledge of programming and optimization and they neglect important aspects (see Fig. 17a). However, this situation changed with the integration of stochastic optimization algorithms in product development aiming to solve the engineering problems in a more realistic way. Due to their strengths, first successful applications of stochastic optimization techniques in the context of tolerance-cost optimization were not long in coming after their initial introductions, e.g of SA in 1983 [316], GA in 1989 [317] or PSO in 1995 [318] (see Fig 17a). Since then, these methods have become more and more popular and are frequently used to solve the different multi-constrained, single- and multiobjective optimization problems with continuous but also discrete variables (see Fig. 7). The rapid development of computer technology has made a significant contribution to this change [12, 233, 319]. While the limited computer performance severely restricted the applicability of optimization algorithms in the beginning, today’s computer technology enables the solving of complex, computing-intensive tolerance-cost optimization problems [53].

Concurrent tolerance design

Fostered by the increasing technical possibilities, the method itself has further been improved with respect to the cost and tolerance analysis model. The traditional separation of the individual divisions has changed to a concurrent perception of product development (see Section 2.1). Thus, the increasing merge of manufacturing and design is reflected by the rising concurrent allocation of design and manufacturing tolerances (see Fig. 8). Although the solely consideration of design tolerances still predominates the optimal tolerance allocation, an increasing link of both disciplines in tolerance-cost optimization can be recognized (see Fig. 17b).

Quality Loss

Focusing on the tolerance-cost model, it can be seen that Taguchi’s idea of quality was already recognized in the early 90s and integrated into tolerance-cost optimization (see Fig. 7). The loss of quality significantly shaped the subsequent research activities and is considered additionally to the manufacturing costs in context of robust tolerance design (see Fig. 17c).

Technical system and tolerance analysis model

Although most problems in engineering are 3D problems, they are mostly reduced to 1D or 2D. Thus, the geometrical KCs are mostly described by linear and simple nonlinear KCs to reduce the complexity of tolerance analysis and thus the computational effort (see Fig. 17d). In comparison with tolerance analysis, optimal tolerance allocation is mainly based on dimensional tolerances [39]. Geometrical tolerances are just rarely allocated and current standards are often neglected (see Fig. 17e). The strengths of statistical tolerancing have already been recognized at the beginnings and have mostly been applied over the years (see Fig. 17f). Worst-case approaches are usually only used if other aspects are mainly in focus and the aspects of tolerance analysis are moved to the background. However, simplified statistical approaches, especially the root sum square approach, are preferred to sampling techniques due to shorter computing times (see Fig. 8).

4.2 Current drawbacks and future research needs

Since its first ideas in the middle of the twentieth century, tolerance-cost optimization tremendously evolved to a powerful instrument for optimal tolerance allocation. Nevertheless, several problems are still unsolved and currently an obstacle for its consistent industrial implementation.

Sophisticated tolerance analysis models

While industry struggles with high system complexity mostly driven by increasing digitalization and mechatronization, most studies focus on relatively simple applications under more but rather less realistic simplifications and assumptions (see Section 4.1). To ensure the applicability of tolerance-cost optimization to industrial problems, the tolerance analysis model must consequently be tailored to the present and future needs of industry. This will require a further expansion of the methods to consider the various effects on non-geometrical KCs with focus on (robust) tolerance design. Hence, the convenient assumption that problems can easily be reduced to 1D or at least 2D, is often too optimistic and unrealistic. Rather, tolerance-cost optimization must be enhanced to efficiently consider 3D effects. Therefore, the obsolete idea of a tolerance specification only based on dimensional tolerances must continuously be discarded. New approaches and strategies are essential to properly consider GD&Ts in alignment with current standards in tolerance-cost optimization. This consequently implies the development of mathematical models to efficiently and properly represent geometrical part deviations. However, especially when sampling techniques are used in combination with stochastic optimization algorithms, current approaches reach the limit of a reasonable computing time, especially for the optimization of time-variant and over- and under-constrained systems. The development of efficient optimization algorithms and procedures will thus become even more important in future to cope with the compellingly increasing complexity of tolerance analysis models.

Availability of tolerance-cost data

However, all these efforts to improve the tolerance analysis model are in vain if the tolerance-cost data and thus the objective function are too imprecise [88]. Since it beginnings, the lack of suitable and accurate tolerance-cost information has been criticized in literature over and over [9, 18, 81, 88, 97, 177, 178, 320]. However, little progress has been made over the years and reliable, up-to-date tolerance-cost data is still missing [178]. As a consequence, tolerance-cost optimization cannot thoroughly address new manufacturing technologies, e.g. additive manufacturing or the manufacturing of fibre-reinforced plastic parts, since reliable tolerance-cost data has not been published yet. While academic literature mostly deals with randomly chosen or obsolete tolerance-cost data, it is not really known whether and to what extent tolerance-cost data is available in industry and used for tolerance-cost optimization [9, 18]. Despite the well-known benefits of tolerance-cost optimization, the huge effort to gather, to process and to provide appropriate data in sufficient quantities often prevents industry from its application. Information from manufacturing and measurement must consequently flow back to tolerance design to provide up-to-date data taking advantage of the increasing digitalization of product development [321]. Therefore, suitable strategies and methods for the automatic acquisition and conversion of information from measurement and manufacturing into tolerance-cost models have to be developed. In addition, currently missing information from manufacturing, assembly and measurement must also be integrated in the total framework of tolerance-cost optimization. Even though design and manufacturing are more closely linked by concurrent tolerance design today (see Fig. 17b), a further shift from a mere product-related to a process-oriented tolerance allocation is necessary [18].

Applicability

Last but not least, the initially discussed complexity of tolerance-cost optimization often dissuades from using it. Therefore, countermeasures, e.g. in the form of expert systems or the development of more easy-applicable optimization algorithms, are important and have to further be investigated to ensure and improve its usability of the steadily enhanced method. In addition, a comprehensible presentation of tolerance-cost optimization in literature is essential to make the method more accessible and transparent for practitioners and researchers.

5 Conclusion

Tolerance-cost optimization has been studied for over half a century. In comparison with tolerance analysis, it is more sophisticated and complex since it requires knowledge in optimization, tolerancing, manufacturing, cost modelling and programming. Although its strengths and benefits are well known in research and industry, its potential remains mostly unused since the method with its different, interrelated aspects is often not correctly and fully understood.

With the aim to overcome this drawback, this review article gave a holistic overview of tolerance-cost optimization. The first part of this article illustrated the fundamental idea of tolerance-cost optimization step-by-step and thus is particularly suitable for inexperienced readers. In the second part, a comprehensive mind map covering all relevant aspects of tolerance-cost optimization was presented and discussed in detail. A retrospect on the last fifty years of research studying 290 publications with focus on tolerance-cost optimization illustrated its historical development and served as a basis to identify the current drawbacks and future research needs.

Appendices

Appendix

A Summary of literature references

The references used to outline the development of tolerance-cost optimization in Section 4.1 are chronologically summarized in Table 2 including a selection of representative keywords. They were mostly chosen following to Figs. 7 and 8 emphasizing their main focus.

Table 2 List of references for the historical analysis in Section 4.1