Robust unit commitment with $n-1$ security criteria

Abstract

The short-term unit commitment and reserve scheduling decisions are made in the face of increasing supply-side uncertainty in power systems. This has mainly been caused by a higher penetration of renewable energy generation that is encouraged and enforced by the market and policy makers. In this paper, we propose a two-stage stochastic and distributionally robust modeling framework for the unit commitment problem with supply uncertainty. Based on the availability of the information on the distribution of the random supply, we consider two specific models: (a) a moment model where the mean values of the random supply variables are known, and (b) a mixture distribution model where the true probability distribution lies within the convex hull of a finite set of known distributions. In each case, we reformulate these models through Lagrange dualization as a semi-infinite program in the former case and a one-stage stochastic program in the latter case. We solve the reformulated models using sampling method and sample average approximation, respectively. We also establish exponential rate of convergence of the optimal value when the randomization scheme is applied to discretize the semi-infinite constraints. The proposed robust unit commitment models are applied to an illustrative case study, and numerical test results are reported in comparison with the two-stage non-robust stochastic programming model.

1 Introduction

The recent increase in the deployment of renewable energy resources such as wind power is having a significant impact on the short-term operational and long-term investment decisions in power systems due to their non-dispatchability and intermittent nature. In the short term, the higher penetration of wind power and the lack of efficient storage facilities have an adverse effect on the stability of generation output. One of the most crucial decision problems that are affected by the short-term supply uncertainty is the unit commitment (UC for short) problem (Takriti 1996; Padhy 2004). The objective of the UC problem is to minimize the overall generation cost by determining the hourly unit commitment and the reserve schedule for the day ahead given the demand and wind forecasts.

Classical models for the UC problem are often deterministic and consider supply and demand for electricity in the day ahead to be known in advance. Whilst the demand forecast for the day ahead can be reasonably estimated, the high reliance of the generation output on the unreliable wind power potentially renders optimal solutions of a deterministic model either heavily infeasible or non-optimal under realized supply (Nemirovski 2012). Stochastic and robust optimization models provide an alternative approach to incorporating the increased uncertainties associated with the wind and load forecasts into power system operations. In this sense, approaches to account for the uncertainty in renewable energy generation in the UC problem fall into three categories: (two-stage) stochastic programming, chance-constrained stochastic programming, and robust optimization.

The first approach of two-stage stochastic optimization Shapiro et al. (2009) has been used widely for solving the UC problem (Tuohy et al. 2009; Papavasiliou et al. 2011; Wang et al. 2008), where energy and reserve generation are jointly scheduled to meet demand under stochastic wind supply. Pozo and Contreras (2013) and Wang et al. (2012) propose a chance-constrained programming approach to deal with the joint energy and reserve scheduling UC where one or several constraints must be satisfied with a given probability. One of the key assumptions in two-stage stochastic programming and chance-constrained programming is that the decision maker has complete information on the distribution of the uncertain parameters. However, limited predictability and high volatility of the renewable supply often make this assumption unrealistic.

In the third approach of classical robust optimization, the only available information on the uncertain parameters is its support, i.e., the set of all scenarios or possible realizations of the unknown parameters (Soyster (1973); Bertsimas and Sim 2004); Ben-Tal and Nemirovski 2000)). For the basic concept and a thorough survey of robust optimization, we refer the interested readers to review papers by Kouvelis and Yu (1997), Aissi et al. (2009) and Ben-Tal et al. (2009). In the context of the UC problem, Jiang et al. (2012) and Bertsimas et al. (2013) provide a robust optimization formulation and an adaptive robust optimization to address the wind power and demand uncertainty, respectively.

The min–max robust optimization approach is often criticized for being over conservative and/or not utilizing available partial information about the distribution of the uncertainty such as the mean and variance. Distributionally robust optimization, as part of the robust modeling framework, is considered a powerful remedy where the optimal decision is based on the worst probability distribution rather than worst scenario from a set of distributions constructed through the partial information.

There is extensive research published on UC models where energy and reserve are scheduled together. Table 1 summarizes some of those references that are closely related to the models proposed in this paper.

Table 1 A survey of UC models with security criteria

For a comparison between the existing models in the literature and the proposed distributionally robust UC model in this paper, we provide some classification criteria as follows.

• The uncertainty sources and their available information Contingencies, demand and wind production are some common sources of uncertainty in the UC problem with security criterion. Contingency events are usually considered as scenarios to include a deterministic or stochastic UC constraint. A bunch of post-contingency power flow operation equations are included in the problem to model how the system remains stable under the loss of one or more unit or line (see Bouffard and Galiana 2004, 2005a; Arroyo and Galiana 2005; Bouffard et al. 2005b, c; Restrepo and Galiana 2011; Karangelos and Bouffard 2012). Probability of the contingencies may be known (e.g. in Bouffard and Galiana 2004, 2005a; Restrepo and Galiana 2011; Karangelos and Bouffard 2012) or may not be known (e.g. in Arroyo and Galiana 2005; Street et al. 2011; Pozo and Contreras 2013). Bouffard and Galiana (2008), Restrepo and Galiana (2011) and Pozo and Contreras (2013) include stochastic demand and wind with full knowledge of probability distributions of the uncertainties. Bertsimas et al. (2013) include stochastic demand with partial information, where the uncertainty set is defined as box uncertainty with a budget constraint.

  Here we model the wind production as the only uncertain parameter with partial information on its probability distribution such as moments and scope of the distribution (representation as a mixture of some know distributions).

• The number of simultaneous contingencies The purpose of security criteria is to keep the system stable in case of one ($n-1$ criterion) or more outages ($n-K$ criteria) of a generating unit or line, where reserve planning is justified to compensate for possible outages. The $n-1$ criterion has been extensively applied to the UC problem (Arroyo and Galiana 2005; Bouffard and Galiana 2005a; Bouffard et al. 2005b, c; Bouffard and Galiana 2008; Restrepo and Galiana 2011; Karangelos and Bouffard 2012). Street et al. (2011) and Pozo and Contreras (2013) extend the security criterion up to K simultaneous contingencies. However, more strict criteria increases the complexity of the model and its tractability.

  Here we propose a model where a $n-1$ security criterion is included in the sense that if one unit is lost, the demand is met with the scheduled reserve from the first stage under any wind scenario.

• Modeling of contingencies Outages can be treated as deterministic parameters and the preventive actions are taken pre-contingency and through inclusion of deterministic constraints. These security constraints will ensure sufficient resources for the normal operation of the system in the event of a contingency (see Arroyo and Galiana 2005). On the other hand, outages can be treated as stochastic parameters, in which case the objective function includes expected value of the second-stage recourse costs. Contingencies probabilities should be known for this model, and the set of post-contingencies equations, one for each outage, is incorporated into the model (see Bouffard and Galiana 2008; Bouffard et al. 2005b). Note that, when other sources of uncertainty exist, post-contingencies equations should be extended for each scenario, which may lead to an intractable problem. Because of that, some authors limit the scenarios of contingencies to an umbrella of credible contingencies (Arroyo and Galiana 2005; Bouffard and Galiana 2005a; Bouffard et al. 2005b, c; Karangelos and Bouffard 2012; Bouffard and Galiana 2008). Another approach to deal with security criteria is posing an optimization problem to determine the worst contingency/contingencies. The works by Street et al. (2011) and Pozo and Contreras (2013) propose a worst-case optimization problem embedded into a deterministic and chance-constrained UC model, respectively.

  Here we formulate the security criterion as a deterministic constraint for the worst-case outage. We show that this worst-case outage is always the worst in any wind scenario. In this sense, we do not need to add up post-contingency equations for each plausible outage (all generating units) and each wind scenario. There is no cost term in the objective function to account for the extra cost of the corrective actions taken in the event of a contingency. This is a reasonable approach because contingencies have a very low probability of occurrence.

• Mathematical model and numerical methodologyBouffard and Galiana (2004) and Arroyo and Galiana (2005) propose a deterministic modeling framework, Bouffard and Galiana (2008) and Bouffard et al. (2005b) develop a two-stage stochastic programming model, Pozo and Contreras (2013) consider a chance-constrained problem, and Street et al. (2011) Bertsimas et al. (2013) present a robust optimization formulation. Most of these models are solved through their deterministic counterparts and further as mixed integer programming (MILP for short).

  Here we propose a two stage stochastic programming model to describe the decision making process and then develop a distributionally minimax robust optimization formulation of the two stage stochastic program to address the risks arising from uncertainty of wind power supply. Monte Carlo sampling methods have been applied to solve the resulting mathematical models. Compared to the existing minimax robust optimization model, the distributionally robust minimax model is less conservative.

Bertsimas et al. (2013) propose a two-stage deterministic robust optimization model for UC problems, where the uncertainty set is defined through a deterministic set. The solution of the proposed adaptive robust model provides immunity against all realizations of the uncertain data within the deterministic uncertainty set. However, this robust model does not take into account the distributional information of the random variables. In contrast, our model accounts for the available, or partially available, information on the probability distribution of the uncertain data. Furthermore the first-stage decision variables in Bertsimas et al. (2013) consist of the on/off commitment variables and the second stage solves an economic dispatch; therefore, they do not need to schedule reserve for the second-stage uncertainty deviations (North American’s UC outlook). However, in our model, the first-stage decision variables are the set of on/off decisions and scheduled energy and reserve (European’s UC outlook). Scheduled reserve is used in the second stage as a corrective action to meet the demand under wind production deviations and/or the outage of one generating unit.

Despite the fact that there is a rich body of literature focussing on two-stage stochastic and robust UC with endogenous reserve scheduling and wind-generation models, a distributionally robust UC approach has not been presented yet. The main contributions of this paper are summarized as follows:

• We propose a distributionally robust approach for UC problems with $n-1$ security criteria to tackle the risks arising from day-ahead wind uncertainty. Two specific models are considered: i) a moment model where the mean values of the random wind power supply are known, and ii) a mixture distribution model where the true probability distribution can be represented as a convex combination of some known distributions.

• For the moment model, we reformulate the distributionally minimax two stage robust problem as a semi-infinite programming problem through Lagrange duality and propose a random discretization approach for solving the latter. Under some moderate conditions, we demonstrate exponential rate of convergence of the randomization scheme as sample size increases. For the mixture distribution model, we reformulate the robust model as a one-stage stochastic program through duality, and develop a solution method based on sample average approximation (SAA) to reformulate the problem as a mixed integer linear programming problem (MILP).

• We have undertaken numerical experiments for the proposed new mathematical model carried out comparative analysis with two-stage stochastic UC model in terms of stability of the optimal solutions against variation of the mean and covariance.

The remainder of this paper are organized as follows. Section 2 sets out a standard two-stage stochastic programming model for the unit commitment problem with uncertainty in wind power generation and a distributionally robust formulation by explicitly considering ambiguity of the true probability distribution of the underlying uncertainty. Sections 3 and 4 detail the robust formulations and reformulations by considering some specific structures of the ambiguity set and develop corresponding numerical schemes for solving the mathematical models. Section 5 presents some case studies and comparative analysis of the new models and numerical schemes. Some conclusions are drawn in Sect. 6.

2 Stochastic unit commitment problem

The unit commitment and generation scheduling problems involve inherent uncertainties stemming from the short-term volatility of demand and unpredictability of wind power. The recent progress in the field of stochastic programming makes it an attractive approach for modeling the UC problem under uncertainty. Research carried out by Carpentier et al. (1996), Takriti (1996) and Dentcheva and Römisch (1998) were amongst the first which formulate the UC problem as a two-stage stochastic program. In this section, we first introduce a two-stage stochastic unit commitment problem (Sto-UC) by taking into account the wind uncertainty and additional technical information. We then further extend the stochastic framework to include the uncertainty on the distribution of the uncertainty and develop a two-stage distributionally robust model.

2.1 Two-stage stochastic UC with uncertain net load

Consider a unit commitment problem with a set of conventional generating units, denoted by $\mathcal {I}=\{1,\ldots ,I\}$, over a time horizon denoted by $\mathcal {T}=\{1,\ldots ,T\}$. The net load at time $t \in \mathcal {T}$ is stochastic and denoted by $\xi _t$.

The stochasticity of the load reflects uncertainty of renewable power supply such as wind power. Mathematically, we denote by $\varvec{\xi }= (\xi _t), t \in \mathcal {T}$ a vector of random variables defined over measurable space $(\Omega , {\mathcal {F}})$ with sigma-algebra. We use $\Xi$ to denote the support set of $\varvec{\xi }$. In this context, we can assume with out loss of generality that $\Xi$ is a compact set (bounded and closed).

A standard two-stage stochastic programming model for the UC problem includes a first-stage decision on the planning of unit power operation before realization of the uncertainty and a second-stage adjustment (recourse action) after the uncertainty is observed. The system operator aims to minimize the total generation costs which comprising the planned generation cost and the expected ‘adjustment’ cost. Specifically, the framework for the two-stage UC problem can be described as follows.

The first-stage (here and now) decisions are taken prior to realization of uncertain net load $\varvec{\xi }$. These include the on/off decisions denoted by $u_{it}$, for generator i and time period t, i.e.,

the energy dispatch variable $q_{it}$, and the up and down scheduled reserves $r_{it}^{up}, r_{it}^{dw}$ for generator i at time t. Each generator $i \in \mathcal {I}$ has a fixed on cost of $c_i^{f}$ and, if on, it has a unit generation cost of $c_i^l$. The upper and lower generation capacities of generator i are given by $\overline{q}_i$ and $\underline{q}_i$ while the upper and lower limits for reserve up/down for generator i are given by $\overline{r}_{it}^{up}/\overline{r}_{it}^{dw}$ and $\underline{r}_{it}^{up}/\underline{r}_{it}^{dw}$, respectively. The unitary costs of scheduling reserve up $c_i^{r,up}$ and reserve down $c_i^{r,dw}$ for generator i are given as an input of the problem.

The second stage decisions include deployed actual up and down reserves, denoted by $\hat{r}_{it}^{up}(\xi ), \hat{r}_{it}^{dw}(\xi )$. The unitary costs for the actual deployment of the reserve up and down are denoted by $\hat{c}_i^{up}$ and $\hat{c}_i^{dw}$.

To avoid imbalance in the supply and demand for energy in the second stage, we introduce additional auxiliary variables for load shedding and wind spillage. The load-shedding variable is denoted by $S_t(\xi )$ and represents the excess demand which cannot be met by the total generation output at time period t and has to be shed at high penalty cost of $c_t^{ls}$. On the other hand, the wind-spillage variable, denoted by $W_t(\xi )$, is equal to the excess wind power that cannot be utilized upon the realization of the net load. Wind spillage incurs an unitary opportunity cost of $c_t^{ws}$.

The resulting mathematical model of the two-stage stochastic UC problem with $n-1$ security criterion and ramping constraints can be presented as follows,

(2.1)

$$\begin{aligned}&q_{it} - r_{it}^{dw}\ge \underline{q}_i u_{it},\quad \forall \; t, i,\end{aligned}$$

(2.2)

$$\begin{aligned}&\underline{r}_i^{up} \le r_{it}^{up}\le \overline{r}_i^{up},\quad \forall \; t, i,\end{aligned}$$

(2.3)

$$\begin{aligned}&\underline{r}_i^{dw} \le r_{it}^{dw}\le \overline{r}_i^{dw},\quad \forall \; t, i,\end{aligned}$$

(2.4)

$$\begin{aligned}&q_{it},r_{it}^{dw},r_{it}^{up} \in \mathbb {R}^+ ,~ u_{it} \in \{0,1\},\quad \forall \; t, i, \end{aligned}$$

(2.5)

where $\mathbb {E}_P$ denotes the mathematical expectation w.r.t. the distribution of $\varvec{\xi }$ over probability space $(P,\Omega ,{\mathcal {F}})$, and $g(\mathbf {u,q,r},\varvec{\xi })$ is the optimal value of the second-stage problem defined as

(2.6)

$$\begin{aligned}&0 \le \hat{r}^{up}_{it}(\xi ) \le r^{up}_{it},\quad \forall \;t,i, \end{aligned}$$

(2.7)

$$\begin{aligned}&0 \le \hat{r}^{dw}_{it}(\xi ) \le r^{dw}_{it},\quad \forall \;t,i, \end{aligned}$$

(2.8)

(2.9)

$$\begin{aligned}&\hat{q}_{it}(\xi )=q_{it} + \hat{r}_{it}^{up}(\xi ) - \hat{r}_{it}^{dw}(\xi ), \quad \forall \;t,i,\end{aligned}$$

(2.10)

$$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi ) \le RU_i u_{i(t-1)} +SU_i(1-u_{i(t-1)}),\quad \forall \;t, i, \end{aligned}$$

(2.11)

$$\begin{aligned}&\hat{q}_{i(t-1)}(\xi )-\hat{q}_{it}(\xi )\le RD_i u_{it} +SD_i(1-u_{it}),\quad \forall \;t, i. \end{aligned}$$

(2.12)

In the first stage, constraints (2.1) and (2.2) represent the generation limits including the up and down scheduled reserves. The constraints (2.3) and (2.4) bound the minimum and maximum reserves to be scheduled.

In the second-stage problem, constraint (2.6) represents the energy balance for each hour t and net load wind scenario $\xi$. Constraints (2.7) and (2.8) ensure that the actual up and down reserves used are within the limits of the nominal reserve scheduled in the first stage. Furthermore, constraint (2.9) represents the $n-1$ reliability requirement which ensures that the demand will be met under the failure of up to one generating unit, where $Q_t$ is the total generation upper limit and is the worst (lowest) realization of wind output at time t. When the time index t is clear from the context, we use as a shorthand notation for . For example, is equivalent to and denotes the load shedding that corresponds to the worst realization of the wind output at time t. Constraint (2.10) provides the formulation for the actual power output of unit i at time t and scenario $\xi$. Finally, constraints (2.11) and (2.12) represent the ramp constraint with $RU_i$, $RD_i$, $SU_i$, $SD_i$ are the ramp up, ramp down, starting up and starting down ramps, respectively. Details about how the reliability and $n-1$ security constraints and the ramp constraints are formed are presented in “Appendix 1”.

2.2 Distributionally robust UC problem

Under the stochastic programming framework (Sto-UC), we assume that the “true” probability distribution P of the random wind variables is known. In practice, however, such distribution is often unknown and hence it has to be estimated through partial information or subjective judgements. One of the possible ways to deal with this issue is to use available information to construct a set of distributions, denoted by $\mathcal {P}$, in which the true probability distribution is assumed to lie. The robust optimization approach for the two-stage stochastic problem with respect to this ambiguity aims to make a decision which is optimal for the worst probability distribution from $\mathcal {P}$.

To ease the exposition, we write x for the first stage decision variables $(\mathbf {u,q,r})$ with feasible domain $\mathcal {X}$. Likewise we write y for the second stage decision variables $({\hat{\mathbf {r}},W,S})$. Furthermore, we denote the first-stage cost parameters by $c=(\mathbf {c}^f,\mathbf {c}^l,\mathbf {c}^{r,up},\mathbf {c}^{r,dw})$ and the second-stage cost parameters by $h=(\hat{\mathbf {c}}^{up},\hat{\mathbf {c}}^{dw},\mathbf {c}^{ls},\mathbf {c}^{ws})$. The corresponding mathematical model can be formulated as

(2.13)

where $g(x,\varvec{\xi })$ is the optimal value of the second-stage problem

(2.14)

and $\mathcal {Y}(x,\varvec{\xi })$ is the second-stage feasible set depending on x and $\varvec{\xi }$. In the literature of robust optimization, (2.13) is known as a distributionally robust formulation where the robustness is in the sense that the worst probability distribution rather than the worst scenario of the random vector $\varvec{\xi }$ is taken into account. This kind of robust optimization framework can be traced back to the earlier work by Scarf Scarf et al. (1958) which was motivated to address incomplete information on the underlying uncertainty in supply chain and inventory control problems. In such problems, historical data may be insufficient to estimate future distribution either because sample size of past demand is too small or because there is a reason to suspect that future demand will come from a different distribution that governing past history. Compared to minimax robust optimization model, the distributionally robust formulation is obviously less conservative and hence more compelling in the circumstances where an optimal decision based on the former model may incur excessive economic and/or computational costs to prevent a rare event. Over the past few decades, DRO models have found many applications in operations research, finance and management sciences, see for instances Bertsimas and Popescu (2005), Delage and Ye (2010), Goh and Sim (2010), Mehrotra and Papp (2014), Wiesemann et al. (2012), Wiesemann et al. (2013) and Wozabal (2014) for various applications and numerical schemes. In particular, Bertsimas et al. (2010) propose a distributionally robust formulation of two stage linear programming model with applications in finance and facility location planning.

A key element in (R-UC) is the ambiguity set $\mathcal {P}$. Various statistical methods have been proposed in the literature for constructing ambiguity set. Here we consider two popular ones where $\mathcal {P}$ is constructed through moments and mixture distribution.

3 Moment model and sample approximation approach

In this section, we investigate the robust unit commitment problem where the first moment condition of the underlying random wind generation is known. Let $\varvec{\mu }\in \mathbb {R}^T$ denote the mean of $\varvec{\xi }$. We consider the ambiguity set $\mathcal {P}$ being defined as follows:

$$\begin{aligned} \mathcal {P} = \left\{ P\in \mathscr {P}: \mathbb {E}_{P}[\varvec{\xi }]=\varvec{\mu }\right\} , \end{aligned}$$

(3.1)

where $\mathscr {P}$ denotes the set of all probability measures of measurable space $(\Xi , \mathscr {B})$ induced by $\varvec{\xi }$. For each fixed $x\in {\mathcal {X}}$, we consider the worst expected value of $g(x,\varvec{\xi })$ over the ambiguity set $\mathcal {P}$:

$$\begin{aligned} H(x):=\sup _{P \in \mathcal {P}}\mathbb {E}_P [g(x,\varvec{\xi })]. \end{aligned}$$

(3.2)

Using the moment conditions, we can write H(x) as the optimal value of the following maximization problem

(3.3)

where $\mathscr {M}^+$ denotes the set of all non-negative finite measures on measurable space $(\Xi , \mathscr {B})$, and $\mu _t$ is the $t^\text {th}$ component of $\varvec{\mu }$. Problem (3.3) is a typical form of classical moment problem. We refer interested readers to a monograph by Landau (1987) for a comprehensive discussion of the historical background of the latter. In order to deal with difficulties associated with solving such an infinite dimensional problem, duality theory is often used; for example, see Rockafellar (1974). Here we follow Shapiro (2001, Proposition 3.1) to derive the Lagrange dual associated with the moment problem (3.3).

Proposition 3.1

For a given $x \in \mathcal {X}$, the Lagrange dual of problem (3.2) is

(3.4)

where $\alpha _t \in \mathbb {R}$, $t=0,1,\ldots ,T$, denotes the dual variables corresponding to moment problem constraints and $\Xi \subset \mathbb {R}^T$ is the support set of $\varvec{\xi }$, and $H_D(x)=H(x)$.

Proof

The derivation of the dual formulation is standard and can be found in Shapiro et al. (2009). Since $\Xi$ is compact and the underlying function are continuous in $\xi$, the strong duality follows from Shapiro et al. (2009, p. 308). $\square$

Using Proposition 3.1, we can reformulate (R-UC) as

(3.5)

Moreover, through a simple analysis, we can show that problem (3.5) is equivalent to the following program which incorporates the details of the second-stage problem

(3.6)

In the rest of the paper, we discuss numerical methods for solving (3.5) or (3.6). If we are able to obtain a closed form of $g(x,\xi )$ and show that g is a linear or a quadratic function of $\xi$, then we may reformulate the semiinfinite constraints of problem (3.5) as a semidefinite constraint and consequently solve the resulting semidefinite programming (SDP) problem with existing methods for SDP. Indeed, this is the main stream work for distributionally robust optimization, see for instance Wiesemann et al. (2012), Wiesemann et al. (2013) and references therein. Unfortunately, here g is not linear or quadratic in $\xi$. Likewise, the underlying functions in the constraints of problem (3.6) are also nonlinear, non-quadratic which makes it impossible to reformulate the semiinfinite constraints as semidefinite constraints. This motivates us to solve (3.6) through other methods

3.1 Sample approximation scheme

One of the well-known solution approaches for semi-infinite programs is random discretization. The basic idea is to construct a tractable sub-problem by considering a randomly drawn finite subset of constraints. The approach has been shown numerically efficient and it has been widely applied to various stochastic and robust programs (see Calafiore and Campi 2005). In a more recent development, Anderson et al. (0000) propose a CVaR approximation scheme to a semi-infinite constraint system, and then apply the well-known sample average approximation to the CVaR (of the constraint function); see also Liu and Xu (2014) where the approach is applied to mathematical programs with semi-infinite complementarity constraints.

Let $\varvec{\xi }^1,\ldots , \varvec{\xi }^{S}$ be random variables which are independent and follow identical distribution to that of $\varvec{\xi }$. Let $\mathcal {S}=\{1,\ldots ,S\}$. We consider the following discretization problem as an approximation to problem (3.6):

(3.7)

where $\xi ^s$ is a realization of $\varvec{\xi }$ for $s\in \mathcal {S}$. In what follows, we show the convergence of the optimal value of (3.7) to its true counterpart as the sample size increases. To this end, we consider an equivalent form of (3.7) which is presented in terms of the optimal value function of the second-stage problem:

(3.8)

A clear benefit of the formulation above is that the decision variables are independent of the sample and this will particularly facilitate the convergence analysis.

To minimize the dependence on the specific details of the objective and constraints functions of problem (3.8) for the convergence analysis and also for the purpose of potential applications of the convergence result, we consider the following general optimization problem

(3.9)

where X is a compact set in a finite dimensional space, $\psi$ and f are continuous functions which map from $\mathbb {R}^n$ and $\mathbb {R}^n\times \mathbb {R}^k$ to $\mathbb {R}$ respectively, $\xi$ is the parameter which takes values over a compact set $\Xi$.

Let $\xi ^1,\ldots ,\xi ^N$ be independent and identically distributed random variables with the same distribution as $\xi$. We consider the discretized problem

(3.10)

Let v and $v_N$ denote, respectively, the optimal values of program (3.9) and program (3.10).

Lemma 3.1

Assume that (a) $\psi$ is Lipschitz continuous, (b) $\Xi$ is a compact set, (c) $\xi$ is a continuously distributed¹ and there exist positive constants K and $\tau$ independent of x, such that for each $x\in X$ there exist $\alpha _{0}(x)<f^{*}(x) :=\max \limits _{y\in \Xi } f(x,y)$ with

$$\begin{aligned} 1-F_{x}(\alpha )\ge K\left( f^{*}(x)-\alpha \right) ^{\tau },\text { for all }\alpha \in (\alpha _{0}(x),f^{*}(x)), \end{aligned}$$

(3.11)

where $F_x$ denotes the cumulative distribution function of $f(x,\xi )$,² and (d) f is Lipschitz continuous in x with integrable Lipschitz modulus (w.r.t. the distribution of $\xi$). Then for any positive number $\epsilon$, there exist positive constants $C(\epsilon )$ and $A(\epsilon )$ such that

$$\begin{aligned} \mathrm{{Prob}}(|v_N-v|\ge \epsilon ) \le C(\epsilon )e^{-A(\epsilon )N} \end{aligned}$$

(3.12)

for N sufficiently large.

Proof

The thrust of the proof is to use CVaR and its sample average approximation to approximate the semi-infinite constraints of (3.9) which is similar to the convergence analysis in Anderson et al. [2]. However, there are a few important distinctions: (a) the convergence here is for the randomization scheme (3.10) rather than the sample average approximation of the CVaR approximation of the semi-infinite constraints, (b) the underlying functions in the objective and constraints are not necessarily convex, and (c) the decision vector may consist of some integer variables.

Let

and let $\mathcal {F}$ and $\mathcal {F}^N$ denote the feasible set of problem (3.9) and problem (3.10) respectively. Then

Moreover, since $\Phi _N(x)\le \Phi (x)$, $\mathcal {F}\subset \mathcal {F}^N.$ For $\beta \in (0,1)$, let

$$\begin{aligned} \text{ CVaR }_{\beta }(f(x,\xi )) :=\sup _{\eta }\Big \{\eta +\frac{1}{1-\beta }\int _{y\in Y}(f(x,y)-\eta )_{+}\rho (y)dy\Big \} \end{aligned}$$

and

$$\begin{aligned} \Psi ^N_\beta (x):=\sup _{\eta }\Big \{ \eta +\displaystyle {\ \frac{1}{(1-\beta )N} \sum _{j=1}^{N}}(f(x,\xi ^{j})-\eta )_{+}\Big \} \end{aligned}$$

where $\rho (\cdot )$ denotes the density function of the random variable $\xi$, $(a)_+=\max (0,a)$ for $a\in \mathrm{I\!R}$. In the literature, $\text {CVaR}_\beta \left( f(x,\xi )\right)$ is known as conditional value at risk and $\Psi ^N_\beta (x)$ is its sample average approximation (see Rockafellar and Uryasev 2000; Anderson et al. 0000). It is well known that the maximum w.r.t. $\eta$ in the above formulation is achieved at a finite $\eta$. In other words, we may restrict the maximum to be taken within a closed interval $[-a,a]$ for a sufficiently large, see Rockafellar and Uryasev (2000). It is easy to verify that

$$\begin{aligned} \Psi ^N_\beta (x) \le \Phi _N(x)\le \Phi (x). \end{aligned}$$

(3.13)

We proceed the rest of the proof in four steps.

Step 1. By the definition of CVaR,

$$\begin{aligned} \text {CVaR}_\beta \left( f(x,\xi )\right) \le \Phi (x) \end{aligned}$$

for any $\beta \in (0,1)$ (see [2]). Moreover, under condition (c), it follows by ([2], Theorem 2.1) that

$$\begin{aligned} |\text {CVaR}_\beta \left( f(x,\xi )\right) - \Phi (x)| \le \dfrac{1}{K^{1/\tau }}\dfrac{\tau }{1+\tau }(1-\beta )^{1/\tau }. \end{aligned}$$

(3.14)

Therefore by driving $\beta$ to 1, we obtain

$$\begin{aligned} \sup _{x\in X} |\text {CVaR}_\beta \left( f(x,\xi )\right) - \Phi (x)|\rightarrow 0. \end{aligned}$$

Step 2. Using the inequalities (3.13), we have

$$\begin{aligned} |\Phi _N(x)- \Phi (x)|\le & {} |\Psi ^N_\beta (x)- \Phi (x)| \nonumber \\\le & {} |\Psi ^N_\beta (x)- \text {CVaR}_\beta \left( f(x,\xi )\right) | + |\text {CVaR}_\beta \left( f(x,\xi )\right) - \Phi (x)|.\nonumber \\ \end{aligned}$$

(3.15)

Let $\delta$ be a small positive number. By (3.14), we may set $\beta$ sufficiently close to 1 such that

$$\begin{aligned} \sup _{x\in X} |\text {CVaR}_\beta \left( f(x,\xi )\right) - \Phi (x)| \le \frac{\delta }{2}. \end{aligned}$$

On the other hand, since $\Xi$ is compact and f is Lipschitz continuous in x with integrable modulus, by virtue of Shapiro and Xu (2008, Theorem 5.1), there exist positive constants $C(\delta )$ and $A(\delta )$ such that

$$\begin{aligned}&\text {Prob}\Big ( \sup _{x\in X}|\Psi ^N_\beta (x) - \text {CVaR}_\beta \left( f(x,\xi )\right) | \ge \delta /2 \Big )\\&\quad \le \text {Prob}\Big (\frac{1}{1-\beta }\sup _{x\in X}\sup _{\eta \in [-a,a]}\left| \frac{1}{N} \sum _{j=1}^{N}(f(x,\xi ^{j})-\eta )_{+}-\mathbb {E}_P [(\eta -f(x,\xi ))_+]\right| \ge \delta /2 \Big )\\&\quad \le C(\delta )e^{-A(\delta )N} \end{aligned}$$

when N is sufficiently large. Here, in the first inequality, we are using the fact that the maximum w.r.t. $\eta$ is achieved in $[-a,a]$ for some appropriate positive constant a; see similar discussions in Xu and Zhang (2009). Therefore,

$$\begin{aligned}&\text {Prob}\Big (\sup _{x\in X} |\Phi _N(x)- \Phi (x)| \ge \delta \Big )\nonumber \\&\quad \le \text {Prob}\Big (\sup _{x\in X}|\text {CVaR}_\beta ^N \left( f(x,\xi )\right) - \text {CVaR}_\beta \left( f(x,\xi )\right) | \ge \delta /2 \Big )\nonumber \\&\quad \le C(\delta )e^{-A(\delta )N}. \end{aligned}$$

(3.16)

Step 3. For small positive number t, let

$$\begin{aligned} R(t)= \min \limits _{x}\Big \{\Phi (x): d(x,\mathcal {F})\Big \}\ge t, \end{aligned}$$

where $d(x,\mathcal {F})$ denotes the distance from point x to set $\mathcal {F}$. Obviously $R(t)>0$, it is monotonically increasing, and $R(t)\rightarrow 0$ as $t\downarrow 0$. Therefore, it is easy to observe that

$$\begin{aligned} d(x,\mathcal {F})\ge t \Longleftrightarrow \Phi (x) \ge R(t). \end{aligned}$$

Let

$$\begin{aligned} \mathbb {D}(\mathcal {F}^N,\mathcal {F}) :=\sup _{x \in \mathcal {F}^N}d(x,\mathcal {F}) \end{aligned}$$

and

$$\begin{aligned} \mathbb {H}(\mathcal {F}^N,\mathcal {F}) := \max \big (\mathbb {D}(\mathcal {F}^N,\mathcal {F}),\mathbb {D}(\mathcal {F},\mathcal {F}^N)\big ), \end{aligned}$$

where $\mathbb {H}$ is the Hausdorff distance between $\mathcal {F}^N$ and $\mathcal {F}$. Since both $\mathcal {F}^N$ and $\mathcal {F}$ are bounded, the Hausdorff distance is well defined. Moreover, since $\mathcal {F}\subset \mathcal {F}^N$, $\mathbb {H}(\mathcal {F}^N,\mathcal {F})=\mathbb {D}(\mathcal {F}^N,\mathcal {F})$. In what follows, we estimate $\text {Prob}\Big (\mathbb {D}(\mathcal {F}^N,\mathcal {F}) \ge \delta \Big )$. For any $x_N \in F^N$, since $\Phi _N(x_N)=0$, then

$$\begin{aligned} \Phi (x_N) \ge R(t)\Longleftrightarrow \Phi (x_N)-\Phi _N(x_N) \ge R(t). \end{aligned}$$

Therefore,

$$\begin{aligned} \text {Prob}\Big (\mathbb {D}(\mathcal {F}^N,\mathcal {F}) \ge t\Big )\le & {} \text {Prob}\left( \sup _{x\in \mathcal {F}^N} |\Phi (x)| \ge R(t)\right) \nonumber \\\le & {} \text {Prob}\left( \sup _{x\in X} |\Phi (x)-\Phi _N(x)| \ge R(t)\right) . \end{aligned}$$

(3.17)

Step 4. Let $x^*\in \mathcal {F}$ and $x^N\in \mathcal {F}^N$ be the optimal solutions to (3.9) and (3.10). Then, by the Lipschitz continuity of $\psi$,

$$\begin{aligned} |v^N-v^*| =|\psi (x^N)-\psi (x^*)| \le L\Vert x^N-x^*\Vert \le L \mathbb {H}(\mathcal {F}^N,\mathcal {F}) \end{aligned}$$

where L denotes the Lipschitz modulus of $\psi$. By (3.17), we deduce

$$\begin{aligned} \text {Prob}(|v^N-v^*|\ge \epsilon )\le & {} \text {Prob}\Big (\mathbb {H}(\mathcal {F}^N,\mathcal {F}) \ge \epsilon /L\Big )\\\le & {} \text {Prob}\left( \sup _{x\in X} |\Phi (x)-\Phi _N(x)| \ge R(\epsilon /L)\right) . \end{aligned}$$

The rest follows from (3.16) with $\delta = R(\epsilon /L)$. The proof is complete. $\square$

With Lemma 3.1, we are ready to state the convergence of problem (3.8).

Theorem 3.1

Let ${\vartheta }$ and ${\vartheta }_N$ denote the optimal value of (SIP-UC) and (3.8) respectively. Assume that $\xi$ follows a uniform distribution.³ Then for any positive number $\epsilon$, there exists positive constants $C(\epsilon )$ and $\beta (\epsilon )$ such that

$$\begin{aligned} \mathrm{{Prob}}(|{\vartheta }_N-{\vartheta }|\ge \epsilon ) \le C(\epsilon )e^{-\beta (\epsilon )N} \end{aligned}$$

(3.18)

for N sufficiently large.

Proof

It suffices to verify the conditions of Lemma 3.1. Conditions (a) and (b) are obvious since the objective function is linear and $\Xi$ is compact problem (3.8). Condition (c) is satisfied because $g(x,\xi )$ also follows a uniform distribution for each fixed x and the cumulative distribution function of $g(x,\xi )$ is a linear function. Let us verify condition (d). Following Walkup and Wets (1969) and Nožička (1974) (see also Liu et al. 2014, Lemma 4.3) that $g(x,\xi )$ is Lipschitz continuous w.r.t. x and $\xi$ and since $\Xi$ is compact, $g(x,\xi )$ is Lipschitz continuous in x with integrable Lipschitz modulus. The proof is complete. $\square$

In Theorem 3.1, we assume that $\xi$ follows a uniform distribution. It might be interesting to show the conclusion when $\xi$ follows a general continuous distribution with positive density function in the interior of $\Xi$; that is, $g(x,\xi )$ satisfies (3.11). We leave this for our future work.

The detailed formulation for the sample approximation of (SIP-UC) problem is given by the mixed integer linear program below,

where the first five constraints are the first-stage constraints, and the last six constraints represent the remaining constraints in problem (3.7).

4 Mixture distribution approach

In the absence of complete information on the underlying distribution of random variables, the decision maker could integrate information obtained through various channels to construct a mixture probability distribution. The use of mixture distribution in the context of robust optimization could be traced back to Peel and McLachlan (2000) and more recently in Zhu and Fukushima (2009) for portfolio optimization problems.

To define the ambiguity set corresponding to the robust problem (2.13), let $P_j, j=1,\ldots ,L$ be a set of probability measures such that $\mathbb {E}_{P_j} [g(x,\varvec{\xi })]$ is well defined for $j=1,\ldots ,L$. The ambiguity set under mixture distribution can then be defined as follows,

$$\begin{aligned} \mathcal {P}:= \Big \{\sum _{j=1}^L \gamma _j P_j:\quad \sum _{j=1}^L \gamma _j =1, \quad \gamma _j \ge 0,\quad \forall j=1,\ldots ,L \Big \}, \end{aligned}$$

where $\gamma _j$ denotes the weight of distribution j. The probability distributions $P_1, \ldots , P_L$ are assumed to be known and true probability distribution is assumed to be in their convex hull. For any realization of the distribution ${P}:= \sum _{j}\gamma _j P_j$ we have

$$\begin{aligned} \mathbb {E}_P [g(x,\varvec{\xi })]=\sum _{j=1}^L \gamma _j\mathbb {E}_{P_j}[g(x,\varvec{\xi })]. \end{aligned}$$

Under the mixture distribution, the inner maximization problem in (2.13) can then be rewritten as follows,

(4.1)

Let $\lambda$ be the dual variable corresponding to the first constraint in (4.1). Then the dual of the above problem can be written as

(4.2)

Proposition 4.1

In the case when $\varvec{\xi }$ has a finite discrete distribution with the support set containing a finite number of values $\varvec{\xi }^1, \ldots , \varvec{\xi }^N$ and for a given first-stage decision x, model (4.2) is equivalent to

(4.3)

where $p_j^k$ is the probability measure of $P_j$ in scenario k.

Proof

If $\varvec{\xi }$ has a discrete distribution with a finite number of scenarios $\varvec{\xi }^1, \ldots , \varvec{\xi }^N$, then model (4.2) can be written as

where $g(x,\varvec{\xi }^k)$ refers to the second-stage problem

Let us denote the optimal solution of the above problem as

$$\begin{aligned} \hat{y}^k= & {} \mathop {{{\mathrm{arg\,min}}}}\limits _{y\in \mathcal {Y}(x,\varvec{\xi }^k)} {h}^{T} y,\quad \forall k. \end{aligned}$$

Then we have $g(x,\varvec{\xi }^k)=h^T\hat{y}^k$. Let us define $\hat{\lambda }= \sum _{k=1}^N p^k_j({h}^{T} \hat{y}^k)$. It is clear that $(\hat{\lambda },\hat{y})$ is a feasible solution to problem (4.3). Let $(\tilde{\lambda }, \tilde{y}^k:k=1,\ldots ,N)$ be an optimal solution to problem(4.3). Then $h^T \tilde{y}^k \ge h^T\hat{y}^k$ for all k by the definition of $\hat{y}^k$. Thus, we have

$$\begin{aligned} \begin{array}{lll} \sum \limits _{k=1}^N p^k_j({h}^{T} \tilde{y}^k)\ge & {} \sum \limits _{k=1}^N p^k_j({h}^{T} \hat{y}^k), \quad \forall j. \end{array} \end{aligned}$$

Therefore

$$\begin{aligned} \begin{array}{lll} \min \limits _j \Bigg \{\sum \limits _{k=1}^N p^k_j({h}^{T} \tilde{y}^k)\Bigg \}\ge & {} \min \limits _j \Bigg \{\sum \limits _{k=1}^N p^k_j({h}^{T} \hat{y}^k)\Bigg \} \end{array} \end{aligned}$$

and $\tilde{\lambda }~\ge ~ \hat{\lambda }$. Since $(\hat{\lambda },\hat{y})$ is a feasible solution of (4.3), it must also be an optimal solution. $\square$

Thus, when $\varvec{\xi }$ has a finite discrete distribution, the original robust problem (2.13) can be rewritten as

(4.4)

Note that when $P_j$ follows a continuous distribution, it might be difficult to compute the expected value of the functions in the constraints of (4.2). A well-known approach to resolving this issue is to use sample average approximation (SAA). For a fixed j, let $\varvec{\xi }^1_j, \ldots , \varvec{\xi }^{N_j}_j$ denote independent and identically random sampling of $\varvec{\xi }$. Then $\mathbb {E}_{p_j} [g(x,\varvec{\xi })]$ can be approximated by

$$\begin{aligned} \dfrac{1}{N_j} \sum _{k=1}^{N_j} g(x,\varvec{\xi }_j^k). \end{aligned}$$

Consequently, problem (4.4) can be approximated by

(4.5)

The overall SAA of the Mix-UC problem can be written as follows,

Note that the SAA approach for Mix-UC results in a mixed integer linear program (MILP).

5 Case study

In this section, we carry out some numerical experiments to evaluate the proposed mathematical methods and numerical schemes. To facilitate further exposition and reading, we develop a list of models in Table 2.

Table 2 Reference of the methodologies

5.1 Data

We consider an illustrative case study based on a system with 10 generating units. The data for the generators are based on work by Pozo and Contreras (2013) and includes the cost and limitation of the generation and reserve utilization as summarised in Table 3.

Table 3 Ten-unit system: generation and reserve cost and capacities

5.1.1 Stochastic base case

The hourly power demand is assumed to be known, and under the two-stage stochastic setting (Sto-UC) the wind output is assumed to follow a multivariate normal distribution $\mathcal {N}(\varvec{\mu },\Sigma )$ with mean $\varvec{\mu }$, standard deviation $\sigma$, correlation C and covariance $\Sigma = \sigma C \sigma ^T$. The hourly demand, wind output mean values $\varvec{\mu }$, and the standard deviations $\sigma$ for a 24-h period are given in Table 4. The corresponding mean values for the stochastic net load are also presented in Fig. 1.

Table 4 Hourly demand and mean/standard deviation of the wind

The correlation matrix C is based on the hourly Danish wind output data⁴ for the year 2013 and is given by

Fig. 1

Nominal values of demand and mean wind

5.1.2 SIP formulation

In the SIP formulation, we assume that only the first moment of the uncertain wind power is known and is given by $\varvec{\mu }$. Based on this assumption, we implement the first proposed model and formulate the problem as a robust SIP (SIP-UC). In solving the SIP problem, we limit the support set of random hourly wind to 150 values generated from a multivariate uniform distribution.

5.1.3 Mixture distribution formulation

In the second approach of mixture distribution, we consider a case where the information on the uncertain net load is received through various resources, e.g. advice from a group of experts. While each alternative net load model provides a specific distribution and parameters such as the mean and the covariance, there is no consensus among the decision makers on which model contains the true distribution. Therefore, instead of relying on a particular expert model, we use the mixture model (Mix-UC) to combine all these potential distributions. Specifically, we assume that we are given three different distributions for the stochastic net load, shown in Table 5. We assume that three distributions are equally relevant and therefore they have equal weights in the construction of the mixture distribution. We construct the uncertainty set by drawing 50 random samples from each distribution.

Table 5 Potential distributions for wind power

5.2 Numerical results

We compare the solutions produced by three different models: (a) a two-stage stochastic UC that uses the known distribution of the random supply as described in Sect. 2.1, (b) the robust UC that uses only information on the mean value of the random supply as described in Sect. 3, and (c) the robust UC that ‘knows’ only a convex hull of a finite set of known distributions containing the true probability distribution as described in Sect. 4. Table 6 shows the size of each problem as well as the running time for solving each problem. The models have been tested on an MacBook Air Intel Core i5 processor at 1.6 GHz and 4 GB of RAM memory using CPLEX 12.6.1 under MATLAB R2014a.

Table 6 Problems size and computational times

The sizes of the three models are dependent on the number of scenarios generated and are very similar to each other in this case study. We generate 150 scenarios for each of the models so that the computational time is reasonable. Our main interest lies in assessing the quality of the solutions proposed by the stochastic model and their robust counterparts.

The cumulative first-stage decisions as well as the second-stage decisions and the total costs for each solution are presented in Table 7. It can be observed that robust solutions result in higher expected costs than the stochastic solution in both the first stage and the second stage. This is contributed to mostly by the increase in the first-stage generation to hedge against the ambiguity of the distribution of the underlying net load uncertainty. The increase of the expected costs makes sense because the stochastic solution was produced by using the truth distribution of the net load; i.e. the truth information is known, while the robust solutions only have the uncertainty set containing the truth distribution. Note that, in practice, we often do not have the truth distribution and hence the stochastic solution must use some ‘guess’ distribution in the uncertainty set. In that case, the resulting expected cost might be higher than those suggested by the robust solutions as we will demonstrate in the sensitivity analysis later on.

Table 7 Stochastic versus robust solutions

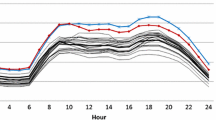
The hourly cumulative first-stage generation and reserve levels are presented in Fig. 2. It can be observed that, in the case of the Mix-UC solution, the hourly pattern of total generation is generally higher than the base Sto-UC solution. Additionally, the SIP-UC solution provides a greater flexibility for the second stage through a higher level of up and down reserves. It can also be observed that the hourly patterns of the generation and the reserve schedule are similar to the net load quantities, and at the peak hours the maximum generation capacity of generators are scheduled either in term of generation (Mix-UC) or generation with reserve (Sto-UC and SIP-UC).

Fig. 2

UC first-stage solutions. a Sto-UC. b Mix-UC. c SIP-UC

5.2.1 Sensitivity of solutions to variation of the wind distribution

The first-stage decisions of the UC models determines the flexibility of the solution to changes in the actual realization of the wind distribution in the second stage, i.e. we expect the robust solutions to provide greater flexibility if the actual distribution of the uncertainty was different from the assumed distribution. To compare the performance of the Sto-UC model, MIX-UC model, and SIP-UC model, we analyze the effect of deviation of the distribution parameters such as the mean and the covariance matrix from the nominal values. In doing so, we consider a two-stage stochastic structure for each instance, in which the first stage unit commitment and reserve schedules are fixed as the first-stage solutions of the Sto-UC model, MIX-UC model, and SIP-UC model. In each instance, we then solve the second-stage problem using a distribution with different means or covariances for the uncertain wind.

We first study the sensitivity of solution to changes in the actual mean of the distribution. We compare the Sto-UC, Mix-UC, and SIP-UC for instances with the following wind distributions: $\mathcal {N}(a\varvec{\mu }, \Sigma ), a=\{0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5\}$ bounded away from zero (i.e. truncated normal distributions). For each choice of a, we carry out 100 independent runs, each generating 150 i.i.d samples from the corresponding distribution, and use these i.i.d samples as input to solve the second-stage problem. The solutions of 100 runs for each instance are summarised as a box plot and are presented in Fig. 3a–c. The average values of the objective function (total expected cost) for the 100 runs of each instance are also shown in Fig. 3d.

Fig. 3

Sensitivity of solutions to variation in mean. a Sto-UC. b Mix-UC. c SIP-UC. d Mean objective values for 100 runs

It can be observed that when the actual wind distribution is $\mathcal {N}=(\varvec{\mu },\Sigma )$, i.e. when $a=1$, the Sto-UC solution performs better than Mix-UC and SIP-UC solutions as expected since the assumed distribution in Sto-UC coincides with the actual distribution. The Sto-UC solution also performs better for all the instances with the mean of distribution greater than $\varvec{\mu }$, i.e. when the mean of wind level is greater than expected in Sto-UC model. This is due to the ability of the system operator to dispatch higher levels of energy using the excess wind power rather than utilizing the costly reserve. On the other hand, the Mix-UC (SIP-UC) solution performs better when the mean of the wind distribution is less than 90 % (80 %) of the anticipated value in the Sto-UC model. In other words the Mix-UC and SIP-UC robust solutions have lower total costs than the Sto-UC solution when the wind output is less than what decision maker assumed under the Sto-UC model.

In the second set of sensitivity test instances, we compare the performances of the Sto-UC, Mix-UC, and SIP-UC solutions to the possible changes in the covariances of the wind distribution.

Fig. 4

Sensitivity of solutions to variation in covariance. a Sto-UC. b Mix-UC. c SIP-UC. d Mean objective values for 100 runs

We specifically consider the following truncated normal distributions for the second-stage uncertain wind $\mathcal {N}(\varvec{\mu }, (b)^2\Sigma )$, where $b=\{0.4, 0.6, 0.8, 1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.4, 2.6\}$. Similar to previous tests, we draw 150 i.i.d samples from the corresponding distribution in each instance and repeat each instance for 100 runs. The corresponding box plots for test instances for all three models are presented in Fig. 4a–c. Furthermore, the mean value of the objective function for 100 tests in each instance and each model is shown in Fig. 4d. It can be observed that the SIP-UC solution has the least sensitivity to change in covariance of the distribution, since the only available information for the SIP-UC model was the first moment condition of the distribution and there was no assumption on the covariance of the distribution. However, this additional flexibility comes at a cost and it can be observed that the SIP-UC solution is more conservative and costly for instances with covariance coefficients around 2, when compared to the Sto-UC solutions. For the instances with $b \ge 2.2$ the SIP-UC performs better than both the Sto-UC and Mix-UC solutions.

The sensitivity of the Mix-UC and Sto-UC solutions to changes in covariance are very similar and the difference between the two curves is almost unchanged across the test instances. This is due to the covariance assumptions in construction of the mixture model, i.e. covariance of all distributions used to construct the mixture model was equal to $\Sigma$. We have also constructed the mixture distribution using the following distributions:

$$\begin{aligned} \mathcal {N}\big (\mu ,(0.8)^2\Sigma \big ),\mathcal {N}\big (\mu ,\Sigma \big ),\mathcal {N}\big (\mu ,(1.2)^2\Sigma \big ). \end{aligned}$$

The solution of this mixture model was very similar to the solutions of the Sto-UC model.

The final sensitivity test that we have performed is to randomly draw the wind input from historical Danish wind data. Specifically, we perform 100 independent runs, each includes 150 daily wind speed data drawn out of 263 historical daily wind speed by using sampling with replacement. For each of these 100 independent runs, the first stage solutions of the STO-UC, the MIX-UC and the SIP-UC are tested for performance against the corresponding 150 daily wind data. We then report the corresponding total costs of these solutions on the 100 runs. Figure 5a shows the box-plot of these total costs and Fig. 5b shows their quantile plots. These quantile plots provide us with the relative comparison between STO-UC, MIX-UC and SIP-UC on different quantiles. For example, at quantile 1, the figure shows us the worst total cost among these three strategies while at quantile 0 it shows the best cases. We can see from the Fig. 5b that MIX-UC does not performs well compared to the others. This could be because of the belief on mixed distribution does not apply to the Danish wind data. The SIP-UC, on the other hand, always outperforms STO-UC in all the quantiles. This implies that using only a belief on the mean is more ‘robust’ against sampling with replacement on the Danish wind data.

Fig. 5

Sensitivity of solutions to variation in samples from historical wind data. a Mean objective values for 100 runs. b Mean objective values for 100 runs

5.3 Medium and large cases

We have also tested the limit of the models computationally by considering a medium-sized problem with 50 generator and a large-sized problem with 100 generators. The time period T is set to equal to 12. We set the stopping criteria as either 5 h computer-running time or an optimality gap of no more than 1 %, whichever reaches first. Sensitivity results for these cases are included in the “Appendix 2”. Table 8 shows the computational times and optimality gaps on these two instances in addition to the small instance with 10 generators.

Table 8 Computational performance on different problem sizes

We can see that the computational time increases significantly when the number of generator increases. This is because the number of binary variables, the number of continuous variables and the number of constraints in each of the STO-UC, MIX-UC and SIP-UC increase proportionally with the number of generators. For the case of 50 generators, the STO-UC can reach 0.94 % optimality gap within around 40 min. The MIX-UC took less than 18 min to reach 0.85 % optimality gap while the STO-UC stops after 5 h when it reached 2.09 % optimality gaps. For the case of 100 generators, only the MIX-UC reach the 1 % optimality gap stopping criteria after 104 min while the STO-UC stops slightly higher at 1.01 % optimality gap after 5 h. There was no sign of the SIP-UC to reach reasonable optimality gap after 5 h.

One interesting observation is that the MIX-UC actually took less time compared to the STO-UC. This is a bit counter-intuitive as the distributionally robust optimization models are build on the two-stage with one extra layer of optimization, i.e. a min–max–min problem with a worst-case max operator in the middle, and hence, we would generally expect it to be more difficult to solve than the stochastic counterpart. In fact, through dualization, the reformulated models for the MIX-UC and the SIP-UC are actually not much bigger than the stochastic counterpart. Specifically, the MIX-UC has one additional variables and two additional constraints compared to the STO-UC. The corresponding numbers of additional variables and constraints for the SIP-UC are 25 and 150, respectively. MIX-UC, however, looks very much the same structure with the stochastic model while the SIP-UC, however, has extra variable $\alpha$ appearing in the objective function and KnT constraints. This make sthe problem much harder to solve

We have programmed the entire models for the STO-UC, MIX-UC and SIP-UC into MATLAB and calling the CPLEX solver directly. It is possible to apply techniques for solving stochastic programming (e.g. by using Bender’s decomposition) to improve the performance of these models and we expect that these could improve the numerical computation significantly. Using that method, we envisage that the increase in the number of generators would not impose significant computational issues as the number of binary variables only grow linearly. Nevertheless, we leave this enhanced methods for future research direction.

6 Conclusion

In this paper, we present a two-stage distributionally robust model that provides a novel and practical approach to deal with the uncertainty of the distribution of random wind output in the unit commitment problem. The model includes the technical ramping constraints as well as reliability condition against failure of up to one generating unit. The robustness takes into account the available information on uncertainty in two alternative ways. First, we assume that only the first-moment information of the random wind is given and use duality theory to formulate the problem as a linear semi-infinite program. The SIP model is then solved using sampling because the structure of the problem does not allow us to reformulate the semiinfinite constraints as semidefinite constraints. We establish exponential rate of convergence of the optimal value when the randomization scheme is applied to discretize the semi-infinite constraints.

Second, we assume that the information on probability distribution of uncertain wind is received through various sources, and we construct a mixture model to include these into decision making. The mixture model is also reformulated using duality theory and solved through the sample average approximation approach. Empirical tests have been carried out using an illustrative UC case study, taken from the literature, in order to illustrate the performance of the proposed robust models. The robust UC solutions may lose the potential of utilizing the wind power in high-wind climate; however, they perform much better in a low-wind climate as compared to the solutions that do not consider the uncertainty of the distribution (Sto-UC).

As one of the referees observed, the model has some limitations in absence of network constraints and second order moment information. In the unit commitment literature, transmission network has a very important impact on the UC decisions, particularly when there is significant wind power generation. Moreover, transmission line outages are an important factor for the (n-1) security constraints. Likewise, if we interpret the first order moment $\mu$ as a persistence forecast for each time period of the planning horizon, then the forecast routines used to generate $\mu$ may constitute standard deviations. We envisage that these are new directions for further research of the model but require significant new work on numerical schemes to cope with the additional complexity from network constraints and higher order moment conditions.

Appendices

Appendix 1: Ramp constraints and reliability and $n-1$ security constraint

1.1 Ramp constraints

For conventional generation units, it is important to take into account the short-term dynamics of generation output over the consecutive periods. Such requirements are often referred to as ramp constraints which limit the maximum increase or decrease of generated power from one time period to the next, reflecting the thermal and mechanical inertia which need to be overtaken in order for the generating unit to increase or decrease its output.

In a two-stage stochastic framework, we need to define the ramp constraints for any possible realization of the net load $\xi$. At the second stage after the realization of the uncertain net load, the scheduled energy $q_{it}$ does not change and the generating units adapt their production to accommodate the realized net load. To do this, up and down reserves ($\hat{r}_{it}^{up}(\xi )$, $\hat{r}_{it}^{dw}(\xi )$) are used. We denote the actual power output of unit i at time t and scenario $\xi$ by $\hat{q}_{it}(\xi )$ which is defined as follows:

$$\begin{aligned} \hat{q}_{it}(\xi )=q_{it} + \hat{r}_{it}^{up}(\xi ) - \hat{r}_{it}^{dw}(\xi ), \quad \forall t,i,\xi . \end{aligned}$$

Note that up and down reserves should not be simultaneously positive. We consider the ramp constraints for all four combinations of on-off decisions between any two consecutive periods $t-1$ and t as follows,

• 1. If $u_{i(t-1)}=1$ and $u_{it}=1$, then the generating unit i is coupled for both hours, and ramp limitations in hour t are bounded by the ramp up and down rates, $RU_i$ and $RD_i$, respectively. The ramp constraints will then be as follows:

  $$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi )\le RU_i,\qquad \forall t, i, \xi , \end{aligned}$$

  (R1)
  $$\begin{aligned}&\hat{q}_{i(t-1)}(\xi ) -\hat{q}_{it}(\xi ) \le RD_i,\qquad \forall t, i,\xi . \end{aligned}$$

  (R2)

• 2. If $u_{i(t-1)}=0$ and $u_{it}=1$, generating unit i starts up at the beginning of period t and hence the limitation for hour t should be the starting up ramp $SU_i$. The ramp constraints will then be

  $$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi )\le SU_i, \qquad \forall t, i, \xi , \end{aligned}$$

  (R1)
  $$\begin{aligned}&\hat{q}_{i(t-1)}(\xi ) -\hat{q}_{it}(\xi ) \le RD_i, \qquad \forall t, i,\xi . \end{aligned}$$

  (R2)

  Note that (R2) always holds because $\hat{q}_{i(t-1)}(\xi )=0$, $\hat{q}_{it}(\xi ) \ge 0$ and $RD_i \ge 0$.

• 3. If $u_{i(t-1)}=1$ and $u_{it}=0$, generating unit i shutdowns at the beginning of time period t and hence limitation during the hour t should be the shut-down ramp $SD_i$. The ramp constraints then become

  $$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi )\le RU_i, \qquad \forall t, i, \xi , \end{aligned}$$

  (R1)
  $$\begin{aligned}&\hat{q}_{i(t-1)}(\xi ) -\hat{q}_{it}(\xi ) \le SD_i, \qquad \forall t, i,\xi . \end{aligned}$$

  (R2)

  Note that (R1) always holds because the left hand side is always negative whereas the right hand side is always positive.

• 4. If $u_{i(t-1)}=0$ and $u_{it}=0$, then generating unit i is off during both periods and the ramp constraints are

  $$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi )\le SU_i, \qquad \forall t, i, \xi , \end{aligned}$$

  (R1)
  $$\begin{aligned}&\hat{q}_{i(t-1)}(\xi ) -\hat{q}_{it}(\xi ) \le SD_i, \qquad \forall t, i,\xi . \end{aligned}$$

  (R2)

A summary of ramp limitations for all of the scenarios discussed above is presented in Table 9:

Table 9 Ramp limitations

Having defined the ramp constraints for all on/off decision scenarios over two time periods, we can generalize them in relation to decision variable $u_{it}$ as follow,

$$\begin{aligned}&\hat{q}_{it}(\xi ) - \hat{q}_{i(t-1)}(\xi )\le RU_i u_{i(t-1)} +SU_i(1-u_{i(t-1)}),&\forall t, i, \xi ,\\&\hat{q}_{i(t-1)}(\xi ) -\hat{q}_{it}(\xi ) \le RD_i u_{it} +SD_i(1-u_{it}),&\forall t, i,\xi . \end{aligned}$$

1.2 Reliability and $n-1$ security constraint

To ensure the secure operation of the system under the failure of up to one scheduled generator, we consider the worst-case scenario that the system could possibly face; that is, for any given time period, the generator with the highest total scheduled generation and actual up reserve fails under the lowest level of wind (highest net load) available. This can be modeled as

$$\begin{aligned}&\sum _i \left( q_{it} + {r}_{it}^{up} \right) -\max _i \{q_{it}+\hat{r}_{it}^{up}(\xi )\}+ S_t(\xi ) \ge d_t - \min \limits _{\xi }\{w_t(\xi ) \},&\forall t, \xi . \end{aligned}$$

(6.1)

In the literature of energy management, this is known as $n-1$ criteria. Let us denote the worst (lowest) realization of wind output at time t by

and let denote the corresponding load shedding for this realization. Since the actual up reserve used has to be less than the scheduled up reserve, i.e. $\hat{r}^{up}_{it}(\xi ) \le {r}^{up}_{it}$ for every scenario $\xi$, the inequality (6.1) can be rewritten as

(6.2)

Let us denote the upper limit of total generation and reserve schedules at time t as

$$\begin{aligned} Q_t= \sum _i \left( q_{it} + {r}_{it}^{up} \right) , \qquad \forall t. \end{aligned}$$

The inequality constraint (6.2) can be rewritten as

Appendix 2: Numerical results for medium and large cases

See Figs. 6 and 7.

Fig. 6

Sensitivity of solutions to variation in mean and variance for a medium-sized problem with 50 generators (with $T = 12$, $S = 150$). a Mean objective values for 100 runs. b Mean objective values for 100 runs

Fig. 7

Sensitivity of solutions to variation in mean and variance for a medium-sized problem with 100 generators (with $T = 12$, $S = 150$). a Mean objective values for 100 runs. b Mean objective values for 100 runs