Abstract
We reconsider the inside patent holders’ optimal licensing problem of non-drastic and (super-) drastic innovations under incomplete information, taking into account restrictions concerning royalty rates and the use of exclusive licenses implied by antitrust rules. We employ methods developed in the analysis of license auctions with downstream interaction and optimal control theory. Our analysis differs from the literature which assumed particular patterns of cost reductions across firms induced by the innovation and either complete information or particular probability distributions.

Similar content being viewed by others
Notes
An extension of this analysis to three firms is in Wang et al. (2013).
This symmetry assumption is not essential and used only to simplify the notation.
By the well-known revelation principle, using a direct mechanism is simply a methodological device to solve optimal mechanisms. The optimal mechanism is equivalent to an indirect mechanism that offers a menu of contracts, (r, f), from which the licensee can choose freely, without asking the licensee to report his unit cost.
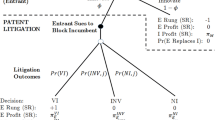
In the present framework, the rival’s output can be inferred. Inspection is only necessary if demand is subject to shocks or if there are more than two firms. However, inspection may be necessary in order to be prepared for the event of litigation.
According to the Antitrust Guidelines for the Licensing of Intellectual Property in the U.S.: “Generally, an exclusive license may raise antitrust concerns only if the licensees themselves, or the licensor and its licensees, are in a horizontal relationship. Examples of arrangements involving exclusive licensing that may give rise to antitrust concerns include ...acquisitions of intellectual property rights” (US Department of Justice and Federal Trade Commission 1995, Section 4.1.2).
Licensing agreements for intellectual property are typically illegal if they involve naked price-fixing, output restrictions, or market division (US Department of Justice and Federal Trade Commission 1995).
To the best of our knowledge, the upper-bound constraint is generally used in the literature that deals with licensing in oligopoly markets and cares about antitrust concerns. The constraint is not invoked when a license is awarded to a firm that is already a monopoly, as in Macho Stadler and Pérez-Castrillo (1991, Sec. 3) and Sen (2005). We also mention that some authors allow for slightly negative royalty rates (see, for example, Liao and Sen 2005; Anderson 2014).
“Quite appropriately, contracts of this form would likely be held to be illegal by antitrust authorities” (Katz and Shapiro 1985, p. 513).
For example, in the theory of price discrimination by Maskin and Riley (1984) screening requires the use of two state-dependent variables: price and quantity.
The exact values are: \(\left( x_1, x_2, \hat{x}\right) = \left( 0.025, \, 0.058, \, 0.134 \right) \), and \((r(x),f(x))=\left( 0 , \,\, {57917}/{720000} - {5x}/{36}+{x^2}/{9} \right) \) for \(x \le x_1\), \((r(x),f(x))= \left( 5 x - {1}/{8},\,\, {12463}/{80000}\right. \) \(\left. - {7 x}/{2} +14 x^2 \right) \) for \(x_1 \le x \le x_2\), and \((r(x),f(x))= \left( {850 -3 \sqrt{35259}/}{1600} - {x}/{4}, \,\,0 \right) \) for \(x \ge x_2\).
The no distortion at the top is a typical feature in standard adverse selection problems. However, in the present framework, with downstream interaction, it cannot occur if \(\underline{x} \ge d \).
However, the distribution function of a non-negative random variable cannot be log-convex everywhere (Block et al. 1998, Corollary 2.1).
This result generalizes Heywood et al. (2014) who use a binary model and assume that the patentee is at least as efficient as the potential licensee with probability one.
The detailed proof is in an earlier version of our paper which is available on request from the authors.
Note, we consider a particular mechanism that is restricted to implement a monopoly (see the restriction (19) below). If we allowed for implementing a duopoly in some states, the analysis would be far more complicated.
Note, if only non-exclusive licenses were permitted, constraint (19) would have to be replaced by: \(r(x) \le 2d- 1-x\).
According to the Antitrust Guidelines: “If the Agencies conclude ...that a restraint in a licensing arrangement is unlikely to have an anticompetitive effect, they will not challenge the restraint” (US Department of Justice and Federal Trade Commission 1995, Section 4.2).
The proof is straightforward and hence omitted.
The present control problem is subject to inequality constraints concerning the state variables and some free and fixed endpoints. The corresponding conditions for optimality can be found in (Kamien and Schwartz 1991, p. 230ff.).
We extend G outside its support in the obvious way. Therefore the equation has a solution, which may however be below \(\underline{x}\).
In one case we prove incentive compatibility by showing that \(\Pi _2(x,z)\) is pseudoconcave in z. The function \(\Pi _2(x,z)\) is “pseudoconcave” in z if, for all x, it is increasing to the left of its stationary point and decreasing to the right. Due to the first-order condition for incentive compatibility \(\Pi _2(x,z)\) has a stationary point at \(z=x\), i.e.,
 for all x. Evidently, pseudoconcavity assures that the stationary points are global maxima.
for all x. Evidently, pseudoconcavity assures that the stationary points are global maxima.
References
Amir, R., Encaoua, D., Lefouili, Y.: Optimal licensing of uncertain patents in the shadow of litigation. Games Econ. Behav. 88, 320–338 (2014)
Anderson, F.: Licensing to a more efficient rival. Manch. Sch. 82, 653–676 (2014)
Bagnoli, M., Bergstrom, T.: Log-concave probability and its applications. Econ. Theory 26, 445–469 (2005)
Beggs, A.: The licensing of patents under asymmetric information. Int. J. Ind. Organ. 10, 171–191 (1992)
Block, H., Savits, T., Singh, H.: The reversed hazard rate function. Probab. Eng. Inf. Sci. 12, 69–90 (1998)
Brousseau, E., Coeurderoy, R., Chaserant, C.: The governance of contracts: empirical evidence on technology licensing agreements. J. Inst. Theor. Econ. 163, 205–235 (2007)
Calvert, R.: The Encyclopedia of Patent Practice and Invention Management. Reinhold, New York (1964)
Choi, J.: Technology transfer with moral hazard. Int. J. Ind. Organ. 19, 249–266 (2001)
Das Varma, G.: Bidding for a process innovation under alternative modes of competition. Int. J. Ind. Organ. 21, 15–37 (2003)
Encaoua, D., Lefouili, Y.: Licensing ‘weak’ patents. J. Ind. Econ. 57, 492–525 (2009)
Fan, C., Jun, B., Wolfstetter, E.: Licensing process innovations when losers’ messages determine royalty rates. Games Econ. Behav. 82, 388–402 (2013)
Fan, C., Jun, B., Wolfstetter, E.: Licensing a common value innovation in oligopoly when signaling strength may backfire. Int. J. Game Theory 43, 215–244 (2014)
Farrell, J., Shapiro, C.: How strong are weak patents? Am. Econ. Rev. 98, 1347–1369 (2008)
Gallini, N., Wright, B.: Technology transfer under asymmetric information. RAND J. Econ. 21(1), 147–160 (1990)
Giebe, T., Wolfstetter, E.: License auctions with royalty contracts for (winners and) losers. Games Econ. Behav. 63, 91–106 (2008)
Goeree, J.: Bidding for the future: signaling in auctions with an aftermarket. J. Econ. Theory 108, 345–364 (2003)
Heywood, J., Li, J., Ye, G.: Per unit vs. ad valorem royalties under asymmetric information. Int. J. Ind. Organ. 37, 38–46 (2014)
Jones, M.: Kumaraswamy’s distribution: a beta-type distribution with some tractability advantages. Stat. Methodol. 6, 70–81 (2009)
Kamien, M.: Patent licensing. In: Aumann, R., Hart, S. (eds.) Handbook of Game Theory, vol. I, pp. 331–354. Elsevier, Amsterdam (1992)
Kamien, M., Schwartz, N.: Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management, 2nd edn. North-Holland, Amsterdam (1991)
Kamien, M., Tauman, Y.: The private value of a patent: a game theoretic analysis. J. Econ. 4, 93–118 (1984)
Kamien, M., Tauman, Y.: Fee versus royalties and the private value of a patent. Q. J. Econ. 101, 471–491 (1986)
Kamien, M., Tauman, Y.: Patent licensing: the inside story. Manch. Sch. 70, 7–15 (2002)
Katz, M., Shapiro, C.: On the licensing of innovations. RAND J. Econ. 16(4), 504–520 (1985)
Kumaraswamy, P.: A generalized probability density function for double-bounded random processes. J. Hydrol. 46, 79–88 (1980)
Lemley, M., Shapiro, C.: Probabilistic patents. J. Econ. Perspect. 19, 75–98 (2005)
Liao, H., Sen, D.: Subsidy in licensing: optimality and welfare implications. Manch. Sch. 73, 281–299 (2005)
Macho-Stadler, I., Pérez-Castrillo, D.: Contrats de licences et asymétrie d’information. Ann. Econ. Stat. 24, 189–208 (1991)
Macho-Stadler, I., Martínez-Giralt, X., Pérez-Castrillo, D.: The role of information in licensing contract design. Res. Policy 25, 25–41 (1996)
Maskin, E., Riley, J.: Monopoly with incomplete information. RAND J. Econ. 15, 171–196 (1984)
Milgrom, P.: Auction theory. In: Bewley, T.E. (ed.) Advances in Economic Theory, Econometric Society Monographs, vol. 12, pp. 1–32. Cambridge University Press, Cambridge (1987)
Poddar, S., Sinha, U.: Patent licensing from a high-cost firm to a low-cost firm. Econ. Rec. 86, 384–395 (2010)
Rostoker, M.: A survey of corporate licensing. IDEA 24, 59–92 (1984)
Seierstad, A., Sydstæter, K.: Sufficient conditions in optimal control theory. Int. Econ. Rev. 18, 367–391 (1977)
Sen, D.: On the coexistence of different licensing schemes. Int. Rev. Econ. Finance 14, 393–413 (2005)
Sen, D., Tauman, Y.: General licensing schemes for a cost-reducing innovation. Games Econ. Behav. 59, 163–186 (2007)
Shapiro, C.: Patent licensing and R&D rivalry. Am. Econ. Rev. Pap. Proc. 75(2), 25–30 (1985)
Taylor, C., Silberston, Z.: The Economic Impact of the Patent System. Cambridge University Press, Cambridge (1973)
US Department of Justice and Federal Trade Commission: Antitrust Guidelines for Licensing of Intellectual Property. Washington, DC. (1995)
Vishwasrao, S.: Royalties vs. fees: How do firms pay for foreign technology? Int. J. Ind. Organ. 25, 741–759 (2007)
Wang, K., Liang, W., Chou, P.: Patent licensing under cost asymmetry among firms. Econ. Model. 31, 297–307 (2013)
Wang, X.: Fee versus royalty licensing in a Cournot duopoly model. Econ. Lett. 60, 55–62 (1998)
Acknowledgements
We thank the anonymous referees for detailed and constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Financial support by the National Natural Science Foundation of China (Grant: 71371116), Korea University (Grant: K1509111), and the Deutsche Forschungsgemeinschaft (SFB Transregio 15, “Governance and Efficiency of Economic Systems”) is gratefully acknowledged.
A Appendix
A Appendix
1.1 A.1 Proof of Proposition 1
As a preliminary, note that it is optimal to adopt the highest possible fixed fee. This allows us to replace the participation constraint (13) by
Step 1: Consider the patentee’s maximization problem:
We solve (A.2) as an optimal control problem for given \(\hat{x}\), then characterize the optimal \(\hat{x}\), and confirm that the ignored constraint is never binding.
To translate (A.2) into an optimal control problem define the control variable, \(u(x){:}=r'(x)\), the state variables r(x), f(x), the constraint functions \(g_1, g_2, k_1, k_2\), the co-state variables, \(\lambda _1(x)\), \(\lambda _2(x)\), \(\eta _1(x)\), \(\eta _2(x)\) and the Hamiltonian, \(H(x, r,f,u,\lambda _1, \lambda _2, \eta _1, \eta _2)\):
There, \(g_2\) corresponds to the incentive compatibility conditions (10), and \(k_1, k_2\) to the constraints, (14), (15). The endpoints \(f(\hat{x})\) and \(r(\hat{x})\) are not free (see A.1) and the endpoints \(f(\underline{x})\), \(r(\underline{x})\) are free.
The maximum principle requires that the following conditions are satisfied:Footnote 22
Step 2: Deriving r(x). (A.9) and (A.13) yield \(\lambda _2(x)= -G(x)\). Inserting this into (A.7) yields
Differentiating (A.16) and equating with (A.8) yields:
Define \(\eta {:}=(\eta _1,\eta _2)\) and:

Consider the function  . Because
. Because  , by (18), the equation
, by (18), the equation  has a unique solution denoted by \(x_1\) and:Footnote 23
has a unique solution denoted by \(x_1\) and:Footnote 23

Similarly, consider the function  . Because
. Because  , the equation
, the equation  has a unique solution denoted by \(x_2\) (which may be above \(\hat{x}\) or even \(\bar{x}\)) and:
has a unique solution denoted by \(x_2\) (which may be above \(\hat{x}\) or even \(\bar{x}\)) and:

By the definition of \(x_1\) we have \(r_0(x_1)=0\); hence

which implies \(x_1 < x_2\).
Also we have


We now derive the asserted r(x) function.

r(x) is zero on \([\underline{x},x_1]\), increasing on \([x_1,x_2]\), which confirms that the ignored constraint is not binding there, and decreasing on \([x_2,\hat{x}]\), as asserted.
Step 3: Deriving f(x). Denote the unique solution to the equation \(c-x=r_0(x)\) by \(x_0\), then we have

We distinguish three cases: Case 1: \(\varvec{\hat{x}} \ge \varvec{x}_0\). In this case we have \(x_1\le x_2\le \hat{x}\) by (A.24) and \(r(\hat{x})=c-\hat{x}\). Thus \(f(\hat{x})=0\).
In this case f(x) is positive and decreasing on \([\underline{x}, x_2)\) and equal to zero on \([x_2,\hat{x}]\).
Case 2: \(\varvec{\hat{x}} <\varvec{x}_0~\text {and}~\varvec{\hat{x}}>\varvec{x}_1\). In this case we have \(x_1< \hat{x} <x_2\) by (A.24). Thus, \(k_2(\hat{x})>0\), which implies \(r(\hat{x})<c-\hat{x}\), and \(f(\hat{x})=\pi _2(q_1^*(\hat{x}), q_2^*(\hat{x});\hat{x}+r(\hat{x}))- \Pi _2^N>0\).
In this case f(x) is positive and decreasing on \([\underline{x}, \hat{x}]\).
Case 3: \(\varvec{\hat{x}} <\varvec{x}_0~\text {and}~\varvec{\hat{x}}\le \varvec{x}_1~(\le \varvec{x}_2)\). In this case we have \(f(\hat{x})=\pi _2(q_1^*(\hat{x}), q_2^*(\hat{x});\hat{x}+r(\hat{x}))- \Pi _2^N\).
In this case f(x) is positive and decreasing.
Step 4: Global incentive compatibility and second-order conditions.
Next, we confirm incentive compatibility.Footnote 24
-
(a)
For \(x,z \ge x_2\), we have \(\Pi _2(x,x) = \Pi _2(x,z)=\frac{1}{36} (2-4 c+2 d+3 \hat{x}-3 x)^2\).
-
(b)
For \(x,z \in [x_1, x_2]\), we have \(\partial _{zx}\Pi _2(x,z)=\frac{1}{6} \left( 1+4 r'(z)\right) >0\).
-
(c)
For \(x_1\le z<x_2\le x\), we have \(\Pi _2(x_2,x_2)-\Pi _2(x_2,z)\ge 0\) from (b) and
$$\begin{aligned} \left( \Pi _2(x,x)-\Pi _2(x,z)\right) -\left( \Pi _2(x_2,x_2)-\Pi _2(x_2,z)\right) = \frac{2}{3} (x-x_2)k_2(z) \ge 0, \end{aligned}$$which implies \(\Pi _2(x,x)-\Pi _2(x,z)\ge 0\).
-
(d)
For \(x_1 \le x<x_2\le z\), we have \(\Pi _2(x,x)\ge \Pi _2(x,x_2)=\Pi _2(x,z)\).
-
(e)
For \(x,z \le x_1\), we have \(\Pi _2(x,z) =\frac{1}{36} (2+2 d-3 x-z)^2-f(x_1)-\frac{1}{9}(x_1-z)(1+d-x_1-z)\). Thus, \(\partial _{zx} \Pi _2(x,z) ={1}/{6}>0\).
-
(f)
For \(x\le x_1 <z \le x_2\), we have \(\Pi _2(x_1,x_1)-\Pi _2(x_1,z)\ge 0\) from (b) and
$$\begin{aligned}&\left( \Pi _2(x,x)-\Pi _2(x,z)\right) -\left( \Pi _2(x_1,x_1)-\Pi _2(x_1,z)\right) \\&= \frac{x_1-x}{12}\left( 8r_0(z)+ 2z-x_1-x\right) \ge 0, \end{aligned}$$which implies \(\Pi _2(x,x)-\Pi _2(x,z)\ge 0\).
-
(g)
For \(z< x_1 \le x \le x_2\), we have \(\Pi _2(x,x)\ge \Pi _2(x,x_1)=\Pi _2(x,z) +\frac{x_1-z}{12}\left( 2x-x_1-z\right) > \Pi _2(x,z)\).
-
(h)
For \(x\le x_1, z \ge x_2\), we have \(\Pi _2(x_1,x_1)-\Pi _2(x_1,z)\ge 0\) from (d) and
$$\begin{aligned}&\left( \Pi _2(x,x)-\Pi _2(x,z)\right) -\left( \Pi _2(x_1,x_1)-\Pi _2(x_1,z)\right) \\&= \frac{x_1-x}{12}\left( 8r_2(z)+ 2z-x_1-x\right) \ge 0, \end{aligned}$$which implies \(\Pi _2(x,x)-\Pi _2(x,z)\ge 0\).
-
(i)
For \(x\ge x_2, z\le x_1\), we have \(\Pi _2(x_2,x_2)-\Pi _2(x_2,z)\ge 0\) from (b) and (g) and
$$\begin{aligned} \left( \Pi _2(x,x)-\Pi _2(x,z)\right) -\left( \Pi _2(x_2,x_2)-\Pi _2(x_2,z)\right) = \frac{x-x_2}{6} (4 c-3 \hat{x}-z) \ge 0, \end{aligned}$$which implies \(\Pi _2(x,x)-\Pi _2(x,z)\ge 0\).
Therefore, incentive compatibility is satisfied.
The Arrow Sufficiency Theorem (Seierstad and Sydstæter 1977, Theorem 3) applies, because, at the optimum, \(\lambda _1 g_1 + \lambda _2 g_2 =0\) and \(H^*{:}=\max _u H\) is concave in r and f.
Step 5: \(\hat{x}> \underline{x}\). Denote the maximum expected payoff of the patentee by \(\Pi _1^*(\hat{x})\). We now prove that a contract is awarded with positive probability by showing

We consider three cases: (i) \(\underline{x} \ge x_2\), (ii) \(\underline{x} \in [x_1,x_2)\), (iii) \(\underline{x}<x_1\).
Case (i): If \(\underline{x} \ge x_2\), then \(r(\underline{x})=r_2(\underline{x})\) and we have

Case (ii): If \(\underline{x} \in [x_1,x_2)\), then \(r(\underline{x})=r_0(\underline{x})\) and we have

because the second term in the big bracket is a concave function of d which takes the minimum value 0 at \(d=2c-1\) on \([2c-1,c]\).
Case (iii): If \(\underline{x} <x_1\), then \(r(\underline{x})=0\) and we have

Depending upon the parameters, the optimal \(\hat{x}\) is either a corner solution, \(\hat{x}= \bar{x}\) (no-exclusion), or an interior solution (exclusion). \(\square \)
1.2 A.2 Supplement to the proof of Proposition 2
Here, we supplement the proof of Proposition 2 and show that \(\Pi _1^*(\hat{x})\) increases on \([x_1,x_2)\).
On the interval \([x_1,x_2)\) one has \(r(x)=r_0(x)\). First, suppose \(x_1 < \underline{x}\). Then, the patentee’s expected revenue can be written as
Its derivative with respect to \(\hat{x}\) is
which is positive because \(d>2c-1\).
Next, suppose \(x_1 \ge \underline{x}\). Then, \(r(x)=r_1(x)\) on \([\underline{x},x_1]\), and \(\Pi _1\) can be written as
The derivative of \(\Pi _1^*(\hat{x})\) with respect to \(\hat{x}\) is exactly the same as above, which completes the proof. \(\square \)
1.3 A.3 Supplement to the proof of Proposition 3
By Proposition 1 it is sufficient to show that \(x_2 \le \underline{x}\). This holds true if and only if  , which confirms as follows:
, which confirms as follows:

\(\square \)
Rights and permissions
About this article
Cite this article
Fan, C., Jun, B.H. & Wolfstetter, E.G. Optimal licensing under incomplete information: the case of the inside patent holder. Econ Theory 66, 979–1005 (2018). https://doi.org/10.1007/s00199-017-1077-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-017-1077-5




 for all x. Evidently, pseudoconcavity assures that the stationary points are global maxima.
for all x. Evidently, pseudoconcavity assures that the stationary points are global maxima.