Skip to main content
SpringerLink
Log in

A Glimpse of the Conformal Structure of Random Planar Maps

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

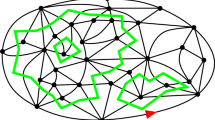
We present a way to study the conformal structure of random planar maps. The main idea is to explore the map along an SLE (Schramm–Loewner evolution) process of parameter \({ \kappa = 6}\) and to combine the locality property of the SLE6 together with the spatial Markov property of the underlying lattice in order to get a non-trivial geometric information. We follow this path in the case of the conformal structure of random triangulations with a boundary.

Under a reasonable assumption called (*) that we have unfortunately not been able to verify, we prove that the limit of uniformized random planar triangulations has a fractal boundary measure of Hausdorff dimension \({\frac{1}{3}}\) almost surely. This agrees with the physics KPZ predictions and represents a first step towards a rigorous understanding of the links between random planar maps and the Gaussian free field (GFF).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahlfors, L.V.: Conformal Invariants: Topics in Geometric Function Theory. McGraw-Hill Series in Higher Mathematics. McGraw-Hill Book Co., New York (1973)

  2. Ambjørn, J., Durhuus, B., Jonsson, T.: Quantum Geometry: A Statistical Field Theory Approach. Cambridge Monographs on Mathematical Physics. Cambridge University Press, Cambridge (1997)

  3. Angel, O.: Scaling of percolation on infinite planar maps, I. arXiv:0501006

  4. Angel O.: Growth and percolation on the uniform infinite planar triangulation. Geom. Funct. Anal. 13, 935–974 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  5. Angel, O., Curien, N.: Percolations on infinite random maps, half-plane models. Ann. Inst. H. Poincaré Probab. Stat. (to appear)

  6. Angel, O., Ray, G.: Classification of half planar maps. Ann. Probab. (to appear)

  7. Angel O., Schramm O.: Uniform infinite planar triangulation. Commun. Math. Phys. 241, 191–213 (2003)

    ADS  MATH  MathSciNet  Google Scholar 

  8. Barral, J., Mandelbrot, B.B.: Non-degeneracy, moments, dimension, and multifractal analysis for random multiplicative measures (Random multiplicative multifractal measures. II). In: Fractal Geometry and Applications: A Jubilee of Benoît Mandelbrot, Part 2. Proceedings of Symposia in Pure Mathematics, vol. 72, pp. 17–52. American Mathematical Society, Providence (2004)

  9. Beffara, V.: Is critical 2D percolation universal? In: In and Out of Equilibrium, vol. 2. Progress in Probability, vol. 60, pp. 31–58. Birkhäuser, Basel (2008)

  10. Benjamini I., Curien N.: Simple random walk on the uniform infinite planar quadrangulation: subdiffusivity via pioneer points. Geom. Funct. Anal. 23, 501–531 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  11. Benjamini, I., Schramm, O.: Recurrence of distributional limits of finite planar graphs. Electron. J. Probab. 6, 23, 13 pp (2001) (electronic)

  12. Benjamini I., Schramm O.: KPZ in one dimensional random geometry of multiplicative cascades. Commun. Math. Phys. 289, 653–662 (2009)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  13. Bertoin J.: Lévy Processes. Cambridge Tracts in Mathematics, vol. 121. Cambridge University Press, Cambridge (1996)

    Google Scholar 

  14. Bertoin, J.: Subordinators: examples and applications. In: Lectures on Probability Theory and Statistics (Saint-Flour, 1997). Lecture Notes in Mathematics, vol. 1717, pp. 1–91. Springer, Berlin (1999)

  15. Curien, N., Ménard, L., Miermont, G.: A view from infinity of the uniform infinite planar quadrangulation. ALEA Lat. Am. J. Probab. Math. Stat. 10(1), 45–88 (2013)

  16. Curien, N., Miermont, G.: Uniform infinite planar quadrangulations with a boundary. arXiv:1202.5452

  17. Duplantier, B., Miller, J., Sheffield, S.: Liouville quantum gravity as a mating of trees. arXiv:1409.7055

  18. Duplantier B., Sheffield S.: Liouville quantum gravity and KPZ. Invent. Math. 185, 333–393 (2011)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  19. Garban, C.: Quantum gravity and the KPZ formula. Séminaire Bourbaki, vol. 64 (2012)

  20. Gill J.T., Rohde S.: On the Riemann surface type of random planar maps. Rev. Mat. Iberoam. 39(3), 1071–1090 (2014)

    MathSciNet  Google Scholar 

  21. Grandell J.: Point processes and random measures. Adv. Appl. Probab. 9, 502–526 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  22. Hongler C., Smirnov S.: Critical percolation: the expected number of clusters in a rectangle. Probab. Theory Relat. Fields 151, 735–756 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  23. Jacod, J., Shiryaev, A.N.: Limit theorems for stochastic processes. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 288, 2nd edn. Springer, Berlin (2003)

  24. Kahane J.-P.: Sur le chaos multiplicatif. Ann. Sci. Math. Qué. 9, 105–150 (1985)

    MATH  MathSciNet  Google Scholar 

  25. Kallenberg O.: Random Measures. Akademie-Verlag, Berlin (1976)

    MATH  Google Scholar 

  26. Knizhnik V.G., Polyakov A.M., Zamolodchikov A.B.: Fractal structure of 2 D-quantum gravity. Mod. Phys. Lett. A 3, 819–826 (1988)

    Article  ADS  MathSciNet  Google Scholar 

  27. Kontoyiannis I., Meyn S.P.: Spectral theory and limit theorems for geometrically ergodic Markov processes. Ann. Appl. Probab. 13, 304–362 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  28. Lawler, G., Schramm, O., Werner, W.: Conformal restriction: the chordal case. J. Am. Math. Soc. 16, 917–955 (electronic) (2003)

  29. Lawler G.F.: Conformally Invariant Processes in the Plane. Mathematical Surveys and Monographs, vol. 114. American Mathematical Society, Providence (2005)

    Google Scholar 

  30. Lawler G.F., Schramm O., Werner W.: The dimension of the planar Brownian frontier is 4/3. Math. Res. Lett. 8, 401–411 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  31. Le Gall J.-F.: The topological structure of scaling limits of large planar maps. Invent. Math. 169, 621–670 (2007)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  32. Le Gall J.-F.: Uniqueness and universality of the Brownian map. Ann. Probab. 41, 2880–2960 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  33. Le Gall J.-F., Paulin F.: Scaling limits of bipartite planar maps are homeomorphic to the 2-sphere. Geom. Funct. Anal. 18, 893–918 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  34. Lyons R., Pemantle R., Peres Y.: Ergodic theory on Galton–Watson trees: speed of random walk and dimension of harmonic measure. Ergod. Theory Dyn. Syst. 15, 593–619 (1995)

    Article  MathSciNet  Google Scholar 

  35. Ménard, L., Nolin, P.: Percolation on uniform infinite planar maps. Electron. J. Probab. 19, 19 (2014)

  36. Meyn, S., Tweedie, R.L.: Markov Chains and Stochastic Stability, 2nd edn. Cambridge University Press, Cambridge (2009). (With a prologue by Peter W. Glynn)

  37. Miermont G.: On the sphericity of scaling limits of random planar quadrangulations. Electron. Commun. Probab. 13, 248–257 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  38. Miermont G.: The Brownian map is the scaling limit of uniform random plane quadrangulations. Acta Math. 210, 319–401 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  39. Miller, J., Sheffield, S.: Quantum Loewner evolution (2013).arXiv:1312.5745

  40. Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 293, 3rd edn. Springer, Berlin (1999)

  41. Rhodes R., Vargas V.: KPZ formula for log-infinitely divisible multifractal random measures. ESAIM Probab. Stat. 15, 358–371 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  42. Rhodes, R., Vargas V.: Gaussian multiplicative chaos and applications: a review. Probab. Surv. (2013, to appear)

  43. Robert R., Vargas V.: Gaussian multiplicative chaos revisited. Ann. Probab. 38, 605–631 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  44. Schaeffer, G.: Conjugaison d’arbres et cartes combinatoires aléatoires. PhD thesis (1998)

  45. Sheffield, S.: Conformal weldings of random surfaces: SLE and the quantum gravity zipper. arXiv:1012.4797

  46. Smirnov S.: Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris Sér. I Math. 333, 239–244 (2001)

    Article  ADS  MATH  Google Scholar 

  47. Sugarcult: Bouncing off the walls. Start Static (2001)

  48. Werner, W.: Random Planar Curves and Schramm–Loewner Evolutions. In: Lectures on Probability Theory and Statistics. Lecture Notes in Mathematics, vol. 1840, pp. 107–195. Springer, Berlin (2004)

Download references

Author information

Authors and Affiliations

  1. CNRS, Université Paris 6, Paris, France

    Nicolas Curien

Authors
  1. Nicolas Curien
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nicolas Curien.

Additional information

Communicated by F. Toninelli

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Curien, N. A Glimpse of the Conformal Structure of Random Planar Maps. Commun. Math. Phys. 333, 1417–1463 (2015). https://doi.org/10.1007/s00220-014-2196-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-014-2196-5

Keywords

Search

Navigation