Skip to main content
SpringerLink
Log in

A new insight into the interaction of thermoelasticity with mass diffusion for a half-space in the context of Moore–Gibson–Thompson thermodiffusion theory

  • Published:
Applied Physics A Aims and scope Submit manuscript

Abstract

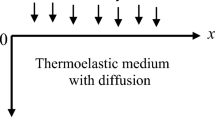
Thermal and mass diffusion processes are important issues in a variety of engineering applications and scientific disciplines. The main objective of this research is to develop a new model that demonstrates diffusion in thermoelastic solids and compares the strain/temperature fields and mass diffusion. The proposed model is an extension of the Quintanilla model [1]. In the new model, Fourier’s and Fick’s laws have been improved by including the relaxation times in the Green–Naghdi theory in the framework of Moore–Gibson–Thompson (MGT) heat equation. Based on the introduced model, a one-dimensional half-space problem is considered. The surface surrounding the half-space is exposed to chemical potential and thermal shocks. Our findings indicate that the considered physical fields have a non-zero value only in a limited area and disappear outside this area. This result fully demonstrates the validity of the proposed model because the nature of velocities is limited by heat and diffusive waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Abbreviations

λ,μ:

Lam´e’s constants

α_t:

Thermal expansion coefficient

αc :

Linear diffusion coefficient

β1=(3λ+2μ) αt :

Thermal coupling parameter

T_0:

Reference temperature

θ=T-T0 :

Temperature change

T:

Absolute temperature

Ce :

Specific heat

e=div ⁡u:

Dilatation

σij :

Stress components

eij :

Strain components

ui :

Displacement components

q:

Heat flux vector

η:

Flow of diffusing mass vector

K:

Thermal conductivity

ρ:

Density of material

Q:

Heat source

β2=(3λ+2μ) αc :

Coupling diffusion

δ_ij:

Kronecker's delta function

∇^2:

Laplacian operator

τ_0:

Thermal relaxtaion time

τ_1:

Diffusion relaxtaion time

K* :

Rate of thermal conductivity

C:

Concentration

a:

Thermoelastic diffusion effect

D:

Diffusion coefficient

P:

Chemical potential

References

  1. R. Quintanilla, Moore-Gibson-Thompson thermoelasticity. Math. Mech. Solids 24, 4020–4031 (2019)

    MathSciNet  MATH  Google Scholar 

  2. M. Ezzat, M. Zakaria, A. Abdel-Bary, Generalized thermoelasticity with temperature dependent modulus of elasticity under three theories. J. Appl. Math. Comput. 14, 193–212 (2004)

    MathSciNet  MATH  Google Scholar 

  3. M.A. Biot, Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27(3), 240–253 (1957)

    ADS  MathSciNet  MATH  Google Scholar 

  4. H.W. Lord, Y. Shulman, A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15(5), 299–309 (1967)

    ADS  MATH  Google Scholar 

  5. A.E. Green, K.A. Lindsay, Thermoelasticity. J. Elast. 2, 1–7 (1972)

    MATH  Google Scholar 

  6. A.E. Green, P.M. Naghdi, A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. 432, 171–194 (1991)

    ADS  MathSciNet  MATH  Google Scholar 

  7. A.E. Green, P.M. Naghdi, On undamped heat waves in an elastic solid. J. Therm. Stresses 15(2), 253–264 (1992)

    ADS  MathSciNet  Google Scholar 

  8. A.E. Green, P.M. Naghdi, Thermoelasticity without energy dissipation. J. Elast. 31(3), 189–208 (1993)

    MathSciNet  MATH  Google Scholar 

  9. D.S. Chandrasekharaiah, Hyperbolic thermoelasticity: a review of recent literature. Appl. Mech. Rev. 51(12), 705–729 (1998)

    ADS  Google Scholar 

  10. D.Y. Tzou, The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass Transf. 38(17), 3231–3240 (1995)

    Google Scholar 

  11. J. Alihemmati, Y.T. Beni, Y. Kiani, Application of Chebyshev collocation method to unified generalized thermoelasticity of a finite domain. J. Therm. Stresses 44(5), 547–565 (2021)

    Google Scholar 

  12. J. Alihemmati, Y.T. Beni, Y. Kiani, LS-based and GL-based thermoelasticity in two dimensional bounded media: a Chebyshev collocation analysis. J. Therm. Stresses (2021). https://doi.org/10.1080/01495739.2021.1922112

    Article  Google Scholar 

  13. A.E. Abouelregal, W.W. Mohammed, H. Mohammad-Sedighi, Vibration analysis of functionally graded microbeam under initial stress via a generalized thermoelastic model with dual-phase lags. Arch. Appl. Mech. 91, 2127–2142 (2021)

    ADS  Google Scholar 

  14. A.E. Abouelregal, Modified fractional thermoelasticity model with multi-relaxation times of higher order: application to spherical cavity exposed to a harmonic varying heat. Waves Rand. Compl. Med. (2019). https://doi.org/10.1080/17455030.2019.1628320

    Article  Google Scholar 

  15. A.E. Abouelregal et al., Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Universitatis Series-Mech. Eng. (2021). https://doi.org/10.22190/FUME201222024A

    Article  Google Scholar 

  16. A.E. Abouelregal, On Green and Naghdi thermoelasticity model without energy dissipation with higher order time differential and phase-lags. J. App. Compu. Mech. (2019). https://doi.org/10.22055/JACM.2019.29960.164

    Article  Google Scholar 

  17. A.E. Abouelregal, Two-temperature thermoelastic model without energy dissipation including higher order time-derivatives and two phase-lags. Mater. Res. Exp. (2019). https://doi.org/10.1088/2053-1591/ab447f

    Article  Google Scholar 

  18. A.E. Abouelregal, A novel model of nonlocal thermoelasticity with time derivatives of higher order. Mathe. Method. App. Sci. (2020). https://doi.org/10.1002/mma.6416

    Article  MathSciNet  MATH  Google Scholar 

  19. R. Quintanilla, Moore-Gibson-Thompson thermoelasticity with two temperatures. App. Eng. Sci. 1, 100006 (2020)

    Google Scholar 

  20. M. Dreher, R. Quintanilla, R. Racke, Ill-posed problems in thermomechanics. Appl. Math. Lett. 22, 1374–1379 (2009)

    MathSciNet  MATH  Google Scholar 

  21. M. Conti, V. Pata, R. Quintanilla, Thermoelasticity of Moore–Gibson–Thompson type with history dependence in the temperature. Asympt. Anal. 120(1–2), 1–21 (2020)

    MathSciNet  MATH  Google Scholar 

  22. M. Pellicer, R. Quintanilla, On uniqueness and instability for some thermomechanical problems involving the Moore–Gibson–Thompson equation. Z. Angew. Math. Phys. 71, 84 (2020)

    MathSciNet  MATH  Google Scholar 

  23. A.E. Abouelregal, I.-E. Ahmed, M.E. Nasr, K.M. Khalil, A. Zakria, F.A. Mohammed, Thermoelastic processes by a continuous heat source line in an infinite solid via Moore–Gibson–Thompson thermoelasticity. Materials 13(19), 4463 (2020)

    ADS  Google Scholar 

  24. A.E. Aboueregal, H.M. Sedighi, The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore Gibson Thompson heat conduction model Proceedings of the Institution of Mechanical Engineers Part L. J Mater Design Appl (2021). https://doi.org/10.1177/1464420720985899

    Article  Google Scholar 

  25. N. Bazarra, J.R. Fernandez, R, , Quintanilla, Analysis of a Moore–Gibson–Thompson thermoelasticity problem. J Comput App Mathe 382, 113058 (2021)

    MATH  Google Scholar 

  26. M. Conti, V. Pata, M. Pellicer, R. Quintanilla, On the analyticity of the MGT-viscoelastic plate with heat conduction. J. Differential Equ 269(10), 7862–7880 (2020)

    ADS  MathSciNet  MATH  Google Scholar 

  27. J.R. Fernández, R. Quintanilla, Moore-Gibson-Thompson theory for thermoelastic dielectrics. App Mathe Mech (English Edition) 42, 309–316 (2021)

    Google Scholar 

  28. A.E. Aboueregal, H.M. Sedighi, A.H. Shirazi, M. Malikan, V.A. Eremeyev, Computational analysis of an infinite magneto-thermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach. Continuum Mech. Thermodyn. (2021). https://doi.org/10.1007/s00161-021-00998-1

    Article  Google Scholar 

  29. A.E. Abouelregal, H. Ahmad, T.A. Nofal, H. Abu-Zinadah, Moore–Gibson–Thompson thermoelasticity model with temperature-dependent properties for thermo-viscoelastic orthotropic solid cylinder of infinite length under a temperature pulse. Phys. Scr. (2021). https://doi.org/10.1088/1402-4896/abfd63

    Article  Google Scholar 

  30. C. Xiong, Y. Guo, Electromagneto-thermoelastic diffusive plane waves in a half-space with variable material properties under fractional order thermoelastic diffusion. Int. J. Appl. Electromagnet Mech 53(2), 251–269 (2017)

    Google Scholar 

  31. W. Nowacki, Dynamical problems of thermodiffusion in solids. Bull. Acad. Pol. Sci. Ser. Sci. Tech. 22, 55–64 (1974)

    MathSciNet  MATH  Google Scholar 

  32. W. Nowacki, Dynamical problems of thermodiffusion in solids II. Bull. Acad. Pol. Sci. Ser. Sci. Tech 22, 129–135 (1974)

    MathSciNet  MATH  Google Scholar 

  33. W. Nowacki, Dynamical problems of thermo diffusion in solid III. Bull. Acad. Pol. Sci. Ser. Sci. Tech. 22, 266–275 (1974)

    Google Scholar 

  34. H.H. Sherief, F. Hamza, H. Saleh, The theory of generalized thermoelastic diffusion. Int. J. Eng. Sci. 42, 591–608 (2004)

    MathSciNet  MATH  Google Scholar 

  35. A.E. Abouelregal, Generalized mathematical novel model of thermoelastic diffusion with four phase lags and higher-order time derivative. The Eur Phy J Plus 135, 263 (2020)

    Google Scholar 

  36. A.E. Abouelregal, M.A. Elhagary, A. Soleiman, K.M. Khalil, Generalized thermoelastic-diffusion model with higher-order fractional time-derivatives and four-phase-lags. Mech. Based Des. Struct. Mach. (2020). https://doi.org/10.1080/15397734.2020.1730189

    Article  Google Scholar 

  37. T. Kansal, Fundamental solution of the system of equations of pseudo oscillations in the theory of thermoelastic diffusion materials with double porosity. Multid. Model. Mater. Structures 15(2), 317–336 (2019)

    Google Scholar 

  38. M.A. El-hagary, A two-dimensional generalized thermoelastic diffusion problem for a thick plate subjected to thermal loading due to laser pulse. J. Therm. Stresses 37, 1416–1432 (2014)

    Google Scholar 

  39. T. Rosnitschek, F. Hueter, B. Alber-Laukant, FEM-based modelling of elastic properties and anisotropic sinter shrinkage of metal EAM. Int J Simul Modell 19(2), 197–208 (2020)

    Google Scholar 

  40. M.A. Fahmy, Boundary element algorithm for nonlinear modeling and simulation of three-temperature anisotropic generalized micropolar piezothermoelasticity with memory-dependent derivative. Int. J. Appl. Mech. 12(03), 2050027 (2020)

    Google Scholar 

  41. H.H. Sherief, E. Hussein, Contour integration solution for a thermoelastic problem of a spherical cavity. Appl. Math. Comput. 320, 557–571 (2018)

    MathSciNet  MATH  Google Scholar 

  42. H.H. Sherief, M. El-Maghraby, A thick plate problem in the theory of generalized thermoelastic diffusion. Int. J. Thermophys. 30(6), 2044–2057 (2009)

    ADS  Google Scholar 

  43. M. Aouadi, B. Lazzari, R. Nibbi, A theory of thermoelasticity with diffusion under Green-Naghdi models. Z. Angew. Math. Mech. 94(10), 837–852 (2013)

    MathSciNet  MATH  Google Scholar 

  44. B. Lazzari, R. Nibbi, Energy decay in green-naghdi thermoelasticity with diffusion and dissipative boundary controls. J. Therm. Stresses 40(7), 917–927 (2016)

    Google Scholar 

  45. C. Giorgi, D. Grandi, V. Pata, On the green-naghdi type III heat conduction model. Disc Contin Dyn Sys Series B 19(7), 2133–2143 (2014)

    MathSciNet  MATH  Google Scholar 

  46. C. Cattaneo, On a form of heat equation which eliminates the paradox of instantaneous propagation. CR Acad. Sci Paris 247, 431–433 (1958)

    MATH  Google Scholar 

  47. K.K. Tamma, X. Zhou, Macroscale and micro-scale thermal transport and thermo- mechanical interactions: Some noteworthy perspectives. J. Therm. Stresses 21(3–4), 405–449 (1988)

    Google Scholar 

  48. E. Samaniego, C. Anitescu, S. Goswami, V.M. Nguyen-Thanh, H. Guo, K. Hamdia, X. Zhuang, T. Rabczuk, An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comp Method Appl Mech Eng 362, 112790 (2020)

    MathSciNet  MATH  Google Scholar 

  49. I. Goodfellow, Y. Bengio, A. Courville, Deep Learning (MIT press, Cambridge, 2016)

    MATH  Google Scholar 

  50. G. Honig, U. Hirdes, A method for the numerical inversion of Laplace Transform. J. Comp. Appl. Math. 10, 113–132 (1984)

    MathSciNet  MATH  Google Scholar 

  51. D.Y. Tzou, Macro to Micro-Scale Heat Transfer: The Lagging Behavior (Taylor and Francis, Washington DC, 1996)

    Google Scholar 

Download references

Acknowledgements

H.M. Sedighi is grateful to the Research Council of Shahid Chamran University of Ahvaz for its financial support (Grant No. SCU.EM99.98).

Author information

Authors and Affiliations

  1. Department of Mathematics, College of Science and Arts, Jouf University, Al-Qurayyat, Saudi Arabia

    Ahmed E. Abouelregal

  2. Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt

    Ahmed E. Abouelregal

  3. Mechanical Engineering Department, Faculty of Engineering, Shahid Chamran University of Ahvaz, 61357-43337, Ahvaz, Iran

    Hamid M. Sedighi

  4. Drilling Center of Excellence and Research Center, Shahid Chamran University of Ahvaz, Ahvaz, Iran

    Hamid M. Sedighi

Authors
  1. Ahmed E. Abouelregal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hamid M. Sedighi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamid M. Sedighi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abouelregal, A.E., Sedighi, H.M. A new insight into the interaction of thermoelasticity with mass diffusion for a half-space in the context of Moore–Gibson–Thompson thermodiffusion theory. Appl. Phys. A 127, 582 (2021). https://doi.org/10.1007/s00339-021-04725-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00339-021-04725-0

Keywords

Search

Navigation