1 Introduction

The scramjet engine is highly anticipated to be the most likely used propulsion system for the next-generation hypersonic transporter. Since the scramjet is impacted to such a considerable extent by the vehicle shape and configuration, one of the key technical issues is assessing the totally integrated vehicle, in terms of aerodynamic stability and propulsion performance. Although flight tests are one of the most desirable options for the integrated vehicle assessment, the testing cost is high, and the number of the test and flight conditions is both limited. Conversely, shock tunnels have been commonly used for hypersonic aerothermodynamic research at a reasonable operating cost. They can easily produce free-stream test flow over Mach 8 with the Reynolds number equivalent to actual flight condition, and many scramjet studies were conducted with such facilities (Stalker and Morgan 1982; Paull et al. 1995; Holden 2000; Itoh et al. 2002; Hannemann et al. 2014; Jiang et al. 2021). Since the facilities’ test time is a few milliseconds, this precludes conventional force balances due to the excessive response time. Although the last couple of decades have seen many studies conducted using the force measurement technique, nevertheless it remains state-of-the-art. Most previous studies were limited to single-component (thrust) measurements, though several multi-component studies have been reported (Robinson et al. 2004, 2006; Doherty et al. 2015; Hannemann et al. 2015). Moreover, less attention was paid to the measurement precision, which is crucial to determine actual vehicle aerodynamic characteristics. For an integrated scramjet-powered vehicle, the longitudinal vehicle stability, namely pitching motion, should be assessed, including the measurement precision.

In the present study, a free-flight aerodynamic force measurement technique was applied to measure a scramjet vehicle’s aerodynamic characteristics in the free-piston shock tunnel HIEST (Itoh et al. 2002), and a new analytical method using multiple single-axis accelerometers was developed. The three-component aerodynamic coefficients (Drag, Lift, and Pitching moment) of the 1.1-m long fully integrated scramjet vehicle MoDKI (Model of Demonstrator Kakuda Initiative) were successfully measured, and measurement precision is discussed.

2 Free-flight technique in short test duration

$$m\frac{{d}^{2}x}{d{t}^{2}}+c\frac{dx}{dt}+kx=F$$
(1)

A general aerodynamic force measurement system (Fig. 1) can be modeled as a one-dimensional forced vibration (Eq. (1)). In this equation, \(F\) denotes the aerodynamic load, \(m\) is the mass of the model, \(c\) is the damping coefficient, and \(k\) is the stiffness of the support device (e.g., sting). In conventional wind tunnels, mechanical vibration is damped by an extended test time, and the aerodynamic force can be measured as the elastic force \(kx\). Conversely, in impulsive facilities, the mechanical vibration typically does not dampen within the short test duration, resulting in less accurate measurement. In this case, by reducing the stiffness \(k\) as smaller as possible, the aerodynamic force can be measured as the inertial force \(m{(d}^{2}x/d{t}^{2})\). Based on the idea above, Duryea and Sheeran (1969) developed the so-called ‘acceleration balance.’ These balances have been used in several shock tunnel measurements (Reddy 1983; Joshi and Reddy 1986). In this technique, the models were weakly constrained by wires, rubbers, or springs instead of a rigid support system. The aerodynamic load can be obtained from the products of the measured acceleration and the mass of the model. However, due to the non-negligible drag produced by the weakly restrained support systems, sufficient measurement accuracy is not guaranteed, especially for multi-component force measurement (Tanno et al. 2009).

Fig. 1
figure 1

Conventional aerodynamic measurement system and 1D vibration model

Full size image

Free-flight force measurement techniques are one of the solutions for the issue. A good summary of previous researches can be found in Bernstein (1975). Most previous works were based on optical measurements using a high-speed camera system. Displacements were obtained directly from test-model images. Accelerations were then derived by double differentiation of displacement curves. However, since the measurement accuracy directly depends on the model displacement resolution, it will be naturally more challenging to keep the resolution as the test time becomes short. Instead of optical tracking, Naumann et al. (1993) used miniature accelerometers mounted inside the model in his shock tunnel measurement. Nevertheless, the model injection system and umbilicals may have produced aerodynamic interference, and such interference would become mostly undesirable when pitching moment measurements are required.

A new free-flight technique was developed to keep the resolution and avoid the interferences using specially designed model-onboard data recording systems (Tanno et al. 2014). Since the test model is in free-fall during the test duration resulting in an entirely unconstrained motion, aerodynamic interference and mechanical vibration are eliminated. In his study, a pair of translational accelerometers was adopted to measure rotational motions instead of gyroscopes. A gyroscope is a favorable option to measure non-restrained or weakly restrained objects (Padgaonkar et al. 1975). However, the general gyroscope’s frequency response, namely up to a few hundred Hz, is insufficient for short-duration impulsive facilities such as HIEST. Instead, a translational accelerometer represents a reasonable option due to its high-frequency response (> 10 kHz), low cost, and availability. Theoretically, rotational motion can be identified with a pair of translational accelerometers offset from the rotation center. However, there is sensor-to-sensor variability on the accelerometers and errors associated with mounting location, just a single (for translation) or a pair (for rotation) of accelerometers may not suffice to improve precision. Moreover, when mounted, accelerometers may not always be optimally positioned given the general limitations on models in space. In fully integrated scramjet vehicle models, the available space may be limited due to the onboard fuel and electrical systems such as gas-fuel bottles, fuel-valves, solid-state timers, and batteries. These constraints make the design of the model challenging and could significantly impair the quality of the measurements. The following section introduces a new analytical approach applied to deal with the issues above.

3 Analysis method for aerodynamic coefficient

3.1 Equation for the rotational motion of a rigid body

Acceleration \({{\varvec{A}}}_{{\varvec{P}}}(t)\) at an arbitrary point,\({\varvec{P}}\), within a rigid body is expressed by the following equation Eq. (2) with the distance from the center of rotation, \({\varvec{r}}\), the translational acceleration \({{\varvec{A}}}_{0}\left(t\right)\), the centrifugal acceleration \({\varvec{\omega}}\left(t\right)\times{\varvec{\omega}}\left(t\right)\times {\varvec{r}}\), the angular acceleration \(\dot{{\varvec{\omega}}}\left({\varvec{t}}\right)\times {\varvec{r}}\), and the gravitational acceleration \({\varvec{g}}\). The coordinate system includes the accelerations around the y-axis, as shown in Fig. 2.

Fig. 2
figure 2

Coordinate system of a measuring point. Centrifugal and angular acceleration were indicated around the y-axis

Full size image
$${{\varvec{A}}}_{{\varvec{P}}}\left(t\right)={{\varvec{A}}}_{0}\left(t\right)+{\varvec{\omega}}\left(t\right)\times{\varvec{\omega}}\left(t\right)\times {\varvec{r}}+\dot{{\varvec{\omega}}}\left(t\right)\times {\varvec{r}}+{\varvec{g}}$$
(2)

Given the very limited test time (in the order of a few milliseconds) and a model weight as heavy as several dozen kilograms, the angular velocity can be assumed to be small (\({\varvec{\omega}}\left(t\right)\approx 0\)).

Thus, the centrifugal acceleration term should be

$${\varvec{\omega}}\left(t\right)\times{\varvec{\omega}}\left(t\right)\times {\varvec{r}}\approx 0$$
(3)

Since the variation in model attitude was ignorable (\({\varvec{\omega}}\left(t\right)\approx 0\)), the gravitational acceleration \({\varvec{g}}\) can be regarded as constant during the test period. Besides, the accelerometers are of differential type (AC-response accelerometer such as a piezoelectric type), making it possible to ignore the gravitational effects. From the above, Eq. (2) can be hence rewritten as follows.

$${A}_{P}\left(t\right)={A}_{0}\left(t\right)+\dot{\omega }\left(t\right)\times r$$
(4)

From Eq. (4), only translational and angular accelerations are included in the measured acceleration values.

3.2 Calculation of multi-component force for the overdetermined system

As mentioned in Sect. 2, two accelerometers per axis are theoretically required to measure moments with single-axis accelerometers. Since translational force can be measured simultaneously with moments, at least six accelerometers are necessary to determine the six-degree of freedom motion. However, actual instrumentation generally requires more accelerometers because of the issues described in Sect. 2. Consequently, the measurement system becomes an overdetermined system, which is solved using linear regression theory.

For a measurement system with N accelerometers, Eq. (4) can be expressed as the following matrix from Eq. (5).

$$\begin{gathered} \left\{ A \right\} = \left[ R \right]\left\{ v \right\} \hfill \\ \quad \left\{ A \right\} = \left\{ {\begin{array}{*{20}c} {a_{1} } \\ \quad {a_{2} } \\ \quad \vdots \\ \quad {a_{n} } \\ \quad \end{array} } \right\}, \hfill \\ \quad \left[ R \right] = \left\{ {\begin{array}{*{20}c} {r_{x1} } \\ \quad {r_{x2} } \\ \quad \vdots \\ \quad {r_{xn} } \\ \quad \end{array} \begin{array}{*{20}c} {r_{y1} } \\ \quad {r_{y2} } \\ \quad \vdots \\ \quad {r_{yn} } \\ \quad \end{array} \begin{array}{*{20}c} {r_{z1} } \\ \quad {r_{z2} } \\ \quad \vdots \\ \quad {r_{zn} } \\ \quad \end{array} \begin{array}{*{20}c} { \delta_{x1} } \\ \quad { \delta_{x2} } \\ \quad \vdots \\ \quad { \delta_{xn} } \\ \quad \end{array} \begin{array}{*{20}c} {\delta_{y1} } \\ \quad {\delta_{y2} } \\ \quad \vdots \\ \quad {\delta_{yn} } \\ \quad \end{array} \begin{array}{*{20}c} {\delta_{z1} } \\ \quad {\delta_{z2} } \\ \quad \vdots \\ \quad {\delta_{Zn} } \\ \quad \end{array} } \right\}, \hfill \\ \quad \left\{ v \right\} = \left\{ {\begin{array}{*{20}c} {\dot{\omega }_{x} } \\ \quad {\dot{\omega }_{y} } \\ \quad {\dot{\omega }_{z} } \\ \quad {a_{x} } \\ \quad {a_{y} } \\ \quad {a_{z} } \\ \quad \end{array} } \right\} \hfill \\ \quad \end{gathered}$$
(5)

The coefficient matrix \([R]\) expresses the values representing the position \({\varvec{r}}\) and sensing direction \(\delta\) of the accelerometers. Subscripts \(x\), \(y\), and \(z\) represent the axial, normal, and side directions, respectively. For the six degrees of freedom, \(\left\{v\right\}\) represents translational accelerations (axial, normal, and side) and angular acceleration (rolling, pitching, and yawing) of each axis at the center of rotation (the center of gravity) of the model. The sensing axes \({\delta }_{x}\), \({\delta }_{y}\), and \({\delta }_{z}\) are defined as follows.

$$\begin{gathered} x - {\text{direction}}: \{ \delta_{xn} ,\delta_{yn} ,\delta_{zn} \} = \left\{ {\begin{array}{*{20}c} {1,0,0\} } \\ \end{array} } \right. \hfill \\ y - {\text{direction}}: \{ \delta_{xn} ,\delta_{yn} ,\delta_{zn} \} = \left\{ {\begin{array}{*{20}c} {0,1,0\} } \\ \end{array} } \right. \hfill \\ z - {\text{direction}}:\{ \delta_{xn} ,\delta_{yn} ,\delta_{zn} \} = \left\{ {\begin{array}{*{20}c} {0,0,1\} } \\ \end{array} } \right. \hfill \\ \end{gathered}$$
(6)

For an arbitrary mounting direction, \(\delta\) can be adjusted -1 \(\le \delta \le\) 1.

Solving Eq. (5), the three-component force and \(\left\{v\right\}={\left\{\begin{array}{ccc}{\omega }_{x}& {\omega }_{y} {\omega }_{z} {a}_{x}& {a}_{y} {a}_{z}\end{array}\right\}}^{T}\) can be obtained. Since the matrix equation is an overdetermined system, and \(\left[R\right]\) is a singular matrix, no unique solution can be determined.

$${\left[R\right]}^{+}={\left({\left[R\right]}^{T}\left[R\right]\right)}^{-1}{\left[R\right]}^{T}$$
(7)

Introducing the pseudo-inverse matrix \({\left[\mathrm{R}\right]}^{+}\), \(\left\{v\right\}\) can be calculated as follows.

$$\left\{v\right\}={\left[R\right]}^{+}\left\{A\right\}$$
(8)

Since this method is based on least square regression, the variance in the measurement corresponds to normal distribution. Accordingly, the variance, or the precision, is reduced theoretically with 1/\(\sqrt{N-1}\) (\(N\) representing the number of accelerometers). However, some of the accelerometers were placed in an orthogonal direction, it should be noted that not all accelerometers have the scope to improve the variance.

This method has additional favorable features. The model’s mechanical vibration may not be damped within the test time for models without sufficient stiffness, impacting measurement precision. This method is expected to mitigate such vibrations through the averaging process with several accelerometers. Besides, since the method allows flexible relocation of the accelerometers to arbitrary locations, vibration can be reduced by placing the accelerometers appropriately (such as at vibration node points). However, precise prediction via finite element computations or pretests is needed to determine the optimum location.

4 Experimental setup

4.1 MoDKI model

During the free-flight test, the ‘Model of Demonstrator Kakuda Initiative (MoDKI),’ a fully integrated scramjet vehicle around 1.1 m long, was used. The standout feature is a scramjet underneath the fuselage. All the fuel injection and electric instruments were included onboard the scramjet model, including a gas-fuel tank and line, a fast-acting valve, data recorders, timers, and batteries. The dimension and onboard instruments of MoDKI are shown in Fig. 3 and Table 1, respectively. The model is made of aluminum alloy/YH75 (which resembles extra super duralumin A7075). This model is equipped with two magnetic stainless steel pads at the front and rear of the top and can be secured by electromagnets on the ceiling inside the shock tunnel’s test section.

Fig. 3
figure 3

a Drawings of the MoDKI and b onboard instruments

Full size image
Table 1 MoDKI dimensions
Full size table

An inert gas (Helium gas) injection test was conducted, and the standard operation of the total injection system was confirmed. The gas injection test results are excluded from this article.

4.2 Moment of inertia

The moment of inertia of MoDKI was measured with the two-support wires’ torsional pendulum.

As shown in Fig. 4, the MoDKI model is suspended by two parallel threads and oscillates the vertical axis when twisted. The moment of inertia \(J\) can be calculated by the frequency \(f\) of this vibration measured.

Fig. 4
figure 4

Schematic of two-support wires vertical-axis torsional pendulum

Full size image
$$J=\frac{mgab}{4{\pi }^{2}{f}^{2}l}$$
(9)

While \(m\) is the mass of the model, \(a\), \(b\) represents the distance between each suspension wire from the center of the mass, and \(l\) is the length of the suspension wire.

4.3 Onboard sensors and data recorders

For the surface pressure measurement, MoDKI has seven pressure transducers that were flush-mounted on the model surface. They were piezoresistive type XCQ-093 or XCL-072 (Kulite Semiconductor Products Inc.), and their locations are shown in Fig. 5 and Table 2. For the force measurement, eight accelerometers were instrumented: the piezoelectric miniature single-axis accelerometer PCB352C65 (PCB Piezoelectronics, Inc.), which has a resonant frequency less than 35 kHz. Four of the eight accelerometers are arranged in the X-axis direction and the remainder in the Z-axis direction. The positions and sensing axis of the test series accelerometers are shown in Fig. 5 and Table 3 (the sensing axis is shown in parentheses to the right of each accelerometer number). The location uncertainty depends on the machining accuracy and is less than 0.05 mm in this model.

Fig. 5
figure 5

Location of the accelerometers and pressure transducers mounted in MoDKI

Full size image
Table 2 Pressure transducer location
Full size table
Table 3 Accelerometer location
Full size table

An onboard miniature data recorder is the critical technology for the present free-flight onboard measurements. In this study, two JAXA original data recorders (Tanno et al. 2014) were onboard in MoDKI, which records at a sampling rate of 500 kHz with a 16-bit resolution. A total of 16 channels were used, 8 each for piezoelectric sensors (accelerometers) and piezoresistive sensors (pressure transducers). The recorder’s total measurement time is 800 ms, which sufficed to capture the entire test period.

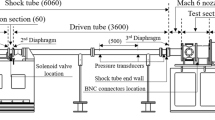
4.4 HIEST (High-Enthalpy Shock Tunnel)

Figure 6 shows an overview of HIEST, a free-piston shock tunnel operated by JAXA Kakuda Space Center, which can be used to test aerodynamic models up to 50 cm long and scramjet models up to 3 m long. Due to the tuned operation (Itoh et al. 1998), the facility can produce high enthalpy and high Reynolds number flow with a comparatively long test time. Low-enthalpy conditions were used in the present study, equivalent to the flight conditions approximately at Mach 8. Figure 7 shows an example of pressure traces (stagnation pressure, free-stream Pitot pressure) and heat-flux measured with hemisphere probe (radius 10 mm). HIEST test airflow conditions were calculated using the JAXA axisymmetric nozzle flow code (Takahashi et al. 2009), and the calculated free-stream parameters are shown in Table 4.

Fig. 6
figure 6

Free-piston shock tunnel HIEST

Full size image
Fig. 7
figure 7

Example of traces; stagnation pressure (shock tube end pressure), free-stream Pitot pressure, and a hemisphere (10 mm radius) probe heat-flux at the current condition

Full size image
Table 4 HIEST test airflow conditions
Full size table

4.5 Test procedure

Figure 8 shows an image of the free-flight test procedure. In the initial status, MoDKI was held to the HIEST test section ceiling with two electromagnets. The model was released, deactivating the electromagnets 400 ms before the test flow arrival. The model release trigger was adjusted to position the free-falling model at the nozzle core flow during the test time. Since the onboard data recorder is pre-triggered, the pressure and acceleration histories were recorded throughout the entire test duration. Finally, the model drops onto the shock-absorbing catcher and is retrieved for data transfer from the data recorders to the host PC. Figure 9 shows a photograph of MoDKI installed on the HIEST test section ceiling and a high-speed camera image of MoDKI during free flight.

Fig. 8
figure 8

Image of the free-flight procedure

Full size image
Fig. 9
figure 9

a MoDKI installed on the HIEST test section ceiling. b Free-flying MoDKI during free flight

Full size image

The exact angle of attack during the test time was monitored with an optical technique (Laurence 2012), which adopted Schlieren images taken with the high-speed camera (SHIMADZU Hypervision), and the model angle of attack was measured for each shot. The AOA (angle of attack) varied from 0.7 to 3.4 degrees in the current test series. The test-to-test variation in measured AOA was \(\pm\) 0.5 from the targeted angle.

5 Results and discussion

5.1 Pressure history

Figure 10 shows an example of the model surface pressure traces. The surface pressure traces’ starting process shows a gentle slope compared to the free-stream Pitot pressure trace (shown in Fig. 7) due to the flow establishment process of the model. The traces show virtually constant pressure from t = 2 to 6 ms. The four milliseconds duration was hence defined as the test time.

Fig. 10
figure 10

Example of surface pressure histories

Full size image

5.2 Aerodynamic characteristics of the MoDKI model

As described in Sect. 4.3, the number of accelerometers was thus limited to eight due to the onboard data recorder’s available channels. The measurement was limited to the three degrees of freedom (namely, three components), and components of the matrices are reduced as follows:

$$\begin{gathered} \left\{ A \right\} = \left[ R \right]\left\{ v \right\} \hfill \\ \quad \left\{ A \right\} = \left\{ {\begin{array}{*{20}c} {a_{1} } \\ \quad {a_{2} } \\ \quad {a_{3} } \\ \quad {a_{4} } \\ \quad {a_{5} } \\ \quad {a_{6} } \\ \quad {a_{7} } \\ \quad {a_{8} } \\ \quad \end{array} } \right\}, \hfill \\ \quad \left[ R \right] = \left\{ {\begin{array}{*{20}c} {r_{1} } \\ \quad {r_{2} } \\ \quad {r_{3} } \\ \quad {r_{4} } \\ \quad {r_{5} } \\ \quad {r_{6} } \\ \quad {r_{7} } \\ \quad {r_{8} } \\ \quad \end{array} \begin{array}{*{20}c} { \delta_{x1} } \\ \quad {\delta_{x2} } \\ \quad {\delta_{x3} } \\ \quad {\delta_{x4} } \\ \quad {\delta_{x5} } \\ \quad {\delta_{x6} } \\ \quad {\delta_{x7} } \\ \quad {\delta_{x8} } \\ \quad \end{array} \begin{array}{*{20}c} {\delta_{z1} } \\ \quad {\delta_{z2} } \\ \quad {\delta_{z3} } \\ \quad {\delta_{z4} } \\ \quad {\delta_{z5} } \\ \quad {\delta_{z6} } \\ \quad {\delta_{z7} } \\ \quad {\delta_{z8} } \\ \quad \end{array} } \right\}, \hfill \\ \quad \left\{ v \right\} = \left\{ {\begin{array}{*{20}c} {\dot{\omega }_{y} } \\ \quad {a_{x} } \\ \quad {a_{z} } \\ \quad \end{array} } \right\} \hfill \\ \quad \end{gathered}$$
(10)

By applying the data reduction process above, bidirectional translational accelerations (X and Z-axes) and angular acceleration around the Y-axis (in pitch direction) were calculated.

$${F}_{D}=m\left({a}_{x}cos\theta +{a}_{z}sin\theta \right)$$
(11)
$${F}_{L}=m\left({a}_{z}cos\theta -{a}_{x}sin\theta \right)$$
(12)
$${M}_{y}=J{\dot{\omega }}_{y}$$
(13)

From the products of mass and three accelerations calculated above, drag force \({F}_{D}\), lift force \({F}_{L}\), and pitching moment \({M}_{y}\) can be obtained. Since the current coordinate is the body axis system, the axial and normal force should be converted to drag and lift force as the above equations Eq. (11)–(13), where theta is the angle of attack and \(J\) is the moment of inertia determined in Sect. 4.2.

$${C}_{D}=\frac{{F}_{D}}{\frac{1}{2}{\rho }_{\infty }{{U}_{\infty }}^{2}S}$$
(14)
$${C}_{L}=\frac{{F}_{L}}{\frac{1}{2}{\rho }_{\infty }{{U}_{\infty }}^{2}S}$$
(15)
$${C}_{M}=\frac{{M}_{y}}{\frac{1}{2}{\rho }_{\infty }{{U}_{\infty }}^{2} SL}$$
(16)

The representative length \(L\) is the total length of the model in the longitudinal direction. The representative area \(S\) is that of the front cross section, which was calculated from CAD data. An example of the traces of the three-component aerodynamic coefficients is shown in Fig. 11. The traces were filtered with a Fourier filter with a cutoff frequency of 367 Hz (time constant 2.7 ms). Low-frequency oscillation remains in the pitching moment trace, which may result from the model’s primary bending mode. However, the coefficients appear constant throughout the test time.

Fig. 11
figure 11

An example of the measured aerodynamic coefficients. a Drag coefficient, b Lift coefficient, and c Pitching moment coefficient

Full size image

Averaging the traces of the coefficients over the defined test time (2–6 ms), eleven data sets were obtained. These data sets are plotted in Figs. 12 and 13 to show the relationship between the angle of attack and aerodynamic coefficients and lift-drag ratio. A 95% prediction interval band is overlapped as a hatch area on each coefficient line to show each measurement’s precision. The standard deviation of all the aerodynamic coefficients at the present data set (degrees of freedom was ten) is summarized in Table 5.

Fig. 12
figure 12

The relationship between the model angle of attack and aerodynamic coefficient. a Drag coefficient, b Lift coefficient, and c Pitching moment coefficient

Full size image
Fig. 13
figure 13

The relationship between the model angle of attack and the lift-drag ratio

Full size image
Table 5 The standard deviation of the current measurement
Full size table

In Fig. 12 (a, b), drag and lift coefficients show positive linear relationships with the angle of attack from 0.7 to 3.4 degrees. In Fig. 12(c), \({C}_{M}\) also increased in line with the angle of attack, making the model aerodynamically unstable. However, this is particular to the current model, in which the center of gravity is shifted downstream due to the batteries’ location in the aft of the model.

6 Conclusion

In this study, the three-component aerodynamic coefficients (Drag, Lift, and Pitching moment) of an airframe-engine integrated scramjet vehicle model MoDKI were successfully obtained in the free-piston shock tunnel HIEST. A free-flight force measurement technique was also adopted. A new analytical method was developed for multiple single-axis piezoelectric accelerometers based on an overdetermined system analysis. The current approach itself is not novel because it is based on general linear regression theory. However, a unique assumption, which is satisfied under short measurement time, heavy model, and differential-type (piezoelectric type) accelerometers, successfully simplified the dynamic equation of motion. The method allows multi-component forces and moments to be measured with a straightforward calculation using several single-axis accelerometers. It improves uncertainties originating from the measurement variability of each acceleration. Moreover, it also mitigates the troublesome issues for positioning accelerometers and may circumvent interference with the model’s natural vibrations. Despite the relatively limited applicable scope (short-duration tests), the method should help free-flight force measurement in impulsive facilities.