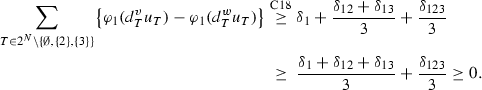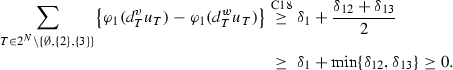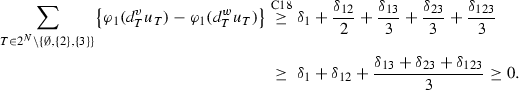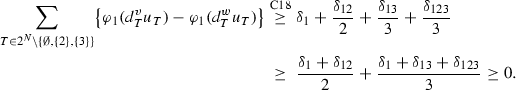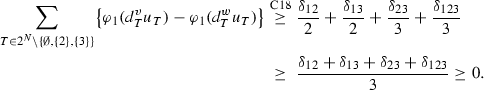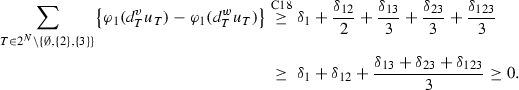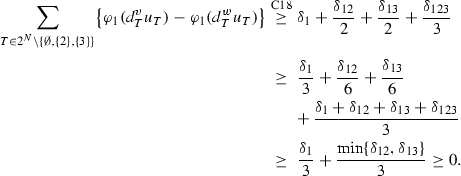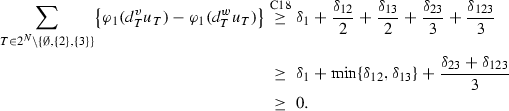Abstract
The purpose of this study is to provide a comprehensive characterization of linear solutions to cooperative games by using monotonicity. A monotonicity axiom states an increase in certain parameters of a game as a hypothesis and states an increase in a player’s payoff as a conclusion. We focus on various parameters of a game and introduce new axioms. Combined with previous results, we prove that efficiency, symmetry and a monotonicity axiom characterize (i) four linear solutions in the literature, namely, the Shapley value, the equal division value, the CIS value and the ENSC value, and (ii) a class of solutions obtained by taking a convex combination of the above solutions. Our methodological contribution is to provide a new linear algebraic approach for characterizing solutions by monotonicity. Using a new basis of the linear space of TU games, we identify a class of games in which a solution that satisfies monotonicity is linear. Our approach provides some intuition for why monotonicity implies linearity.
Similar content being viewed by others
Notes
We denote a singleton set \(\{i\}\) simply by i.
This solution is also called the \(\alpha \)-egalitarian Shapley value (Joosten 1996).
When \(\alpha =1/2\), \(\varPsi ^\alpha \) coincides with the consensus value by Ju et al. (2007).
For example, in public good provision problems (Moulin 1995, Chapter 5), the voluntary participation axiom states that a player should receive no less than his individual worth.
By our characterization results, a solution in a column does not satisfy the axiom with an empty cell.
See, for example, Theorem 1.42 of Sundaram (1996).
Sp is an abbreviation of Span. Mathematically speaking, \(\text {Sp}(V)\) is the linear subspace in \({\mathbb {R}}^{2^n-1}\) spanned by the vectors in V.
We can prove \(\psi _3(u_1-u_2)=0\) in the following way: by efficiency and symmetry, \(\psi _3({\mathbf {0}})=0\), and by \(cont+gr+sur\)-monotonicity, \(\psi _3({\mathbf {0}})=\psi _3(u_1-u_2)\).
Note that \((u^1+u^2)(i)=(u^1+u^2)(j)\) for all \(i,j\in N\) and \({\bar{u}}_T(i)=0\) for all \(T\subseteq N\), \(|T|\ge 3\), \(i\in N\).
The coefficient \(d^v_T\) is called the dividend of T.
References
Casajus A (2015) Monotonic redistribution of performance-based allocations: a case for proportional taxation. Theor Econ 10(3):887–892
Casajus A, Huettner F (2013) Null players, solidarity, and the egalitarian Shapley values. J Math Econ 49(1):58–61
Casajus A, Huettner F (2014) Weakly monotonic solutions for cooperative games. J Econ Theory 154:162–172
Driessen T, Funaki Y (1991) Coincidence of and collinearity between game theoretic solutions. OR Spektrum 13(1):15–30
Joosten R (1996) Dynamics, equilibria and values. Dissertation, Maastricht University
Ju Y, Borm P, Ruys P (2007) The consensus value: a new solution concept for cooperative games. Soc Choice Welf 28(4):685–703
Moulin H (1995) Cooperative microeconomics: a game theoretic approach. Prentice Hall, Englewood Cliffs
Oishi T, Nakayama M, Hokari T, Funaki Y (2016) Duality and anti-duality in TU games applied to solutions, axioms, and axiomatizations. J Math Econ 63:44–53
Pintér M (2015) Young’s characterization of the Shapley value: a new proof. Ann Oper Res 235(1):665–673
Shapley LS (1953) A value for n-person games. In: Roth AE (ed) The Shapley value. Cambridge University Press, Cambridge, pp 41–48
Sundaram RK (1996) A first course in optimization theory. Cambridge University Press, Cambridge
van den Brink R (2007) Null or nullifying players: the difference between the Shapley value and equal division solutions. J Econ Theory 136(1):767–775
van den Brink R, Funaki Y (2009) Axiomatizations of a class of equal surplus sharing solutions for TU-games. Theory Decis 67(3):303–340
van den Brink R, Funaki Y, Ju Y (2013) Reconciling marginalism with egalitarianism: consistency, monotonicity, and implementation of egalitarian Shapley values. Soc Choice Welf 40(3):693–714
Yokote K, Funaki Y (2014) Several bases of a game space and an application to the Shapley value. Institute of Research in Contemporary Political and Economic Affairs Working Paper No.E1419, Waseda University. http://www.waseda.jp/fpse/winpec/en/public/working-paper/. Accessed 20 April 2017
Yokote K, Funaki Y (2015) Weak Surplus Monotonicity characterizes convex combination of egalitarian Shapley value and Consensus value. Institute of Research in Contemporary Political and Economic Affairs Working Paper No.E1504, Waseda University. http://www.waseda.jp/fpse/winpec/en/public/working-paper/. Accessed 20 April 2017
Young HP (1985) Monotonic solutions of cooperative games. Int J Game Theory 14(2):65–72
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors thank an associate editor and anonymous referees for their valuable comments and suggestions. This work was supported by JSPS KAKENHI Grant Numbers JP26380247, JP23530231, JP24220033, JP26245026.
Appendix
Appendix
The purpose of this appendix is to introduce a solution \(\varphi \) for \(n=3\) that satisfies efficiency, symmetry, \(cont+sur\)-monotonicity, but is not a convex combination of linear solutions. Since \(cont+sur\)-monotonicity is stronger than \(cont+gr+sur\)-monotonicity, this solution is a counterexample to Theorems 1 and 2 for \(n=3\).
Let \(N=\{1,2,3\}\). We first focus on the unanimity games. For \(\lambda \in {\mathbb {R}}\) and \(T\subseteq N\), \(T\ne \emptyset \), we define \(\varphi (\lambda u_T)\) as follows:
Since \(\{u_T\}_{\emptyset \ne T\subseteq N}\) is a basis of \(\varGamma \), we can uniquely express \(v\in \varGamma \) as a linear combination of \(\{u_T\}_{\emptyset \ne T\subseteq N}\). Let \(\{d^v_T\}_{\emptyset \ne T\subseteq N}\) denote the coefficients in the linear combination.Footnote 10 We define \(\varphi \) for a general game \(v\in \varGamma \) as follows:
Let \(v,w\in \varGamma \) be games such that \(\varDelta _1v(S) \ge \varDelta _1w(S)\) for all \(S\subseteq N\backslash 1\) and \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N}w(i)\). Our goal is to prove that
For each \(T\subseteq N\), \(T\ne \emptyset \), let \(\delta _T=d^v_T-d^w_T\). We provide a claim that immediately follows from the definition of \(\varphi \).
Claim 18
The following two statements hold :
-
(i)
Let \(i\in N\backslash \{1\}\). If \(\delta _{1i}\ge 0,\) then \(\varphi _1(d^v_{1i}u_{1i})-\varphi _1(d^w_{1i}u_{1i})\ge \frac{\delta _{1i}}{3}\). If \(\delta _{1i}\le 0,\) then \(\varphi _1(d^v_{1i}u_{1i})-\varphi _1(d^w_{1i}u_{1i})\ge \frac{\delta _{1i}}{2}\).
-
(ii)
If \(\delta _{23}\ge 0,\) then \(\varphi _1(d^v_{23}u_{23})-\varphi _1(d^w_{23}u_{23})\ge 0\). If \(\delta _{23}\le 0,\) then \(\varphi _1(d^v_{23}u_{23})-\varphi _1(d^w_{23}u_{23})\ge \frac{\delta _{23}}{3}\).
In what follows, Claim 18 is abbreviated as C18.
If \(\delta _1<0\), then \(v(1)<w(1)\), which is a contradiction with \(\varDelta _1 v(S)\ge \varDelta _1 w(S)\) for all \(S\subseteq N\backslash 1\). Thus, \(\delta _1\ge 0\). Depending on the signs of \(\delta _{12}\), \(\delta _{13}\), \(\delta _{23}\) and \(\delta _{123}\), we consider 16 cases.
If \(\delta _T\ge 0\) for all \(T\subseteq N\), \(|T|\ge 2\), then \(\varphi _1(v)\ge \varphi _1(w)\) immediately holds. If \(\delta _T<0\) for all \(T\subseteq N\), \(|T|\ge 2\), we obtain a contradiction with \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N} w(i)\). In what follows, we consider other 14 cases.
-
Case 1: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\), we must have \(\delta _1\ge -\delta _{12}\). Then,
$$\begin{aligned} \sum _{T\in 2^N\backslash \{\emptyset , \{2\}, \{3\}\}}\bigl \{\varphi _1(d^v_T u_T)-\varphi _1(d^w_T u_T)\bigr \}\mathop {\ge }\limits ^{\text {C18}} \delta _1+\frac{\delta _{12}}{2} \ge \delta _1+\delta _{12} \ge 0. \end{aligned}$$ -
Case 2: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
This case can be proved in the same way as Case 1.
-
Case 3: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<0\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
In order that \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N}w(i)\), we must have \(\delta _{12}+\delta _{13} +\delta _{123}\ge -\delta _{23}\). Then,
$$\begin{aligned} \sum _{T\in 2^N\backslash \{\emptyset , \{2\}, \{3\}\}}\bigl \{\varphi _1(d^v_T u_T)-\varphi _1(d^w_T u_T)\bigr \} \mathop {\ge }\limits ^{\text {C18}} \frac{\delta _{12}+\delta _{13}+\delta _{123}}{3}+\frac{\delta _{23}}{3} \ge 0. \end{aligned}$$ -
Case 4: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
In order that \(v(N)-v(23)\ge w(N)-w(23)\), we must have \(\delta _1+\delta _{12}+\delta _{13}\ge -\delta _{123}\). Then,
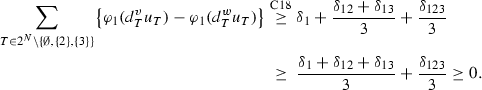
-
Case 5: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\) and \(v(13)-v(3)\ge w(13)-w(3)\), we must have \(\delta _1\ge -\min \{\delta _{12}, \delta _{13}\}\). Then,
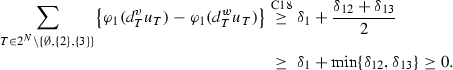
-
Case 6: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\), we must have \(\delta _1\ge -\delta _{12}\). In order that \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N} w(i)\), we must have \(\delta _{13} +\delta _{123}\ge -\delta _{12}-\delta _{23}\ge -\delta _{23}\). Then,
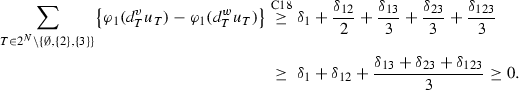
-
Case 7: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}< \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
This case can be proved in the same way as Case 6.
-
Case 8: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\) and \(v(N)-v(23)\ge w(N)-w(23)\), we must have \(\delta _1\ge -\delta _{12}\) and \(\delta _{1}+\delta _{13}\ge -\delta _{12}-\delta _{123}\ge -\delta _{123}\). Then,
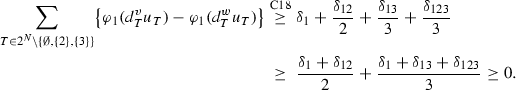
-
Case 9: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}< \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
This case can be proved in the same way as Case 8.
-
Case 10: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
In order that \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N} w(i)\), we must have \(\delta _{12} +\delta _{13}\ge -\delta _{23}-\delta _{123}\). Then,
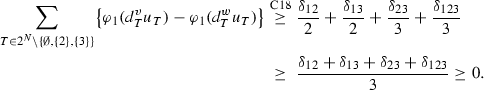
-
Case 11: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\), we must have \(\delta _1\ge -\delta _{12}\). In order that \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N} w(i)\), we must have \(\delta _{13}\ge -\delta _{12} -\delta _{23}-\delta _{123}\ge -\delta _{23}-\delta _{123}\). Then,
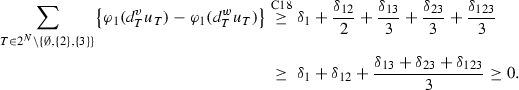
-
Case 12: \({\varvec{\delta }}_{\mathbf{12}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
This case can be proved in the same way as Case 11.
-
Case 13: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}\ge \mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}<\mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\) and \(v(13)-v(3)\ge w(13)-w(3)\), we must have \(\delta _1\ge -\min \{\delta _{12}, \delta _{13}\}\). In order that \(v(N)-v(23)\ge w(N)-w(23)\), we must have \(\delta _1\ge -\delta _{12}-\delta _{13}-\delta _{123}\). Then,
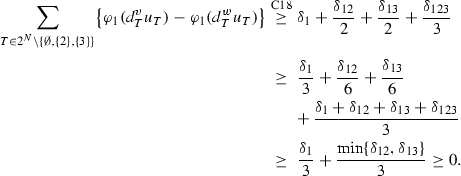
-
Case 14: \({\varvec{\delta }}_{\mathbf{12}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{13}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{23}}<\mathbf{0}\), \({\varvec{\delta }}_{\mathbf{123}}\ge \mathbf{0}\).
In order that \(v(12)-v(2)\ge w(12)-w(2)\) and \(v(13)-v(3)\ge w(13)-w(3)\), we must have \(\delta _1\ge -\min \{\delta _{12}, \delta _{13}\}\). In order that \(v(N)-\sum _{i\in N} v(i)\ge w(N)-\sum _{i\in N} w(i)\), we must have \(\delta _{123}\ge -\delta _{12} -\delta _{13}-\delta _{23}\ge -\delta _{23}\). Then,
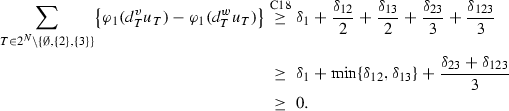
Rights and permissions
About this article
Cite this article
Yokote, K., Funaki, Y. Monotonicity implies linearity: characterizations of convex combinations of solutions to cooperative games. Soc Choice Welf 49, 171–203 (2017). https://doi.org/10.1007/s00355-017-1056-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-017-1056-6