Trefftz-unsymmetric finite element for bending analysis of orthotropic plates

Abstract

This work develops a new four-node quadrilateral displacement-based Trefftz-type plate element for bending analysis of orthotropic plates within the framework of the unsymmetric finite element method (FEM). In the present formulation, the modified isoparametric interpolations are employed to formulate the element’s test functions in which the deflection is effectively enriched by the nodal rotation degrees of freedom (DOFs). Meanwhile, the element’s trial functions are determined based on the Trefftz functions that can a prior satisfy the governing equations of orthotropic Mindlin–Reissner plates. Numerical benchmark tests reveal that the new unsymmetric plate element is free of shear locking problem and can produce satisfactory results for both the displacement and stress resultant. In particular, it exhibits quite good tolerances to the gross mesh distortion.

Appendix

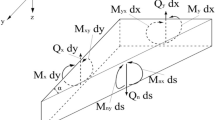
This section provides the detailed calculations of the matrices ${{\varvec{\uplambda}}}$, ${{\varvec{\Lambda}}}$ and ${{\varvec{\upchi}}}$ shown in Eq. (29). The components of ${{\varvec{\uplambda}}}$ can be expressed as:

$$ {{\varvec{\uplambda}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\uplambda}}}^{w} } \\ {{{\varvec{\uplambda}}}^{\phi } } \\ \end{array} } \right], $$

(37)

in which the first part ${{\varvec{\uplambda}}}^{w}$ is

$$ {{\varvec{\uplambda}}}^{w} = \left[ {\begin{array}{*{20}c} {w^{0}_{1} \left( {x_{1} ,y_{1} } \right)} & {w^{0}_{2} \left( {x_{1} ,y_{1} } \right)} & {w^{0}_{3} \left( {x_{1} ,y_{1} } \right)} & {\ldots} & {w^{0}_{12} \left( {x_{1} ,y_{1} } \right)} \\ {w^{0}_{1} \left( {x_{2} ,y_{2} } \right)} & {w^{0}_{2} \left( {x_{2} ,y_{2} } \right)} & {w^{0}_{3} \left( {x_{2} ,y_{2} } \right)} & {\ldots} & {w^{0}_{12} \left( {x_{2} ,y_{2} } \right)} \\ {w^{0}_{1} \left( {x_{3} ,y_{3} } \right)} & {w^{0}_{2} \left( {x_{3} ,y_{3} } \right)} & {w^{0}_{3} \left( {x_{3} ,y_{3} } \right)} & {\ldots} & {w^{0}_{12} \left( {x_{3} ,y_{3} } \right)} \\ {w^{0}_{1} \left( {x_{4} ,y_{4} } \right)} & {w^{0}_{2} \left( {x_{4} ,y_{4} } \right)} & {w^{0}_{3} \left( {x_{4} ,y_{4} } \right)} & {\ldots} & {w^{0}_{12} \left( {x_{4} ,y_{4} } \right)} \\ \end{array} } \right], $$

(38)

while ${{\varvec{\uplambda}}}^{\phi }$ is obtained by

$$ {{\varvec{\uplambda}}}^{\phi } = {\mathbf{T}}_{n} {{\varvec{\Phi}}}, $$

(39)

in which

$$ ~{\mathbf{\Phi }} = \left[ {\begin{array}{*{20}c} {\psi _{{x1}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} & {\psi _{{x2}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} & \ldots & {\psi _{{x12}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} \\ {\psi _{{y1}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} & {\psi _{{y2}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} & \ldots & {\psi _{{y12}}^{0} \left( {x_{{A1}} ,y_{{A1}} } \right)} \\ \ldots & \ldots & {} & \ldots \\ {\psi _{{x1}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} & {\psi _{{x2}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} & \ldots & {\psi _{{x12}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} \\ {\psi _{{y1}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} & {\psi _{{y2}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} & \ldots & {\psi _{{y12}}^{0} \left( {x_{{B4}} ,y_{{B4}} } \right)} \\ \end{array} } \right], $$

(40)

$$ {\mathbf{T}}_{n} = \left[ {\begin{array}{*{20}c} {{\mathbf{T}}_{1} } & {} & {} & {} \\ {} & {{\mathbf{T}}_{2} } & {} & {} \\ {} & {} & {{\mathbf{T}}_{3} } & {} \\ {} & {} & {} & {{\mathbf{T}}_{4} } \\ \end{array} } \right], $$

(41)

with

$$ {\mathbf{T}}_{i} = \left[ {\begin{array}{*{20}c} {l_{ij} } & {m_{ij} } & {} & {} \\ {} & {} & {l_{ij} } & {m_{ij} } \\ \end{array} } \right],\;\;\left( {ij = 12,\;23,\;34,\;41} \right), $$

(42)

where $l_{ij}$ and $m_{ij}$ are the direction cosines of the element edge ij.

The matrix ${{\varvec{\Lambda}}}$ can also be divided into two parts as follows:

$$ {{\varvec{\Lambda}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\Lambda}}}^{w} } \\ {{{\varvec{\Lambda}}}^{\phi } } \\ \end{array} } \right], $$

(43)

in which the first part is

$$ {{\varvec{\Lambda}}}^{w} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & 1 & 0 & 0 & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & 1 & 0 & 0 & {} & {} & {} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & 1 & 0 & 0 \\ \end{array} } \right], $$

(44)

while the second part can be calculated by:

$$ {{\varvec{\Lambda}}}^{\phi } = \left[ {\begin{array}{*{20}c} {{{\varvec{\Lambda}}}_{11}^{\phi } } & {{{\varvec{\Lambda}}}_{12}^{\phi } } & {} & {} \\ {} & {{{\varvec{\Lambda}}}_{22}^{\phi } } & {{{\varvec{\Lambda}}}_{23}^{\phi } } & {} \\ {} & {} & {{{\varvec{\Lambda}}}_{33}^{\phi } } & {{{\varvec{\Lambda}}}_{34}^{\phi } } \\ {{{\varvec{\Lambda}}}_{41}^{\phi } } & {} & {} & {{{\varvec{\Lambda}}}_{44}^{\phi } } \\ \end{array} } \right], $$

(45)

with

$$ {{\varvec{\Lambda}}}_{11}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{12} }}\left( {1 - s_{A1} } \right)y_{12} } & {\frac{1}{{l_{12} }}\left( {1 - s_{A1} } \right)x_{12} } \\ 0 & { - \frac{1}{{l_{12} }}\left( {1 - s_{B1} } \right)y_{12} } & {\frac{1}{{l_{12} }}\left( {1 - s_{B1} } \right)x_{12} } \\ \end{array} } \right],\;\;{{\varvec{\Lambda}}}_{12}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{12} }}s_{A1} y_{12} } & {\frac{1}{{l_{12} }}s_{A1} x_{12} } \\ 0 & { - \frac{1}{{l_{12} }}s_{B1} y_{12} } & {\frac{1}{{l_{12} }}s_{B1} x_{12} } \\ \end{array} } \right], $$

(46)

$$ {{\varvec{\Lambda}}}_{22}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{23} }}\left( {1 - s_{A2} } \right)y_{23} } & {\frac{1}{{l_{23} }}\left( {1 - s_{A2} } \right)x_{23} } \\ 0 & { - \frac{1}{{l_{23} }}\left( {1 - s_{B2} } \right)y_{23} } & {\frac{1}{{l_{23} }}\left( {1 - s_{B2} } \right)x_{23} } \\ \end{array} } \right],\;\;{{\varvec{\Lambda}}}_{23}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{23} }}s_{A2} y_{23} } & {\frac{1}{{l_{23} }}s_{A2} x_{23} } \\ 0 & { - \frac{1}{{l_{23} }}s_{B2} y_{23} } & {\frac{1}{{l_{23} }}s_{B2} x_{23} } \\ \end{array} } \right], $$

(47)

$$ {{\varvec{\Lambda}}}_{33}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{34} }}\left( {1 - s_{A3} } \right)y_{34} } & {\frac{1}{{l_{34} }}\left( {1 - s_{A3} } \right)x_{34} } \\ 0 & { - \frac{1}{{l_{34} }}\left( {1 - s_{B3} } \right)y_{34} } & {\frac{1}{{l_{34} }}\left( {1 - s_{B3} } \right)x_{34} } \\ \end{array} } \right],\;\;{{\varvec{\Lambda}}}_{34}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{34} }}s_{A3} y_{34} } & {\frac{1}{{l_{34} }}s_{A3} x_{34} } \\ 0 & { - \frac{1}{{l_{34} }}s_{B3} y_{34} } & {\frac{1}{{l_{34} }}s_{B3} x_{34} } \\ \end{array} } \right], $$

(48)

$$ {{\varvec{\Lambda}}}_{44}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{41} }}\left( {1 - s_{A4} } \right)y_{41} } & {\frac{1}{{l_{41} }}\left( {1 - s_{A4} } \right)x_{41} } \\ 0 & { - \frac{1}{{l_{41} }}\left( {1 - s_{A4} } \right)y_{41} } & {\frac{1}{{l_{41} }}\left( {1 - s_{A4} } \right)x_{41} } \\ \end{array} } \right],\;\;{{\varvec{\Lambda}}}_{41}^{\phi } = \left[ {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{41} }}s_{A4} y_{41} } & {\frac{1}{{l_{41} }}s_{A4} x_{41} } \\ 0 & { - \frac{1}{{l_{41} }}s_{B4} y_{41} } & {\frac{1}{{l_{41} }}s_{B4} x_{41} } \\ \end{array} } \right], $$

(49)

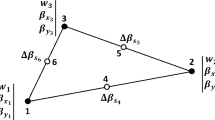
where $S_{Ai}$ and $S_{Bi}$ are illustrated as shown in Fig. 3.

Finally, the matrix ${{\varvec{\upchi}}}$ is given by:

$$ {{\varvec{\upchi}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\upchi}}}^{w} } \\ {{{\varvec{\upchi}}}^{\phi } } \\ \end{array} } \right], $$

(50)

with

$$ {{\varvec{\upchi}}}^{w} = \left[ {\begin{array}{*{20}c} {w^{*} \left( {x_{1} ,y_{1} } \right)} \\ {w^{*} \left( {x_{2} ,y_{2} } \right)} \\ {w^{*} \left( {x_{3} ,y_{3} } \right)} \\ {w^{*} \left( {x_{4} ,y_{4} } \right)} \\ \end{array} } \right], $$

(51)

$$ {{\varvec{\upchi}}}^{\phi } = {\mathbf{T}}_{n} {{\varvec{\Phi}}}^{*} , $$

(52)

in which ${\mathbf{T}}_{n}$ is also given by Eq. (41) and

$$ {{\varvec{\Phi}}}^{*} = \left[ {\begin{array}{*{20}c} {\psi_{x}^{*} \left( {x_{A1} ,y_{A1} } \right)} \\ {\psi_{y}^{*} \left( {x_{A1} ,y_{A1} } \right)} \\ {\ldots} \\ {\psi_{x}^{*} \left( {x_{B4} ,y_{B4} } \right)} \\ {\psi_{y}^{*} \left( {x_{B4} ,y_{B4} } \right)} \\ \end{array} } \right]. $$

(53)