Skip to main content
SpringerLink
Log in

Flapwise bending vibration analysis of a rotating double-tapered Timoshenko beam

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

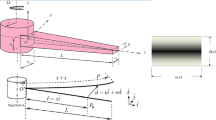
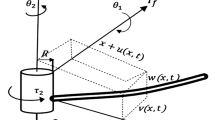
In this study, free vibration analysis of a rotating, double-tapered Timoshenko beam that undergoes flapwise bending vibration is performed. At the beginning of the study, the kinetic- and potential energy expressions of this beam model are derived using several explanatory tables and figures. In the following section, Hamilton’s principle is applied to the derived energy expressions to obtain the governing differential equations of motion and the boundary conditions. The parameters for the hub radius, rotational speed, shear deformation, slenderness ratio, and taper ratios are incorporated into the equations of motion. In the solution, an efficient mathematical technique, called the differential transform method (DTM), is used to solve the governing differential equations of motion. Using the computer package Mathematica the effects of the incorporated parameters on the natural frequencies are investigated and the results are tabulated in several tables and graphics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

cross-sectional area

b 0 :

beam breadth at the root section

c b :

breadth taper ratio

c h :

height taper ratio

E :

Young’s modulus

EA :

axial rigidity of the beam cross section

EI :

bending rigidity of the beam cross section

G :

shear modulus

h 0 :

beam height at the root section

\(\vec{i}, \vec{j}, \vec{k}\) :

unit vectors in the x, y, and z directions

I y :

second moment of inertia about the y axis

k :

shear correction factor

kAG :

shear rigidity

L :

beam length

P :

reference point after deformation

P 0 :

reference point before deformation

r :

inverse of the slenderness ratio S

\(\vec{r}_{0}\) :

position vector of P 0

\(\vec{r}_{1}\) :

position vector of P

R :

hub radius

S :

slenderness ratio

t :

time

T :

centrifugal force

u 0 :

axial displacement due to the centrifugal force

U b :

potential energy due to bending

U s :

potential energy due to shear

V x , V y , V z :

velocity components of point P

W[k], θ[k ]:

transformed functions

w :

flapwise bending displacement

w′:

flapwise bending slope

x :

spanwise coordinate

\(\bar{x}\) :

spanwise coordinate parameter

x0, y0, z0:

coordinates of P 0

x1, y1, z1:

coordinates of P

δ :

hub radius parameter

γ :

shear angle

\(\varepsilon_{0}\) :

uniform strain due to the centrifugal force

\(\varepsilon_{{ij}}\) :

classical strain tensor

\(\varepsilon_{{xx}}\) :

axial strain

\(\varepsilon_{{\eta \eta}}, \varepsilon_{{\xi \xi}}\) :

transverse normal strains

η :

sectional coordinate corresponding to major principal axis for P 0 on the elastic axis

μ :

natural frequency parameter

ξ :

sectional coordinate for P 0 normal to η axis at the elastic axis

ρ :

density of the blade material

ρA :

mass per unit length

θ :

rotation angle due to bending

ω :

circular natural frequency

Ω:

constant rotational speed

\(\bar{\Omega}\) :

rotational speed parameter

References

  1. Banerjee J.R. (2001). Dynamic stiffness formulation and free vibration analysis of centrifugally stiffened Timoshenko beams. J. Sound Vib. 247(1): 97–115

    Article  Google Scholar 

  2. Banerjee J.R. and Williams F.W. (1985). Exact Bernoulli–Euler dynamic stiffness matrix for a range of tapered beams. Int. J. Numer. Methods Eng. 21: 2289–2302

    Article  MATH  Google Scholar 

  3. Bazoune A. and Khulief Y.A. (1992). A finite beam element for vibration analysis of rotating tapered Timoshenko beams. J. Sound Vib. 156: 141–164

    Article  MATH  Google Scholar 

  4. Downs B. (1977). Transverse vibrations of cantilever beam having unequal breadth and depth tapers. ASME J. Appl. Mech. 44: 737–742

    Google Scholar 

  5. Eringen A.C. (1980). Mechanics of continua. Robert E. Krieger, Huntington

    Google Scholar 

  6. Grossi R.O. and Bhat R.B. (1991). A note on vibrating tapered beams. J. Sound Vib. 147: 174–178

    Article  Google Scholar 

  7. Hodges, D.H., Dowell, E.H.: Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades. NASA TN D-7818 (1974)

  8. Kaya M.O. (2006). Free vibration analysis of rotating Timoshenko beams by differential transform method. Aircr. Eng. Aerosp. Tech. 78(3): 194–203

    Article  Google Scholar 

  9. Khulief Y.A. and Bazoune A. (1992). Frequencies of rotating tapered Timoshenko beams with different boundary conditions. Comput. Struct. 42: 781–795

    Article  Google Scholar 

  10. Kim C.S. and Dickinson S.M. (1988). On the analysis of laterally vibrating slender beams subject to various complicating effects. J. Sound Vib. 122: 441–455

    Article  Google Scholar 

  11. Klein L. (1974). Transverse vibrations of non-uniform beam. J. Sound Vib. 37: 491–505

    Article  Google Scholar 

  12. Lau J.H. (1984). Vibration frequencies of tapered bars with end mass. ASME J. Appl. Mech. 51: 179–181

    Google Scholar 

  13. Lee S.Y. and Kuo Y.H. (1992). Exact solution for the analysis of general elastically restrained non-uniform beams. ASME J. Appl. Mech. 59: 205–212

    Google Scholar 

  14. Lee S.Y. and Lin S.M. (1994). Bending vibrations of rotating non-uniform Timoshenko beams with an elastically restrained root. J. Appl. Mech. 61: 949–955

    MATH  Google Scholar 

  15. Lee S.Y., Ke H.Y. and Kuo Y.H. (1990). Analysis of non-uniform beam vibration. J. Sound Vib. 142: 15–29

    Article  Google Scholar 

  16. Naguleswaran S. (1994). Vibration in the two principal planes of a non-uniform beam of rectangular cross-section, one side of which varies as the square root of the axial co-ordinate. J. Sound Vib. 172: 305–319

    Article  MATH  Google Scholar 

  17. Ozdemir Ozgumus O. and Kaya M.O. (2006). Flexural vibration analysis of double tapered rotating Euler–Bernoulli beam by using the differential transform method. Meccanica 41(6): 661–670

    Article  MATH  Google Scholar 

  18. Özdemir Ö. and Kaya M.O. (2006). Flapwise bending vibration analysis of a rotating tapered cantilevered Bernoulli–Euler beam by differential transform method. J. Sound Vib. 289: 413–420

    Article  Google Scholar 

  19. Storti D. and Aboelnaga Y. (1987). Bending vibration of a class of rotating beams with hypergeometric solutions. ASME J. Appl. Mech. 54: 311–314

    Article  MATH  Google Scholar 

  20. Swaminathan M. and Rao J.S. (1977). Vibrations of rotating, pretwisted and tapered blades. Mech. Mach. Theory 12: 331–337

    Article  Google Scholar 

  21. To C.W.S. (1979). Higher order tapered beam finite elements for vibration analysis. J. Sound Vib. 63: 33–50

    Article  Google Scholar 

  22. Williams F.W. and Banerjee J.R. (1985). Flexural vibration of axially loaded beams with linear or parabolic taper. J. Sound Vib. 99: 121–138

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Istanbul Technical University, Faculty of Aeronautics and Astronautics, 34469, Maslak, Istanbul, Turkey

    O. Ozdemir Ozgumus & M. O. Kaya

Authors
  1. O. Ozdemir Ozgumus
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. O. Kaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. O. Kaya.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ozdemir Ozgumus, O., Kaya, M.O. Flapwise bending vibration analysis of a rotating double-tapered Timoshenko beam. Arch Appl Mech 78, 379–392 (2008). https://doi.org/10.1007/s00419-007-0158-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-007-0158-5

Keywords

Search

Navigation